Subject-Specific Estimation of Respiratory Navigator Tracking Factor for Free-Breathing Cardiovascular MR

Abstract

A mean respiratory navigator tracking factor of 0.6 is commonly used to estimate the respiratory motion of the heart from the displacement of the right hemi-diaphragm. A constant tracking factor can generate significant residual error in estimation of the respiratory motion of the heart for the cases where the actual tracking factor highly deviates from 0.6. In this study, we implemented and evaluated a robust method to calculate a subject-specific tracking factor for free-breathing high resolution cardiac MR. The subject-specific tracking factor was calculated from two consecutive navigator signals placed on the right hemi-diaphragm (RHD) and the basal left ventricle (LV) in a training phase. To verify the accuracy of the estimated subject-specific tracking factor, nineteen subjects were recruited for comparing the estimated tracking factor in real-time with an image-based tracking factor, calculated off-line. Subsequently, in seven adult subjects, whole-heart or targeted coronary artery MR images were acquired using the estimated subject-specific tracking factor and visually compared with those acquired using a constant (0.6) tracking factor. It was shown that the proposed method can accurately estimate the subject-specific tracking factor and improve the quality of coronary images when the subject-specific tracking factor differs from 0.6.

INTRODUCTION

Magnetic resonance imaging (MRI) is a noninvasive imaging modality useful for the assessment of coronary artery disease. Both targeted and whole-heart image acquisitions have been used for coronary artery MRI (1–5). In the targeted approach, each artery is imaged using either a double oblique or axial thin slab prescription (6–8). In the whole-heart coronary MRI, a large axial slab covering the entire heart is used to image all major branches of coronaries in a single acquisition (4,9,10). To reduce the cardiac motion in coronary MRI, data acquisition is usually performed during a short (70–120 ms) diastolic quiescent period. High spatial resolution and a short quiescent period necessitate a free-breathing approach with a real-time respiratory motion correction algorithm to improve the acquisition efficiency (11–13).

Respiratory navigators have been used over the past two decades as a robust technique to monitor and correct for the respiratory motion of the heart (12–15). Linear navigators, such as spin echo with orthogonal planes for excitation and refocusing and two-dimensional (2D) pencil-beam, are commonly available from different MR manufacturers. In the pencil-beam navigator implementation, a 2D spiral radio frequency (RF) excitation pulse is placed on the dome of the right hemi-diaphragm (RHD) to monitor the motion. Alternatively, respiratory self-gating navigators (16–22) have also been used to directly measure the respiratory motion of the heart from the acquired images. In this method, the k-space line passing through the center of k-space and corresponding to the zero phase and slice encoding gradients has been used to acquire the projection profile of the heart along the superior and inferior (SI) direction (19). The variations in the projection profile due to the respiration are then utilized to directly measure and correct for respiratory motion of the heart in the acquired images. This method has been shown to be affected by the thorax, chest wall, and back signals superimposed on the projection profiles of the heart; a dual projection algorithm has been proposed to average out these extra signals (16). Dual projection has been extended to retrospectively correct the respiratory motion of the heart along the anterior-posterior (AP), right-left (RL), and SI directions using three pairs of dual projection along these directions (21). Three-dimensional (3D) navigators have also been proposed for detection and correction of respiratory motion by monitoring the three orthogonal motions (23). Although improvements in some patients have been reported, this method is limited by the indirect measurement of the respiratory motion of the heart from the RHD. Affine transformation has been presented to directly model and correct the respiratory motion of the heart (24–27). This technique reduces the respiratory motion of the heart so as to delineate the arteries; but requires an additional pre-scan calibration and segmentation to define the subject-specific affine parameters.

Pencil-beam navigators remain the most robust method currently available on most clinical MR scanners. Pencil-beam navigators indirectly estimate the motion of the heart by applying a fixed tracking factor, often 0.6 (15,28), to the motion of the RHD. This navigator is based on the assumption that the respiratory motion of the heart and RHD is linearly correlated by the constant tracking factor for all subjects (28). However, the tracking factor has been shown to be subject dependent (29,30); using a fixed tracking factor can potentially degrade the coronary artery delineation by creating residual motion artifacts (31,32). Furthermore, due to the non-rigidity of the respiratory motion, the tracking factor varies for different anatomical locations. For example, a smaller tracking factor of 0.45 has been used in pulmonary vein (PV) imaging (33). Hence, methods to calculate a subject-specific tracking factor for different heart locations are appealing.

The purpose of this study is to develop and validate a robust method for calculating the subject-specific respiratory tracking factor to facilitate high resolution coronary MRI without additional scan time or off-line processing.

MATERIALS and METHODS

Two navigators, centered at the dome of the RHD and the basal left ventricle (LV) of the heart, were acquired consecutively in a training phase. The motion of the edges of the RHD and LV is monitored in a training phase, permitting estimation of the relative displacements. Because pencil-beam navigators have a small diameter of 30 mm, we also investigated a projection navigator approach with a thickness of 50 mm and 5 ms temporal resolution to cover the entire basal portion of the heart. Although the diameter of the pencil-beam navigator can be increased to match the projection navigator, it might become more sensitive to the inhomogeneity; therefore, we chose to evaluate both approaches.

In two separate acquisitions in a randomized order, we evaluated the projection and pencil-beam navigators for the estimation of the tracking factor. In each acquisition, an identical navigator method (projection or pencil-beam) was used to acquire both RHD and LV displacements. The data acquisition for the estimation of the tracking factor was integrated into the training phase of the navigator, where the center of the acceptance/rejection window (gating window) is defined.

To validate the accuracy of the estimated tracking factor using each method, a 2D single-shot steady state free precession (SSFP) sequence with electrocardiogram (ECG) triggering was modified to acquire real-time 2D images of the RHD and the LV in a coronal orientation. The real-time images were acquired immediately after the acquisition of the navigators and used for off-line calculation of an image-based tracking factor. This tracking factor was then compared to the prospectively estimated tracking factor from either the projection or pencil-beam navigator.

In the following sections, we will describe the various steps of the proposed method:

Projection Navigator

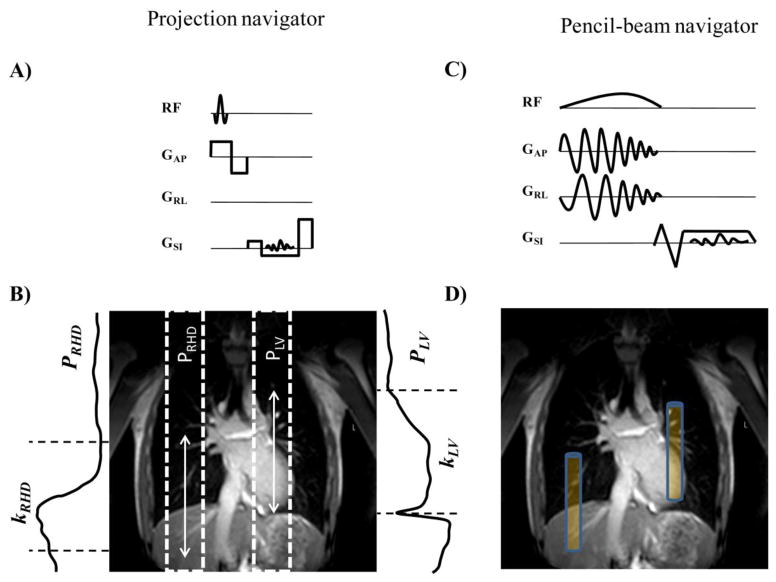
We implemented a projection navigator which directly measured the motion of targeted locations (Figure 1a). The navigator signal was acquired in a single repetition time (TR = 6 ms) and consisted of a slab selective RF followed by readout gradients. A sinc-Gaussian (RF) pulse with 20° flip angle and duration of 0.5 ms was used for excitation. The readout length, bandwidth, and field of view (FOV) were 1.56 ms, 164 kHz, and 256 mm, respectively. Two sagittal slabs were prescribed to excite the RHD and the LV (Figure 1b). The k-space line passing through the center of k-space and corresponding to the zero phase and slice encoding gradients was measured along the readout (SI) direction. The Fourier transform of the measured k-space line was calculated to obtain the projection profiles of the RHD (p_RHD) and the LV (p_LV). The acquired profiles consisted of signals originating from the liver, lungs, heart, thorax, chest wall, and back. To eliminate the superposition of the thorax, chest wall, and back signals, which could dominate the projection signals of the acquired projection profiles, two spatially-selective saturation slabs placed on the chest-wall and the back, were applied prior to the projection navigators.

Figure 1.

Schematic of the projection navigator (a) and associated profile and kernel (b) for RHD (P_RHD, k_RHD) and LV (P_LV, k_LV). Pencil-beam navigator sequence (c) and its associated prescription (d). The white arrows in (c) and blue boxes in (d) depict the size of kernel.

The acquired projection profiles vary due to the respiratory motion. The first pair of acquired projection profiles was set as the reference pair ( $p_{\mathit{RHD}}^0$ and $p_{LV}^0$). To track the respiratory-induced motion of the RHD and the LV, two regions of interest, so called kernels (k_RHD and k_LV), were manually determined on the projection profiles using a scout image (Figure 1b). The center of the kernels were placed at the edge of the RHD covering the liver and lung and the edge of the LV covering the LV and lung, respectively, to provide reliable landmarks to track the RHD and LV displacement in the succeeding projection profiles. Cross-correlation between the projection profile and each kernel of the RHD and the LV was calculated to estimate and track the new displacement of the RHD and the LV (34). The length of the kernel, w, can be adjusted but was set to a constant value of 80 mm for all navigators. Reducing the length of the kernel may lead to a weak correlation between the projection profile and the kernels of the RHD and the LV, and therefore induce failures in tracking the edges of the RHD and the LV.

During the training phase (the first 15 acquired images), the displacement of the RHD is monitored to calculate the maximum position; the kernel is updated with this position, which corresponds to the end-expiration. The center of the acceptance window was also defined and updated in the navigator training phase using the maximum position of the RHD.

After updating the kernels in the first 15 heart beats, the next N heart beats were used in the second training phase to calculate the tracking factor, α, and the intercept between the estimated displacement of the RHD and the LV using a linear regression model.

Pencil-beam Navigator

The pencil-beam navigator was acquired in approximately 20 ms with a diameter of 30 mm and consisted of a 2D pencil-beam RF excitation pulse with 25° flip angle and 16 RF cycles (Figure 1c). The readout length, bandwidth, and FOV were 2.94 ms, 54 kHz, and 256 mm, respectively. The readout gradients had flow compensations and partial echo with a factor of 0.625. Navigator positioning (Figure 1d), processing, and calculation of the subject-specific tracking factor were identical to those of the projection navigator and were calculated in real-time.

Evaluation of the Estimated Tracking Factor using Real-time Images

To validate the estimated tracking factor, a 2D single-shot ECG-triggered SSFP image was acquired after the acquisition of two navigator signals during the imaging phase. Both projection and pencil-beam navigators were used in different scans and performed randomly one after the other with the same sequence parameters. The image acquisition was repeated 50 times to cover multiple respiratory phases and the hysteresis effect.

The calculation of the image-based tracking factor was performed off-line in Matlab (V 7.9, The MathWorks, Natick, MA). Regions of interest (ROIs) of the RHD and the LV were manually defined on the first acquired real-time image. Two kernels were then generated by excluding the signal outside these regions. A 2D normalized cross-correlation algorithm was used to calculate the cross-correlations between the kernels of the RHD and the LV and the succeeding acquired real-time images along the SI direction.

Imaging Protocol

Before any image acquisition, written informed consent was obtained from all participants and all imaging protocols were approved by our Institutional Review Board (IRB).

Thirteen healthy adult subjects (4 males, 24 ± 12 years, 22.8 body mass index (BMI)) and 6 patients, referred to our center for clinical cardiac MRI (3 males, 53 ± 10 years, 27.3 BMI), were imaged supinely on a 1.5T MRI scanner (Achieva, Philips Healthcare, Best, NL) with a 5-channel phased array coil. In each scan, scout images were acquired to localize the anatomy using a SSFP sequence with 3.1 × 3.1 mm² in-plane resolution and 10 mm slice thickness. Each subject received two additional scans: one using the projection navigators and another using the pencil-beam navigators. The parameters for the real-time 2D images were as follows: TE/TR/α = 1.49/3/60°, FOV = 270×338 mm² with a spatial resolution of 1.5×2.5 mm² reconstructed to 1.0×1.0 mm², slice thickness 15 mm, accelerated imaging using SENSE (35) with an acceleration factor of 3, and a navigator acceptance window of 100 mm to accept all images in different respiratory cycles.

To demonstrate improvements that can be achieved using a more accurate tracking factor, whole-heart and targeted coronary MRI were acquired in seven healthy adult subjects (4 females, 26 ± 9 years old, 22.3 BMI) using the subject-specific and fixed (0.6) tracking factor in a subsequent pilot study. To acquire the whole-heart images, a free-breathing ECG-triggered SSFP sequence with the following parameters were used: TE/TR/α = 2.2/4.4/90°, FOV = 300×255×112 mm³ with spatial resolution of 1.3×1.3×1.5 mm³ reconstructed to 0.59×0.59×0.75 mm³. To compensate for the respiratory motion, a pencil-beam navigator was placed at the edge of the RHD to gate and track the acquired images with the acceptance window of 7 mm. The Soap-bubble post-processing tool (36) was used to generate the reformatted images. This technique is based on the assumption that the coronary anatomy fits to a fairly smooth three-dimensional (3D) curved convex-hull defined by the points of the coronary trees. The convex-hull is then projected onto a plane to generate the image displaying a planar reconstruction of the coronary branches (36).

To acquire targeted coronary MR images, a free-breathing ECG-triggered SSFP sequence with the following parameters were used: TE/TR/α = 2.8/5.7/110°, FOV = 290×290×45 mm³ with spatial resolution of 1.0×1.0×3.0 mm³ reconstructed to 0.57×0.57×1.5 mm³, and acceptance window of 7 mm. Whole-heart acquisition has higher through-plane resolution while the targeted acquisition has higher in-plane resolution.

Non-reformatted images, acquired using the subject-specific tracking factor, were visually compared with those acquired using the conventional tracking factor of 0.6.

Statistical Analysis

For each of the 19 subjects, we estimated the tracking factor between the displacement of the RHD and the LV measured by the pencil-beam and projection navigators, respectively. We used a random coefficient model (37) which incorporated the data from all 19 subjects and assumed that the intercept and tracking factor for each subject were randomly distributed around a fixed estimate of intercept and tracking factor for the population parameters. Using a restricted maximum likelihood estimation method, we obtained the best linear unbiased predictors for the intercepts and tracking factors for all of the subjects. Thus, four sets of these individual-level intercepts and tracking factors were obtained for each navigator and its corresponding real-time images. To compare the tracking factor estimates between the projection navigator and real-time images, we used the fixed effect estimate of the tracking factor (about which the random slopes average), which represents the average tracking factor of all subjects and estimated the 95% confidence interval. Likewise, the same procedure was performed to compare the tracking factor of the pencil-beam navigator and real-time images. The magnitude and range of the confidence interval were examined to compare of the estimated tracking factors. The correlation coefficient of the individual-level tracking factor between each navigator and real-time images was also measured. SAS/STAT software (V9.2, SAS Institute Inc., Cary, NC) was used to carry out all the analyses.

RESULTS

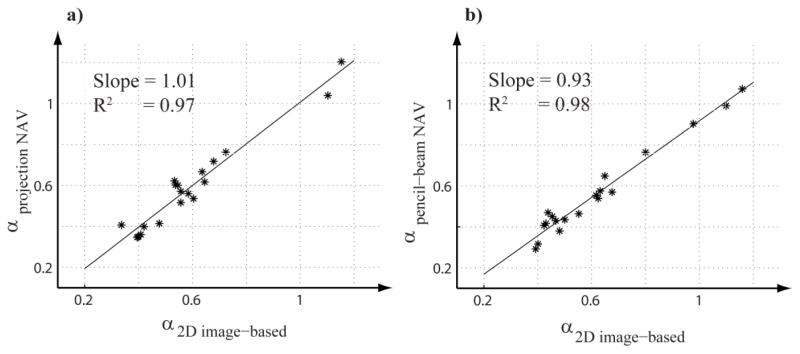
Figure 2 shows the regression lines for the estimated tracking factors using the projection navigator and its corresponding real-time 2D images (a); and the pencil-beam navigator and its corresponding real-time 2D images (b), respectively. The observed data demonstrates that there is a high degree of similarity between the tracking factors estimated from the projection navigator and the real-time 2D images. Also, strong similarity is observed between the tracking factors estimated from the pencil-beam navigator and real-time 2D images. The estimated tracking factors using the projection and pencil-beam navigators, respectively, range between 0.35 – 0.72, and 0.31 – 0.99 in healthy subjects, and 0.35 – 1.2, and 0.29–1.07 in patients.

Figure 2.

Regression lines and estimated tracking factors using the projection navigator (NAV) versus its corresponding real-time 2D images (a), and the pencil-beam NAV versus its corresponding real-time 2D images (b), respectively. Note the high correlation with the slope of near 1.0.

Table 1 displays the results from the random coefficient models in which the estimated tracking factors and standard errors represent the overall average tracking factor estimate of all subjects. It can be seen that the estimates of the overall tracking factors between the projection navigators and real-time 2D images are identical, and those for the pencil-beam navigators and real-time 2D images are strongly similar. The correlation estimates also show a high degree of similarity between the estimated tracking factor using the projection navigators and real-time 2D images, and the pencil-beam navigators and real-time 2D images.

Table 1.

Estimated adjusted mean tracking factor, from the linear mixed effects (random intercept and tracking factor) model, for the linear relationship between the RHD and LV displacements. The correlations between the estimated tracking factors using the projection navigators and associated real-time 2D images, and the pencil-beam navigators and associated real-time 2D images are also listed.

Statistical parameters	Experiment one		Experiment two
	Projection	2D images	Pencil-beam	2D images
Mean slope	0.59	0.59	0.56	0.62
Standard error	0.05	0.05	0.05	0.05
95% confidence interval	0.49–0.69	0.49–0.69	0.46–0.66	0.51–0.72
Correlation	0.96		0.98

In the coronary MR images acquired from seven healthy adult subjects, four subjects had a tracking factor close to 0.6 and therefore no difference was observed between the images acquired using the subject-specific and constant tracking factor of 0.6. The other three datasets had a tracking factor of 0.4, 0.2, and 0.35, respectively, with visual improvement in the coronary MR images acquired using the subject-specific tracking factor, as shown in Figures 3, 4, and 5.

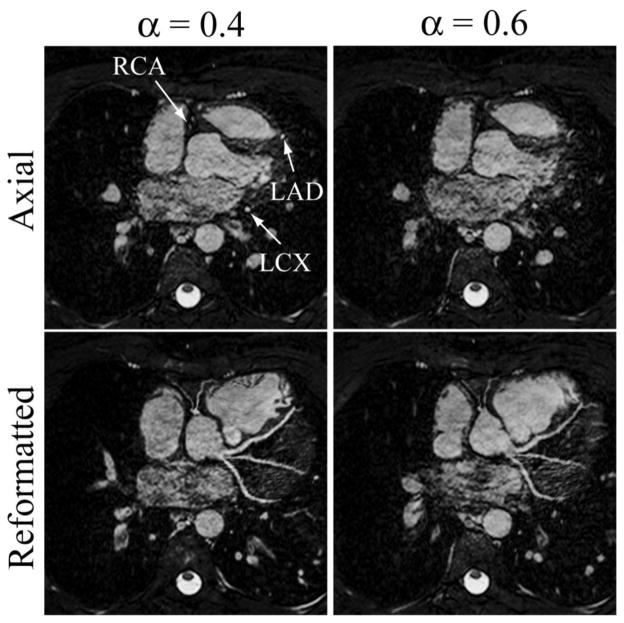
Figure 3.

Axial slice and reformatted images of the whole-heart coronary MRI from one subject showing the right coronary artery (RCA), left anterior descending (LAD), and left circumflex (LCX) using the pencil-beam navigator with the subject-specific tracking factor (0.4) and fixed tracking factor (0.6), respectively. The Soap-bubble tool (36) was used to generate the reformatted images.

Figure 4.

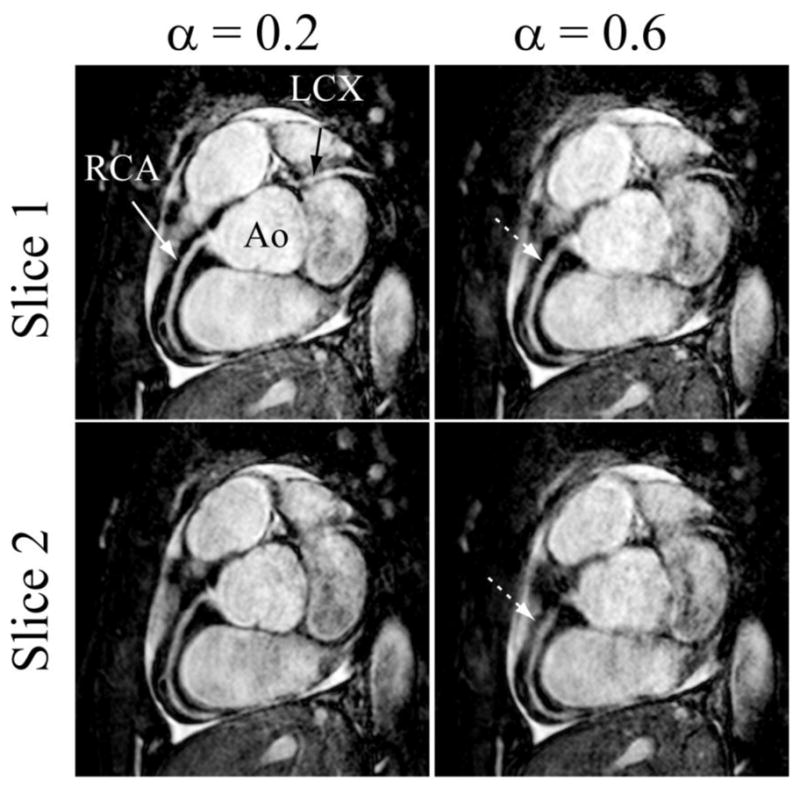
Two different slices of the targeted coronary MRI from one subject showing the right coronary (RCA) and left circumflex (LCX) acquired using the pencil-beam navigator with the subject-specific tracking factor (0.2) and fixed tracking factor (0.6), respectively.

Figure 5.

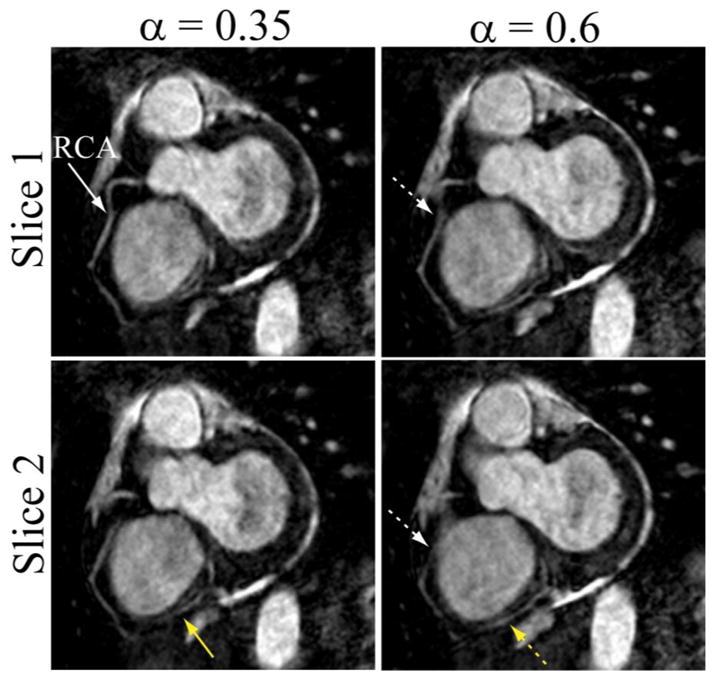
Two different slices of the targeted coronary MRI showing the middle and distal regions of RCA acquired using the pencil-beam navigator with the subject-specific tracking factor (0.35) and fixed tracking factor (0.6). White and yellow arrows indicate the mid and distal regions of RCA, respectively.

Figure 3 shows an example axial slice and reformatted images of the whole-heart acquisition from a healthy subject using the pencil-beam navigator with the subject-specific (0.4) and fixed (0.6) tracking factors. The size of gating window and gating efficiency for the two acquisitions were 7 mm and 75%, respectively. Improved delineation of the coronary arteries in images using the subject-specific tracking factor is evident.

Figure 4 shows two slices of a targeted coronary MRI acquired from a subject using the pencil-beam navigator and the subject-specific (0.2) and fixed (0.6) tracking factors. As shown, the right coronary and left circumflex arteries are sharper and have enhanced vessel definition in the images acquired with the subject-specific tracking factor.

Figure 5 shows two slices of a targeted coronary MRI acquired from another subject using the pencil-beam navigator and the subject-specific (0.35) and fixed (0.6) tracking factors. As shown, the right coronary artery images acquired using the subject-specific tracking factor is sharper.

DISCUSSIONS

We implemented and validated a method to estimate the tracking factor to accurately compute the respiratory-induced heart motion from the motion of the RHD. Both projection and pencil-beam navigators accurately estimate the tracking factor, as measured with the real-time 2D images.

The proposed method was used to measure the respiratory motion of the basal LV. However, due to the non-rigidity of the respiratory motion, different heart locations may have different motions with respect to the RHD (27). For example, it is expected that the tracking factor for the apex and pulmonary veins to be greater and less than 0.6, respectively, due to their distance from the RHD. The proposed algorithm could potentially be used to calculate the tracking factors of those regions by placing the navigator and its kernel at the designated areas. However, it should be emphasized that the proposed method can only compensate for the bulk respiratory motion of the heart at targeted regions.

The projection navigator excites a larger volume and measures a stronger signal than the pencil-beam navigator. Therefore, if the diaphragm edge is included in the kernel, which is tracking the respiratory motion of the heart, then the projection navigator tends to follow the diaphragm edge more dominantly than the heart, causing overestimation of the displacement of the heart (16). Therefore, the kernel of the projection should be carefully chosen such that the edge of the RHD is not within the region of interest.

The robustness of the proposed method in calculation of the tracking factor depends on the length of the kernels and the signal-to-noise ratio of the acquired projection profiles. If the kernel size is not large enough due to the noise the displacement of the RHD and the LV may not be accurately estimated.

With a small acceptance window (≤5mm) and moderate spatial resolution, the impact of the subject-specific tracking factor becomes negligible. However, with larger acceptance window sizes or higher spatial resolution, an accurate estimation of the tracking factor will improve the accuracy of the computed respiratory motion of the heart from the RHD. Thus, a subject-specific tracking factor will only improve image quality in patients whose tracking factor significantly deviates from 0.6. Recent studies utilize various approaches to constrain the motion, such as the use of abdominal banding (38). An accurate estimation of the relative motion of the RHD to the heart may benefit these approaches. In this study, we have chosen an acceptance window size of 7 mm, which is fairly wide compared to the SI directional displacement of 15–20 mm. This size is commonly used for whole heart coronary MRI (39), although a smaller window size is employed for targeted coronary acquisition with a higher in-plane resolution (40). A smaller acceptance window will result in a longer scan acquisition time, thereby making the scan more susceptible to the variations in the R-R intervals, quiescent period of coronaries, and respiratory drift. Furthermore, in contrast-enhanced coronary MRI (41,42), a longer scan acquisition time will impact the contrast-to-noise and signal-to-noise ratios due to variations in the optimal inversion time and changes in the T₁ of blood and myocardium. To mitigate these issues, the ideal acceptance window size for whole heart coronary MRI acquisition is considered to be higher than that of the targeted coronary MRI acquisition. Recent studies have also demonstrated increasing the size of acceptance window using a retrospective respiratory motion correction algorithm to improve scan efficiency and reduce scan time (43,44). A more accurate tracking factor will allow increasing the size of acceptance window by shortening the scan acquisition time. Further studies are required to investigate the optimal size of the acceptance window.

The proposed technique only monitors and corrects for respiratory motion of the heart along the SI direction. However, there is residual motion along the AP and RL directions that is not accounted for in the proposed approach and requires correction (45,46). The rigid-body motion may not adequately model the non-rigid respiratory motion of the heart, but is the simplest approach to compensate for the bulk respiratory-induced heart motion.

Although using a more accurate tracking factor should impact the proximal and mid regions of the coronary arteries closer to the base of the heart, which have a larger distance from the motion of the liver, we have observed slight improvements on the distal region, closer to the LV apex. This may be related to the location of the pencil-beam navigator, the larger deviation of the motion of the liver-heart or the scan variability. The proposed method can be further improved by using multiple navigators in the training phase to track the motion of the RHD, basal and apical LV, thereby enabling calculation of the tracking factor between i) the RHD-basal LV and ii) RHD-apical LV. Subsequently, a weighted combination of these two tracking factors may be used to more reliably account for the respiratory-induced heart motion. Further studies are required to investigate this approach (38).

Despite advances in coronary MRI and its promise as an alternative to invasive coronary angiography methods, its current clinical utilities are still limited to only a few clinical indications such as the assessment of anomalous coronary arteries (47–51). When compared to alternative modalities such as MDCT or x-ray angiography, coronary MRI suffers from lower spatial resolution and longer scan time. A lower spatial resolution reduces the ability to visualize smaller vessels and a long scan time makes the scan more susceptible to variations of the respiratory and cardiac motion. Therefore, further advances in the accelerated imaging and motion correction algorithms as well as increasing the signal-to-noise ratio are essential for advancing coronary MRI as a non-invasive imaging modality for routine assessment of coronary artery disease.

Our performed study has limitations; we did not present a quantitative image quality assessment of the images acquired with the fixed (0.6) and subject-specific tracking factor due to the small size of the imaging population. Furthermore, our population mainly consists of healthy subjects. Further studies in larger patient populations with irregular motion patterns are required to robustly and significantly evaluate the efficacy of the proposed method in estimating the tracking factor and improving the quality of acquired coronary artery images. The validation of the proposed method was based on the real-time 2D images, which have limited spatial and temporal resolution. The proposed algorithm does not account for hysteresis effect between the respiratory motion of the heart and the RHD, since the hysteresis cannot be well-approximated by a linear regression model (16,22). Using both leading and trailing navigators in the training phase might be helpful to approximate the hysteresis with two linear regression lines. Therefore, two tracking factors can be estimated for inspiration to end-expiration, and end-expiration to inspiration for retrospective correction of the respiratory motion of the heart. We also did not study the variation of the tracking factor over time as previously suggested in (52). However, in a long scan where the breathing pattern may vary due to the respiratory drift, the tracking factor may change.

CONCLUSION

We have presented and evaluated a technique to measure the subject-specific tracking factor between the respiratory motion of the RHD and the LV. Both projection and pencil-beam navigators can be used during the training phase of the navigators to reliably estimate the subject-specific tracking factor.