Abstract
The extracellular matrix (ECM) of the vocal fold tissue consists primarily of fibrous and interstitial proteins. The purpose of this study was to investigate the effects of selective enzymatic digestion of two ECM proteins, namely elastin and versican, on the elasticity of rabbit vocal fold tissue. Quasi-static, sinusoidal, uniaxial tensile tests were performed. The data were analyzed within the framework of a model of the ECM as a two-phase composite material consisting of collagen fibrils as the reinforcing fibers and noncollagenous ECM proteins as the matrix. To validate the two-phase model, the regression parameters for the fibers’ volume fraction and shear modulus in a different animal model were compared with corresponding published data. The proposed model was then used to analyze rabbit vocal fold tissues. The mean value and the standard deviation of the fiber volume fraction were found to be 8.49 ±3.75% for the control samples (n =4), 0.59 ±1.13 % after elastin removal (n =4), and 8.22 ±1.06% after versican removal (n =4). The results suggest that elastin removal may lead to a reduction in tissue stiffness, through counteracting the reinforcement of collagen fibrils.
Keywords: Vocal folds, Hyperelasticity, Fiber-reinforced model, Elastin, Chondroitin
1 Introduction
The human vocal folds may be idealized as multilayered structures that include the epithelium, the lamina propria, and the thyroarytenoid muscle. The lamina propria consists of various extracellular matrix (ECM) molecules, including fibrous proteins such as collagen and elastin and interstitial elements such as proteoglycan, glycoprotein, and glycosaminoglycan (GAG). The composition and the distribution of ECM proteins are known to determine the elasticity of the vocal folds. The elastic properties of the lamina propria must lie within a fairly narrow range to support and maintain proper phonatory function. It is conceivable to engineer the lamina propria with specific elasticity through selective addition or degradation of ECM components. The objective of the present study was to evaluate the role of ECM elastin and versican on vocal fold elasticity using a combined experimental and modeling approach. We hypothesized that the biochemical digestion of elastin and versican may compromise tissue elasticity (Kronick and Sacks 1994; Ventre et al. 2009).
Collagen and elastin fibers both contribute to the elasticity of vocal fold tissue. The role of collagen in the mechanical response of the tissue when it is under load has been thoroughly investigated [e.g., (Miri et al. 2013)], but the role of elastin has received comparatively less attention (Moore and Thibeault 2012). Versican, which is the largest macromolecule among the proteoglycans, was recently identified in the vocal fold lamina propria (Buhler et al. 2011). Versicans are attached to hyaluronic acid, which are believed to regulate vocal fold viscosity.
Vocal fold tissue was treated here as a homogenous material at the millimeter scale, with bulk properties governed by contributions from two distinct phases at the sub-micrometer scale. A homogenization method used for composite materials (Hashin and Rosen 1964; Hill 1972) was used to determine the bulk mechanical behavior of the vocal fold lamina propria based on the properties of each of its phases. The homogenization method includes finding the effective strain energy of the composite as a function of the average of the deformation gradient over the microstructure.
The second-order homogenization method [e.g., Avazmohammadi and Ponte Castañeda (2012)], which makes use of a linear comparison composite approach (Ponte Castañeda (1991)), yields the effective strain-energy function for soft materials with a random-particulate microstructure under general loading conditions. For the case of uniaxial tension along the direction of collagen fibers, the use of a cylinder assemblage can provide the framework for the linear comparison composite approach [see, for example, DeBotton (2005), Avazmohammadi and Naghdabadi (2009)]. The filament elements in the tissue may be modeled as long circular fibers embedded in a homogeneous soft matrix (Agoras and Lopez-Pamies 2009). Two models of fiber-reinforced composites were used to estimate the contributions of the two different phases on the mechanical response of the tissue. The role of the tissue microstructure on the observed macroscopic behavior was inferred from the two-phase model constants.
Two well-known constitutive models, the logarithmic Gent model and the exponential Fung model, describe the strain-stiffening effect of soft materials (Destrade and Ní Annaidh 2009). The Gent model features a limiting chain (i.e., fiber extension) parameter, and the Fung model exhibits an exponential increase in stress with respect to strain. The main focus of this study was the strain-stiffening effect imposed by noncollagenous ECM molecules such as elastin fibers; hence, a composite hyperelastic model based on both the Gent and Fung models for the matrix phase was developed here. Rabbit vocal folds were subjected to uniaxial tensile testing following submersion in protease and control solutions.
2 Materials and methods
2.1 Sample preparation
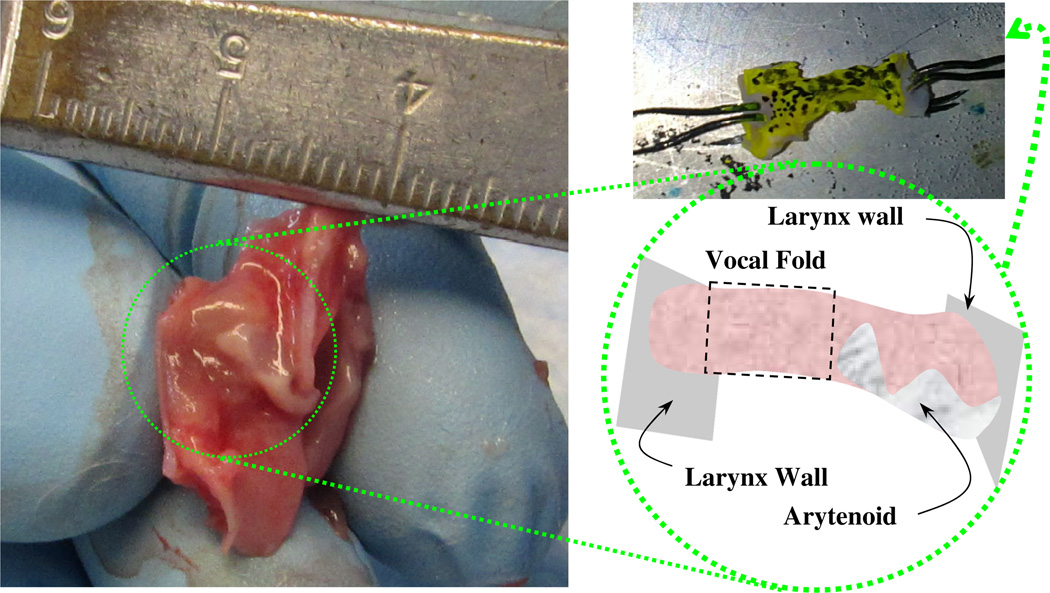
Twelve New-Zealand rabbits (6 number of males, 6 number of females; with an age of 5 months and a weight of 2.9–3.4 kg) were donated from commercial vendors. Upon euthanization, larynges were harvested en bloc and quickly frozen in liquid nitrogen. Each larynx was thawed at room temperature, then bisected into two hemi-larynges, and soaked in one of three enzymatic solutions for 24 hours at 4°C with gentle agitation. Pilot tests showed that this digestion time allowed maximum elastin and versican digestions, while maintaining the integrity of tissue structure for the subsequent tensile testing. One enzymatic solution was included for elastin removal, one was for versican removal, and one was a control buffer, respectively. For elastin removal, the enzymatic solution was 1 mg elastase (Sigma-Aldrich E7885) in 5ml of Tris (pH 8.0) buffer. The amount of protease was optimized based on the sample size (< 2 mm in thickness and 20mm2 area), the saturation time (~ 24 hours), and incubation time (~ 2.5 hours) (Ventre et al. 2009). For versican removal, the enzymatic solution was prepared using the same Tris buffer solution with 60 mM Sodium Acetate and 2-UN Chondroitinase ABC (Sigma-Aldrich, C2905). Kronick and Sacks (1994) showed that this treatment on calfskin reduces the uronic acid content, which is related to the GAG content, by 70%. chondroitinase solution also degrades the versican molecules of the vocal fold tissue into disaccharidic soluble units, as observed by Buhler et al. (2011). Lastly, the Tris buffer solution without any enzyme served as the control medium. After saturation in the enzymatic solution, the vocal folds were dissected from their hemilarynges using small scissors. Additional tissue from the larynx wall and portions of the arytenoid cartilage were kept to help gripping the sample for mechanical testing, as depicted in Fig. 1. Each dissected vocal fold was subjected to uniaxial tensile tests before and after enzymatic digestion. Following the second tensile tests, each sample was fixed in 4% formaldehyde overnight at 4°C for histological analysis.
Fig. 1.
A rabbit hemilarynx and the orientation of the vocal fold sample used for mechanical tensile tests
Histology was used to confirm the effectiveness of the digestion protocols. A commercial elastic van Gieson kit (EVG; Newcomer Supply Inc., Middleton, WI) was used to stain elastin fibers black and collagen fibrils brown. Sulfated GAGs that are cross-linked to versicans were stained using the cationic dye 1,9-dimethylmethylene blue (DMMB; Sigma-Aldrich # 341088-1G) in 0.1 N HCl, containing 0.04 M NaCl and 0.04 M glycine (Sigma-Aldrich # 50046-50G) (Buhler et al. 2011). Positive reactions revealed sulfated GAGs in purple when viewed using bright-field light microscopy. Elastin and versicans were not completely removed to retain the tissue integrity necessary for mechanical testings. In addition, EVG and DMMB staining provided information on the presence or absence of elastin and versican is present or absent in the section, respectively. The interpretation of mechanical and modeling results, however, do not require the data about the absolute concentrations of elastin or versican.
2.2 Mechanical testing protocols
Tensile tests were performed using an EnduraTEC tester (ElectroForce (ELF) 3200, Bose Inc., Eden Prairie, MN). A digital camera (Flea2, Point Grey Research Inc., Richmond, BC) captured the surface deformation of the sample under mechanical traction (Miri et al. 2012a). The apparatus was operated in a displacement-control mode. The thickness of the sample was measured using a caliper (Mitutoyo, Tokyo, Japan) with a 1 µm precision. A speckle pattern was applied onto the surface, as shown in Fig. 1. The sample was then installed between two grips via two black silk (5.0 metric) sutures on each end. The sample was submerged in Tris buffer solution (pH 8.0) 37°C±0.5°C, such that a thin layer of fluid covered the upper surface (i.e., the epithelium). A fiber-optic light source (Cole-Parmer Instrument Co, Montreal, QC) was used to illuminate the sample. A cyclic sinusoidal loading unloading was imposed with a 4.5 mm displacement amplitude at a frequency of 0.1 Hz, following five cycles of preconditioning. This constitutes the first round of tensile tests (i.e., R1). The tissue was then submerged in one of the two digestion solutions, using a small aluminum pan, or kept in the same buffer solution while gently stirring. The temperature was held constant at 37°C for the control buffer and for the versican removal, but at 25°C in the case of elastin removal for enzymatic activation of the elastase. After 2.5 hour of incubation, the pan was removed and the second round of tensile tests was performed (i.e., R2). The duration of each test was around 10 minutes.
2.3 Mechanical modeling
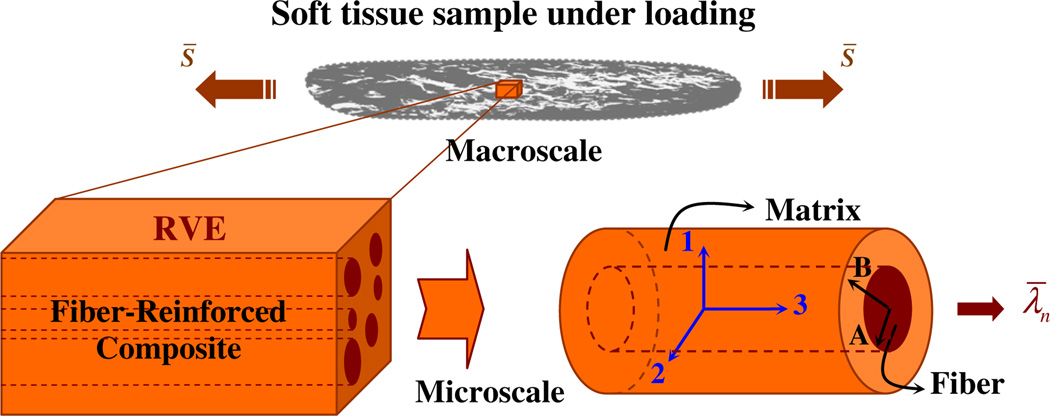
The characteristic size of tissue structural inhomogeneities was assumed to be much smaller than the size of the tissue sample and the scale of spatial variations of the applied loads. As a two-phase composite material, we assumed that the tissue consists of an elastomeric matrix surrounding a random distribution of aligned, circular, cylindrical fibers, as illustrated in Fig. 2. The undeformed composite material occupies a volume, Ωo, with a defined boundary, ∂Ωo. The undeformed cylindrical fibers are oriented along the longitudinal direction,e3 (Fig. 2), where the basis vectors [ei], i =1,2,3 define the fixed Cartesian coordinates. The deformation gradient tensor, F, has Cartesian components Fij = ∂xi /∂Xj where j =1,2,3 and the vectors X and x represent the position vectors of a material point, respectively, in the undeformed and deformed configuration. The polar decomposition of F is written as F=RU, where U and R denote the stretch and rotation tensors, respectively. The tensor C=FT F=U2 is the right Cauchy–Green deformation tensor (Humphrey 2002).
Fig. 2.
Schematic of the tissue sample under uniaxial loading, and one representative volume element (RVE) for unidirectional composite materials, and the equivalent cylindrical assemblage
The matrix (phase 1) and the fibers (phase 2) are assumed to be incompressible, isotropic, hyperelastic materials. Their constitutive behaviors are defined by strain-energy functions W(1)(F) and W(2)(F), respectively. The strain-energy function has the general form, for both phases,
| (1) |
where I1 = tr(C) and I2 = [(I1)2 − tr (C2)]/2 are the first and second invariants of the right Cauchy–Green deformation tensor. The third invariant is J = det (F) =1 because of the incompressibility assumption. The twice- differentiable functions g(i)(I1, I2) must satisfy g(i)(3, 3) =0 and dg(i)(3, 3)/dI1 + dg(i)(3, 3)/dI2 = µ(i)/2, with µ(i) as the linear shear modulus in phase i.
We assume that the composite material undergoes a macroscopic deformation gradient, F̄, which is consistent with an affine displacement boundary condition along ∂Ωo. Following the homogenization framework presented by Hill (1972), an effective constitutive relation for the sample can be defined as
| (2) |
where Ŵ (F̄), denoting the effective strain-energy function, is obtained using the principle of minimum potential energy, i.e.,
| (3) |
In the potential energy expression, K (F̄) denotes the set of kinematically admissible deformation gradients (Hill 1972),
| (4) |
The macroscopic deformation gradient associated with uniaxial tension is written as
| (5) |
where λ̄n denotes the stretch along the fibers’ direction, and is obtained from the macroscopic incompressibility constraint, J̄ = det(F̄) = 1.
A RVE of the composite material was selected to study the macroscopic behavior of the tissue sample. Assuming that the size of the RVE is much larger than the size of the fibers, and much smaller than the size of the sample, the macroscopic quantities such as the effective energy and the stress tensor can be obtained from the RVE. Given the simple macroscopic deformation gradient in Eq. (5), the composite cylinder assemblage model introduced by Hashin and Rosen (1964) was used to represent the random microstructure of the composite material. The study of one composite cylinder element is sufficient to determine the macroscopic behavior of the composite material (Hill 1972). This type of element has been frequently used to represent a fiber-reinforced solid under axisymmetric loadings (DeBotton et al. 2006; Hashin and Rosen 1964). The element consists of a cylindrical fiber of radius A surrounded by a concentric cylindrical matrix with a different material and outer radius B (Fig. 2). The initial fiber volume fraction, c0, is defined by c0 = A2/B2.
For the sake of convenience, a cylindrical coordinate system (R,Θ, Z) is used. The boundary conditions on the outer surface of the composite element are , θ = Θ, and z = λ̄n Z, where (r, θ, z) denotes the cylindrical coordinate of material points in the deformed configuration. Making use of the local incompressibility constraint, an exact and uniform local deformation field is obtained as (Humphrey 2002)
| (6a) |
| (6b) |
| (6c) |
Correspondingly, tensors F̄(1) and F̄(2), denoting the deformation gradient tensors of phase 1 and phase 2, are given by
| (7) |
Because the deformation gradient within the cylinder is constant for each phase, the effective strain-energy function of the composite material, defined in Eq. (3), is
| (8) |
where and . The axial component of the macroscopic first Piola-Kirchhoff stress tensor, S̄, is obtained from Eq. (2),
| (9) |
Specific forms of the material functions, g(i)(I1, I2), were used for the tissues under study. Strain stiffening is most commonly observed during the extension of biological soft tissues (Fung 1990). Among many constitutive models developed to capture this effect, two strain-energy function models, namely the Gent (Gent 1996) and Fung (Fung 1990) models, were shown to provide simple and efficient simulations of the strain-stiffening effect. The incompressible form of the Gent strain-energy function is written as
| (10) |
where λj (j = 1, 2, 3) is the stretch along the direction ej, and (> 0; i = 1, 2) denotes a nondimensional stiffening parameter whose value identifies the extensibility limit. For the case of the Fung model, the strain- energy function is formulated as
| (11) |
where (> 0; i = 1, 2) is the associated nondimensional stiffening parameter. Finally, from Eq. (9), the effective stress measure, S̄n, in the composite materials with the strain-energy functions (10) and (11] for both the matrix and fiber phases, is, respectively, given by [see also (deBotton and Shmuel 2010) to find a more general formulation)
| (12a) |
| (12b) |
where c0 denotes the initial fiber volume fraction. The Gent and Fung models converge to the simple neo-Hookean model as Jm → ∞ and Fm → 0. Because noncollagenous ECM components, including elastin and versican, are the main subject of the present study, the incompressible neo-Hookean model was used to represent the constitutive behavior of the fiber phase. The associated strain-energy function reads
| (13) |
and the associated term inside the bracket in Eq. (12a) is reduced to c0µ(2).
3 Results and discussion
3.1 Morphological changes after protein removal
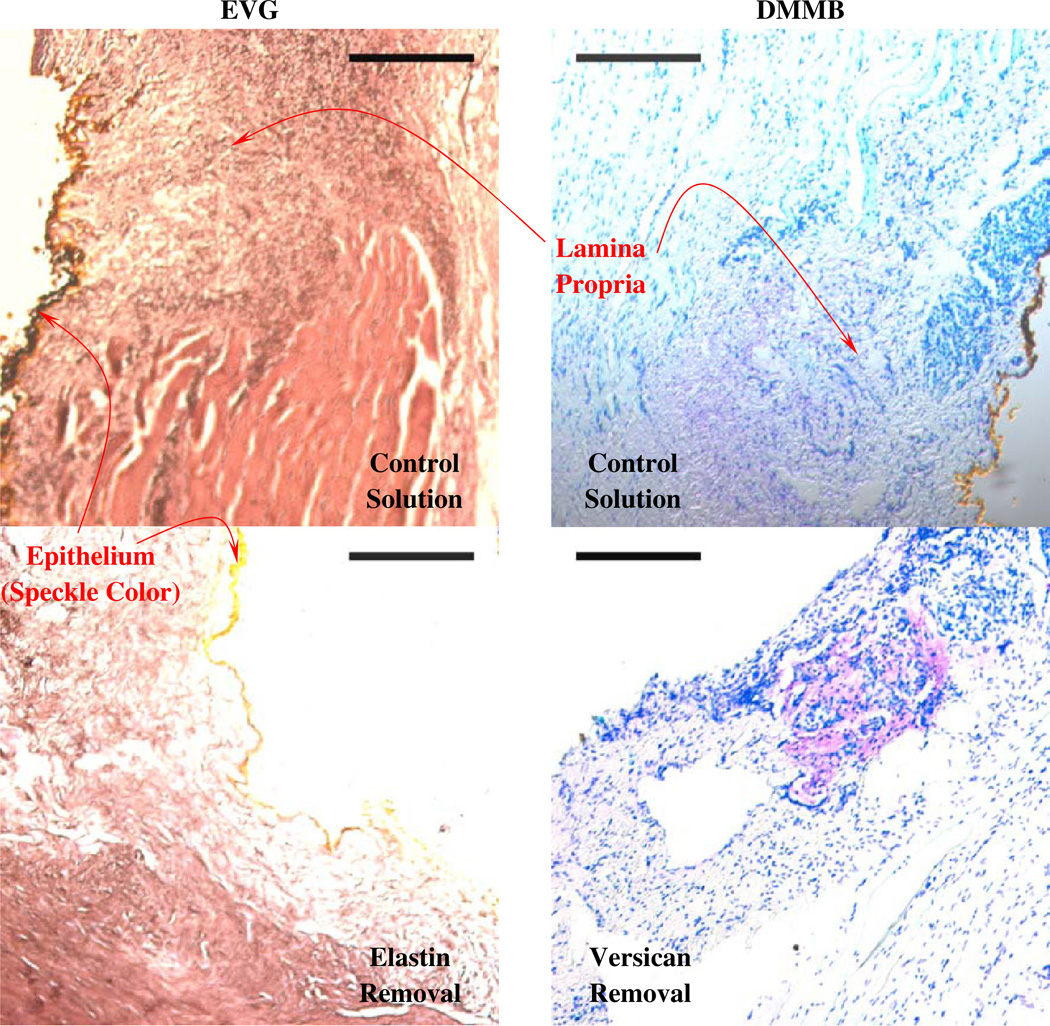
The effectiveness of the enzymatic digestion protocols was evaluated subjectively using EVG and DMMB staining, as shown in Fig. 3. For elastin digestion, EVGstaining shows collagen fibrils in red-brown and elastin fibers in black. The large red bundles indicate the vocalis muscle, which is free of elastin fibers (Fig. 3). The histology results indicate that the rabbit tissue samples included both the lamina propria and the muscle. The distribution of the elastin and collagen fibers was significantly altered following elastin removal. Sulfated GAGs, in purple (Fig. 3), were found throughout the lamina propria in the control samples. The results show that the removal of sulfated GAGs, which are attached to Versican, did not lead to a complete reduction in DMMB stain.
Fig. 3.
Representative elastic van Gieson (EVG) and 1,9-dimethylmethylene blue (DMMB) staining of rabbit vocal folds in coronal sections. The scale bar is 200µm
The digestion protocols used in this study may not provide a complete removal of both molecules. This fact may prevent quantifying the correlation between the protein removal and the mechanical properties of the tissue, although the model parameters are used to investigate and understand the behavior of the ECM under those circumstances. This work provides a preliminary study for the quantification of correlations between the ECM content and the mechanical properties of the vocal fold tissue.
3.2 Model validation
The composite material model developed herein was validated by a comparison of the regression parameters for the uniaxial tensile testing data (Miri et al. 2012a) with published mechanical and structural data for porcine vocal fold lamina propria (Miri et al. 2013; Miri et al. 2012b). The model parameters were obtained from a least-square minimization of the differences (R2 > 0.90) between experimental data and predictions from Eq. (12a), as summarized in Table 1. The secant slope of the stress–stretch curves, between λ1 =1 and λ1 =1.15, was used as the bulk modulus (i.e., (1- c0)µ(1) + c0µ(2)) to determine the matrix modulus, µ(2). The two strain-stiffening parameters (Table 1) fall within the range of values obtained for arteries (Destrade and Ní Annaidh 2009). The fiber volume fraction was found to be 18.4 ± 7.7 % from the Gent model and 20.7 ± 8.2 % from the Fung model. Previous nonlinear laser microscopy imaging study yielded an area fraction of 14.6 ± 3.7 % for collagen fibrils in the porcine vocal fold lamina propria (Miri et al. 2013). Quantitative histological results (Hahn et al. 2006) showed that collagen made up 52.6 % ± 1.9 % of total protein in porcine vocal fold lamina propria, which considering the fluid mass fraction of porcine vocal folds (~ 80 %) and the effective specific volume of collagen (~ 1.8 ml/g) yield a fiber volume fraction of 18.9 % ± 2.7 %. The fiber elastic modulus predicted by the present models, however, is one order of magnitude lower than that from nanoindentation tests, ~ 1 MPa (Miri et al. 2013). This could be because of loose connections between collagen fibrils and other ECM components, while the proposed formulation assumes an affine deformation of the two phases.
Table 1.
Averaged model parameters and their standard deviations for porcine vocal folds (m = 10): Fung and Gent models (R2 > 0.90)
| Model | Fm/Jm | c0 (%) | 3×µ(1) (kPa) |
| Fung | 3.79 ± 1.67 | 20.69 ± 8.24 | 80.92 ± 26.08 |
| Gent | 1.01 ± 0.58 | 18.36 ± 7.65 | 78.63 ± 32.78 |
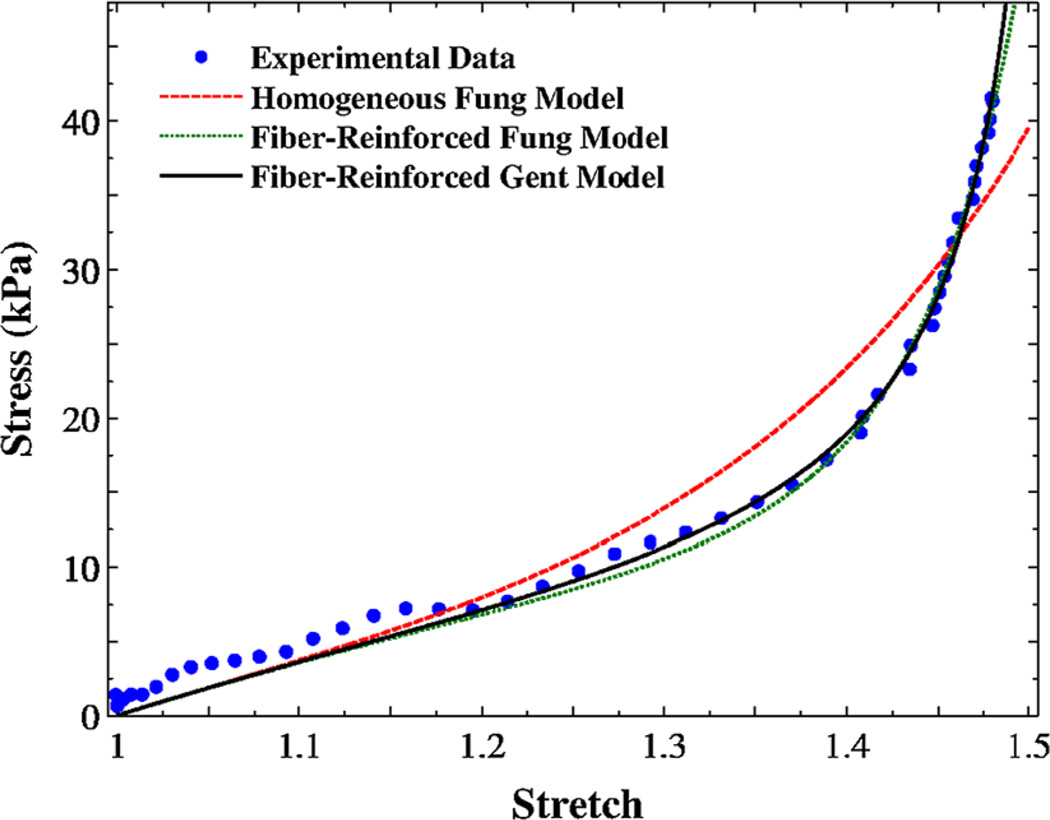
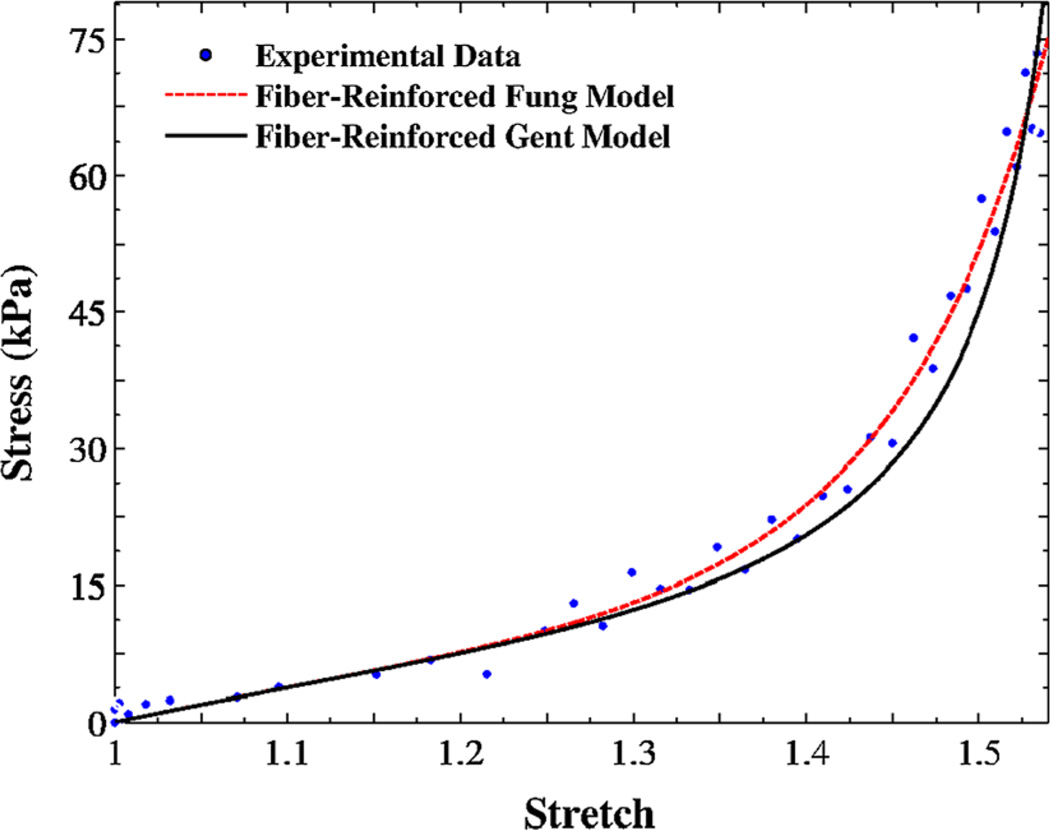
A regression of the fiber-reinforced composite models [Eq. 12a)] is shown, along with the single-phase Fung model, in Fig. 4. The composite Fung model provided a better fit than the homogenous model, particularly at large stretches. The experimental data for one rabbit vocal fold sample along with its regressions using the present models are shown in Fig. 5. There is only a slight difference between the two models outputs. A comparison of experimental data in Figs. 4 and 5 may yield higher signal variations (i.e., higher uncertainties) in rabbit vocal fold samples than porcine samples. Larger experimental noise was expected for rabbit tissue because of a lower range of force values in the data.
Fig. 4.
The variation of Cauchy stress versus stretch for one porcine vocal fold sample under uniaxial traction testing for verification; Regression curves from three models: single-phase solid Fung model, fiber-reinforced Fung model, and fiber-reinforced Gent model
Fig. 5.
The variation of Cauchy stress versus stretch for one rabbit vocal fold sample under uniaxial traction testing in the control solution; Regression curves from fiber-reinforced Fung and Gent models
The two models are in good agreements with experimental data (Figs. 4, 5), but the Fung model is generally recommended for large-deformation problems as it involves no locking stretches, at which the stress would rise significantly (compare the curves at high stretches in Fig. 5). The present composite models allow predictions of the mechanical behavior of the vocal folds along with physical interpretations of the constituents. They can model pathological conditions in which the collagen fibrils have distinctive physical properties. For example, vocal fold scarring is a common complication of phonosurgery that can induce excessive collagen deposition and remodeling, i.e., higher fiber volume fractions (e.g., in acute injuries). The proposed model may help predict the uniaxial tensile response of scarred vocal folds from microstructural data alone without the need for independent tensile testing (see also Supplementary Materials).
3.3 Effects of elastin removal on mechanical properties
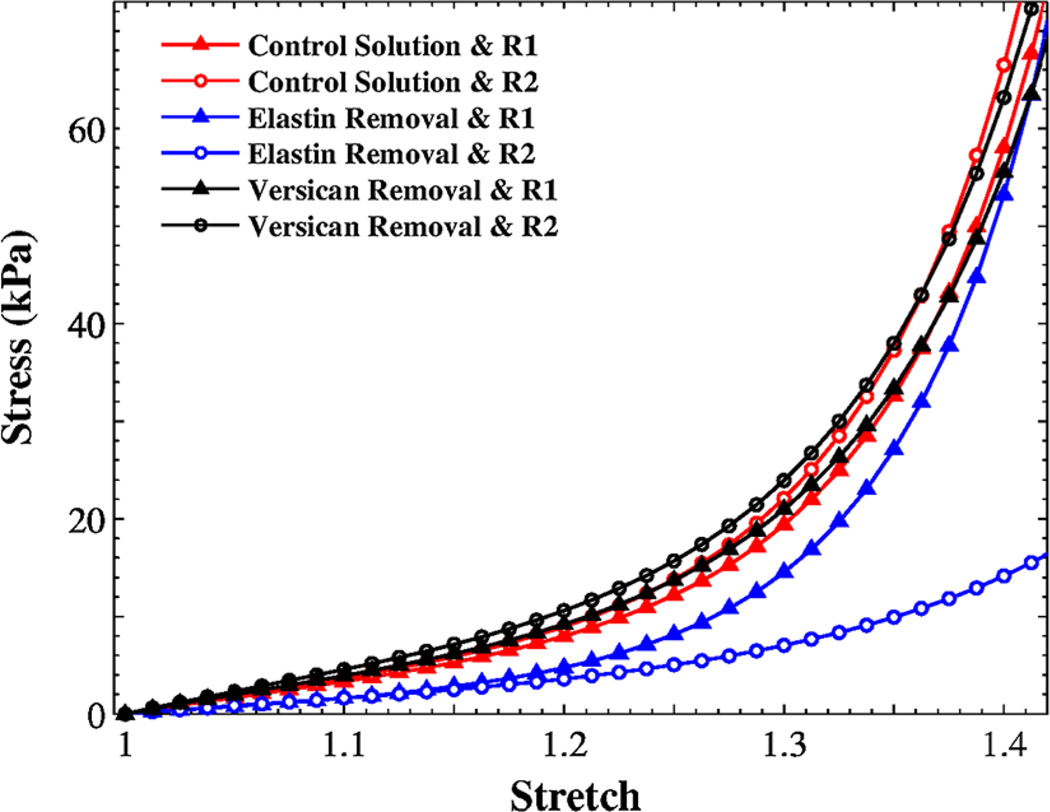
Owing to the large deformations involved in the tensile tests, it is unlikely that collagen is the sole constituent responsible for the observed mechanical behavior. For instance, the elastin network is believed to have chemical bonds with many other ECM proteins (Moore and Thibeault 2012). Interfibrillar ECM components appear to play a significant role in the mechanical response of collagen-rich vocal folds. The Fung model was used to simulate the tissue behavior for both rounds of uniaxial tensile tests, as shown in Fig. 6, using the regression constants in Table 2 that were calculated as described in Sect. 3.2.
Fig. 6.
The variation of Cauchy stress versus stretch for rabbit vocal fold samples (m = 4) using the average values reported in Table 2, for three different protocols (R1 & R2 denote first and second rounds, respectively)
Table 2.
Averaged Fung parameters and their standard deviations for rabbit vocal folds (m = 4) subjected to the three protocols; R denotes the round tensile tests (R=1, 2)
| Protocol | R | Fm | c0 (%) | 3×µ(1) (kPa) |
| Control | 1 | 6.48 ± 1.54 | 7.29 ± 4.13 | 69.34 ± 4.94 |
| Solution | 2 | 6.45 ± 1.21 | 8.49 ± 3.75 | 59.32 ± 18.09 |
| Elastin | 1 | 7.19 ± 1.86 | 1.04 ± 2.07 | 29.92 ± 53.85 |
| Removal | 2 | 3.43 ± 1.42 | 0.59 ± 1.13 | 16.81 ± 33.62 |
| Versican | 1 | 5.59 ± 0.22 | 6.94 ± 0.53 | 69.11 ± 5.19 |
| Removal | 2 | 5.64 ± 0.69 | 8.22 ± 1.06 | 73.75 ± 9.43 |
The elastase treatment caused a significant reduction in the tangent bulk modulus of the tissue, particularly for large stretches (see Fig. 6). The small-deformation tangent modulus undergoes a similar, but more-subtle reduction after the enzymatic treatment. The model predicted a negligible value for the fiber volume fraction (i.e., c0= 0.59–1.04%). The fibrous network interruption resulted in much lower strainstiffening effects of the matrix phase, as the mean Fm was reduced from 7.19 ± 1.86 to 3.43 ± 1.42 (Table 2). In the vocal fold lamina propria, the elastin three-dimensional network is interconnected with thin collagen fibrils (Miri et al. 2013). Thus, elastin removal may affects the distribution of collagen fibrils (Fig. 3), which in turn affect the overall tissuemechanical response. As shown in the histological results (Fig. 3), the elastase treatment resulted in a change in cross-linking between the collagen fibrils and the elastin fibers separating the two networks, rather than systematic dissolution of the elastin fibers. Because of the enzymatic activation of elastase at room temperature, the tissue was weaker than the control samples during the first round of tensile tests.
3.4 Effects of versican removal on mechanical properties
Chondroitinase was expected to digest chondroitin sulfate and hyaluronic acid of the ECM (Yamagata et al. 1968). This treatment did not have significant effects on the uniaxial tensile testing data despite the fact that chondroitinase did appear to digest the polysaccharidic components of the ECM based on theDMMBstaining in Fig. 3. Thismay be due to the cleaving mechanism of the chondroitinase (Yamagata et al. 1968). This mechanism releases the GAG sidechains while preserving the core protein, which constitutes a considerable fraction of the total mass of the glycoprotein (Fig. 3). This enzyme does not digest other interfibrillar proteins, thus keeping the collagen network unaffected. In fact, a partial glycosaminoglycan removal could allow collagen fibrils to undergo increased slippage and reconfiguration.
Under quasi-static tensile loading, proteoglycans that control the fluid content might migrate throughout the interstitial space between ECM structural proteins; thus, the collagen fibrils would untwist and remodel to provide the resistance forces. In other words, collagen fibril motion is modified by the change of ECM composition. For instance, the removal of a specific ECM component creates additional volume for the collagen fibrils to deform, leading to a slight increase in the fiber volume fraction from 6.94 ± 0.53 % to 8.22 ± 1.06 % (Table 2). The fiber shear modulus accordingly increased from 69.11 ± 5.19 kPa to 73.75 ± 9.43 kPa, but the change was not statistically significant. The effects of versican treatment are more prominent at larger stretches as the collagen fibrils had a greater contribution to the tissue response, shown by a comparison between R1 and R2 in Fig. 6.
4 Concluding remarks
The rabbit laryngeal model has a structure and size that is appropriate to study vocal fold pathologies. However, their size is too small to prepare standard dog-bone traction test specimens with rabbit vocal fold tissues (see Fig. 1). The measurement uncertainties are significant when considering the principal assumptions of uniaxial tension. Stress was defined here as the ratio of the measured force to an average specimen cross-sectional area, assuming a rectangular cubic shape with uniform cross-sectional area. The axial strain was also extracted by digital image correlation, assuming planar deformation. Therefore, the main experimental uncertainties consist of errors in the cross-sectional area, the uniformity of loading, and the strain measurement.
An error analysis reveals the accuracy of the measurements. Because the resolution of the optical images is much greater than that required for the calculation of strain components, the errors or uncertainties are dominated by the strain numerical analysis. The associated uncertainty selected in the image correlation analysis was less than 0.01. The rabbit vocal fold samples had a resistive force around 0.02 N, a thickness less than 1mm, and a width around 2 mm. The uncertainty in stress measurements was in a range of 0.5– 1.0 kPa for 1.15–1.20 stretch, while the absolute stress values were within 2–5kPa. The overall uncertainty was not greater than the variability of the model parameters.
The rabbit samples used in this study included lamina propria (~ 0.2–0.3mm thickness) and the muscle (~ 0.5– 1mm thickness). The rabbit vocal fold microstructure is different than that of the porcine tissue. These facts, along with the degree of experimental uncertainties here, explain the difference between the model predictions of rabbit vocal fold (Table 2; control samples) and those of porcine vocal fold (Table 1). Unpublished data on nonlinear laser scanning microscopy of rabbit vocal fold showed a higher (and lower) dispersion (density) of collagen fibrils, compared with those in porcine vocal folds.
The objective of the present work was to understand the role of elastin and versican on the elasticity of vocal fold tissue. Elastase and chondroitinase enzymes, following two commercially available protocols (see Ventre et al. (2009)), were used to digest the elastin and sulfated GAGs in rabbit vocal folds, respectively. The lamina propria was found to be more sensitive to elastase digestion than to chondroitinase digestion, as microscopy observations showed a higher tissue damage when digested in the elastase solution. The disruption of the elastin network yielded a significant decrease in both the linear and nonlinear tangent moduli, suggesting that the relative spatial assembly of elastin and collagen dominates the tensile behavior of the tissue.
An analytical fiber-reinforced composite model was developed to simulate the uniaxial tensile testing response of the vocal fold tissue in terms of the volume fraction and elastic modulus of collagen fibrils. The strain-stiffening effect was included in the matrix phase. The model parameters were identified using data regressions. A more specific digestion of ECM components is required to obtain conclusive results. These results can be useful as benchmarks for tissue engineering of the vocal folds and to develop strategies to design novel scaffolds that promote functionally graded ECM assembly.
Supplementary Material
Acknowledgments
This work was supported by National Institute of Health Grant Nos. R01-DC005788 (Luc Mongeau, principal investigator) and R01-DC004336 (Susan Thibeault, principal investigator).
Footnotes
Electronic supplementary material The online version of this article (doi:10.1007/s10237-014-0585-5) contains supplementary material, which is available to authorized users.
Contributor Information
Amir K. Miri, Email: amir.miriramsheh@mail.mcgill.ca, Department of Mechanical Engineering, McGill University, 817 Sherbrooke Street West, Montreal, Quebec H3A 0C3, Canada.
Nicole Y. K. Li, Department of Hearing and Speech Sciences, University of Maryland-College Park, College Park, MD, USA
Reza Avazmohammadi, Department of Mechanical Engineering and Applied Mechanics, University of Pennsylvania, Philadelphia, PA, USA.
Susan L. Thibeault, Division of Otolaryngology-Head and Neck Surgery, Department of Surgery, University of Wisconsin-Madison, Madison, WI, USA
Rosaire Mongrain, Department of Mechanical Engineering, McGill University, 817 Sherbrooke Street West, Montreal, Quebec H3A 0C3, Canada.
Luc Mongeau, Department of Mechanical Engineering, McGill University, 817 Sherbrooke Street West, Montreal, Quebec H3A 0C3, Canada.
References
- Agoras M, Lopez-Pamies O. A general hyperelastic model for incompressible fiber-reinforced elastomers. J Mech Phys Solids. 2009;57(2):268–286. [Google Scholar]
- Avazmohammadi R, Ponte Castañeda P. Tangent secondorder estimates for the large-strain, macroscopic response of particle-reinforced elastomers. J Elast. 2013;112(2):139–183. [Google Scholar]
- Avazmohammadi R, Naghdabadi R. Strain energy-based homogenization of nonlinear elastic particulate composites. Int J Eng Sci. 2009;47(10):1038–1048. [Google Scholar]
- Buhler RB, Sennes LU, Tsuji DH, Mauad T, Saldiva PN. Collagen type I, collagen type III, versican in vocal fold lamina propria. Arch Otolaryngol-Head Neck Surg. 2011;137(6):604–608. doi: 10.1001/archoto.2011.88. [DOI] [PubMed] [Google Scholar]
- DeBotton G. Transversely isotropic sequentially laminated composites in finite elasticity. J Mech Phys Solids. 2005;53(6):1334–1361. [Google Scholar]
- DeBotton G, Hariton I, Socolsky E. Neo-Hookean fiber-reinforced composites in finite elasticity. J Mech Phys Solids. 2006;54(3):533–559. [Google Scholar]
- deBotton G, Shmuel G. A new variational estimate for the effective response of hyperelastic composites. J Mech Phys Solids. 2010;58(4):466–483. [Google Scholar]
- Destrade M, Ní Annaidh A. Bending instabilities of soft biological tissues. Int J Solids Struct. 2009;46(25):4322–4330. [Google Scholar]
- Fung Y. Biomechanics: motion, flow, stress, and growth. New York: Springer; 1990. [Google Scholar]
- Gent A. A new constitutive relation for rubber. Rubber Chem Technol. 1996;69(1):59–61. [Google Scholar]
- Hahn MS, Kobler JB, Zeitels SM, Langer R. Quantitative and comparative studies of the vocal fold extracellularmatrix II: collagen. Ann Otol Rhinol Laryngol. 2006;115(3):225–232. doi: 10.1177/000348940611500311. [DOI] [PubMed] [Google Scholar]
- Hashin Z, Rosen BW. The elastic moduli of fiber-reinforced materials. J Appl Mech. 1964;31(2):223–232. [Google Scholar]
- Hill R. On constitutive macro-variables for heterogeneous solids at finite strain. Proc R Soc Lond Math Phys Sci. 1972;326(1565):131–147. [Google Scholar]
- Humphrey JD. Cardiovascular solid mechanics. 2nd edn. New York: Springer; 2002. [Google Scholar]
- Kronick P, Sacks M. Matrix macromolecules that affect the viscoelasticity of calfskin. J Biomech Eng. 1994;116(2):140–145. doi: 10.1115/1.2895712. [DOI] [PubMed] [Google Scholar]
- Miri AK, Barthelat F, Mongeau L. Effects of dehydration on the viscoelastic properties of vocal folds in large deformations. J Voice. 2012a;26(6):688–697. doi: 10.1016/j.jvoice.2011.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miri AK, Mongrain R, Chen LX, Mongeau L. Quantitative assessment of the anisotropy of vocal fold tissue using shear rheometry and traction testing. J Biomech. 2012b;45:2943–2946. doi: 10.1016/j.jbiomech.2012.08.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miri AK, Heris HK, Tripathy U, Wiseman PW, Mongeau L. Microstructural characterization of vocal folds toward a strainenergy model of collagen remodeling. Acta Biomater. 2013;9(8):7957–7967. doi: 10.1016/j.actbio.2013.04.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moore J, Thibeault S. Insights into the role of elastin in vocal fold health and disease. J Voice. 2012;26(3):269–275. doi: 10.1016/j.jvoice.2011.05.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ponte Castañeda P. The effective mechanical properties of nonlinear isotropic composites. J Mech Phys Solids. 1991;39:45–71. [Google Scholar]
- Ventre M, Mollica F, Netti PA. The effect of composition and microstructure on the viscoelastic properties of dermis. J Biomech. 2009;42(4):430–435. doi: 10.1016/j.jbiomech.2008.12.004. [DOI] [PubMed] [Google Scholar]
- Yamagata T, Saito H, Habuchi O, Suzuki S. Purification and properties of bacterial chondroitinases and chondrosulfatases. J Biol Chem. 1968;243(7):1523–1535. [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.