What affects detectability of lesion–deficit relationships in lesion studies?

Abstract

Elucidating the brain basis for psychological processes and behavior is a fundamental aim of cognitive neuroscience. The lesion method, using voxel-based statistical analysis, is an important approach to this goal, identifying neural structures that are necessary for the support of specific mental operations, and complementing the strengths of functional imaging techniques.

Lesion coverage in a population is by nature spatially heterogeneous and biased, systematically affecting the ability of lesion–deficit correlation methods to detect and localize functional associations. We have developed a simulator that allows investigators to model parameters in a lesion–deficit study and characterize the statistical bias in lesion deficit detection coverage that will result from specific assumptions. We used the simulator to assess the signal detection properties and localization accuracy of standard lesion–deficit correlation methods, under a simple truth model — that a critical region of interest (CR), when damaged, gives rise to a deficit. We considered voxel-based lesion-symptom mapping (VLSM) and proportional MAP-3 (PM3). Using regression analysis, we examined if the pattern of outcome statistics can be explained by simulation parameters, factors that are inherent to anatomic parcels, and lesion coverage of the population, which consisted of a representative sample of 351 subjects drawn from the Iowa Patient Registry. We examined the effect of using nonparametric versus parametric statistics to obtain thresholded maps and the effect of correcting for multiple comparisons using false discovery rate or cluster-based correction.

Our results, which are derived from samples of realistic lesions, indicate that even a simple truth model yields localization errors that are systematic and pervasive, averaging 2 cm in the standard anatomic space, and tending to be directed towards areas of greater anatomic coverage. This displacement positions the center of mass of the detected region in a different anatomical region 87% of the time. This basic result is not affected by the choice of PM3 vs VLSM as the fundamental approach, nor is localization error ameliorated by incorporation of lesion size as a covariate in the VLSM approach, or by data distribution-driven approaches to controlling multiple spatial comparisons (false discovery rate or cluster-based correction approaches).

Our simulations offer a quantitative basis for interpreting lesion studies in cognitive neuroscience. We suggest ways in which lesion simulation and analysis frameworks could be productively extended.

Highlights

• •We assessed the signal detection properties and localization accuracy of lesion–deficit correlation methods
• •Localization errors are pervasive regardless of statistical method or whether controlling for multiple comparisons
• •The power of lesion deficit analysis is limited by the number of subjects with a lesion and a deficit
• •The detected center of mass tends to be skewed towards regions of higher coverage, and is a function of the spatial distribution of lesion coverage
• •The simulator approach offers a way to evaluate modifications to the lesion method to address weaknesses of the method

1. Introduction

The lesion method in cognitive neuroscience is based on the establishment of a descriptive and/or statistical relationship between a circumscribed region of brain damage and a behavioral and/or cognitive impairment. It uses brain lesions, which result from human disease and are identified in digital images, as probes of hypothesized large-scale systems supporting behavior and cognition (Damasio and Damasio, 1989). Productive application of the lesion method is a difficult endeavor, requiring recruitment and detailed anatomical and cognitive characterization of many suitable subjects with damage in various brain regions.

Contemporary theories of brain–behavior relationships demand methods to characterize lesion–deficit associations with respect to anatomical structures that are finer than, and often variable with respect to, macroscopic landmarks. Thus methods have been developed that utilize the same standard space frameworks employed in functional brain imaging studies. Once lesion data from multiple subjects with behavioral measures of impairment have been mapped to a common anatomical space, the standard approach is to construct a voxel-level statistical map of the lesion–deficit association, with the purpose of identifying the region(s) critical for the support of a particular function. Our studies have utilized approaches wherein lesion status and deficit are binary variables, notably the proportional MAP-3 (PM3) statistic (Kemmerer et al., 2012; Philippi et al., 2014; Rudrauf et al., 2008; Tranel et al., 2008). Bates et al. (2003) demonstrated a method they termed voxel-based lesion symptom-mapping (VLSM). They performed a voxelwise t-test contrasting the dependent behavioral variables between the group of subjects whose lesion included that coordinate and the group which did not have a lesion at that coordinate. This approach potentially takes advantage of informative variance in deficit severity, and also is applicable to measures of “ability” as opposed to measures of deficit in ability.

One well-known issue with lesion studies is that brain lesions do not sample the brain randomly. They are the product of neurological disease, and their nature is determined by intrinsic neural system vulnerabilities, cerebrovascular anatomy, surgical techniques, and other factors. All of these factors introduce systematic effects on lesion location, size, shape, and extent, and therefore must affect the anatomical accuracy, sensitivity, and spatial resolution of lesion methods. For example, strokes are most prone to affect the middle cerebral artery territory. The insula, situated in the core of this vascular territory, is rarely infarcted without additional damage in adjacent regions. On the other hand, border zones between the vascular territories are less frequently infarcted (Caviness et al., 2002). Some lesions, e.g. anterior temporal resections, are relatively stereotyped. Although these issues are acknowledged in a general way, few studies report these relationships in such a fashion as to clarify the extent and density of brain coverage or quantify regional biases (Mah et al., 2014).

In this paper, we examine what factors affect detectability of lesion–deficit associations using both discrete (PM3) and continuous (VLSM) approaches to incorporation of deficit. Our approach is to conduct systematic simulations based on lesion data in the Iowa Patient Registry, which provides a representative lesion sample with heterogeneous brain coverage. These simulations allow us to analyze the effect of factors such as sample size, location of the critical area of interest, probability of association of deficit with the lesion, and threshold of significance on sensitivity, specificity and localization bias.

2. Methods

We developed a simulator in Python and Matlab that, given parameters describing the sample size, probability of deficit, and truth model, computes the statistically significant region that is associated with a deficit. Fig. 1 shows the overview of the lesion simulator (see the details below). The primary statistical metrics used for the simulation are PM3 (Rudrauf et al., 2008), and voxel-based lesion-symptom mapping (VLSM: Bates et al., 2003). PM3 is the proportion of subjects with a lesion at a given voxel and a deficit among those with a deficit, minus the proportion of subjects with a lesion and no deficit among those with no deficit, or Eq. (1). We also report on performance of M3, defined as the number of subjects with a lesion at voxel and a deficit (N_LD) minus the number of subjects with a lesion at voxel but no deficit (N_L ~ D), (Eq. (2)). VLSM compares the continuous behavioral scores for subjects who have a lesion and those who do not at each voxel. VLSM is currently the most widely used lesion-symptom mapping statistic. PM3 statistics are preferable to M3 statistics, which are skewed with respect to their significance due to basic normalization issues (Rudrauf et al., 2008). Essentially, M3 values with the same level of significance can be very different, and will vary across voxels, as it depends strongly on lesion coverage and proportions of subject with and without deficit in the sample. However, we included M3 because it has been used as a descriptive statistic in earlier studies, and the current work informs their interpretation (Ralph Adolphs et al., 2002; Adolphs et al., 2000; Damasio et al., 2004; Tranel et al., 2001; Tranel et al., 1997; Tranel et al., 2003; Tranel et al., 2009; Young et al., 2010). Exact analytical expressions for the distributions of probability of the M3 and PM3 distributions are described in Rudrauf et al. (2008).

$$PM3=\frac{N_{LD}}{N_D}-\frac{N_{L~D}}{N_{~D}}$$ (1)

$$M3=N_{LD}–N_{L~D}$$ (2)

Fig. 1.

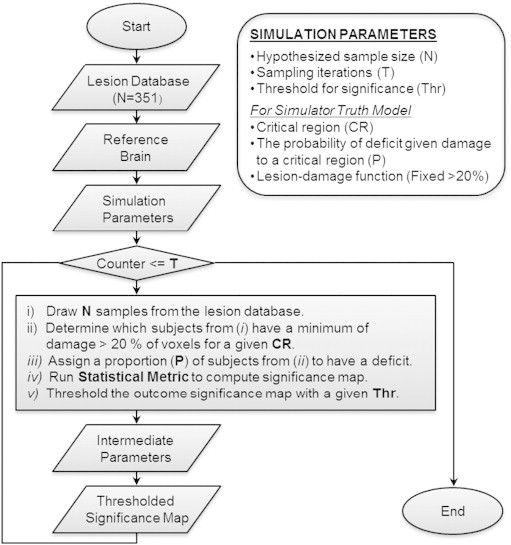
Overview of the simulator. Input data are the lesion database, the parcellated reference brain, and a set of simulation parameters. We ran the simulation for M3 and PM3 statistics separately for 100 critical region, varying systematically the sample size (N = 25, 50, 75, 100, 125, 150), proportion of lesions in the critical parcel that were accompanied by deficit probability (P = .25, .5, .75, 1), and significance threshold (Thr = .001, .005, .01, .05), for 100 iterations (T = 100).

We performed simulations using PM3 for 100 critical regions (Fig. 2), varying systematically the sample size (25, 50, 75, 100, 125, 150), proportion of lesions in the critical parcel that were accompanied by deficit (.3, .5, .75, 1), and the uncorrected threshold for statistical significance (.001, .005, .01, .05), followed by statistical evaluations of the simulation outputs.

Fig. 2.

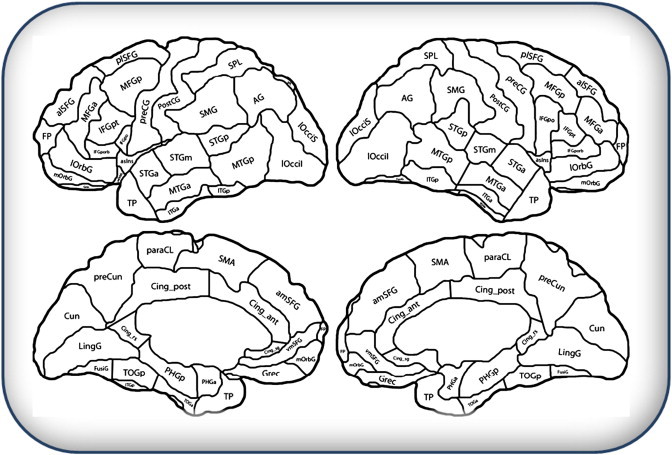
Cortical parcellation showing critical regions of interest (ROIs) used in simulations. The parcellation is based on Desikan et al.(2006), and mapped onto the anatomy of a single reference brain by Hanna Damasio and Joel Bruss.

VLSM was implemented in Matlab in our simulator as described in Bates et al. (2003). Because of computational demands, we limited our simulations of VLSM to a sample size of 150 and the case where all lesions causing suprathreshold damage to the critical parcel were associated with a deficit. We examined VLSM with a simulated behavioral deficit proportional to the damage in the critical parcel, and with and without covarying for lesion size. We controlled for lesion size by first regressing out the total lesion size from the simulated behavioral deficit, and using the residual in the final model. This hierarchical regression implementation is conceptually identical to the ANCOVA framework proposed by Bates et al. (2003).

To explore the effects of correction for multiple comparisons, we examined the effect of false discovery rate (FDR) correction and cluster-based correction using the null distribution of the maximum cluster size. Finally, we examined the effect of using nonparametric versus parametric thresholding of uncorrected t statistics with VLSM.

The details of the simulator, output measures, and the evaluation procedure of the stimulation outputs are as follows.

2.1. Simulator overview

2.1.1. Input data to the simulator

The simulator draws samples from a real lesion database. The input data in this study consists of (a) a lesion database consisting of 351 lesion masks drawn from and representative of the patient registry of the University of Iowa's Division of Behavioral Neurology and Cognitive Neuroscience, in NIfTI format; and (b) an anatomically parcellated reference brain, in NIfTI format. Lesions were regions of circumscribed tissue destruction caused by cerebrovascular disease, herpes simplex encephalitis, or surgical resection. The lesions were expertly traced (by Dr. Hanna Damasio and students under her supervision) on a 3D T1-weighted MRI image of a standard normal reference brain, respecting anatomic landmarks, according to the MAP-3 procedure developed in the Laboratory of Human Neuroanatomy and Neuroimaging (Damasio and Damasio, 1989; Damasio and Frank, 1992; Damasio et al., 2004; Frank et al., 1997) and converted to binary masks.

2.1.2. Simulator truth model

The simulations incorporate an assumed association between a lesion and a deficit (the “truth model”) that permits evaluation of the ability of an analysis and sampling approach to recover this truth model. In this report we adopt a simple truth model in which there is assumed to exist a single “critical region (CR)” which, when damaged gives rise to a deficit with a defined probability (P). The critical region is operationalized as one of the functional anatomic parcels depicted in Fig. 2. The threshold for damage causing deficit is also a free parameter, but was fixed at 20% of the voxels in the CR for the purpose of this study, as it interacts with sample size and deficit probability to change the number of subjects who have a lesion in a specific region. This damage threshold was chosen to correspond to the rule used to interpret lesion data in practice (Damasio and Damasio, 1989), i.e. in the Iowa Patient Registry, regions with more than 20% destruction are recorded as lesioned (Damasio and Damasio, 1989).

2.1.3. Parameters that control the simulator

Parameters that control the simulator are (a) a critical region (CR), (b) a hypothesized sample size (N), (c) the probability of deficit given damage to a critical region (P), (d) the number of sampling iterations (T), and (e) a threshold for significance (Thr) (Fig. 1).

2.1.4. Basic simulator algorithm

For each statistical metric and for each combination of a set of parameters (CR, N, P, T, Thr) a random sample of N subjects is drawn from the lesion database. These subjects are inspected to determine whether they meet the criteria for having a lesion following a lesion-damage function (i.e. a minimum of damage to 20% of voxels in the critical region). Of those subjects who have lesions in the CR, some fraction (P) are assigned a deficit. Then, the statistics (either PM3 or M3) are calculated and thresholded significance maps are output for each of the given thresholds (Thr). This sampling process and creation of threshold significance maps are repeated for T iterations. Certain important intermediate parameters are calculated in the simulator loop, for each combination of input parameters. These are (a) the number of subjects with a lesion, (b) the number of subjects with a deficit, and (c) the number of subjects with a lesion and a deficit. These intermediate parameters are functions of the input data and the simulator parameters, more immediately determine the simulator output, and are typically known in real lesion studies.

2.1.5. Simulator output statistics

After all the thresholded significance maps are computed, the simulator calculates a variety of output statistics. These include measures of localization error, signal detection theory statistics (e.g., sensitivity, specificity, accuracy), and percentage of trials that detect any significant voxels. The output statistics that we selected for our analysis are (1) the distance between the center of mass of the critical region and the center of mass of the identified significant region, or localization error, (2) voxel-level true negative rate, or specificity, (3) the total number of false negative voxels, or type II error — the number of nonsignificant voxels within a CR, and (4) two measures of true positives: a) the voxel-level true positive rate, or sensitivity, and b) the rate at which a significant association was found in the CR.

2.1.6. Example simulator run

Fig. 3 illustrates the flow of the simulator. The CR in which we postulate a lesion–deficit relationship is the left pars opercularis (Fig. 3A). We draw a sample of N = 100 subjects from the total population of N = 351 (Fig. 3B). Of these subjects, 15 subjects have at least 20% of the CR involved in the simulated lesion and thus meet truth model requirement to model presence of a deficit. These 15 subjects are shown in Fig. 3C. Because our deficit probability is .5 (P = 0.5), half of the subjects in Fig. 3C are randomly selected to manifest a deficit (Fig. 3D). PM3 statistics are then estimated to obtain the map shown in Fig. 3E.

Fig. 3.

Simulation example for one trial (CR = LIFGpo, N = 100, P = 0.5). (A) Critical region — pars opercularis in the left hemisphere. The cumulative map of lesions for: (B) lesion maps randomly selected for this trial (n = 100), (C) those identified as having more than 20% damage in the critical region (n = 15), of which (D) 50 % are then randomly selected to have a deficit (n = 8). (E) The lesion deficit relationship estimated by PM3 statistics (P < 0.01).

2.2. Evaluations of the simulator outputs

After running the simulator, we conducted statistical analyses to reduce and interpret the simulator outcomes. This involved characterizing the CRs and identifying how CR characteristics and simulator parameters related to simulator outcomes. This is because anatomical variability is an important implicit input variable. For example, some regions are more susceptible to damage, and will be more represented in the lesion database. To characterize this variability, we computed various measures describing the nature of the anatomic parcels (CRs), and lesion coverage of the CR given the population. These descriptive statistics included CR size, the average number of subjects with damage in the CR, and the proportion of damaged voxels in the CR (see Table 1 for the list of the CR descriptive statistics). We identified these statistics using the intuition that the qualitative nature of lesion coverage would be an important factor affecting our results. To eliminate collinearity among these arbitrarily chosen statistics, we performed a principal component analysis (PCA) of the statistics characterizing the CR.

Table 1.

ROI description statistics.

Name	Description
ttlvox	Total number of voxels (size of ROI in voxels)
dist_cm_cg	Distance (in voxel) between the center of mass of the ROI and the center of the gravitya of the ROI
sum_pdmg_n351	Sum of (the number of lesioned voxels within ROI divided by a total number of voxels (ROI size) for each subject)
prob_dmg_5p	Proportion of the people (out of 351) with damages in a given ROI where the damage threshold is >5%
prob_dmg_10p	Proportion of the people (out of 351) with damages in a given ROI where the damage threshold is >10%
prob_dmg_20p	Proportion of the people (out of 351) with damages in a given ROI where the damage threshold is >20%
prob_dmg_40p	Proportion of the people (out of 351) with damages in a given ROI where the damage threshold is >40%
prob_dmg_60p	Proportion of the people (out of 351) with damages in a given ROI where the damage thresholds is >60%
prob_dmg_80p	Proportion of the people (out of 351) with damages in a given ROI where the damage thresholds is >80%
avg_num_lesVox	Average (number of lesioned voxels within ROI for each subject)
num_subj_anydmg	Total number subject with ANY damage to the ROI
avg_num_lesVox_anydmg	Average (umber of voxels within the ROI for each subject who had any damaged to that ROI)
num_sum_20pdmg	Total number of subject with lesion >20% for the ROI
avg_num_lesVox_20pdmg	Average (number of voxels within the ROI for each subject who had damage >20% to that ROI)
pro_lesionedROI	Average of [(number of damaged voxels in the ROI) divided by (total number of damaged voxels in the brain) for each subject]
pro_lesionedROI_subj_anydmg	Average of [(number of damaged voxels in the ROI) divided by (total number of damaged voxels in the brain) for each subject who had any damage]
pPro_lesionedROI_subj_20pdmg	Average of [(number of damaged voxels in the ROI) divided by (total number of damaged voxels in the brain) for each subject who had damage >20% to that ROI]
avg_num_lesVox	Average of (number of lesioned voxels within ROI for each subject)

^aThe center of gravity is computed based on lesion coverage for the population (n = 351).

On the basis of this dimensionality reduction, we used the components describing the CR in combination with the simulator inputs (sample size, deficit probability, and significance threshold) as independent variables in regression analyses to predict each dependent variable, or outcome statistics, selected for these analyses.

3. Results

3.1. Overall simulation results

Table 2 shows the mean and standard deviation of the output statistics for PM3 and M3 across all parameterizations and iterations. On average, 85% of trials yielded a significant association in some voxels. The mean localization error over all conditions for PM3 is approximately 2 cm (SD = 0.61 cm). The voxelwise sensitivity across all parameterizations and iterations for PM3 is 0.52 (SD = 0.28), suggesting that PM3 results in many false negatives. In absolute terms, the volume of tissue that are false negatives is 2.85 cm³ (SD = 2.52 cm³). The voxelwise true negative rate is high (all cortical voxels outside of the CR), as a consequence of how we model the deficit, but the number of false positives vary as a systematic effect of coverage. Because the true negative rate is so high relative to false positives, specificity is high (.95, SD = .04). Results for M3 are qualitatively similar, with the exception that M3 has a higher rate of false negative voxels.

Table 2.

Summary outcome statistics.

	PM3		M3
	Mean	SD	Mean	SD
Localization error (mm)	20.88	6.05	18.86	5.56
Voxel-level TPR (sensitivity)	0.52	0.28	0.40	0.30
Voxel-level SPC (specificity)	0.95	0.04	0.98	0.03
FN (false negatives, cm3)	2.85	2.52	3.48	2.86
Percent of trials with sig. association	85%		74%

3.2. Characterization of critical regions

Of the 17 variables selected in Table 1 to characterize the critical regions, three components were sufficient to explain 86.6% of the variance. Examining the patterns of orthogonal loadings (see Table 3), we suggest descriptions for these factors as follows: Component 1 (C1), which explains 48.4% of the variance in our descriptive variables, is a measure of high coverage of the CR by the lesion sample. Component 2 (C2), which explains 31.5% of the variance, describes local heterogeneity of coverage within the CR and its systematic relationship to large CR size. The region with the largest value of C2 is the precentral gyrus and the region with the lowest is the pars orbitalis. Component 3 (C3), which explains 6.7% of the variance, seems to reflect a measure of the degree to which the CR is the main locus of damage versus peripheral to the main locus of damage. As a caveat, it is clear that our initial choice of descriptive metrics biases the specific component structure, and PCA was used only as a data reduction technique to simplify analysis.

Table 3.

Principal component analysis loadings on ROI characteristics.

	Component
ROI characteristic	1	2	3
ttlvox	.048	.912	−.084
dist_cm_cg	−.252	.565	.404
sum_pdmg_n351	.917	−.229	.217
prob_dmg_5p	.819	−.306	−.024
prob_dmg_10p	.848	−.351	−.038
prob_dmg_20p	.869	−.403	−.060
prob_dmg_40p	.827	−.490	−.111
prob_dmg_60p	.772	−.520	−.149
prob_dmg_80p	.669	−.518	−.220
avg_num_lesVox	.742	.631	.044
num_subj_anydmg	.512	.419	.614
avg_num_lesVox_anydmg	.742	.631	.044
num_sum_20pdmg	.923	−.113	.288
avg_num_lesVox_20pdmg	.796	.549	.001
pro_lesionedROI	.555	.776	−.049
pro_lesionedROI_subj_anydmg	.545	.704	.403
pro_lesionedROI_subj_20pdmg	.079	.779	−.451
avg_num_lesVox	.742	.631	.044

3.3. Factors that affect outcome statistics

Table 4 summarizes the results from the regression analyses, including the standardized beta weights from each analysis. The deficit probability and the threshold were the two major predictor variables for localization error for PM3. As the deficit probability increases, the localization error decreases. Conversely, with more stringent thresholds (smaller values of Thr), the localization error decreases. Moving from the lowest deficit probability or the least stringent threshold to the highest deficit probability or most stringent threshold decreases localization error by an average of 4.9 cm across all conditions.

Table 4.

Standardized regression coefficients.

		Std. beta
Dependent variable	R2	Sample size (N)	Deficit prob (P)	Threshold (Thr)	CR coverage (C1)	CR size/skew (C2)	CR main/ peripheral (C3)
PM3
localization error	0.333	−0.242	−0.274	0.394	−0.214	0.000	0.011
						(P = .966)	(P = .195)
TPR (sensitivity)	0.62	0.289	0.376	0.529	0.285	−0.193	−0.023
SPC (specificity)	0.666	−0.169	−0.184	−0.752	−0.129	0.072	−0.132
FN (false negatives)	0.67	−0.169	−0.218	−0.325	−0.123	0.688	−0.008
							(P = .201)
% of trials w/ any significant voxels	0.573	0.378	0.172	0.029	0.616	−0.045	0.138
M3
localization error	0.378	−0.203	−0.452	0.286	−0.008	−0.076	0.11
					(P = .330)	(P = .002)
TPR (sensitivity)	0.783	0.348	0.707	0.329	0.32	−0.166	0.014
							(P = .005)
SPC (specificity)	0.613	−0.238	−0.502	−0.483	−0.328	0.093	−0.14
FN (false negatives)	0.743	−0.196	−0.397	−0.193	−0.134	0.72	−0.041
% of trials w/ any significant voxels	0.625	0.552	0.206	0.213	0.466	−0.033	0.118

All are significant at P < .001, except noted otherwise not significant at P < .05.

For sensitivity, the major predictive variables for PM3 were the threshold and deficit probability. If the deficit probability increases, then the number of false negative voxels decreases and the number of false positive voxels increases. This causes the sensitivity to increase and the specificity to decrease. As the threshold becomes less stringent the sensitivity increases and specificity decreases.

For the measurement of false negative voxels, the size/skew of CR (C2) was the major predictor for PM3. Larger CRs with more heterogeneity will lead to failure to associate the CR with the deficit.

The major predictor variable of the percentage of trials with significant voxels was CR coverage (C1) for PM3. When the CR coverage (C1) increases, so does the proportion of trials yielding significant voxels. Sample size was the second most important factor in determining the percentage of trials with significant voxels. Although on average the probability of detecting a lesion–deficit relationship with our simulation parameters was .85, it climbed to .95 with a sample size of 150. We can see from Fig. 4 that there is a nonlinear relationship between coverage and probability of detecting a significant association that is dependent upon the number of subjects in the sample with a lesion. No relationship can be detected unless there are subjects with a lesion and a deficit in a CR. The total N required to meet this condition varies with the deficit probability and sample size. However, as we make the threshold more stringent, this number increases to 2–3. This is because to detect a significant association, there must be more subjects with a lesion and a deficit at a voxel than subjects who have a lesion and no deficit. Because subjects need to have at least 20% of damage to CR to have a lesion and a deficit, subjects can have incidental damage to the CR without an accompanying deficit. Given the patterns of coverage, the probability of having the same number of subjects with damage and no deficit as those with damage and a deficit becomes very small in these simulations when 2–3 subjects have a lesion and a deficit (see Discussion).

Fig. 4.

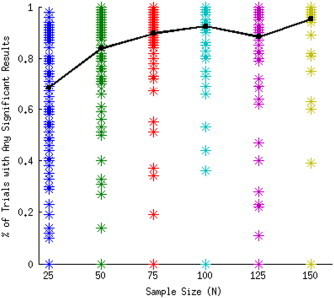
Percentage of trials with significant results by sample size for deficit probability P = 1.0 and threshold Thr = .001. Each asterisk in a column represents a CR in a different anatomic location. Trend line graphs the mean of all CRs.

M3 statistics show a pattern similar to PM3 with some exceptions. Localization error for M3 (Table 4) loads on C2 and C3 (components describing the skew of coverage) and localization error for PM3 loads only on C1 (coverage). For M3, the effect of increasing deficit probability is greater than that for PM3 on sensitivity and specificity because PM3 adjusts for the number of subjects with and without a deficit. Sample size is consequently less important a predictor for PM3 than for M3 in both specificity and sensitivity.

As shown in Fig. 1, the inputs to the simulator result in the ultimate selection of a number of subjects with lesion, N_L (who have greater than 20% damage to the CR) and assignment of some of those to have a lesion and a deficit (N_LD) or a lesion and no deficit (N_L~D). It can be seen from Eqs. (1) and (2) that these three parameters are sufficient to describe the M3 and PM3 statistics. The number of subjects with a lesion N_L is determined by the lesion coverage in the lesion database. As we increase the sample size N, N_L increases proportionally, because our sample is drawn from the same distribution. Therefore, if N_L is proportional to N, the M3 and PM3 maps will be similar for any selections of deficit probability and N where P × N₁=P × N₂, given the simple truth model tested in our simulations.

3.4. Characteristics of identified regions

For PM3, across all conditions, when a significant association was identified, the center of mass was located in the cerebral cortex (one of the parcels in Fig. 2) 94.6% of the time. However, the center of mass was located in the CR (as specified by the truth model) only 13.2% of the time. Under the simulation conditions that would seem most favorable (150 subjects, deficit probability = 1, and threshold = .001) this probability rose to 21.4%. The center of mass is attracted away from the region specified by the truth model towards neighboring regions with higher coverage, as illustrated in Fig. 5. This is the practical impact of the increase in false positive voxels that results with more lenient thresholds and increasing statistical power. These false positive voxels tend to implicate regions that are not the critical region but that tend to also be damaged in subjects with damage affecting the critical region. Furthermore, regions with higher statistical power (i.e. to detect a relationship in the first place, whether it corresponds to the truth model or not) generally correspond to regions with higher lesion coverage in the sampling population (Fig. 6). As a result, the map of localization bias and the map of lesion coverage resemble each other.

Fig. 5.

Simulation example for one trial (CR = LMTGp, N = 100, P = 0.5), illustrating localization error in the direction of higher lesion coverage. (A) Critical region — posterior middle temporal gyrus in the left hemisphere. The cumulative map of lesions for: (B) lesion maps randomly selected for this trial (n = 100), (C) those identified as having more than 20% damage in the critical region (n = 6), of which (D) 50% are then randomly selected to have a deficit (n = 3). (E) The lesion deficit relationship estimated by PM3 statistics (P < 0.01).

More specifically, the accuracy and reliability of results depends on the proximity to regions with high spatial gradient in lesion coverage. The gradient acts as an attractor for the localization bias (as illustrated in Fig. 5). Thus, regions of lower statistical power that are far away from regions of strong spatial gradient in lesion coverage can demonstrate better localization accuracy than regions of higher statistical power near such high gradients.

3.5. Comparison of PM3 with VLSM

Because of computational requirements, we ran VLSM (with and without the lesion size as a covariate) for all parcels, with N = 150 and P = 1.0, a favorable set of conditions. We computed the P values for the voxelwise t statistics in two ways: first using standard parametric distributional assumptions, and second using nonparametric permutation testing with 1000 permutations. Table 5 shows the results comparing PM3 and M3 to VLSM for N = 150 and P = 1.0 On average, VLSM using parametric statistics has higher localization error and lower sensitivity than PM3 and M3. However, VLSM with nonparametric statistics has comparable localization error, sensitivity, and specificity to M3 and PM3.

Table 5.

Non-FDR corrected summary outcome statistics (N = 150 and P = 1).

	PM3		M3		VLSM (parametric)		VLSM (nonparametric)		VLSM (parametric, lesion size as covariate)
	Mean	SD	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Localization error (mm)	16.51	6.61	14.15	5.75	19.14	6.89	16.52	6.25	26.21	13.72
Voxel-level TPR (sensitivity)	0.82	0.25	0.82	0.23	0.60	0.26	0.83	0.26	0.64	0.26
Voxel-level SPC (specificity)	0.92	0.06	0.94	0.05	0.99	0.01	0.99	0.01	0.98	0.01
FN (false negatives, cm2)	1.15	1.87	1.15	1.80	2.03	1.78	1.05	1.83	1.86	1.78
Percent of trials with sig. association	100%		100%		100%		100%		100%

3.6. Correction for multiple comparisons

We examined the effect of correcting for multiple comparisons using FDR correction for all parcels with N = 150 and P = 1.0. Table 6 shows these results. Correcting for multiple comparisons had only a modest effect upon localization error. We further compared FDR correction for multiple comparisons to nonparametric cluster correction for two parcels, one with high coverage (LIFGpo) and one with lower coverage (LMTGp) (Table 7). Cluster correction for multiple comparisons did not significantly improve localization error, as long as a nonparametric approach was used to threshold the t statistic maps.

Table 6.

FDR corrected summary outcome statistics (N = 150 and P = 1).

	PM3		M3		VLSM (parametric)		VLSM (lesion size as covariate)
	Mean	SD	Mean	SD	Mean	SD	Mean	SD
Localization error (mm)	15.61	9.92	12.37	5.31	18.76	6.77	24.82	12.93
Voxel-level TPR (sensitivity)	0.65	0.35	0.75	0.28	0.60	0.26	0.63	0.26
Voxel-level SPC (specificity)	0.99	0.01	0.99	0.00	0.99	0.01	0.99	0.01
FN (false negatives, cm2)	2.13	2.68	1.58	2.15	2.06	1.79	1.89	1.79
Percent of trials with sig. association	94%		92%		100%		100%

Table 7.

FDR and cluster-corrected summary outcome statistics for VLSM with no covariate (LIFGpo and LMTGp only, N = 150 and P = 1).

		FDR parametric VLSM		Nonparametric VLSM		Cluster-corrected nonparametric VLSM
		Mean	SD	Mean	SD	Mean	SD
LIFGpo	Localization error (mm)	14.31	2.67	12.62	3.11	12.55	3.10
	Voxel-level TPR (sensitivity)	0.29	0.16	1.00	0.00	1.00	0.00
	Voxel-level SPC (specificity)	0.99	0.00	.99	0.00	0.99	0.00
	FN (false negatives, cm2)	1.00	0.23	0.00	0.22	0.00	0.22
	Percent of trials with sig. association	100.00		100.00		100.00
LMTGp	Localization error (mm)	16.40	3.45	14.83	4.52	14.63	4.04
	Voxel-level TPR (sensitivity)	0.86	0.12	0.80	0.17	0.80	0.17
	Voxel-level SPC (specificity)	0.99	0.00	0.99	0.00	0.99	0.00
	FN (false negatives, cm2)	1.19	1.06	1.70	1.48	1.74	1.50
	Percent of trials with sig. association	100.00		100.00		100.00

4. Discussion

In this article we quantify and evaluate the impact of lesion sampling characteristics, anatomical heterogeneity of lesion coverage, and their interaction on the detectability and accuracy of localization of lesion deficit relationships. We do so using simulations, which are a powerful tool for evaluating the ability of specific statistical approaches to recover a lesion–deficit relationship defined by a truth model. The conclusions from such simulations pertain to the underlying truth model and simulator parameters. Even using a simple truth model, our simulations offer a quantitative basis for interpreting lesion studies in cognitive neuroscience.

Our results indicate that, given samples of realistic lesions, even a simple truth model yields localization errors that are systematic and pervasive, averaging 2 cm in the standard anatomic space, and tending to be directed to areas of greater anatomic coverage. This displacement positions the center of mass of the detected region in a different anatomical region 87% of the time, given a parcellation dividing the cerebral cortex in regions of a size comparable to Brodmann areas. This basic result is not affected by the choice of PM3 vs VLSM as the fundamental approach, nor is localization error ameliorated by incorporation of lesion size as a covariate in the VLSM approach, or by data distribution-driven approaches to controlling multiple spatial comparisons (false discovery rate or cluster-based correction approaches).

Our results also suggest that VLSM performs significantly better in terms of sensitivity, and slightly but significantly better in terms of localization error, when nonparametric significance testing is performed instead of parametric t-testing. Performance with the nonparametric significance testing is essentially equivalent to PM3, for the models used here. Rorden et al. (2007) show that the Liebermeister approach for voxel-based lesion mapping is more sensitive than the chi-square test when the clinical measure is binomial, and that a test described by Brunner and Munzel is more appropriate than the t test for nonbinomial data, because neuropsychological data often violate the assumptions of the t-test (see also Medina et al. (2010) for description of a correction for small N).

An advantage of the VLSM framework is that its models are extensible to covariates like lesion size. However, covarying lesion size did not reduce localization error. Due to computational constraints we were not able to explore nonparametric thresholding for this case.

We performed multiple comparison correction primarily using the FDR approach. FDR correction did not substantially affect the sensitivity, specificity, or localization error resulting from these simulations. The failure of FDR correction to improve localization error is due in part to our decision to model only one critical zone, with no (false positive) associations outside the critical zone. Our purpose in doing so was to isolate as much as possible the effect of localization bias. Thus it is probably most significant to note that alternative approaches to multiple comparison correction (nonparametric thresholding, cluster based correction) did not result in less localization bias than FDR (or indeed no correction).

Our results converge with a recent paper by Mah et al. (2014), which found a mean of 15.7 mm mislocalization across the brain. In contrast to our simulation approach, which was designed to explore the effects of different parameters on localization error, Mah et al. used all data available in a large database to quantify localization error. Their approach was to calculate a vector showing the displacement of the identified center of gravity from each voxel lesioned in more than four subjects. Thus, the magnitude of mislocalization they identified represents the best case scenario using standard lesion mapping approaches. Making their model more similar to ours (that a critical region was damaged if 20% of its voxels were affected, and further assigning a deficit probability of 90%) increased the mean displacement slightly. As we have shown, if the number of subjects with a lesion and a deficit is smaller, the mean displacement is likely to be larger and the probability of finding a significant association where one exists is reduced.

These studies were designed to shed light on lesion distribution as a factor affecting accuracy and sensitivity of voxel-based lesion–deficit mapping approaches. To do so, we used a simple truth model, in which there existed only one critical region, and in which there existed no deficits not caused by damage in the critical region. Even under these artificial conditions, the simulator was useful in demonstrating and quantifying localization error. With these simulations, a significant association in a CR between a lesion and a deficit could be detected when there were 2–3 brain-damaged subjects with a lesion at that CR and a deficit. We caution that in practice, lesion–deficit relations are certainly more complex. For example, cognition and behavior are critically supported by systems of distributed cortical regions, and damage to various components of the system may generate similar deficits. There are also factors such as degeneracy of neural systems (Friston and Price, 2011; Noppeney et al., 2004) and collateral damage to underlying white matter tracts (Mehta et al., 2012; Rudrauf et al., 2008) to consider. These factors will conspire to require a larger number of subjects with damage in the CR to detect a lesion–deficit relationship. Simulations using a more complex truth model that assumes distributed and individually critical regions supporting the target function/behavior represent an important future direction for this work.

In its current form, lesion deficit analysis is limited first by the number of subjects with a lesion and a deficit (given the coverage of the CR, number of subjects and deficit probability) and thereafter by the tendency of the center of mass to be skewed along the gradient of coverage, towards regions of higher coverage. The localization bias caused by displacement along the gradient of coverage is a factor even when the number of subjects with a deficit is large, and is a function of the spatial distribution of lesion coverage. This suggests that one might consider a form of biased sampling or weighting that considers lesion size: The smaller a lesion associated with a deficit, the less it contributes to localization error. Our framework thus offers a number of ways forward, incorporating other truth models, statistical frameworks, and variations of the lesion method that may begin to address these weaknesses.

Besides the PM3 and VLSM methods we implemented in this simulation, other statistical approaches have been described to identify whether an association between a lesioned area and a behavior may be statistically significant. Karnath et al. (2004) developed an approach named Voxel-based Analysis of Lesions (VAL). In VAL, a voxelwise logistic multiple regression is conducted where the dependent variable in the regression is a dichotomized behavioral score. A potential advantage of this approach is the formal modeling of lesion-related parameters. In Karnath et al. the independent variables are whether or not the voxel is part of the lesion (dichotomous) and the size of the lesion (continuous). An exploration of this method was beyond the scope of the simulations reported here.

A different approach to lesion behavior mapping that attempts to accommodate a somewhat more complex truth model is Anatomo-Clinical Overlapping Mapping (AnaCOM) (Kinkingnéhun et al., 2007), which contrasts the behavior of patients who have damage to a specific voxel to a group of healthy controls. An advantage of AnaCOM is that patients with the same behavioral deficit but no overlap in damaged voxels will not serve as controls for each other. In cases where more than one region may be responsible for a deficit, the approach therefore improves statistical power, though AnaCOM still relies on the spatial overlap of brain-damaged regions across multiple subjects to detect/localize anatomical–functional correspondence. Rorden et al. (2009) find that the increased statistical power of this method may come at the expense of decreased specificity.

Natural extensions of the simulator can accommodate more realistic truth models and address the competency of the lesion method to generate knowledge in the systems' framework. For example, an area can be rendered dysfunctional due to a lesion that disconnects it from others and not because it is lesioned directly. We can thus extend the simulator to systems of critical regions. We can also formally model an impact of disconnection of these critical regions on function (Rudrauf et al., 2008).

In summary, our contribution is to implement a simulation framework for testing the expected association between lesion and deficit. Our characterization of the effects of experimental parameters on the ability to detect a significant lesion–deficit association allows us to make certain pragmatic recommendations for interpretation of studies using of the PM3 statistics, or VLSM t-statistics. Simulations offer a way forward for examining the usefulness and validity of alternative approaches, and, given specific truth models and samples, a means to evaluate the feasibility of lesion studies prospectively.

Fig. 6.

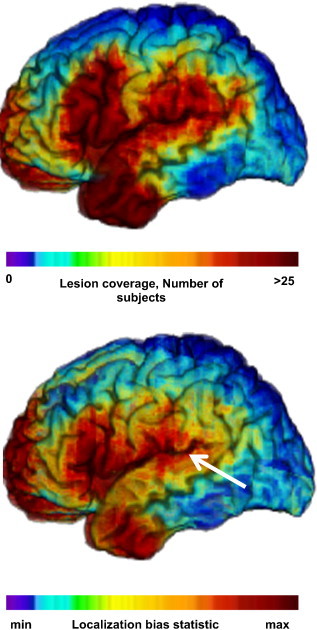
Lesion coverage and regions attracting center of mass, driving localization error. Top. Lesion coverage map (N = 351): number of subjects with damage at a given voxel. Bottom. Localization bias map (simulation parameters: N = 100, deficit probability = 0.5, statistical threshold = .01). Arrow shows vector of localization error for the case illustrated in Fig. 5. Left lateral aspect of the brain.