Free Energetics of Arginine Permeation into Model DMPC Lipid Bilayers: Coupling of Effective Counterion Concentration and Lateral Bilayer Dimensions

Abstract

Mechanisms and underlying thermodynamic determinants of translocation of charged cationic peptides such as cell-penetrating peptides across the cellular membrane continue to receive much attention. Two widely-held views include endocytotic and non-endocytotic (diffusive) processes of permeant transfer across the bilayer. Considering a purely diffusive process, we consider the free energetics of translocation of a mono-arginine peptide mimic across a model DMPC bilayer. We compute potentials of mean force for the transfer of a charged mono-arginine peptide unit from water to the center of a 1,2-Dimyristoyl-sn-Glycero-3-Phosphocholine (DMPC) model lipid bilayer. We use fully atomistic molecular dynamics simulations coupled with the adaptive biasing force (ABF) method for free energy estimation. The estimated potential of mean force difference from bulk to bilayer center is 6.94 ± 0.28 kcal/mol. The order of magnitude of this prediction is consistent with past experimental estimates of arginine partitioning into physiological bilayers in the context of translocon-based experiments, though the correlation between the bench and computer experiments is not unambiguous. Moreover, the present value is roughly one-half of previous estimates based on all-atom molecular dynamics free energy calculations. We trace the differences between the present and earlier calculations to system sizes used in the simulations, and the dependence of the contributions to the free energy from various system components (water, lipids, ions, peptide) on overall system size. By varying the bilayer lateral dimensions in simulations using only sufficient numbers of counterions to maintain overall system charge neutrality, we find the possibility of an inherent convergent transfer free energy value.

II. INTRODUCTION

Cell-penetrating peptides (CPP) are short cationic proteins that permeate across biological membranes. The HIV transactivator of transcription (TAT) protein (containing 6 arginines and 2 lysines) was found to translocate across biological membranes for the first time in 1988^1,2. Among the CPPs, the arginine-rich cell-penetrating peptides (RRP), such as TAT and polyarginines, have garnered extensive attention. Arginine-rich cell-penetrating peptides (RRP) are considered a promising trans-membrane delivery platform for potential therapeutic molecules with inherently low cellular permeability such as peptides, nucleic acids, macromolecules, and so on³. The translocation efficiency of cell penetrating peptides positions RRP’s as a viable potential approach to treat diseases such as cancers⁴. It is reported that polyargine fused p53 proteins, a transcription factor and tumor suppressor, can effectively penetrate the plasma membrane of glioma cells associated with pyrenebutyrate⁵. In spite of the potential, broad application of RRPs for delivery purposes, the exact molecular mechanism of their translocation is currently not fully understood^6–11. Two dominantly-held views about the translocation mechanism are espoused first, an endocytotic mechanism, and second, an energy-independent (non-endocytotic) path. Importantly, even the endocytotic mechanism must consider the exit of the peptide from the endosome, again, requiring some mechanistic interpretation to account for the efficient entry of this class of peptides into cellular nuclei¹².

A recent study¹³ demonstrated a non-endocytic uptake mode of arginine-rich cell-penetrating peptides. Studies show that in conditions lacking endocytosis, CPPs including RRPs are able to translocate across giant plasma membrane vesicles (GPMVs)¹⁴. Thus, the existence of a non-endocytotic pathway is plausible at the present time within the context of available experimental data.

The notion of highly charged species in membranes and bilayers is not only relevant with respect to RRP’s, but numerous other physiological contexts as well. These processes range from voltage gating in select ion channels,^15–17 translocation of cationic residue enriched cell-penetrating peptides for transporting cargo across the cellular membrane,^13,18–23 and the action of anti-microbial peptides upon interaction with native cellular membranes. Furthermore, from purely physical arguments, continuum electrostatic models suggest a large free energy barrier need overcome by translocating cationic particles from a high dielectric bulk water to low dielectric center of membrane. The Born-type free energy required is ca. 40 kcal/mol to translocate a positive charged arginine into the center of membrane²⁴. However, translocon-based experiments indicate a barrier of about 2.5 kcal/mol for transferring arginine into a physiological membrane²⁵. Molecular dynamics simulations using all-atom models indicate that the free energy difference between bulk and bilayer-centered states of model arginine analogues such as methyl guanidinium (and methyl guanidinium as a side-chain in a polyleucine helix) is significantly higher, on the order of 20 kcal/mol. Considering the deformation of membrane caused by the internalization the arginine to be a factor to allow for some stabilization of the arginine charge by polar and charged groups of the lipid molecule, the consensus penetration free energies are still as high, about 15 ~ 18 kcal/mol, in both continuum model²⁶ and all-atom model^27,28.

Spurred by ongoing experiments giving rise to varying experimental evidence for possible translocation mechanisms, atomistic and coarse-grained molecular dynamics simulations have added to the molecular- scale knowledge of determinants to the transfer process. These include deformation at the single-lipid level of the model bilayer as well as the formation of water pores or water defects that provide a solvation shell around the charged permeant, thus alleviating a portion of the desolvation penalty incurred during the transfer process as modeled in the context of such simulations. Recent studies have focused on unloaded linear and cyclic poly-arginine peptides^13,29 as well as RPP’s with carbon nanomaterial loads³⁰. In particular, the study by Huang et al²⁹ demonstrates the thermodynamic stability contributed by water pore formation along the translocation coordinate as compared to one without a pore. This result is consistent with many previous molecular dynamics studies of translocation of polar molecules, and provides context within which to compare our results. Finally we note that several experimental and theory/computation groups have shown that the transfer of arginine into model bilayers is non-additive^28,31–33. Though we do not address this explicitly in this work, continuing studies aim to probe this behavior further.

Computational experiments measuring the reversible work (potential of mean force, PMF) for transferring permeants from bulk aqueous environment to bilayer centers enjoy a long history as a means to explore thermodynamics and molecular determinants of translocation processes^{24,27,29,34–36}. In this work, we continue to explore the free energetics of cationic arginine, translocating across a model lipid bilayer. Model DMPC bilayers of two different sizes are considered as proxies for physiological membranes. To simplify the simulations, no salts are added into the systems, and we consider the infinite dilution case of a single arginine translocating across the membrane. We use the Adaptive Biasing Force (ABF) method to calculate PMFs. We compute a PMF barrier of about 13.48 kcal/mol for the translocation of arginine into the center of small membrane (64 DMPC lipids, 32 lipids per leaflet) consistent with previous simulations on similarly sized membranes. However, we find that, to penetrate into a larger membrane (288 DMPC, 144 lipids per leaflet) requires 6.94 kcal/mol for monomer arginine. This estimate is remarkably within a factor of 2 to 3 of the experimental translocon-based measurements, suggesting that the inherent free energetics of translocation predicted by current force field methods may be more accurate than previously considered. Comparing to the large membrane system, about 6.54 kcal/mol of the penetration free energy is overestimated in the small membrane system. To obtain insights and understand the differences observed for the PMFs, we decompose the PMFs into contributions from system components, and track the differences in the two systems. Finally, the membrane deformation, and side chain orientations are compared. These results have implications for system size dependencies in simulations of potentials of mean force of charged molecules across lipid bilayers, and continue to shed light on the molecular-scale details of the translocation process and determinants arising from specific molecular interactions modeled with current state of the art methods.

III. METHODS

A. Force Fields

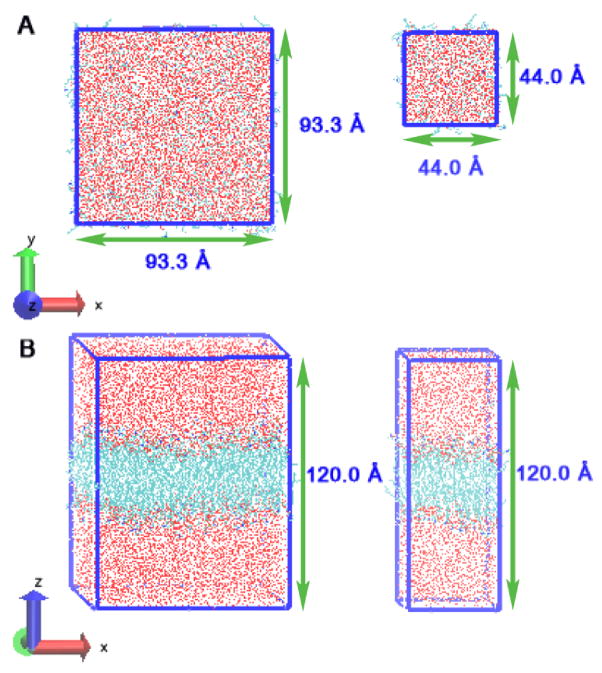
All simulations use the CHARMM force fields (CHARMM22 for proteins including phi, psi cross term map (CMAP) correction, and CHARMM36 for lipids)^37–41, which have been in large measure developed for proteins and lipids. All simulations were performed using the parallel, scalable MD program NAMD 2.9b3⁴². Cationic arginine was patched with standard NH₂ (CT2) group at the C-terminus, and acetyl (ACE) group at the N-terminus. We consider only the protonated methyl guanidinium model compound for our studies. Recent studies^27,36,43 have explored the shift in stability of the protonated and unprotonated species, as manifested in pKa shifts, along the bilayer normal. For thin membranes, it has been suggested that the protonated state is plausible, and sustained by a combination of lipid membrane deformation and long-lived polar (water and lipid) pores across the bilayer stabilizing the charge. Furthermore, Harms et al⁴⁴ demonstrated the stability of the charged form of arginine in the hydrophobic core of staphylococcal nuclease (essentially no pKa shift) across a series of mutants isolating the arginine at several locations (via denaturation by guanidinium chloride monitored via intrinsic tryptophan fluorescence). Acknowledging these studies, we focus here on the free energetics of partitioning of the charged species. One chloride anion was added to neutralize the +1 charge of the single arginine. For the current study, we forgo using excess salt solutions in order to first systematically consider the translocation free energetics in the absence of low-concentration electrolyte which introduces unique issues related to sampling. For instance, as discussed in Huang et al²⁹, cations associated with excess salt have been shown to associate with lipid head groups and carbonyl groups, giving rise to a priori uncontrollable asymmetry leading to net potentials across the bilayer⁴⁵. Furthermore, with lower electrolyte concentrations, there are issues related to equilibration of the salt configurational distribution, though we acknowledge the use of high salt concentrations as has been done in previous molecular dynamics studies^24,27,28. 1,2-Dimyristoyl-sn-Glycero-3-Phosphocholine (DMPC) molecules were employed as the model lipids. We confirmed the surface area per lipid of the pure DMPC bilayer to be 60.5±0.3 Ų in the small membrane system, and 60.3±0.2 Ų in the large membrane system, within the uncertainty of a recently reported value of 〈SA〉 = 60.6 ± 0.5 Ų based on X-ray scattering experiments⁴⁶ above the temperature of the liquid-gel phase transition^47,48 (the main transition temperature of pure DMPC is 297K). Water is modeled using the TIP3P model⁴⁹. Two systems with different membrane dimensions were built for comparison (see Figure 1). The small membrane system was constructed with 64 DMPC molecules (32 lipid molecules per leaflet) and 5474 water molecules, one cationic monoarginine, and one chloride anion; the large membrane system was constructed with 288 DMPC molecules (144 lipid molecules per leaflet) and 24635 water molecules, one cationic monoarginine, and one chloride anion; respectively. A time step of 1 femtosecond was used to integrate the equations of motion. The hydrogen-oxygen and hydrogen-hydrogen distances in water are constrained to the nominal length using the SHAKE algorithm⁵⁰. Average equilibrium x, y, and z dimensions of the simulation box are about 44.0 Å × 44.0 Å × 120.0 Å for 64 lipids system and about 93.5 Å × 93.5 Å × 120.0 Å for 288 lipids system. Periodic boundary conditions (PBC) were applied in all three spatial directions. Particle Mesh Ewald (PME)⁵¹ was implemented to treat conditionally convergent long-range electrostatic interactions(using a grid of 64 × 64 × 128 points for the small membrane system and 128 × 128 × 128 points for the large membrane system). In both systems, the cutoff for van der Waals (VDW) interactions was set to 12 Å with smoothing functions activated at 10 Å and ended at 12 Å. The pairlist distance is set at 14 Å. The temperature was kept constant by appliying the Langevin friction force scheme (1ps⁻¹ was used for the damping coefficient). The pressure of 1 atm was maintained in the direction perpendicular to the water-membrane interface by a combination of the Nosé-Hoover^52,53 constant pressure method with piston fluctuation control implemented using Langevin dynamics. The long-range Coulombic forces were updated every four steps. VMD was used for visualization⁵⁴.

FIG. 1.

System Size of large membrane system (left) and small membrane system (right). (A) top view of the systems (B) front view of the systems

B. Potential of Mean Force Calculations

Potentials of mean force were calculated using NAMD with the Adaptive Biasing Force (ABF)^55,56 (discussed more fully in Section III C) extensions integrated in the Collective Variables module and under the same conditions as described for MD simulations. The Helmholtz free energy profile, A(z), for transferring a peptide across the DMPC-water interface is calculated as a function of an order parameter (“reaction coordinate”) z, defined as the z component of the distance between the center of mass of the peptide and a dummy atom located at the position (x=0.0, y=0.0, z=0.0) close to the center of mass of the DMPC bilayer; we have monitored the drift of the bilayer center of mass from the Cartesian coordinate frame origin, and find that the Root Mean Squared deviation from 0 is about 0.085 Å in the large membrane system, and 0.122 Å in the small membrane system. We note that this choice of reaction coordinate is in great part determined from the implementation limitations of the Collective Variable module in NAMD; specifically, due to parallel performance losses when using large atom groups with which to define collective variables, it is recommended to use small atomic groups⁵⁷.

Free energy methods generally rely on computing the mean force on the reaction coordinate (in this case the peptide center of mass) at positions along the reaction coordinate. The potential of mean force in principle is then obtained by integration of this mean force over the domain of the reaction coordinate. Alternatively, as done in the ABF method, a biasing force opposing the actual force arising from system components is periodically applied to the reaction coordinate to generate what is effectively a random walk along the reaction coordinate (purely diffusive dynamics). Since we need a mean value of a property (force) that depends on a continuous variable (in this case the z-position of the peptide center of mass), we must integrate over the probability density distribution function of the reaction coordinate (〈F_com(z_com) 〉 = ∫P(z_com)F_com(z_com)dz_com). This distribution is represented by the aggregate of configurations generated from the MD simulation. To enhance sampling of the distribution of configurations where the reaction coordinate holds a particular value, the reaction coordinate is restrained within a certain narrow range (instead of its entire span). At the boundaries of the narrow range of interest, relevant restraint potentials are introduced on the reaction coordinate in order to prevent it from moving outside of the desired range. In this work, we construct fourteen overlapping “windows” along the positive z-direction ranging from bulk solution to the bilayer center. Each window is 3.0 Å wide, and 0.5 Å on the upper and lower ends overlap with adjoining windows. The spans of the windows going from bulk solution to bilayer center (in Å) are: [33.5:36.5], [31:34], [28.5:31.5], [26:29], [23.5:26.5], [21:24], [18.5:21.5], [16:19], [13.5:16.5], [11:14], [8.5:11.5], [6:9], [3.5:6.5], [1:4], [−1.5: 1.5]. Forces are accumulated in smaller bins of width 0.02 Å within each window as per the ABF protocol. During the production free energy calculations, the ABF method introduces a biasing force acting on the peptide; the bias force is equal in magnitude and opposite in sign to the actual mean force on the peptide. The mean force is an average over the preceding 500 molecular dynamics steps.

The starting structures for each ABF window, from bulk solution to bilayer center, are constructed as follows. Initially, a single monoarginine was placed and equilibrated in the bulk solvent region of a previously equilibrated DMPC/water simulation cell; the simulation with unrestrained monoarginine in solution is referred to as simulation A. The initial structure for the bulk water window (i.e., [33.5 Å:36.5 Å]) of the ABF sampling coordinate was picked from one snapshot of simulation Å when the center of mass of the single monoarginine was within the range [33.5 Å: 36.5 Å]. We use this configuration to start another 4-nanosecond simulation, B, during which the monoarginine undergoes diffusive motion along the reaction coordinate and is restrained within the relevant window by harmonic potentials at the boundaries of the window; after 4ns of simulation B, we select a snapshot where the position of the monoarginine center-of-mass is close to the lower boundary of the current window to serve as the starting configuration for the contiguous window moving toward the bilayer center. We repeat this process for the remaining windows, transfering arginine into the bilayer center. For each window, we allowed at least 4 ns of equilibration in total before considering the rest of the simulation data as production data (i.e., for purposes of obtaining the mean force in the bins of that window). For each window in both systems, we randomly selected five or six snapshots from the window and started multiple simulations with different initial random seeds for the initial velocity assignment. For the small membrane system, we performed two independent simulations in order to assess the reproducibility of the PMF (see figure S5 in Supplementary Information).

C. Potential of Mean Force

The ABF free energy gradient is estimated from the force (F_ξ0), which is accumulated in small finite bins of width δξ₀^56,58,59. The applied biasing force, which is along the translocation pathway ξ₀, is calculated as^60,61:

$$F^{\mathit{ABF}}={\nabla }_x\stackrel{\sim }{A}({\xi }_0)=-<F_{{\xi }_0}{>}_{{\xi }_0}$$ (1)

Here, ξ₀ is the reaction coordinate, <F_ξ0>_ξ0 is the current average of F_ξ0 along reaction coordinate. As the estimate of the free energy derivative, ∇_xÃ, is refined with more sampling over the course of the simulation, the biasing force F^ABF applied will compensate the system force. As a result, no net force will act along the reaction coordinate ξ₀ over time allowing the whole system dynamics to be diffusive.

The instantaneous force associated with reversible work is given via application of Leibniz’ Rule as^60–62:

$$F_{{\xi }_0}={\left(\frac{\partial V}{\partial q_{\xi }}-\frac{1}{\beta }\frac{\partial ln\mid J\mid }{\partial q_{\xi }}\right)}_{{\{q_{m\ne \xi }\}}^{N-1}}-\frac{1}{\beta }\sum _{m\ne \xi }^{N-1}\left[\delta (q_m-l_{U_m})\frac{{dl}_{U_m}(q_{\xi })}{d{q}_{\xi }}-\delta (q_m-l_{L_m})\frac{{dl}_{L_m}(q_{\xi })}{d{q}_{\xi }}\right]$$ (2)

where V is the potential energy of the system. N is the number of degrees of freedom q_m · q_ξ = ξ₀, and q_ξ is the generalized coordinate. |J| is the Jacobian determinant of coordinates transformation from generalized coordinates to Cartesian coordinates. The upper and lower integration limits for q_m are denoted as l_Um and l_Lm respectively. The differentiation of the free energy profile with respect to ξ₀⁶²:

$$\begin{array}{l}\\ \frac{dA({\xi }_0)}{d{\xi }_0}={\langle {\left(\frac{\partial V}{\partial q_{\xi }}\right)}_{{\{q_{m\ne \xi }\}}^{N-1}}\rangle }_{{\xi }_0}-{\langle \frac{1}{\beta }\frac{1}{\mid J\mid }{\left(\frac{\partial \mid J\mid }{\partial q_{\xi }}\right)}_{{\{q_{m\ne \xi }\}}^{N-1}}\rangle }_{{\xi }_0}\\ -\frac{1}{\beta }{\langle \sum _{m\ne \xi }^{N-1}\left[\delta (q_m-l_{U_m})\frac{{dl}_{U_m}(q_{\xi })}{d{q}_{\xi }}-\delta (q_m-l_{L_m})\frac{{dl}_{L_m}(q_{\xi })}{d{q}_{\xi }}\right]\rangle }_{{\xi }_0}\\ =-{\langle F_{{\xi }_0}\rangle }_{{\xi }_0}\end{array}$$ (3)

where 〈…〉_ξ0 is the ensemble average over all configurations in each bin along the reaction coordinate. The potential of mean force computed from NAMD ABF method, is from the ensemble-average of the first term and the second term in this equation. The Leibnitzian term and the Jacobian terms vanish as we retain the Cartesian representation in a reaction coordinate being the Cartesian z-projection of the distance between the center of mass of the peptide and the position z=0 of the system. The reference position, z=0, is chosen for technical reasons since the performance of NAMD is optimal when collective variable groups are chosen to be of small size. We have monitored the drift of the center of mass of the membrane during the simulations to assess the effects of this technical constraint. We observe slight fluctuations of the bilayer center of mass (both positive and negative) from z=0 of the order of less than 0.5 Å, which we believe sufficiently small.

Contributions to the mean force, and subsequently the potential of mean force, from various components of the system (i.e., water, ions, peptide, etc.) are estimated by first noting that the total reversible work for transfer of peptide from bulk to bilayer center is:

$$\mathrm{\Delta }A=\mathrm{\Delta }{W}_{\mathit{reversible}}=-{\int }_{{\xi }_0=0.0}^{{\xi }_0=36.5}\langle F_z({\xi }_0)\rangle d{\xi }_0$$ (4)

where ξ₀ is the z-component of the center of mass of arginine, 〈F_z(ξ₀)〉 is the average force in the z-direction (normal of the bilayer) experienced by the arginine when it is at position ξ₀. The PMF represents the reversible work associated in changing the relative center of mass distance from a value of 36.5 Å (arginine in bulk solution) to 0.0 Å (arginine in bilayer center). Finally, we consider the total force acting on the arginine as well as the decomposition of the total force into constituent contributions:

$$\begin{array}{c}\mathrm{\Delta }W=-{\int }_{{\xi }_0=0.0}^{{\xi }_0=36.5}\langle F_{z,\text{Ion}-\text{Arg}}({\xi }_0)\rangle d{\xi }_0-{\int }_{{\xi }_0=0.0}^{{\xi }_0=36.5}\langle F_{z,\text{Water}-\text{Arg}}({\xi }_0)\rangle d{\xi }_0\\ -{\int }_{{\xi }_0=0.0}^{{\xi }_0=36.5}\langle F_{z,\text{Lipid}-\text{Arg}}({\xi }_0)\rangle d{\xi }_0-{\int }_{{\xi }_0=0.0}^{{\xi }_0=36.5}\langle F_{z,\text{Arg}-\text{Arg}}({\xi }_0)\rangle d{\xi }_0\end{array}$$ (5)

Uncertainty estimates for the ABF PMF are determined using Equation 22 of Henin and Chipot⁵⁵, which is proposed by Rodriguez-Gomez et al.^55,59; variances are obtained with the blocking method of Flyvbjerg et al⁶³. The pmf was considered converged once the pmf difference between center of the bilayers and the bulk water reached a stable value. The assessments of the convergence of the PMF for both systems over 100ns simulation time are shown in Figure S1 of Supplementary Information.

IV. RESULTS AND DISCUSSION

A. Total PMF

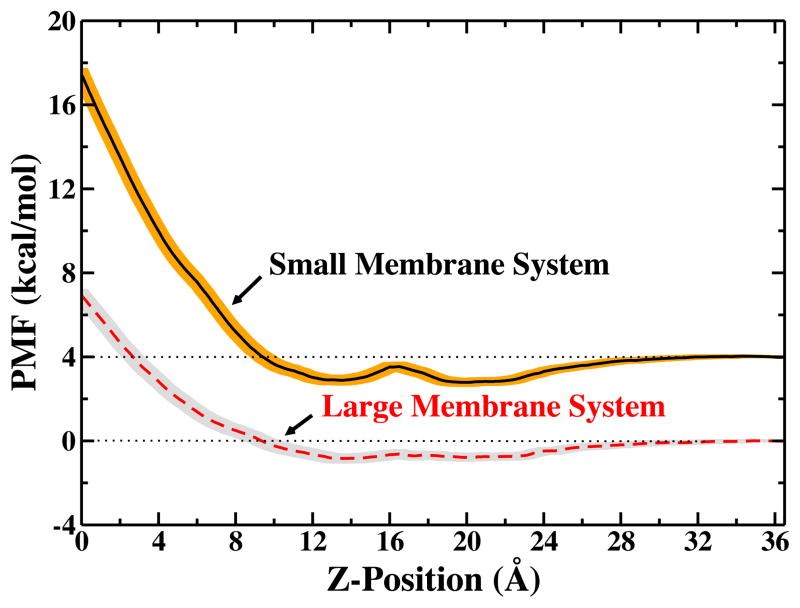
The total PMFs with uncertainties of arginine traversing the lipid bilayers in both systems are shown in Figure 2 (solid curve: small membrane system, dash curve: large membrane system), on the right side is the bulk water region, and on the left side is the center of membrane; the solid curve is shifted by 4.0 kcal/mol for clarity. The production simulation time (excluding equilibration) of each window is shown in Supplementary Information Table S1. The aggregate simulation time (all windows) of each system is more than 1.5 microseconds. The least sampling in each bin is greater than 50,000 sample points, and the fluctuation of the arginine position is sufficient both at the bulk water region and the center of membrane region, shown in Figure S2, S3 of Supplementary Information. The force collected in each bin is Gaussian distributed, see Figure S4 of Supplementary Information.

FIG. 2.

Potential of mean forces of arginine from bulk water into DMPC lipid bilayer. solid curve: small membrane system; dashed curve: large membrane system. The solid curve is shifted by 4.0 kcal/mol for clarity. Shading indicates the uncertainty.

The free energy cost of the arginine translocation in the small membrane system (64 DMPC) is about 13.48 kcal/mol. This result is close to the free energy of cationic arginine translocating into 72 DPPC-lipid bilayer surrounded with electrolyte reported by Allen et al²⁷ (about 17.8 kcal/mol), and also close to the value for translocation of single arginine into a 64 DOPC-lipid bilayer system (with bulk electrolyte) reported by Tieleman et al²⁸ (about 14.46 kcal/mol). Moreover, the present results are in accord with PMF estimates of arginine in polyleucine transmembrane helices predicting bulk to bilayer center PMF differences on the order of 22 kcal/mol⁶. Recently Ou et al⁶⁴ found that the free energy of translocation of methyl guanidinium across 72 DPPC bilayer (no bulk electrolyte) system is equivalent to that for a 1 M potassium chloride salt system; the aggregate influence of bulk electrolyte on the PMF appears to be quite small. Thus, acknowledging the differences in force fields, our PMF in the small membrane system is consistent with numerous previous simulation results. Finally, for the small membrane system, we computed the PMF using two independent starting points and have demonstrated the reproducibility of the PMF difference between bulk solution and bilayer center for the small membrane system (see Supplementary Information, Figure S5).

For the 288 DMPC-lipid bilayer, the bulk solution to bilayer center PMF difference is 6.94 kcal/mol. The PMF difference between small and large systems is 6.54 kcal/mol, suggesting that about 94 % of the free energy in the small membrane system may be overestimated. Interestingly, the free energy barrier in the 288 DMPC-lipid bilayer system is closer to the value of 2.5 kcal/mol reported by Hessa et al²⁵.

The PMFs show a minimum of −1.14 kcal/mol for small membrane system and −0.84 kcal/mol for the large membrane system at position 13.50 Å and 13.88 Å, respectively, in the region of lipid headgroups (see density profiles in Figure S6 of Supplementary Information). The free energy from these minima to the center of the bilayer is 14.62 kcal/mol in the small system, and 7.78 kcal/mol in the large system. In the 64 lipid bilayer, one more minimum of −1.24 kcal/mol is observed at the interface of the membrane, ca. 20 Å. In light of the uncertainty estimates at these positions, we suggest that in actuality, there is a broad basin in the region from 12 to 28.0 Å that supports the charged cation.

B. PMF decomposition

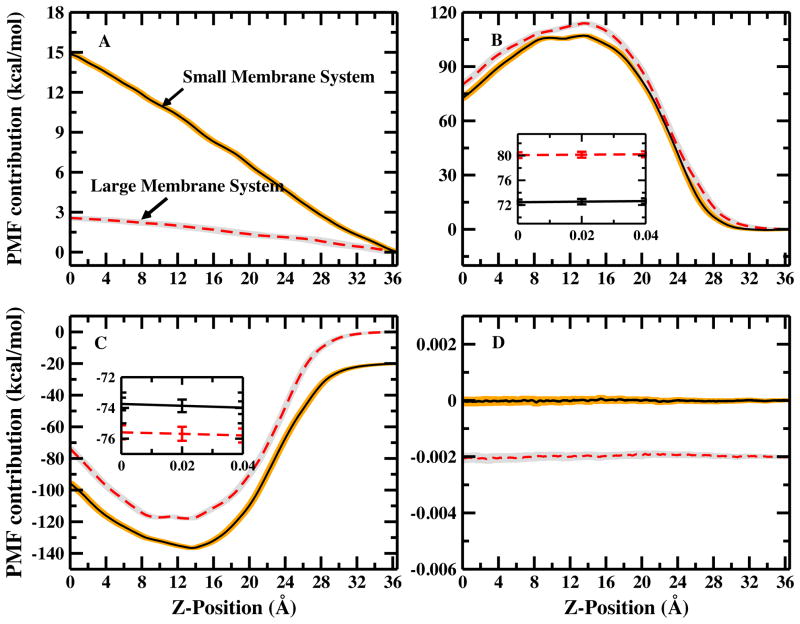
To explore possible origins of the PMF differences between the two membrane systems, we decompose the PMF into constituent contributions via equation 5. Figure 3 shows the contributions from the single chloride counterion, all water, and the peptide. The solid curve in Figure 3C is shifted by −20.0 kcal/mol, and the dash curve in figure 3D is shifted by −0.002 kcal/mol for clarity. Figure 3A demonstrates the greater destabilizing contribution of chloride in the small membrane system (14.88 kcal/mol) that is about five times larger than in the large membrane system (2.6 kcal/mol). Possible origins of this difference are discussed in Section IV C. Figure 3B shows the water contribution to the PMFs. The water contribution in the larger bilayer system is more destabilizing relative to that in the small bilayer system by about 7.6 kcal/mol. However, the water destabilization in the large system is not commensurate to the stability gained by the reduction in the chloride anion contribution. This leaves a large part of the residual difference in PMFs from the chloride anion. Figure 3C shows the contributions from the lipid bilayers. The inset shows that the total membrane contribution is about 1.85 kcal/mol more favorable for the large membrane system. Finally, Figure 3D shows the peptide self-contribution is negligibly small for both systems. The PMF decomposition data are summarized in Table I. We discuss in further detail the chloride anion and water contributions in the next Sections.

FIG. 3.

Decomposition of the PMF. Solid curves represent small membrane system, dashed curves represent large membrane system. (A) Ion contribution; (B) Water contribution from large and small membrane systems; (C) Membrane contribution and the solid curve is shifted by −20.0 kcal/mol; no shift in the inset figure; (D) arginine self-contribution, and the solid curve is shifted by −0.002 kcal/mol for clarity. Shades indicates the uncertainty.

Table I.

Potential of mean forces of the small and large membrane and the contributions from different components

Free Energy (kcal/mol)	ΔGtotal	ΔGion–arg	ΔGwater–arg	ΔGlipid–arg	ΔGarg–arg
Small Membrane System (64 lipids)	13.48(0.29)	14.88(0.05)	72.46(0.44)	−73.74(0.46)	0.00012(0.0001)
Large Membrane System (288 lipids)	6.94(0.28)	2.57(0.02)	80.08(0.48)	−75.59(0.41)	0.00011(0.0001)
ΔΔG	6.54	12.31	−7.62	1.85	0.00001

C. Chloride ion contribution

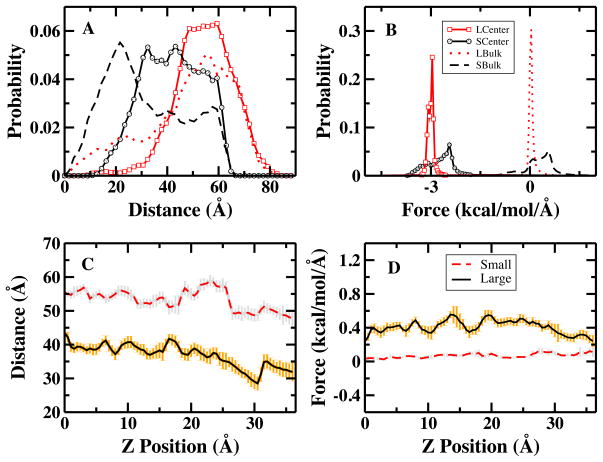
Attractive electrostatic interactions between chloride anion and arginine’s guanidinium group disfavor the peptide translocating into the lipid bilayer. Although we include only one chloride anion (for total system charge neutrality) in each system, we see unfavorable contributions to the PMF up to 15 kcal/mol. The relatively large destabilizing single anion contribution in the small system is consistent with the 12.5 kcal/mole contribution obtained for chloride anion contribution to methyl guanidinium translocation into a 72-lipid DPPC bilayer (surrounded by pure water with single chloride anion) using polarizable charge equilibration force fields⁶⁴. Considering the slightly larger size of lipid and different type of model lipid, the ion contribution we obtain for the small system is consistent with the the result of that in the methyl guanidinium system. Use of a larger 288-lipid DMPC bilayer (and thus lower effective Cl⁻ concentration when accounting for the additional water added to the system) results in a significantly lower ion contribution of 2.57 kcal/mol. Since the component contributions are determined in our analysis from forces, we consider how changing the system size might affect forces from the anion acting on the peptide. Since the force is distance-dependent, it is plausible to consider that a characteristic distance between ion and guanidinium group changes with different overall system sizes. Figure 4A is the distribution of peptide-anion distances computed using data from the 100 ns simulation for windows where the peptide is at the center of bilayer and in the bulk water region. The curves with LCenter and LBulk (SCenter and SBulk) symbols represent the large (small) membrane system. When arginine resides at bilayer center, the anion cannot approach the guanidinium group to within as close a distance as when the arginine is in bulk water. Thus, though in both large and small bilayer systems we observe significant probability of peptide-anion distance being a large value (greater than 40 Å) when the peptide resides in the extreme windows, universally we see enhancement of probability of smaller separations when the peptides is in bulk water, as one would expect. Since the large membrane system size is about 4.5 times the small one there is more accessible volume for chloride anion. The larger system is overall entropically stabilized by the higher number of configurational states available. Figure 4C shows that the average ion-peptide distance is roughly 15 Å larger in the large membrane system. The larger average separation weakens the average electrostatic interaction, thus increasing the probabilities of smaller electrostatic forces from peptide-ion interactions contributing to the PMF in the large membrane system, see Figure 4B. Finally, the average forces from ion at peptide positions along along the reaction coordinates in the large membrane system is much smaller than the force in the small membrane system, see Figure 4D.

FIG. 4.

LCenter (SCenter): the center of bilayer windows [−1.5: 1.5] Å in the large (small) membrane system; LBulk (SBulk): the bulk water windows [33.5: 36.5] Å in the large (small) membrane system. (A) the distribution of the distance between chloride and guanidinium carbon; (B) the distribution of the force acting on arginines from ion in both systems, the solid lines show the center of bilayer windows, shifted by −3 kcal/mol/Å for clarification, and dash and dotted lines show the bulk water windows; In figures C and D, dash line: small membrane system; solid line: large membrane system. (C)the average distance between ion and guanidinium carbon; (D) the average force along the reaction coordinate.

D. Water contribution

In a molecular simulation, water in aggregate stabilizes the arginine when it resides at bilayer center, the dominant stabilizing forces arising from what have been termed “core” water molecules as reported previously^24,65,66. This stability comes from local, solvation water. In Supplementary Information, Figure S7, we show the core water contributions from the present simulations using large and small systems. The “core” water is taken to be water within ±13 Å of the bilayer center as in previous studies ²⁷. In both large and small systems, we observe similar contributions to the total PMF from “core” water (which incidentally counteracts the strongly destabilizing contribution from the lipids), indicating possible underlying similarities in the local hydration structure and water environment in the central bilayer region. We thus quantify the local hydration around the arginine by computing hydration water numbers (the average number of water oxygen within 4.85 Å of arginine heavy atoms) around arginine side chains (Figure S8 of Supplementary Information). About 8 water molecules are found coordinate to the arginine at the center of the bilayer, and 48 water in the first solvation shell in bulk water leading to a loss of about 6 ~ 7 water-arginine hydrogen bonds, see Figures S8 and S9 of Supplementary Information (H-bond geometric criteria⁶⁷: Donor-acceptor distance is less or equal to 3.6 Å, hydrogen-acceptor distance is less or equal to 2.6 Å, and donor-hydrogen-acceptor angle is between 90 and 180 degree). The dehydration free energy penalty²⁷, however, is partly compensated by the new hydrogen bonds formed between deformed membrane lipids and arginine. The net change in hydrogen bond number between the arginine and other polar components going from bulk water to bilayer center is thus about four.

The overall water free energy contributions are shown in Figure 3B. In the small membrane system, the water destabilizes the cation in the bilayer center by about 72.46 kcal/mol relative to when it is located in the bulk, and in the large membrane system the destabilization is greater and reaches about 80.08 kcal/mol. The free energy of the water contributions at the bulk water regions from 36.5 Å to 20.0 Å are almost the same, the biggest differences appearing when the cation is at the bilayer center. Since the large membrane system contains 24635 water molecules, while there are 5474 water molecules in the small membrane system, we attempt to consider qualitatively whether simply having more water molecules in the system introduces, asymmetrically, more destabilizing water; that is, water molecules that effectively exert a force on the cation towards the bulk water region. Water molecules on the side closer to the cation (in our case in the region of the simulation cell with z > 0.0) will asymmetrically exert a larger destabilizing force on the cation.

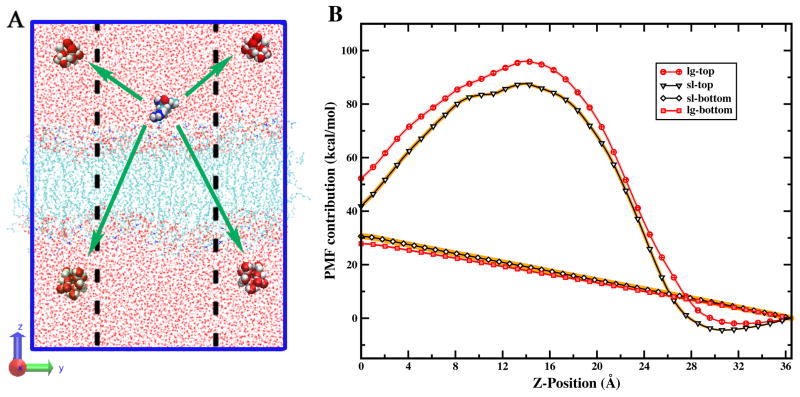
To probe the issue of asymmetry of the water (as a primary requirement for the observed effect of water on the side of the arginine), we compute the PMF contribution from the water located in the bottom and top layers of the bilayer. In Figure 5B, we show the results of this analysis. The results show that the forces from water on the side closer to the arginine are the more dominant contribution to the PMF. The water in the top layer of the large membrane contribute about 52.2 kcal/mol, which is about 10 kcal/mol more than that in the small membrane (41.8 kcal/mol). The difference coming from the bottom layer water is about 2 kcal/mol. In the large membrane system, water in the region closer to the cation exerts an asymmetrically higher destabilizing force, leading to a more positive PMF contribution relative to that in the small membrane system. Interestingly, there is a differential stabilization from forces from water approaching the bilayer-water interface; in the region of 26 to 32 Å the PMF contribution from water in the small system exhibits a deeper, broader well compared to the large system. To summarize, the extra water present in the larger membrane system asymmetrically leads to more destabilization of the arginine until it penetrates sufficiently deep into the bilayer such that the major contribution to the PMF comes from “core” water.

FIG. 5.

(A) Schematic of the relative distances between arginine and the water molecules in top and bottom regions of the simulation cell. The dashed lines represent the lateral dimension of the smaller system for comparison. (B) Decomposition of water contribution. lg-top: the top layer water (oxygen of water greater than zero) in large membrane; lg-bottom: the bottom layer water (oxygen of water smaller than zero) in large membrane; sl-top: the top layer water in small membrane; sl-bottom: the bottom layer water in small membrane. The x-axis is the position of the center of mass of the peptide and the y-axis is the PMF arising from water acting on the peptide.

E. Decomposition of Membrane contribution

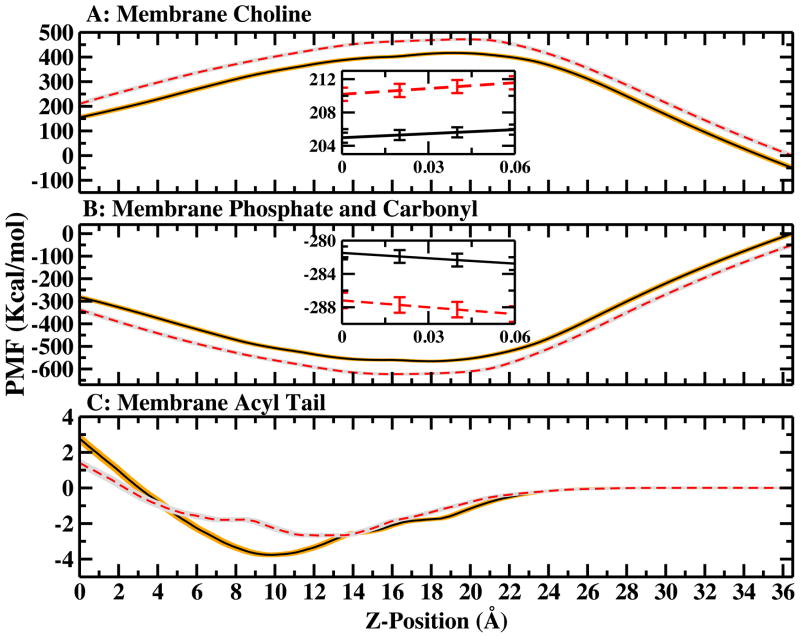
The membrane contribution is decomposed into three parts: contributions from choline, phosphate and carbonyl (combined), and the acyl tail groups. The free energetic contributions of each group are show in Figure 6. The solid curve in figure 6A and the solid curve 6B are shifted by 50.0 kcal/mol and −50.0 kcal/mol, respectively, for clarity. No shift was made for the inset figures. In both systems, all the choline groups(from all lipids in aggregate) destabilize the arginine at membrane center by roughly 205 kcal/mol, while the negatively-charged phosphate and polar carbonyl groups overall stabilize the peptide by about −280 kcal/mol. The acyl tail contribution is less than 5 kcal/mol. As one would expect, the choline groups initially force the cation away from the interface (in conjunction with the positive membrane dipole potential) and then work to favor the bilayer center state for the arginine; this effect is rationalized by the strong coulomb repulsion between the positively-charged groups. In contrast, the effect of the negatively-charged phosphate/carbonyl groups is opposite. In the large membrane, the choline contribution is more destabilizing by roughly 5.21 kcal/mol, while the phosphate/carbonyl group contribution decreases by about 5.70 kcal/mol. Overall, the contribution from these two groups (headgroups), is 0.49 kcal/mol stabilizing for the bilayer center state. Figure 6C shows that the acyl tail contribution in the large membrane is lower by 1.36 kcal/mol. The contribution in both large and small systems is almost the same in the bulk water region. As arginine moves into the headgroups region, the small membrane system shows a slightly favorable contribution. However, after it moves out of the headgroup region (10 to 20 Å), the contribution increases sharply in the small membrane system. We suggest that these differences are mainly due to differences in local membrane deformation, on the scale of individual lipid molecules as opposed to large scale (nanometer-scale) undulations. We consider the deformation of the bilayers Section IV F.

FIG. 6.

Decompositon of Membrane free energy contributions. Solid curves represent small membrane system, dash curves represent large membrane system. The dash curve in figure 6A and the dash curve 6B are shifted by 50.0 kcal/mol and −50.0 kcal/mol, respectively, for clarity. No shift was made for the inset figures. (A) membrane choline group contribution; it is defined as (CH₃)₃NCH₂CH₂− (B) membrane phosphate and carbonyl group contribution; it is defined as PO₄CH₂CH(OCOCH₂−)₂ (C) membrane acyl tails contribution; it is defined as CH₃(CH₂)₁₂−.

F. Further Implications: Membrane Deformation

Because bilayers harboring embedded proteins (of widely varying dimensions) must structurally adapt to accommodate these macromolecules, perturbations of the membrane are inevitable. In the context of discussing deformations at the atomic/molecular level via atomistic molecular simulations and the relation of the properties of these perturbations to the dimensions of the systems employed to represent model bilayers, it is reasonable to think that system size may influence the nature of membrane structural perturbations. Effectively, the system dimension imposes a severe constraint on the relaxation of the membrane. We next consider the implications of system size on structural perturbations of the bilayer in this relatively simple system. Perturbations of the bilayer leaflet structure in the local region around the translocating species has been widely reported as in Li et al²⁷, Vorobyov et al³⁴, MacCallum et al²⁸. The deformation helps to spatially modulate the interface between low and high electrostatic potential regions, thus stabilizing the charged translocating species in a favorable electrostatic environment³⁴. The nonadditivity of multiple arginine translocation as a result of membrane deformation and water pore/defect formation has also been demonstrated by MacCallum et al.²⁸ Our results exhibiting membrane structure perturbation support numerous earlier studies pointing to the importance of water defects on a local scale in facilitating structural and dynamic aspects of membrane biophysics.^66,68,69

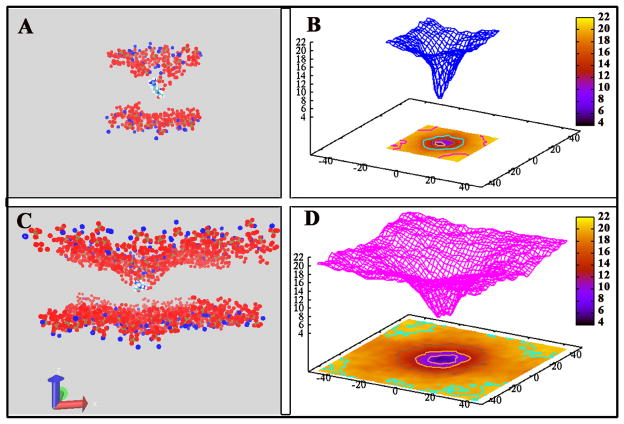
To visualize membrane deformation, the average z positions of nitrogen, phosphate and carbonyl of membrane are calculated over all snapshots. The lateral coordinates of all the atoms in the system are shifted relative to the center of mass of the arginine first, and then the z coordinates of the relevant atoms are averaged in bins spaced at a resolution of 2Å × 2Å in the x-y plane. Membrane deformations were observed in both large and small membrane systems, shown in Figure 7. The shape of the phosphate surface is shown in Figure 7B and 7D when the arginine is located at the membrane center, and nitrogen, carbonyls deformations as well as the bulk water window are shown in Supplementary Information, Figures S10, S11 and S12. In both systems, the deformations give similar funnel shape of the membranes. However, the nature of this deformation is strikingly variable depending on the system size. The small membrane accommodates a smaller number of lipids associating with the cation, in a rather narrow, elongated region around the translocating cation. The elongated nature of this deformation (described by the phosphate positions) suggests a constraint on the orientation of the cation, which we will briefly discuss in the next section. For the large membrane system, the deformation is broader, with the cation being accommodated by a larger number of lipids that associate with it to a greater depth within the bilayer. The broader deformation, supported by the less severe size constraint imposed through a larger box, suggests that the orientation of the cation is different than in the small membrane system. A further interesting difference between the deformations in the large and small membrane systems concerns the bottom (distal) leaflet’s perturbation as the arginine resides in the bilayer center. Figures S14, S15, and S16 in Supporting Information show density profiles of nitrogen atoms, phosphate atoms, and carbonyl oxygen atoms, respectively, when the arginine is at bilayer center. In the small membrane case, we observe that the lower leaflet is perturbed to some degree, with a visible atom density near the arginine as the lipids of the lower leaflet are pulled towards the arginine. We see no such signal in the density profiles for the larger membrane system. An implication of this size dependence is that formation of pores bridging the two leaflets with a water/headgroup environment appear to be more facile to access in small systems rather than in larger systems. This has bearing on interpretations of mechanism in solute translocation through bilayers, and this suggests avenues for further study.

FIG. 7.

Deformation of membrane. (A) and (C): snapshots of window [−1.5: 1.5] Å, the center of membrane region. Nitrogen, Oxygen and Phosphate are shown in blue, red and brown spheres. (B) and (D): the average z coordinate position of phosphate atoms over the total time scale. The lateral coordinates of all the atoms in the system are shifted relative to the center of mass of the arginine first, and then the z coordinates of the interested atoms are averaged in bins spaced at a resolution of 2Å × 2Å in xy plane.

The deformation contribution might be estimated by using membrane elasticity theory²⁶, though it is not pursued in this manuscript. However, we note that the nature of our observed deformation is similar to that described by Choe et al²⁶ as well as the deformations observed in numerous earlier studies. Using elasticity theory (Helfrich functional for a deformable sheet), the authors compute the shape of a deformed membrane-water interface adjacent to an inserted peptide. This shape turns out remarkably to be similar to the funnel-shape deformations we observe as well (Figure 4 in Choe et al²⁶). The authors estimate a deformation free energy up to 5 kcal/mol. Though we do not make any connections to this number in the present work, ongoing work will explore the differences in the deformation free energy based on system size.

G. Further Implications: Side Chain Orientation

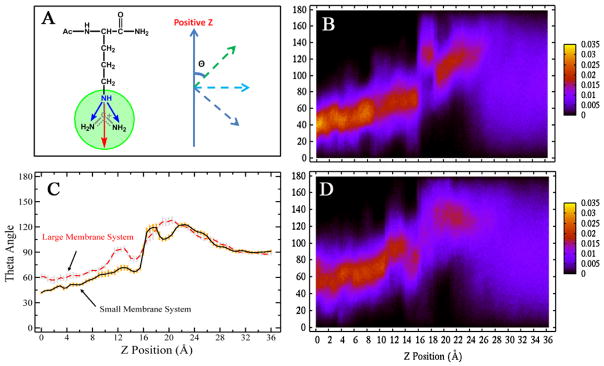
Due to the strong interaction between the guanidinium group of arginine and membrane, it’s found that the side chains are oriented toward the membrane headgroup region. The angle between the membrane normal and the side chain nitrogen bisector changes as the arginine translocates into the center of the membrane, shown in Figure 8. When arginine is located at the bulk water region, the distance between arginine and membrane is too far to affect the orientation of the side chain, so the angles are randomly distributed. As a result, the average angles at bulk water are about 90 degree in Figure 8C. The second Legendre polynomial order parameter P₂ =< 1/2(3cos²θ − 1) > at the bulk water region is 0, shown in Supplementary Information Figure S17, confirming the random orientation of side chain. As arginine approaches the membrane-water interface, the interaction of the side chain with polar/charged headgroup moieties orients the side chain relative to the membrane, and the theta (θ) angle is larger than 90 degrees; when arginine translocates past the headgroup region and moves into the center of membrane, the drive to maintain these favorable interactions reverses the orientation, directing the charged components of the sidechain towards the positive z direction, and this angle is smaller than 90 degrees.

FIG. 8.

Arginine side chain orientation. (A) the model of the theta (θ) angle between the positive z and bisector of the two NH-NH₂ vectors; (C) the average theta (θ) angle (degree) along the reaction coordinate; (B) and (D): two dimensional angle distribution along reaction coordinate–B is the small membrane system and D is large membrane system.

In Figure 8C, we observe that when the arginine is at the center of the bilayer, the sidechain is more oriented along the membrane plane in the large system than in the small system. This correlates with the observed lipid deformations discussed in the previous section. Since the larger membrane size accommodates greater perturbations of a larger number of lipids, the arginine cation is able to achieve a more planar orientation, thus maximizing favorable, predominantly electrostatic interactions with charged/polar components of the lipid.

V. SUMMARY AND CONCLUSIONS

In this work, we investigated the thermodynamics of arginine translocation through model DMPC bilayers of different lateral dimensions using the ABF method. We obtained the potential of mean force for the reversible transfer of arginine through the bilayer. We further decomposed the overall PMFs into contributions from various system components including ion, water, arginine, lipid choline group, phosphate and carbonyl group, and acyl tails. We explored the effects of the membrane size to the total PMFs.

With respect to the overall free energetics of arginine translocation through membrane, the free energy cost of our small membrane system is about 13.48 kcal/mol, and it is qualitatively in agreement with a range of previous similar membrane size simulation studies. We find a remarkably less destabilizing free energy in the large membrane system. Only 6.94 kcal/mol of reversible work are required to translocate the arginine into the center of the bilayer. This is surprisingly close to the experimental trans-locon based result of ca. 2.5 kcal/mol. By decomposing the overall free energy profile into contributions from various components, we find that the ion destabilizing contribution is notably reduced by about 12.31 kcal/mol in the large membrane. The larger accessible volume allows the ion to sample further distances from the arginine, and reduce the probability of strong electrostatic interactions between ion and arginine. This is an entropically stabilizing effect. The overall water contribution primarily destabilizes arginine. The additional amount of water due to solvating the larger membrane size makes the water contribution more unfavorable in the large membrane system. Lipid in total confers a stabilizing contribution. The large membrane system allows a slight amount of more favorable contribution, about 1.85 kcal/mol. By decomposing the membrane into three parts, the free energy change from lipid choline group almost offset the change from the phosphate and carbonyl group. The destabilizing acyl tails contribution in the large membrane system is reduced.

An implication of the constraints imposed by system dimensions is the impact on sustainable structural perturbations of the bilayer, at least locally around the permeant. We find that the nature of the deformations of arginine-associated lipids is ostensibly quite different between the large and small systems. We observe that the membrane deformation in the large system broader and slightly deeper than in the small system. Consistent with the variations in structural perturbations, we observe that the orientations of the arginine sidechain in the large and small systems are accordingly different, the orientations in the two cases being accommodated by the deformations allowed under the constraint of the system size. In the small system, the sidechain is oriented more along the bilayer normal, matching the narrow, elongated shape of the membrane deformation; in contrast, the arginine side chain is oriented more in the plane of the bilayer in the larger system, as evidenced by the broader deformation. In the latter case, the additional lipids associated with the permeant in the bilayer center contribute stabilizing electrostatic forces.

In summary, we observe non-trivial system size effects (coupled to the presence of counterions) on estimated thermodynamics of charged species translocating through model lipid bilayers via computer simulations. On going work seeks to extract the convergent behavior of the PMF difference and analytic approximations that may prove useful in using results of small system sizes to extrapolate to larger systems.