Positive Semidefinite Rank-based Correlation Matrix Estimation with Application to Semiparametric Graph Estimation

Abstract

Many statistical methods gain robustness and flexibility by sacrificing convenient computational structures. In this paper, we illustrate this fundamental tradeoff by studying a semi-parametric graph estimation problem in high dimensions. We explain how novel computational techniques help to solve this type of problem. In particular, we propose a nonparanormal neighborhood pursuit algorithm to estimate high dimensional semiparametric graphical models with theoretical guarantees. Moreover, we provide an alternative view to analyze the tradeoff between computational efficiency and statistical error under a smoothing optimization framework. Though this paper focuses on the problem of graph estimation, the proposed methodology is widely applicable to other problems with similar structures. We also report thorough experimental results on text, stock, and genomic datasets.

1 Introduction

Undirected graphical models provide a powerful framework for exploring relationships between a large number of variables (Lauritzen, 1996; Wille et al., 2004; Honorio et al., 2009). More specifically, we can represent a d-dimensional random vector X = (X₁, …, X_d)^T by an undirected graph 𝒢 = (V,E), where V contains nodes corresponding to the d variables in X, and the edge set E describes the conditional independence relationships between X₁, …, X_d. Let X_\{j,k} = {X_ℓ : ℓ ≠ j,k}, the distribution of X is Markov to 𝒢 if X_j is independent of X_k given X_\{j,k} for all (j,k) ∉ E. In this paper, we aim to estimate the graph 𝒢 based on n data points of X.

A popular distributional assumption for estimating high dimensional undirected graph is multivariate Gaussian, i.e., X ~ N(μ, Σ). Under this assumption, the graph estimation problem can be solved by examining the sparsity pattern of the precision matrix Ω = Σ⁻¹ (Dempster, 1972). There are two major approaches for estimating high dimensional Gaussian graphical models: (i) graphical lasso (Banerjee et al., 2008; Yuan and Lin, 2007; Friedman et al., 2007), which maximizes the ℓ₁-penalized Gaussian likelihood and simultaneously estimates the precision matrix Ω and the graph 𝒢, (ii) neighborhood pursuit (Meinshausen and Bühlmann, 2006), which maximizes the ℓ₁-penalized pseudo-likelihood and only estimates the graph structure 𝒢. Scalable software packages such as glasso and huge have been developed to implement these algorithms (Zhao et al., 2012a; Friedman et al., 2007). Both methods are consistent in graph recovery under suitable conditions (Meinshausen and Bühlmann, 2006; Ravikumar et al., 2011). However, these two methods have been observed to behave differently in practical applications. In many applications, the neighborhood pursuit method is preferred due to its computational simplicity. Many other Gaussian graph estimation methods have also been proposed and most of them fall in these two categories (Li and Gui, 2006; Lam and Fan, 2009; Peng et al., 2009; Shojaie and Michailidis, 2010; Yuan, 2010; Cai et al., 2011; Yin and Li, 2011; Jalali et al., 2012; Sun and Li, 2012; Sun and Zhang, 2012).

The Gaussian graphical model crucially relies on the normality assumption, which is restrictive in real applications. To relax this assumption, Liu et al. (2009) propose the semiparametric nonparanormal model. They assume that there exists a set of nondecreasing transformations $\mathit{f}={\{f_j\}}_{j=1}^d$, which make the transformed random vector f(X) = (f₁(X₁), …, f_d(X_d))^T follow a Gaussian distribution, i.e., f(X) ~ N(0, Ω⁻¹). Liu et al. (2009) show that, under the nonparanormal model, the graph 𝒢 is still encoded by the sparsity pattern of Ω. To estimate Ω, Liu et al. (2012) propose a rank-based estimator named nonparanormal skeptic, which first calculates a transformed Kendall’s tau correlation matrix, and then plugs the estimated correlation matrix into the graphical lasso. Such a procedure has been proven to attain the same parametric rates of convergence as the graphical lasso (Liu et al., 2012). However, the transformed Kendall’s tau correlation matrix has no positive semidefiniteness guarantee, and directly plugging it into the neighborhood pursuit may lead to a nonconvex formulation. Therefore applying the transformed Kendall’s tau matrix to the neighborhood pursuit approach is challenging to both computational and theoretical analyses.

In this paper, we propose a novel projection algorithm to handle this challenge. More specifically, we project the possibly indefinite transformed Kendall’s tau matrix into the cone of all positive semidefinite matrices with respect to a smoothed elementwise ℓ_∞ norm, which is induced by the smoothing approach (Nesterov, 2005). We provide both computational and theoretical analyses of the obtained procedure. Computationally, the smoothed elementwise ℓ_∞ norm has nice computational properties that allow us to develop an accelerated proximal gradient algorithm with a convergence rate of O(ε^−1/2), where ε is the desired accuracy of the objective value (Nesterov, 1988). Theoretically, we prove that the proposed projection method preserves the concentration property of the transformed Kendall’s tau matrix in high dimensions. This important result enables us to prove graph estimation consistency of the neighborhood pursuit method for nonparanormal graph estimation (Meinshausen and Bühlmann, 2006).

Besides these new computational and theoretical analyses, we also provide an alternative view to analyze the tradeoff between computational efficiency and statistical error under the smoothing optimization framework. In existing literature (Nesterov, 2005; Chen et al., 2012), the smoothing approach is usually considered as a tradeoff between computational efficiency and approximation error. Thus the smoothness has to be controlled to avoid a large approximation error, which results in a slower convergence rate O(ε⁻¹). In this paper, we analyze this tradeoff by directly considering the statistical error. We show that the smoothing approach simultaneously preserves the good statistical properties and enjoys the computational efficiency. Some preliminary results in this paper first appeared in Zhao et al. (2012b) without the technical proofs. Here we provide detailed proofs, more experimental results (including both simulated and real datasets), and a comprehensive comparison between the projection method and other competitors.

Although this paper targets the semiparametric graph estimation problem, the proposed methodology is widely applicable to other statistical methods for nonparanormal models, such as copula discriminant analysis and the semiparametric sparse inverse column operator (Han et al., 2013; Zhao and Liu, 2013). Taking the result in this paper as an initial start, we expect more sophisticated and stronger follow-up work that applies to problems with similar structure.

The rest of this paper is organized as follows: In §2 we briey review the transformed Kendall’s tau estimator; In §3, we describe the projection algorithm and nonparanormal neighborhood pursuit algorithm; In §4, we analyze the statistical properties of the proposed procedures; In §5 and §6, we present experimental results on both simulated and real datasets; In §7, we discuss other related correlation estimators and draw conclusions.

2 Background

We start with some notations. Given a vector υ = (υ₁, …, υ_d)^T ∈ ℝ^d, we define vector norms

$${\Vert \mathit{\upsilon }\Vert }_1=\sum _j|{\upsilon }_j|,{\Vert \mathit{\upsilon }\Vert }_2^2=\sum _j{\upsilon }_j^2,{\Vert \mathit{\upsilon }\Vert }_{\infty }=\underset{j}{\text{max}}|{\upsilon }_i|.$$

Given two symmetric matrices A = [A_jk] ∈ ℝ^d×d and B = [B_jk] ∈ ℝ^d×d, we de note Λ_min(A) and Λ_max(A) as the smallest and largest eigenvalues of A respectively; We also denote 〈A, B〉 = tr(A^TB) as the inner product of A and B. We define matrix norms as

$${\Vert |\mathbf{A}|\Vert }_1=\sum _{j,k}|{\mathbf{A}}_{jk}|,{\Vert |\mathbf{A}|\Vert }_{\infty }=\underset{j,k}{\text{max}}|{\mathbf{A}}_{jk}|,{\Vert \mathbf{A}\Vert }_{\mathrm{F}}^2=\sum _{j,k}{|{\mathbf{A}}_{jk}|}^2,\text{and}{\Vert \mathbf{A}\Vert }_{\infty }=\underset{j}{\text{max}}\sum _k|{\mathbf{A}}_{jk}|.$$

We denote υ_\j = (υ₁,…, υ_j−1, υ_j+1, …, υ_d)^T ∈ ℝ^d−1 as the subvector of υ with the j^th entry removed. We denote A_\i,\j as the submatrix of A with the i^th row and the j^th column removed. We denote A_i,\j as the i^th row of A with its j^th entry removed. If I and J are two sets of indices, then A_{I J} denotes the submatrix of A whose rows and columns are indexed by I and J.

2.1 Nonparanormal skeptic

The nonparanormal distribution extends the Gaussian distribution by separately modeling the conditional independence structure and marginal distributions. It assumes that there exists a set of transformations such that the transformed random vector follows a Gaussian distribution.

Definition 2.1. Let f = {f₁, …, f_d} be a collection of nondecreasing univariate functions and Σ* ∈ ℝ^d×d be a correlation matrix with diag(Σ*) = 1. We say that a d-dimensional random vector X = (X₁, …, X_d)^T follows a nonparanormal distribution, denoted by

$$\mathit{X}~NPN(\mathit{f},{\mathbf{\Sigma }}^{*}),$$

if f(X) = (f₁(X₁), …, f_d(X_d))^T ~ N (0, Σ*).

For continuous distributions, Liu et al. (2009) prove that the nonparanormal family is equivalent to the Gaussian copula family (Klaassen and Wellner, 1997; Tsukahara, 2005). Moreover, the nonparanormal models have the same nice property as Gaussian models that the conditional independence graph can be characterized by the sparsity pattern of Ω* = (Σ*)⁻¹. To estimate Ω*, Liu et al. (2012) propose a rank-based method – namely nonparanormal skeptic for estimating the correlation matrix. They exploit the Kendall’s tau statistic to directly estimate the unknown correlation matrix. This approach avoids explicitly calculating the marginal transformation functions ${\{f_j\}}_{j=1}^d$ and achieves the optimal parametric rates of convergence.

More specifically, let x¹, …, xⁿ be n independent observations of X, where ${\mathit{x}}^i={(x_1^i,\dots ,x_d^i)}^T$. Then the Kendall’s tau statistic τ̂_jk is defined as follows,

$${\mathrm{\tau ̂}}_{jk}=\{\begin{array}{cc}\frac{2}{n(n-1)}\sum _{i<i\prime }\text{sign}(x_j^i-x_j^{i\prime })(x_k^i-x_k^{i\prime })\hfill & k\ne j\hfill \\ 1\hfill & k=j\hfill \end{array}.$$

Though τ̂_jk is not consistent for ${\mathbf{\Sigma }}_{jk}^{*}$, the bias can be corrected by resorting to a transformed Kendall’s tau estimator Ŝ = [Ŝ_jk] ∈ ℝ^d×d, defined as

$${\mathbf{Ŝ}}_{jk}=\text{sin}(\frac{\pi }{2}{\mathrm{\tau ̂}}_{jk}).$$

Liu et al. (2012) further characterize the following concentration property of the transformed Kendall’s tau estimator.

Lemma 2.2 (Liu et al. (2012)). Suppose that X ~ N P N (f, Σ*). There exists a universal constant κ₁, such that

$$\mathbb{P}({\Vert |\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le {\kappa }_1\sqrt{\frac{\text{log}d}{n}})\ge 1-\frac{1}{d^3}.$$ (2.1)

Existing literature often uses (2.1) as an important condition to achieve parameter estimation and model selection consistency in high dimensions (Meinshausen and Bühlmann, 2006; Ravikumar et al., 2011; Liu et al., 2012). Therefore in the next section, we propose a projection method to obtain a positive semidefinite replacement of Ŝ, which also preserves this concentration property.

2.2 Possible Indefiniteness

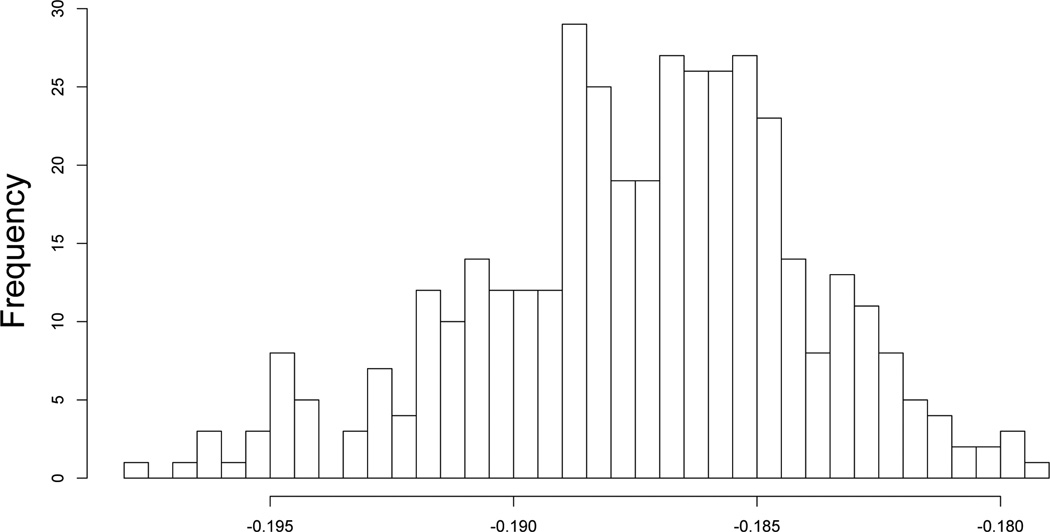
Here we present a typical example to illustrate the possible indefiniteness of the transformed Kendall’s tau matrix. We sample 100 data from a 200-dimensional normal distribution N(0, I₂₀₀) and calculate the minimum eigenvalue of the transformed Kendall’s tau matrix. We repeat the sampling for 400 times and present the histogram of minimum eigenvalues in Figure 1. We see that these minimum eigenvalues are close to −0.187. For all 400 replications, the minimum eigenvalues are always negative.

Figure 1.

The histogram of minimum eigenvalues of the transformed Kendall’s tau matrix. Across all 400 replications, the minimum eigenvalues are always negative.

Such indefiniteness causes trouble when we apply the neighborhood pursuit algorithm to nonparanormal graph estimation. The main reason is that the neighborhood pursuit is formulated as a quadratic program, when the transformed Kendall’s tau matrix in the quadratic term is indefinite, the objective function is no longer convex. Thus existing quadratic programming solvers cannot guarantee a global solution in polynomial time. In the next section, we present a projection method to circumvent this difficulty.

3 Methodology

Before introducing the proposed method, we first motivate our interest in the nonparanormal neighborhood pursuit.

3.1 Neighborhood Pursuit v.s. Graphical lasso

Ravikumar et al. (2011) study the sufficient conditions for perfect graph recovery for the graphical lasso and neighborhood pursuit. They numerically verify that the neighborhood pursuit has better sample complexity than the graphical lasso.

In many real applications, neighborhood pursuit and graphical lasso behave differently. For example, we apply both methods to a stock market dataset (See §6 for more details). We calculate the solution paths over a grid of regularization parameters and align the obtained paths by their sparsity levels. We further calculate the proportion of edges on which these two methods disagree with each other. More specifically, we adjust the regularization parameters of the neighborhood pursuit and graphical lasso such that the obtained graphs have approximately the same number of edges. For example, if one graph has 100 edges and the other graph has 102 edges— with 40 shared edges—the disagreement between these two graphs is (60/100 + 62/102)/2 = 0.6039. As shown in Figure 2(a), there exists a large amount of disagreement between the graphical lasso estimate and the neighborhood pursuit estimate. A similar phenomenon is also found in Figure 2(b), where the nonparanormal neighborhood pursuit shows significant difference from the nonparanormal graphical lasso. In addition, we compare the Gaussian graph estimation and nonparanormal graph estimation in the same way. From Figures 2(c) and 2(d), we see that the neighborhood pursuit and graphical lasso also behave differently from their corresponding nonparanormal based methods.

Figure 2.

The quantitative comparison between the solution paths recovered by the graphical lasso, neighborhood pursuit, nonparanormal graphical lasso, and nonparanormal neighborhood pursuit. The neighborhood pursuit shows a large amount of disagreement with the graphical lasso in both Gaussian and nonparanormal graph estimation. Additionally, the neighborhood pursuit and graphical lasso also behave differently from their corresponding nonparanormal based methods.

Given the above merit of the neighborhood pursuit in graph recovery and its different empirical behavior, we are interested in extending this method to the nonparanormal graph estimation.

3.2 Nonparanormal Neighborhood Pursuit

Recall that f(X) = (f₁(X₁), …, f_d(X_d))^T, and let f_\j(X_\j) be the (d − 1)-dimensional subvector of f(X) with the j^th entry f_j(X_j) removed. Since the conditional distribution of f_j(X_j) given f_\j(X_\j) remains Gaussian, i.e.,

$$f_j(X_j)|{\mathit{f}}_{\backslash j}({\mathit{X}}_{\backslash j})~N({\mathbf{\Sigma }}_{j,\backslash j}^{*}{({\mathbf{\Sigma }}_{\backslash j,\backslash j}^{*})}^{-1}{\mathit{f}}_{\backslash j}({\mathit{X}}_{\backslash j}),{\mathbf{\Sigma }}_{j,j}^{*}-{\mathbf{\Sigma }}_{j,\backslash j}^{*}{({\mathbf{\Sigma }}_{\backslash j,\backslash j}^{*})}^{-1}{\mathbf{\Sigma }}_{\backslash j,j}^{*}),$$ (3.1)

then (3.1) can be equivalently represented by a linear regression model:

$$f_j(X_j)={\mathit{f}}_{\backslash j}{({\mathit{X}}_{\backslash j})}^T{\mathbf{B}}_{\backslash j,j}^{*}+Z_j,$$

where $Z_j~N(0,{\mathbf{\Sigma }}_{j,j}^{*}-{\mathbf{\Sigma }}_{j,\backslash j}^{*}{({\mathbf{\Sigma }}_{\backslash j,\backslash j}^{*})}^{-1}{\mathbf{\Sigma }}_{\backslash j,j}^{*})$ and B* ∈ ℝ^d×d is defined as

$${\mathbf{B}}_{\backslash j,j}^{*}={({\mathbf{\Sigma }}_{\backslash j,\backslash j}^{*})}^{-1}{\mathbf{\Sigma }}_{\backslash j,j}^{*}\text{and}{\mathbf{B}}_{j,j}^{*}=0\text{for all}1\le j\le d.$$ (3.2)

Consequently, the nonparanormal neighborhood pursuit solves

$${\mathbf{B̂}}_{\backslash j,j}=\underset{{\mathbf{B}}_{j,j}=0}{\text{argmin}}{\mathbf{B}}_{\backslash j,j}^T{\mathbf{S̃}}_{\backslash j,\backslash j}{\mathbf{B}}_{\backslash j,j}-2{\mathbf{S̃}}_{\backslash j,j}^T{\mathbf{B}}_{\backslash j,j}+\lambda {\Vert {\mathbf{B}}_{\backslash j,j}\Vert }_1\text{for all}j=1,\dots ,d,$$ (3.3)

where S̃ is a positive semidefinite replacement of the transformed Kendall’s tau matrix Ŝ. The optimization problem in (3.3) can be efficiently solved by the coordinate descent algorithm (Friedman et al., 2007). Since B̂ may not be symmetric, we need an additional symmetrization procedure to obtain a graph estimator. That is, let E* be the adjacency matrix of the underlying graph 𝒢*, we estimate E* by

$$\mathbf{Ê}=[{\mathbf{Ê}}_{jk}]=[I(\text{max}\{|{\mathbf{B̂}}_{jk}|,|{\mathbf{B̂}}_{kj}|\}>0)].$$

In the next subsection, we explain how to obtain the positive semidefinite replacement S̃ with theoretical guarantees in high dimensions.

3.3 Positive Semidefinite Projection

Our proposed projection method is motivated by the following problem:

$$\mathbf{S̅}=\underset{\mathbf{S}}{\text{argmin}}{\Vert |\mathbf{Ŝ}-\mathbf{S}|\Vert }_{\infty }\text{subject to}\mathbf{S}⪰0.$$ (3.4)

Since S̅ is the minimizer of (3.4), and Σ* is a feasible solution to (3.4), by the triangle inequality, we have

$${\Vert |{\mathbf{\Sigma }}^{*}-\mathbf{S̅}|\Vert }_{\infty }\le {\Vert |\mathbf{Ŝ}-\mathbf{S̅}|\Vert }_{\infty }+{\Vert |\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le 2{\Vert |\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }.$$ (3.5)

Thus combining (3.5) with Lemma 2.2, it is straightforward to show that

$${\Vert |\mathbf{S̅}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }=O_P(\sqrt{\text{log}d/n}).$$ (3.6)

However, (3.4) is computationally expensive because of its nonsmoothness. To gain computational efficiency, we apply the smoothing approach in Nesterov (2005) to solve (3.4) at the expense of a controllable accuracy loss. For any matrix A ∈ ℝ^d×d, we consider the following smooth surrogate of the elementwise ℓ_∞ norm

$${\Vert |\mathbf{A}|\Vert }_{\infty }^{\mu }=\underset{{\Vert |\mathbf{U}|\Vert }_1\le 1}{\text{max}}\langle \mathbf{U},\mathbf{A}\rangle -\frac{\mu }{2}{\Vert \mathbf{U}\Vert }_{\mathrm{F}}^2,$$ (3.7)

where μ > 0 is a smoothing parameter. The first term in (3.7) is well known as the Fenchel’s dual representation, and the second term is the proximity function of U. We call ${\Vert |·|\Vert }_{\infty }^{\mu }$ smoothed elementwise ℓ_∞ norm. The next lemma characterizes the solution to (3.7).

Lemma 3.1. Let ${\mathbf{Ũ}}^{(\mathbf{A})}=[{\mathbf{Ũ}}_{jk}^{(\mathbf{A})}]$ be the optimal solution to (3.7), we have

$${\mathbf{Ũ}}_{jk}^{(\mathbf{A})}=\text{sign}({\mathbf{A}}_{jk})\text{max}\left\{\right|\frac{{\mathbf{A}}_{jk}}{\mu }|-\gamma ,0\},$$ (3.8)

where γ is the minimum nonnegative constant such that ‖|Ũ^(A)|‖₁ ≤ 1.

The proof of Lemma 3.1 is provided in the supplementary materials. The naive algorithm for calculating γ is to sort the matrix, which has an average-case complexity of O(d² log d). See the supplementary materials for a more efficient algorithm with an average-case complexity of O(d²).

Figure 3 shows several two-dimensional examples of the elementwise ℓ_∞ norm smoothed by different μ’s. We see that increasing μ makes the function smoother, but induces a larger approximation error. The smoothed elementwise ℓ_∞ norm is convex, and has a gradient as follows,

$$\nabla {\Vert |\mathbf{Ŝ}-\mathbf{S}|\Vert }_{\infty }^{\mu }=\frac{\partial {\Vert |\mathbf{Ŝ}-\mathbf{S}|\Vert }_{\infty }^{\mu }}{\partial (\mathbf{Ŝ}-\mathbf{S})}·\frac{\partial (\mathbf{Ŝ}-\mathbf{S})}{\partial \mathbf{S}}=-{\mathbf{Ũ}}^{(\mathbf{Ŝ}-\mathbf{S})}.$$ (3.9)

Figure 3.

The elementwise ℓ_∞ norm (a) and smoothed elementwise ℓ_∞ norms with μ = 0.1, 0.5, 1 (b–d). Increasing μ makes the function smoother, but induces a larger approximation error.

Recall that Ũ^(Ŝ−S) is essentially a soft thresholding function, therefore it is continuous in S with a Lipchitz constant 1/μ. Since the smoothed elementwise ℓ_∞ norm has the above nice computational properties with a controllable loss in accuracy (See §4 for more details), we focus on the following smooth relaxed optimization problem,

$$\mathbf{S̃}=\underset{\mathbf{S}}{\text{argmin}}{\Vert |\mathbf{Ŝ}-\mathbf{S}|\Vert }_{\infty }^{\mu }\text{subject to}\mathbf{S}⪰0.$$ (3.10)

3.4 Accelerated Proximal Gradient Algorithm

We propose an accelerated proximal gradient algorithm as in Nesterov (1988) to solve the optimization problem in (3.10). Unlike most existing accelerated proximal gradient algorithms for unconstrained minimization problems (Ji and Ye, 2009; Chen et al., 2012; Zhao and Liu, 2012; Nesterov, 2005; Beck and Teboulle, 2009), the proposed algorithm can handle the positive semidefinite constraint in (3.10). Before we proceed with the details of the algorithm, we first define the projection operator as

$${\mathrm{\Pi }}_{+}(\mathbf{A})=\underset{\mathbf{B}}{\text{argmin}}{\Vert \mathbf{B}-\mathbf{A}\Vert }_{\mathrm{F}}^2\text{subject to}\mathbf{B}⪰0,$$ (3.11)

where A ∈ ℝ^d×d is a symmetric matrix. Π₊(A) is the projection of the symmetric matrix A to the cone of all positive semidefinite matrices with respect to the Frobenius norm. Π₊(A) has a closed form solution as shown in the following lemma.

Lemma 3.2. Suppose that A has an eigenvalue decomposition $\mathbf{A}={\sum }_{j=1}^d{\sigma }_j{\mathit{\upsilon }}_j{\mathit{\upsilon }}_j^T$, where σ_j’s are the eigenvalues, and υ_j’s are the corresponding eigenvectors. We have

$${\mathrm{\Pi }}_{+}(\mathbf{A})=\sum _{j=1}^d\text{max}\{{\sigma }_j,0\}{\mathit{\upsilon }}_j{\mathit{\upsilon }}_j^T.$$ (3.12)

The proof of Lemma 3.2 is provided in the supplementary materials.

Now we start to derive the algorithm. We define two sequences of auxiliary variables M^(t) and W^(t) with M⁽⁰⁾ = W⁽⁰⁾ = S⁽⁰⁾, and a sequence of weights θ_t = 2/(1 + t) for t = 1, 2, …. At the t^th iteration, we calculate the auxiliary variable M^(t) as

$${\mathbf{M}}^{(t)}=(1-{\theta }_t){\mathbf{S}}^{(t-1)}+{\theta }_t{\mathbf{W}}^{(t-1)}.$$ (3.13)

We then evaluate the gradient using

$${\mathbf{G}}^{(t)}=\frac{\partial {\Vert |\mathbf{Ŝ}-{\mathbf{M}}^{(t)}|\Vert }_{\infty }^{\mu }}{\partial {\mathbf{M}}^{(t)}}=[-\text{sign}({\mathbf{Ŝ}}_{jk}-{\mathbf{M}}_{jk}^{(t)})·\text{max}\{|\frac{{\mathbf{Ŝ}}_{jk}-{\mathbf{M}}_{jk}^{(t)}}{\mu }|-\gamma ,0\left\}\right].$$ (3.14)

We consider the following quadratic approximation:

$$Q(\mathbf{W},{\mathbf{W}}^{(t-1)},\mu )={\Vert |\mathbf{Ŝ}-{\mathbf{W}}^{(t-1)}|\Vert }_{\infty }^{\mu }+\langle {\mathbf{G}}^{(t)},\mathbf{W}-{\mathbf{W}}^{(t-1)}\rangle +\frac{1}{2{\eta }_t{\theta }_t}{\Vert \mathbf{W}-{\mathbf{W}}^{(t)}\Vert }_{\mathrm{F}}^2,$$ (3.15)

where η_t is the step-size for the t^th iteration. Then we take

$${\mathbf{W}}^{(t)}=\underset{\mathbf{W}⪰0}{\text{argmin}}Q(\mathbf{W},{\mathbf{W}}^{(t-1)},\mu )={\mathrm{\Pi }}_{+}({\mathbf{W}}^{(t-1)}-\frac{{\eta }_t}{{\theta }_t}{\mathbf{G}}^{(t)}).$$ (3.16)

We further calculate S^(t) for the t^th iteration as follows,

$${\mathbf{S}}^{(t)}=(1-{\theta }_t){\mathbf{S}}^{(t-1)}+{\theta }_t{\mathbf{W}}^{(t)}.$$ (3.17)

Let ε be the target precision, the algorithm stops when $|{\Vert |\mathbf{Ŝ}-{\mathbf{S}}^{(t)}|\Vert }_{\infty }^{\mu }-{\Vert |\mathbf{Ŝ}-{\mathbf{S}}^{(t-1)}|\Vert }_{\infty }^{\mu }|\le \epsilon \mu$.

Remark 3.3. A conservative choice of η_t is η_t = μ in all iterations. Since μ is the Lipchitz constant of G^(t), we always have

$${\Vert |\mathbf{Ŝ}-{\mathbf{S}}^{(t)}|\Vert }_{\infty }^{\mu }\le {\Vert |\mathbf{Ŝ}-{\mathbf{M}}^{(t)}|\Vert }_{\infty }^{\mu }+\langle {\mathbf{G}}^{(t)},{\mathbf{S}}^{(t)}-{\mathbf{M}}^{(t)}\rangle +\frac{1}{2\mu }{\Vert {\mathbf{S}}^{(t)}-{\mathbf{M}}^{(t)}\Vert }_{\mathrm{F}}^2\le {\Vert |\mathbf{Ŝ}-{\mathbf{M}}^{(t)}|\Vert }_{\infty }^{\mu }+\langle {\mathbf{G}}^{(t)},{\mathbf{S}}^{(t)}-{\mathbf{M}}^{(t)}\rangle +\frac{1}{2\mu {\theta }_t}{\Vert {\mathbf{S}}^{(t)}-{\mathbf{M}}^{(t)}\Vert }_{\mathrm{F}}^2=Q({\mathbf{S}}^{(t)},{\mathbf{M}}^{(t)},\mu ),$$

where the second inequality comes from θ_t ≤ 1. To gain a better empirical performance, we can adopt the backtracking line search with a sequence of non-increasing step-sizes η _t’s for t = 1, 2…. More specifically, we start with a large enough η₁, and within each iteration we choose the minimum integer z such that

$${\Vert |\mathbf{Ŝ}-{\mathbf{S}}^{(t)}|\Vert }_{\infty }^{\mu }\le Q({\mathbf{S}}^{(t)},{\mathbf{M}}^{(t)},{\eta }_t)\mathit{\text{with}}{\eta }_t=\text{max}\{\mu ,m^z{\eta }_{t-1}\},$$ (3.18)

where m ∈ (0, 1) is the shrinkage parameter.

The following theorem establishes the worst-case convergence rate of the proposed accelerated proximal gradient algorithm.

Theorem 3.4. To achieve the desired accuracy ε such that ${\Vert |\mathbf{Ŝ}-{\mathbf{S}}^{(t)}|\Vert }_{\infty }^{\mu }-{\Vert |\mathbf{Ŝ}-\mathbf{S̃}|\Vert }_{\infty }^{\mu }<\epsilon$, the required number of iterations is at most

$$t=\sqrt{\frac{2{\Vert {\mathbf{S}}^{(0)}-\mathbf{S̃}\Vert }_{\mathrm{F}}^2}{\mu \epsilon }}-1=O({\epsilon }^{-1/2}{\mu }^{-1/2}).$$

Theorem 3.4 is a direct result of Nesterov (1988). It guarantees that our derived algorithm achieves the optimal convergence rate for minimizing (3.10) over all first order computational algorithms. Existing literature considers the smoothing approach as a tradeoff between computational efficiency and approximation error (Nesterov, 2005; Chen et al., 2012). Therefore they analyze the convergence rate with respect to the optimal solution to the original problem (3.4). They choose to set the smoothing parameter μ small enough (e.g., μ = ε/2) to avoid a large approximation error, and eventually get a slower convergence rate O (ε⁻¹).

In contrast, we directly analyze the tradeoff between the computational efficiency and statistical error (Agarwal et al., 2012). Although S̃ is not the optimal solution to the original problem (3.4), our analysis in §4 will show that choosing a larger μ (e.g., $\mu \asymp \sqrt{\text{log}d/n}$) can still make S̃ concentrate to Σ* with a rate similar to (2.1) in high dimensions. This boosts the computational performance.

4 Statistical Theory

We first present the rate of convergence of S̃ under the elementwise ℓ_∞ norm.

Theorem 4.1. Suppose that X ~ N P N(f, Σ*), there exist universal constants κ₂ and κ₃ such that by taking $\mu ={\kappa }_2\sqrt{\text{log}d/n}$, we have the optimum to (3.10), S̃ satisfying

$$\mathbb{P}({\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le {\kappa }_3\sqrt{\frac{\text{log}d}{n}})\ge 1-\frac{1}{d^3}.$$ (4.1)

The proof of Theorem 4.1 is provided in Appendix A. Theorem 4.1 implies that we can choose a reasonably large μ to gain the computational efficiency without losing statistical efficiency.

Remark 4.2. By plugging $\mu ={\kappa }_2\sqrt{\text{log}d/n}$ into Theorem 3.4, we obtain a more refined convergence rate of the proposed computational algorithm as O(ε^−1/2(log d/n)^−1/4).

Now we analyze the graph recovery performance of the nonparanormal neighborhood pursuit under suitable conditions. Let I_j denote the set of the neighbors of node j, and J_j denote the set of the non-neighbors of node j. For all j = 1, …, d, we assume that

$$\begin{array}{cc}\text{Assumption}1\hfill & {\Vert {\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }\le \alpha ,\hfill \\ \text{Assumption}2\hfill & {\mathrm{\Lambda }}_{\text{min}}({\mathbf{\Sigma }}_{I_j{I}_j}^{*})\ge \delta ,{\Vert {({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }\le \psi ,\hfill \end{array}$$

where α ∈ (0, 1), δ > 0, and ψ < ∞ are all constants. Assumptions 1 and 2 have been extensively studied in existing literature (Zhao and Yu, 2006; Zou, 2006; Wainwright, 2009). Assumption 1 is known as the irrepresentable condition, which requires that the correlation between the non-neighborhood and neighborhood moderate. Assumption 2 is known as the minimum curvature condition, which requires that the correlation within the neighborhood cannot be too large. We then present the results on graph recovery consistency.

Theorem 4.3. Recall that E* denotes the adjacency matrix of 𝒢*, and

$$\tau =\underset{{\mathbf{E}}_{jk}^{*}\ne 0}{\text{min}}|{\mathbf{B}}_{jk}^{*}|,$$ (4.2)

we assume that Σ* satisfies Assumptions 1 and 2. Let s = max_j |I_j|. If we choose λ ≤ min {τ/ψ, 2}, then for large enough n such that

$$\sqrt{\frac{\text{log}d}{n}}\le \text{min}\{\frac{\lambda (1-\alpha )}{26\psi \alpha {\kappa }_{3}s},\frac{\lambda (1-\alpha )}{26\psi {\kappa }_{3}s},\frac{\lambda (1-\alpha )}{26(\alpha +1)},\frac{\tau }{14{\psi }^{2}s{\kappa }_3},\frac{\tau }{14\psi {\kappa }_3},\frac{\delta }{2s{\kappa }_3}\},$$

we have

$$\mathbb{P}(\mathbf{Ê}={\mathbf{E}}^{*})\ge 1-\frac{1}{d^3}.$$

Moreover, we have ℙ (Ê = E*) → 1, if the following conditions hold:

• Condition 1: α, δ, and ψ are constants, which do not scale with n, d, and s;

• Condition 2: τ scales with n, d, and s as

  $$\frac{s\text{log}d}{{\tau }^{2}n}\to 0\mathit{\text{and}}\frac{s^2\text{log}d}{n}\to 0;$$
• Condition 3: λ scales with τ, n, d, and s as

  $$\frac{\lambda }{\tau }\to 0\mathit{\text{and}}\frac{s^2\text{log}d}{{\lambda }^{2}n}\to 0.$$

The proof of Theorem 4.3 is provided in Appendix B. It guarantees that we can correctly recover the underlying graph structure with high probability.

5 Numerical Simulations

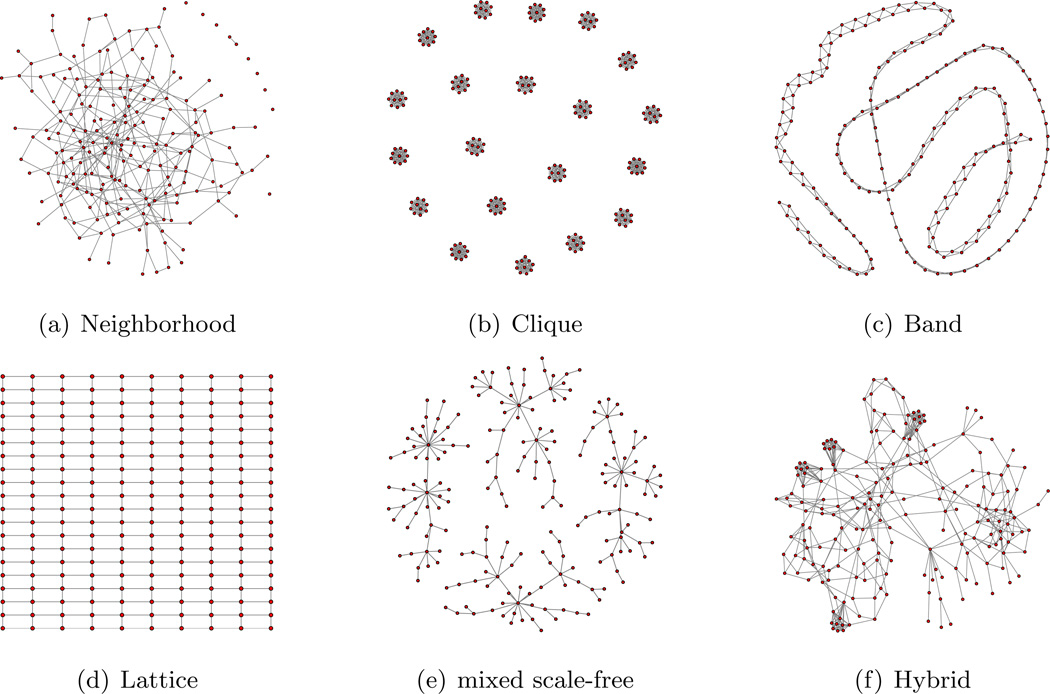
In our numerical simulations, we use six different graphs with 200 nodes (d = 200) including neighborhood graph, clique graph, band graph, lattice graph, mixed scale-free graph, and hybrid graph to generate the precision matrix Ω* (shown in Figure 4). We then generate 100 observations from the Gaussian distribution with covariance matrix (Ω*)⁻¹. We further adopt the power function g(t) = t⁵ to convert the Gaussian data to the nonparanormal data. See the supplementary materials for more details about the graph and covariance matrix generation.

Figure 4.

Six different graph patterns in the simulation studies.

We use an ROC curve to evaluate the graph recovery performance. Since d > n, we cannot obtain the solution paths for the full range of sparsity levels, therefore we restrict the range of false positive rates to be from 0 to 0.1 for computational convenience. For the proposed accelerated proximal gradient algorithm, we set the target precision ε = 10⁻³ and the shrinkage parameter of the backtracking line search m = 0.5.

5.1 Positive Semidefiniteness v.s. Indefiniteness

In this subsection, we first demonstrate the effiectiveness of the proposed projection method. The empirical performance of our computational algorithm using different smoothing parameters (μ = 0.4603, 0.1455, 0.0460, 0.0146, and 0.0046) are presented in Tables 1 and 2 on all six graphs (averaged over 100 replications with standard errors in parentheses). We evaluate the computational performance based on the objective value ‖|Ŝ−S̃|‖_∞ and the estimation error ‖|Σ*− S̃|‖_∞. We see that smaller μ’s attain smaller objective values because of smaller approximation errors.

Table 1.

Quantitive comparison between the proposed projection method and transformed Kendall’s tau estimator on the neighborhood, clique, and band graphs. “Kendall” denotes the transformed Kendall’s tau estimator. Timing results are evaluated in seconds.

Neighborhood	μ = 0.4603	μ = 0.1455	μ = 0.0460	μ = 0.0146	μ = 0.0046	Kendall
Timing	0.7542 (0.0372)	1.3353 (0.0521)	3.3128 (0.1173)	6.4969 (0.3719)	15.395 (2.1716)	N.A. (N.A.)
Obj. Val.	0.0102 (0.0001)	0.0094 (0.0001)	0.0086 (0.0001)	0.0085 (0.0001)	0.0082 (0.0017)	N.A. (N.A.)
Est. Err.	0.4184 (0.0234)	0.4183 (0.0236)	0.4186 (0.0239)	0.4186 (0.0240)	0.4183 (0.0243)	0.4250 (0.0248)

Clique	μ = 0.4603	μ = 0.1455	μ = 0.0460	μ = 0.0146	μ = 0.0046	Kendall
Timing	0.7359 (0.0301)	1.3650 (0.0449)	3.3983 (0.1349)	6.2133 (0.1888)	15.872 (1.4772)	N.A. (N.A.)
Obj. Val.	0.0103 (0.0002)	0.0094 (0.0001)	0.0085 (0.0001)	0.0082 (0.0001)	0.0079 (0.0003)	N.A. (N.A.)
Est. Err.	0.4170 (0.0271)	0.4168 (0.0268)	0.4170 (0.0268)	0.4171 (0.0268)	0.4174 (0.0268)	0.4245 (0.0271)

Band	μ = 0.4603	μ = 0.1455	μ = 0.0460	μ = 0.0146	μ = 0.0046	Kendall
Timing	0.7110 (0.0200)	1.2955 (0.0342)	3.2849 (0.0908)	6.4094 (0.3692)	16.6467 (2.2016)	N.A. (N.A.)
Obj. Val.	0.0104 (0.0002)	0.0094 (0.0001)	0.0086 (0.0001)	0.0082 (0.0001)	0.0080 (0.0001)	N.A. (N.A.)
Est. Err.	0.4311 (0.0319)	0.4309 (0.0318)	0.4309 (0.0317)	0.4310 (0.0317)	0.4308 (0.0312)	0.4832 (0.0316)

Table 2.

Quantitive comparison between the proposed projection method and transformed Kendall’s tau estimator on the lattice, mixed scale-free, and hybrid graphs. “Kendall” denotes the transformed Kendall’s tau estimator. Timing results are evaluated in second.

Lattice	μ = 0.4603	μ = 0.1455	μ = 0.0460	μ = 0.0146	μ = 0.0046	Kendall
Timing	0.8290 (0.1110)	1.3592 (0.0527)	3.2477 (0.0679)	6.0479 (0.1312)	14.516 (3.8660)	N.A. (N.A.)
Obj. Val.	0.0104 (0.0002)	0.0094 (0.0001)	0.0086 (0.0001)	0.0084 (0.0001)	0.0082 (0.0011)	N.A. (N.A.)
Est. Err.	0.4098 (0.0185)	0.4098 (0.0185)	0.4099 (0.0181)	0.4098 (0.0180)	0.4100 (0.0181)	0.4176 (0.0180)

Mixed Scale-free	μ = 0.4603	μ = 0.1455	μ = 0.0460	μ = 0.0146	μ = 0.0046	Kendall
Timing	0.7045 (0.0833)	1.2641 (0.0920)	3.3132 (0.1382)	6.3076 (0.1331)	16.7927 (1.8876)	N.A. (N.A.)
Obj. Val.	0.0103 (0.0002)	0.0094 (0.0001)	0.0085 (0.0001)	0.0082 (0.0002)	0.0082 (0.0006)	N.A. (N.A.)
Est. Err.	0.4224 (0.0223)	0.4228 (0.0221)	0.4230 (0.0221)	0.4231 (0.0221)	0.4231 (0.0220)	0.4310 (0.0221)

Hybrid	μ = 0.4603	μ = 0.1455	μ = 0.0460	μ = 0.0146	μ = 0.0046	Kendall
Timing	0.7939 (0.0791)	1.4681 (0.1459)	3.7757 (0.1722)	6.2499 (0.3817)	14.2512 (2.2610)	N.A. (N.A.)
Obj. Val.	0.0104 (0.0002)	0.0094 (0.0001)	0.0085 (0.0001)	0.0085 (0.0006)	0.0081 (0.0006)	N.A. (N.A.)
Est. Err.	0.4113 (0.0223)	0.4108 (0.0221)	0.4112 (0.0232)	0.4112 (0.0232)	0.4111 (0.0232)	0.4187 (0.0234)

However, we see that changing μ does not make much difference in the estimation error. In terms of the computational cost, $\mu =0.0046\approx 0.002\sqrt{\text{log}d/n}$ is up to 24 times slower than $\mu =0.4603\approx 2\sqrt{\text{log}d/n}$. Therefore a reasonably large μ can greatly reduce computational burden with almost no loss of statistical efficiency. Moreover, we also find that our projection method not only guarantees the positive semidefiniteness but also attains smaller estimation error than the original transformed Kendall’s tau matrix.

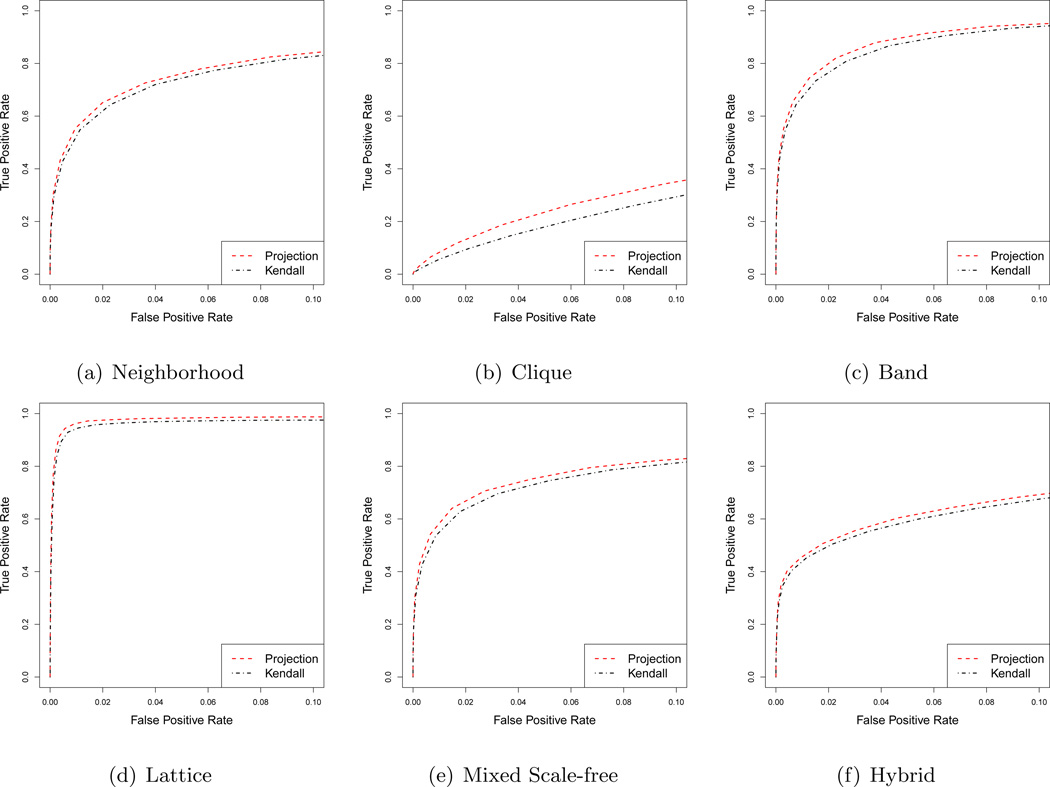
We then compare the graph recovery performance of the projection method with the original transformed Kendall’s tau estimator. Figure 5 shows the average ROC curves over 100 replications. The ROC curves from different replications are first aligned by regularization parameters. The averaged ROC curve shows the false positive and true positive rate averaged over all replications w.r.t. each regularization parameter. Since ROC curves corresponding to different μ’s are almost identical, we only present the ROC curves corresponding to μ = 0.4603, which is of our main interest. We see that the projection method achieves better performance than the transformed Kendall’s tau estimator in graph recovery for all six graphs.

Figure 5.

Average ROC curves of the neighborhood pursuit when combing with different correlation estimators. “Kendall” represents the transformed Kendall’s tau estimator, and “Projection” represents the projection method. We see that the proposed projection method achieves better graph recovery performance than the transformed Kendall’s tau estimator for all the six graphs.

In summary, these simulation results show that the projection method provides a computational tractable solution and achieves better graph recovery performance than the indefinite transformed Kendall’s tau estimator.

5.2 Nonparanormal Neighborhood Pursuit v.s. Gaussian Neighborhood Pursuit

This subsection is similar to the numerical studies in Liu et al. (2012), and we compare our proposed method with the Gaussian neighborhood pursuit, which directly combines the Pearson correlation estimator with the neighborhood pursuit and graphical lasso approaches. The main difference is that our experiment is conducted under the setting d > n. The smoothing parameter μ is chosen to be 0.4603. The average ROC curves over 100 replications are presented in Figure 6. As can be seen, the nonparanormal neighborhood pursuit outperforms the Gaussian neighborhood pursuit and Gaussian graphical lasso throughout all the 6 graphs.

Figure 6.

Average ROC curves of the nonparanormal neighborhood pursuit, Gaussian neighborhood pursuit, and Gaussian graphical lasso. “N-Neighborhood pursuit” represents our proposed nonparanormal neighborhood pursuit. “G-Neighborhood pursuit” represents Gaussian neighborhood pursuit, which combines the neighborhood pursuit and the Pearson correlation estimator. “G-Graphical Lasso” represents Gaussian neighborhood pursuit, which combines the graphical lasso and the Pearson correlation estimator. We see that the nonparanormal neighborhood pursuit outperforms the Gaussian neighborhood pursuit and Gaussian graphical lasso for all the six graphs.

5.3 Nonparanormal Neighborhood Pursuit v.s. Nonparanormal Graphical Lasso

In this subsection, we compare the proposed method with the nonparanormal graphical lasso. The smoothing parameter μ is chosen to be 0.4603. The average ROC curves over 100 replications are presented in Figure 7. We see that the nonparanormal neighborhood pursuit achieves better graph recovery performance than the nonparanormal graphical lasso for all the 6 graphs.

Figure 7.

Average ROC curves of the nonparanormal neighborhood pursuit and nonparanormal graphical lasso. “N-Neighborhood Pursuit” represents the nonparanormal neighborhood pursuit. “N-Graphical Lasso” represents the nonparanormal graphical lasso. We see that the nonparanormal neighborhood pursuit achieves better graph recovery performance than the nonparanormal graphical lasso for all the six graphs.

6 Data Analysis

We present three real data examples. Throughout this subsection, Gaussian graphs are obtained by combining the neighborhood pursuit with the Pearson correlation estimator, while nonparanormal graphs are obtained by the nonparanormal neighborhood pursuit.

We use the following stability graph estimator (Meinshausen and Bühlmann, 2010; Liu et al., 2010) to conduct graph selection:

1. Calculate the solution path using all samples and choose the regularization parameter at sparsity level θ;

2. Randomly select ξ × 100% of all samples without replacement, and estimate the graph using the selected samples with the regularization parameter chosen in (1);

3. Repeat (2) for 500 times and retain edges that appear with frequency no less than 95%.

We select (θ, ξ) based on two criteria: (1) The obtained graphs should be sparse to ease visualization, interpretation, and computation. (2) The obtained results should be stable. Thus by manually tuning the regularization parameter over a refined grid, we eventually set (θ, ξ) as (0.04, 0.1), (0.1, 0.5), and (0.10, 0.75) respectively for the topic modeling, stock market, and arabidopsis datasets.

6.0.1 Topic Graph

The topic graph is originally used in Blei and Lafferty (2007) to illustrate the effectiveness of the correlated topic modeling for extracting K “topics” that occur in a collection of documents (corpus). We first estimate the topic proportion for each document. The topic proportion of each document is represented in a K-dimensional simplex. The whole corpus used by Blei and Lafferty (2007) contains 16,351 documents with 19,088 unique terms. Blei and Lafferty (2007) set K = 100 and fit a topic model to the articles published in Science from 1990 to 1999. Thus each document is represented by a 100-dimensional vector, with each entry corresponding to one of the 100 topics.

Here we are interested in visualizing the relationship among the topics using the following topic graph: The nodes represent individual topics and neighboring nodes represent highly related topics. In Blei and Lafferty (2007), the topic proportion is assumed to be approximately normal after the log-transformation. To obtain the topic graph, they calculate the Pearson correlation matrix of 100 topics, and plug it into the neighborhood pursuit. When we perform the Kolmogorov-Smirnov test for each topic, however, we find that some of them strongly violate the normality assumption (See the supplementary materials for more details). This motivates our choice of the nonparanormal neighborhood pursuit approach.

The estimated topic graphs are shown in Figures 8, where the clustering information can be read directly from the graphs. See the supplementary materials for zoomed-in figures. Here each topic is labelled with the most frequent word and an index. See http://www.cs.cmu.edu/lemur/science/topics.html for more details about topic summaries. The nonparanormal graph contains 6 mid-size modules and 6 small modules, while the Gaussian graph contains 1 large module, 2 mid-size modules, and 6 small modules. We see that the refined structures discovered by the nonparanormal approach clearly improves the interpretability of the graph. Here we provide a few examples:

1. Topics closely related to the climate change in Antarctica, such as “ice-68”, “ozone-23”, and “carbon-64”, are clustered in the same module;

2. Topics closely related to the environmental ecology, such as “monkey-21”, “science-4”, “species-86”, and “environmental-67”, are clustered in the same module;

3. Topics closely related to modern physics, such as “quantum-29”, “magnetic-55”, “pressure-92”, and “solar-62”, are clustered in the same module;

4. Topics closely related to the material mechanics, such as “structure-38”, “material-78”, “force-79”, “metal-39”, and “reaction-41”, are clustered in the same module.

Figure 8.

Two topic graphs estimated using the nonparanormal neighborhood pursuit and Gaussian neighborhood pursuit. The nonparanormal graph contains 6 mid-size modules and 6 small modules, while the Gaussian graph contains 1 large module, 2 mid-size modules, and 6 small modules.

In contrast, we see that the Gaussian graph mixes all these topics together and clusters them into a large module.

Moreover, with a subsampling ratio of 0.1, the sample size (n = 1,635) is much larger than the dimension (d = 100). We find that all transformed Kendall’s tau estimates are positive definite. Thus the proposed projection method is not required.

6.0.2 S&P 500 Stock Market Graph

We acquire closing prices of all S&P 500 stocks for all the days when the market was open between January 1, 2003 and January 1, 2005. It results in 504 samples of the 452 stocks. The dataset is transformed by calculating the log-ratio of the price at time t to price at time t − 1, and further standardized by mean zero and variance one. By examining the data points (See the supplementary materials for more details), we see that a large number of potential outliers exist, and they may affect the quality of the estimated graph. Since the transformed Kendall’s tau estimator is rank-based, it is more robust to outliers than the Pearson correlation estimator.

These 452 stocks belong to 10 different Global Industry Classification Standard (GICS) sectors. We present the obtained graphs in Figure 9. Each stock is represented by a node, which is colored according to its GICS sector. We see that stocks from the same GICS sectors show the tendency to be clustered with each other. We highlight several densely connected modules in the nonparanormal graph, and by color coding we see that the nodes in the same dense module belong to the same sector of the market. In contrast, these modules are shown to be sparse in the Gaussian graph. Especially for the blue nodes, many of them are observed as isolated nodes, which means the stocks they represent are (both marginally and conditionally) independent to the others. This is contrary to common beliefs. Overall, we see that the nonparanormal graph has more refined structures than Gaussian graph such that more meaningful relationships could be revealed.

Figure 9.

Stock Graphs. Several densely connected modules are found in the nonparanormal graph, while they are sparser in the corresponding Gaussian graph. The color shows all nodes in this module belong to the same sector of the market.

Moreover, with a subsampling ratio of 0.5, the sample size (n = 252) is smaller than the dimension (d = 452) and the transformed Kendall’s tau estimator is indefinite. By the positive semidefinite projection, we can exploit the convexity of the problem and obtain a high quality graph estimator. The smoothing parameter for the projection method $\mu =0.3115\approx 2\sqrt{\text{log}d/n}$ is the same as our previous simulations.

6.0.3 Gene Graph

This dataset includes 118 gene expression profiles from arabidposis thaliana that originally appeared in Wille et al. (2004). Our analysis focuses on gene expression from 39 genes involved in two isoprenoid pathways: 16 from the mevalonate (MVA) pathway are located in the cytoplasm, 18 from the plastidial (MEP) pathway are located in the chloroplast, and 5 are located in the mitochondria. While the two pathways generally operate independently, crosstalk is known to happen (Wille et al., 2004). Our goal is to recover the gene regulatory graph (network), with special interest in crosstalk.

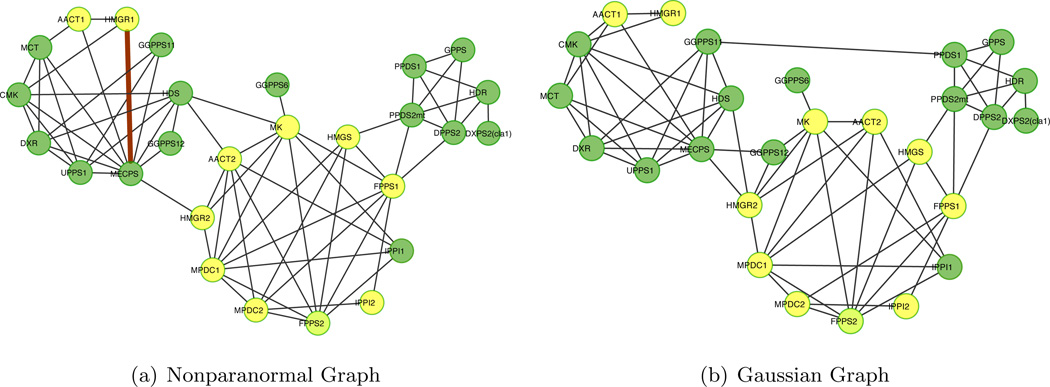
Though the estimated graphs shown in Figure 10 are similar, there exist subtle differences with potentially interesting implications. Both highlight three tightly connected clusters. With the exception of AACT1 and HMGR1 which are part of the MVA pathway (yellow), most of the genes in the cluster to the left are from the MEP pathway (green). The only gene that changes clusters in the two estimated graphs is GGPPS12; This gene, which is also a member of the MEP pathway, is correctly positioned in the nonparanormal graph. MECPS is clearly a hub gene for this pathway.

Figure 10.

Gene regulatory graphs with isolated notes omitted. Genes belonging to the MVA and MEP pathways are colored in yellow and green, respectively. GGPPS12 is correctly positioned by the nonparanormal neighborhood pursuit. Our analysis also suggests that a link between “HMGR1” and “MECPS” constitutes another key point of crosstalk between these two pathways.

Prior investigation suggests that the connections from genes AACT1 and HMGR2 to hub gene MECPS indicate primary sources of the crosstalk between the MEP and MVA pathways and these edges are present in both graphs. We highlight the edge connecting HMGR1 and MECPS, which appears only in the nonparanormal graph. Our analysis suggests that this link constitutes another possible crosstalk between these two pathways. Further investigation of the gene expression levels reveals that the distribution of MECPS is strongly non-Gaussian (See the supplementary materials). This lack of normality might explain why the Gaussian neighborhood pursuit does not detect the link between HMGR1 and MECPS.

Moreover, with a subsampling ratio of 0.75, the sample size (n = 88) is much larger than the dimension (d = 39). We find that all transformed Kendall’s tau estimates are positive definite. Thus the proposed projection method is not required.

7 Discussion and Conclusion

In addition to the projection method, there are two alternative heuristic approaches to obtain a positive semidefinite replacement of Ŝ. One approach is based on the following optimization problem (Rousseeuw and Molenberghs, 1993),

$$\mathbf{S̃}=\underset{\mathbf{S}}{\text{argmin}}{\Vert \mathbf{Ŝ}-\mathbf{S}\Vert }_{\mathrm{F}}^2\text{subject to}\mathbf{S}⪰0.$$ (7.1)

By Lemma 3.2, (7.1) has a closed form solution as

$$\mathbf{S̃}=\sum _{j=1}^d\text{max}\{{\sigma }_j,0\}·{\mathit{\upsilon }}_j{\mathit{\upsilon }}_j^T,$$ (7.2)

where σ_j’s are eigenvalues of Ŝ, and υ_j’s are the corresponding eigenvectors.

Remark 7.1. Similar to our projection method, (7.1) also projects Ŝ onto the cone of all positive semidefinite matrices, but with respect to the Frobenius norm. The theoretical property of such a “truncation” estimator is not clear.

The other approach is directly adding a positive value to all diagonal entries of Ŝ as follows,

$$\mathbf{S̃}=\mathbf{Ŝ}+|\underset{j}{\text{min}}{\sigma }_j|·\mathbf{I}.$$ (7.3)

Such a “perturbation” estimator has been used in many classical statistical methods such as the regularized linear discriminant analysis (Guo et al., 2007) and the ridge regression (Hoerl and Kennard, 1970). However, no theoretical analysis has been established for this approach.

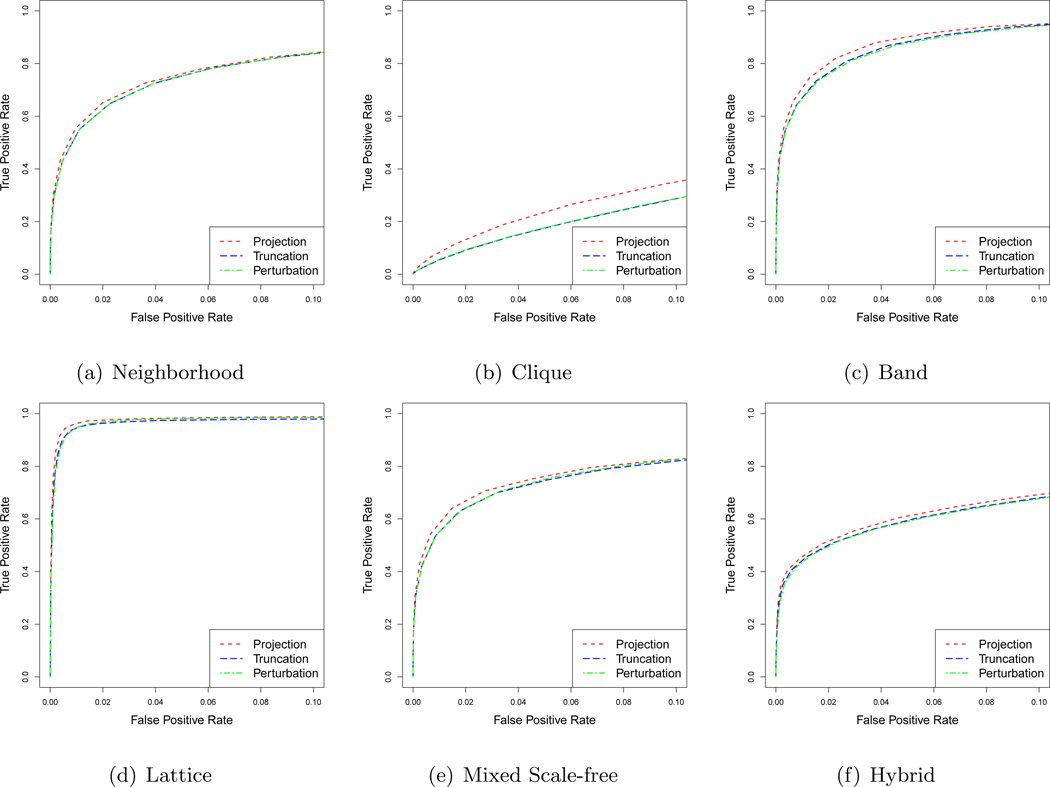
We compare the proposed projection method in §3.10 with the above two estimators using the same settings as our simulations in §5. Figure 11 shows the average ROC curves over 100 replications. We see that the projection method achieves better graph recovery performance than the competitors for all the six graphs.

Figure 11.

Average ROC curves of the neighborhood pursuit when combing with different correlation estimators. “Projection” represents the projection method. “Truncation” represents the estimator defined in (7.2). “Perturbation” represents the estimator defined in (7.3). We see that the projection method achieves better graph recovery performance than the other two estimators for all the six graphs.

Two closely related methods are copula discriminant analysis (Han et al., 2013), and semiparametric sparse inverse column operator (Zhao and Liu, 2013). Similar to the nonparanormal neighborhood pursuit, both methods are formulated as ℓ₁ regularized quadratic programs. When the transformed Kendall’s tau matrix is indeginite, their computational formulations become non-convex. Thus the proposed projection approach can also benefit these two methods to achieve better empirical performance with theoretical guarantees. More details can be found in Han et al. (2013); Zhao and Liu (2013).

In this paper, we propose a projection method to handle the possible indefiniteness of the transformed Kendall’s tau matrix in semiparametric graph estimation. We derive a computationally tractable optimization algorithm to secure the positive semidefiniteness of the estimated correlation matrix in high dimensions. The theoretical study, combined with the proposed projection method, shows that the neighborhood pursuit achieves graph estimation consistency for nonparanormal models under suitable conditions. More importantly, this nonparanormal graph estimation problem illustrates a fundamental tradeoff between statistics and computation. Our result shows that it is possible to simultaneously gain robustness of estimation and modeling flexibility without losing good computational structures such as convexity and smoothness. The proposed methodology is theoretically justifiable and applicable to a wide range of problems.

Appendix A

A Proof of Theorem 4.1

Proof. We define

$$\mathbf{Û}=\underset{{\Vert |\mathbf{U}|\Vert }_1\le 1}{\text{argmax}}\langle \mathbf{U},\mathbf{A}\rangle .$$ (A.1)

This implies that

$${\Vert |\mathbf{A}|\Vert }_{\infty }-\frac{\mu }{2}\stackrel{(\mathrm{i})}{\le }\langle \mathbf{Û},\mathbf{A}\rangle -\frac{\mu }{2}{\Vert \mathbf{Û}\Vert }_{\mathrm{F}}^2\stackrel{(\mathrm{i}\mathrm{i})}{\le }{\Vert |\mathbf{A}|\Vert }_{\infty }^{\mu }\le \langle \mathbf{Ũ},\mathbf{A}\rangle \stackrel{(\mathrm{i}\mathrm{i}\mathrm{i})}{\le }{\Vert |\mathbf{A}|\Vert }_{\infty },$$ (A.2)

where (i) comes from the fact ${\Vert \mathbf{Û}\Vert }_{\mathrm{F}}^2\le {\Vert |\mathbf{Û}|\Vert }_1^2$, (ii) comes from the fact that ${\Vert |\mathbf{A}|\Vert }_{\infty }^{\mu }$ is obtained by maximizing (3.7), and (iii) comes from the fact that Û is the maximizer to (A.1). A direct result of (A.2) is

$${\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le {\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }^{\mu }+\frac{\mu }{2}.$$ (A.3)

Since S̅ is a feasible solution to (3.10), we have

$${\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }^{\mu }\le {\Vert |\mathbf{S̅}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }^{\mu }.$$ (A.4)

Recall (3.5), we further have

$${\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }^{\mu }\le {\Vert |\mathbf{S̅}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le 2{\Vert |\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }.$$ (A.5)

Combing (A.3) and (A.5), we further have

$${\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le 2{\Vert |\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }+\frac{\mu }{2}.$$ (A.6)

Since $\mu ={\kappa }_2\sqrt{\text{log}d/n}$, combining (A.6) and Lemma 2.2, we eventually have

$$\mathbb{P}({\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le {\kappa }_3\sqrt{\frac{\text{log}d}{n}})\ge \mathbb{P}({\Vert |\mathbf{Ŝ}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le {\kappa }_1\sqrt{\frac{\text{log}d}{n}})\ge 1-\frac{1}{d^3},$$ (A.7)

where κ₃ = 2κ₁ + κ₂/2.

Appendix B

B Proof of Theorem 4.3

Before we proceed with the proof, we need to introduce the following lemmas. Their detailed proofs are provided in the supplementary materials.

Lemma B.1. Let A, B ∈ ℝ^d×d be two symmetric matrices, we have ‖AB‖_∞ ≤ ‖A‖_∞‖B‖_∞.

Lemma B.2. Let B, B̂ ∈ ℝ^d×d be two invertible symmetric matrices and ${\Vert \mathbf{B}-\mathbf{B̂}\Vert }_{\infty }{\Vert {\mathbf{B}}^{-1}\Vert }_{\infty }<\frac{1}{2}$, then we have

$${\Vert {\mathbf{B̂}}^{-1}-{\mathbf{B}}^{-1}\Vert }_{\infty }\le 2{\Vert {\mathbf{B}}^{-1}\Vert }_{\infty }^2{\Vert \mathbf{B̂}-\mathbf{B}\Vert }_{\infty }.$$ (B.1)

Lemma B.3. Let A, B ∈ ℝ^d×d be invertible symmetric matrices with

$${\Vert \mathbf{A}{\mathbf{B}}^{-1}\Vert }_{\infty }\le \alpha ,{\Vert {\mathbf{B}}^{-1}\Vert }_{\infty }\le \psi \mathit{\text{and}}{\Vert \mathbf{B}-\mathbf{B̂}\Vert }_{\infty }{\Vert {\mathbf{B}}^{-1}\Vert }_{\infty }<\frac{1}{2}.$$ (B.2)

We have

$${\Vert \mathbf{Â}{\mathbf{B̂}}^{-1}-\mathbf{A}{\mathbf{B}}^{-1}\Vert }_{\infty }\le 2\psi {\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\infty }+2\alpha \psi {\Vert \mathbf{B̂}-\mathbf{B}\Vert }_{\infty }.$$ (B.3)

Lemma B.4. Let Â, A ∈ ℝ^d×d be symmetric matrices and υ̂, υ ∈ ℝ^d be vectors, we have

$${\Vert \mathbf{Â}\mathit{\upsilon ̂}-\mathbf{A}\mathit{\upsilon }\Vert }_{\infty }\le {\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\infty }{\Vert \mathit{\upsilon ̂}-\mathit{\upsilon }\Vert }_{\infty }+{\Vert \mathbf{Â}-\mathbf{A}\Vert }_{\infty }{\Vert \mathit{\upsilon }\Vert }_{\infty }+{\Vert \mathbf{A}\Vert }_{\infty }{\Vert \mathit{\upsilon ̂}-\mathit{\upsilon }\Vert }_{\infty }.$$ (B.4)

Lemma B.5. Assuming that Σ* satisfies Assumption 2 and ${\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le {\kappa }_3\sqrt{\text{log}d/n}$ and s = max_j |I_j|, we have

$${\Vert {\mathbf{S̃}}_{I_j{I}_j}-{\mathbf{\Sigma }}_{I_j{I}_j}^{*}\Vert }_{\infty }\le {\kappa }_{3}s\sqrt{\frac{\text{log}d}{n}},$$ (B.5)

$${\Vert {\mathbf{S̃}}_{J_j{I}_j}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}\Vert }_{\infty }\le {\kappa }_{3}s\sqrt{\frac{\text{log}d}{n}},$$ (B.6)

$${\Vert {\mathbf{S̃}}_{\backslash j,j}-{\mathbf{\Sigma }}_{\backslash j,j}^{*}\Vert }_{\infty }\le {\kappa }_3\sqrt{\frac{\text{log}d}{n}}.$$ (B.7)

Moreover, for large enough n, we have that S̃_IjIj is invertible and Λ_min(S̃_IjIj) ≥ δ/2.

Proof. We adopt a similar strategy in Zhao and Yu (2006); Meinshausen and Bühlmann (2006); Zou (2006); Wainwright (2009); Mai et al. (2012), and all the analysis assumes that the following condition holds,

$${\Vert |\mathbf{S̃}-{\mathbf{\Sigma }}^{*}|\Vert }_{\infty }\le {\kappa }_3\sqrt{\frac{\text{log}d}{n}}.$$ (B.8)

Thus by Lemma B.5, for large enough n, S̃_IjIj is invertible and positive definite.

We define the following optimization problem with an auxiliary variable β̂ ∈ ℝ^d,

$${\mathit{\beta ̂}}_{I_j}=\underset{{\mathit{\beta }}_{I_j}}{\text{argmin}}{\mathit{\beta }}_{I_j}^T{\mathbf{S̃}}_{I_j{I}_j}{\mathit{\beta }}_{I_j}-2{\mathbf{S̃}}_{I_j,j}^T{\mathit{\beta }}_{I_j}+\lambda {\Vert {\mathit{\beta }}_{I_j}\Vert }_1.$$ (B.9)

Since S̃_IjIj is positive definite, (B.9) is strongly convex and has an unique solution

$${\mathit{\beta ̂}}_{I_j}={({\mathbf{S̃}}_{I_j{I}_j})}^{-1}({\mathbf{S̃}}_{I_j,j}-\frac{\lambda }{2}{\mathit{\zeta }}_{I_j}),$$ (B.10)

where ζ_Ij is the subgradient of ‖β_Ij‖₁ at β_Ij = β̂_Ij. We set β̂_Jj = 0 and β̂_j = 0. Thus β̂ exactly recovers the neighborhood structure of node j, if β̂_Ij does not contain any zero entry.

Now we will show that given (B.8) and large enough n, β̂ is the optimal solution to (3.3). We need to verify the optimality conditions of (3.3) as follows:

$${\mathbf{S̃}}_{I_j{I}_j}{\mathit{\beta ̂}}_{I_j}-{\mathbf{S̃}}_{I_j,j}+\frac{\lambda }{2}{\mathit{\zeta }}_{I_j}=0,$$ (B.11)

$${\mathbf{S̃}}_{J_j{I}_j}{\mathit{\beta ̂}}_{I_j}-{\mathbf{S̃}}_{J_j,j}+\frac{\lambda }{2}{\mathit{\zeta }}_{J_j}=0.$$ (B.12)

Note that (B.10) already implies (B.11). By plugging (B.10) into (B.12), we have

$${\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}\frac{\lambda }{2}{\mathit{\zeta }}_{I_j}-{\mathbf{S̃}}_{J_j,j}+\frac{\lambda }{2}{\mathit{\zeta }}_{J_j}=0,$$ (B.13)

where ζ_Jj is the subgradient of ‖β_Jj‖₁ at β_Jj = 0. Therefore, we only need to verify

$${\Vert {\mathit{\zeta }}_{J_j}\Vert }_{\infty }\le 2{\lambda }^{-1}{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{\mathbf{S̃}}_{J_j,j}\Vert }_{\infty }+{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathit{\zeta }}_{I_j}\Vert }_{\infty }\le 2{\lambda }^{-1}{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{\mathbf{S̃}}_{J_j,j}\Vert }_{\infty }+{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }+\alpha ,$$ (B.14)

where the last inequality comes from ‖ζ_Ij ‖_∞ ≤ 1, Assumption 1, and the triangle inequality. It suffices to show that

$$2{\lambda }^{-1}{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{\mathbf{S̃}}_{J_j,j}\Vert }_{\infty }+{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }<1-\alpha .$$ (B.15)

By (3.2) we have ${\mathbf{\Sigma }}_{\backslash j,\backslash j}^{*}{\mathbf{B}}_{\backslash j,j}^{*}={\mathbf{\Sigma }}_{\backslash j,j}^{*}$ and ${\mathbf{B}}_{J_j,j}^{*}=0$, we can further rewrite (3.2) as

$${\mathbf{\Sigma }}_{I_j,I_j}^{*}{\mathbf{B}}_{I_j,j}^{*}={\mathbf{\Sigma }}_{I_j,j}^{*}\text{and}{\mathbf{\Sigma }}_{J_j,I_j}^{*}{\mathbf{B}}_{I_j,j}^{*}={\mathbf{\Sigma }}_{J_j,j}^{*},$$ (B.16)

which implies that

$${\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}{\mathbf{\Sigma }}_{I_j,j}^{*}={\mathbf{\Sigma }}_{J_j,j}^{*}.$$ (B.17)

Thus we have

$${\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{\mathbf{S̃}}_{J_j,j}\Vert }_{\infty }\le {\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{\mathbf{\Sigma }}_{J_j,j}^{*}\Vert }_{\infty }+{\Vert {\mathbf{S̃}}_{J_j,j}-{\mathbf{\Sigma }}_{J_j,j}^{*}\Vert }_{\infty }\stackrel{(\mathrm{i}\mathrm{v})}{=}{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}{\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }+{\Vert {\mathbf{S̃}}_{J_j,j}-{\mathbf{\Sigma }}_{J_j,j}^{*}\Vert }_{\infty }\le {\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }{\Vert {\mathbf{S̃}}_{I_j,j}-{\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }+{\Vert {\mathbf{S̃}}_{J_j,j}-{\mathbf{\Sigma }}_{J_j,j}^{*}\Vert }_{\infty }+{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }{\Vert {\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }+{\Vert {\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }{\Vert {\mathbf{S̃}}_{I_j,j}-{\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }\stackrel{(\mathrm{v})}{\le }{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }{\Vert {\mathbf{S̃}}_{\backslash j,j}-{\mathbf{\Sigma }}_{\backslash j,j}^{*}\Vert }_{\infty }+{\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j})}^{-1}\Vert }_{\infty }+(\alpha +1){\Vert {\mathbf{S̃}}_{\backslash j,j}-{\mathbf{\Sigma }}_{\backslash j,j}^{*}\Vert }_{\infty },$$ (B.18)

where (iv) comes from (B.17) and (v) comes from Lemma B.4 with  = S̃_JjIj (S̃_IjIj)⁻¹S̃_Ij,j, $\mathbf{A}={\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}$, υ̂ = S̃_Ij,j, and $\mathit{\upsilon }={\mathbf{\Sigma }}_{I_j,j}^{*}$. When ${\Vert {\mathbf{S̃}}_{\backslash j,j}-{\mathbf{\Sigma }}_{\backslash j,j}^{*}\Vert }_{\infty }\le 1$, we need to verify

$$(1+\frac{4}{\lambda }){\Vert {\mathbf{S̃}}_{J_j{I}_j}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }+\frac{2(\alpha +1)}{\lambda }{\Vert {\mathbf{S̃}}_{\backslash j,j}-{\mathbf{\Sigma }}_{\backslash j,j}^{*}\Vert }_{\infty }<1-\alpha .$$ (B.19)

Then by Lemma B.3 with  = S̃_JjIj, $\mathbf{A}={\mathbf{\Sigma }}_{J_j{I}_j}^{*}$, B̂ = S̃_IjIj ; and $\mathbf{B}={\mathbf{\Sigma }}_{I_j{I}_j}^{*}$, we only need to verify that, when λ ≤ 2,

$$12\psi \alpha {\Vert {\mathbf{S̃}}_{I_j{I}_j}-{\mathbf{\Sigma }}_{I_j{I}_j}^{*}\Vert }_{\infty }+12\psi {\Vert {\mathbf{S̃}}_{J_j{I}_j}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}\Vert }_{\infty }+2(\alpha +1){\Vert {\mathbf{S̃}}_{\backslash j,j}-{\mathbf{\Sigma }}_{\backslash j,j}^{*}\Vert }_{\infty }<\lambda (1-\alpha ).$$

It is easy to see that given λ ≤ 2 and α < 1, the above inequality holds when

$${\Vert {\mathbf{S̃}}_{I_j{I}_j}-{\mathbf{\Sigma }}_{I_j{I}_j}^{*}\Vert }_{\infty }<\frac{\lambda (1-\alpha )}{26\psi \alpha },{\Vert {\mathbf{S̃}}_{J_j{I}_j}-{\mathbf{\Sigma }}_{J_j{I}_j}^{*}\Vert }_{\infty }<\frac{\lambda (1-\alpha )}{26\psi },{\Vert {\mathbf{S̃}}_{\backslash j,j}-{\mathbf{\Sigma }}_{\backslash j,j}^{*}\Vert }_{\infty }<\frac{\lambda (1-\alpha )}{26(\alpha +1)}<1.$$ (B.20)

Then we need to show that β̂_Ij has no zero elements. Here we aim to secure a sufficient condition $\tau >{\Vert {\mathit{\beta ̂}}_{I_j}-{\mathbf{B}}_{I_j,j}^{*}\Vert }_{\infty }$. Since

$${\Vert {\mathit{\beta ̂}}_{I_j}-{\mathbf{B}}_{I_j,j}^{*}\Vert }_{\infty }={\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}{\mathbf{\Sigma }}_{I_j,j}^{*}-\frac{\lambda }{2}{({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathit{\zeta }}_{I_j})\Vert }_{\infty }\le {\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}{\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }+\frac{\lambda }{2}{\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}\Vert }_{\infty },$$ (B.21)

by Lemma B.4 with  = (S̃_IjIj)⁻¹, $\mathbf{A}={({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}$, υ̂ = S̃_Ij,j, and $\mathit{\upsilon }={\mathbf{\Sigma }}_{I_j,j}^{*}$, we have

$${\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}{\mathbf{S̃}}_{I_j,j}-{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}{\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }\le {\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }{\Vert {\mathbf{S̃}}_{I_j,j}-{\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }+{\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }+\psi {\Vert {\mathbf{S̃}}_{I_j,j}-{\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }\le 2{\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }+\psi {\Vert {\mathbf{S̃}}_{\backslash ,j}-{\mathbf{\Sigma }}_{\backslash ,j}^{*}\Vert }_{\infty },$$ (B.22)

where the last inequality holds when ${\Vert {\mathbf{S̃}}_{I_j,j}-{\mathbf{\Sigma }}_{I_j,j}^{*}\Vert }_{\infty }\le 1$. Combining

$$\frac{\lambda }{2}{\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}\Vert }_{\infty }\le \frac{\lambda }{2}{\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }+\frac{\lambda \psi }{2}$$

with (B.22), we have

$${\Vert {\mathit{\beta ̂}}_{I_j}-{\mathbf{B}}_{I_j,j}^{*}\Vert }_{\infty }\le (\frac{\lambda }{2}+2){\Vert {({\mathbf{S̃}}_{I_j{I}_j})}^{-1}-{({\mathbf{\Sigma }}_{I_j{I}_j}^{*})}^{-1}\Vert }_{\infty }+\psi {\Vert {\mathbf{S̃}}_{\backslash ,j}-{\mathbf{\Sigma }}_{\backslash ,j}^{*}\Vert }_{\infty }+\frac{\lambda \psi }{2}\le (\lambda +4){\psi }^2{\Vert {\mathbf{S̃}}_{I_j{I}_j}-{\mathbf{\Sigma }}_{I_j{I}_j}^{*}\Vert }_{\infty }+\psi {\Vert {\mathbf{S̃}}_{\backslash ,j}-{\mathbf{\Sigma }}_{\backslash ,j}^{*}\Vert }_{\infty }+\frac{\lambda \psi }{2},$$ (B.23)

where the last inequality comes from Lemma B.2. Now we only need to show that

$$6{\psi }^2{\Vert {\mathbf{S̃}}_{I_j{I}_j}-{\mathbf{\Sigma }}_{I_j{I}_j}^{*}\Vert }_{\infty }+\psi {\Vert {\mathbf{S̃}}_{\backslash ,j}-{\mathbf{\Sigma }}_{\backslash ,j}^{*}\Vert }_{\infty }<\frac{\tau }{2},$$ (B.24)

when λψ ≤ and λ ≤ 2. It is easy to verify that (B.24) holds when

$${\Vert {\mathbf{S̃}}_{I_j{I}_j}-{\mathbf{\Sigma }}_{I_j{I}_j}^{*}\Vert }_{\infty }<\frac{\tau }{14{\psi }^2}\text{and}{\Vert {\mathbf{S̃}}_{\backslash ,j}-{\mathbf{\Sigma }}_{\backslash ,j}^{*}\Vert }_{\infty }<\frac{\tau }{14\psi }.$$ (B.25)

By applying Lemma B.5 and Theorem 4.1 to (B.20) and (B.25), for large enough n such that

$$\sqrt{\frac{\text{log}d}{n}}\le \text{min}\{\frac{\lambda (1-\alpha )}{26\psi \alpha {\kappa }_{3}s},\frac{\lambda (1-\alpha )}{26\psi {\kappa }_{3}s},\frac{\lambda (1-\alpha )}{26(\alpha +1)},\frac{\tau }{14{\psi }^{2}s{\kappa }_3},\frac{\tau }{14\psi {\kappa }_3},\frac{\delta }{2s{\kappa }_3}\},$$

we have

$$\mathbb{P}(\mathbf{Ê}={\mathbf{E}}^{*})\ge 1-\frac{1}{d^3}.$$

Under Conditions 1, 2, and 3, we obtain ℙ(Ê = E*) → 1.