Identifying Genetic Variants for Addiction via Propensity Score Adjusted Generalized Kendall’s Tau

Abstract

Identifying replicable genetic variants for addiction has been extremely challenging. Besides the common difficulties with genome-wide association studies (GWAS), environmental factors are known to be critical to addiction, and comorbidity is widely observed. Despite the importance of environmental factors and comorbidity for addiction study, few GWAS analyses adequately considered them due to the limitations of the existing statistical methods. Although parametric methods have been developed to adjust for covariates in association analysis, difficulties arise when the traits are multivariate because there is no ready-to-use model for them. Recent nonparametric development includes U-statistics to measure the phenotype-genotype association weighted by a similarity score of covariates. However, it is not clear how to optimize the similarity score. Therefore, we propose a semiparametric method to measure the association adjusted by covariates. In our approach, the nonparametric U-statistic is adjusted by parametric estimates of propensity scores using the idea of inverse probability weighting. The new measurement is shown to be asymptotically unbiased under our null hypothesis while the previous non-weighted and weighted ones are not. Simulation results show that our test improves power as opposed to the non-weighted and two other weighted U-statistic methods, and it is particularly powerful for detecting gene-environment interactions. Finally, we apply our proposed test to the Study of Addiction: Genetics and Environment (SAGE) to identify genetic variants for addiction. Novel genetic variants are found from our analysis, which warrant further investigation in the future.

1 INTRODUCTION

Identifying genetic risk variants for addiction (substance dependence) has drawn much attention due to the popularity of genome-wide association studies (GWAS) based on high throughput data. Many genetic signals for addiction have been discovered using GWAS in recent years. Studies focusing on nicotine dependence include Bierut et al. (2007), Uhl et al. (2007), Luo et al. (2008), Drgon et al. (2009), Rice et al. (2012), and Wang et al. (2012), among others. Similarly, there are many important discoveries for alcohol dependence, including but not limited to, Reich et al. (1998), Treutlein et al. (2009), Edenberg et al. (2010), Bierut et al. (2010), Johnson et al. (2006), Kendler et al. (2011), Heath et al. (2011), Wang et al. (2011), and Frank et al. (2012).

Despite these important findings, it still remains to be a very challenging problem to identify genetic variants for addiction, especially taking into account the following two issues. First, comorbidity of addiction is widely observed in the existing literature (National Institute on Drug Abuse, 2010). For example, Zuo et al. (2012a) and Zuo et al. (2012b) studied the risk gene regions in alcohol and nicotine co-dependence. Substance dependence can also be comorbid with other diseases such as depression (Edwards et al., 2012). Second, environmental factors (covariates) are known to play an important role in the association analysis between genetic risk factors and addiction. Examples include stress and history of violence. These factors can potentially produce confounding effects, or they can interact with genotypes known as the gene-environment interactions.

In this work, we aim to analyze the data from the Study of Addiction: Genetics and Environment (SAGE), which is part of the Gene Environment Association Studies initiative (GENEVA) funded by the National Human Genome Research Institute. In the SAGE data, addiction to six different substances were measured simultaneously for the subjects, including alcohol, nicotine, marijuana, cocaine, opiates, and other drugs. A preliminary analysis shows that different addictions are dependent. In the data, there are about 45% subjects who are addicted to nicotine and 47% subjects addicted to alcohol. The nicotine and alcohol co-dependence rate is 32%, much higher than the rate if assuming these two traits are statistically independent. Moreover, information about important environmental factors was also collected. Environmental factors such as history of sexual abuse or violence and socioeconomic status have a non-negligible effect on substance dependence. To analyze the SAGE data, it remains an open question on how to properly adjust for these important covariates with such a complicated constitution of phenotypes. This motivates us to develop a new statistical method to fill this gap.

Traditionally, covariates were usually adjusted in GWAS by being added into a parametric association model such as a binary or an ordinal logistic regression model (Wang et al., 2006). However, there are two major drawbacks when using a parametric model-based approach for analysis of comorbidity of multiple traits. First, it is challenging to build a parametric model for multiple traits especially with different scales. Second, it is not clear how to remove the confounding effects through the model. Therefore, nonparametric tools were recently proposed. To handle comorbidity, Zhang et al. (2010) proposed a nonparametric U-statistic to measure association, called the “generalized Kendall’s tau”, which can take any hybrid of dichotomous, ordinal and quantitative traits. The generalized Kendall’s tau is applicable to both population-based and family-based designs. It is also noteworthy that the family-based association tests (FBAT) (Laird et al., 2000; Rabinowitz and Laird, 2000) are a special case of the generalized Kendall’s tau. To further adjust for environmental factors in a nonparametric setting, Zhu et al. (2012) and Jiang and Zhang (2011) proposed weighted versions of generalized Kendall’s tau. For the weight function, Zhu et al. (2012) used covariates themselves while Jiang and Zhang (2011) used propensity scores (Rosenbaum and Rubin, 1983). The weighted nonparametric tests have shown their power for detecting genetic effects after considering environmental effects.

The weighted tests are proven useful but still face difficulties. For instance, researchers are often required to select the tuning parameters in the weight function (Jiang and Zhang, 2011; Zhu et al., 2012). Although suggestions were made, this extra step makes the tests less accessible. In this work, we propose an alternative that is more natural and convenient. Instead of directly weighting the generalized Kendall’s tau, we employ the idea of “inverse probability weighting” from the applications of propensity scores (Rosenbaum, 1987; Robins et al., 2000; Lunceford and Davidian, 2004). First, we use a parametric model to estimate the genomic propensity scores (Zhao et al., 2009) which summarize all covariates. Then, we apply the inverse probability weighting using the parametric propensity score estimates to the genotype kernel of the nonparametric U-statistic. These procedures result in our proposed semiparametric measurement of association adjusted by covariates.

In an observational study, the inverse probability weighting method aims to construct an unbiased estimator of treatment effect. Similarly, we show that our U-statistic is an asymptotically unbiased estimator of the phenotype-genotype association under the null hypothesis, while the non-weighted and other weighted U-statistics are not necessarily asymptotically unbiased. Moreover, the inverse probability weighted U-statistic is free of tuning parameters. Another contribution of this work is to provide the null distribution of our test statistic incorporating the estimation step of propensity scores. Interestingly, we find that if the propensity scores are estimated consistently ($\sqrt{n}$-consistency indeed), the U-statistic has even a smaller variance than the one with true propensity scores. This confirms a surprising but known fact that “it is better to use the ‘estimated propensity score’ than the true propensity score even when the true score is known” (Robins et al., 1992). Nonetheless, it is the first time (to the best of our knowledge) to rigorously formalize this idea either from a U-statistic viewpoint or in the framework of genome-wide association tests.

To evaluate the performance of our proposed test, we perform simulation studies to compare with the generalized Kendall’s tau and its weighted versions in terms of type I error and power. The simulation results show that our test possesses a higher power in most situations we examined and is particularly powerful for detecting gene-environment interactions.

Finally, we apply our proposed test to the SAGE data, together with non-weighted and other weighted tests, for comorbidity of multiple addictions. We also compare the comorbidity based analyses with the analysis from a single addiction at a time. Interestingly, besides a few overlapped markers, novel regions have been detected using multiple phenotypes, and different approaches may be more powerful under different settings; for example, a comorbidity genetic analysis is more powerful only for shared genes. Among the tests for multiple addictions, we clearly see the advantage of adjusting for important covariates in our analysis. Without any adjustment, no SNP was identified to be genome-wide significant. With adjustment, different adjusted tests work complementarily to each other. Our proposed test, in particular, reveals SNPs/genes that are not discovered by other tests. For example, the SNP rs251133 (on chromosome 5) achieves the genome-wide significance only using our proposed test. The new findings from our analyses warrant further investigation with either a replication study or a biological verification.

2 SEMIPARAMETRIC ASSOCIATION TEST

2.1 Non-weighted and Weighted Association Measurements

Suppose we observe a vector of traits ${\mathbf{Y}}_i=\{Y_i^{\left(1\right)},\dots ,Y_i^{\left(p\right)}\}\prime$, a test-locus genotype G_i, and a vector of covariates ${\mathbf{Z}}_i=\{Z_i^{\left(1\right)},\dots ,Z_i^{\left(q\right)}\}\prime$ for the ith subject in the n study subjects from a population association study. Our data are independent samples $\{({\mathbf{Y}}_i^{\prime },G_i,{\mathbf{Z}}_i^{\prime })\prime :i=1,\dots ,n\}$. In the following, we denote Y = {Y₁, … , Y_n} and Z = {Z₁, … , Z_n} for all the traits and covariates, respectively. We present here a few nonparametric association statistics to measure the association between the multiple traits and the genetic marker.

The first statistic was proposed by Zhang et al. (2010). For individuals i and j, let Y_i and Y_j be their vectors of traits respectively. Then, a trait kernel is defined as

$${\varphi }_t({\mathbf{Y}}_i,{\mathbf{Y}}_j)=\left[f_1\{Y_i^{\left(1\right)}-Y_j^{\left(1\right)}\},\dots ,f_p\{Y_i^{\left(p\right)}-Y_j^{\left(p\right)}\}\right]\prime ,$$

where function f_k(·) (k = 1, … , p) can be chosen as the identity function for a quantitative or binary trait (Rabinowitz, 1997), or the sign function for an ordinal trait (Zhang et al., 2006). Traditionally, a genotype kernel is chosen as

$${\varphi }_g(G_i,G_j)=G_i-G_j.$$

Based on these two kernels, Zhang et al. (2010) proposed a nonparametric U-statistic to measure the association between the phenotype and genotype as

$$\mathbf{U}={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}{\varphi }_t({\mathbf{Y}}_i,{\mathbf{Y}}_j){\varphi }_g(G_i,G_j),$$ (1)

which is a generalization of Kendall’s tau (Kendall, 1938). This U-statistic was used there to test the null hypothesis that there is no phenotype-genotype association.

For the purpose of adjusting for the covariates, Zhu et al. (2012) introduced another statistic, which is a weighted version of U in (1). Let w(Z_i, Z_j) be a weight function measuring the similarity between Z_i and Z_j. For instance, the most intuitive weight function w(Z_i, Z_j) can be defined as a function of the distance or similarity of the two covariate vectors Z_i and Z_j. Afterwards, they defined the weighted U-statistic as

$${\mathbf{U}}_{\mathrm{w},1}={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}{\varphi }_t({\mathbf{Y}}_i,{\mathbf{Y}}_j){\varphi }_g(G_i,G_j)w({\mathbf{Z}}_i,{\mathbf{Z}}_j).$$ (2)

This weighted U-statistic is used to measure the covariate-adjusted association between the multiple traits and the genetic marker.

Considering the fact that there exist potentially continuous (such as age) and categorical (such as gender) covariates, their distance or similarity can become arbitrary and complicated especially when we have many covariates. Therefore, Jiang and Zhang (2011) proposed to summarize all the covariates, continuous or categorical, into the propensity score (Rosenbaum and Rubin, 1983; Zhao et al., 2009). Its definition is the likelihood of an individual having a particular test-locus genotype based on that individual’s covariate makeup, which can be explicitly stated as

$$\mathbf{p}\left({\mathbf{z}}_i\right)=\left\{P(G_i=g\mid {\mathbf{Z}}_i={\mathbf{z}}_i):g\in \mathcal{𝒢}\right\}\prime ,$$

with 𝒢 being the set of possible values for the genotype G; while in our context, 𝒢 = {0, 1, 2} representing {aa, Aa, AA} for a SNP marker with two alleles A and a. Then the weighted U-statistic in (2) becomes

$${\mathbf{U}}_{\mathrm{w},2}={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}{\varphi }_t({\mathbf{Y}}_i,{\mathbf{Y}}_j){\varphi }_g(G_i,G_j)w\left(\mathbf{p}\left({\mathbf{Z}}_i\right),\mathbf{p}\left({\mathbf{Z}}_j\right)\right).$$ (3)

These weighted U-statistics (2) and (3) were proposed to adjust the association taking into account the covariate effects. They have been proven useful in both theory and application especially when the covariates have direct or indirect effects on the traits (Jiang and Zhang, 2011; Zhu et al., 2012).

2.2 Inverse Probability Weighting

In the case without covariates, a natural choice of measurement of genotype-phenotype association is given by U in (1). One property of U is its unbiasedness under the null hypothesis. That is, E(U | Y) = 0 when there is no association between the genotype and phenotype (Zhang et al., 2010). It is noteworthy that conditioning on the traits is necessary to eliminate the need for assumptions about the phenotypic distribution (Laird et al., 2000).

When the covariate information is available, however, in order to remove the confounding effects of the covariates, one needs to test the conditional independence between the genotype and phenotype conditional on the covariates (Zhu et al., 2012). That is ℋ₀ : Y_i ⊥ G_i | Z_i, i = 1, … , n. Under the new null hypothesis ℋ₀, however, the U-statistic U in (1) is not necessarily an unbiased measure. The reason is that, under ℋ₀,

$$E(\mathbf{U}\mid \mathbf{Y})={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}{\varphi }_t({\mathbf{Y}}_i,{\mathbf{Y}}_j)\{E(G_i\mid {\mathbf{Y}}_i)-E(G_j\mid {\mathbf{Y}}_j)\},$$

which is a similar association measurement to U in (1) with the genotype G_i replaced by its conditional mean E(G_i | Y_i). This implies that E(U | Y) would have a non-degenerate distribution (when Y_i’s are regarded as random) unless all E(G_i | Y_i)’s are equal. Therefore, E(U | Y) cannot always be zero. The same conclusion holds for the weighted U-statistics U_W,1 and U_W,2 in (2) and (3). They are also not necessarily unbiased under the null hypothesis ℋ₀.

Therefore, we need to revise the above-mentioned U-statistics to ensure the theoretical unbiasedness. Borrowing the idea of the inverse probability weighting method for propensity scores (Rosenbaum, 1987; Robins et al., 2000; Lunceford and Davidian, 2004), we revise the genotype kernel from ϕ_g(G_i, G_j) = G_i − G_j to

$${\varphi }_g(G_i,G_j;{\mathbf{Z}}_i,{\mathbf{Z}}_j)=\frac{G_i}{e\left({\mathbf{Z}}_i\right)}-\frac{G_j}{e\left({\mathbf{Z}}_j\right)},$$

where e(z_i) = E(G_i | Z_i = z_i) is the conditional expectation of G_i given Z_i = z_i. In general, e(z_i) can be directly obtained from the propensity score as

$$e\left({\mathbf{z}}_i\right)=\sum _{g\in \mathcal{𝒢}}gP(G_i=g\mid {\mathbf{Z}}_i={\mathbf{z}}_i).$$

Then we propose the propensity score-inverse probability weighted U-statistic as

$${\mathbf{U}}_{\text{IPW}}={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}{\varphi }_t({\mathbf{Y}}_i,{\mathbf{Y}}_j){\varphi }_g(G_i,G_j;{\mathbf{Z}}_i,{\mathbf{Z}}_j).$$ (4)

From (4), we see that

$$E({\mathbf{U}}_{\text{IPW}}\mid \mathbf{Y})={\left(\begin{array}{c}\hfill n\hfill \\ \hfill 2\hfill \end{array}\right)}^{-1}\sum _{i<j}{\varphi }_t({\mathbf{Y}}_i,{\mathbf{Y}}_j)E\left[E\left\{{\varphi }_g(G_i,G_j;{\mathbf{Z}}_i,{\mathbf{Z}}_j)\mid {\mathbf{Z}}_i,{\mathbf{Z}}_j\right\}\mid \mathbf{Y}\right]=0,$$

as E{ϕ_g(G_i, G_j; Z_i, Z_j) | Z_i, Z_j} = 0 under ℋ₀. This shows that U_IPW is an unbiased estimator of the conditional association between the genotype and phenotype under ℋ₀, provided that the true values of propensity scores are known.

2.3 Asymptotic Distribution with True Propensity Scores

As illustrated by Zhu et al. (2012), the asymptotic distribution of U_IPW may be derived conditioning on both traits Y = y and covariates Z = z. Write ${\stackrel{‒}{\mathbf{u}}}_i=\frac{1}{n}{\sum }_{j=1}^n{\varphi }_t({\mathbf{Y}}_i,{\mathbf{Y}}_j)$, then

$${\mathbf{U}}_{\text{IPW}}=\frac{2}{n-1}\sum _{i=1}^n{\stackrel{‒}{u}}_i{G}_i∕e\left({\mathbf{Z}}_i\right).$$

Conditioning on both traits and covariates, the mean of U_IPW is still zero under ℋ₀. The asymptotic distribution of U_IPW can be derived by applying the central limit theorem. Theorem 1 reveals that U_IPW has an asymptotic normal distribution after normalization by its variance.

Theorem 1. Let v(z_i) = var(G_i | Z_i = z_i). Assume inf_n,i |e(z_i)| > 0 and inf_n,i |v(z_i)| > 0. Suppose ${\text{max}}_{1\le i\le n}\parallel {\stackrel{‒}{\mathbf{u}}}_i{\parallel }^2=o\left\{{\lambda }_{\text{min}}\left({\sum }_{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{\stackrel{‒}{\mathbf{u}}}_i^{\prime }\right)\right\}$, where λ_min represents the minimum eigenvalue. Then, under the null hypothesis ℋ₀,

$$\sqrt{n}{\sum }^{-1∕2}{\mathbf{U}}_{\text{IPW}}\to N(0,{\mathbf{I}}_p)$$

in distribution, conditioning on all the traits and covariates, where

$$\sum =\frac{4}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_i{\stackrel{‒}{u}}_i^{\prime }\nu \left({\mathbf{z}}_i\right)∕e^2\left({\mathbf{z}}_i\right).$$

U_ipw is a linear combination of the independent genotypes G₁, … , G_n. This observation inspires the application of Corollary 1.3 in Shao (2003) to prove Theorem 1. The conditions inf_n,i |e(z_i)| > 0 and inf_n,i |v(z_i)| > 0 are assumed to ensure the positive definiteness of the covariance matrix Σ. Moreover, the condition ${\text{max}}_{1\le i\le n}\parallel {\stackrel{‒}{\mathbf{u}}}_i{\parallel }^2=o\left\{{\lambda }_{\text{min}}\left({\sum }_{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{\stackrel{‒}{\mathbf{u}}}_i^{\prime }\right)\right\}$ is used to control the contribution of each term in the linear combination so that no term is dominant of all the others (see the regularity condition in Corollary 1.3 in Shao (2003)).

2.4 Test Statistic with Estimated Propensity Scores

In Section 2.3, U_IPW involves the true values of the propensity score p(z_i) and the mean e(z_i). However, in the real situation, the propensity scores are always estimated from the samples, i.e., by $\widehat{\mathbf{p}}\left({\mathbf{Z}}_i\right)$. So is the mean e(z_i) in the statistic U_IPW, estimated by $\widehat{e}\left({\mathbf{Z}}_i\right)$. In this case, the test statistic becomes

$${\widehat{U}}_{\text{IPW}}=\frac{2}{n-1}\sum _{i=1}^n{\stackrel{‒}{u}}_i{G}_i∕\widehat{e}\left({\mathbf{Z}}_i\right).$$

Therefore, we aim to find the asymptotic distribution of the test statistic ${\widehat{\mathbf{U}}}_{\text{IPW}}$ in this subsection. This distribution will serve as the reference distribution for our association test.

We assume a parametric model indexed by parameters θ ∈ R^d to estimate the propensity scores. Therefore, we call ${\widehat{\mathbf{U}}}_{\text{IPW}}$ a semiparametric measurement given both its parametric and nonparametric components. To estimate p(z_i) and further e(z_i), we make use of the maximum likelihood estimator or the root of the likelihood equations $\widehat{\theta }$ from this model. It is noteworthy that we do not limit ourselves to any specific form of models. Instead, we build the theory upon the following general parametric form,

$$P(G_i=g\mid {\mathbf{Z}}_i={\mathbf{z}}_i)=p_g({\mathbf{z}}_i;\theta ),g=0,1,2;i=1,\dots ,n,$$ (5)

with ${\sum }_{g=0}^2{p}_g({\mathbf{z}}_i;\theta )=1$. For clarity, θ₀ is used for the true values of θ. Thus, e_θ0(z_i) and v_θ0(z_i) denote the true values of e(z_i) and v(z_i), respectively.

With model (5), we observe that ${\widehat{\mathbf{U}}}_{\text{IPW}}={\mathrm{U}}_{\text{IPW}}\left(\widehat{\theta }\right)$ is a statistic with estimated parameters $\widehat{\theta }$. To derive the asymptotic distribution of ${\widehat{\mathbf{U}}}_{\text{IPW}}$, we follow the approach suggested by Pierce (1982) and Randles (1982). The idea is to derive the asymptotic joint distribution of $\{{\mathbf{U}}_{\text{IPW}}^{\prime }\left({\theta }_0\right),\widehat{\theta }\prime \}\prime$ and then to approximate the distribution of ${\widehat{\mathbf{U}}}_{\text{IPW}}$ using the mean value theorem.

Before presenting the main theoretical result, we need to introduce some necessary notation. With i = 1, … , n, the log-likelihood function log ℓ_i(θ) of model (5) is

$$\text{log}{\ell }_i\left(\theta \right)=\sum _{g=0}^{2}I(G_i=g)\text{log}{p}_g({\mathbf{z}}_i;\theta ).$$

We assume the score function ψ_θ(G_i, z_i) and information matrix I_θ(z_i) are well defined as

$${\psi }_{\theta }(G_i,{\mathbf{z}}_i)=\frac{\partial }{\partial \theta }\text{log}{\ell }_i\left(\theta \right)=\sum _{g=0}^{2}I(G_i=g)p_g^{-1}({\mathbf{z}}_t;\theta )\frac{\partial }{\partial \theta }{p}_g({\mathbf{z}}_i;\theta ),$$ (6)

$$I_{\theta }\left({\mathbf{z}}_i\right)=E\left\{{\psi }_{\theta }(G_i,{\mathbf{z}}_i){\psi }_{\theta }^{\prime }(G_i,{\mathbf{z}}_i)\right\}=\sum _{g=0}^2{p}_g^{-1}({\mathbf{z}}_i;\theta )\frac{\partial }{\partial \theta }{p}_g({\mathbf{z}}_i;\theta )\frac{\partial }{\partial \theta \prime }{p}_g({\mathbf{z}}_i;\theta ).$$ (7)

In addition, define the following matrices,

$$\begin{array}{cc}\hfill \sum _{{\theta }_0}& =\frac{4}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_i{\stackrel{‒}{u}}_i^{\prime }{\nu }_{{\theta }_0}\left({\mathbf{z}}_i\right)∕e_{{\theta }_0}^2\left({\mathbf{z}}_i\right),\hfill \\ \hfill {\Gamma }_{{\theta }_0}& =\frac{2}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_i\sum _{g=0}^2\left(g\frac{\partial }{\partial \theta \prime }{p}_g\{{\mathbf{z}}_i;{\theta }_0)\right\}∕e_{{\theta }_0}\left({\mathbf{z}}_i\right),\hfill \end{array}$$ (8)

and vectors (for i = 1, … , n),

$$\begin{array}{cc}\hfill {\gamma }_{i1}& ={\left\{{\stackrel{‒}{u}}_i^{\prime }∕e_{{\theta }_0}\left({\mathbf{z}}_i\right),p_1^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta \prime }{p}_1({\mathbf{z}}_i;{\theta }_0)-p_0^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta \prime }{p}_0({\mathbf{z}}_i;{\theta }_0)\right\}}^{\prime },\hfill \\ \hfill {\gamma }_{i2}& ={\left\{2{\stackrel{‒}{u}}_i^{\prime }∕e_{{\theta }_0}\left({\mathbf{z}}_i\right),p_2^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta \prime }{p}_2({\mathbf{z}}_i;{\theta }_0)-p_0^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta \prime }{p}_0({\mathbf{z}}_i;{\theta }_0)\right\}}^{\prime }.\hfill \end{array}$$

Theorem 2 presents the asymptotic distribution of the test statistic ${\widehat{\mathbf{U}}}_{\text{IPW}}$, with the detailed derivation provided in the Appendix.

Theorem 2. Let the parameter space Θ be an open set. Suppose that, there exist some δ > 0 andc_θ0 > 0 such that p_g(z_i; θ) ∈ [δ, 1 − δ] for all θ satisfying ∥θ − θ₀∥ ≤ c_θ0 with g = 0, 1, 2 and i = 1, … , n; ℓ_i(θ) is twice continuously differentiable; for each g = 0, 1, 2,

$$\underset{1\le i\le n}{\max }\underset{\Vert \theta -{\theta }_0\Vert \le c_{{\theta }_0}}{\text{sup}}\Vert \frac{\partial }{\partial \theta }{p}_g({\mathbf{z}}_i;\theta )\Vert =O\left(1\right),\underset{1\le i\le n}{\max }\underset{\Vert \theta -{\theta }_0\Vert \le c_{{\theta }_0}}{\text{sup}}\Vert \frac{{\partial }^2}{\partial \theta \partial \theta \prime }{p}_g({\mathbf{z}}_i;\theta )\Vert =O\left(1\right),$$ (9)

and there exists constants C_θ0 > 0 and α > 0 such that for all θ satisfying ∥θ − θ₀∥ ≤ c_θ0,

$$\frac{1}{n}\sum _{i=1}^n\Vert \frac{{\partial }^2}{\partial \theta \partial \theta \prime }{p}_g({\mathbf{z}}_i;\theta )-\frac{{\partial }^2}{\partial \theta \partial \theta \prime }{p}_g({\mathbf{z}}_i;{\theta }_0)\Vert \le C_{{\theta }_0}\Vert \theta -{\theta }_0{\Vert }^{\alpha },$$ (10)

where ∥A∥ = {tr(A′A)}^1/2 is the Frobenius norm for any matrix A; there exists a positive definite matrix I_θ0 such that $\frac{1}{n}{\sum }_{i=1}^n{\mathbf{I}}_{{\theta }_0}\left({\mathbf{z}}_i\right)\to {\mathbf{I}}_{{\theta }_0};{\lambda }_{\text{max}}\left({\sum }_{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{\stackrel{‒}{\mathbf{u}}}_i^{\prime }\right)=O\left(n\right)$ and ${\text{max}}_{1\le i\le n}\parallel {\stackrel{‒}{\mathbf{u}}}_i{\parallel }^2=o\left(n\right)$; furthermore, ${\text{max}}_{1\le i\le n}{\lambda }_{\text{max}}({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })=o\left[{\lambda }_{\text{min}}\left\{{\sum }_{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}\right]$ and ${\lambda }_{\text{min}}\left\{{\sum }_{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}\ge nϵ$ for some ϵ > 0, where λ_max represents the maximum eigenvalue. Let ${\Lambda }_{{\theta }_0}={\sum }_{{\theta }_0}-{\Gamma }_{{\theta }_0}{\mathbf{I}}_{{\theta }_0}^{-1}{\Gamma }_{{\theta }_0}^{\prime }$. Then, under the null hypothesis ℋ₀,

$$\sqrt{n}{\Lambda }_{{\theta }_0}^{-1∕2}{\widehat{U}}_{\text{IPW}}\to N(0,{\mathbf{I}}_p),$$

in distribution, conditioning on all the traits and covariates.

The condition ${\text{max}}_{1\le i\le n}{\lambda }_{\text{max}}({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })=o\left[{\lambda }_{\text{min}}\left\{{\sum }_{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}\right]$ in Theorem 2 has the same role as the condition ${\text{max}}_{1\le i\le n}\parallel {\stackrel{‒}{\mathbf{u}}}_i{\parallel }^2=o\left\{{\lambda }_{\text{min}}\left({\sum }_{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{\stackrel{‒}{\mathbf{u}}}_i^{\prime }\right)\right\}$ in Theorem 1. It is a typical requirement of the central limit theorem for a weighted sum of independent random variables. That is, none of the weights would dominate all the others in an asymptotic sense.

Theorem 2 implies the asymptotic unbiasedness of the semiparametric statistic ${\widehat{\mathbf{U}}}_{\text{IPW}}$ under our null hypothesis ℋ₀, when the propensity scores are estimated using a parametric model. This property has not been achieved by either the non-weighted or the weighted statistics in the previous work (Zhang et al., 2010; Jiang and Zhang, 2011; Zhu et al., 2012). This agrees with our observation in Section 2.2 when the true values of propensity scores are assumed to be known.

In addition, a comparison between Theorems 1 and 2 reveals that the asymptotic variance of ${\widehat{\mathbf{U}}}_{\text{IPW}}$ is smaller than that of U_IPW, the U-statistic with true propensity scores. This confirms a surprising but known fact that “it is better to use the ‘estimated propensity score’ than the true propensity score even when the true score is known” (Robins et al., 1992). This phenomenon has been revealed by both theory (Rosenbaum, 1987; Robins et al., 1992) and empirical studies (Gu and Rosenbaum, 1993). Nonetheless, it is the first time (to the best of our knowledge) to rigorously formalize the idea either from a U-statistic viewpoint or in the framework of association tests.

2.5 A Specific Example

As a specific example of model (5), we consider the ordinal logistic regression model

$$\text{logit}\{G_i\le g\mid {\mathbf{Z}}_i={\mathbf{z}}_i\}={\lambda }_g+\beta \prime {\mathbf{z}}_i,g=0,1;i=1,\dots ,n,$$ (11)

where λ₀ < λ₁ are ascending level parameters, and β reflects the association between the gene and covariates. Using the notation in Section 2.4, θ = (λ₀, λ₁, β′)′ ∈ R^q+2 and d = q + 2.

Let

$$q_g({\mathbf{z}}_i;\theta )=\frac{\text{exp}({\lambda }_g+\beta \prime {\mathbf{z}}_i)}{1+\text{exp}({\lambda }_g+\beta \prime {\mathbf{z}}_i)},g=0,1,$$

be the cumulative probabilities with q_g(z_i; θ) = Σ_g′≤g p_g′(z_i; θ), then the first-order derivatives in (6) can be explicitly written as follows,

$$\begin{array}{cc}\hfill \frac{\partial }{\partial \theta }{p}_0({\mathbf{z}}_i;\theta )& =\pi \left\{q_0({\mathbf{z}}_i;\theta )\right\}{\varphi }_{10i},\hfill \\ \hfill \frac{\partial }{\partial \theta }{p}_1({\mathbf{z}}_i;\theta )& =\pi \left\{q_1({\mathbf{z}}_i;\theta )\right\}{\varphi }_{01i}-\pi \left\{q_0({\mathbf{z}}_i;\theta )\right\}{\varphi }_{10i},\hfill \\ \hfill \frac{\partial }{\partial \theta }{p}_2({\mathbf{z}}_i;\theta )& =-\pi \left\{q_1({\mathbf{z}}_i;\theta )\right\}{\varphi }_{01i},\hfill \end{array}$$

with π(x) = x(1 − x), ${\varphi }_{10i}=(1,0,{\mathbf{z}}_i^{\prime })\prime$ and ${\varphi }_{01i}=(0,1,{\mathbf{z}}_i^{\prime })\prime$. The second-order derivatives in (9) and (10) can also be explicitly written as

$$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial \theta \partial \theta \prime }{p}_0({\mathbf{z}}_i;\theta )& =\varpi \left\{q_0({\mathbf{z}}_i;\theta )\right\}{\varphi }_{10i}{\varphi }_{10i}^{\prime },\hfill \\ \hfill \frac{{\partial }^2}{\partial \theta \partial \theta \prime }{p}_1({\mathbf{z}}_i;\theta )& =\varpi \left\{q_1({\mathbf{z}}_i;\theta )\right\}{\varphi }_{01i}{\varphi }_{01i}^{\prime }-\varpi \left\{q_0({\mathbf{z}}_i;\theta )\right\}{\varphi }_{10i}{\varphi }_{10i}^{\prime },\hfill \\ \hfill \frac{{\partial }^2}{\partial \theta \partial \theta \prime }{p}_2({\mathbf{z}}_i;\theta )& =-\varpi \left\{q_1({\mathbf{z}}_i;\theta )\right\}{\varphi }_{01i}{\varphi }_{01i}^{\prime },\hfill \end{array}$$

with $\varpi \left(x\right)=x(1-x)(1-2x)$. In this way, we can write the explicit form of the information matrix in (7) as

$${\mathbf{I}}_{\theta }\left({\mathbf{z}}_i\right)=\left[\frac{1}{p_0({\mathbf{z}}_i;\theta )}+\frac{1}{p_1({\mathbf{z}}_i;\theta )}\right]{\pi }^2\left\{q_0({\mathbf{z}}_i;\theta )\right\}{\varphi }_{10i}{\varphi }_{10i}^{\prime }+\left[\frac{1}{p_1({\mathbf{z}}_i;\theta )}+\frac{1}{p_2({\mathbf{z}}_i;\theta )}\right]{\pi }^2\left\{q_1({\mathbf{z}}_i;\theta )\right\}{\varphi }_{01i}{\varphi }_{01i}^{\prime }-\frac{1}{p_1({\mathbf{z}}_i;\theta )}\pi \left\{q_0({\mathbf{z}}_i;\theta )\right\}\pi \left\{q_1({\mathbf{z}}_i;\theta )\right\}({\varphi }_{10i}{\varphi }_{10i}^{\prime }+{\varphi }_{01i}{\varphi }_{10i}^{\prime }),$$ (12)

and the matrix Γ_θ0 in (8) as

$${\Gamma }_{{\theta }_0}=-\frac{2}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_i[\pi \left\{q_0({\mathbf{z}}_i;{\theta }_0)\right\}{\varphi }_{10i}^{\prime }+\pi \left\{q_1({\mathbf{z}}_i;{\theta }_0)\right\}{\varphi }_{01i}^{\prime }]∕e_{{\theta }_0}\left({\mathbf{z}}_i\right).$$ (13)

The main result in Theorem 2 follows as long as its conditions are satisfied. Indeed, some of the conditions become redundant in this specific example, such as the twice continuous differentiability of the likelihood function. Moreover, conditions (9) and (10) can be simplified into a simple condition max_1≤i≤n ∥z_i∥ = O(1). In summary, we present the following corollary parallel to Theorem 2 specifically for this example.

Corollary 1. Assume model (11) holds. Suppose that, there exist some δ > 0 andc_θ0 > 0 such that p_g(z_i; θ) ∈ [δ, 1 − δ] for all θ satisfying ∥θ − θ₀∥ c_θ0 with g = 0, 1, 2 and i = 1, … , n; max_1≤i≤n ∥z_i∥ = O(1), ${\text{max}}_{1\le i\le n}\parallel {\stackrel{‒}{\mathbf{u}}}_i{\parallel }^2=o\left(n\right)$, and ${\lambda }_{\text{max}}\left({\sum }_{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{\stackrel{‒}{\mathbf{u}}}_i^{\prime }\right)=O\left(n\right);{\text{max}}_{1\le i\le n}{\lambda }_{\text{max}}({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })=o\left[{\lambda }_{\text{min}}\left\{{\sum }_{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}\right]$ and ${\lambda }_{\text{min}}\left\{{\sum }_{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}\ge nϵ$ for some ϵ > 0, where

$$\begin{array}{cc}\hfill {\gamma }_{i1}& ={\{{\stackrel{‒}{u}}_i^{\prime }{e}_{{\theta }_0}^{-1}\left({\mathbf{z}}_i\right),-1-p_{i0}{p}_{i2}{p}_{i1}^{-1},p_{i2}+p_{i0}{p}_{i2}{p}_{i1}^{-1},-(p_{i0}+p_{i1}){\mathbf{z}}_i^{\prime }\}}^{\prime },\hfill \\ \hfill {\gamma }_{i2}& ={\{2{\stackrel{‒}{u}}_i^{\prime }{e}_{{\theta }_0}^{-1}\left({\mathbf{z}}_i\right),-p_{i1}-p_{i2},-p_{i0}-p_{i1},-(1+p_{i1}){\mathbf{z}}_i^{\prime }\}}^{\prime },\hfill \end{array}$$

with the simplified notation p_ig = p_g(z_i; θ₀); there exists a positive definite matrix I_θ0 such that $\frac{1}{n}{\sum }_{i=1}^n{\mathbf{I}}_{{\theta }_0}\left({\mathbf{z}}_i\right)\to {\mathbf{I}}_{{\theta }_0}$ with I_θ0(z_i) in (12). Then, the conclusion of Theorem 2 holds with the explicit form of Γ_θ0 given in (13).

Following the asymptotic distribution of ${\widehat{\mathbf{U}}}_{\text{IPW}}$ in Corollary 1, we define the test statistic

$${\widehat{T}}_{\text{IPW}}=n{\widehat{U}}_{\text{IPW}}^{\prime }{\widehat{\Lambda }}^{-1}{\widehat{U}}_{\text{IPW}},$$

where $\widehat{\Lambda }={\Lambda }_{\widehat{\theta }}$ is the estimator of Λ_θ0. The consistency of $\widehat{\Lambda }$ can be verified under the conditions of Corollary 1. Therefore, it is clear that

$${\widehat{T}}_{\text{IPW}}\to {\chi }_p^2,$$

in distribution, conditioning on all the traits and covariates. This serves as the reference distribution in our numerical studies.

2.6 Genotype Coding

As mentioned in Section 2.1, the genotype G is coded as 0, 1, 2 representing aa, Aa, AA respectively, which record the number of a reference allele A. The choice of a different reference allele a leads to a different coding of genotype such as G′ = 2 − G. We illustrate in this subsection the effect of different genotype codings on the association measurements we studied in Sections 2.1–2.2.

Firstly, notice that the genotype kernel ϕ_g(G_i, G_j) in (1) is invariant to the change of genotype coding from G to G′, i.e., ${\varphi }_g(G_i,G_j)={\varphi }_g(G_i^{\prime },G_j^{\prime })$. Therefore, the non-weighted U-statistic U in (1) and the weighted U-statistic U_W,1 in (2) are both invariant to the genotype codings.

Secondly, the propensity score vector p(z_i) = {P(G_i = g | Z_i = z_i) : g ∈ 𝒢}′ in the weighted U-statistics U_W,2 in (3) is invariant except that the order of its elements is reversed. It leads to the invariance of U_W,2, as long as the weight function w(u₁, u₂) in (3) is not changed by the synchronous permutation of the elements in u₁ and u₂. This is often the case. For example, Jiang and Zhang (2011) used w(u₁, u₂) = exp(−∥u₁−u₂∥²/2), which satisfies the above condition.

Finally, we should note that our proposed measurement U_IPW does not possess the invariance property under the two genotype codings. The revised genotype kernel ϕ_g(G_i, G_j; Z_i, Z_j) is not invariant under codings G and G′. Using a different genotype coding will actually change our association measurement U_IPW and further change the test result. This is understandable because we apply a new weighting scheme. In the non-weighted U-statistic U, the genotypes G_i are treated equally in the genotype kernel. However, to achieve the unbiasedness under ℋ₀, the new U-statistic U_IPW inversely weights the genotypes by their expected values conditional on the covariates. It is the new weighting scheme that violates the invariance but achieves the unbiasedness. From the practical viewpoint, the new method can give us more flexibility to choose a genotype coding which better fits the real situation.

For clarity, we recommend the simple genotype coding. We choose the major allele as the reference allele for practical reasons. In practice, the inverse probability weighting often encounters the difficulty of small weights in the denominator. However, it is fairly easy to see that the above choice is much less likely to result in small denominators e(z_i) (or $\widehat{e}\left({\mathbf{z}}_i\right)$) in U_IPW (or ${\widehat{\mathbf{U}}}_{\text{IPW}}$) than the other choice. Therefore, we try to avoid the situation where the weights e(z_i) (or $\widehat{e}\left({\mathbf{z}}_i\right)$) in the denominator are close to zero.

3 SIMULATION STUDIES

3.1 Settings

We conduct simulation studies to compare the performance of our semiparametric association test ${\widehat{T}}_{\text{IPW}}$ with the three methods mentioned in Section 2.1. They are the non-weighted and weighted tests derived from the association measures (1)–(3), denoted by T, T_W,1 and T_W,2 respectively. We utilize the same “conditional independence” null hypothesis ℋ₀ (see Section 2.2) for all four tests for a fair comparison. The simulation results are obtained from samples with size of 500, which are generated as follows.

Step 1: For the ith sample, a continuous covariate Z_i1 is simulated from N(0, 1) distribution, and a binary covariate Z_i2 is randomly sampled from {−1, 1} with equal probabilities.

Step 2: For the relationship between the covariates and the test-locus genotype G_i, we generate G_i from the ordinal logistic regression model

$$\text{OLR:}\text{logit}\left\{P(G_i\le g\mid Z_{i1},Z_{i2})\right\}={\mu }_g-{\nu }_1{Z}_{i1}-{\nu }_2{Z}_{i2},g=0,1,$$

where ν₁ and ν₂ control the association between the genotype and the covariates. An alternative genotype model is to generate G_i according to a binomial distribution Bin(2, r_i) with probability r_i satisfying

$$\text{BIN:}\text{logit}\left(r_i\right)=\mu +{\nu }_1{Z}_{i1}+{\nu }_2{Z}_{i2}+{ϵ}_i,$$

where ϵ_i ∼ N(0, 1) is a random error. We refer to the former model “OLR” and the latter model “BIN”. The former model is the one we specified in Section 2.5, while the latter model is used to assess the effect of model misspecification with ϵ_i deliberately added for additional complexity.

Step 3: Conditional on the genotype G_i and the covariates Z_i1 and Z_i2, two binary traits ${\mathbf{Y}}_i=(Y_i^{\left(1\right)},Y_i^{\left(2\right)})\prime$ are generated according to a logistic regression phenotype model,

$$\text{logit}\left\{P(Y_i^{\left(j\right)}=1\mid G_i,Z_{i1},Z_{i2})\right\}={\alpha }_j+{\beta }_G{G}_i+{\beta }_{Z_1}{Z}_{i1}+{\beta }_{Z_2}{Z}_{i2}+{\beta }_{G{Z}_1}{G}_i{Z}_{i1}+{\beta }_{G{Z}_2}{G}_i{Z}_{i2}+{ϵ}_{ij},$$

with i = 1, … , n; j = 1, 2; and (ϵ_i1, ϵ_i2)′ ∼ N(0,Σ_ϵ).

In the two genotype models (OLR and BIN), the minor allele frequency (MAF) of the simulated genotype depends on the values of μ₀, μ₁, μ and ν₁, ν₂. To investigate the possible effect of different minor allele frequencies on our results, we fix ν₁ = ν₂ = 1 and select appropriate values of μ₀, μ₁ and μ. Their values are chosen so that the simulated minor allele frequency is equal to one of the following values: 0.05, 0.10, 0.15, … , 0.40. These choices give a broad and reasonable range for evaluating how an association test performs with different minor allele frequencies.

In the phenotype model, we set α₁ = −0.75, α₂ = −1, and ${\sum }_{ϵ}=\left(\begin{array}{cc}\hfill 1\hfill & \hfill 0.25\hfill \\ \hfill 0.25\hfill & \hfill 1\hfill \end{array}\right)$. The choices of the coefficients (β_G, β_Z1, β_Z2, β_GZ1, β_GZ2)′ are provided by Table 1 as different phenotype models. The models N1 and N2 are null models under ℋ₀ in which Y_i and G_i are independent conditional on (Z_i1, Z_i2), and the models A1–A6 are under our alternative hypothesis.

Table 1.

Phenotype models

Null Models
N1	βG = 0	βZ1 = βZ2 = 0	βGZ1 = βGZ2 = 0
N2	βG = 0	βZ1 = βZ2 = 0.5	βGZ1 = βGZ2 = 0
Alternative Models
A1	βG = 0.5	βZ1 = βZ2 = 0	βGZ1 = βGZ2 = 0
A2	βG = 0.5	βZ1 = βZ2 = 0.5	βGZ1 = βGZ2 = 0
A3	βG = 0.5	βZ1 = βZ2 = 0	βGZ1 = βGZ2 = 1
A4	βG = 0.5	βZ1 = βZ2 = 0.5	βGZ1 = βGZ2 = 1
A5	βG = 0.5	βZ1 = βZ2 = 0	βGZ1 = βGZ2 = 2
A6	βG = 0.5	βZ1 = βZ2 = 0	βGZ1 = βGZ2 = 2

3.2 Results for Bivariate Phenotypes

In this subsection, we present simulation results for the generated bivariate phenotypes. In terms of type I error, Table 2 presents the empirical type I error of the four tests based on 10,000 replications when the nominal level is set to 0.001. Table 2 also includes the type I error results when the nominal level is 5 × 10⁻⁷. To save the computational time, we fix the minor allele frequency at 0.10 there. This smaller nominal level provides an additional comparison among different methods in a situation similar to the real application (Burton et al., 2007). To illustrate the necessity of utilizing the “conditional independence” null hypothesis ℋ₀, we also include T′, the non-weighted test under the original “unconditional independence” null hypothesis ${\mathcal{\mathscr{H}}}_0^{\prime }$—no association between phenotype and genotype. In terms of power, Figures 1-4 present the statistical power of the four tests with respect to a wide range of minor allele frequencies. Figures 1-2 correspond to the nominal level 0.001 and Figures 3-4 correspond to the nominal level 5 × 10⁻⁷.

Table 2.

Type I error for bivariate phenotypes

MAF	T	T W,1	T W,2	${\widehat{T}}_{\text{IPW}}$	T ′	T	T W,1	T W,2	${\widehat{T}}_{\text{IPW}}$	T ′
	Model OLR (Nominal Level: 0.001)
	Model N1					Model N2
0.05	1.0e-3	0.9e-3	1.6e-3	1.1e-3	0.5e-3	0.5e-3	0.8e-3	0.6e-3	1.1e-3	0.2358
0.10	0.7e-3	0.7e-3	0.7e-3	1.0e-3	0.7e-3	0.4e-3	0.9e-3	1.2e-3	0.9e-3	0.4913
0.15	1.4e-3	0.8e-3	0.8e-3	1.3e-3	0.6e-3	0.5e-3	0.6e-3	0.7e-3	1.0e-3	0.6463
0.20	1.0e-3	0.7e-3	0.9e-3	1.0e-3	0.7e-3	1.0e-3	1.1e-3	1.0e-3	1.4e-3	0.7249
0.25	0.8e-3	0.9e-3	0.6e-3	0.7e-3	0.5e-3	0.8e-3	1.0e-3	1.1e-3	1.1e-3	0.7804
0.30	0.9e-3	0.9e-3	1.0e-3	1.1e-3	0.7e-3	0.7e-3	1.2e-3	0.8e-3	0.7e-3	0.8049
0.35	0.9e-3	0.6e-3	0.8e-3	1.5e-3	0.8e-3	0.5e-3	0.8e-3	1.4e-3	0.9e-3	0.8250
0.40	0.9e-3	1.3e-3	1.0e-3	1.0e-3	1.3e-3	0.5e-3	0.9e-3	0.5e-3	1.2e-3	0.8391
	Model BIN (Nominal Level: 0.001)
	Model N1					Model N2
0.05	0.5e-3	1.1e-3	0.5e-3	0.8e-3	0.8e-3	0.2e-3	0.1e-3	0.3e-3	0.7e-3	0.1937
0.10	1.2e-3	1.2e-3	0.7e-3	1.7e-3	1.3e-3	0.2e-3	0.4e-3	0.5e-3	0.6e-3	0.4293
0.15	0.8e-3	0.7e-3	0.4e-3	0.9e-3	0.8e-3	0.6e-3	1.1e-3	0.8e-3	1.7e-3	0.5950
0.20	1.1e-3	1.2e-3	1.0e-3	1.5e-3	1.5e-3	0.6e-3	0.6e-3	0.7e-3	1.1e-3	0.6954
0.25	0.5e-3	0.6e-3	0.7e-3	0.5e-3	1.1e-3	0.4e-3	0.6e-3	0.6e-3	0.7e-3	0.7691
0.30	1.2e-3	0.9e-3	0.8e-3	1.7e-3	1.3e-3	0.6e-3	1.1e-3	1.2e-3	0.8e-3	0.8072
0.35	0.7e-3	0.7e-3	0.5e-3	1.4e-3	0.8e-3	1.0e-3	1.6e-3	1.4e-3	0.7e-3	0.8263
0.40	1.1e-3	1.2e-3	1.4e-3	0.9e-3	1.3e-3	0.8e-3	0.9e-3	1.2e-3	0.8e-3	0.8437
	Model OLR (Nominal Level: 5 × 10−7)
	Model N1					Model N2
0.10	2e-7	2e-7	6e-7	3e-7	2e-7	3e-7	6e-7	7e-7	5e-7	0.0466208
	Model BIN (Nominal Level: 5 × 10−7)
	Model N1					Model N2
0.10	2e-7	4e-7	1e-7	5e-7	5e-7	1e-7	1e-7	1e-7	5e-7	0.0331154

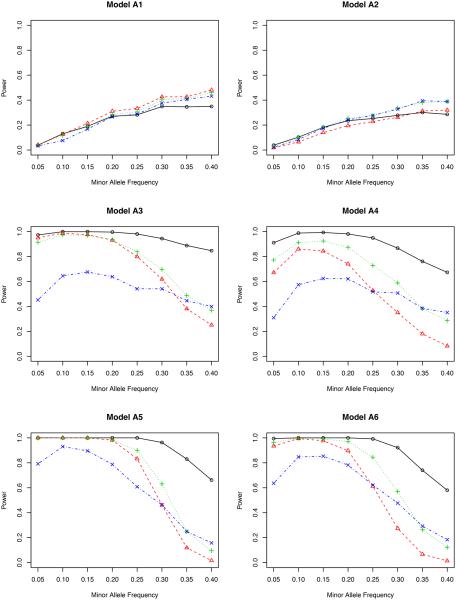
Figure 1.

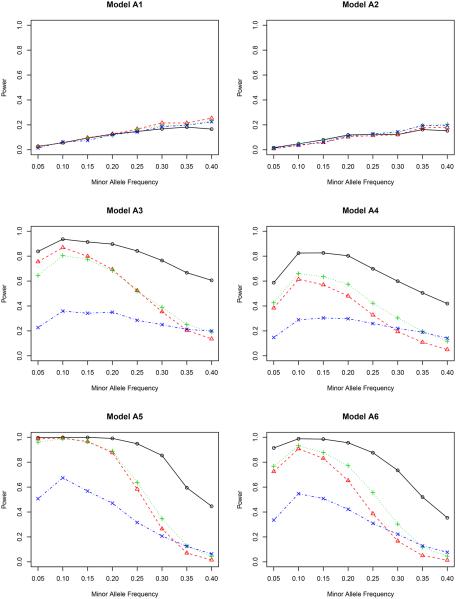
Power versus minor allele frequency for bivariate phenotypes. The significance level is 0.001. The genotype is simulated using model OLR. Solid line with circles: inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$; dashed line with triangles: non-weighted test T; dotted line with pluses: covariate weighted test T_W,1; dotdash line with crosses: propensity score weighted test T_W,2.

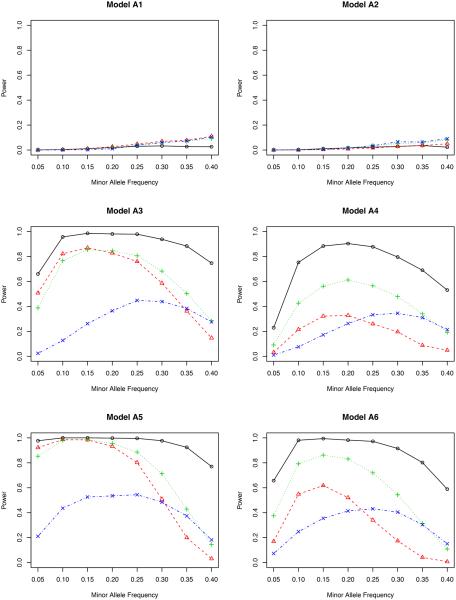
Figure 4.

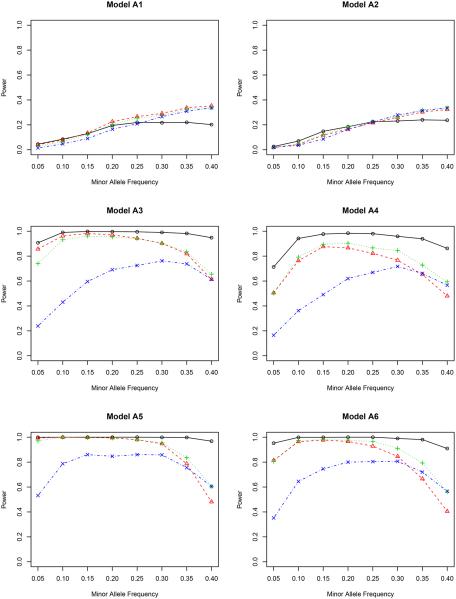
Power versus minor allele frequency for bivariate phenotypes. The significance level is 5 × 10⁻⁷. The genotype is simulated using model BIN. Solid line with circles: inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$; dashed line with triangles: non-weighted test T; dotted line with pluses: covariate weighted test T_W,1; dotdash line with crosses: propensity score weighted test T_W,2.

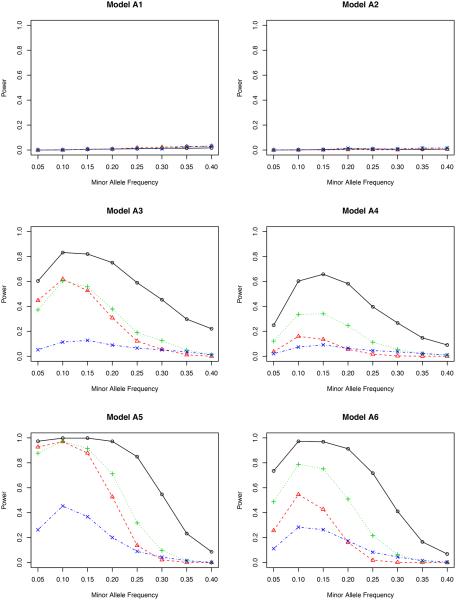
Figure 2.

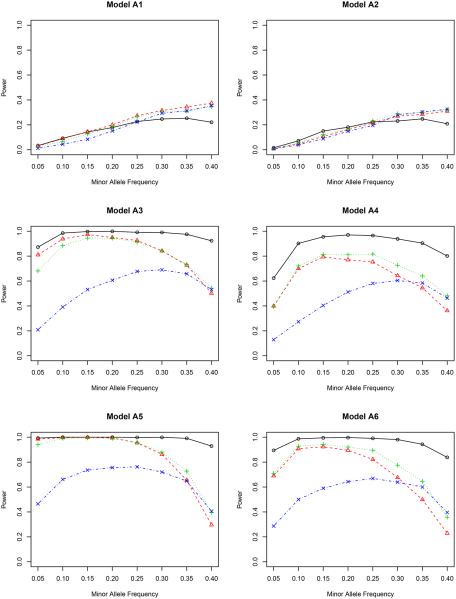
Power versus minor allele frequency for bivariate phenotypes. The significance level is 0.001. The genotype is simulated using model BIN. Solid line with circles: inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$; dashed line with triangles: non-weighted test T; dotted line with pluses: covariate weighted test T_W,1; dotdash line with crosses: propensity score weighted test T_W,2.

Figure 3.

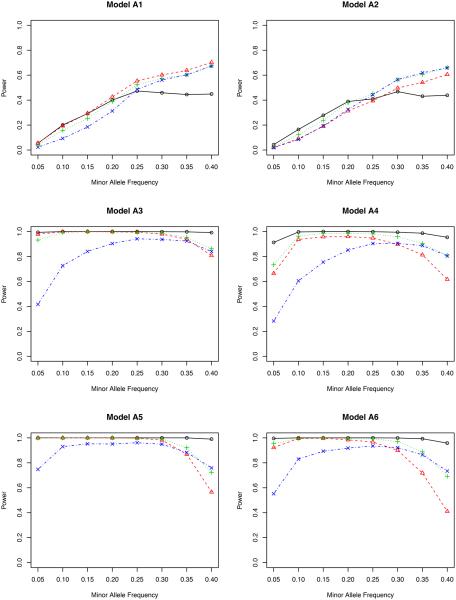
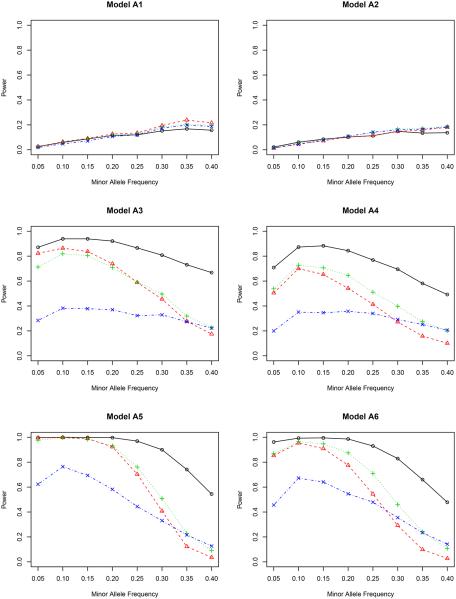
Power versus minor allele frequency for bivariate phenotypes. The significance level is 5 × 10⁻⁷. The genotype is simulated using model OLR. Solid line with circles: inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$; dashed line with triangles: non-weighted test T; dotted line with pluses: covariate weighted test T_W,1; dotdash line with crosses: propensity score weighted test T_W,2.

From the perspective of type I error (in models N1 and N2), we find that all four tests under ℋ₀ behave fairly well since they all possess reasonably accurate type I errors under both nominal levels. This is partially due to the fact that ℋ₀ removes the confounding effects of covariates. By contrast, T′ cannot control its type I error in model N2. The reason is clear: T′ does not remove the confounding effect in model N2 (Jiang and Zhang, 2011; Zhu et al., 2012).

From the perspective of power, we consider models A1–A6. Models A1–A2 are from a phenotype model without the gene-environment interaction, and A3–A6 are with an interaction. To assess situations with different gene-environment interactions, in models A5–A6, we double the interaction coefficients from models A3–A4, respectively.

In model A1 with the genetic effect only, the non-weighted test T possesses the highest power among all four methods, although their differences are actually quite small. This agrees with our expectation since it is not necessary to adjust for covariates in this case. But adjusting for covariates does not harm the statistical power. In model A2 with both genetic and environmental effects, the non-weighted test T performs the worst for most values of minor allele frequency. The other three methods are slightly better, indicating the essentiality of including covariates in the association test. It is noteworthy that the proposed inverse probability weighted test favors the region of a small minor allele frequency in both models A1 and A2. Compared to other weighted tests, the proposed test is comparable or even better for low MAF’s, but is slightly underpowered when the MAF is higher than 0.30.

By including gene-environment interactions (models A3–A4), different methods perform quite differently. It is fairly clear from all figures that the proposed test ${\widehat{T}}_{\text{IPW}}$ outperforms all competitors for all minor allele frequencies. When the nominal level is 0.001, the proposed test has a power close to 1, which means that it can identify the genetic signal in almost every replicate of the simulated data. The covariate weighted test T_W,1 wins the second place in terms of power. The non-weighted test T and the propensity score weighted test T_W,2 do not have a comparable power for a wide range of minor allele frequencies.

A further study with stronger gene-environment interactions (models A5–A6) provides additional evidence for our conclusion drawn from models A3–A4. When the gene-environment interactions dominate both genetic and environmental effects, the semiparametric inverse probability weighted test outperforms other tests in all minor allele frequencies we considered, showing the power of the proposed test in detecting the gene-environment interactions.

Comparing the two genotype models (OLR versus BIN), we have not observed a major impact from the misspecified model on testing the associations. When the genotype is generated using the binomial distribution, our test derived from the ordinal logistic regression (Section 2.5) still has a quite accurate type I error and also a high power (even higher in some cases) to detect either genetic effects or gene-environment interactions.

Between the two nominal levels (0.001 and 5 × 10⁻⁷), the statistical power becomes smaller with the lower nominal level given the same effect sizes (β’s in Table 1), especially in models A1–A2. All methods are underpowered there; with the sample size of 500, it is expected that we cannot achieve a reasonable power for a full GWAS scan, but unfortunately, the simulation for a much larger sample size takes a very long time to complete. Since our objective is to compare the relative power, we can achieve this goal with the modest sample size. In fact, for models A3–A6, the power of our proposed test is only slightly affected by this small nominal level, and it still dominates all others. In a situation similar to the real application (nominal level 5×10⁻⁷), it is clear that some adjustment is necessary when there is a gene-environment interaction.

3.3 Results for Individual Phenotypes

In addition to the simulation results for the bivariate phenotypes in Section 3.2, we also present the results for each individual phenotype Y⁽¹⁾ and Y⁽²⁾ separately. For simplicity, we fix the nominal level to be 0.001 throughout this subsection. In terms of type I error, Table 3 presents the empirical type I error of the tests based on 10,000 replications. In terms of power, Figures 5-8 present the statistical power of the four tests with respect to a wide range of minor allele frequencies, where Figures 5-6 correspond to the first phenotype and Figures 7-8 correspond to the second phenotype.

Table 3.

Type I error for individual phenotypes

MAF	T	T W,1	T W,2	${\widehat{T}}_{\text{IPW}}$	T ′	T	T W,1	T W,2	${\widehat{T}}_{\text{IPW}}$	T ′
	Phenotype Y(1), Model OLR
	Model N1					Model N2
0.05	0.7e-3	0.9e-3	0.5e-3	0.9e-3	1.2e-3	0.4e-3	0.6e-3	0.8e-3	0.7e-3	0.1288
0.10	1.2e-3	1.2e-3	1.3e-3	1.1e-3	0.6e-3	0.3e-3	0.6e-3	0.6e-3	0.9e-3	0.2689
0.15	1.0e-3	0.8e-3	1.2e-3	1.0e-3	0.9e-3	0.4e-3	0.4e-3	1.1e-3	0.8e-3	0.3703
0.20	1.4e-3	1.3e-3	1.1e-3	1.2e-3	1.1e-3	0.9e-3	1.2e-3	1.0e-3	1.1e-3	0.4441
0.25	1.3e-3	1.5e-3	1.0e-3	0.6e-3	0.7e-3	1.1e-3	1.2e-3	1.2e-3	1.7e-3	0.4966
0.30	1.0e-3	1.0e-3	0.7e-3	1.0e-3	1.0e-3	0.5e-3	0.9e-3	0.8e-3	0.9e-3	0.5173
0.35	0.7e-3	0.7e-3	0.9e-3	0.8e-3	0.7e-3	0.7e-3	1.2e-3	1.0e-3	1.3e-3	0.5402
0.40	1.2e-3	1.1e-3	1.3e-3	1.6e-3	0.7e-3	0.5e-3	0.9e-3	1.1e-3	0.9e-3	0.5566
	Phenotype Y(1), Model BIN
	Model N1					Model N2
0.05	0.6e-3	0.2e-3	0.6e-3	0.7e-3	1.2e-3	0.3e-3	0.3e-3	0.5e-3	1.2e-3	0.1099
0.10	0.5e-3	0.6e-3	0.2e-3	1.0e-3	1.5e-3	1.0e-3	1.2e-3	0.8e-3	1.8e-3	0.2319
0.15	0.5e-3	0.8e-3	0.7e-3	1.2e-3	1.4e-3	0.6e-3	0.3e-3	0.3e-3	1.0e-3	0.3321
0.20	1.0e-3	1.3e-3	1.2e-3	1.2e-3	1.0e-3	1.0e-3	1.2e-3	1.3e-3	1.5e-3	0.4100
0.25	0.6e-3	1.1e-3	0.9e-3	1.2e-3	1.1e-3	0.7e-3	0.9e-3	0.7e-3	1.1e-3	0.4768
0.30	0.5e-3	0.4e-3	0.3e-3	0.9e-3	1.0e-3	0.3e-3	0.7e-3	0.4e-3	1.4e-3	0.5136
0.35	1.3e-3	1.4e-3	1.2e-3	1.3e-3	0.8e-3	0.5e-3	0.8e-3	0.9e-3	0.7e-3	0.5491
0.40	1.2e-3	1.1e-3	0.7e-3	0.7e-3	1.1e-3	0.8e-3	0.8e-3	1.2e-3	0.7e-3	0.5665
	Phenotype Y(2), Model OLR
	Model N1					Model N2
0.05	0.9e-3	0.7e-3	0.7e-3	0.9e-3	0.8e-3	0.7e-3	1.0e-3	0.9e-3	1.1e-3	0.1246
0.10	0.6e-3	0.9e-3	0.6e-3	0.4e-3	0.3e-3	0.3e-3	0.9e-3	1.0e-3	0.9e-3	0.2586
0.15	1.2e-3	1.4e-3	1.5e-3	1.3e-3	1.1e-3	0.5e-3	0.7e-3	0.6e-3	0.7e-3	0.3620
0.20	1.7e-3	1.3e-3	1.7e-3	1.3e-3	1.4e-3	0.5e-3	0.6e-3	1.5e-3	1.3e-3	0.4232
0.25	1.0e-3	0.8e-3	1.0e-3	0.9e-3	0.9e-3	0.7e-3	1.1e-3	0.9e-3	1.0e-3	0.4678
0.30	1.0e-3	0.7e-3	1.3e-3	0.8e-3	0.9e-3	0.5e-3	0.9e-3	0.5e-3	1.0e-3	0.5047
0.35	1.1e-3	0.9e-3	1.2e-3	1.3e-3	0.6e-3	0.9e-3	0.9e-3	0.9e-3	1.1e-3	0.5170
0.40	0.4e-3	0.7e-3	0.6e-3	0.7e-3	1.0e-3	0.7e-3	1.4e-3	1.5e-3	1.2e-3	0.5235
	Phenotype Y(2), Model BIN
	Model N1					Model N2
0.05	0.7e-3	0.7e-3	1.2e-3	0.8e-3	0.9e-3	0.5e-3	0.8e-3	0.4e-3	1.3e-3	0.1091
0.10	0.3e-3	0.4e-3	0.6e-3	0.7e-3	0.6e-3	0.7e-3	0.7e-3	0.2e-3	1.0e-3	0.2282
0.15	0.8e-3	0.9e-3	0.5e-3	0.8e-3	0.5e-3	0.2e-3	0.5e-3	0.2e-3	0.9e-3	0.3195
0.20	0.7e-3	0.7e-3	0.4e-3	1.0e-3	0.9e-3	0.9e-3	1.1e-3	0.9e-3	1.6e-3	0.4007
0.25	0.7e-3	0.6e-3	0.4e-3	1.0e-3	1.0e-3	0.5e-3	0.6e-3	1.1e-3	0.8e-3	0.4558
0.30	0.4e-3	0.6e-3	0.6e-3	0.3e-3	1.0e-3	0.7e-3	0.9e-3	1.0e-3	0.6e-3	0.4942
0.35	0.5e-3	0.7e-3	0.5e-3	1.4e-3	0.7e-3	1.1e-3	1.1e-3	1.3e-3	1.4e-3	0.5106
0.40	0.8e-3	0.9e-3	0.7e-3	1.2e-3	1.0e-3	0.6e-3	0.7e-3	1.0e-3	0.8e-3	0.5313

Figure 5.

Power versus minor allele frequency for phenotype Y⁽¹⁾. The significance level is 0.001. The genotype is simulated using model OLR. Solid line with circles: inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$; dashed line with triangles: non-weighted test T; dotted line with pluses: covariate weighted test T_W,1; dotdash line with crosses: propensity score weighted test T_W,2.

Figure 8.

Power versus minor allele frequency for phenotype Y⁽²⁾. The significance level is 0.001. The genotype is simulated using model BIN. Solid line with circles: inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$; dashed line with triangles: non-weighted test T; dotted line with pluses: covariate weighted test T_W,1; dotdash line with crosses: propensity score weighted test T_W,2.

Figure 6.

Power versus minor allele frequency for phenotype Y⁽¹⁾. The significance level is 0.001. The genotype is simulated using model BIN. Solid line with circles: inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$; dashed line with triangles: non-weighted test T; dotted line with pluses: covariate weighted test T_W,1; dotdash line with crosses: propensity score weighted test T_W,2.

Figure 7.

Power versus minor allele frequency for phenotype Y⁽²⁾. The significance level is 0.001. The genotype is simulated using model OLR. Solid line with circles: inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$; dashed line with triangles: non-weighted test T; dotted line with pluses: covariate weighted test T_W,1; dotdash line with crosses: propensity score weighted test T_W,2.

In our simulations, the single-trait results are very similar to the bivariate-trait results in Section 3.2. From the perspective of type I error, all four tests under ℋ₀ behave fairly well since they all possess reasonably accurate type I errors. By contrast, T′ cannot control its type I error in model N2. From the perspective of power, we observe that the inverse probability weighted test is generally comparable to others when there is only genetic effects and/or environmental effects, and it outperforms others when there are gene-environment interactions.

3.4 Impact of Model Misspecification

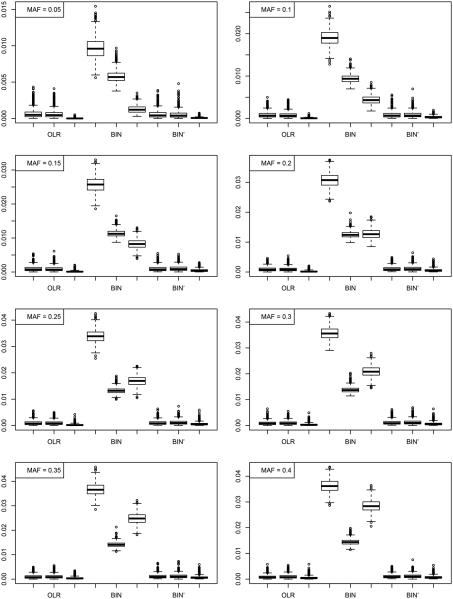
In Sections 3.2–3.3, we observed no major impact on testing the genetic associations caused by a possibly misspecified parametric gene-environment model. To better understand how the model misspecification affects the estimation of the propensity scores, we compare the estimation results under the two genotype models (OLR and BIN) used in Section 3.1. Figure 9 provides the boxplot of the mean squared errors of the estimated propensity scores ${\widehat{p}}_0,{\widehat{p}}_1$ and ${\widehat{p}}_2$ from random samples with size of 500 based on 1, 000 replications.

Figure 9.

Mean squared error of the estimated propensity scores ${\widehat{p}}_0,{\widehat{p}}_1$ and ${\widehat{p}}_2$. Each panel includes the boxplots for mean squared errors of the estimated propensity scores ${\widehat{p}}_0,{\widehat{p}}_1$ and ${\widehat{p}}_2$, in that particular order, from genotype models OLR, BIN, and BIN’, respectively.

Since we use the ordinal logistic regression model to estimate the propensity scores (Section 2.5), when the genotype is simulated using model OLR, the estimation performance is the best. The mean squared errors of the estimated propensity scores are higher when the genotype data are simulated from model BIN.

We would like to note that we deliberately added a random error ϵ_i in model BIN for additional complexity, which can cause spurious estimation errors. For a more fair comparison, we also simulate genotype data using model BIN without the random error (referred to as model BIN’) and further present the results for BIN’ in Figure 9. From the results, it is obvious that the extra estimation error for model BIN is mainly caused by the random error we added. There is no significant difference between the estimation errors for models OLR and BIN’, indicating that the difference between the estimation performance under the two genotype models is negligible if no additional noise is included.

4 DATA ANALYSIS

4.1 Data and Methods

The Study of Addiction: Genetics and Environment (SAGE) aims to identify susceptible genetic factors that contribute to substance dependence through three large-scale genomewide association studies: the Collaborative Study on the Genetics of Alcoholism (COGA), the Family Study of Cocaine Dependence (FSCD), and the Collaborative Genetic Study of Nicotine Dependence (COGEND). These three studies have been reported separately in previous work (Reich et al., 1998; Hartel et al., 2006; Luo et al., 2008; Bierut et al., 2008). The SAGE data include 4,121 subjects for whom the addiction to alcohol, nicotine, marijuana, cocaine, opiates, and other drugs and genome-wide SNP data (ILLUMINA Human 1M platform) were available. Lifetime dependence on these six categories of substances was diagnosed in accordance with the Diagnostic and Statistical Manual of Mental Disorders, Fourth Edition (DSM-IV). We hypothesize that there is a common genetic effect for the comorbidity including the addiction to the six categories of substances. We thus use multivariate traits, each of which stands for whether or not the subject is addicted to a single substance. The six phenotypes are coded into binary scales according to whether the subject is addicted to a particular substance.

In our study, we excluded 60 duplicate genotype samples and removed nine subjects with ethnic backgrounds other than African origin (black) or European origin (white). In total we have 3,627 unrelated subjects for whom we have both genotype and phenotype data. Following Chen et al. (2011), we performed a separate analysis for both race (black or white) and gender (female or male), due to the complexity of substance dependence with possible environmental components. Therefore, our analysis was performed in each of the four subpopulations: 1,393 white women, 1,131 white men, 568 black women, and 535 black men (Chen et al., 2011). In addition, we filtered SNPs by setting thresholds for call rate (> 90%), minor allele frequency (MAF) in each sub-population (> 1%), and Hardy-Weinberg equilibrium in each sub-population (p-value > 0.0001).

As we have already split the data by the covariates race and gender, they were not adjusted in the further analysis in each subset. Hence, the remaining covariates include age and some environmental risk factors, such as whether experienced rape/sexual assault, whether experienced physical assault, and whether experienced non-assaultive trauma. Some other risk factors, such as whether experienced neglect as a child, whether experienced physical abuse as a child, and childhood sexual abuse, were not included due to their high rates of missing values.

Similar to the simulation study, we compare four association tests: non-weighted test T, covariate-weighted test T_W,1, propensity score-weighted test T_W,2, and our semiparametric propensity score-inverse probability weighted test ${\widehat{T}}_{\text{IPW}}$. With the above selected covariates, the weight functions w(·, ·) in both weighted tests T_W,1 and T_W,2 are chosen following previous work (Jiang and Zhang, 2011; Zhu et al., 2012) with default parameters. Meanwhile, we continue to use the ordinal logistic regression model for the genotype-covariate relationship in our proposed test. In addition to the above tests with multivariate traits, we also tabulate the results from analyses using a single trait at a time. For each of the six traits, we utilize two approaches to analyze them. Firstly, we fit a logistic regression model including both genotype and the selected covariates. The statistical significance is drawn from a likelihood ratio test based on the logistic regression model. Secondly, we apply the same association tests T, T_W,1, T_W,2, and ${\widehat{T}}_{\text{IPW}}$ as above to each trait, and present the significant findings.

4.2 Summary Statistics

We provided in Table 4 the co-dependence information of the six substances among the 3,627 unrelated subjects included in our final analysis. The diagonal entries are the rates of each substance dependence, and the lower-diagonal entries are the co-dependence rates of each pair of substances. Comparing a lower-diagonal entry to its two corresponding diagonal entries suggests the statistical dependence among the six addictions. For example, there are 1,625 subjects (45%) who are addicted to nicotine and 1,693 subjects (47%) addicted to alcohol. The co-dependence rate of nicotine and alcohol is 32% (1,154 out of 3,627), which is much higher than the rate if assuming these two addictions are statistically independent. This observation supports the existence of comorbidity among the six addictions in this data set.

Table 4.

Dependence and co-dependence rate of six substances. nic: nicotine; mj: marijuana; coc: cocaine; op: opiates; alc: alcohol; oth: other drugs. The percentage in the parenthesis is the dependence or co-dependence rate in the 3,627 unrelated subjects.

	Substance Dependence
	nic (%)	mj (%)	coc (%)	op (%)	alc (%)	oth (%)
nic	1625 (45)
mj	486 (13)	620 (17)
coc	686 (19)	464 (13)	937 (26)
op	203 (6)	145 (4)	217 (6)	258 (7)
alc	1154 (32)	577 (16)	820 (23)	238 (7)	1693 (47)
oth	332 (9)	258 (7)	335 (9)	168 (5)	406 (11)	432 (12)

Table 5 summarizes the addiction distribution in each subset of data split by race and sex. We can see that the addiction to some categories of substances is homogeneous across the four subpopulations, such as nicotine, with addiction rates 47%, 48%, 47% and 41% respectively. However, other substance dependencies differ by race (e.g., cocaine, 46% and 36% for black men and women versus 27% and 12% for white men and women) and/or sex (e.g., alcohol, 62% and 62% for black and white men versus 39% and 31% for black and white women). Throughout our analysis, the data are divided into four subsets according to sex and race of the subjects. Therefore, we focus on the subset specific analysis, removing the heterogeneity across the subpopulations.

Table 5.

Summary of substance dependence in each subpopulation. nic: nicotine; mj: marijuana; coc: cocaine; op: opiates; alc: alcohol; oth: other drugs. The percentage in the parenthesis is the substance dependence rate in each subpopulation.

Subset	Total	Substance Dependence
		nic (%)	mj (%)	coc (%)	op (%)	alc (%)	oth (%)
Black Men	535	254 (47)	136 (25)	248 (46)	44 (8)	332 (62)	61 (11)
Black Women	568	271 (48)	78 (14)	206 (36)	35 (6)	224 (39)	37 (7)
White Men	1131	528 (47)	285 (25)	309 (27)	112 (10)	704 (62)	203 (18)
White Women	1393	572 (41)	121 (9)	174 (12)	67 (5)	433 (31)	131 (9)
Total	3627	1625 (45)	620 (17)	937 (26)	258 (7)	1693 (47)	432 (12)

4.3 Single-Trait Results

Before presenting the multiple-trait results, we summarize the single-trait results from logistic regression models and the association tests in Table 6 and Table 7, respectively. The p-values in bold characters indicate that they reach the genome-wide significance level after Bonferroni correction for the number of traits (p-value < 5 × 10⁻⁷/6) (Burton et al., 2007).

Table 6.

Significant SNPs in the genome-wide association study of a single substance dependence from logistic regression. nic: nicotine; mj: marijuana; coc: cocaine; op: opiates; alc: alcohol; oth: other drugs.

Chr	SNP	Gene	MAF	p-values
				nic	mj	coc	op	alc	oth
White Women
3	rs445057	FHIT	0.174	5.9e-1	2.2e-2	2.0e-4	1.7e-1	4.5e-8	1.8e-2

Table 7.

Significant SNPs in the genome-wide association study of a single substance dependence from association tests. op: opiates; oth: other drugs.

Chr	SNP	MAF	Gene	p-values
				T	T W,1	T W,2	${\widehat{T}}_{\text{IPW}}$
op
Black Men
2	rs2377339	0.019	NCK2	1.1e-8	1.1e-9	1.4e-9	8.2e-9
16	rs2042360	0.066	–	9.2e-7	6.5e-8	4.3e-7	9.6e-7
17	rs17544779	0.017	–	5.6e-8	6.3e-6	1.8e-6	4.6e-8
White Men
13	rs9529180	0.111	PCDH9	1.5e-7	4.6e-7	4.9e-8	1.1e-7
13	rs9540995	0.112	PCDH9	2.2e-7	7.0e-7	5.9e-8	1.5e-7
13	rs9529185	0.111	PCDH9	1.6e-7	4.7e-7	5.2e-8	1.1e-7
Black Women
5	rs2441010	0.012	–	1.0e-7	1.1e-4	8.2e-5	7.6e-8
7	rs2528381	0.084	UBE2D4	1.9e-5	5.1e-8	2.9e-5	1.6e-5
7	rs1182398	0.014	UBE3C	1.9e-7	5.6e-8	1.2e-6	1.1e-7
10	rs7911634	0.011	PCDH15	7.2e-5	2.7e-9	3.1e-6	6.6e-5
14	rs17197261	0.020	0R10G3	1.3e-5	4.5e-8	1.4e-3	1.0e-5
White Women
19	rs3745816	0.016	EML2	2.2e-5	4.4e-11	2.0e-5	1.3e-5
19	rs4445998	0.015	EML2	1.2e-5	1.2e-11	2.4e-5	6.7e-6
19	rs1545040	0.020	EML2	1.5e-3	5.7e-8	2.5e-3	1.1e-3
oth
Black Women
11	rs11603357	0.041	–	2.5e-7	2.6e-8	1.1e-8	1.5e-7
White Women
17	rs3098945	0.187	ANKRD13B	4.5e-6	1.8e-8	6.0e-7	1.1e-6

From Table 6, only one SNP achieves the genome-wide significance level (after Bonferroni correction) in the subpopulation of white women: rs445057 in gene FHIT is identified as a significant marker for addiction to alcohol. Very recently, FHIT has been documented to be in correlation with lifetime cigarette addiction (Antczak et al., 2013). This existing result, combined with our finding that FHIT is associated with alcohol dependence, partially supports the hypothesis that common genes underlie the comorbidity of multiple substance dependencies.

From Table 7, we have identified several significant SNP markers for each of the two phenotypes: addiction to opiates and addiction to other drugs, using the association tests T, T_W,1, T_W,2, and ${\widehat{T}}_{\text{IPW}}$.

For the addiction to opiates, three SNPs are identified to be genome-wide significant in black men. Among these SNPs, rs2377339 is located within gene NCK2, which has a strong association with normal angle glaucoma (Akiyama et al., 2008; Fuse, 2010). Furthermore, a meta-analysis (Bonovas et al., 2004) reported that smoking is a risk factor for glaucoma. These findings indicate some intriguing interplay between smoking and NCK2. A more recent study also verified the association of NCK2 with opiates addiction (Liu et al., 2013).

Three SNPs, all in gene PCDH9, are significantly associated with opiates dependence in white men. PCDH9 was discovered to contain variants that contribute to general addiction vulnerability (Liu et al., 2006), agreeing with our current finding.

Five additional SNPs, located in four known genes, achieve the genome-wide significance in black women. Among these genes, UBE3C has recently been discovered to be one of the four particularly promising candidate genes susceptible to cocaine dependence and major depressive episode (Yang et al., 2011); PCDH15 was also found to be associated with nicotine dependence by multiple human genome-wide association studies (Uhl et al., 2008; Lind et al., 2010). These results partially support our findings about the association between these two genes and opiates dependence.

Three SNPs in gene EML2 are discovered for addiction to opiates in white women. EML2 was found to be one of the potential candidate genes for bipolar disorder comorbid with alcoholism in mice (Le-Niculescu et al., 2008). However, no human studies have suggested the association of EML2 with substance dependence yet.

In addition to opiates, we have two more findings for addiction to other drugs, for which we have not found supporting evidence in the literature. All these single-trait findings can be potentially important for researchers to better understand the genetic components of substance dependence.

4.4 Multiple-Trait Results

The results from the analysis of multivariate traits are summarized in Table 8, with the p-values in bold characters indicating that they reach the genome-wide significance level (p-value < 5 × 10⁻⁷) (Burton et al., 2007). Comparing the four tests for multivariate traits, it is fairly clear to see the advantage of adjusting for important covariates in this data set. Without any adjustment, no SNP can be identified at the genome-wide significance level using test T. In addition, we find that different adjusted tests work complementarily to each other. These three tests (T_W,1, T_W,1 and ${\widehat{T}}_{\text{IPW}}$) have some common findings and also non-overlapping discoveries. The results of the weighted tests might depend on the strength of the genetic signals and/or gene-environment interactions, as illustrated by our simulation studies. Similar conclusions can also be drawn from the comparison among different methods for single-trait results in Table 7.

Table 8.

Significant SNPs in the genome-wide association study of multiple substance dependencies. The symbol * indicates that the same SNP is also found by single-trait analysis in Table 7.

Chr	SNP	MAF	Gene	p-values
				T	T W,1	T W,2	${\widehat{T}}_{\text{IPW}}$
Black Men
2	rs2377339*	0.019	NCK2	1.1e-06	6.2e-08	1.4e-07	9.0e-07
5	rs251133	0.406	STARD4-AS1	5.3e-07	5.2e-06	2.8e-05	4.2e-07
5	rs10483285	0.037	ADCY4	2.4e-03	1.3e-07	5.0e-05	2.0e-03
White Men
3	rs4016435	0.042	CTNNB1	7.3e-07	6.2e-07	1.5e-07	2.6e-07
8	rs1477908	0.177	MMP16	1.1e-05	2.3e-05	2.3e-07	4.1e-06
Black Women
1	rs2175254	0.035	RASAL2	2.6e-05	4.1e-07	1.0e-05	1.7e-05
8	rs10504824	0.014	WWP1	1.1e-06	9.1e-09	2.7e-07	5.9e-07
8	rs17609515	0.014	CPNE3	1.1e-06	9.1e-09	2.7e-07	5.9e-07
10	rs7911634*	0.011	PCDH15	1.7e-04	1.1e-08	1.3e-05	1.6e-04
White Women
2	rs16866493	0.011	–	6.1e-04	1.9e-07	5.2e-04	3.3e-04
2	rs878167	0.010	–	1.3e-04	4.8e-08	1.0e-04	6.4e-05
2	rs6731600	0.039	–	2.1e-05	9.7e-06	7.1e-08	5.2e-06
2	rs6721762	0.039	MPV17	3.2e-05	1.1e-05	2.3e-07	8.7e-06
11	rs955396	0.068	TOLLIP/MUC5B	4.4e-05	1.5e-06	9.3e-08	4.4e-05
19	rs3745816*	0.016	EML2	5.2e-05	8.8e-10	1.7e-04	4.6e-05
19	rs4445998*	0.015	EML2	5.4e-05	3.8e-10	3.1e-04	4.6e-05
19	rs1545040*	0.020	EML2	6.7e-04	1.6e-07	2.4e-03	6.8e-04

Interestingly, we have several common findings between the multiple-trait results in Table 8 and the single-trait results in Table 7. These common genes, such as NCK2, PCDH15, and EML2, can be of particular interest to the addiction research. In the following, we provide a brief overview of the multiple-trait findings.

Three SNPs, rs2377339, rs251133 and rs10483285, which are located in genes NCK2, STARD4-AS1 and ADCY4 respectively, reach the genome-wide significance in black men. In addition to NCK2, previous research has also provided evidence for ADCY4: it is associated with opioid dependence (Wang et al., 2005; Li et al., 2008). All these results support NCK2 and ADCY4 as potentially relevant genes to substance dependence.

Two other SNPs, rs4016435 and rs1477908, in genes CTNNB1 and MMP16, achieve the genome-wide significance level in white men. It has come to our attention that the gene CTNNB1 has been suggested by microarray studies of nicotine exposure in rats (Sullivan et al., 2004), but it is the first time that this gene is discovered to be related to substance dependence in a human study. In addition, MMP16 belongs to a family of genes (matrix metalloproteinases, i.e., MMPs) that is known to play an important role in drug addiction (Wright and Harding, 2009).

Four SNPs located in four different genes are discovered to be associated with substance dependence in black women. Similar to CTNNB1, RASAL2 is also a candidate gene for nicotine dependence from pathway analysis (Sullivan et al., 2004). Furthermore, multiple human genome-wide association studies identified PCDH15 to be associated with nicotine dependence (Uhl et al., 2008; Lind et al., 2010). These existing results provide partial support to our findings.

Eight other SNPs are identified using multiple addictions in white women. Similar to EML2, previous microarray study in mice has provided evidence that MPV17 is associated with alcohol dependence (Li et al., 2008). However, no human studies have suggested the association of these two genes with substance dependence yet.

Besides the SNPs/genes discussed above, there are other SNPs/genes showing strong evidence of association with substance dependence in our study, and those SNPs/genes warrant further investigation.

5 DISCUSSION

Understanding comorbidity related with addictions is one of the most pressing challenges with enormous public health significance (National Institute on Drug Abuse, 2010). In this work, we studied genetics of multiple addictions by analyzing the data from the Study of Addiction: Genetics and Environment (SAGE). To properly utilize the information collected by this study, we propose a novel statistical method to incorporate environmental factors into a nonparametric U-statistic (generalized Kendall’s tau) which can handle comorbidity of multiple traits. Compared with directly imposing a weight function on the U-statistic, the idea of inverse probability weighting is more natural and convenient. On the one hand, the inverse probability weighted U-statistic is asymptotically unbiased under the null hypothesis while the non-weighted and other weighted tests are not necessarily. On the other hand, the proposed test is free of tuning parameters, which is more convenient and accessible than other weighted tests.

A byproduct of our theoretical work is to confirm a previous finding that estimated propensity scores can be preferable to their true values in applications. It is shown that our semiparametric U-statistic has a smaller asymptotic variance with $\sqrt{n}$-consistent propensity score estimates than with true propensity scores. Although this phenomenon has been revealed before, to the best of our knowledge this is the first time to formalize it in the areas of U-statistics and genetic association tests. Moreover, a recently proposed multiple-trait association test called “Scaled Multiple-phenotype Association Test” (SMAT) (Schifano et al., 2013) was brought to our attention by a referee. It is noteworthy that SMAT can only handle continuous phenotypes while our proposed test can take any hybrid of dichotomous, ordinal and quantitative traits. Since we focus on binary responses in our current investigation of addictions, we will leave the comparison study with SMAT to our future work.

We have demonstrated numerical performance of our method, and should note the topics that deserve further research. For example, a key assumption for the distribution of our statistic is that the propensity scores are estimated under the correct parametric model. We assessed the impact of model misspecification in simulation studies, and our empirical results did not reveal a major impact. Nonetheless, a deeper theoretical understanding is still important. Another issue is the choice of genotype coding in our method. As discussed in Section 2.6, our test is not invariant to the genotype coding and we provided a practical suggestion. Although it is not the focus of the current study, it warrants some future investigations.

Applying the new method (together with other methods) to the SAGE data leads to a few interesting findings. Firstly, the multiple-trait analysis reveals new markers that were not identified by the single addiction analysis. When a genetic signal is not strong enough for any single addiction and yet underlies multiple ones, it can become stronger (to a detectable level) by combining different substance dependencies.

Secondly, our analysis of the SAGE data reveals an advantage of adjusting for environmental factors. To study comorbidity, adjusted tests identified a few genetic variants to addiction but the unadjusted test did not have any findings. This agrees with the observations from our simulation studies. Most of the time, the inclusion of important environmental factors can increase the power to detect either the genetic effect or the gene-environment interaction. Even under the situation with a genetic effect only (no environmental effects), an unnecessary adjustment for the environmental factors has little effect on the power of a test.

Lastly, tests with different adjustments behave differently. Due to the nature of the real data analysis, we cannot really tell which method performs the best. In a real application, it is usually not practical to have one method that is always superior to all others. Therefore, it is useful that different adjusted tests work complementarily to each other in this data set.

A APPENDIX

We split our derivation of Theorem 2 into three steps as follows. The first step is to obtain an asymptotic representation of $\widehat{\theta }$. Under regularity conditions, there exists a $\sqrt{n}$-consistent estimator $\widehat{\theta }$ of θ₀. The following lemma presents the result, with its proof given in Appendix A.1.

Lemma 1. Let the parameter space Θ be an open set. Suppose that, there exists some δ > 0 and c_θ0 > 0 such that p_g(z_i; θ) ∈ [δ, 1 − δ] for all θ satisfying ∥θ − θ₀∥ ≤ c_θ0 with g = 0, 1, 2 and i = 1, … , n; ℓ_i(θ) is twice continuously differentiable; for each g = 0, 1, 2, condition (9) holds, and there exists constants C_θ0 > 0 and α > 0 such that for all θ satisfying ∥θ − θ₀∥ ≤ c_θ0, condition (10) holds; there exists a positive definite matrix I_θ0 such that $\frac{1}{n}{\sum }_{i=1}^n{\mathbf{I}}_{{\theta }_0}\left({\mathbf{z}}_i\right)\to {\mathbf{I}}_{{\theta }_0}$. Then, there exists a root of the likelihood equations $\widehat{\theta }$ of θ₀ which has the following representation

$$\sqrt{n}(\widehat{\theta }-{\theta }_0)={\mathbf{I}}_{{\theta }_0}^{-1}\frac{1}{\sqrt{n}}\sum _{i=1}^n{\psi }_{{\theta }_0}(G_i,{\mathbf{z}}_i)+o_p\left(1\right).$$ (A.1)

The result of Lemma 1 is fairly standard for a root of the likelihood equations $\widehat{\theta }$ in the framework of maximum likelihood. We refer to Theorem 5.21 in van der Vaart (1998) and Theorem 4.17 in Shao (2003) as similar conclusions. A distinct part of this lemma is that the samples are only independent but not identically distributed due to the conditional inference given all the covariates. In other words, the covariates are regarded as non-random. This characteristic results in the unique conditions (9) and (10) involving the covariate z_i’s, compared with the traditional theories. Thus, we provide a proof in Appendix A.1 for being clear and self-contained.

The second step is to investigate the asymptotic joint distribution of $\{{\mathbf{U}}_{\text{IPW}}^{\prime }\left({\theta }_0\right),\widehat{\theta }\prime \}\prime$. The idea becomes clear with the conclusion of Lemma 1, as both U_IPW(θ₀) and $\widehat{\theta }-{\theta }_0$ can be written in the form of a sum of independent random vectors. Hence, $\{{\mathbf{U}}_{\text{IPW}}^{\prime }\left({\theta }_0\right),(\widehat{\theta }-{\theta }_0)\prime \}\prime$ becomes a sum of independent random vectors, on which we can apply the central limit theorem. Thus, we leave the proof in Appendix A.2 and present the result in the following lemma.

Lemma 2. In addition to the conditions in Lemma 1, assume that ${\lambda }_{\text{max}}\left({\sum }_{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{\stackrel{‒}{\mathbf{u}}}_i^{\prime }\right)=O\left(n\right)$ and ${\text{max}}_{1\le i\le n}{\lambda }_{\text{max}}({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })=o\left[{\lambda }_{\text{min}}\left\{{\sum }_{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}\right]$. Then, under the null hypothesis ℋ₀,

$$\sqrt{n}{\Omega }_{{\theta }_0}^{-1∕2}\left[\begin{array}{c}\hfill {\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)\hfill \\ \hfill \widehat{\theta }-{\theta }_0\hfill \end{array}\right]\to N(0,{\mathbf{I}}_{p+d}),$$ (A.2)

in distribution, conditioning on all the traits Y = y and covariates Z = z. In (A.2),

$${\Omega }_{{\theta }_0}=\left(\begin{array}{cc}\hfill \sum _{{\theta }_0}\hfill & \hfill {\Gamma }_{{\theta }_0}{\mathbf{I}}_{{\theta }_0}^{-1}\hfill \\ \hfill {\mathbf{I}}_{{\theta }_0}^{-1}{\Gamma }_{{\theta }_0}^{\prime }\hfill & \hfill {\mathbf{I}}_{{\theta }_0}^{-1}\hfill \end{array}\right),$$

where Σ_θ0 and Γ_θ0 are defined in Section 2.4.

Finally, as the last step, the asymptotic distribution of ${\widehat{\mathbf{U}}}_{\text{IPW}}$ follows from the joint asymptotic distribution of U_IPW(θ₀) and $\widehat{\theta }$, borrowing the idea from Pierce (1982) and Randles (1982). The proof of this step can be found in Appendix A.3.

A.1 Proof of Lemma 1

In this section, all probability related arguments/operations will be conditioning on the covariates. However, to simplify the notation, we still write E(·) or var(·) instead of E(· | Z = z) or var(· | Z = z).

We first prove that $\sqrt{n}(\widehat{\theta }-{\theta }_0)=O_p\left(1\right)$. This is implied by the fact that for any ϵ > 0, there exists C > 0 and n₀ > 1 such that

$$P\{\text{log}\ell \left(\theta \right)-\text{log}\ell \left({\theta }_0\right)<0\text{for all}\theta \in \partial B_n\left(C\right)\}\ge 1-ϵ,n>n_0,$$ (A.3)

where $\text{log}\ell \left(\theta \right)={\sum }_{i=1}^n\text{log}{\ell }_i\left(\theta \right)$ and ∂B_n(C) is the boundary of $B_n\left(C\right)=\{\theta :\sqrt{n}\parallel \theta -{\theta }_0\parallel \le C\}$. Let ${\Psi }_n\left(\theta \right)=\frac{1}{n}{\sum }_{i=1}^n{\psi }_{\theta }(G_i,{\mathbf{z}}_i)$. The Taylor expansion gives that

$$\frac{1}{n}\{\text{log}\ell \left(\theta \right)-\text{log}\ell \left({\theta }_0\right)\}={\Psi }_n^{\prime }\left({\theta }_0\right)(\theta -{\theta }_0)+\frac{1}{2}(\theta -{\theta }_0)\prime \frac{\partial {\Psi }_n\left(\stackrel{\sim }{\theta }\right)}{\partial \theta \prime }(\theta -{\theta }_0),$$ (A.4)

where $\stackrel{\sim }{\theta }$ is the generic notation of a vector lying between θ₀ and θ. We will show at the end that,

$$\Vert {\Psi }_n\left({\theta }_0\right)\Vert =O_p\left(n^{-1∕2}\right),\frac{\partial {\Psi }_n\left(\stackrel{\sim }{\theta }\right)}{\partial \theta \prime }+{\mathbf{I}}_{{\theta }_0}=o_p\left(1\right).$$ (A.5)

Combining (A.4) and (A.5),

$$\frac{1}{n}\{\text{log}\ell \left(\theta \right)-\text{log}\ell \left({\theta }_0\right)\}=\Vert \theta -{\theta }_0\Vert O_p\left(n^{-1∕2}\right)-\frac{1}{2}(\theta -{\theta }_0)\prime \{{\mathbf{I}}_{{\theta }_0}+o_p\left(1\right)\}(\theta -{\theta }_0),$$

therefore (A.3) holds with large enough C and n₀. The $\sqrt{n}$-consistency of $\widehat{\theta }$ is proved.

To obtain the asymptotic representation (A.1) of $\widehat{\theta }$, we consider the Taylor expansion of ${\Psi }_n\left(\widehat{\theta }\right)$ at θ₀. On the one hand, ${\Psi }_n\left(\widehat{\theta }\right)=0$ by the definition of a root of the likelihood equations; on the other hand,

$${\Psi }_n\left(\widehat{\theta }\right)={\Psi }_n\left({\theta }_0\right)+\frac{\partial {\Psi }_n\left(\stackrel{\sim }{\theta }\right)}{\partial \theta \prime }(\widehat{\theta }-{\theta }_0),$$ (A.6)

where $\stackrel{\sim }{\theta }$ lies between θ₀ and $\widehat{\theta }$. Then the representation (A.1) in Lemma 1 holds by (A.6), $\sqrt{n}(\widehat{\theta }-{\theta }_0)=O_p\left(1\right)$, and the same result as the second part of (A.5) but with $\stackrel{\sim }{\theta }$ denoting a vector between θ₀ and $\widehat{\theta }$ (which will be proved immediately).

At the end, we provide the proof of (A.5). For Ψ_n(θ₀), it is seen that

$$E\left\{{\Psi }_n\left({\theta }_0\right)\right\}=0,n\text{var}\left\{{\Psi }_n\left({\theta }_0\right)\right\}=\frac{1}{n}\sum _{i=1}^n{\mathbf{I}}_{{\theta }_0}\left({\mathbf{z}}_i\right)\to {\mathbf{I}}_{{\theta }_0},$$

because of the exchangeability of the partial derivative and integration with respect to a discrete measure. Then, for any ϵ > 0, we can choose C_ϵ large enough such that

$$P\{\Vert \sqrt{n}{\Psi }_n\left({\theta }_0\right)\Vert >C_{ϵ}\}\le C_{ϵ}^{-2}E\left\{n{\Vert {\Psi }_n\left({\theta }_0\right)\Vert }^2\right\}=C_{ϵ}^{-2}\text{tr}\left[n\text{var}\left\{{\Psi }_n\left({\theta }_0\right)\right\}\right]<ϵ,$$

This is the first part of (A.5). For the second part, we need to show it holds for $\stackrel{\sim }{\theta }$ satisfying either $\sqrt{n}\parallel \stackrel{\sim }{\theta }-{\theta }_0\parallel \le C$ or $\sqrt{n}\parallel \stackrel{\sim }{\theta }-{\theta }_0\parallel =O_p\left(1\right)$. In either case, we have that

$$\frac{\partial {\Psi }_n\left(\stackrel{\sim }{\theta }\right)}{\partial \theta \prime }=\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }+op\left(1\right),$$ (A.7)

$$E\left\{\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }\right\}=\frac{1}{n}\sum _{i=1}^n{\mathbf{I}}_{{\theta }_0}\left({\mathbf{z}}_i\right)\to -{\mathbf{I}}_{{\theta }_0},$$ (A.8)

$$\text{var}\left\{\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }c\right\}=\frac{1}{n^2}\sum _{i=1}^n\text{var}\left[\left\{\frac{\partial }{\partial \theta \prime }{\psi }_{{\theta }_0}(G_i,{\mathbf{z}}_i)\right\}\mathbf{c}\right]\to 0,$$ (A.9)

for an arbitrary d-dimensional vector c. (A.7) follows from the following equation

$$\frac{\partial {\Psi }_n\left(\theta \right)}{\partial \theta \prime }=\frac{1}{n}\sum _{i=1}^n\sum _{g=0}^{2}I(G_i=g)\left\{p_g^{-1}({\mathbf{z}}_i;\theta )\frac{{\partial }^2}{\partial \theta \partial \theta \prime }{p}_g({\mathbf{z}}_i;\theta )-p_g^{-2}({\mathbf{z}}_i;\theta )\frac{\partial }{\partial \theta }{p}_g({\mathbf{z}}_i;\theta )\frac{\partial }{\partial \theta \prime }{p}_g({\mathbf{z}}_i;\theta )\right\}$$

and the conditions (9) and (10) in Lemma 1. (A.8) follows from the exchangeability of the partial derivative and integration with respect to a discrete measure. (A.9) follows from the condition (9) in Lemma 1. By Markov’s inequality, for any ϵ > 0,

$$\begin{array}{cc}\hfill P\left[\Vert \left\{\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }+{\mathbf{I}}_{{\theta }_0}\right\}\mathbf{c}\Vert >ϵ\right]& \le {ϵ}^{-2}E\left[{\Vert \left\{\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }-E\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }\right\}\mathbf{c}\Vert }^2\right]+{ϵ}^{-2}E\left[{\Vert \left\{E\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }+{\mathbf{I}}_{{\theta }_0}\right\}\mathbf{c}\Vert }^2\right]\hfill \\ \hfill & ={ϵ}^{-2}\text{tr}\left[\text{var}\left\{\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }\mathbf{c}\right\}\right]+{ϵ}^{-2}{\Vert \left\{E\frac{\partial {\Psi }_n\left({\theta }_0\right)}{\partial \theta \prime }+{\mathbf{I}}_{{\theta }_0}\right\}\mathbf{c}\Vert }^2\to 0.\hfill \end{array}$$ (A.10)

The second part of (A.5) is implied by (A.7) and (A.10).

A.2 Proof of Lemma 2

In the next two subsections (Sections A.2 and A.3), all probability related arguments/operations will be conditioning on the traits and covariates. However, to simplify the notation, we still write E(·) or var(·) instead of E(· | Y = y, Z = z) or var(· | Y = y, Z = z).

From the Cramér-Wold device, it suffices to find the asymptotic distribution of ${\mathbf{c}}_1^{\prime }{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)+{\mathbf{c}}_2^{\prime }(\widehat{\theta }-{\theta }_0)$ for arbitrary p- and d-dimensional vectors c₁ and c₂. As $\sqrt{n}{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)=O_p\left(1\right)$ from Theorem 1 and the condition ${\lambda }_{\text{max}}\left({\sum }_{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{\stackrel{‒}{\mathbf{u}}}_i^{\prime }\right)=O\left(n\right)$, it is seen that

$$\sqrt{n}\{{\mathbf{c}}_1^{\prime }{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)+{\mathbf{c}}_2^{\prime }(\widehat{\theta }-{\theta }_0)\}=\frac{1}{\sqrt{n}}\sum _{i=1}^n[2{\mathbf{c}}_1^{\prime }{\stackrel{‒}{u}}_i{G}_i∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)+{\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}{\psi }_{{\theta }_0}(G_i,{\mathbf{z}}_i)]+o_p\left(1\right).$$ (A.11)

A direct calculation gives its variance

$$\begin{array}{cc}\hfill {\sigma }_n^2& =\text{var}\left[\frac{1}{\sqrt{n}}\sum _{i=1}^n\{2{\mathbf{c}}_1^{\prime }{\stackrel{‒}{u}}_i{G}_i∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)+{\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}{\psi }_{{\theta }_0}(G_i,{\mathbf{z}}_i)\}\right]\hfill \\ \hfill & ={\mathbf{c}}_1^{\prime }\left[\frac{4}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_i{\stackrel{‒}{u}}_i^{\prime }{\nu }_{{\theta }_0}\left({\mathbf{z}}_i\right)∕e_{{\theta }_0}^2\left({\mathbf{z}}_i\right)\right]{\mathbf{c}}_1+{\mathbf{c}}_2^{\prime }\left[{\mathbf{I}}_{{\theta }_0}^{-1}\frac{1}{n}\sum _{i=1}^n{\mathbf{I}}_{{\theta }_0}\left({\mathbf{z}}_i\right){\mathbf{I}}_{{\theta }_0}^{-1}\right]{\mathbf{c}}_2\hfill \end{array}$$ (A.12)

$$+2{\mathbf{c}}_1^{\prime }\left[\frac{2}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_{i}E\{G_i,{\psi }_{{\theta }_0}^{\prime }(G_i,{\mathbf{z}}_i)\}{\mathbf{I}}_{{\theta }_0}^{-1}∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)\right]{\mathbf{c}}_2,$$ (A.13)

where we have in (A.12) that

$${\mathbf{c}}_2^{\prime }\left[{\mathbf{I}}_{{\theta }_0}^{-1}\frac{1}{n}\sum _{i=1}^n{\mathbf{I}}_{{\theta }_0}\left({\mathbf{z}}_i\right){\mathbf{I}}_{{\theta }_0}^{-1}\right]{\mathbf{c}}_2\to {\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}{\mathbf{c}}_2,n\to \infty ,$$

and in (A.13) that

$$\begin{array}{cc}\hfill & 2{\mathbf{c}}_1^{\prime }\left[\frac{2}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_{i}E\left\{G_i{\psi }_{{\theta }_0}^{\prime }(G_i,{\mathbf{z}}_i)\right\}{\mathbf{I}}_{{\theta }_0}^{-1}∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)\right]{\mathbf{c}}_2\hfill \\ \hfill =& 2{\mathbf{c}}_1^{\prime }\left(\frac{2}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_i\sum _{g=0}^2\left[E\left\{G_{i}I(G_i=g)\right\}{p}_g^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta \prime }{p}_g({\mathbf{z}}_i;{\theta }_0)\right]{\mathbf{I}}_{{\theta }_0}^{-1}∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)\right){\mathbf{c}}_2\hfill \\ \hfill =& 2{\mathbf{c}}_1^{\prime }\left[\frac{2}{n}\sum _{i=1}^n{\stackrel{‒}{u}}_i\sum _{g=0}^2\left\{g\frac{\partial }{\partial \theta \prime }{p}_g({\mathbf{z}}_i;{\theta }_0)\right\}{I}_{{\theta }_0}^{-1}∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)\right]{\mathbf{c}}_2.\hfill \end{array}$$

Therefore,

$${\sigma }_n^2={\mathbf{c}}_1^{\prime }\sum _{{\theta }_0}{\mathbf{c}}_1+{\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}{\mathbf{c}}_2+2{\mathbf{c}}_1^{\prime }{\Gamma }_{{\theta }_0}{\mathbf{I}}_{{\theta }_0}^{-1}{\mathbf{c}}_2+o\left(1\right).$$

In order to apply the central limit theorem as in Corollary 1.3 in Shao (2003), we need to rewrite (A.11) into

$$\frac{1}{\sqrt{n}}\sum _{i=1}^n[2{\mathbf{c}}_1^{\prime }{\stackrel{‒}{\mathbf{u}}}_i{G}_i∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)+{\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}{\psi }_{{\theta }_0}(G_i,{\mathbf{z}}_i)]=\frac{1}{\sqrt{n}}\sum _{i=1}^n{\mathbf{d}}_i^{\prime }\{{\mathbf{R}}_i-E\left({\mathbf{R}}_i\right)\},$$

with d_i = (d_i1, d_i2)′, R_i = {I(G_i = 1), I(G_i = 2)}′, and

$$\begin{array}{cc}\hfill d_{i1}& =2{\mathbf{c}}_1^{\prime }{\stackrel{‒}{\mathbf{u}}}_i∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)+{\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}\left\{p_1^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta }{p}_1({\mathbf{z}}_i;{\theta }_0)-p_0^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta }{p}_0({\mathbf{z}}_i;{\theta }_0)\right\}=(2{\mathbf{c}}_1^{\prime },{\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}){\gamma }_{i1},\hfill \\ \hfill d_{i2}& =4{\mathbf{c}}_1^{\prime }{\stackrel{‒}{\mathbf{u}}}_i∕e_{{\theta }_0}\left({\mathbf{z}}_i\right)+{\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}\left\{p_2^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta }{p}_2({\mathbf{z}}_i;{\theta }_0)-p_0^{-1}({\mathbf{z}}_i;{\theta }_0)\frac{\partial }{\partial \theta }{p}_0({\mathbf{z}}_i;{\theta }_0)\right\}=(2{\mathbf{c}}_1^{\prime },{\mathbf{c}}_2^{\prime }{\mathbf{I}}_{{\theta }_0}^{-1}){\gamma }_{i2}\hfill \end{array}$$

using the notation introduced in Lemma 2.

From the condition ${\text{max}}_{1\le i\le n}{\lambda }_{\text{max}}({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })=o\left[{\lambda }_{\text{min}}\left\{{\sum }_{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}\right]$, we see that

$$\underset{1\le i\le n}{\max }\Vert {\mathbf{d}}_i{\Vert }^2∕\sum _{i=1}^n\Vert {\mathbf{d}}_i{\Vert }^2\to 0.$$

The conditions in Lemma 2 also lead to inf_n,i λ_min({var(R_i)}) > 0 and sup_n,i E(∥R_i∥^2+δ) < ∞ for δ = 2. These regularity conditions imply that

$$\frac{1}{{\sigma }_n}\sqrt{n}\{c_1^{\prime }{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)+c_2^{\prime }(\widehat{\theta }-{\theta }_0)\}\to N(0,1)$$

in distribution. If Ω_θ0 is positive definite, then substituting $({\mathbf{c}}_1^{\prime },{\mathbf{c}}_2^{\prime })=({\stackrel{\sim }{\mathbf{c}}}_1^{\prime },{\stackrel{\sim }{\mathbf{c}}}_2^{\prime }){\Omega }_{{\theta }_0}^{-1∕2}$ already leads to the result in Lemma 2.

The last piece to prove is the positive definiteness of Ω_θ0. Let V_i = var(R_i) and ${\mathbf{A}}_i=\text{diag}(2{\mathbf{I}}_p,{\mathbf{I}}_{{\theta }_0}^{-1})({\gamma }_{i1},{\gamma }_{i2})$, then

$${\Omega }_{{\theta }_0}=\frac{1}{n}({\mathbf{A}}_1,\dots ,{\mathbf{A}}_n)\text{diag}({\mathbf{V}}_1,\dots ,{\mathbf{V}}_n)({\mathbf{A}}_1,\dots ,{\mathbf{A}}_n)\prime +o\left(1\right).$$

We see that inf_n[λ_min{diag(V₁, … , V_n)}] > 0. In addition, there exists some δ_n > 0,

$${\Vert (\mathbf{x}\prime ,\mathbf{y}\prime )({\mathbf{A}}_1,\dots ,{\mathbf{A}}_n)\Vert }^2=(2\mathbf{x}\prime ,\mathbf{y}\prime {\mathbf{I}}_{{\theta }_0}^{-1})\left\{\sum _{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}(2\mathbf{x}\prime ,\mathbf{y}\prime {\mathbf{I}}_{{\theta }_0}^{-1})\prime \ge {\delta }_n{\Vert (\mathbf{x}\prime ,\mathbf{y}\prime )\Vert }^2,$$

for arbitrary p- and d-dimensional vectors x and y. Therefore, for n sufficiently large,

$$(\mathbf{x}\prime ,\mathbf{y}\prime ){\Omega }_{{\theta }_0}(\mathbf{x}\prime ,\mathbf{y}\prime )\prime \ge \{{\delta }_n∕\left(2n\right)\}\underset{n}{\text{inf}}\left[{\lambda }_{\text{min}}\left\{\text{diag}({\mathbf{V}}_1,\dots ,{\mathbf{V}}_n)\right\}\right]{\Vert (\mathbf{x}\prime ,\mathbf{y}\prime )\Vert }^2,$$ (A.14)

which implies the positive definiteness of Ω_θ0.

A.3 Proof of Theorem 2

The proof follows from the idea in Pierce (1982) and Randles (1982) who provided a general guidance of deriving the asymptotic distribution of statistics with estimated parameters. In our situation, the statistic is ${\widehat{\mathbf{U}}}_{\text{IPW}}={\mathbf{U}}_{\text{IPW}}\left(\widehat{\theta }\right)$ where $\widehat{\theta }$ are the estimated parameters. The proof starts from the following fact,

$${\widehat{\mathbf{U}}}_{\text{IPW}}={\mathbf{U}}_{\text{IPW}}\left(\widehat{\theta }\right)={\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)+\frac{\partial }{\partial \theta \prime }{\mathbf{U}}_{\text{IPW}}\left(\stackrel{\sim }{\theta }\right)(\widehat{\theta }-{\theta }_0),$$ (A.15)

with some $\stackrel{\sim }{\theta }$ lying between θ₀ and $\widehat{\theta }$. As

$${\mathbf{U}}_{\text{IPW}}\left(\theta \right)=\frac{2}{n-1}\sum _{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{G}_i∕e_{\theta }\left({\mathbf{Z}}_i\right),$$

it is seen that

$$\begin{array}{cc}\hfill \frac{\partial }{\partial \theta \prime }{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)& =-\frac{2}{n-1}\sum _{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{G}_i\frac{\partial }{\partial \theta \prime }{e}_{{\theta }_0}\left({\mathbf{Z}}_i\right)∕e_{{\theta }_0}^2\left({\mathbf{Z}}_i\right)\hfill \\ \hfill & =\frac{2}{n-1}\sum _{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{G}_i\sum _{g=0}^2\left\{g\frac{\partial }{\partial \theta \prime }{p}_g({\mathbf{Z}}_i;{\theta }_0)\right\}∕e_{{\theta }_0}^2\left({\mathbf{Z}}_i\right)\hfill \\ \hfill & =-{\Gamma }_{{\theta }_0}\{1+o\left(1\right)\}+o_p\left(1\right).\hfill \end{array}$$ (A.16)

The equality in (A.16) follows from the facts that

$$\begin{array}{cc}\hfill E\left\{\frac{\partial }{\partial \theta \prime }{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)\right\}& =-\frac{n}{n-1}{\Gamma }_{{\theta }_0},\text{and}\hfill \\ \hfill \text{var}\left\{\frac{\partial }{\partial \theta \prime }{\mathbf{U}}_{\text{IPW}}^{\left(l\right)}\left({\theta }_0\right)\right\}& =\frac{4}{{(n-1)}^2}\sum _{i=1}^n{\left\{{\stackrel{‒}{u}}_i^{\left(l\right)}\right\}}^2{v}_{{\theta }_0}\left({\mathbf{z}}_i\right)\sum _{g=0}^2\left\{g\frac{\partial }{\partial \theta }{p}_g({\mathbf{z}}_i;{\theta }_0)\right\}\sum _{g=0}^2\left\{g\frac{\partial }{\partial \theta \prime }{p}_g({\mathbf{z}}_i;{\theta }_0)\right\}∕e_{{\theta }_0}^4\left({\mathbf{z}}_i\right)\hfill \\ \hfill & \to 0,\hfill \end{array}$$

due to the condition ${\text{max}}_{1\le i\le n}\parallel {\stackrel{‒}{\mathbf{u}}}_i{\parallel }^2=o\left(n\right)$ and the first part of condition (9). In addition, since $\stackrel{\sim }{\theta }-{\theta }_0=O_p\left(n^{-1∕2}\right)$,

$$\frac{\partial }{\partial \theta \prime }{\mathbf{U}}_{\text{IPW}}\left(\stackrel{\sim }{\theta }\right)-\frac{\partial }{\partial \theta \prime }{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)=\frac{{\partial }^2}{\partial \theta \partial \theta \prime }{\mathbf{U}}_{\text{IPW}}\left({\stackrel{\sim }{\theta }}^{\ast }\right)(\stackrel{\sim }{\theta }-{\theta }_0)=o_p\left(1\right),$$ (A.17)

with ${\stackrel{\sim }{\theta }}^{\ast }$ between θ₀ and $\stackrel{\sim }{\theta }$. The equality in (A.17) follows from the fact that for each l = 1, … , p,

$$\begin{array}{cc}\hfill \frac{{\partial }^2}{\partial \theta \partial \theta \prime }{U}_{\text{IPW}}^{\left(l\right)}\left({\stackrel{\sim }{\theta }}^{\ast }\right)& =-\frac{2}{n-1}\sum _{i=1}^n{\stackrel{‒}{u}}_i^{\left(l\right)}{G}_i\sum _{g=0}^2\left\{g\frac{{\partial }^2}{\partial \theta \partial \theta \prime }{p}_g({\mathbf{Z}}_i;{\stackrel{\sim }{\theta }}^{\ast })\right\}∕e_{{\stackrel{\sim }{\theta }}^{\ast }}^2\left({\mathbf{Z}}_i\right)+\frac{4}{n-1}\sum _{i=1}^n{\stackrel{‒}{u}}_i^{\left(l\right)}{G}_i\sum _{g=0}^2\left\{g\frac{\partial }{\partial \theta }{p}_g({\mathbf{Z}}_i;{\stackrel{\sim }{\theta }}^{\ast })\right\}\sum _{g=0}^2\left\{g\frac{\partial }{\partial \theta \prime }{p}_g({\mathbf{Z}}_i;{\stackrel{\sim }{\theta }}^{\ast })\right\}∕e_{{\stackrel{\sim }{\theta }}^{\ast }}^3\left({\mathbf{Z}}_i\right)\hfill \\ \hfill & =o_p\left(\sqrt{n}\right),\hfill \end{array}$$

by the condition ${\text{max}}_{1\le i\le n}\parallel {\stackrel{‒}{\mathbf{u}}}_i{\parallel }^2=o\left(n\right)$ and the condition (9). Substituting (A.16) and (A.17) into (A.15) leads to

$$\begin{array}{cc}\hfill \sqrt{n}{\Lambda }_{{\theta }_0}^{-1∕2}{\widehat{\mathbf{U}}}_{\text{IPW}}& =\sqrt{n}{\Lambda }_{{\theta }_0}^{-1∕2}{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)-{\Lambda }_{{\theta }_0}^{-1∕2}{\Gamma }_{{\theta }_0}\sqrt{n}(\widehat{\theta }-{\theta }_0)+o_p\left(1\right)\hfill \\ \hfill & ={\Lambda }_{{\theta }_0}^{-1∕2}\sqrt{n}\{{\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)-{\Gamma }_{{\theta }_0}(\widehat{\theta }-{\theta }_0)\}+o_p\left(1\right)\hfill \end{array}$$ (A.18)

$$=\left\{{\Lambda }_{{\theta }_0}^{-1∕2}({\mathbf{I}}_p,-{\Gamma }_{{\theta }_0}){\Omega }_{{\theta }_0}^{1∕2}\right\}\sqrt{n}{\Omega }_{{\theta }_0}^{-1∕2}\left[\begin{array}{c}\hfill {\mathbf{U}}_{\text{IPW}}\left({\theta }_0\right)\hfill \\ \hfill \widehat{\theta }-{\theta }_0\hfill \end{array}\right]+o_p\left(1\right).$$ (A.19)

The equality in (A.18) follows if

$${\Vert {\Gamma }_{{\theta }_0}\Vert }_2=O\left(1\right)\text{and}{\Vert {\Lambda }_{{\theta }_0}^{-1∕2}\Vert }_2=O\left(1\right),$$ (A.20)

where ∥A∥₂ = {λ_max(A′A)}^1/2 is the spectral norm for any matrix A. We will prove (A.20) at the end. Combining Lemma 2 and the fact that

$$\left\{{\Lambda }_{{\theta }_0}^{-1∕2}({\mathbf{I}}_p,-{\Gamma }_{{\theta }_0}){\Omega }_{{\theta }_0}^{1∕2}\right\}\left\{{\Lambda }_{{\theta }_0}^{-1∕2}({\mathbf{I}}_p,-{\Gamma }_{{\theta }_0}){\Omega }_{{\theta }_0}^{1∕2}\right\}\prime ={\mathbf{I}}_p,$$

(A.19) leads to the following convergence in distribution

$$\sqrt{n}{\Lambda }_{{\theta }_0}^{-1∕2}{\widehat{\mathbf{U}}}_{\text{IPW}}\to N(0,{\mathbf{I}}_p).$$

At the end, we verify (A.20) to complete our proof. There exists a constant C > 0 such that

$$\begin{array}{cc}\hfill {\Vert {\Gamma }_{{\theta }_0}\Vert }_2& \le C\sum _{g=0}^2\frac{1}{n}{\Vert \sum _{i=1}^{n}g{\stackrel{‒}{\mathbf{u}}}_i\frac{\partial }{\partial \theta }{p}_g({\mathbf{Z}}_i;{\theta }_0)\Vert }_2\hfill \\ \hfill & \le C\sum _{g=0}^2\frac{2}{n}{\Vert \sum _{i=1}^n{\stackrel{‒}{\mathbf{u}}}_i{\stackrel{‒}{\mathbf{u}}}_i^{\prime }\Vert }_2^{1∕2}{\Vert \sum _{i=1}^n\frac{\partial }{\partial \theta }{p}_g({\mathbf{Z}}_i;{\theta }_0)\frac{\partial }{\partial \theta \prime }{p}_g({\mathbf{Z}}_i;{\theta }_0)\Vert }_2^{1∕2}\hfill \\ \hfill & =\frac{1}{n}O\left(\sqrt{n}\right)O\left(\sqrt{n}\right)=O\left(1\right).\hfill \end{array}$$

Also, for an arbitrary x ∈ R^p,

$$\begin{array}{cc}\hfill \mathbf{x}\prime {\Lambda }_{{\theta }_0}\mathbf{x}& =\mathbf{x}\prime ({\mathbf{I}}_p,-{\Gamma }_{{\theta }_0}){\Omega }_{{\theta }_0}({\mathbf{I}}_p,-{\Gamma }_{{\theta }_0})\prime \mathbf{x}\hfill \\ \hfill & =(\mathbf{x}\prime ,-\mathbf{x}\prime {\Gamma }_{{\theta }_0}){\Omega }_{{\theta }_0}(\mathbf{x}\prime ,-\mathbf{x}\prime {\Gamma }_{{\theta }_0})\prime \hfill \\ \hfill & \ge \underset{n}{\text{inf}}\left\{{\lambda }_{\text{min}}\left({\Omega }_{{\theta }_0}\right)\right\}{\Vert \mathbf{x}\Vert }^2,\hfill \end{array}$$

With the condition ${\lambda }_{\text{min}}\left\{{\sum }_{i=1}^n({\gamma }_{i1}{\gamma }_{i1}^{\prime }+{\gamma }_{i2}{\gamma }_{i2}^{\prime })\right\}\ge nϵ$ in Theorem 2, δ_n in (A.14) can be replaced with nδ for some δ > 0, which in turn implies that inf_n{λ_min(Ω_θ0)} > 0. Then we know inf_n{λ_min(Λ_θ0)} > 0 according to (A.21). So $\Vert {\mathbf{\Lambda }}_{{\theta }_0}^{-1∕2}{\Vert }_2=O\left(1\right)$.