Abstract
Studies of the evolution of collective behavior consider the payoffs of individual versus social learning. We have previously proposed that the relative magnitude of social versus individual learning could be compared against the transparency of payoff, also known as the “transparency” of the decision, through a heuristic, two-dimensional map. Moving from west to east, the estimated strength of social influence increases. As the decision maker proceeds from south to north, transparency of choice increases, and it becomes easier to identify the best choice itself and/or the best social role model from whom to learn (depending on position on east–west axis). Here we show how to parameterize the functions that underlie the map, how to estimate these functions, and thus how to describe estimated paths through the map. We develop estimation methods on artificial data sets and discuss real-world applications such as modeling changes in health decisions.
Introduction
In studies of decision-making and health, social influence is becoming increasingly recognized. Coordinated behavior has benefits for groups and the individuals within them. When successful behaviors of the community are socially learned, cooperation can evolve in social networks extending beyond the limits of Hamiltonian inclusive fitness among kin [1]–[8]. Provided that some fraction of agents learn individually [9], either as “specialists” or “generalists” [10], social learning can be seen as an adaptive strategy among “scroungers” for the exploitation of the information gains made by the “producers” who track the environment through individual learning [11]–[13]. Most evolutionary approaches expect the most adaptive state to equilibrate to a mix of individual and social learners whose proportions are dictated by the degree of spatial and temporal autocorrelation of the environment and the cost of individual learning [7], [12], [14]–[18]. This assumption of adaptive equilibrium is an ideal, however, and not necessarily attainable in conditions of continual transition. As social learners increase in frequency, they are increasingly copying from each other, and so the quality of their information about decision payoffs likely diminishes [12]. At the same time, individual learners may be overwhelmed by rapid change, poor information, or simply too much information in order to make informed decisions.
For this reason, there is the important factor of how well informed decision makers are — what we might call the “transparency” of payoffs in their decisions. A relevant question about online social media, for example, is whether their searchability makes decision makers more well informed, or whether the deluge of social influence and similar options makes decisions less transparent in terms of payoffs [19]. Traditional decision theory typically assumes that agents are informed about their behavioral options, or if not, then are at least knowledgeable about the people from whom they might learn, preferably the most skilful, informed, or prestigious members of the group [12], [20]–[22]. In contrast, models of collective flocking or herding behavior assume no such knowledge — agents are often represented by vectors, with choice as the direction and transparency as the magnitude. Even as most agents follow neighbors with no particular preference, a collective direction (consensus) can nonetheless favor of the minority, if there exists high transparency of choice [23]–[25].
We see two major factors in decision making: social/individual learning and transparency of choice [19], as depicted in Figure 1. This heuristic map represents the relative magnitude of social versus individual learning on the horizontal axis and the transparency of a decision on the vertical axis. Following the call for evolutionary theory as the integrating principle of behavioral science [26], the map is intended to unify quantitative approaches from multiple branches of social science, ranging from rational-actor approaches in the northwest, to more anthropological social-learning theory in the northeast, to the “information overload” of the southwest and southeast.
Figure 1. Summary of the four-quadrant map for understanding different domains of human decision making, based on whether a decision is made independently or socially and the transparency of options and payoffs [19].
At the macro scale, the map reduces the complexity of social decision process analysis to the coarse-grained simplicity of two axes, analogous to a principal components analysis reduced to two dominant factors. The north–south axis, which we parameterize as 
, represents a measure of transparency in the payoff differences among available alternatives, from opaque at the south (
) to absolutely transparent in the north (
). Along the east–west axis, the measured parameter 
increases from west to east, from a decision made individually at the western edge (
) to pure social decision making — copying, for example — at the eastern edge (
).
The framework has broad applicability, and one particular application we envisage is toward fertility decisions for example, using an exceptional long-term dataset on about 250,000 people, collected in the Matlab region of Bangladesh since 1966 [27]. Those data are excellent, long-term monthly records of the decisions that have been made over many years, along with associated (anonymous) details of the individuals making those decisions, such as total fertility, religion, surviving children, age at marriage, household income, education and other observable covariates that impact fertility. We can also consider social variables as well, such as density of the behaviour within the local social network. Other health-related examples would be smoking, where national health services such as the NHS in the United Kingdom or the ALSPAC dataset at University of Bristol hold long-term data on anonymous individuals and their relevant binary choices (to smoke or not, be vaccinated or not), along with a wealth of covariate information on the individuals (wealth, education, religion, and so on) but also often on social visibility (e.g., kin members in the same dataset).
Work on peer effects in smoking behavior is vast, but we have not found any work that attempts to estimate the dynamics of the intensity of choice function, as we propose. Work that is most closely related to ours [28], [29] attempts to control for the effects of self-selection into peer groups, correlated unobservables, and contextual effects that tend to bias received estimates of peer effects on smoking (e.g., estimates of our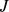 
parameter). This valuable precedent, however, does not estimate the intensity of selection function as we propose.
Our approach could be applied to far different scenarios than health, including criminal records or consumer sales, where long-term choice data are available alongside individual covariates. We see the framework as especially appropriate to online choices in the big-data era, as the covariate data could be comprehensive, including vast records of previous choices. In all cases, the characterization on social influence and transparency of choice would provide a novel insight into the decision dynamics at the population scale.
We previously described the map in terms of generalized data patterns diagnostic of each of its four quadrants [19]. We focused on population-scale data patterns and left specific empirical estimation concerning individuals to future work. Here we show how real-world data could be plotted as locations on the map in Figure 1 and, if the data allow, as trajectories across the map through time. This requires us to develop a method to estimate 
and 
, either for each agent or for each agent's group, from real-world data. We assume the available data include the (a) covariates that may influence the agent's choice, (b) variability of the agent's choices, and (c) strength of social influences upon the agent's choices. All three of these associations may change through time.
The Model
In parametarizing our two-dimensional map, we divide transparency of choice into separable components for intrinsic utility and social influence. Our model builds on previous work in discrete choice theory by parameterizing the transparency of choice as a function of observable covariates (see Methods). To begin, let there be 
groups with 
players in each group. We can think of 
as being a large number so that the law of large numbers gives a good approximation in what follows. For now, assume the groups are disjoint, i.e., nonoverlapping. Agent 
in group 
chooses choice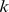 
if the random utility agent 
gets from choice 
is greater than the random utility available from any other choice,
 |
(1) |
at time 
for all 
. Here, symbols with a 
denote random variables (deterministic quantities will not have tildes).
Assume that
 |
(2) |
where the 
are deterministic and the random variables 
are Independent and Identically Distributed Extreme Values (IIDEV) across all dates, choices, groups, and individuals. Then the transparency of choice is inversely proportional to how strongly the noise in the payoff is amplified,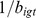 
. We then choose units so the constant of proportionality is one (so that when noise is small, transparency is high). As we will see, this noise can occur in intrinsic utility and/or social utility of the choice. The probability, 
, that agent 
in group 
chooses 
is then the term for choice 
divided by the sum of terms across all choices, 
:
 |
(3) |
where 
, 
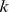and 
take the integer index values from 1 to 
, 
, and 
, respectively. The higher the transparency of choice is, the more sensitive the probability is to the utility. Note that when transparency of choice 
is zero, utility has no effect on choice, and agents are effectively just guessing among all the choices, i.e., 
when 
.
In order to incorporate the “east-west” axis of social influence, one option is to add a term for frequency-dependent social learning [30], whereas another is to add a social component by which agent 
makes pairwise expectations on choices of 
others [31]. Building on both, we define utility with respect to choice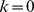 
and then divide 
by 
, so that the partition function, 
, cancels out from equation 3, such that
 |
(4) |
If we then take the natural logarithm of both sides, we are left with the transparency 
multiplied by the difference in utility 
. We can then expand the utility function into an individual component and a social component as follows:
 |
(5) |
for agent 
, for choice 
, in group 
, at date 
(recall that 
is the fraction of group 
that chose 
at date 
).
Table 1 in the Methods section (below) summarizes the different parameters and variables involved. Equation 5 separates, from left to right on its right-hand side, an individual-choice component, 
, and a social component, 
. The individual component of choice is governed by 
and acts on the payoff difference between options 
. The social-influence component, governed by 
, acts on the popularity of the option 
that is expressed as the relative popularity of choice 
compared to the choice of reference 
. Although the transparency of choice parameter, 
, is part of both the individual term and the social-learning term, our map depicts the transparency of choice and social influence as orthogonal dimensions.
Table 1. Parameters and variables of the model.
| Parameter or variable | Description |
|
Total utility payoff function (total) |
|
Individual index, from 1 to 
|
|
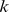
Choice index, from 1 to 
|
|
Group index, from 1 to 
|
|
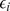
Random idiosyncrasies (noise) associated with agent 
|
|
transparency of choice for agent  at time  . Depends on  and  . |
|
Social influence for agent  at time  . Depends on  and  . |
|
Individual sensitivity to differences in choice 
|
|
Social choice transparency (parameter vector) |
|
Covariates for choice transparency (parameter vector) |
|
Scalar for individual choice |
|
Scalar for presence of social influence |
|
Scalar for variability of choices through time |
|
Observable characteristics of agent  , consisting of 
|
The model is intended to allow the estimation 
and 
from the data and potentially map a trajectory through time for agent 
in group 
. The transparency of choice, 
, increases from south to north on the map and the social influence, 
, increases from west to east (Figure 1). We may estimate 
once we have adequate time series data set on a vector of covariates, 
, and we have parameterized the transparency of choice function, 
. The parameter vectors 
and 
can be normalized to fit the functional specification, 
, and social-utility function,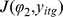 
, respectively (discussed below).
The covariates for each agent include those that predict the propensity of the behavior, denoted by 
, those associated with the presence of social influence 
, and those that relate how variable the choices were through time, 
. These realities are amplified by 
(individual) and 
(social), which govern the sensitivity to inherent differences of the choice and social influence, respectively. In other words, the parameter vectors 
, and 
operate on aspects of the real world denoted by positive scalars 
, and 
, respectively. Estimating the parameter vector 
determines the individual sensitivity to differences in choice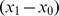 
. Estimating the parameter vector 
, along with the scalar observable 
, determines the transparency of choice, 
. Estimating the parameter vector 
specifies the social-influence function, 
.
We tested to see how these estimates can be used to describe a path,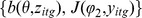 
, through the map for each agent 
in each group 
for which we have data at date 
.
Results
We generated artificial data to yield four different paths through the map to test whether our suggested estimation procedure actually works (see Methods). We can use equation 5 for a log odds regression,
 |
(6) |
where 
is the fraction of group 
that chose 
at date 
. We then specified the social-influence and transparency of choice functions as follows,
 |
(7) |
We can now use this parameterisation to explore how the parameterised map applies to artificial datasets (see Methods on how these data were generated). In Figure 2, we show simulations of the binary choice (e.g., to have a child or not) with 
, and 
from equation 7, with group size 
and 
agents per group. We then vary the initial starting proportions of the 10,000 agents (over all groups) choosing one (blue) versus the other (red). We can see that all simulations converge to nearly 100% of agents choosing the blue option in fewer than ten time steps, even if we start with a majority choosing red at the starting point. This is what we expect when both 
is positive and 
is high and positive — the population selects the option with the better payoff.
Figure 2. Simulations of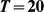 
time steps, with group size
and
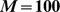agents per group.
From equation 7, we set 
, and 
. The noise component, 
has mean 0 and 
. Shown are proportions of the 10,000 total agents who have made one of the two possible two choices, one shown as red and one shown as blue, through time. The different plots show simulations with varying starting points for each proportion. The payoffs 
and 
are chosen from from time-varying normal distributions 
, and 
and 
are both chosen from time-varying normal distributions 
. Gray bounds show 95% quantiles for sample paths over group and red/blue curves show the mean paths for proportion over groups.
The specification in equation 7 allows other variations that yield more novel results. To convey the effects of varying 
and 
, Figure 3 shows the change in behavior for a binary choice under different values of 
and 
(for clarity, Figure 3 shows just the proportion of one of the two choices). In varying these two parameters, we find variation not only in final outcomes after 30 time steps, but in the dynamics of choice as well (Figure 3). When 
is negative, for example, we move toward social independence, and, for positive 
, decisions tend to be made socially. Similarly, when 
is negative, we move south toward ambivalence, and, as 
increases, we move north toward a transparency between the binary options. If 
is low and 
high, a member (or a whole group) might be able to choose something different from the norm. This event, however, becomes rarer as social influence increases.
Figure 3. Simulations of binary choice model with varying choice intensity 
and social influence intensity 
.
For clarity the plots only show the proportion of agents making one of the two choices (e.g., non-parent). The panels show 16 different combinations of 
and 
, with 
for all. Each panel shows results of simulation with 30 time steps, 100 groups and 200 agents per group, noise component 
with mean 0 and 
, and starting proportion 80% for the choice shown (so the choice not shown starts at 20%). The payoffs 
and 
are chosen from 
, and 
and 
are both chosen from 
. Gray bounds show 95% quantiles for sample paths over group for the proportion of non-parents over groups.
We then used the modelling to explore how the parameters 
and 
can be estimated from the simulated data. Figure 4 shows how some estimates of the parameters, based on the data generated via simulation, vary as we move along the axis on the map displayed in Figure 1. We use a nonlinear least squares (NLLS) method to estimate 
and 
; for 
large (Figure 3, bottom row), for example, estimating 
accurately is nearly impossible because there is little variation in behaviour as the social dominance of the group dominates individual utilities.
Figure 4. Map of the chosen values of 
and
used in
Figure 3
.
The red dots represent the true parameter values and are linked to their corresponding nonlinear least squares estimates in blue.
Discussion
In these tests, we found that estimation is reasonable for 
but less precise for 
. We see the source of this “weak identification” problem in equation 5 where, because 
multiplies 
and 
, there can be difficulty in disentangling parameters in 
from 
and parameters in 
unless we have the right kind of specifications of 
and 
as well as variation in the observables that go into estimating their parameters. In equation 11 we can also see the challenge in disentangling the size of 
for the size of the variance of the random variable on the right-hand side (multiplying numerator and denominator by a scalar cancels out). This suggests that the variance of the numerator has to be normalized to one, say, in order to identify parameter theta in 
.
We note that the inability to correctly estimate 
for large values of 
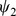is not important because the uncertainty around 
when 
is large shows that payoff/costs are irrelevant when social influence is extremely high. In future work we will focus on how to better estimate 
. Moreover, as we focus on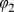 
and 
, we may consider that 
is unnecessary. We prefer to keep 
embedded in the model, as it allows for a priori assumptions regarding the strength of individual vs social learning — from 
(aversion to choice 1) to 
(no individual bias) to 
(bias towards choice 1). Further, removing 
would change the inference on 
and 
; that is,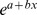 
and 
can be equivalent representations when 
and 
are positive, but otherwise the relevance of 
depends on the magnitude of 
in the former and allows negative outputs in the latter.
The simple bi-axial map of behavior in Figure 1 aims to extract from aggregated data the transparency of decisions (north–south) and the extent to which a behavior is acquired socially versus individually (east–west). We have proposed a means by which to parameterize the functions that underlie the map and thus estimate paths through it. Rather than assume how well agents are informed in their learning, we can let transparency of choice be a variable parameter in our models, with the aim of using the models to infer transparency of choice from real data [19], [23]. For example, we might have a vector 
such that the transparency of choice would be parameterized as the specification 
.
A hypothetical real-world example for 
might be the fraction of unvaccinated in group 
at time 
. We would consider an idealized binary choice of whether or not to get vaccinated at time 
, where 
would designate vaccinated and 
designate not vaccinated. In this example, 
grows linearly with 
, which would imply that the more unvaccinated there were in the group, the more transparent the decisions would become about vaccination. Other binary-choice examples might include whether or not to use contraception, smoke, use hand sanitizer, or perhaps the fertility decision of whether or not to have a child.
Social-influence studies that treat transparency of choice as a variable suggest that it has a complex interaction with social learning. Some of this interaction might be captured, for example, by a specification such as 
, by which, assuming 
is positive, the presence of social influence increases with the scalar 
. Hypothetical real-world examples for a group-specific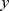 
include the fraction in the group that are high income or perhaps the Gini coefficient of the group. Given the formulation for 
, the scalar factor 
then affects the social influence associated with other observables.
These parameters relate to debates on modelling fertility decisions, for example, as explanations range from an intrinsic individual utility decision [27] versus the social influence of the frequency of a particular fertility level in their local community [32]. For example, it may be that poor, uneducated women living in a wealthy, educated group tend to adopt the low-fertility level of the group rather than the higher fertility that would otherwise be associated with their low income and low education as individuals [32]. In this case the social-choice transparency, 
, might reflect the tendency to have the same number of children as other mothers, whose success and/or education has become more socially visible.
Fertility research also generates the sort of long-term, time-stratified demographic datasets that are appropriate to our proposed estimation method for the map. More generally, the growth of so-called “big data” on collective decisions also seems suited to this map [19], which links different scales of analysis, such as the microprocesses that produce observed scaling relationships in social-network formation [33].
As new digital technologies filter and search social influences and information, transparency of choice may be increased, but conversely if agents are overwhelmed the online deluge of information, options, and social influences [34], [35], then transparency of choice, 
, may decrease (by decreasing 
and/or 
). This may be central to herding effects in online product ratings [36], for example. Also, the transparency of payoffs may well be changing for many health decisions - the rapidly changing conditions of the modern world may effectively lower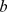 
as the connection between the decision and its actual future payoffs are obscured by the “noise” of socio-economic change. Seemingly straightforward social interventions may therefore have unanticipated consequences [37].
The dimensions of the map are also relevant to studies that compare technological complexity with population size [38]–[41], which assumes relatively transparent individual and social learning. Adding agents who are uninformed (payoffs not transparent) tends to cause a group consensus to regress to a single mode [24], [42]. When it is much easier, and less costly (essentially free), to see what others do, then the balance could shift to the east and south. When survey respondents, for example, can see the aggregated guesses from other people, they simply change from their original, individual guesses in linear proportion to the distance from the group mean [43].
Conclusion
Having presented a two dimensional map (Figure 1) as a schematic abstraction of human decision-making [19], we have now gone further toward making this into an empirical tool to project population-scale decision data onto axes of social influence and transparency of choice. As the decision maker proceeds from south to north, the precision of understanding which choice is best increases. As the decision maker moves from west to east, the strength increases of social influence or peer group influence on which choice is best. Starting with a basis in discrete-choice modeling with social influence, we have discussed how a path through the map for a group of decision makers can be estimated from data sets. Through experiments with artificial data sets, we showed how the suggested estimation methods work and how parametric specifications can be estimated. For smaller datasets, we recommend maximum likelihood as the best way to estimate a path through the map, and then for larger datasets it becomes possible to use NLLS as the estimation method.
The map can now be applied to real-world case studies, especially those that feature large, time-stratified demographic data sets on binary decisions, such as those regarding health decisions. The parametrization we have presented allows us to extract, from these sorts of datasets, locations on the map representing degree of social learning and transparency of choice. As we apply this method in the future, we may be surprised to find that standard, universal assumptions regarding certain decisions may be becoming less appropriate, as the nature of such decisions changes through time or in different cultural contexts.
Methods
Artificial data generation
We generated data for 
periods, 
groups with 
members each as follows. We first generated a random noise component, 
, for each agent choice over the time span, which means 
logistic random variates with mean 0 and variance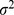 
. We then simulated variability in payoffs and social influence for all of these choices as well. In doing so, we generated three sets of 
normally distributed random numbers, each with time varying means and variance, one set for the 
's, one set for the 
's and one set for the 
's. In this case we allowed the means of 
, and 
to increase over time, by choosing 
and 
from normal distributions with mean 
and variance 0.1, and choosing both 
and 
from normal distributions with mean 
and variance 1. In generating these artificial data sets, we found that our simulation outcomes were well determined after 
time steps, during which the effect of varying group size and members per group was minimal when both 
and 
are greater than 100. We then specified the social-influence and transparency of choice functions as indicated in equation 7.
Functional forms and estimation
In order to identify parameters of the model that describe movements across the map, we need to separate transparency of choice from social influence. To do this, we start with the north–south axis of the map (the transparency of choice) and then add, via the east–west axis, social influence on individual choices. We can start with the north–south axis. In discrete-choice theory, we assume we have a certain number of choices available and a certain amount of utility that is divided up among those choices. We then effectively toss the choices randomly into bins of a certain utility and find how many choices we expect in each bin. To start, consider a population of individuals making a binary choice (
or 
), each seeking to maximize payoff function 
:
 |
(8) |
in which 
represents the binary choice and 
represents covariates of agent 
such as family, peer group, previous choices, or education level. The parameter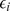 
represents idiosyncrasies, which are treated as random, even if privately sensible to each individual agent. Following [31], we will assume that the values of 
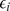are what are known as Independent and Identically Distributed Extreme Values (IIDEV).
For a given individual, a standard approach assumes the probability to make a particular choice is equivalent to the probability that the difference in idiosyncrasies,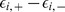 
, is less than some threshold 
:
 |
(9) |
where 
is transparency of choice for agent 
. To illustrate, Figure 5 shows, for two values of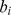 
, how the probability that option 
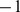(versus option 
) is chosen depends on this payoff difference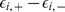 
. The probability transition is more abrupt or decisive for the higher value of 
(farther north on our map), representing greater transparency of choice.
Figure 5. From
equation 9
, showing how the probability that option 
(versus option 
) is chosen depends on this payoff difference 
, two values of 
.
Our use of the Fermi/Boltzmann function as our equation (9) is fairly standard in discrete-choice theory, but it is also seen in some studies of evolutionary games in finite populations, in which a “temperature,” or “noise,” parameter is varied (e.g., taken to zero) in order to characterize the equilibrium in terms of cooperators in the population. The same function has been used, for example, to model the probability of outcome between two randomly selected individuals playing Prisoners Dilemma or related pairwise game [44], [45]. In that case, the parameter (analogous to temperature in the Boltzmann function) is intensity of selection rather than our transparency of choice, which operates on the payoff difference. The difference in our approach from game-theoretic approaches is twofold. First, rather than play pairwise games, agents choose among available options and the model relates how well choice popularity corresponds to covariates among the individuals of the population. Second, our focus is on econometric identification of parameters and estimation of parameters as well as on the ability to retrieve the model parameters from noisy data. In particular, we are interested in estimating the intensity of selection as a function of observable covariates. This effort appears new to the literature on estimation of social influences on choice, and it raises difficult identification issues that we have addressed through simulation methods. We developed this approach in order to show that our method works before applying it to field data.
Although this established approach does not model social influence directly, it has been used as a baseline to infer it from appropriate datasets. Aral et al. [46], for example, applied this to daily data on the social network links and the date when individuals downloaded a certain mobile-service application (app). Aral et al. [46] considered individuals of similar propensity, 
, to have adopted the app by time 
, which for agent 
was estimated using a logistic regression equivalent to:
 |
(10) |
where 
functions as transparency of choice and 
is a vector of observable characteristics and behaviors for agent 
at time 
(we have subsumed one of their other parameters into the idiosyncrasies term 
). Having collected data over a 4-month period, Aral et al. [46] were able to distinguish homophily — the tendency of similar individuals to associate with each other — from genuine influence (roughly 50/50 in their final estimation).
Now, to build from this background to an explicit consideration of social influence and transparency of choice, suppose that we have 
different subpopulations, each with 
individuals. Within each population 
individuals are considered potential peers. Suppose we have observed covariates for all dates 
and each agent 
in every group 
, as well as the estimated propensity to be vaccinated, denoted by 
. Also suppose, based on previous studies, we have another set of social-influence covariates, 
, on agent 
and group 
at date 
, and yet another set of covariates, 
, that relate how variable the choices were through time.
Our goal is to plot 
and 
for each agent 
for each date 
for each group 
on the map, by which we could describe a temporal path for each agent 
in each group 
. We start with the scalar covariate case where choice number 1 is made over choice 0 at date 
. This happens when the utility of choice 
versus choice 
, comprising the individual and social-choice components, exceeds the random variable given the choice transparency, i.e.,
 |
(11) |
where, again, the covariates, 
, are all positive, one-dimensional scalars. Note that 
and 
can be either positive or negative. Table 1 (below) summarizes the different parameters and variables involved. The parameter vector, 
, represents the intrinsic and social sensitivities, given the transparency of payoffs. The estimates of these from the data set are denoted 
— we use “hats” to denote estimates.
With sufficient data on 
, and 
from a particular case study, we can estimate the parameter vector, 
, of the structural model in equations 3 and 5 using the observed fractions 
of vaccinated individuals in group 
at date 
(recall that the estimates are denoted by 
). The model predicts that agent 
in group 
gets vaccinated at date 
if the difference in noisy payoff 
is greater than zero. In other words, the probability of positive payoff for vaccination, 
, is equivalent to the probability favoring the intrinsic plus social payoffs of parenting over the random idiosyncrasies of choice:
 |
(12) |
Here, 
is the cumulative distribution function of the random variable, 
.
Functional forms for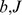 
To specify 
we might start with the simple specification 
, with 
representing the variability of choices through time 
. With this specification, the larger 
is, the less variable the choices of agent 
are through time.
We can then discuss several different specifications of the social-influence function 
. To work within the borders of the map we might, for example, specify the social-influence function as
 |
(13) |
This function allows 
to take the value zero with positive probability, and we require the function 
, i.e., to not allow 
, so that the farthest west part of the map corresponds to 
. In the absence of social influence, the value of 
. If we assume that 
for an open set of 
's implies 
, and that 
for an open set of 
's implies 
, then the absence of social influence 
implies
 |
(14) |
Further, we see that if the data have a wide enough range over individuals, groups, and dates, of values of 
, it must be the case that
 |
(15) |
i.e., social influence is zero for all values of the parameters that cannot be specified by the data alone. This level of identification can be enough when we simply want to determine the strength of social influence over time for different individuals and groups in different choice settings. We discuss another specification of the social-influence function 
in Section 5, where we test the estimation procedure on artificial data.
Estimation methods
In order to consider two popular estimation methods, Maximum Likelihood (ML) and Non-Linear Least Squares (NLLS), we consider a binary decision via equation 12, with the probability statement
 |
(16) |
where 
is the cumulative distribution function of the random variable, 
. We have added a constant term,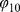 
, and a slope term, 
, in equation 16 to capture variation among agents in how they respond to different alternatives, independent of social influences.
Now, denote by 
the random variable, which is either 1 if agent 
in group 
succeeds (or chooses “yes”) at date 
or 0 if agent 
in group 
fails (or chooses “no”) at date 
. From equation 16 we can write the likelihood function for the probability of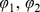 
, and 
, given the real-world data ([47], section 17.3), which relates to how well the model predicts all the observed successes (yeses) and failures (nos):
 |
(17) |
where 
is the cumulative distribution function of the random variable,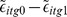 
, and
 |
(18) |
In the standard versions of estimation of discrete-choice models, the transparency of choice, 
, is typically assumed to be constant (absorbed into the other parameters by a normalization convention). We are interested in how 
varies, however, so we must modify the conventional textbook approach [47]. One popular way of proceeding is to formulate dynamic discrete-choice models [48], which often use Markov chain formulations or hazard-function formulations. However, for simplicity we wish to remain as close as possible to the static framework with independent stochastic drivers. Therefore, we shall work with the likelihood function (equation 3.7) above, where the ultimate stochastic drivers are IIDEV across individuals, groups, and dates.
In the scalar case, formulas for the partial derivatives of the likelihood function with respect to 
are straightforward. The maximum-likelihood estimator, at the peak of the likelihood function, is found by setting these four partial derivatives of the likelihood function equal to zero. This yields four nonlinear equations in four unknowns. When one takes these four partial derivatives and sets the four resulting equations equal to zero, one will see that when, for some reason, the social-influence function is always zero, then the pair 
is determined only up to scale. The nonlinearity of the social influence helps resolve this particular identification problem.
If the social-influence function is zero, however, or restricted to be zero, we normalize the four equations by dividing the equations by 
, which can be further simplified by setting 
and solving the remaining three equations for 
, and 
. Three nonlinear equations in three unknowns is still more challenging than simple Ordinary Least Squares regression analysis.
Packages such as Matlab or R are good for general ML estimation, which works well when we have few observations per cell and enough observations per cell to allow for logistic regression [49]. Also, ML estimation does not assume that errors follow a specific distribution, whereas NLLS assumes normality of the errors, and one can use least squares estimators as starting points on the ML solver. ML estimation is less demanding of data sets than NLLS [47, chapter 14], but in cases where there is a large amount of data, we can also consider NLLS estimation methods that require larger data sets. Equation 5 suggests the NLLS regression equation of the log odds of agent 
in group 
of choosing choice 1 rather than choice zero at date 
,
 |
(19) |
in which the right-hand side again consists of transparency of choice multiplied by individual, social, and noise components (note that the noise terms 
in equation 19 are part of the standard regression equation framework and are not the same as the 
terms in the logit equations above). Here, we assume the standard regression orthogonality condition on the regression errors,
 |
(20) |
so that parameter estimates are consistently estimated as sample size tends to infinity.
Note that equation 20 implies
 |
(21) |
by taking iterated expectations. Equation 21 assures us that if we estimate the parameters in equation 19 by NLLS, the estimates will have good properties, provided that the parameter vector, 
, in the structural model in equation 19 is identified ([47], chapter 7). Of course, since the function induces heteroskedasticity in the residuals, 
, of the NLLS regression equation 19, this heteroskedasticity can be exploited to produce more efficient estimates ([47], chapter 7). To avoid some problems of large sample size and data overflow, an improved NLLS estimation process might use a growing window in time, i.e., start with points corresponding to time 
and locate a plausible region on the parameter space, add more points for time 
and update, and so on.
Consider the functional-form specifications for the transparency of choice function and the social-influence function,
 |
(22) |
Substituting 22 into 19, NLLS proceeds by selecting the parameter vector, 
, to minimize the sum of squared errors (SSE),
 |
(23) |
where
 |
(24) |
is the prediction error of the model. In other words, NLLS chooses the parameter vector to minimize the sum of prediction errors. Taking the four partial derivatives of SSE with respect to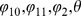 
, and setting all four of them equal to zero, we have the four following four nonlinear equations in four unknowns:
 |
(25) |
We can see that if for some reason the term 
is always zero, then the pair of parameters, 
, of the direct utility difference is determined only up to scale. To put it another way: if we set the social-influence function 
equal to zero, then the parameter pair, 
, is not identified, i.e. any parameter pair 
will solve the last equation of 25 with the third equation dropped for all values of 
. We resolve this problem if it occurs by “normalizing” by setting 
and dropping the first equation of 25. We recommend the same procedure for the ML estimation above.
Acknowledgments
This research was partially supported by the Leverhulme Trust “Tipping Points” program. Correspondence should be addressed to Alex Bentley at r.a.bentley@bristol.ac.uk.
Data Availability
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper.
Funding Statement
This research was partially supported by the Leverhulme Trust “Tipping Points” program. The funder had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1. Helbing D, Yu W (2009) The outbreak of cooperation among success-driven individuals under noisy conditions. Proceedings of the National Academy of Sciences USA 106: 3680–3685. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Henrich J, Boyd R, Bowles S, Gintis H, Fehr E, et al. (2006) “economic man” in cross-cultural perspective: Ethnography and experiments from 15 small-scale societies. Behavioral and Brain Sciences 28: 795–855. [DOI] [PubMed] [Google Scholar]
- 3. Hill KR, Walker R, Božičević M, Eder J, Headland T, et al. (2011) Co-residence patterns in hunter-gatherer show unique human social structure. Science 331: 1286–1289. [DOI] [PubMed] [Google Scholar]
- 4.Hrdy SB (2009) Mothers and Others: The Evolutionary Origins of Mutual Understanding. Cambridge, MA: Harvard University Press.
- 5.Nowak MA (2006) Evolutionary Dynamics. Harvard University Press.
- 6. Rand DG, Dreber A, Ellingsen T, Fudenberg D, Nowak M (2009) Positive interactions promote public cooperation. Science 325: 1272–1275. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Rendell L, Fogarty L, Hoppitt W, Morgan T, Webster MM, et al. (2011) Cognitive culture: theoretical and empirical insights into social learning strategies. Trends in Cognitive Sciences 15: 68–76. [DOI] [PubMed] [Google Scholar]
- 8.Turchin P, Currie TE, Turner EAL, Gavrilets S (2013) War, space, and the evolution of old world complex societies. Proceedings of the National Academy of Sciences USA 110: pages. [DOI] [PMC free article] [PubMed]
- 9.Boyd R, Richerson PJ (1985) Culture and the Evolutionary Process. Chicago: University of Chicago Press.
- 10. Baronchelli A, Chater N, Christiansen HM, Pastor-Satorras R (2013) Evolution in a changing environment. PLoS ONE 8: e52742. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Henrich J, McElreath R (2003) The evolution of cultural evolution. Evolutionary Anthropology 12: 123–135. [Google Scholar]
- 12. Mesoudi A (2008) An experimental simulation of the “copy-successful-individuals” cultural learning strategy. Evolution and Human Behavior 29: 350–363. [Google Scholar]
- 13. O'Brien MJ, Bentley RA (2011) Stimulated variation and cascades: Two processes in the evolution of complex technological systems. Journal of Archaeological Method and Theory 9: 1–17. [Google Scholar]
- 14. Laland KM (2004) Social learning strategies. Learning and Behavior 32: 4–14. [DOI] [PubMed] [Google Scholar]
- 15.McElreath R, Boyd R (2007) Mathematical Models of Social Evolution. Chicago: University of Chicago Press.
- 16.Mesoudi A (2011) Cultural evolution: How Darwinian theory can explain human culture and synthesize the social sciences. Chicago: University of Chicago Press.
- 17. Nettle D (2009) Ecological influences on human behavioural diversity: A review of recent findings. Trends in Ecology and Evolution 24: 618–624. [DOI] [PubMed] [Google Scholar]
- 18.Kempe M, Mesoudi A (2014) An experimental demonstration of the effect of group size on cultural accumulation. Evolution and Human Behavior 35: in press.
- 19. Bentley RA, O'Brien MJ, Brock WA (2014) Mapping collective behavior in the big-data era. Behavior and Brian Sciences 37: 63–119. [DOI] [PubMed] [Google Scholar]
- 20. Henrich J (2004) Demography and cultural evolution: How adaptive cultural processes can produce maladaptive losses. American Antiquity 69: 197–214. [Google Scholar]
- 21. Henrich J, Broesch J (2011) On the nature of cultural transmission networks: Evidence from fijian villages for adaptive learning biases. Philosophical Transactions of the Royal Society B 366: 1139–1148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Mesoudi A, O'Brien MJ (2008) The learning and transmission of hierarchical cultural recipes. Biological Theory 3: 63–72. [Google Scholar]
- 23. Bentley RA, O'Brien MJ (2012) Tipping points, animal culture and social learning. Current Zoology 58: 298–306. [Google Scholar]
- 24. Couzin ID, Ioannou CC, Demirel G, Gross T, Torney CJ, et al. (2011) Uninformed individuals promote democratic consensus in animal groups. Science 334: 1578–1580. [DOI] [PubMed] [Google Scholar]
- 25. Mann R, Perna A, Strömbom D, Garnett R, Herbert-Read J, et al. (2013) Multi-scale inference of interaction rules in animal groups using bayesian model selection. PLoS Computational Biology 9(3): e1002961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Gintis H (2007) A framework for the unification of the behavioral sciences. Behavioral and Brain Sciences 30: 1–61. [DOI] [PubMed] [Google Scholar]
- 27. Shenk M, Towner MC, Kress HC, Alam N (2013) A model comparison approach shows stronger support for economic models of fertility decline. Proceedings of the National Academy of Sciences USA 110: 8045–8050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28. Krauth B (2006) Simulation-based estimation of peer effects. Journal of Econometrics 133: 243–271. [Google Scholar]
- 29. Krauth B (2007) Peer and selection effects on youth smoking in california. Journal of Business and Economic Statistics 25: 288–298. [Google Scholar]
- 30. McElreath R, Bell AV, Efferson C, Lubell M, Richerson PJ, et al. (2008) Beyond existence and aiming outside the laboratory: estimating frequency-dependent and pay-off-biased social learning strategies. Philosophical Transactions of the Royal Society B 363: 3515–3528. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Brock WA, Durlauf SN (2001) Interactions-based models. In: Heckman J, Leamer E, editors, Handbook of Econometrics, Amsterdam: Elsevier Science. pp. 3297–3380.
- 32. Colleran H, Jasienska G, Nenko I, Galbarczyk A, Mace R (2014) Community-level education accelerates the cultural evolution of fertility decline. Proceedings of the Royal Society B 281: 20132732. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Snijders TA, Steglich CE (2013) Representing micro-macro linkages by actor-based dynamic network models. Sociological Methods and Research 42: in press. [DOI] [PMC free article] [PubMed]
- 34. Goncalves B, Perra N, Vespignani A (2011) Validation of dunbar's number in twitter conversations. PLoS ONE 6(8): e22656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Dean D, Webb C (2011) Recovering from information overload. McKinsey Quarterly Jan: 1–9.
- 36. Sridhar S, Srinivasan R (2012) Social influence effects in online product ratings. Journal of Marketing 76: 70–87. [Google Scholar]
- 37. Gibson M, Gurmu E (2012) Rural to urban migration as an unforeseen impact of development intervention in ethiopia. PLoS ONE 7: e48708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Powell A, Shennan SJ, Thomas MG (2009) Late pleistocene demography and the appearance of modern human behavior. Science 324: 1298–1301. [DOI] [PubMed] [Google Scholar]
- 39. Hausmann R, Hidalgo CA (2011) The network structure of economic output. Journal of Economic Growth 16: 309–342. [Google Scholar]
- 40.Henrich J (2010) The evolution of innovation-enhancing institutions. In: O'Brien M, Shennan S, editors, Innovation in cultural systems, Boston: MIT Press. pp. 99–120.
- 41. Malakoff D (2013) Are more people necessarily a problem? Science 333: 544–546. [DOI] [PubMed] [Google Scholar]
- 42. Palfrey TR, Poole KT (1987) The relationship between information, ideology, and voting behavior. American Journal of Political Science 31: 511–530. [Google Scholar]
- 43. Mavrodiev P, Tessone C, Schweitzer F (2013) Quantifying the effects of social influence. Scientific Reports 3: 1360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Traulsen A, Nowak MA, Pacheco JM (2007) Stochastic payoff evaluation increases the temperature of selection. Journal of Theoretical Biology 244: 349–356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45. Traulsen A, Pacheco JM, Nowak MA (2007) Pairwise comparison and selection temperature in evolutionary game dynamics. Journal of Theoretical Biology 246: 522–529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Aral S, Muchnik L, Sundararajan A (2009) Distinguishing influence-based contagion from homophily-driven diffusion in dynamic networks. Proceedings of the National Academy of Sciences USA 106: 21544–21549. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Greene WH (2012) Econometric Analysis. Saddle River, NJ: Prentice Hall.
- 48. Arcidiacono P, Bayer P, Bugni F, James J (2013) Approximating high dimensional dynamic models: Sieve value function iteration. Advances in Econometrics 31: 45–96. [Google Scholar]
- 49. Amemiya T (1981) Qualitative response models: A survey. Journal of Economic Literature 19: 1483–1536. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The authors confirm that all data underlying the findings are fully available without restriction. All relevant data are within the paper.