Atlas-Based Under-Segmentation

Abstract

We study the widespread, but rarely discussed, tendency of atlas-based segmentation to under-segment the organs of interest. Commonly used error measures do not distinguish between under- and over-segmentation, contributing to the problem. We explicitly quantify over- and under-segmentation in several typical examples and present a new hypothesis for the cause. We provide evidence that segmenting only one organ of interest and merging all surrounding structures into one label creates bias towards background in the label estimates suggested by the atlas. We propose a generative model that corrects for this effect by learning the background structures from the data. Inference in the model separates the background into distinct structures and consequently improves the segmentation accuracy. Our experiments demonstrate a clear improvement in several applications.

1 Introduction

Atlas-based segmentation exploits knowledge from previously labeled training images to segment the target image. In this paper, we focus on multi-atlas segmentation methods that map all labeled images onto the target image, which helps to reduce segmentation errors [6,8,11]. Label fusion combines the transferred labels into the final segmentation [9]. A common tendency of atlas-based segmentation to under-segment has largely been ignored in the field. We conjecture that one of the reasons that this phenomenon has not received more attention is that common error metrics do not capture the under-segmentation effect. For instance, the Dice volume overlap [3] and the Hausdorff distance [4] do not indicate if the segmentation is too large or too small. We are only aware of one recent article that addresses the spatial bias in atlas-based segmentation [12]. In that work, the bias is approximated by spatial convolution with an isotropic Gaussian kernel, modeling the distribution of residual registration errors. This model implies under-segmentation of convex shapes and over-segmentation of concave shapes. To reduce the spatial bias, a deconvolution is applied to the label maps. Results were reported for the segmentation of the hippocampus [12].

We present an alternative hypothesis for the bias in segmentation and propose a strategy to correct for such bias. First, we quantify the under-segmentation in atlas-based segmentation with new volume overlap measures. Our hypothesis ties the under-segmentation to the asymmetry of most segmentation setups where we seek to identify a single organ and merge all surrounding structures into one large background class. We show that this foreground-background segmentation strategy exhibits stronger bias than multi-organ segmentation. We propose a generative model of the background to correct under-segmentation even if the segmentation labels for multiple organs are not available. The posterior probability distribution of the Dirichlet process mixture model yields the splitting of the background into several components. Our experiments illustrate that this refined voting scheme improves the segmentation accuracy.

2 Under-Segmentation in Multi-atlas Segmentation

In multi-atlas segmentation, the training set includes images = {I₁, …, I_n} with the corresponding manual segmentations = {S₁, …, S_n} and S_i(x) ∈ {1, …, η}, where η is the number of labels. The objective is to infer segmentation S for a new input image I. Probabilistic label maps 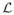= {L¹, …, L^η} specify the likelihood of each label l ∈ {1, …, η} at location x ∈ Ω in the new image

$$L^l(x)=\sum _{i=1}^{n}p(S(x)=l\mid S_i)·p(I(x)\mid I_i).$$ (1)

The label maps satisfy Σ_l L^l(x) = 1 and 0 ≤ L^l(x) ≤ 1. For obtaining label likelihood, we register all training images 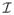to the test image I, yielding deformation fields {ϕ₁, …, ϕ_n}, and define

$$p(S(x)=l\mid S_i)=\{\begin{array}{ll}1\hfill & \text{if}{S}_i({\varphi }_i(x))=l,\hfill \\ 0\hfill & \text{otherwise}.\hfill \end{array}$$ (2)

Alternatively, probabilistic segmentations S_i can be included in the label likelihood, with the rest of the analysis unchanged. For majority voting (MV) [6,8], the image likelihood is constant, p(I(x)|I_i) ∝ 1. For intensity-weighted (IW) voting [9], also referred to as locally-weighted voting, the likelihood depends on image intensities

$$p(I(x)\mid I_i)\propto exp(-{(I(x)-I_i({\varphi }_i(x)))}^2/2{\sigma }^2),$$ (3)

where σ² is the variance of the image noise. We obtain the final segmentation Ŝ(x) by choosing the most likely label

$$\widehat{S}(x)=arg\underset{l}{max}{L}^l(x).$$ (4)

For one structure (η=2), we directly compare foreground and background likelihoods to obtain the segmentation by identifying image locations x for which L^f(x) > L^b(x), or equivalently L^f(x) > 0.5.

2.1 Quantifying Under-Segmentation

Since the Dice volume overlap [3] and the Hausdorff distance [4] do not capture the type of segmentation error, we introduce two measures that explicitly quantify the over- and under-segmentation. Given the manual segmentation S̄ and the automatic segmentation Ŝ, we define

$$O(\widehat{S},\overline{S})=\frac{\mid \widehat{S}\backslash \overline{S}\mid }{\mid \overline{S}\mid }\text{and}U(\widehat{S},\overline{S})=\frac{\mid \overline{S}\backslash \widehat{S}\mid }{\mid \overline{S}\mid }$$ (5)

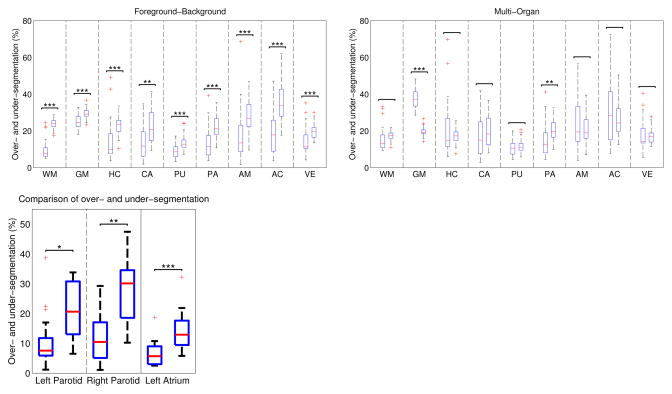
to quantify over- and under-segmentation, respectively. To examine the problem of under-segmentation, we compute and report statistics in three different segmentation applications using intensity-weighted voting in Fig. 1. The applications target the segmentation of (i) nine brain structures in magnetic resonance (MR) images, (ii) left and right parotid glands in CT images, and (iii) the left atrium of the heart in magnetic resonance angiography (MRA) images. For the brain, we perform foreground-background segmentation by segmenting each brain structure separately and merging all other structures into a background label. The structures we segment are white matter (WM), gray matter (GM), hippocampus (HC), caudate (CA), putamen (PU), pallidum (PA), amygdala (AM), accumbens (AC), ventricles (VE). Under-segmentation errors are significantly higher than over-segmentation errors in all three applications, suggesting a bias towards under-segmentation in atlas-based segmentation.

Fig. 1.

Statistical analysis of over-segmentation O (left bar) and under-segmentation U (right bar). Top: Segmentation of brain structures with foreground-background (left panel) and multi-organ (right panel) scheme. Left: Segmentation statistics for foreground-background segmentation of parotid glands and left atrium. Red line indicates the median, the boxes extend to the 25^th and 75^th percentiles, and the whiskers reach to the most extreme values not considered outliers (red crosses). *, **, and *** indicate statistical significance levels at 0.05, 0.01, and 0.001, respectively.

2.2 Foreground-Background Segmentation Causes Spatial Bias

Our hypothesis for the cause of under-segmentation is the asymmetry in how the foreground and background labels are treated by binary classification methods. Merging all surrounding structures into background causes this new meta-label to dominate in the voting process even if the evidence for the foreground label is stronger than that for any of the surrounding structures. We illustrate this phenomenon on the example of the amygdala in Fig. 2. The atlas-based segmentation with the foreground-background scheme yields an under-segmentation (yellow outline). Investigating the votes for one location (black voxel in the left image), we observe that labels from several structures are present. Amygdala is assigned the highest number of votes and would win the voting in a multi-organ scheme. However, merging all other structures into a background label causes the background to win, leading to a segmentation error. To further illustrate the impact of merging neighboring structures, we examine the drop in the Dice volume overlap as we accumulate more and more structures into the background label (Fig. 2, right panel).

Fig. 2.

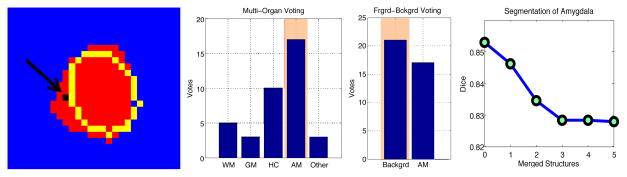
Left: Manual segmentation of amygdala is shown in red, the outline of the automatic segmentation with foreground-background scheme is shown in yellow. Two middle panels: Distribution of votes for the location marked in black in the image on the left. Multi-organ segmentation correctly assigns the AM label. The foreground-background segmentation assigns the background label, which is an error. Right: Dice volume overlap as a function of the number of merged neighboring structures.

To further quantify the difference between foreground-background and multi-organ segmentation, we report the under- and over-segmentation statistics for the brain segmentation in Fig. 1. In comparison to the foreground-background segmentation, the under-segmentation is reduced and most of the significant differences between over- and under-segmentation are reduced or eliminated when we use multiple labels. Interestingly, the gray matter segmentation changes from under- to over-segmentation, which may be attributed to its complex shape. While it is possible for the brain segmentation algorithms to use multi-organ schemes because many structures have been delineated in training data, it is not possible for many other applications (e.g., left atrium or parotid glands), where no multi-label training data exists.

3 Latent Multi-label Model of the Background

We introduce a generative model that estimates latent labels for the background structures from the available images. We emphasize that the method does not require multi-label training segmentations. We use image intensities of the training data to perform unsupervised separation of the background into K components while simultaneously estimating the number of components K. Estimated components serve as labels in the voting procedure. We assume that image patches P_ix = I_i( 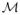(x)), with patch neighborhood 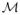, are sampled from a Gaussian mixture model (GMM). Since we do not know the number of components a priori, we employ a Dirichlet process Gaussian mixture model (DP-GMM) [5,10] to account for the potentially infinite number of components. In practice, the number of components is determined as part of the inference procedure. Formally, our generative model and the corresponding graphical model are as follows

where (μ_k, Σ_k) are the mean and covariance of the normal distribution. We choose the conjugate Normal-Wishart distribution H with hyperparameter λ as a prior on the parameters (μ_k, Σ_k) [5]. Mixture weights π follow a stick-breaking process GEM with parameter α [10]. Setting Σ_u = σI, the asymptotic case of σ → 0 yields the DP-means algorithm [7], which is an extension of the k-means algorithm that assumes a variable number of clusters during the estimation procedure. We compare the performance of k-means, DP-means, GMM, and DP-GMM in our experiments. For k-means and DP-means, we use k-means++ seeding for initialization [1].

Once the inference yields a model with K components, the index z_ix ∈ {1, …, K} specifies the component that generates the patch P_ix. Since we only consider background patches, we replace the background label S_i(x) = b with the component index S_i(x) = z_ix in the voting procedure. The labels for the foreground-background segmentation therefore change from {f, b} to {f, 1, …, K}. Voting on this updated label set as defined in Eq. (4) yields the segmentation.

3.1 Model Inference

The increased model complexity of DP mixture models makes the posterior inference difficult. Variational inference algorithms that approximate the result lack convergence guarantees. Instead, we use a recently proposed inference scheme based on efficient Markov chain Monte Carlo sampling, which shows improved convergence properties [2]. The method combines non-ergodic, restricted Gibbs iteration with split-merge moves yielding an ergodic Markov chain.

It is not necessary to perform the inference on the entire background region, as it will affect the voting only in voxels close to the organ boundary. We restrict the inference to the atlas-induced region Γ = {x ∈ Ω : 0.1 < L^f(x) < 0.5}, since our procedure does not change the vote of foreground locations. Within this region, we investigate a global and a local approach. The global approach considers background patches in the region Γ for all training images, 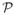= {P_ix : x ∈ Γ, S_i(x) = b}. The local approach selects patches in a small region R around a current location 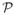(x) = {P_iy : y ∈ R(x), S_i(y) = b}. Considering patches in a small region is necessary to have more relevant samples for learning the parameters. For the local approach, we perform separate inferences for each location on 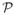(x), instead of one global inference on .

4 Results

We evaluate our approach on three datasets. The first set contains 39 brain MR T1 scans with 1mm isotropic resolution and dimensions 256×256×256 that were used to construct the FreeSurfer atlas. The second dataset includes 18 CT scans from patients with head and neck cancer [11], containing between 80 and 200 axial slices with a slice thickness of 2.5mm. The in-plane resolution is 0.9mm, the slice size is 512 × 512 pixels. The third dataset contains 16 heart MRA images that are electro-cardiogram gated to counteract considerable volume changes of the left atrium and contrast-enhanced (0.2 mmol/kg, Gadolinium-DTPA, CIDA sequence, TR=4.3ms, TE=2.0ms). The in-plane resolution varies from 0.51mm to 0.68mm and slice thickness varies from 1.2mm to 1.7mm with an image resolution of 512 × 512 × 96. We use intensity-weighted voting for creating baseline label maps that serve as input to our algorithm (σ = 10 for brain, σ = 45 for head and neck, σ = 0.5 for heart). We compare to the deconvolution with a generalized Gaussian [12], where we sweep kernel parameters for each application to determine the best setting. We quantify the segmentation accuracy with the Dice volume overlap between manual and automatic segmentation.

We set the patch size to (3, 3, 3) for brain and (3, 3, 1) for the other two applications to account for anisotropy in the data. For the global approach, we evaluate k-means, DP-means, GMM, and DP-GMM. We set α = 0.1 for DP-GMM and create a new cluster in DP-means if the distance to a cluster center exceeds 10 times the average distance within a cluster. For GMM and k-means, we set the number of clusters to 5. For the local approach, we set the region R to (3, 3, 3) and only consider k-means and DP-means because other methods become computationally prohibitive. The number of clusters is set to 3 for the local approach, as we expect fewer structures to be present at one location.

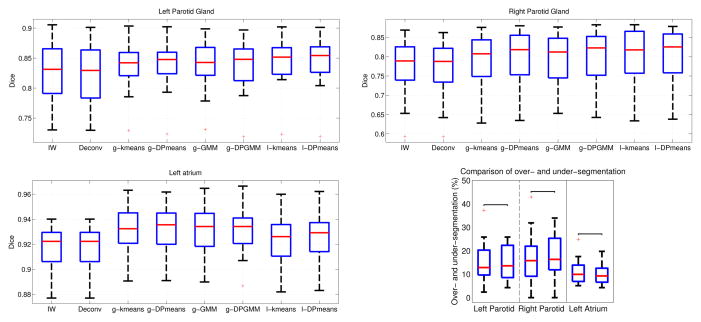
Fig. 3 reports segmentation results of brain structures with the inference of latent background labels using DP-GMM. The under-segmentation is reduced when compared to the foreground-background segmentation in Fig. 1. The latent label estimation offers improvements in accuracy that are comparable to those of the multi-organ scheme, without requiring the multiple organ segmentations for the training set. Fig. 4 illustrates segmentation results for the parotid glands and the left atrium, where we experiment with different inference methods and add the deconvolution approach to the comparison. We also quantify the under-segmentation for the proposed method. We observe that the differences between over- and under-segmentation are no longer significant.

Fig. 3.

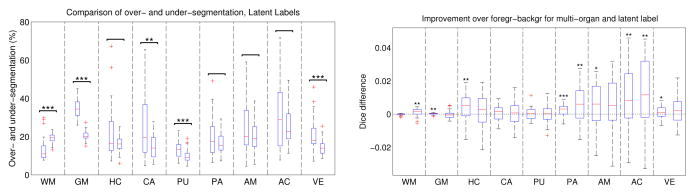
Segmentation statistics for brain data. Left: Over- and under-segmentation for each brain structure after inference of latent labels. Right: Improvement offered by multi-organ (left bar) and latent label estimation (right bar) over foreground-background segmentation.

Fig. 4.

Segmentation accuracy of parotid glands (top) and left atrium (bottom left). We compare global (g-) and local (l-) approaches with intensity-weighted voting (IW) [9] and the deconvolution approach (Deconv) [12] as baseline methods. The plot in the bottom right shows the over- and under-segmentation statistics after latent label estimation for all three structures.

Our results demonstrate the advantage of estimating latent background labels over foreground-background segmentation. The non-parametric methods based on the Dirichlet process yield a slight additional gain compared to their parametric counterparts. This is a consequence of the simultaneous estimation of component membership and number of components, which enables dynamic adaptation to the data. The comparison of global and local approaches indicates that the performance is application dependent. While local approaches perform better for parotid glands, they are slightly worse for the left atrium. Our experiments with majority voting are not included in the article but they confirm the presented results.

5 Conclusion

We demonstrated that a significant bias exists in atlas-based segmentation that leads to under-segmentation. We proposed the asymmetry in foreground-background segmentation as a new hypothesis for the cause of this phenomenon. To reduce the domination of the voting by the background, we introduced a generative model for the background based on the Dirichlet process mixture model. Inference of latent labels yielded partitioning of the background. Segmentation results for brain structures, parotid glands, and the left atrium illustrated clear improvement in the segmentation quality.