Abstract
The visual system summarizes average properties of ensembles of similar objects. We demonstrated an adaptation aftereffect of one such property, mean size, suggesting it is encoded along a single visual dimension (Corbett, et al., 2012), in a similar manner as basic stimulus properties like orientation and direction of motion. To further explore the fundamental nature of ensemble encoding, here we mapped the evolution of mean size adaptation over the course of visually guided grasping. Participants adapted to two sets of dots with different mean sizes. After adaptation, two test dots replaced the adapting sets. Participants first reached to one of these dots, and then judged whether it was larger or smaller than the opposite dot. Grip apertures were inversely dependent on the average dot size of the preceding adapting patch during the early phase of movements, and this aftereffect dissipated as reaches neared the target. Interestingly, perceptual judgments still showed a marked aftereffect, even though they were made after grasping was completed more-or-less veridically. This effect of mean size adaptation on early visually guided kinematics provides novel evidence that mean size is encoded fundamentally in both perception and action domains, and suggests that ensemble statistics not only influence our perceptions of individual objects but can also affect our physical interactions with the external environment.
Keywords: Ensemble statistics, Mean size, Visually guided action, Adaptation aftereffect
We can explicitly conceive only a fraction of the information entering the eyes in each glance. Yet, the visual system can rapidly extract the mean properties of entire sets of objects, such as average size (e.g., Ariely, 2001; Chong & Treisman, 2003). Our experience of stable, thorough perception may be accomplished by integrating occasional detailed samples of the visual world with statistical summaries of the remaining areas (Ariely, 2001), such that statistical, or ensemble representations act in complement to limited capacity attentional resources needed to represent individual objects in detail (e.g., Alvarez, 2011). Along these lines, average properties of sets are extracted automatically (e.g., Oriet & Brand, 2013) and more efficiently than individual object representations (e.g., Im & Halberda, 2013), when attention is distributed broadly across the visual field (e.g., Chong & Treisman, 2005), and even when individual elements cannot be represented (e.g., Corbett & Oriet, 2011; Joo, et al., 2009) or consciously perceived (e.g., Choo & Franconeri, 2010; Parkes, et al., 2001). In addition, ensemble representations persist across eye movements and transfer between different egocentric and allocentric frames of reference (Corbett & Melcher, 2014), providing further support for the proposal that the visual system relies on statistical summaries to efficiently represent large chunks of scenes.
There has been great deal of controversy surrounding the nature of the mechanisms underlying ensemble representations (for a recent review, see Alvarez, 2011). Adaptation is said to reflect the existence of mechanisms that encode a specific visual attribute along a single dimension (e.g., Campbell & Robson, 1968). Several previous reports have demonstrated evidence of perceptual adaptation to ensemble statistics, such as average direction of motion (e.g., Anstis et al., 1998), average orientation (e.g., Gibson & Radner, 1937), average texture density (Durgin, 1995, 2008; Durgin & Huk, 1997), and numerosity (Burr & Ross, 2008). We have recently demonstrated an adaptation aftereffect specific to the average sizes of sets of objects that could not otherwise be attributed to lower-level properties, such as density or spatial frequency, or to adapting to a small sub-sample of individual items (Corbett, Wurnitsch, Schwartz, & Whitney, 2012). When participants adapted to two sets of dots with different mean sizes, the same size dot appeared larger when presented in a region adapted to a set of dots with a smaller mean size than when presented in a region adapted to a set with a comparably larger average diameter. Taken together, these findings provide converging evidence that mean size and other ensemble statistics are encoded as basic dimensions of visual scenes.
Although much recent attention has been paid to how such summary statistical representations may impact visual perception, little has been done towards understanding how ensemble representations may be integrated with visually guided actions. Given that vision mainly functions to facilitate our interactions with the surrounding environment, statistical representations of visual contextual information may also affect actions. Therefore, in the present investigation, we examined how perceptual summaries of the average sizes of sets of objects are integrated over the course of visually guided grasping.
We introduced a novel paradigm combining a visually guided grasping task with the adaptation paradigm used in Corbett et al., (2012). Participants adapted to two sets of dots, simultaneously presented on opposite sides of the screen. They were subsequently instructed to reach to one of two test dots presented in the adapted regions, and then to indicate whether this dot was larger or smaller than the opposite dot. In addition to perceptual reports at the end of each trial, we measured their grip apertures over the entire course of each grasping action. As it has been well established that grip aperture is highly correlated with the size of a single target object (e.g., Jeannerod, 1986), and that reach trajectories can reveal the evolution of dynamic internal cognitive processes (e.g., Song & Nakayama, 2006; 2009), this paradigm allowed us to examine how perceptual summaries influence reach-to-grasp movements over time. Importantly, neither the reaching task, nor the size judgment task explicitly required participants to extract the mean size of the adapting displays.
If summary representations of mean size affect visually guided actions, grip apertures should vary systematically as an inverse function of the average diameter of the dots comprising the adapting displays. Specifically, when participants reach to test dots presented in the region adapted to the larger set of dots, their grip apertures should be comparably smaller than when they reach to the same test dots presented in the region adapted to the smaller mean size set of dots. Their subsequent judgments of the relative sizes of the test dots should show the corresponding pattern (Corbett, et al., 2012), with test dots presented in the large-adapted region perceived as physically smaller than the same dots presented in the small-adapted region. As the perceptual judgment is made after grasping and neither task is executed with the adapting context visible, our paradigm also measures whether the perceptual aftereffect survives even after actions have been completed.
Methods
Participants
12 undergraduate students at Brown University, all right-handed with normal or corrected-to-normal vision, participated in a one-hour session for course credit. All procedures and protocols were in accordance with Brown University's Institutional Review Board.
Tasks
On each trial, after adapting to two side-by-side displays of heterogeneously sized dots, participants were instructed to reach to and grasp one of two side-by-side test dots presented in the adapted regions, between the thumb and forefinger (Grasping task). They then indicated whether that test dot was larger or smaller than the opposite dot, by pressing the “z” key on a computer keyboard if it was smaller, and the “x” key if it was larger (Perceptual comparison).
Apparatus
A Dell PC projected the visual display onto an upright plexi-glass screen (43 cm × 32.5 cm) with a vertical refresh rate of 60 Hz (1280 pixel × 1024 pixel resolution) that was centered 60 cm in front of participants, and recorded responses made using a computer keyboard. Matlab® software (version 2010a) in conjunction with the Psychophysics Toolbox (Brainard 1997; Pelli 1997) controlled all the display, timing, and response functions.
Grip aperture was measured with a Liberty® electromagnetic position and orientation measuring system (Polhemus Inc., Colchester, VT) with a sampling rate of 120 Hz and a measuring error of 0.3 mm root mean square. Two small position-tracking sensors (each 2.26 cm × 1.27 cm × 1.14 cm) were attached to the participant's fingers: one on the index fingertip of the right hand, and the other on the tip of the right thumb. The body midline was approximately aligned with a 3 cm × 3 cm starting position marker on the table 20 cm in front of the participant (40 cm from the screen). Participants were required to rest the index finger on the starting position to initiate each trial. The tracking system was calibrated separately for each sensor with nine points on the screen prior to the start of each experimental session.
Stimuli
As outlined in the Introduction, our goal was to test whether the perceptual aftereffects of mean size adaptation reported in Corbett, et al., (2012) can similarly affect visually guided actions. Therefore, we used the same adapting and test stimuli to replicate this paradigm as closely as possible. The adapting stimulus consisted of two sets of 14 dots. Each set of 14 dots was composed of two concentric rings, an inner ring of six dots subtending 3.5° of visual angle (37.6 mm), and an outer ring of eight dots subtending 7° of visual angle (75.3 mm). The outer eight dots were positioned at one of eight cardinal or 45° intercardinal locations around the outer ring, and then each was jittered independently in the x- and y-directions by a random factor between −0.5° and +0.5° of visual angle (±5.4 mm) on each trial. The six inner dots were initially positioned around the inner ring at the 30°, 90°, 150°, 210°, 270°, and 330° positions, then jittered in the same manner as the outer dots. Within each 14-dot patch, we restricted the positions of the dots such that no individual dot was within 0.125° (1.3 mm) of any other dot in either the x- or y-direction.
Adapting displays
Each two-ringed adapting dot set was 8° of eccentricity from the center of the screen, relative to the horizontal meridian. The smaller adapting set always contained the same 14 individual dots ranging in diameter from 1.0° (10.8 mm) to 2.3° (24.7 mm) in 0.1° (1.1 mm) steps, with a constant mean size of 1.65° of visual angle (17.7 mm). The larger adapting set always contained the same 14 individual dots ranging in diameter from 2.0° (21.5 mm) to 3.3° (35.5 mm) also in 0.1° (1.1 mm) steps, with a constant mean size of 2.65° of visual angle (28.5 mm). The positions of the 14 dots in each set were randomized on every trial, such that no location within either adapting patch consistently contained a dot that was larger or smaller than any other dot in the set; only the difference in mean dot size (diameter) between the two adapting sets was constant over the course of the experiment.
Test displays
The test displays consisted of two single dots, presented side-by-side, one in each adapted region. Unknown to subjects, the dot on the opposite side of the screen from the dot to which they were reaching always served as a standard, and was the same size as the mean size of all 28 dots comprising the adapting displays (2.15°/23.1 mm). The dot to which subjects reached on any given trial was ± 0, 0.12, 0.25, 0.53, or 0.84 standard deviations (of the whole set of 28 adapting dots) larger or smaller than the standard, resulting in 9 possible test dots subtending 1.6°, 1.8°, 1.99°, 2.07°, 2.15°, 2.23°, 2.31°, 2.5°, and 2.7° of visual angle (17.2 mm, 19.4 mm, 21.4 mm, 22.3 mm, 23.1 mm, 24.0 mm, 24.8 mm, 26.9 mm, and 29.0 mm, respectively). We randomized the positions of the test dots within the two adapted regions from trial-to-trial, so that no given location in either adapted region was consistently probed, making it more likely that the mean size of the entire display of adapting dots was responsible for any observed effects on perceived size or grip aperture.
Procedure
Participants were tested individually in a semi-darkened room. They were seated 60 cm in front of the center of the visual display, and asked to remain focused on the 0.5° of visual angle (5.4 mm) fixation cross that was always present in the center of the screen during all adaptation and top-up displays. The experimenter stressed the importance of fixating to ensure adaptation at the start of each session, and remained in the room over the course of the experiment to monitor that participants remained fixated and aligned with the center of the screen during adaptation on each trial. However, during the grasping and perception tasks, participants were free to move their eyes but not heads, such that they were able to naturally monitor hand position and the individual test dots. Each participant performed one practice block of 18 trials, followed by eight experimental blocks of 63 trials each (7 repetitions of each of the 9 possible test dot standard deviation differences, in random sequence) for a total of 504 experimental trials per session. Each experimental session consisted of two repetitions of the 4 possible conditions that resulted from combining the side of the larger adapting set (left or right) and the reach side (left or right). The order of conditions was counterbalanced over observers. At the start of each block, participants were informed to which test dot they should reach for the entire block (left or right), but no information was provided about the relative locations or sizes of the adapting displays.
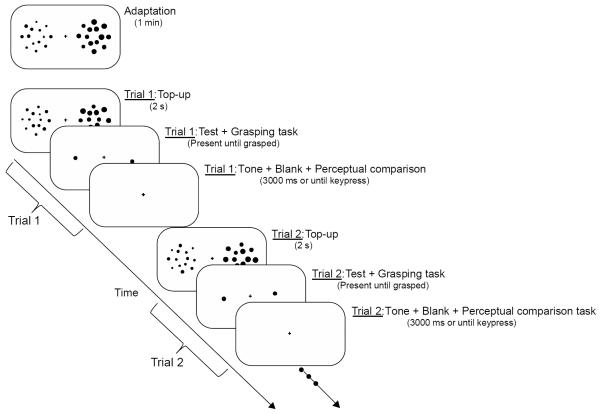
As shown in Figure 1, each block began with an initial adaptation phase, during which participants fixated while viewing a display of the two side-by-side adapting patches for 1 minute. After this initial adaptation, each trial consisted of an adapting top-up display presented for two seconds to ensure participants remained adapted to the two mean sizes over the course of each block. Importantly, the positions of the individual dots comprising each adapting patch in the adaptation displays were randomized on every trial. A test display consisting of the two single dots was presented immediately after each adaptation display. Participants were instructed to reach to the pre-specified test dot as if it was a real object as quickly and accurately as possible on each trial using the thumb (6 o'clock) and index finger (12 o'clock). The experimenter stressed that participants should reach to the test dot immediately after the test display onset so that there was no delay between target onset and movement initiation that may have otherwise increased reliance on stored perceptual information (Hu & Goodale, 2000; Fischer, 2001; Franz, et al., 2009). As previous reports suggest that the absence of visual and tactile feedback changes kinematics and neural control from that of natural grasping movements (e.g., Goodale, et al., 1994; Króliczak, et al., 2007; Schenk, 2012), participants were also instructed to touch the screen so they could see how their grasps overlapped with the test dots, providing continuous visual feedback that allowed them to make online adjustments up until the end of the grasping action and at least some minimal (although not veridical) form of tactile feedback. The test dots remained on the screen until the participant had completed the grasping task. Importantly, only the test stimuli and hand were visible during the planning and execution of each grasping action and there was no interference from obstacle stimuli that could have affected grip scaling (e.g., Haffenden & Goodale, 2000; Haffenden, et al., 2001; Smeets, et al., 2003). Once participants touched the screen to grasp the test dot, the screen blanked except for the fixation cross and a 500 Hz tone sounded for 200 ms, signaling them to make a keypress response to the perceptual test dot comparison task. The screen remained blank until the keypress response, or for 3 seconds, whichever came first. We excluded responses made later than 3 seconds after the display offset from further analysis (less than 1% of trials for any participant).
Figure 1.
Experimental sequence: Each block began with an initial adaptation phase, during which the participant fixated while viewing a display of the two side-by-side adapting patches for 1 minute. After this initial adaptation, each trial consisted of a top-up adapting display presented for 2 seconds (to ensure participants remained adapted to the two mean sizes), followed by a test display of two single dots, which remained on the screen until the participant reached to the pre-specified test dot. Once the participant touched the screen to grasp the test dot, a 500 Hz tone sounded for 200 ms as the screen blanked except for the fixation cross, signaling the participant to make a keypress response to the perceptual comparison task. The screen remained blank until the keypress response, or for 3 seconds, whichever came first. Two consecutive trials are shown above to clarify that there was only a single 1-minute initial adaptation display at the start of each block followed by multiple 2-second top-up displays, as well as to illustrate that although the mean size of the adapting dots was held constant over the course of each block, the dots were arranged in random positions within each presentation of the adapting and test displays.
Results
Regardless of reach side (Left vs. Right), we categorized trials based on whether the reach was made towards the smaller or larger adapting display side (Small vs. Large condition).
Grasping task (Figure 2a)
Figure 2.
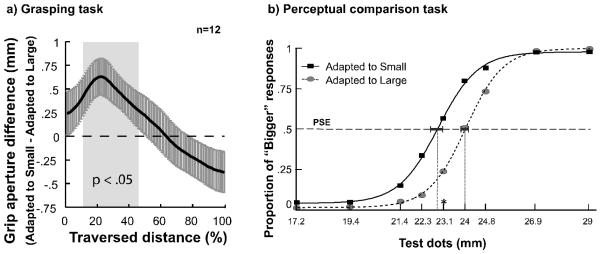
Results; Grasping task (a): Time course (% of total distance traversed) of mean grip aperture differences (in mm) between the Small and Large adapting conditions. Participants made significantly larger grip apertures in the Small relative to the Large adapting condition during the early stage of their reaching movements (between ~12% to 45%; light gray box), but this inverse bias gradually disappeared as their hands moved closer to the target. The black solid line represents the mean aperture difference, and the dark gray vertical error bars represent ± 1 standard error of the mean at each sampling point. The dashed horizontal line delimits the point at which no difference (0 mm; y-axis) was apparent between average grip apertures in the two adapting conditions. The positive number on the ordinate indicates grip aperture in the small condition is larger, whereas the negative number represents the opposite. Perceptual comparison task (b): Grand-averaged logistic fits (lines) and actual data (points) for the average probability of responding that the test dot (sizes are represented in mm for comparison with grasping data) to which the participant was instructed to reach appeared bigger than the dot on the opposite side of the display over the 9 test dots in each adapting condition (Small, Large). On average, observers more often perceived the test dot presented in the region adapted to the small set of dots as bigger relative to when the same dot was presented in the region adapted to the large set of dots. The dashed horizontal line delimits the proportion of responses (y-axis) for which the observer was equally likely to respond that the test dot appeared bigger when it was presented on the Small versus Large adapted side, and the vertical dashed lines mark the corresponding PSEs (x-axis) for each adapting condition in terms of the relative difference in the size of the test dots necessary for this perceived equality. The asterisk on the x-axis indicates the diameter of the standard comparison dot. Dark gray horizontal error bars represent ± 1 standard error of the mean in the respective PSEs for each adapting condition.
In the grasping task, we conducted an off-line analysis of reaching movements. We calculated movement velocity from the 3D position traces after filtering with a low-pass filter (cutoff frequency of 25 Hz). The beginning and end of reaching movements were detected using a velocity criterion (between 8 cm/s and 10 cm/s). The algorithm's identification of movements was inspected to verify its accuracy (Song & Nakayama, 2006; 2007a;b; 2008; 2009; Song, et al., 2008). We defined reaction time as the interval between stimulus and movement onset, and movement time as the interval between movement onset and offset. To quantify potential influences of mean size representations on visually guided actions, we calculated mean grip aperture as a spatial plot of hand aperture against the forward progress of hand transport. We individually normalized the entire distance traversed on each trial by resampling 101 equally spaced points (from 0% to 100%) during reaching movements. Corresponding x, y, and z positions were computed by linear interpolation (e.g., Cuijpers, et al., 2004; Haggard & Wing, 1998; Song & Nakayama, 2008; Spivey et al., 2005). Grasping responses for different test dot sizes were then collapsed for the further analysis.
Paired t-tests showed no differences between participants' averaged reaction times (μS = 337 ms, SDS = 97 ms, μL = 368 ms, SDL = 119 ms; t(11) = 1.889, SEM = 4.03, p = .086, d = .285), and movement times (μS = 517 ms, SDS = 80 ms, μL = 520 ms, SDL = 82 ms; t(11) = .57, SEM = 5.43, p =.577, d = .037) in the Small and Large adapting conditions, respectively. Figure 2a shows the time course of mean grip aperture differences between the Small and Large conditions (Small – Large) as a function of percent distance traversed. We were particularly interested in the early stages of grasping movements most likely to manifest effects of perceptual summaries of mean size, before online visual feedback allows for the metric adjustment of grip aperture as the hand nears the target (e.g., Glover & Dixon, 2001; Health, et al., 2011). Therefore, we performed a t-test at every sampling point to examine how the aftereffect may unfold over the course of the entire movement. On average, participants made significantly larger grip apertures in the Small relative to the Large adapting condition during the early stages of their reaching movements, between ~12% to ~45% of the total distance traversed (paired t-tests, p < .05; indicated by the light gray shading in Figure 2a), demonstrating that their visually guided reach-to-grasp actions were initially affected in-line with an adaptation aftereffect of mean size. However, this bias gradually disappeared as their hands moved closer to the target. These findings are in agreement with Heath and colleagues' (2011) report that although peak grip aperture (at ~70% of total movement) is not affected by perceived size, grip apertures during earlier stages (~10% to 50% of total movement) do show perceptual effects. Taken together, these movement dynamics reveal that the early stage of the reach-to-grasp actions is most strongly affected by the adapting sets, and suggest that the statistical representation of average size is integrated into the motor plan online.
Perceptual comparison task (Figure 2b)
In the perceptual task, which was executed after grasping was completed, participants' average RTs for the perceptual judgment when reaching to the test dot on the side adapted to the display with the larger average size (μL = 1465 ms, SDL = 329 ms) were not significantly different from RTs when reaching to the test dot on the side adapted to the display with the smaller average size (μS = 1403 ms, SDS = 314 ms; t(11) = 1.628, SEM = .038, p = .132, d = .192). Therefore, we computed each participant's average probability of a response that the dot to which they were reaching appeared larger than the standard dot on the opposite side of the test display for each of the 9 test dots in each adapting condition (Small, Large). Using maximum likelihood estimation, we next fit each participant's averaged responses over the 9 test dots to two separate logistic functions (one for the Small adapting condition, and one for the Large adapting condition), with lower and upper bounds of 0 and 1, respectively. Goodness of fit was evaluated with deviance scores, calculated as the log-likelihood ratio between a fully saturated, zero-residual model and the data model. A score above the critical chi-square value indicated a significant deviation between the fit and the data (Wichmann & Hill, 2001). All fits were significant, as all deviance scores were well below the critical chi-square value, χ2(9, 0.95) = 16.92. There was a significant difference between the logistic fits to the grand average over the 12 participants in each adapting condition (t(8) = 3.21, SEM = .037, p = .012, d = .306). The grand averaged fit for the Large adapting condition was shifted rightward relative to the leftward-shifted fit for the Small adapting condition, replicating our previous findings that observers experienced an adaptation aftereffect (Corbett, et al., 2012).
We next defined the magnitude an individual subject's aftereffect for each of the adapting conditions as the Point of Subjective Equality (PSE), the 50% inflection point on the corresponding psychometric function. The PSE quantifies the physical difference in dot size for the two test dots to appear equal in diameter. A paired t-test examining the effect of adapting condition (Small, Large) on participants' PSEs in the two adapting conditions indicated a differential aftereffect over the twelve observers (μPSE_S = 2.13° (22.9 mm), SDPSE_S = .08° (.9 mm), μPSE_L = 2.23° (24 mm), SDPSE_L = .04° (.4 mm); t(11) = 3.85, SEM = .027, p = .003, d = 1.58; Figure 2b).
Discussion
The present investigation uncovered a novel adaptation aftereffect of statistical extraction on visually guided actions. Specifically, the initial stage of participants' grasping actions to test dots presented in regions of the visual field adapted to sets of dots with different mean sizes was biased, such that grip apertures to a particular test dot were inversely dependent on the average dot size of the preceding adapting patch. In addition, extending our recent findings that participants' perceptual judgments of the sizes of the test dots were also biased as an inverse function of the average size of the adapting dot set (Corbett, et al., 2012), we confirmed that this aftereffect persisted even after actions were compensated to overcome the initial aftereffect during later stages of reaching. Most importantly, our results provide the first evidence that ensemble representations of average size not only influence perceptual judgments, but can also affect our physical interactions with objects in the external environment. Taken with findings that mean size adaptation transfers across eye movements and different spatial frames of reference (Corbett & Melcher, 2014), the present finding that mean size adaptation can also affect visually guided actions also offers further support for the proposal that ensemble statistics sub-serve visual stability as we interact with the surrounding environment amidst constantly changing retinal imagery.
The present results support the proposal that mean size and other summary statistical properties are encoded as fundamental visual attributes (Corbett, et al., 2012). There is much debate regarding the mechanisms underlying summary statistical representations. Although there is mounting evidence to suggest such statistical representations involve a calculation of the mean of the entire set of items without the need to encode individual set members (e.g., Ariely, 2001; Choo & Franconeri, 2010; Chong, et al., 2008; Chong & Treisman, 2005; Corbett & Oriet, 2011; Joo, et al., 2009), it has been argued that perceptual averaging can be accomplished by sampling only a handful of the items in each set using focused attention (e.g., Simons & Myczek, 2008; c.f., Ariely, 2008). We have previously used the same paradigm as in the present study to demonstrate that observers are sensitive to the variance in the sizes of the dots in the adapting sets (Corbett, et al., 2012), suggesting that most, if not all of the elements in each set are included in the calculation of the mean. The present demonstration that the aftereffect induced by these same displays also affects visually guided actions provides further evidence that mean size is encoded along a single visual dimension as a basic stimulus attribute that affects visually guided actions in the same manner as the sizes of homogeneous or single elements (e.g., Hu & Goodale, 2000; Pavani, et al., 1999).
Along these lines, our findings that mean size adaptation induces a negative aftereffect are likely related to size contrast illusions induced by Ebbinghaus-Titchener displays, in which the size of a central test circle is perceived as an inverse function of the homogeneous sizes of circles in a surrounding annulus. Although these studies are generally concerned with the long-standing debate about potential dissociations between dorsal and ventral visual processing and not per se with mean size representation, it is likely that a statistical representation of the average (homogeneous) size of the surrounding circles underlies such effects on the perceived size of the central circle, as the average of heterogeneous sizes is represented in the same manner as the size of homogeneous elements (Chong & Treisman, 2003). On the one hand, there have been a number of reports of dissociated size contrast effects of Ebbinghaus-Titchner displays on perceptual size judgments and grasping actions to central test circles (e.g., Aglioti, et al., 1995; Haffenden & Goodale, 1998; Marotta, et al., 1998). These results support Goodale and Milner's (1992) two visual streams hypothesis that relative visual information for object perception and absolute metric information for actions are governed by independent ventral and dorsal pathways. On the other hand, several studies have reported no such dissociations between perception and action (e.g., Pavani, et al., 1999; van Donkelaar, 1999). To explain similar effects in perceptual and motor tasks, Glover and Dixon (2001) proposed a planning and control model of actions, involving common mechanisms for perception and action with decreasing reliance on perceptual representations from movement planning to execution. Although not the focus of the present investigation, our results do offer support for such claims that early planning stages of actions are affected by perceptual representations, but actions are corrected online over the course of the movement (e.g., Glover & Dixon, 2001). In general, whether or not the Ebbinghaus-Titchner illusion similarly biases perceptions and actions has been found to depend on a variety of factors such as the availability of visual feedback (e.g., van Donkelaar, 1999; Haffenden & Goodale, 1998; Pavani, et al., 1999), the onset of reaching movements (e.g., Pavani, et al., 1999), the configuration of display elements (e.g., Pavani, et al., 1999; Aglioti, et al., 1995; Franz, et al., 2000), and whether grip is estimated two- or three-dimensionally (Stöttinger, et al., 2012). Future studies manipulating visual, kinematic, and temporal factors will likely uncover similar effects on vision and action induced by heterogeneously-sized elements as those induced by homogeneously-sized Ebbinghaus-Titchener circles.
In conclusion, the present results demonstrate that mean size adaptation not only affects the perceived size of a single object, but that this ensemble representation can also affect early stages of grasping actions and survives even after actions are completed inline with the physical size of the target. These convergent effects on perception and action provide novel support for the fundamental nature of ensemble representations in both the perception and action domains. On the one hand, such an interaction poses a serious threat, in that actions may fail to be executed in a veridical manner, leading to dreadful outcomes in critical situations. An increased understanding of how statistical representations affect perceptions and visually guided actions can allow for better prediction and prevention of such errors. On the other hand, this interplay between perception and action could be exploited to direct our interactions with the external environment. Especially, as we argue that this sort of summary representation can be constructed even when participants are not explicitly aware of each object comprising the set, such a rapid extraction of average set properties could be used to guide actions, quickly recover texture and depth information, and aid in representing scene “gist,” (e.g., Potter, 1976) without detracting from the resources needed to perform other perceptually intensive tasks in parallel.
Acknowledgements
This project is supported by Brown University Salomon Faculty award and NIGMS-NIH (P20GM103645) to J.H.S.
References
- Aglioti S, DeSouza JFX, Goodale MA. Size-contrast illusions deceive the eye but not the hand. Current Biology. 1995;5(6):679–685. doi: 10.1016/s0960-9822(95)00133-3. [DOI] [PubMed] [Google Scholar]
- Alvarez GA. Representing multiple objects as an ensemble enhances visual cognition. Trends in Cognitive Science. 2011;15(3):122–131. doi: 10.1016/j.tics.2011.01.003. [DOI] [PubMed] [Google Scholar]
- Anstis S, Verstraten F, Mather G. The motion after-effect. Trends in Cognitive Sciences. 1998;2:111–117. doi: 10.1016/s1364-6613(98)01142-5. [DOI] [PubMed] [Google Scholar]
- Ariely D. Seeing sets: Representation by statistical properties. Psychological Science. 2001;12:157–162. doi: 10.1111/1467-9280.00327. [DOI] [PubMed] [Google Scholar]
- Ariely D. Better than average? When can we say that subsampling of items is better than statistical summary representations? Perception & Psychophysics. 2008;70:1325–1326. doi: 10.3758/PP.70.7.1325. [DOI] [PubMed] [Google Scholar]
- Brainard DH. The Psychophysics Toolbox. Spatial Vision. 1997;10:433–436. [PubMed] [Google Scholar]
- Burr D, Ross J. A visual sense of number. Current Biology. 2008;18(6):425–428. doi: 10.1016/j.cub.2008.02.052. [DOI] [PubMed] [Google Scholar]
- Campbell FW, Robson JG. Application of Fourier analysis to the visibility of gratings. Journal of Physiology. 1968;197:551–566. doi: 10.1113/jphysiol.1968.sp008574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chong SC, Joo SJ, Emmanouil T, Treisman A. Statistical processing: Not so implausible after all. Perception & Psychophysics. 2008;70:1327–1334. doi: 10.3758/PP.70.7.1327. [DOI] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Representation of statistical properties. Vision Research. 2003;43:393–404. doi: 10.1016/s0042-6989(02)00596-5. [DOI] [PubMed] [Google Scholar]
- Chong SC, Treisman A. Attentional spread in the statistical processing of visual displays. Perception & Psychophysics. 2005;67(1):1–13. doi: 10.3758/bf03195009. [DOI] [PubMed] [Google Scholar]
- Choo H, Franconeri SL. Objects with reduced visibility still contribute to size averaging. Attention, Perception, & Psychophysics. 2010;72(1):86–99. doi: 10.3758/APP.72.1.86. [DOI] [PubMed] [Google Scholar]
- Corbett JE, Melcher D. Characterizing ensemble statistics: Mean size is represented across multiple frames of reference. Attention, Perception, & Psychophysics. 2014 doi: 10.3758/s13414-013-0595-x. Advance online publication. doi: 10.3758/s13414-013-0595-x. [DOI] [PubMed] [Google Scholar]
- Corbett JE, Oriet C. The whole is indeed more than the sum of its parts: Perceptual averaging in the absence of individual item representation. Acta Psychologica. 2011;138:289–301. doi: 10.1016/j.actpsy.2011.08.002. [DOI] [PubMed] [Google Scholar]
- Corbett JE, Wurnitsch N, Schwartz A, Whitney D. A aftereffect of adaptation to mean size. Visual Cognition. 2012;20(2):211–231. doi: 10.1080/13506285.2012.657261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuijpers RH, Smeets JBJ, Brenner E. On the relation between object shape and grasping kinematics. Journal of Neurophysiology. 2004;91:2598–2606. doi: 10.1152/jn.00644.2003. [DOI] [PubMed] [Google Scholar]
- van Donkelaar P. Pointing movements are affected by size-contrast illusions. Experimental Brain Research. 1999;125:517–520. doi: 10.1007/s002210050710. [DOI] [PubMed] [Google Scholar]
- Durgin FH. Texture density adaptation and the perceived numerosity and distribution of texture. Journal of Experimental Psychology: Human Perception and Performance. 1995;21(1):149–169. [Google Scholar]
- Durgin FH. Texture density adaptation and visual number revisited. Current Biology. 2008;18(18):R855–R856. doi: 10.1016/j.cub.2008.07.053. [DOI] [PubMed] [Google Scholar]
- Durgin FH, Huk AC. Texture density aftereffects in the perception of artificial and natural textures. Vision Research. 1997;37(23):3273–3282. doi: 10.1016/s0042-6989(97)00126-0. [DOI] [PubMed] [Google Scholar]
- Fischer MH. How sensitive is hand transport to illusory context effects? Experimental Brain Research. 2001;136:224–230. doi: 10.1007/s002210000571. [DOI] [PubMed] [Google Scholar]
- Franz VH, Gegenfurtner KR, Bülthoff HH, Fahle M. Grasping visual illusions: No evidence for a dissociation between perception and action. Psychological Science. 2000;11(1):20–25. doi: 10.1111/1467-9280.00209. [DOI] [PubMed] [Google Scholar]
- Gibson JJ, Radner M. Adaptation, after-effect and contrast in the perception of tilted lines. I. Quantitative studies. Journal of Experimental Psychology. 1937;20(5):453–467. [Google Scholar]
- Glover S, Dixon P. Motor adaptation to an optical illusion. Experimental Brain Research. 2001;137:254–258. doi: 10.1007/s002210000651. [DOI] [PubMed] [Google Scholar]
- Goodale MA, Jakobson LS, Keillor JM. Differences in the visual control of pantomimed and natural grasping movements. Neuropsychologia. 1994;32(10):1159–1178. doi: 10.1016/0028-3932(94)90100-7. [DOI] [PubMed] [Google Scholar]
- Goodale MA, Milner AD. Separate visual pathways for perception and action. Trends in Neuroscience. 1992;15(1):20–25. doi: 10.1016/0166-2236(92)90344-8. [DOI] [PubMed] [Google Scholar]
- Haffenden AM, Goodale MA. The effect of pictorial illusion on prehension and perception. Journal of Cognitive Neuroscience. 1998;10(1):122–136. doi: 10.1162/089892998563824. [DOI] [PubMed] [Google Scholar]
- Haffenden AM, Goodale MA. Independent effects of pictorial displays on perception and action. Vision Research. 2000;40(10–12):1597–1607. doi: 10.1016/s0042-6989(00)00056-0. [DOI] [PubMed] [Google Scholar]
- Haffenden AM, Schiff KC, Goodale MA. The dissociation between perception and action in the Ebbinghaus illusion: Nonillusory effects of pictorial cues on grasp. Current Biology. 2001;11(3):177–181. doi: 10.1016/s0960-9822(01)00023-9. [DOI] [PubMed] [Google Scholar]
- Haggard P, Wing A. Coordination of hand aperture with the spatial path of hand transport. Experimental Brain Research. 1998;118:286–292. doi: 10.1007/s002210050283. [DOI] [PubMed] [Google Scholar]
- Heath M, Mulla A, Holmes SA, Smuskowitz LR. The visual coding of grip aperture shows an early but not late adherence to Weber's law. Neuroscience Letters. 2011;490:200–204. doi: 10.1016/j.neulet.2010.12.051. [DOI] [PubMed] [Google Scholar]
- Hu Y, Goodale MA. Grasping after a delay shifts size-scaling from absolute to relative metrics. Journal of Cognitive Neuroscience. 2000;12(5):856–868. doi: 10.1162/089892900562462. [DOI] [PubMed] [Google Scholar]
- Im HY, Halberda J. The effects of sampling and internal noise on the representation of ensemble average size. Attention, Perception, & Psychophysics. 2013;75(2):278–286. doi: 10.3758/s13414-012-0399-4. [DOI] [PubMed] [Google Scholar]
- Jeannerod M. The formation of finger grip during prehension. A cortically mediated visuomotor pattern. Behavioural Brain Research. 1986;19(2):99–116. doi: 10.1016/0166-4328(86)90008-2. [DOI] [PubMed] [Google Scholar]
- Joo SJ, Shin K, Chong SC, Blake R. On the nature of the stimulus information necessary for estimating mean size of visual arrays. Journal of Vision. 2009;9(7):1–12. doi: 10.1167/9.9.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Króliczak G, Cavina-Pratese C, Goodman DA, Culham JC. What does the brain do when you fake it? An fMRI study of pantomimed and real grasping. Journal of Neurophysiology. 2007;97:2410–2422. doi: 10.1152/jn.00778.2006. [DOI] [PubMed] [Google Scholar]
- Marotta JJ, DeSouza JFX, Haffenden AM, Goodale MA. Does a monocularly presented size-contrast illusion influence grip aperture? Neuropsychologia. 1998;36(6):491–497. doi: 10.1016/s0028-3932(97)00154-1. [DOI] [PubMed] [Google Scholar]
- Oriet C, Brand J. Size averaging of irrelevant stimuli cannot be prevented. Vision Research. 2013;79(7):8–16. doi: 10.1016/j.visres.2012.12.004. [DOI] [PubMed] [Google Scholar]
- Parkes L, Lund J, Angelucci A, Morgan M. Compulsory averaging of crowded orientation signals in human vision. Nature Neuroscience. 2001;4:739–744. doi: 10.1038/89532. [DOI] [PubMed] [Google Scholar]
- Pavani F, Boscagli I, Benvenuti F, Rabuffetti M, Farné A. Are perception and action affected differently by the Titchener circles illusion? Experimental Brain Research. 1999;127:95–101. doi: 10.1007/s002210050777. [DOI] [PubMed] [Google Scholar]
- Pelli DG. The VideoToolbox software for visual psychophysics: transforming numbers into movies. Spatial Vision. 1997;10:437–442. [PubMed] [Google Scholar]
- Potter MC. Short-term conceptual memory for pictures. Journal of Experimental Psychology: Human Learning and Memory. 1976;2:509–522. [PubMed] [Google Scholar]
- Schenk T. No dissociation between perception and action in patient DF when haptic feedback is withdrawn. The Journal of Neuroscience. 2012;32(6):2013–2017. doi: 10.1523/JNEUROSCI.3413-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simons DJ, Myczek K. Average size perception and the allure of a new mechanism. Perception & Psychophysics. 2008;70:1335–1336. doi: 10.3758/pp.70.5.772. [DOI] [PubMed] [Google Scholar]
- Smeets JBJ, Glover S, Brenner E. Modeling the time-dependent effect of the Ebbinghaus illusion on grasping. Spatial Vision. 2003;16(3–4):311–324. doi: 10.1163/156856803322467554. [DOI] [PubMed] [Google Scholar]
- Song J-H, Nakayama K. Role of focal attention on latencies and trajectories of visually guided manual pointing. Journal of Vision. 2006;6(9):982–995. doi: 10.1167/6.9.11. [DOI] [PubMed] [Google Scholar]
- Song J-H, Nakayama K. Automatic adjustment of visuomotor readiness. Journal of Vision. 2007a;7(5):1–9. doi: 10.1167/7.5.2. [DOI] [PubMed] [Google Scholar]
- Song J-H, Nakayama K. Fixation offset facilitates saccades and manual reaching for single but not multiple target displays. Experimental Brain Research. 2007b;177(2):223–232. doi: 10.1007/s00221-006-0667-4. [DOI] [PubMed] [Google Scholar]
- Song J-H, Nakayama K. Numeric comparison in a visually-guided manual reaching task. Cognition. 2008;106:994–1003. doi: 10.1016/j.cognition.2007.03.014. [DOI] [PubMed] [Google Scholar]
- Song J-H, Nakayama K. Hidden cognitive states revealed in choice reaching tasks. Trends in Cognitive Sciences. 2009;13:360–366. doi: 10.1016/j.tics.2009.04.009. [DOI] [PubMed] [Google Scholar]
- Song J-H, Takahashi N, McPeek RM. Target selection for visually-guided reaching in macaque. Journal of Neurophysiology. 2008;99:14–24. doi: 10.1152/jn.01106.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spivey MJ, Grosjean M, Knoblich G. Continuous attraction toward phonological competitors. Proceedings of the National Academy of Sciences. 2005;102(29):10393–10398. doi: 10.1073/pnas.0503903102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stöttinger E, Pfusterschmied J, Wagner H, Danckert J, Anderson B, Perner J. Getting a grip on illusions: replicating Stöttinger et al [Exp Brain Res (2010) 202:79–88] results with 3-D objects. Experimental Brain Research. 2012;261:155–157. doi: 10.1007/s00221-011-2912-8. [DOI] [PubMed] [Google Scholar]
- Wichmann FA, Hill NJ. The psychometric function: I. Fitting, sampling, and goodness of fit. Perception & Psychophysics. 2001;63:1293–1313. doi: 10.3758/bf03194544. [DOI] [PubMed] [Google Scholar]