Abstract
Robotic systems have the potential to assist vitreoretinal surgeons in extremely difficult surgical tasks inside the human eye. In addition to reducing hand tremor and improving tool positioning, a robotic assistant can provide assistive motion guidance using virtual fixtures, and incorporate real-time feedback from intraocular force sensing ophthalmic instruments to present tissue manipulation forces, that are otherwise physically imperceptible to the surgeon. This paper presents the design of an FBG-based, multi-function instrument that is capable of measuring mN-level forces at the instrument tip located inside the eye, and also the sclera contact location on the instrument shaft and the corresponding contact force. The given information is used to augment cooperatively controlled robot behavior with variable admittance control. This effectively creates an adaptive remote center-of-motion (RCM) constraint to minimize eye motion, but also allows the translation of the RCM location if the instrument is not near the retina. In addition, it provides force scaling for sclera force feedback. The calibration and validation of the multi-function force sensing instrument are presented, along with demonstration and performance assessment of the variable admittance robot control on an eye phantom.
I. INTRODUCTION
Retinal microsurgery refers to the intraocular surgical treatments of the disorders related to retina, vitreous, and macula. Typical diseases include retina detachment, diabetic retinopathy, macular hole and epiretinal membrane. Retinal microsurgery demands advanced surgical skills that are near or beyond natural human capabilities. During retinal microsurgery, a surgical microscope is placed above the patient to provide magnified visualization of the interior of the eye. The surgeon inserts small instruments (e.g., 25 Ga) through trocars on the sclera, the white part of the eye, to perform delicate tissue manipulation in the posterior of the eye. An example of a common surgical task is epiretinal membrane (ERM) peeling to restore the patient’s vision from ERM distortion. The surgeon carefully peels the thin, semi-transparent scar tissue (the ERM) off the retina using a micro-forceps, as shown in Fig. 1. A more challenging maneuver is internal limiting membrane (ILM) peeling, where the innermost layer of the neurosensory retina is incised a few microns, and delaminated from the rest of the retina. Steady and precise motion is desired, because the thickness of the membranes [1] can be an order of magnitude smaller than the human hand tremor [2]. Additionally the force applied on the membrane has to stay below the strength of the retina tissue. However, the forces exerted between the instrument tip and the retina are well below the human sensory threshold [3]. The absence of force sensing raises the risk of applying excessive force on the retina, which can potentially cause retina hemorrhage and tearing. During the membrane peeling, the eye should be stable to minimize the motion of the target membrane. This requires the tool motion to comply at the sclerotomy site. Only three rotational degrees of freedom (DOF) about the sclera entry point and one translational DOF along the instrument axis are allowed, while lateral translations are prohibited by the sclera constraint. This corresponds to the concept of remote center-of-motion (RCM) in robotics, devised by Taylor et al. [4]. A fixed RCM is often considered to be a fundamental requirement in minimally invasive Surgery (MIS). Unlike MIS, the imaging component of retinal microsurgery, the microscope, is located outside the patient and is rarely moved, as shown in Fig. 1(a). Instead, the retinal surgeon needs to reposition the patient’s eye using the inserted tools, in order to adjust the view and gain tool access to the region of interest. As a result, the location of the RCM point (the sclera entry point) is not necessarily fixed, and can move up to 12 mm during retinal microsurgery [5]. The repositioning of the eye requires all of the instruments inserted in the eye (e.g., a micro-forceps and a light pipe) to move in coordination. Unsynchronized instrument motion can cause cornea striae, which distorts the view of the retina in the microscope. Suboptimal ergonomics and fatigue impose further limitations on the surgical performance.
Fig. 1.
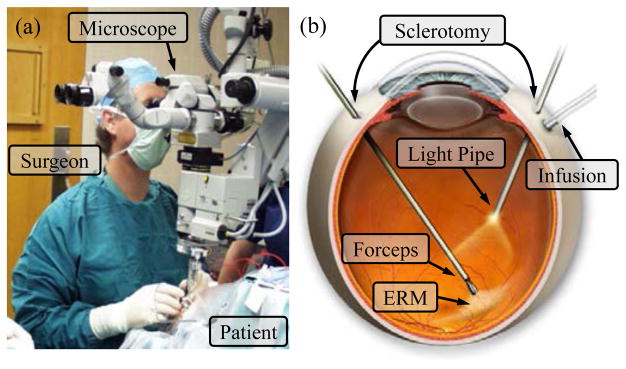
Retinal microsurgery: (a) position of the patient and the lead surgeon in the operating room. (b) the layout of the surgical instruments in the eye during ERM peeling.
Many robotic systems have been developed and investigated to explore the potential to enhance and expand the capabilities of retinal surgery and microsurgery in general. Major approaches include master-slave teleoperated system [6]–[9], handheld robotic devices [10], [11], and untethered micro-robots [12]. Our approach is the Steady-Hand Eye Robot with hands-on cooperative control [13]–[16], where the user and the robot both hold the surgical instrument. The user input force applied on the instrument handle controls the velocity with which the robot follows the user motion. This control approach is also termed admittance velocity control. The human hand tremor is damped by the stiff robot structure. The cooperatively controlled robot provides not only the precision and sensitivity of a machine, but also the manipulative transparency and immediacy of hand-held instruments. This robotic system can further be augmented with virtual fixtures [17], as well as incorporated with smart instruments with various sensing modalities.
Virtual fixtures are algorithms that provide assistive motion guidance with anisotropic robot behavior. The robot motion constraints assist the user to avoid forbidden regions [17], [18], as well as to guide along desired paths [19], [20]. Virtual fixtures can be prescribed [17], [18], generated from patient anatomy [21] or from real-time computer vision [19]. The implementation includes impedance [18] and admittance methods [19], [20], as well as optimization algorithms with desired geometric constraints [21], [22]. With the aid of virtual fixtures, the mental and physical demands on the user to accomplish a desired maneuver are reduced, while the task performance is notably increased. The surgeon can concentrate on the critical surgical tasks (e.g., membrane peeling) if virtual fixtures can manage the inherent surgical motion constraints, such as RCM and tool coordination, by providing an intuitive, guided robot behavior.
Smart instruments with force sensing capability are essential for safe interaction between the robot and the patient. Various force sensors have been developed for microsurgery, micromanipulation, and MIS [23]–[27]. Handle mounted force sensors [28] cannot distinguish forces exerted at the tool tip from those at the trocar. Therefore, a family of force sensing instruments [29]–[32] has been developed with fiber optic sensors integrated into the distal portion of the instrument that is typically located inside the eye. Auditory [33] and haptic [34] force feedbacks have demonstrated the efficacy of regulating the tool-to-tissue interaction force. During a freehand manipulation, the surgeon can often sense the contact force at the sclera entry point, and utilizes it as an important indicator to guide the desired motion, e.g., RCM and tool coordination. However, the stiffness of the Steady-Hand Eye Robot attenuates the user perceptible level of the sclera force, inducing undesired large sclera forces. We devised a dual force sensing instrument [35] to provide force feedback from both tool tip force and sclera force. The drawback is that the force sensor cannot provide the exact sclera force value nor the location where the sclera force is applied on the tool shaft. Instead, it measures the moment attributed to the sclera force.
In this paper, we report a new design of a multi-function force sensing instrument that can sense not only the sclera force in transverse directions, but also the location of the sclera contact point on the tool shaft. This new multi-function force sensing instrument enables a variable admittance robot control to provide an intuitive robot behavior. By varying the robot admittance, the robot behavior can continuously transit from an adaptive virtual fixture mode that enforces RCM and adapts to the current location of the sclerotomy site, to a force scaling mode that provides scaled feedback of the sclera force as well as the ability to reposition the eye. Experiments are conducted to calibrate the new multi-function force sensing instrument, to calibrate the tool tip position with respect to the robot, and to evaluate the force sensor as well as the proposed robot control algorithm. Preliminary results show the potential to increase safety, as well as to enhance the usability and capability of the robotic assistant system.
II. MULTI-FUNCTION FORCE SENSING TOOL
A. Design
The new design improves on the previous dual force sensing instrument [35]. Based on the observation of the surgical procedure, it is assumed that forces are only exerted at no more than two locations: the tool tip and the sclera contact point on the tool shaft. The tool shaft is made of a stainless steel wire with a diameter of 0.5 mm, same as the 25 Ga ophthalmic instrument. The tool shaft is machined to cut three longitudinal channels with V-shape sections. One optical fiber with three fiber Bragg grating (FBG) sensors (Technica S.A., Beijing, China) is embedded into each channel in the tool shaft. Each FBG sensor is 3 mm long. The tool dimension, as well as the specifications of the FBG sensors are shown in Fig. 2.
Fig. 2.
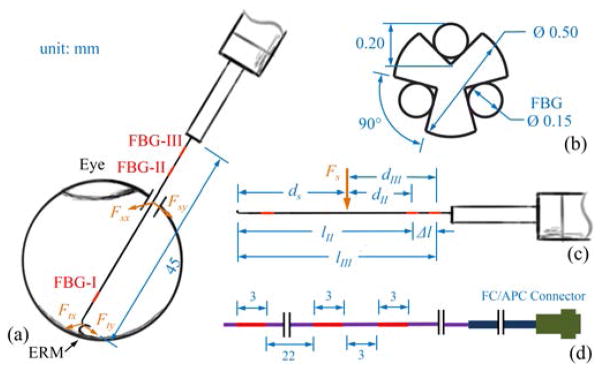
Dimension of the multi-function force sensing instrument (a). The section view of the tool shaft with the FBG sensors (b). The geometry related to tool calibration (c). The dimension of a single fiber with three FBG sensors (d). The center Bragg wavelengths of FBG-I, FBG-II, and FBG-III are 1529 nm, 1545 nm, and 1553 nm, respectively.
The new multi-function force sensing instrument includes nine FBG sensors in total, arranged into three segments of the tool shaft. The three FBG sensors in the same tool shaft segment are 120° apart, and provide strain measurements at that segment of the tool shaft. The first FBG sensing segment, FBG-I, typically remains inside the eye. It is used to measure the transverse force exerted between the tool tip and the eye tissue, because the sclera contact force does not generate strain at the tool tip. FBG-II and FBG-III sensing segments are at least 30 mm proximal from the tool tip, greater than the average diameter of the human eye (25 mm). They are dedicated to measure the transverse force exerted at the sclerotomy, and the location of the sclerotomy with respect to the tool. The axial force component at the sclerotomy is mainly due to friction, thus is correlated to the transverse force, i.e., normal force. Axial force sensing at the tip is not included in this prototype, but is possible as shown in our other work [32]. The total length of the tool shaft is 45 mm. The data acquisition unit is the sm130–700 optical sensing interrogator from Micron Optics (Atlanta, GA) with a refresh rate of 2 kHz and a spectrum range from 1525 nm to 1565 nm.
B. Algorithm to Calculate Forces and Sclerotomy Location
The algorithm to calculate the tool tip and sclera forces is based on the previous methods presented by Iordachita et al. [29] and He et al. [35]. The wavelength shift common mode of the FBG sensors from the same sensing segment represents the strain attributed to axial force and temperature change. The differential mode, termed sensor reading, is defined as follows:
| (1) |
where Δsjk and Δλjk denotes respectively the sensor reading and the wavelength shift of FBG sensor k in sensing segment j, with j= I, II, and III, and k = 1, 2, and 3.
With the assumption that tool-to-tissue interaction forces are always exerted at the tool tip, the sensor readings of FBG-I are linearly dependent on the transverse force at the tool tip:
| (2) |
where ΔSI = [ΔsI1, ΔsI2, ΔsI3]T denotes the sensor readings of FBG-I, Ft = [Ftx, Fty]T denotes the transverse force exerted at the tool tip, and KIt is a 3 × 2 matrix with constant coefficients.
The location where the sclera contact force is exerted on the tool shaft depends on the tool insertion depth inside the eye. Together with the sclera contact force, it contributes to the strain generated at FBG-II and FBG-III. In addition, the FBG sensors also respond to tool tip force, therefore:
| (3) |
| (4) |
where ΔSj = [Δsj1, Δsj2, Δsj3]T denotes the sensor readings of FBG-j, Fs = [Fsx, Fsy]T denotes the transverse force exerted at the sclerotomy, dj denotes the distance from the sclerotomy to FBG-j along the tool shaft, Mj = [Mjx, Mjy]T denotes the moment attributed to Fs at FBG-j, Kjt and Kjs are both 3 × 2 constant coefficients matrices, j = II and III. As shown in Fig. 2, the distance Δl between FBG-II and FBG-III is constant and is always the difference between dII and dIII, which is equal to the difference between lII and lIII:
| (5) |
The coefficient matrices Kjt(j= I, II, and III) and Kjs(j = II and III), as well as the distance Δl between FBG-II and FBG-III are obtained through the tool calibration presented in Section IV-A.
The tool tip force can be calculated using the pseudo-inverse of the coefficient matrix:
| (6) |
where (·)† denotes the matrix pseudo-inverse operator.
The moments attributed to the sclera contact forces at FBG-j (j = II and III) can be calculated using (3) and (6):
| (7) |
The sclera contact force can be solved from the difference in moments MII and MIII:
| (8) |
The distance from the sclerotomy to the FBG-j can be obtained from the magnitude ratio between the moment and the force:
| (9) |
where || · || denotes the vector 2-norm.
This method can calculate transverse forces exerted at the tool tip and at the sclerotomy, as well as the location of the sclerotomy with respect to the tool. However, if the magnitude of the sclera contact force is small, the location of the sclerotomy calculated using (9) can be subject to large error. Therefore, the sclerotomy location is updated with the help of a dead band on the sclera force magnitude. Only when the sclera force magnitude exceeds a given threshold (e.g., 5 mN), the sclerotomy location will be updated using (9), otherwise the previous value of dj will be used.
III. VARIABLE ADMITTANCE ROBOT CONTROL
A variable admittance robot control scheme is devised from previous force scaling and admittance velocity control [34], [36]. In addition to the surgeon’s force input at the tool handle (robot end-effector), it utilizes the new sensing capabilities enabled by the multi-function force sensing instrument, to provide a robot behavior that is transparent and intuitive to the surgeon. This robot behavior enables useful feedbacks and virtual fixtures to increase precision and safety to interact with the patient and the environment. Fig. 3 illustrates the variable admittance control scheme.
Fig. 3.

Variable admittance robot control scheme. Solid lines show the signal flow in current implementation, dashed lines show the signals that can also be incorporated into the control law.
A. Constant Admittance Control with Force Scaling
The previous admittance velocity control is:
| (10) |
| (11) |
where ẋhh and ẋwh are the desired robot handle velocity in the robot handle frame and that in the world Cartesian frame, respectively, Fhh denotes user’s force input measured in the robot handle frame, and α is a constant scalar as the admittance gain, and Adgwh is the adjoint transformation associated with coordinate frame transformation gwh. If we write , where Rwh and pwh denote the rotation and translation of gwh from the local robot handle frame to the world Cartesian frame, then:
| (12) |
where p̂wh denotes the skew symmetric matrix that is associated with the vector pwh.
We modify (10) using force scaling [34], [36] to incorporate sclera force feedback:
| (13) |
where γ is a force scaling factor, and Fhs is the sclera force resolved at the robot handle with the following adjoint transformation:
| (14) |
where Fss denotes the sclera force measured in the sclera frame which is located at the sclerotomy and has the same orientation as the robot handle frame. Let denote the coordinate frame transformation from sclera frame to robot handle frame, then:
| (15) |
where (·)T denotes the matrix transpose. The sclerotomy is not a static point during retinal microsurgery. Therefore, ghs is time-varying. We assume that the tool shaft bending due to sclera force remains in a small range, then Rhs ≈ I, phs ≈ [0, 0, zhs]T, and zhs can be updated by the multifunction force sensing instrument.
B. Variable Admittance Control
The admittance in the previous control law is isotropic. Virtual fixtures can be rendered by commanding anisotropic admittance. We introduce diagonal admittance matrices into (13) and rewrite it in the sclera frame:
| (16) |
where ẋss is the desired velocity of the point where the robot/tool contact the sclerotomy written in the sclera frame, Fsh and Fss are the handle input force and sclera contact force resolved in the sclera frame, respectively, γ denotes the constant scalar as the force scaling factor, α denotes the constant scalar as the admittance gain, and Ash and Ass are the diagonal admittance matrices associated with the handle input force and sclera contact force in the sclera frame, respectively. If Ash = Ass = I, (16) reduces to (13) as force scaling of the sclera force.
A virtual RCM can be realized by setting Ash = diag([0, 0, 1, 1, 1, 1]T) and Ass = I. The handle input force Fsh is resolved in the sclera frame. The admittance matrix Ash removes the transverse force components that can lead to undesired lateral motion, and preserves the 4-DOF motion that is allowed by the RCM constraints. In addition, the sclera force feedback is to servo the sclera contact force toward zero. This strengthens the virtual RCM with robustness against eye motion attributed other instrument and patient movement.
When the surgeon is performing membrane peeling, the tool tip is close to the retina, and an RCM is desired to minimize the motion of the eye and the target membrane. When the surgeon needs to reposition the eye to adjust view, the tool is kept away from the retina to avoid collision. Therefore, the measured insertion depth of the tool can be used to adjust the robot admittance to provide the appropriate robot behavior. For example, we can define:
| (17) |
| (18) |
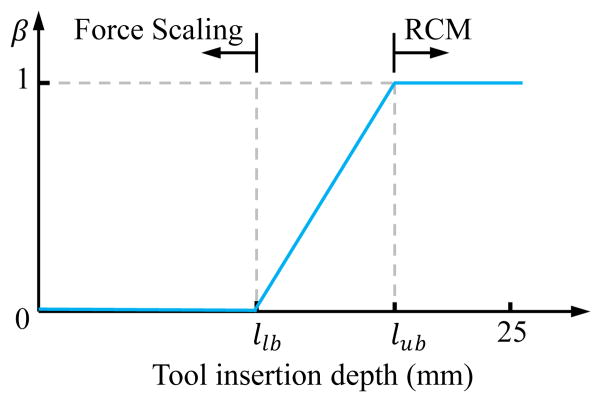
where β ∈ [0, 1] varies along with the tool insertion depth as shown in Fig. 4. When the insertion depth is smaller than the given lower bound llb, β = 0 and Ash = Ass = I. We have the force scaling control mode that provides the freedom to reposition the eye with scaled sclera force feedback. When the insertion depth is larger than the given upper bound lub, β = 1 and it switches to virtual RCM with doubled gain for minimizing the transverse forces at the sclerotomy. Alternatively, the value of β can be controlled by the human operator (e.g., using a foot pedal) to select the preferred operating mode.
Fig. 4.
Admittance varies along with the insertion depth. The section between llb and lub is the transition between pure force scaling of the sclera force and pure RCM.
IV. EXPERIMENTS AND RESULTS
A. Calibration of the Multi-Function Force Sensing Tool
An automated calibration system [32] is used to carry out the calibration. The orientation and position of the tool are controlled by a high precision robot (translation resolution 1 μm, rotation resolution ≤ 0.005°). Actual values of the transverse forces are measured by a precision scale with a resolution of 1 mg.
1) Calibration for Tool Tip Force
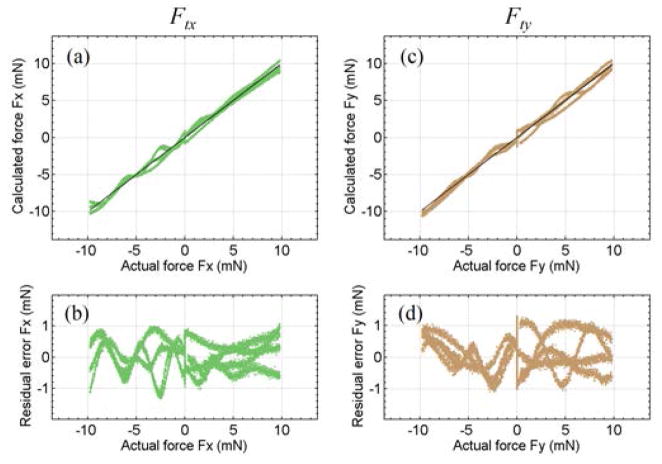
The calibration for tool tip force is the same as for our previous dual force sensing tool [35]. Transverse forces up to 10 mN are applied along X- and Y-axes. The coefficient matrices Kjt, j = I, II, and III, are obtained as least squares solutions of (2) and (3) with MII = MIII = 0. Fig. 5 illustrates the calibration results for the tool tip forces. Fig. 5(a) and (c) show the forces calculated using (6) versus the actual forces. The 45° straight line through the origin represents the ideal results. Fig. 5(b) and (d) show the residual error versus the actual forces. The root mean square (RMS) errors are 0.35 mN for Ftx and 0.53mN for Fty, respectively.
Fig. 5.
Results of tool tip force calibration. The calculated tool tip force along X-axis Ftx versus the actual value (a), its residual error (b). The calculated tool tip force along Y-axis Fty versus the actual value (c), and its residual error (d).
2) Calibration for Sclera Contact Force and Location
Transverse forces are applied at 16 locations on the tool shaft, from 10 mm to 25 mm proximal from the tool tip with 1 mm intervals, shown as ds in Fig. 2(c). The force magnitude ranges from 25 mN at 10 mm from the tool tip, to 100 mN at 25 mm from the tool tip. Because the optical fibers are manually aligned and embedded into the tool shaft, the accurate “center” locations of FBG-II and FBG-III, i.e., lII and lIII in Fig. 2(c), are not known. There is no force applied at the tool tip, hence (4) reduces to:
| (19) |
| (20) |
where dj = lj − ds with j = II and III.
The calibration goal is to find the constant Kjs and lj. Because they are not linearly independent, an optimization problem is constructed to find the best fit:
| (21) |
| (22) |
| (23) |
The optimum minimizes the cost function, i.e., the 2-norm of the residual error of the sensor reading of FBG-j. Fig. 6 illustrates the optimization results. and are 31.3 mm and 37.2 mm, respectively. The difference between FBG-II and FBG-III , is consistent with the nominal value of 6 mm in a single fiber.
Fig. 6.
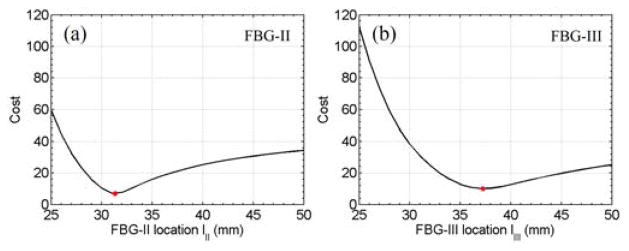
Results of the optimization problem. The optimization cost for FBG-II versus lII (a) and the optimization cost for FBG-III versus lIII (b). The red dots indicate the minimum cost where and .
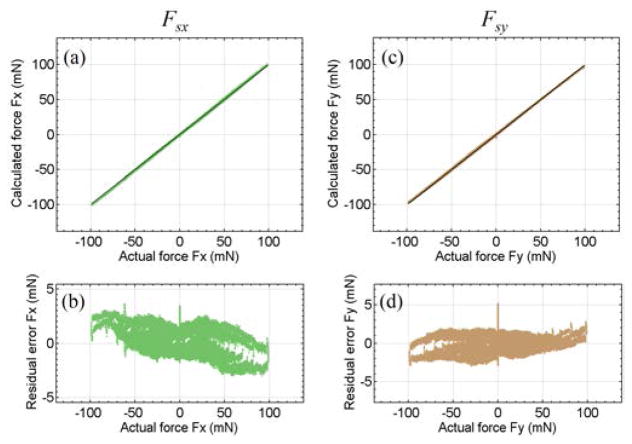
The coefficient matrix Kjs is calculated using (22) with . Calibration results demonstrate sufficient accuracy, as shown in Fig. 7. The RMS errors are 0.82 mN for Fsx and 1.00 mN for Fsy. The location of the sclerotomy is estimated using forces larger than 5 mN in magnitude. Fig. 8 illustrates the estimated sclerotomy location with respect to the tool tip versus the actual value, and the estimation RMS error at each calibrated location. The further the sclerotomy is located from the tool tip, i.e., the closer it is to FBG-II and FBG-III, the more accurate is the location estimation. As shown in the next section, Low pass filtering can further reduce the sensing noise and smooth the estimation.
Fig. 7.
Results of sclera force calibration. The calculated sclera force along X-axis Fsx versus the actual value (a), its residual error (b). The calculated sclera force along Y-axis Fsy versus the actual value (c), and its residual error (d).
Fig. 8.

Results of sclerotomy location calibration. The calculated distance from the tool tip to sclerotomy ds versus the actual value (a), the RMS error at each calibrated location verus the actual distance (b). The further the scleratomy is located from the tool tip, i.e., the closer it is with respect to FBG-II and FBG-III, the smaller is the RMS error. Data points with forces smaller than 5 mN in magnitude is not included to reduce noise, as discussed in Section II-B.
Using the sclera calibration results, we examine the tool tip force cancellation from FBG-II and FBG-III. The sensor readings of FBG-II and FBG-III from calibration with only tool tip forces are plugged into (7) and (8) to calculate the sclera force estimation error due to tool tip force. As shown in Fig. 9, the sclera force errors are not dependent on the tool tip force magnitude, and are possibly due to the system noise. The RMS errors are 0.62 mN for Fsx and 0.74 mN for Fsy, with tool tip forces up to 10 mN.
Fig. 9.
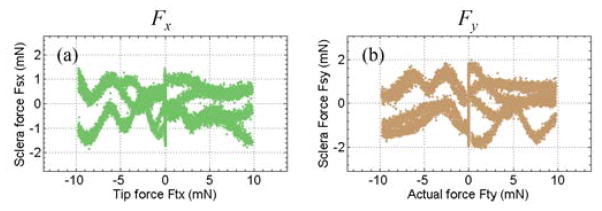
Sclera force estimation error due to tool tip force. The calculated sclera force along X-axis Fsx versus the applied tool tip force along X-axis Ftx (a), and the calculated sclera force along Y-axis Fsy versus the applied tool tip force along Y-axis Fty (b).
3) Validation Experiment for Sclera Contact Force
A validation experiment is carried out using the automated calibration system to test the results obtained from calibration for sclera force and location. The direction and the magnitude of the transverse forces, as well as the location on the tool shaft where the force is applied are generated randomly within the calibrated range. A moving average filter with a window size of 100 samples is applied on the location estimation of sclerotomy. Fig. 10 illustrates the results of the validation experiment. The RMS errors of Fsx and Fsy estimations are 0.56 mN and 1.08 mN respectively. The RMS error of the sclerotomy location estimation is 0.57 mm, comparable to the lowest RMS error obtained in the calibration (at 25 mm from the tool tip).
Fig. 10.
Results of validation experiment for sclera contact force. The calculated sclera force versus the actual value (a), the residual error of force calculation (b). The calculated distance from the tool tip to sclerotomy ds versus the actual value (c), and its residual error (d).
B. Tool-to-Robot Calibration
Incorporating the multi-function force sensing capability into the robot control requires an accurate coordinate transformation from the local tool frame to the robot handle frame. It is reasonable to assume the tool and the robot handle are coaxial. The X- and Y-axes of the tool and the robot handle are manually aligned. The Z-offset zht from the tool tip to the robot handle is about −40 mm measured with a caliper. A traditional pivot calibration is not practical, because the tool shaft is not rigid. We use variable admittance control to enforce the RCM constraint, in order to perform a pseudo pivot calibration. Fig. 11 illustrates the experiment setup. A piece of 0.25 mm thick, stiff paper is taped to a CD clamped to a stable platform. A 0.7 mm hole is punctured in the center of the paper that is exposed through the center hole of the CD. The multi-function force sensing tool is inserted through the hole and pivoted with the RCM constraint by the variable admittance control, as shown in Fig. 11(a).
Fig. 11.
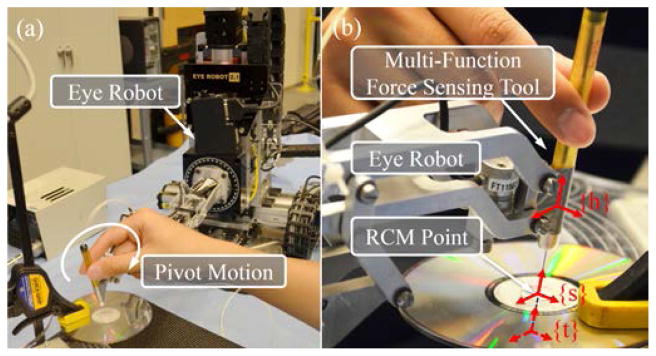
Setup of the pseudo pivot calibration (a) and the close-up with coordinate frames robot handle {h}, sclera {s}, and tool tip {t} (b). Tool tip frame {t} is underneath the CD, shown with dashed arrows.
The sclera location estimations ds from the multi-function force sensing tool and the frame transformations from the robot handle frame to the world Cartesian frame gwh are used to find the tool tip offset from the handle. Let ghs denote the frame transformation from the “sclera” frame located at the RCM point to the robot handle frame. Because we assume the orientation of “sclera” RCM frame is aligned with that of the robot handle frame:
| (24) |
where Rhs = I, phs = [0, 0, zht + ds]T, and zht is the Z-position of the tool tip in the robot handle frame. The RCM point pws can be considered as a static point in the world Cartesian frame. Ideally, all pws computed from the kinematics should converge to one point. Therefore, an optimization problem that finds the to minimize the standard deviation of all pws:
| (25) |
| (26) |
| (27) |
| (28) |
Fig. 12(a) shows the optimization results, . The corresponding trajectories of the RCM point and the tool tip are shown in Fig. 12(b). The standard deviation of the computed RCM positions is 0.38 mm, 0.34 mm and 0.74 mm in the X-, Y-, and Z-direction, respectively. This demonstrates the capability of adaptive RCM constraints enabled by the variable admittance control.
Fig. 12.
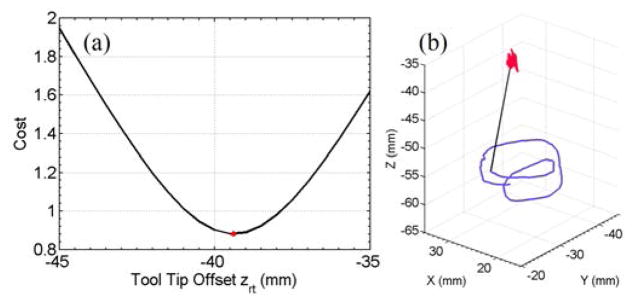
Results of the optimization to find the tool tip offset from the handle along Z-axis (a). The optimum offset is at , shown as the red dot. The corresponding trajectories of the RCM point (red) and the tool tip (purple) (b). The black straight line shows the end position of the tool shaft.
C. Tracing a Retina Vein in an Eye Phantom with Robot Assistance
We further assess the performance of the robot control methods using an eye phantom, as shown in Fig. 13. The tool is mounted in the tool holder of the Steady-Hand Eye Robot and inserted through a 23 Ga trocar on the eye. The tracing task is to make a round trip with the tool tip above a retina vein branch that is about 3 mm long. A stereo video microscope with a 3D display is used for visualization.
Fig. 13.

Setup of the retina vein tracing experiment with robotic assistance.
Five trials are conducted with the variable admittance robot control. Fig. 14 illustrates the recorded sclera forces, as well as the trajectories of the sclerotomy point and the tool tip of one trial. The maximum sclera force magnitude is 3.44 ± 0.21 mN. The sclerotomy position is calculated using the tool-to-robot transformation obtained in Section IV-B. The standard deviation of the sclerotomy position is 0.13 ± 0.03 mm, 0.17 ± 0.06 mm, and 0.38 ± 0.06 mm for X-, Y-, and Z-direction. The experiment results show the RCM behavior with the variable admittance control is precise and repeatable, minimizing both force and motion of the sclerotomy.
Fig. 14.

Sclera force of one retina vein tracing trial (a). The corresponding trajectories of the scleratomy point (red) and the tool tip (purple) (b). The black straight line shows the end position of the tool shaft.
Same task is also attempted with the standard cooperative robot control without sclera force feedback. However, no successful trial was completed. The robot stiffness attenuates the user perceptible level of the sclera force. The excessive tool deflection due to large sclera forces (over 50mN) and the inverted tool motion due to RCM make it very difficult for the user to precisely control the tool tip trajectory. As a result, the pivot motion of the tool and the sclerotomy point are misaligned. In contrast, the variable admittance control enables a fulcrum at the sclerotomy, the user pivots naturally about it with precise control of the tool tip motion.
V. DISCUSSION AND CONCLUSION
Krupa et al. [37] used force control with the help of a force sensor mounted on the robot end-effector to implement an adaptive RCM behavior. However, it was assumed that there is no transverse forces exerted at the instrument tip, therefore the transverse forces measured outside the patient at the robot end-effector is the contact force exerted between the instrument shaft and the trocar. This assumption is not necessary valid in MIS. The multi-function force sensing instrument can provide sufficiently accurate, independent measurements of the tool tip force and the sclera contact force, as well as the location of the sclerotomy. Its design can also be applied to surgical instruments for MIS, to provide additional useful information to improve the surgical robot control. Both impedance and admittance type robots can utilize this sensor to provide safe interaction with the environment. This can be especially pertinent for bilateral cooperative manipulation and master-slave telesurgery.
The variable admittance control takes the sensing advantage from the multi-function force sensing instrument. It reflects the natural physical interaction between the tool and the environment. It can adapt to the current RCM point without the assumption that the RCM point is static. Mechanical RCM does not provide the flexibility to vary the RCM point, while software virtual RCM that uses geometric constraints can incorporate the multi-function force sensing instrument to update the current RCM location. The variable admittance control law can also be incorporated with other virtual fixture methods, such as the constrained optimization framework [21], [22]. Ultimately, it should provide a transparent and intuitive interface that can incorporate useful feedback and natural motion guidance.
We have presented a novel multi-function force sensing instrument designed for vitreoretinal surgery procedures and measures not only the forces at the instrument tip, but also the sclera contact position and the corresponding sclera contact force. A variable admittance robot control method was developed that incorporates this information to provide a transparent and intuitive robot behavior that can minimize eye motion while enabling tool manipulation inside the eye, as well as provide useful sclera force feedback to assist to reposition the eye. This system can potentially provide safe, stable micromanipulation that can improve the outcome of the retinal microsurgery. In the future, we will further investigate this system in phantom and in vivo experiments.
Footnotes
Research supported in part by NIH BRP grant 1 R01 EB 007969, in part by NIH grant R01 EB 000526, in part by Wilmer Eye Institute’s Research to Prevent Blindness, and in part by Johns Hopkins University internal funds. Other equipment and systems infrastructure support were developed within the CISST ERC under NSF grant EEC9731748.
References
- 1.Wilkins JR, Puliafito CA, Hee MR, Duker JS, Reichel E, Coker JG, Schuman JS, Swanson EA, Fujimoto JG. Characterization of epiretinal membranes using optical coherence tomography. Ophthalmology. 1996;103(12):2142–2151. doi: 10.1016/s0161-6420(96)30377-1. [DOI] [PubMed] [Google Scholar]
- 2.Patkin M. Ergonomics applied to the practice of microsurgery. The Australian and New Zealand Journal of Surgery. 1977;47(3):320–9. doi: 10.1111/j.1445-2197.1977.tb04297.x. [DOI] [PubMed] [Google Scholar]
- 3.Gupta P, Jensen P, de Juan E. Surgical forces and tactile perception during retinal microsurgery. International Conference on Medical Image Computing and Computer Assisted Intervention. 1999;1679:1218–1225. [Google Scholar]
- 4.Taylor RH, Funda J, Grossman DD, Karidis JP, LaRose DA. U.S. Patent 5,397,323. Remote center-of-motion robot for surgery. 1995;14
- 5.Hubschman JP, Son J, Allen B, Schwartz SD, Bourges JL. Evaluation of the motion of surgical instruments during intraocular surgery. Eye (London, England) 2011;25(7):947–953. doi: 10.1038/eye.2011.80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Charles S, Das H, Ohm T, Boswell C, Rodriguez G, Steele R, Istrate D. Dexterity-enhanced telerobotic microsurgery. IEEE International Conference on Advanced Robotics; 1997. pp. 5–10. [Google Scholar]
- 7.Ida Y, Sugita N, Ueta T, Tamaki Y, Tanimoto K, Mitsuishi M. Microsurgical robotic system for vitreoretinal surgery. International Journal of Computer Assisted Radiology and Surgery. 2012;7(1):27–34. doi: 10.1007/s11548-011-0602-4. [DOI] [PubMed] [Google Scholar]
- 8.Wei W, Goldman R, Simaan N. Design and theoretical evaluation of micro-surgical manipulators for orbital manipulation and intraocular dexterity. IEEE International Conference on Robotics and Automation; 2007. pp. 10–14. [Google Scholar]
- 9.Yu H, Shen JH, Joos KM, Simaan N. Design, calibration and preliminary testing of a robotic telemanipulator for OCT guided retinal surgery. IEEE International Conference on Robotics and Automation; 2013. pp. 225–231. [Google Scholar]
- 10.Maclachlan RA, Becker BC, Tabar JC, Podnar GW, Lobes LA, Riviere CN. Micron: an actively stabilized handheld tool for microsurgery. IEEE Transactions on Robotics. 2012;28(1):195–212. doi: 10.1109/TRO.2011.2169634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Song C, Park DY, Gehlbach PL, Park SJ, Kang JU. Fiber-optic OCT sensor guided “SMART” micro-forceps for microsurgery. Biomedical Optics Express. 2013;4(7):1045–1050. doi: 10.1364/BOE.4.001045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kummer MP, Member SS, Abbott JJ, Kratochvil BE, Borer R, Sengul A, Nelson BJ. OctoMag: An Electromagnetic System for 5-DOF Wireless Micromanipulation. IEEE Transactions on Robotics. 2010;26(6):1006–1017. [Google Scholar]
- 13.Taylor R, Jensen P, Whitcomb L, Barnes A, Kumar R, Stoianovici D, Gupta P, Wang Z, DeJuan E, Kavoussi L. A Steady-Hand Robotic System for Microsurgical Augmentation. The International Journal of Robotics Research. 1999;18(12):1201–1210. [Google Scholar]
- 14.Mitchell B, Koo J, Iordachita I, Kazanzides P, Kapoor A, Handa J, Hager G, Taylor R. Development and application of a new steady-hand manipulator for retinal surgery. IEEE International Conference on Robotics and Automation; 2007. pp. 623–629. [Google Scholar]
- 15.Uneri A, Balicki MA, Handa J, Gehlbach P, Taylor RH, Iordachita I. New Steady-Hand Eye Robot with micro-force sensing for vitreoretinal surgery. IEEE International Conference on Biomedical Robotics and Biomechatronics; 2010. pp. 814–819. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.He X, Roppenecker D, Gierlach D, Balicki M, Olds K, Gehlbach P, Handa J, Taylor R, Iordachita I. Toward Clinically Applicable Steady-Hand Eye Robot for Vitreoretinal Surgery. ASME 2012 International Mechanical Engineering Congress and Exposition. 2012;2:145–153. [Google Scholar]
- 17.Rosenberg L. Virtual fixtures: Perceptual tools for telerobotic manipulation. IEEE Virtual Reality Annual International Symposium; 1993. pp. 76–82. [Google Scholar]
- 18.Abbott J, Okamura A. Virtual fixture architectures for tele-manipulation. IEEE International Conference on Robotics and Automation; 2003. pp. 2798–2805. [Google Scholar]
- 19.Bettini A, Marayong P, Lang S, Okamura A, Hager G. Vision-assisted control for manipulation using virtual fixtures. IEEE Transactions on Robotics. 2004;20(6):953–966. [Google Scholar]
- 20.Marayong P, Li M, Okamura AM, Hager GD. Spatial motion constraints: theory and demonstrations for robot guidance using virtual fixtures. IEEE International Conference on Robotics and Automation; 2003. pp. 1954–1959. [Google Scholar]
- 21.Li M, Ishii M, Taylor RH. Spatial motion contraints using virtual fixtures generated by anatomy. IEEE Transactions on Robotics. 2007;23(1):4–19. [Google Scholar]
- 22.Kapoor A, Taylor R. Constrained control for surgical assistant robots. IEEE International Conference on Robotics and Automation; 2006. pp. 231–236. [Google Scholar]
- 23.Menciassi A, Eisinberg A, Scalari G, Anticoli C, Carrozza M, Dario P. Force feedback-based microinstrument for measuring tissue properties and pulse in microsurgery. IEEE International Conference on Robotics and Automation; 2001. pp. 626–631. [Google Scholar]
- 24.Seibold U, Kubler B, Hirzinger G. Prototype of Instrument for Minimally Invasive Surgery with 6-Axis Force Sensing Capability. IEEE International Conference on Robotics and Automation; 2005. pp. 496–501. [Google Scholar]
- 25.Peirs J, Clijnen J, Reynaerts D, Van Brussel H, Herijgers P, Corteville B, Boone S. A micro optical force sensor for force feedback during minimally invasive robotic surgery. Sensors and Actuators A: Physical. 2004;115(2–3):447–455. [Google Scholar]
- 26.Puangmali P, Liu H, Seneviratne LD, Dasgupta P, Althoefer K. Miniature 3-Axis Distal Force Sensor for Minimally Invasive Surgical Palpation. IEEE/ASME Transactions on Mechatronics. 2012;17(4):646–656. [Google Scholar]
- 27.Polygerinos P, Ataollahi A, Schaeffter T, Razavi R, Seneviratne LD, Althoefer K. MRI-compatible intensity-modulated force sensor for cardiac catheterization procedures. IEEE Transactions on Biomedical Engineering. 2011;58(3):721–726. doi: 10.1109/TBME.2010.2095853. [DOI] [PubMed] [Google Scholar]
- 28.Berkelman P, Whitcomb L, Taylor R, Jensen P. A miniature microsurgical instrument tip force sensor for enhanced force feedback during robot-assisted manipulation. IEEE Transactions on Robotics and Automation. 2003;19(5):917–921. [Google Scholar]
- 29.Iordachita I, Sun Z, Balicki M, Kang JU, Phee SJ, Handa J, Gehlbach P, Taylor R. A sub-millimetric, 0.25 mN resolution fully integrated fiber-optic force-sensing tool for retinal microsurgery. International Journal of Computer Assisted Radiology and Surgery. 2009;4(4):383–390. doi: 10.1007/s11548-009-0301-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.He X, Balicki M, Kang JU, Gehlbach P, Handa J, Taylor R, Iordachita I. Force sensing micro-forceps with integrated fiber Bragg grating for vitreoretinal surgery. SPIE Phontics West. 2012;8218(82180W):1–7. [Google Scholar]
- 31.Liu X, Iordachita I, He X, Taylor R, Kang JU. Miniature fiber-optic force sensor based on low-coherence Fabry-Pérot interferometry for vitreoretinal microsurgery. Biomedical Optics Express. 2012;3(5):1062–1076. doi: 10.1364/BOE.3.001062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.He X, Handa J, Gehlbach P, Taylor R, Iordachita I. A sub-millimetric 3-dof force sensing instrument with integrated fiber bragg grating for retinal microsurgery. IEEE Transactions on Biomedical Engineering. 2014;61(2):522–534. doi: 10.1109/TBME.2013.2283501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Cutler N, Balicki M, Finkelstein M, Wang J, Gehlbach P, Mc-Gready J, Iordachita I, Taylor R, Handa JT. Auditory force feedback substitution improves surgical precision during simulated ophthalmic surgery. Investigative Ophthalmology & Visual Science. 2013;54(2):1316–1324. doi: 10.1167/iovs.12-11136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Balicki M, Uneri A, Iordachita I, Handa J, Gehlbach P, Taylor R. Micro-force sensing in robot assisted membrane peeling for vitreoretinal surgery. International Conference on Medical Image Computing and Computer Assisted Intervention. 2010;13:303–310. doi: 10.1007/978-3-642-15711-0_38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.He X, Balicki M, Gehlbach P, Handa J, Taylor R, Iordachita I. A novel dual force sensing instrument with cooperative robotic assistant for vitreoretinal surgery. IEEE International Conference on Robotics and Automation; 2013. pp. 213–218. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kumar R, Berkelman P, Gupta P, Barnes A, Jensen P, Whitcomb L, Taylor R. Preliminary experiments in cooperative human/robot force control for robot assisted microsurgical manipulation. IEEE International Conference on Robotics and Automation; 2000. pp. 610–617. [Google Scholar]
- 37.Krupa A, Morel G, de Mathelin M. Achieving high-precision laparoscopic manipulation through adaptive force control. Advanced Robotics. 2004;18(9):905–926. [Google Scholar]