A neurocomputational account of cognitive deficits in Parkinson’s disease

Abstract

Parkinson’s disease (PD) is caused by the accelerated death of dopamine (DA) producing neurons. Numerous studies documenting cognitive deficits of PD patients have revealed impairments in a variety of tasks related to memory, learning, visuospatial skills, and attention. While there have been several studies documenting cognitive deficits of PD patients, very few computational models have been proposed. In this article, we use the COVIS model of category learning to simulate DA depletion and show that the model suffers from cognitive symptoms similar to those of human participants affected by PD. Specifically, DA depletion in COVIS produced deficits in rule-based categorization, non-linear information-integration categorization, probabilistic classification, rule maintenance, and rule switching. These were observed by simulating results from younger controls, older controls, PD patients, and severe PD patients in five well-known tasks. Differential performance among the different age groups and clinical populations was modeled simply by changing the amount of DA available in the model. This suggests that COVIS may not only be an adequate model of the simulated tasks and phenomena but also more generally of the role of DA in these tasks and phenomena.

1. Introduction

Parkinson’s disease (PD) is caused by the accelerated death of dopamine (DA) producing neurons. The pattern of cell loss is opposite from and more severe than in normal aging. Within the substantia nigra pars compacta (SNpc), cell loss is predominately found in the ventral tier with less (but still extensive) damage in the dorsal tier (Fearnley & Lees, 1991; Gibb & Lees, 1991). In contrast, normal aging yields substantially less cell loss and in a dorsal-to-ventral pattern. Parkinsonian motor symptoms appear after a loss of 60–70% of SNpc cells and 70–80% of DA levels in striatal nuclei (Bernheimer, Birkmayer, Hornykiewicz, Jellinger, & Seitelberger, 1973; Gibb & Lees, 1991). Motor symptoms include tremor, rigidity, bradykinesia, and akinesia.

In addition to motor deficits, non-demented PD patients present cognitive symptoms that resemble those observed in patients with frontal damage. Numerous studies documenting cognitive deficits of PD patients have revealed impairment in a variety of tasks related to memory, learning, visuospatial skills, and attention (e.g., ignoring irrelevant and maintaining relevant information: Gotham, Brown & Marsden, 1988). While there are a plethora of studies documenting cognitive deficits of PD patients (for a review, see Price, Filoteo, & Maddox, 2009), very few computational models have been proposed to investigate the variegated landscape of deficits observed in those studies. In this article, we use the COVIS model of category learning (Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Ashby, Paul, & Maddox, 2011) to simulate DA depletion and we show that the depleted model suffers from cognitive symptoms similar to those of human participants affected by PD.

2. The COVIS theory of category learning

COVIS (Ashby et al., 1998) is a neurobiologically detailed theory of category learning that postulates two systems that compete throughout learning—an explicit, hypothesis-testing system that uses logical reasoning and depends on working memory and executive attention, and an implicit system that uses procedural learning. The hypothesis-testing system of COVIS is thought to mediate rule-based category learning. Rule-based category-learning tasks are those in which the category structures can be learned via some explicit reasoning process. Frequently, the rule that maximizes accuracy (i.e., the optimal rule) is easy to describe verbally. In the most common applications, only one stimulus dimension is relevant, and the observer’s task is to discover this relevant dimension and then to map the different dimensional values to the relevant categories. The Wisconsin Card Sorting Test (WCST; Heaton, Chelune, Talley, Kay, & Curtiss, 1993) is a well-known rule-based task. More complex rule-based tasks can require attention to multiple stimulus dimensions. For example, any task where the optimal strategy is to apply a logical conjunction or disjunction is rule-based. The key requirement is that the optimal strategy can be discovered by logical reasoning and is easy for humans to describe verbally.

The procedural system of COVIS is hypothesized to mediate information-integration category learning. Information-integration tasks are those in which accuracy is maximized only if information from two or more stimulus components (or dimensions) is integrated at some pre-decisional stage. Perceptual integration could take many forms—from treating the stimulus as a Gestalt to computing a weighted linear combination of the dimensional values. Typically, the optimal strategy in information-integration tasks is difficult or impossible to describe verbally. Rule-based strategies can be applied in information-integration tasks, but they generally lead to sub-optimal levels of accuracy because rule-based strategies make separate decisions about each stimulus component, rather than integrating this information.

3. Parkinson’s disease and cognitive impairments

Many experiments have contributed to the identification of PD-related cognitive deficits. Although the diverse landscape of impairments may appear disparate, they can largely be attributed to failures in one of the two COVIS learning systems. Impairments in rule-based tasks will be considered first followed by impairments in procedural-learning tasks. The evidence presented here is by no means exhaustive, but instead has been selected as representative of learning failures that are amenable to exposition through model simulation without modifying the existing COVIS model architecture (Ashby et al., 1998, 2011). A fuller treatment of PD cognitive deficits can be found in Price et al. (2009).

3.1. Rule-based learning

PD patients display many of the same deficits in rule-learning tasks as patients with frontal lobe damage (Owen, Roberts, Hodges, & Robbins, 1993). These tasks demand attention, working memory, and logical reasoning to maximize performance. This section reviews empirical evidence for rule-related deficits in PD patients, with a focus on deficits in rule-based category learning, rule maintenance, and perseverative response tendencies. This focus is warranted considering that COVIS is a model of category learning that uses hypothesis-testing as a mechanism for rule learning, and that the goal here is not to design a specific computational model of PD deficits, but rather to simulate PD symptoms using an existing neurobiologically-detailed model (COVIS) without any modifications or additional assumptions. Evidence reviewed in Cools (2006) suggests that these impairments in ‘executive functions’ are DA related. More specifically, Price et al. (2009) reviewed evidence suggesting that rule shifting and rule selection impairments are DA related. Hence, rule-related cognitive symptoms will be simulated in COVIS by reducing DA levels (see Section 5).

Ashby and his colleagues (2003) tested PD patients, age-matched controls, and younger controls in a rule-based categorization task similar to the WCST, except that the stimuli varied on four dimensions instead of three. Like the WCST however, a simple one-dimensional rule could be used to categorize the stimuli perfectly. Each participant was classified as a learner if the rule was successfully learned (i.e., 10 consecutively correct responses) within 200 trials. Compared to controls, significantly more PD patients failed to learn in this task than both the young and age-matched controls.

The above experiment successfully identified a gross impairment in rule learning via simple rule-based categorization. More nuanced deficits have also been identified by using different kinds of rule-based tasks and performance metrics. For example, PD patients tend to demonstrate a failure of rule maintenance. Rule maintenance requires sustained attention to the relevant stimulus dimension (as determined by the rule) while ignoring variations in the other dimensions. Typically, rule maintenance is measured by set loss errors, which are defined as errors following several consecutively correct responses. In the WCST, PD patients exhibit significantly more set loss errors than controls (Beatty, Staton, Weir, Monson, & Whitaker, 1989). Similarly, Filoteo, Maddox, Ing, and Song (2007) observed more set loss errors in a rule-based categorization task when the irrelevant dimensions varied randomly than when there was no variability in the irrelevant dimension.

PD patients also appear to exhibit a perseverative tendency—patients often persist with the previous response strategy despite feedback suggesting a change in the relevant rule. Using a simplified version of the WCST (Nelson, 1976), Gotham et al. (1988) found PD patients to make significantly more perseverative errors than control participants. In addition, Beatty et al. (1989) found greater mean perseverative errors and responses than controls in the standard WCST. Finally, a meta-analysis of PD patient performances in WCST experiments found moderate effect sizes for both perseverative errors and perseverative responses, further supporting the hypothesis that PD patients exhibit perseverative tendencies (Zakzanis & Freedman, 1999).

3.2. Procedural learning

Using a different class of learning problems, some studies have identified a different pattern of learning deficits in PD patients. Procedural learning is important in categorization tasks in which optimal responding cannot be obtained via logical reasoning or by using any explicit rule-based strategy. Shohamy, Myers, Grossman, Sage, and Gluck (2005) reviewed evidence and collected data suggesting that at least some forms of procedural learning are DA-related. As such, procedural-learning deficits are simulated in COVIS by reducing DA levels in the model (see Section 5).

In a now classic study, Knowlton, Mangels, and Squire (1996) tested several patient groups in the Weather Prediction Task (WPT), a probabilistic classification task that requires participants to learn gradually to associate a number of stimuli with the correct outcome. Knowlton and her colleagues found that PD patients performed significantly worse than controls in this task, and PD patients with the most severe symptoms never performed above chance. Importantly, amnesic patients performed as well as controls, thus lending strong evidence that a failure of memorization was not the cause of the PD impairment and indirectly supporting the hypothesis that performance in this task depends on an intact mesostriatal dopamine system.

Ashby and his colleagues (2003) tested PD patients with an information-integration category-learning task that used the same stimuli as in the rule-based task described in Section 3.1. In the information-integration condition, the stimuli were separated into two categories in such a way that no easily verbalized rule would yield optimal performance. Interestingly, PD patients were unimpaired in this task compared to age-matched controls (although both groups were massively impaired relative to young controls). Similarly, PD patients showed no deficits in two other information-integration category-learning tasks that used two-dimensional continuous-valued stimuli when the categories were linearly separable, although they were impaired relative to controls when the categories were non-linearly separable (Filoteo, Maddox, Salmon, & Song, 2005; Maddox & Filoteo, 2001). These results suggest that PD patients are impaired relative to age-matched controls in tasks that rely on procedural learning, but only when the task is sufficiently complex.

3.3. A model-based approach to understanding Parkinson’s disease impairments

Despite the tremendous amount of behavioral research in PD, very few computational models have been proposed that attempt to account for the cognitive impairments concomitant with the disease. In this article, we describe how an implementation of the COVIS theory of category learning (Ashby et al., 1998) can be used to simulate DA depletions and we show that the resulting model mimics some cognitive symptoms of PD patients (Hélie, Paul, & Ashby, 2012). The neurobiological specificity of COVIS uniquely allows this degree of flexibility. Notably, the model requires no substantive modification to account for some neuropsychological patient and normal aging data despite the fact that it was originally built as a model of human category learning in healthy adults, not as a model of PD (Ashby et al., 2011).

While this approach is useful in further testing the COVIS model of categorization, it will, by its very nature, result in an incomplete model of PD symptoms. For instance, COVIS does not include a model of the ventral striatum (e.g., nucleus accumbens). This region is thought to play a major role in reversal learning and feedback processing (e.g., Cools, Altamirano, & D’Esposito, 2006) and, as a result, the present model could not account for reversal learning data without adding additional assumptions (which is not in line with the goal of this work). For this reason, we avoid simulating tasks that include major feedback manipulations in this article.

Likewise, a model of the ventral striatum is required in order to adequately model the effect of dopaminergic medication on cognitive deficits. First, according to the overdose hypothesis (Cools, 2006; Price et al., 2009), the dosage of dopaminergic medication required to improve motor symptoms (i.e., restoring DA levels in the dorsal striatum) may result in too much DA in the ventral striatum (because DA innervation to the dorsal striatum is more affected than DA innervation to the ventral striatum in PD). The overdose hypothesis explains some of PD patients’ cognitive deficits as a result of the dopaminergic medication ‘overdosing’ the ventral striatum (not included in the current version of COVIS). Second, some dopaminergic medications predominantly target the ventral striatum (e.g., D3 agonists; Foll, Gallo, Strat, Lu, & Gorwood, 2009) whereas others similarly increase DA levels in the whole striatum (e.g., levodopa; Cools, 2006). While D3 agonists, such as pramipexole, also bind to other receptors in the D2-class within the dorsal striatum, their effect on the ventral striatum can hardly be ignored. As such, the effect of dopaminergic medication cannot be modeled using the current computational implementation of COVIS.

It should be noted that even if a ventral striatum was added to COVIS, some major challenges would still have to be overcome before it would be possible to account for the published effects of medication on the cognitive performance of PD patients. In addition to the issues discussed above, building such a model is complicated by the fact that a number of different medications are used to treat PD, and many patients are prescribed a cocktail that includes two or more of these. The specific effects of some of these drugs is still unclear (e.g., anticholinergics), and to complicate things even further, a number of drugs have complex interactions that are poorly understood. In addition, there are important individual differences regarding the locus and extent of basal ganglia dysfunction in PD, and most studies do not currently control for these differences. For all these reasons, the simulations described in this article focus on PD patients “ON” medication.

The remainder of this article is organized as follows. First, we describe a computational implementation of COVIS with a focus on the role played by DA in the model. Second, we propose a model of how the DA deficits found in PD patients can be modeled within the COVIS framework. Third, we reproduce some of the PD deficits identified above by simulating five well-known tasks (i.e., rule-based categorization, information-integration categorization, the WPT, the WCST, and the simplified WCST). Fourth, we conclude with a general discussion of alternative models of PD and discuss the implications of computational PD modeling for future research.

4. A computational implementation of COVIS

The computational version of COVIS includes three separate components—namely a model of the hypothesis-testing system, a model of the procedural-learning system, and an algorithm that monitors the output of these two systems and selects a response on each trial. Because the goal of this paper is to provide a COVIS-based account of PD, we present a verbal description of the COVIS subsystems, and only describe the equations directly related to DA levels. Note that none of the processes described in this implementation were added to account for PD cognitive deficits; they were all present in the initial formulation of COVIS published more than a decade ago (Ashby et al., 1998). The reader interested in a more recent full formal description of COVIS is referred to Hélie et al. (2012).

4.1. The hypothesis-testing system

The hypothesis-testing system in COVIS selects and tests explicit rules that determine category membership. The simplest rule is one-dimensional. More complex rules are constructed from one-dimensional rules via Boolean algebra (e.g., to produce logical conjunctions, disjunctions, etc.). The neural structures that have been implicated in this process include the prefrontal cortex, anterior cingulate, head of the caudate nucleus, and hippocampus (Ashby et al., 1998; Ashby, Ell, Valentin, & Casale, 2005; Hélie, Roeder, & Ashby, 2010). The computational implementation of the COVIS hypothesis-testing system is a hybrid neural network that includes both symbolic and connectionist components. The model’s hybrid character arises from its combination of explicit rule selection and switching and its incremental salience-learning component.

On each trial, the hypothesis-testing system computes a response using the following algorithm. Suppose rule R_i is used on trial n. A response for stimulus $\underset{¯}{\chi }$ is selected by computing a discriminant value $h_E(\underset{¯}{\chi })$ on the relevant rule dimension(s) and using the following decision rule:

$$\begin{array}{l}\text{Respond}A\text{on trial}n\text{if}{h}_E(\underset{¯}{x})\le \epsilon ;\\ \text{Respond}B\text{if}{h}_E(\underset{¯}{x})>\epsilon \end{array}$$ (1)

where e is a normally distributed random variable with mean 0 and variance ${\sigma }_E^2$, and $h_E(\underset{¯}{\chi })$ is the signed distance between the stimulus and the category boundary (positive on one side and negative on the other). The variance ${\sigma }_E^2$ increases with trial-by-trial variability in the participant’s perception of the stimulus and memory of the decision criterion (i.e., perceptual and criterial noise). As argued in Ashby and Casale (2003), ${\sigma }_E^2$ is inversely related to cortical DA levels (for similar arguments, see also Durstewitz & Seamans, 2008; Frank, 2005; Moustafa & Gluck, 2010).

After a response is given and feedback has been received, rule selection proceeds as follows: if the response on trial n was correct, then rule R_i is used again on trial n + 1 with probability 1; if the response on trial n was incorrect, then the probability of selecting each rule in the set R for use on trial n + 1 is a function of each rule’s current weight. The weight associated with each rule is determined by the participant’s lifetime history with that rule, the reward history associated with that rule during the current categorization training session, the tendency of the participant to perseverate, and the tendency of the participant to select unusual or creative rules. Together, these factors determine rule salience.

On correct trials, the salience of the current rule is increased, but no further action is required (because the current rule is used again with probability 1). On incorrect trials, the first step is to decrease the salience of the current rule. Next, the salience of each rule is used to produce a weight Y, according to the following procedure. For the rule R_i that was active on trial n,

$$Y_i(n)=Z_i(n)+\gamma$$ (2)

where Z_i(n) is the salience of rule R_i on trial n, and the constant γ is a measure of the tendency of the participant to perseverate on the active rule, even though feedback indicates that this rule is incorrect. If γ is small, then switching will be easy, whereas switching is difficult if γ is large. COVIS assumes that switching of executive attention is mediated within the head of the caudate nucleus, and that the parameter γ is inversely related to basal ganglia DA levels (for a detailed argument, see Ashby et al., 1998).

After the active rule weight has been computed using Eq. (2), a rule is chosen at random from the list of all possible rules (including the active rule¹). Call this rule R_j. The weight for this rule is

$$Y_j(n)=Z_j(n)+\mathbf{X}$$ (3)

where Z_j(n) is the salience of rule R_j on trial n, and X is a random variable that has a Poisson distribution with mean λ. Larger values of λ increase the probability that rule R_j will be selected for the next trial, so λ is called the selection parameter. COVIS assumes that a cortical network including the anterior cingulate and the prefrontal cortex mediates selection, and that λ increases with cortical DA levels (for a detailed argument, see Ashby et al., 1998). The weight of every other rule is set to its previous salience value (i.e., Y_k(n)=Z_k(n)).

Finally, rule R_k (for all k) is selected for use on trial n+1 with probability

$$P_{n+1}(R_k)=\frac{Y_k^a(n)}{{{\displaystyle {\sum }_{s=1}^{m}Y}}_s^a(n)}$$ (4)

where a is a parameter that determines how much variability there is in the selection process. When a<1, the selection is noisy and the probability differences are diminished (making the selection probabilities more uniform). When a<1, the selection becomes more deterministic—the rule with the greatest weight is almost always chosen. Hence, a can be interpreted as a gain parameter and, as such, COVIS assumes that a increases with cortical DA (Ashby & Casale, 2003; for similar arguments, see Durstewitz & Seamans, 2008; Frank, 2005; Moustafa & Gluck, 2010).

This model has a number of attractive properties. First, the more salient the rule, the higher the probability that it will be selected, even after an incorrect trial. Second, after the first trial, feedback is used to adjust the selection probabilities up or down, depending on the success of the rule. Third, the model has separate selection and switching parameters, reflecting the COVIS assumption that these are separate operations. The random variable X models the selection operation. The greater the mean of X (i.e., λ) in Eq. (3), the greater the probability that the selected rule (R_j) will become active. In contrast, the parameter γ from Eq. (2) models switching, because when γ is large, it is unlikely that the system will switch away from to the currently active rule R_i. It is important to note, however, that with both parameters (i.e., λ and γ), optimal performance occurs at intermediate numerical values. For example, note that if λ is too large, some extremely low salience rules will be selected, and if γ is too low then a single incorrect response could cause a participant to switch away from an otherwise successful rule.

4.2. The procedural system

The current implementation of the procedural system is called the Striatal Pattern Classifier (SPC: Ashby, Ennis, & Spiering, 2007; Ashby & Waldron, 1999). The SPC learns to assign responses to regions of perceptual space. In such models, a decision bound could be defined as the set of all points that separate regions assigned to different responses, but it is important to note that in the SPC, the decision bound has no psychological meaning. As the name suggests, the SPC assumes that the key site of learning is at cortical-striatal synapses within the striatum.

The SPC architecture is shown in Fig. 1 for an application to a categorization task with two contrasting categories. This is a straightforward three-layer feedforward network with up to 10,000 units in the input layer and two units each in the hidden and output layers. The only modifiable synapses are between the input and hidden layers. The more biologically detailed version of this model proposed in Ashby et al. (2007) included lateral inhibition between striatal units and between cortical units. In the absence of such inhibition, the top motor output layer in Fig. 1 represents a conceptual placeholder for the striatum’s projection to premotor areas.

Fig. 1.

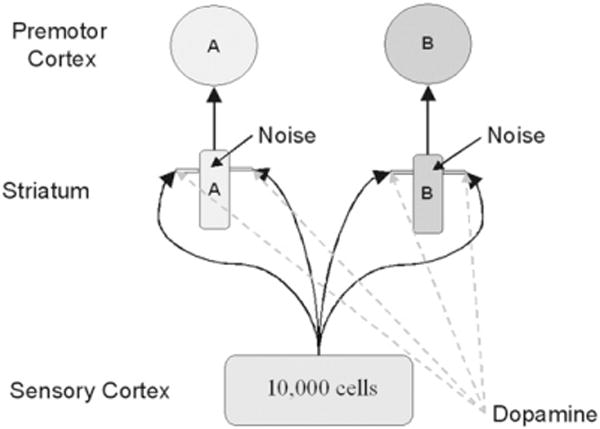
A schematic illustrating the architecture of the COVIS procedural system.

The key structure in the model is the striatum (i.e., the putamen), which is a major input structure within the basal ganglia (Waldschmidt & Ashby, 2011). In humans and other primates, all of extra-striate cortex projects directly to the striatum and these projections are characterized by massive convergence, with the dendritic field of each medium spiny cell innervated by the axons of approximately 380,000 cortical pyramidal neurons (Kincaid, Zheng, & Wilson, 1998). COVIS assumes that, through a procedural-learning process, each striatal unit associates an abstract motor program with a large group of sensory cortical cells (i.e., all that project strongly to it). The dendrites of striatal medium spiny neurons are covered in protuberances called spines. These play a critical role in the model because glutamate projections from sensory cortex and DA projections from the SNpc converge (i.e., synapse) on the dendritic spines of the medium spiny neurons. COVIS assumes that these synapses are a critical site of procedural learning.

Sensory cortex is modeled as an ordered array of up to 10,000 units, each representing a different radial-basis function. The model assumes that each unit responds maximally when its preferred stimulus is presented, and that its response decreases as a Gaussian function of the distance in stimulus space between the stimulus preferred by that unit and the presented stimulus. COVIS assumes that the activation of each striatal unit (within the middle or hidden layer) is determined by the weighted sum of activations in all sensory cortical cells that project to it. The striatal neuron with maximum activation produces more premotor activation and hence determines the model’s response.

The connection weights between sensory cortex and the striatum are modified using a reinforcement learning algorithm (Haykin, 2008). The three factors thought to be necessary to strengthen cortical-striatal synapses are (1) strong pre-synaptic activation, (2) strong post-synaptic activation, and (3) DA levels above baseline (e.g., see Arbuthnott, Ingham, & Wickens, 2000). According to this model, the synapse between a neuron in sensory association cortex and a medium spiny neuron in the striatum is strengthened if the cortical neuron responds strongly to the presented stimulus, the striatal neuron is also strongly activated (i.e., factors 1 and 2 are present) and the participant is rewarded for responding correctly (factor 3). On the other hand, the strength of the synapse will weaken if the participant responds incorrectly (factor 3 is missing), or if the synapse is driven by a cell in sensory cortex that does not produce much activation in the striatum (i.e., factor 2 is missing).

The learning conditions described above require a model that specifies how much DA is released on every trial in response to the feedback signal. The key empirical results are (Schultz, Dayan, & Montague, 1997): (1) midbrain DA cells fire spontaneously (i.e., tonically), (2) DA release increases above baseline following unexpected reward, and the more unexpected the reward the greater the release, and (3) DA release decreases below baseline following unexpected absence of reward, and the more unexpected the absence, the greater the decrease. One common interpretation of these results is that over a wide range, DA firing is proportional to the reward prediction error (RPE), which is defined as the value of the obtained reward minus the value of the expected reward. In all the simulations included herein, we defined the value of obtained reward as +1 if the feedback was positive and −1 if the feedback was negative. Following, Ashby and Crossley (2011), expected reward was computed using the single-operator learning model (Bush & Mosteller, 1955).

Bayer and Glimcher (2005) reported activity in midbrain DA cells as a function of RPE. A simple model that nicely matches their results is

$$D(n)=\{\begin{array}{ll}{D}_{\mathit{max}}\hfill & \text{if}\mathrm{RPE}>\frac{D_{\mathit{max}}-D_{\mathit{base}}}{D_{\mathit{slope}}}\hfill \\ D_{\mathit{slope}}\times \mathrm{RPE}+D_{\mathit{base}}\hfill & \text{if}-\frac{D_{\mathit{base}}}{D_{\mathit{slope}}}\le \mathrm{RPE}\le \frac{D_{max}-D_{\mathit{base}}}{D_{\mathit{slope}}}\hfill \\ 0\hfill & \text{if}\mathrm{RPE}<-\frac{D_{\mathit{base}}}{D_{\mathit{slope}}}\hfill \end{array}$$ (5)

where D_max, D_slope, and D_base are constants. This model is illustrated in Fig. 2. Note that the baseline DA level is D_base (i.e., when the RPE=0) and that DA levels increase linearly with the RPE between 0 and D_max. In general, higher values of D_max allow for a larger increase in DA following unexpected reward, higher values of D_base allow for a larger decrease of DA following the unexpected absence of reward, and higher values of D_slope increase the effect of RPE on DA release. Thus, increasing the value of any of these constants should improve learning in the procedural system (up to a point).

Fig. 2.

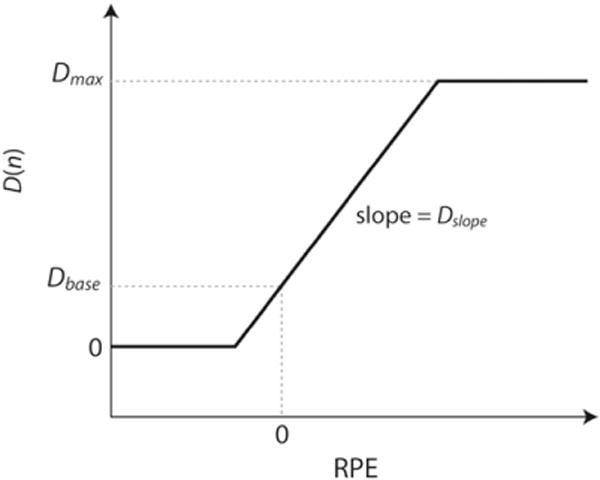
Model used to relate the amount of dopamine (DA) released as a function of the reward prediction error (RPE).

4.3. Resolving the competition between the hypothesis-testing and procedural systems

Because on any trial the model can make only one response, the final task is to decide which of the two systems will control the observable response. In COVIS, this competition is resolved by combining two factors: the confidence each system has in the accuracy of its response, and how much each system can be trusted. In the case of the hypothesis-testing system, confidence equals the absolute value of the discriminant function (as in Eq. (1)). When the value is small, the stimulus is close to the hypothesis-testing system’s decision bound, so the model has no confidence in its ability to predict the correct response. When the discriminant value is large, the stimulus is far from the bound and confidence is high. In the procedural system, confidence is defined as the difference between the maximum striatal activation and the mean striatal activation. Here the rationale is similar to that of the hypothesis-testing system: when the stimulus is equally activating all of the striatal units, the procedural system has no confidence in its ability to predict the correct response, but when one unit is activated much more strongly than the others, the evidence strongly favors one response over the others.

The amount of trust that is placed in each system is a function of an initial bias toward the hypothesis-testing system, and the previous success history of each system. In typical applications, COVIS assumes that the initial trust in the hypothesis-testing system is much higher than in the procedural system, partly because initially there is no procedural learning to use. As the experiment progresses, feedback is used to adjust the two system weights up or down depending on the success of the relevant component system. Finally, confidence and trust are combined multiplicatively and the system with the highest resulting value determines the overall response.

5. Modeling Parkinson’s disease with COVIS

DA cells in the SNpc and the ventral tegmental area (VTA) die in PD, which results in decreased DA levels in the prefrontal cortex and the striatum. In COVIS, DA has a differential effect on the hypothesis-testing and procedural systems. In the hypothesis-testing system, COVIS assumes that selection and switching both depend on brain DA levels. In particular, selection should improve as levels of DA rise in frontal cortex (up to some optimal level), and switching should improve if levels of DA rise in the head of the caudate nucleus (Ashby et al., 1998). Thus, the selection parameter λ should increase with DA levels in frontal cortex, and the switching parameter γ is assumed to decrease with increased DA levels in the caudate nucleus. In addition, it has been argued that DA in the prefrontal cortex increases signal-to-noise ratio (Ashby & Casale, 2003; Frank, 2005; Durstewitz & Seamans, 2008; Moustafa & Gluck, 2010). Hence, a in Eq. (4) should increase with DA levels (similar to λ), and ${\sigma }_E^2$ should decrease with more DA (similar to γ).

In the procedural system, DA plays a crucial role in learning: it provides the reward signal required for reinforcement learning. A decreased DA baseline or range can affect the ability of the procedural system to learn stimulus-response associations. Hence, decreasing DA levels in the striatum should decrease the values assigned to D_base, D_slope, and D_max. Note that the hypothesis-testing and procedural systems mostly rely on different nuclei of the striatum (head of the caudate nucleus and putamen, respectively). As such, striatal DA levels have a different effect on the hypothesis-testing and procedural systems that happen on different time scales: rule switching in the head of the caudate nucleus happens within a trial (for hypothesis-testing) whereas procedural learning in the putamen requires several trials of practice (for dopamine mediated reinforcement learning). This is consistent with lesion studies, which show that lesions to the caudate nucleus generally produce more ‘cognitive’ deficits while lesions to the putamen generally produce more ‘motor’ deficits (Bhatia & Marsden, 1994).

Many factors are known to affect brain DA levels including age, mood, genetic predisposition, drug-taking history, and neuropsychological patient status (Ashby, Isen, & Turken, 1999). For example, brain DA levels are known to decrease by approximately 7% per decade of life due to normal aging, and PD patients are thought to have lost at least 70% of their birth DA levels (Gotham et al., 1988; Price et al., 2009). Also, many studies, including those simulated in this article, do not systematically control the time since the last dose of dopaminergic medication for PD patients “ON” medication. For this reason, it is reasonable to assume that, on average, PD patients “ON” medication have less DA than age-dmatched controls, who in turn have less DA than young control participants. Moreover, the more severe the PD symptoms (as measured by, e.g., the Hoehn and Yahr scale), the lower the DA level. Hence, in COVIS, we model an ordinal relationship where DA(young adults; YC)≥DA(old adults; OC)≥DA(PD)≥DA(severe PD; SPD) (where more DA results in lower γ and ${\sigma }_E^2$, and higher λ, a, D_base, D_slope, and D_max).

Note that D_base and D_max, which represent the range of DA, were calculated to reflect the proportion of DA cells remaining as a function of age and diagnosis (Hélie et al., 2012). For instance, in the studies considered here, young adults (YC) are usually undergraduate students in their late teens or early 20s. Hence, they should have approximately 86% of their birth DA levels (assuming they lost 7% of birth DA per decade of life). Typically, these participants have been modeled with D_base=0.20 and D_base=1.00 (e.g., Ashby & Crossley, 2011; Ashby et al., 2011). Likewise, age-matched controls (OC) are typically about 70 years old and should thus have 50% of their birth DA level. As such, their D_base was set to 0.15 and their D_max was set to 0.60. Finally, on average, PD patients are predicted to have 30% of their birth DA remaining. Hence, their D_base was set to 0.10 and their D_max was set to 0.35.² Thus, only five DA-related parameters were varied in the simulations (i.e., γ, ${\sigma }_E^2$, λ, a, and D_slope).

6. Simulations

In this section, we test the COVIS model of PD patient deficits against data from five well-known tasks, namely rule-based categorization, information-integration categorization, the WPT, the WCST, and the simplified WCST. The values given to the DA-related parameters in all simulations are shown in Table 1. Only these parameters were varied to simulate the different participant populations. In addition to these DA-related parameters, COVIS also requires setting some task-related parameters (which did not vary when modeling the different participant populations). These are shown in Table 2. Note that a single set of parameters was used to simulate the WCST (Beatty et al., 1989) and the simplified WCST (Gotham et al., 1988). However, different parameter values were used in the two perceptual categorization tasks because Ashby et al. (2003) used discrete-value stimuli (modeled using binary values [0, 1]) whereas Filoteo et al. (2005) used continuous-value stimuli (modeled continuously [0,…,100]). The WPT also used a different set of parameter values because of rule complexity.

Table 1.

Dopamine-related parameters in COVIS.

Parameters	Ashby et al. (2003)			Filoteo et al. (2005)		Knowlton et al. (1996)			WCST/simplified WCST
	YC	OC	PD	OC	PD	OC	PD	SPD	OC	PD
${\sigma }_E^2$	0.50	–	–	13.00	14.00	0.30	0.85	5.00	0.25	0.35
γ	10.00	10.00	55.00	5.00	10.00	20.00	55.00	55	2.45	5.03
λ	1.50	1.50	0.15	10.00	5.00	15.00	0.15	0.05	10.47	8.66
a	1.00	–	–	1.00	0.10	10.00	1.00	1.00	1.39	0.39
Dslope	0.80	0.25	0.20	0.70	0.10	00.80	0.15	0.05	0.80	0.15

Note: YC=young control; OC=old control; PD=Parkinson’s disease patients; SPD=severe PD patients. WCST/simplified WCST shows a common set of parameter values for Gotham et al. (1988) and Beatty et al. (1989).

Table 2.

Task-related parameters in COVIS.

Parameters	Ashby et al. (2003)	Filoteo et al. (2005)	Knowlton et al. (1996)	WCST/simplified WCST
ΔC	0.0025	0.0400	0.0380	0.4553
ΔE	0.0200	0.0100	0.0180	0.6827
θNMDA	0.0020	0.1500	0.0020	0.0570
θAMPA	0.0010	0.0010	0.0010	0.0001
ΔOC	0.0100	0.0050	0.0100	0.0500
ΔOE	0.0400	0.0400	0.0200	0.0010

Note: The role of these parameters is described in Ashby et al. (2011) and Hélie et al. (2012). WCST/simplified WCST shows a common set of parameter values for Gotham et al. (1988) and Beatty et al. (1989).

It is important to note that the unit of measurement of almost all parameters in the model is arbitrary (as in most computational models). For example, it is straightforward to rescale parameters in a way that reduces the DA parameters by any arbitrary factor (e.g., in much the same way that a z-transform rescales the variance to a value of 1). This would reduce the change in the value of the DA parameters across applications by the same factor. Thus, the ordering of DA parameters within an application is important, but differences in the magnitude of these values across applications are not.

None of the parameter estimates were optimized; reasonable values were assigned using a rough grid search. Specifically, we used the model to fit the control data in each task. Then, a number of DA-related parameters were varied to fit the experimental group(s). Overall, 24 parameter values were used to account for 33 data points, leaving a total of 9 degrees of freedom to test the model validity. The robustness of the model to exact parameter values was also tested. Specifically, we performed a sensitivity analysis for each DA parameter in each simulation (Hélie et al., 2012). For each parameter listed in Table 1, we successively changed the parameter estimate from the value used to fit the data by 710%. After each change, we simulated the behavior of the model in the same conditions used to simulate the task. Next, after each new simulation (and for each condition), we computed the mean root squared error (MRSE) between the simulated learning curves (used to fit the data) and the learning curve produced by the new version of the model. The MRSE has the advantage of being on the same scale as the simulated dependent variable. To identify the most relevant parameters in each simulation, we also ran the sensitivity analysis with a change of 795% of the parameter values. The results will be discussed in each simulation’s ‘Results and discussion’ subsection.

6.1. Perceptual categorization

The first series of simulations address two key results regarding PD deficits in perceptual categorization. First, PD patients exhibit impaired performance in rule-based categorization compared to normal age-matched controls, but perform as well as age-matched controls in (linear) information-integration categorization (Ashby et al., 2003). Second, follow-up studies replicate the finding that PD patients are not impaired in linear information-integration categorization, but instead observe PD deficits relative to age-matched controls in non-linear information-integration categorization (Filoteo et al., 2005).

6.1.1. Rule-based vs. linear information-integration categorization

Ashby and his colleagues (2003) compared the performances of 16 PD patients in rule-based and information-integration categorization tasks with the performance of 15 aged-matched (OC) controls and 109 undergraduate students (YC). The stimuli varied on the four binary-valued dimensions of background color, symbol color, symbol shape, and number of symbols. The resulting 16 possible stimuli were separated into two categories of equal sizes with a different stimulus assignment in each of the categorization conditions. In the rule-based condition, a stimulus dimension was selected randomly, and stimuli were assigned to different categories based on their value on the selected dimension. In the information-integration condition, one dimension was randomly selected to be irrelevant. Next, one level from each of the remaining dimensions was randomly assigned a numerical value of 1 and the other level was assigned a value of 0. One category included all 8 stimuli for which the sum of the assigned numerical values across the three relevant dimensions was greater than 1.5. The 8 stimuli for which this sum was less than 1.5 were assigned to the contrasting category. Note that the rule-based categories were easily verbalizable (e.g., blue vs. yellow background) whereas no such simple verbalizable rule was available for the information-integration categories.

If a participant was able to correctly classify 10 consecutive stimuli before reaching the 200-trial limit, s/he was classified as a ‘learner’. Otherwise, the participant was classified as a ‘non-learner’. The dependent measure was the proportion of ‘non-learners’ in each participant group in each categorization condition. The results show that, compared with older controls, PD patients were impaired in learning the rule-based categories but not the information-integration categories (see Fig. 3, left panel).

Fig. 3.

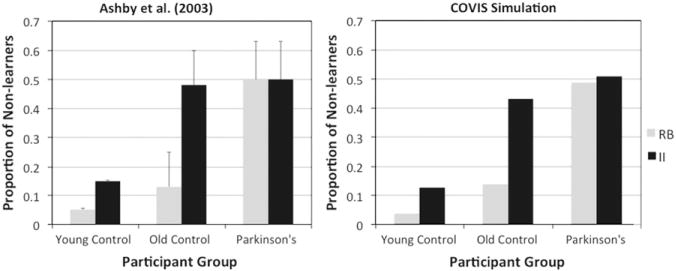
Human and simulation data for the categorization task of Ashby et al. (2003). RB=rule-based; II=information-integration.

6.1.2. Linear vs. non-linear information-integration categorization

Filoteo et al. (2005) further tested the performance of 20 PD patients and 20 aged-matched controls in information-integration categorization. The stimuli were lines that continuously varied in length and orientation and were separated into two different categories using either a linear or a non-linear (quadratic) bound. As in Ashby et al. (2003), no simple verbalizable rule could yield optimal performance in either condition.

Each participant was trained for 600 trials on each category structure (in separate sessions). The dependent measure was the proportion of correct classifications in each block of 100 trials. The results showed that, compared with aged-matched controls, PD patients are impaired in non-linear information-integration but not in linear information-integration category learning (Fig. 4, left column).

Fig. 4.

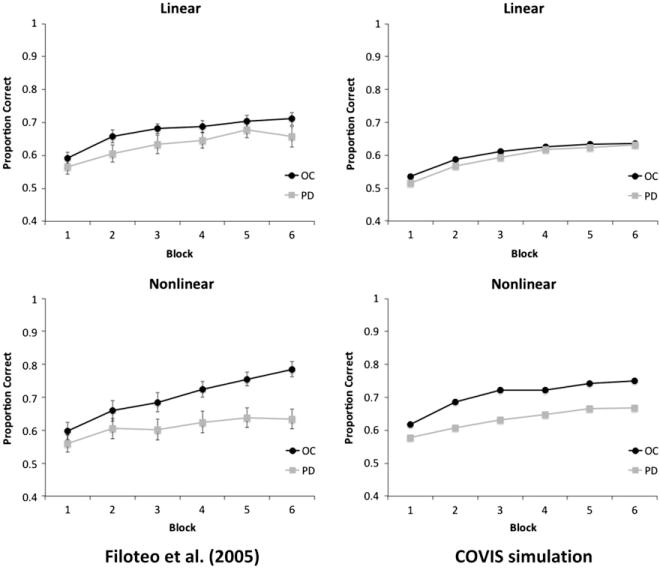
Human and simulation data for the information-integration categorization task of Filoteo et al. (2005).

6.1.3. Simulation

For the Ashby et al. (2003) data, 500 simulations were run for each participant group in each categorization condition with the COVIS model described in Section 4. The procedural system received an object-based representation of the stimuli while the hypothesis-testing system received a feature-based representation. The stimuli were all perceptually distinct, so for the procedural system each stimulus was represented as a 16-dimensional vector. For stimulus i, this vector had a value of 1 in row i and 0 in all other rows. In contrast, the stimuli presented to the hypothesis-testing system were 4-dimensional binary vectors. The entry in row i was set to 1 if feature i had one value and 0 if it had the other. Each system received a separate copy of the feedback. The simulation results are shown in Fig. 3 (right panel).

For the Filoteo et al. (2005) data, 200 simulations were run for each participant group in each condition. The simulation details were the same as for Ashby et al. (2003) except for the following. In this simulation, the stimulus-values were continuous (perceptually confusable) and generated using the same distributions described in Filoteo et al.³ Hence, the procedural system input was modeled using two radial-basis functions (as described in Hélie et al., 2012) centered at (line length, line orientation) coordinates (30, 50) and (70, 50) (respectively) with a common variance of 125 and no covariance. The stimulus presented to the hypothesis-testing system was the (continuous) stimulus value on the dimension specified by the selected rule (either the line length or the line orientation coordinate). The criterion used for each rule was the mean value of the stimulus set on the dimension of the relevant rule. The simulation results are shown in the right column of Fig. 4.

6.1.4. Results and discussion

Figs. 3 and 4 show that COVIS did a good job of simulating the performance of the younger controls, older controls, and PD patients for both rule-based and information-integration category structures. As in the human data, the PD version of the model was impaired compared to the simulated age-matched controls in rule-based and non-linear information-integration categorization, but not in linear information-integration categorization. The performance of the simulated younger controls was better than the older controls and PD patients in rule-based and informationintegration categorization tasks.

The parameter sensitivity analysis shows that changing the DA-related parameters by 7±10% produced a RMSE of only 2.5% for the Ashby et al. (2003) simulation and 1% for the Filoteo et al. (2005) simulation. Further, analyses on individual parameters suggest that the same parameters account for the most variance in both simulations, namely ${\sigma }_E^2$ and D_slope. These parameters correspond to noise on the decision criterion of the hypothesis-testing system and the effect of feedback on DA released in the procedural system (respectively). Overall, these good fits were achieved by varying only DA-related parameters, each of which was theoretically justified and had a clear conceptual meaning.

6.2. Probabilistic classification

This simulation addresses PD deficits in learning probabilistic classification tasks. The main results are that, compared to aged-matched controls, PD patients achieve a lower accuracy score and that the more severe the disease, the larger the deficit.

6.2.1. The Weather Prediction Task (WPT)

The WPT is one of the most popular probabilistic classification tasks (Gluck, Shohamy & Myers, 2002). In the WPT, participants are asked to predict whether the outcome of each trial will be “rain” or “sun” as a function of four possible cue cards. Each cue card is independently associated with the outcome “sun” with probability 0.75, 0.57, 0.43, and 0.25 (respectively). On each trial, the participants see one, two, or three cue cards and make predictions about the trial outcome (i.e., “rain” or “sun”). Accuracy feedback is then provided. The dependent variable is response accuracy.

Knowlton et al. (1996) tested 20 non-demented PD patients and 15 aged-matched controls in the WPT. The results for the first 50 trials are shown in Fig. 5 (left panel). As can be seen, aged-matched controls quickly learned the task and achieved an accuracy of about 70%. In contrast, the PD patients failed to learn the task and only achieved about 55% correct. In addition to these results, Knowlton and her colleagues investigated patients with the most severe PD symptoms (Hoehn and Yahr scale ≥3; n=10). These patients performed at chance throughout the task (SPD in the figure).

Fig. 5.

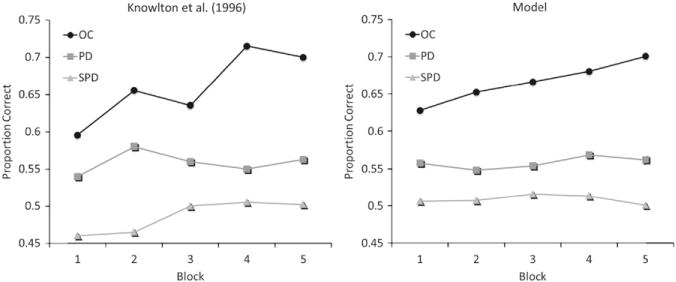
Human and simulation data for the WPT of Knowlton et al. (1996). Each block contains 10 trials. SPD=severe PD.

6.2.2. Simulation

Three hundred simulations were run for each participant group with the COVIS model described in Section 4. The procedural system received an object-based representation of the stimuli while the hypothesis-testing system received a feature-based representation. The stimuli were all perceptually distinct, so for the procedural system each stimulus was represented as a 14-dimensional vector. For stimulus i, this vector had a value of 1 in row i and 0 in all other rows. In contrast, the stimuli presented to the hypothesis-testing system were 4-dimensional binary vectors. The entry in row i was set to 1 if cue card i was present and 0 otherwise. On each trial, the hypothesis-testing system selected a rule that focused its attention on a subset of the cue cards. All possible combinations of cue cards were represented as rules (for a total of 14 rules). In line with COVIS’ assumptions about rule complexity (Ashby et al., 1998), the initial saliency of all the rules focusing on only 1 cue card was set to 0.2 (4 rules), the initial saliency of all rules focusing on 2 cue cards simultaneously was set to 0.025 (6 rules), and the saliency of all rules focusing on 3 cue cards simultaneously was set to 0.0125 (4 rules). On each trial, the hypothesis-testing system chose the most likely outcome by considering only the cue cards specified by the selected rule (i.e., using the conditional probability of the outcomes, as computed in Knowlton, Squire, & Gluck, 1994). As in the previous simulations, each system received a separate copy of the feedback. The simulation results are shown in Fig. 5 (right panel).

6.2.3. Results and discussion

Fig. 5 shows that COVIS did a good job of simulating the performance of the aged-matched controls, PD patients, and severe PD patients in the WPT. As in the human data, the PD version of the model was impaired compared to the simulated age-matched controls, and severe PD performed at chance throughout the experiment. The parameter sensitivity analysis shows that changing the DA-related parameters by ±10% produced a RMSE of only 1%. Analyses on individual parameters suggest that ${\sigma }_E^2$ and λ accounted for the most variance in the simulation. These parameters correspond to noise on the decision criterion of the hypothesis-testing system and rule selection. These are both parameters of the explicit system, which suggests that the model is largely treating the WPT as an explicit task. Empirical evidence suggests humans also solve the WPT using explicit strategies (Gluck et al., 2002), even though the WPT was originally designed as an implicit task. Again, the good fits of COVIS were achieved by varying only DA-related parameters, each of which was theoretically justified and had a clear conceptual meaning.

6.3. Rule maintenance and perseveration

The next two simulations address PD deficits in rule maintenance and perseveration. The key results are that compared to age-matched controls, PD patients display a larger number of set-loss errors and perseverative responses (Beatty et al., 1989). In addition, their more frequent perseverative errors lead to difficulties in achieving a learning criterion (Beatty et al., 1989; Gotham et al., 1988). On the other hand, PD patients do not produce more non-perseverative errors than age-matched controls (Beatty et al., 1989; Gotham et al., 1988). Note that only one set of parameter values was used to simulate the WCST and the simplified WCST.

6.3.1. The Wisconsin Card Sorting Test (WCST)

The WCST is a popular clinical measure of conceptual ability and hypothesis testing. In short, the experimenter has a deck of cards with a variety of figures displayed on each card. The cards differ in the shape, number, and color of the figures. Each one of these dimensions has four possible values (for a total of 43=64 different cards). On each trial, the participant is shown a card and asked to categorize it using a rule on one of the dimensions. After 10 consecutive correct categorizations, the dimension relevant for categorization is changed (without telling the participants). The experiment ends after the participant has reached the categorization criterion six times or the deck of cards has been cycled twice (i.e., 128 stimuli).

Beatty et al. (1989) tested 25 PD patients and 13 age-matched control participants. The dependent measures were the number of sorts completed, the number of perseverative errors (error trials where the previously correct rule is used), the number of non-perseverative errors (error trials that are not perseverative errors), the number of set loss errors (when five or more consecutive correct responses are followed by an error), and the number of perseverative responses. All these measures were calculated as described in Heaton et al. (1993). The results are shown in Fig. 6 (left panel). As evidenced in the figure, the PD patients completed fewer sorts and committed more set-loss errors than age-matched controls. There was also a tendency toward more perseverative errors and responses for the PD patients, but these differences did not reach statistical significance.

Fig. 6.

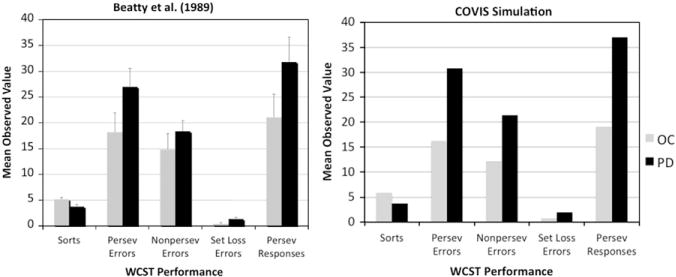
Human and simulation data for the WCST from Beatty et al. (1989).

6.3.2. The simplified WCST

Gotham et al. (1988) compared the performance of 16 PD patients with 16 age-matched controls on a battery of psychological tests. One of the tasks used was the simplified WCST (Nelson, 1976), which is similar to the ‘regular’ WCST but uses only a subset of 24 cards. The criterion for rule switching is 6 consecutive correct responses, and the participants are explicitly told when the rule changes. The experiment ends after 6 sorts have been completed or the entire set of cards has been seen twice (i.e., 48 stimuli). The dependent measures are the number of sorts completed, the number of perseverative errors, and the number of non-perseverative errors. The results showed that PD patients achieved fewer sorts and made more perseverative errors than age-matched controls (see Fig. 7, left panel).

Fig. 7.

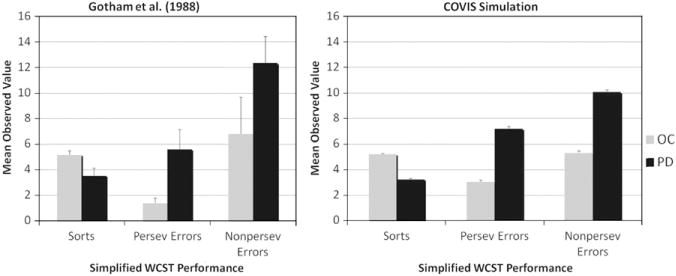
Human and simulation data for the simplified WCST from Gotham et al. (1988).

6.3.3. Simulations

For the WCST, 200 simulations were run for each participant group with the COVIS model described in Section 4. As in the previous simulations, the procedural system received an object-based representation of the stimuli whereas the hypothesis-testing system received a feature-based representation. The stimuli presented to the procedural system were 64-dimensional binary vectors, with a 1 in row i for stimulus i and a 0 in all other rows. The stimuli presented to the hypothesis-testing system were 12-dimensional binary vectors. Rows 1–4 encoded the value of feature 1, with a separate row for each level of the feature. Row i had a value of 1 if feature 1 had value i (i=1,…,4) and the other 3 rows had a value of 0. Rows 5–8 encoded the value of feature 2 using this same coding scheme, and rows 9–12 encoded the value of feature 3. Each system received a separate copy of the feedback. The simulation results are shown in Fig. 6 (right panel).

For the simplified WCST, 200 simulations were run for each participant-group with the COVIS model described in Section 4. The simulation methodology and parameter values were the same as in the WCST. Note that, while the whole deck of WCST cards was represented, only 24 stimuli were used (corresponding to the subset of cards used in the simplified WCST). Because the participants were told when the rule changed, the rule saliences were reset after each sort (i.e., whenever 6 consecutive correct responses occurred). The simulation results are shown in Fig. 7 (right panel).

6.3.4. Results and discussion

For both the WCST and the simplified WCST, the COVIS simulations provide a good match to the PD patient and control data on all five dependent measures using a single set of parameter values. As in the human data, the PD version of the model had a larger number of set-loss errors and perseverative responses, as well as a larger number of perseverative errors, which led to difficulties in achieving the learning criterion (compared with simulated aged-matched controls). Because the sensitivity analysis yields results that are scaled with the simulated dependent variable, a separate analysis was run for each measure. The results are shown in Table 3. As can be seen, the model performance is highly robust on all dependent variables. In addition, the same parameters accounted for the most variance in both tasks, even though the measures are calculated differently in the two versions of the WCST. This further supports the stability of the model. Analyses on individual parameters suggest that, similar to the WPT, ${\sigma }_E^2$ and λ accounted for the most variance overall in both simulations. These parameters correspond to noise on the decision criterion of the hypothesis-testing system and rule selection. It is critical to note that this good fit was achieved by using only DA-related parameter values, without any ad hoc hypotheses or arbitrary parameter changes. This suggests that COVIS is an adequate model of the behavioral deficits observed in PD patient in tasks that evaluate hypothesis-testing performance.

Table 3.

Sensitivity analyses in the WCST and simplified WCST.

Dependent variables	MRSE	Highest variance
WCST
Sorts	0.2	${\sigma }_E^2$, λ
Perseverative errors	2.1	λ,a
Non-perseverative errors	0.8	${\sigma }_E^2$, λ
Set-loss errors	0.1	${\sigma }_E^2$, λ
Perseverative responses	2.4	λ, γ
Simplified WCST
Sorts	0.2	${\sigma }_E^2$, λ
Perseverative errors	0.5	λ,a
Non-perseverative errors	0.5	${\sigma }_E^2$, λ

Note: Each DA-related parameter was varied by ±10% to calculate the MRSE for each dependent measure. Highest variance parameters were identified by varying each DA-related parameter by ±95%.

7. General discussion

This article proposed a formal account of a variety of cognitive deficits commonly displayed by PD patients that is based on the COVIS model of categorization (Ashby et al., 1998). Without adding any extra parameters or assumptions to the COVIS model of categorization (Ashby et al., 1998, 2011), the model achieved a good fit of the data in perceptual categorization, probabilistic classification, the WCST, and the simplified WCST. These tasks were used to highlight PD deficits in rule-based categorization (Ashby et al., 2003), non-linear information-integration categorization (Filoteo et al., 2005), the WPT (Knowlton et al., 1996), and rule maintenance and switching (Beatty et al., 1989; Gotham et al., 1988). It is noteworthy that differential performance between younger adults, older adults, PD patients, and severe PD patients was achieved simply by changing the amount of DA available in the model. This suggests that COVIS may be an adequate model, not only of the tasks and phenomena presented herein but also more generally of the role of DA in these tasks and phenomena. Changing the amount of DA available to the model reproduces behavioral patterns of different human participant populations who correspondingly have different numbers of DA producing cells in the SNpc and the VTA as a consequence of aging or of disease. Sensitivity analyses further suggested that the most important parameters to simulate PD cognitive deficits are ${\sigma }_E^2$, λ, and D_slope. These parameters correspond to noise on the decision criterion of the hypothesis-testing system, the tendency to select new rules, and the sensitivity (i.e., gain) of the DA system to changes in RPE.

7.1. Other computational models of PD

Very few computational models of PD have been proposed. Monchi, Taylor, and Dagher (2000) used a working memory model to simulate PD deficits. Their model include three basal ganglia-thalamocortical loops: two with the prefrontal cortex (one for spatial information and the other for object information), and one through the anterior cingulate gyrus (for strategy selection). PD is simulated in the Monchi et al. model by reducing the connection strengths between the cortex and the caudate, and between the caudate and the internal segment of the globus pallidus (with reduction of the latter strengths being twice as large as the former). The model was used to simulate a delayed response task, a delayed match-to-sample task, and the WCST. In all of these tasks, PD deficits are accounted for by improper encoding of the stimuli in working memory.

An alternative model was proposed by Frank (2005) to explain cognitive deficits in PD. This model includes basal ganglia-thalamocortical loops with an emphasis on a more biologically detailed model of the basal ganglia that included both the direct and indirect pathways. In Frank’s model, PD is simulated by lesioning SNpc DA cells to reduce the range of DA in the basal ganglia. This reduction in DA’s dynamic range reduces activation in the direct pathway (through D1 receptors) and amplifies activation in the indirect pathway (through D2 receptors). In addition, DA plays the role of the reward signal in synaptic plasticity. This model has been used to simulate a probabilistic classification task and a probabilistic reversal learning task. In both tasks, PD deficits were explained by abnormal direct/indirect pathway interactions.

More recently, Moustafa and Gluck (2010, 2011) proposed a new computational model of PD deficits. Their model is a three-layer feed-forward connectionist network where the input activates the prefrontal cortex, which in turn activates the striatum to produce a response. Similar to Frank (2005), the role of tonic DA is to modulate neural activation and the role of phasic DA is to facilitate synaptic plasticity. However, the Moustafa and Gluck model allows for differential effects of DA in the prefrontal cortex and striatum by varying the slope of the transfer functions and learning rates separately for neurons in these two regions. The model has been used to simulate instrumental conditioning, probabilistic classification, and probabilistic reversal learning tasks. PD impairments in these tasks were explained by noisy activation and learning.

7.2. Theoretical implications

One of the main contributions of the COVIS simulation of PD deficits is that it brings into focus the different roles of DA in different brain regions. In the Monchi et al. (2000) and Frank (2005) models, the simulated role of DA was restricted to producing abnormal dynamics in the basal ganglia. Moustafa and Gluck (2010, 2011) were the first to independently simulate the role of DA in the prefrontal cortex and striatum, but the role of DA was the same in both regions: activation gain and learning rate. In COVIS, DA can be independently manipulated in the prefrontal cortex and basal ganglia, but it also has a different role in each region. In the prefrontal cortex, DA facilitates rule selection and increases signal gain (reducing noise). In the basal ganglia, DA facilitates rule switching (in the hypothesis-testing system) and synaptic plasticity (in the procedural system). This dual role is made possible by the COVIS subsystems each relying mostly on different basal ganglia structures (the caudate nucleus and putamen for the hypothesis-testing and procedural systems, respectively). These differential roles of DA in the prefrontal cortex and the basal ganglia not only allowed for the explanation of a wide range of tasks and phenomena, but also allowed for a more fine-grained account of the deficits in each task. For instance, COVIS predicts that in rule-based categorization tasks the primary behavioral effect of DA deficits in the basal ganglia should be to impair rule switching. In information-integration tasks, however, DA reductions in the basal ganglia should mostly affect synaptic plasticity. Previous modeling of PD performance did not allow for this level of specificity.

Another interesting contribution of the present modeling is that it predicts that PD patients may often not be using the same response strategies as control participants. According to COVIS, humans are initially biased toward using their hypothesis-testing system, and switch away to the procedural system only if the hypothesis-testing system does not attain satisfactory performance. However, the hypothesis-testing system is heavily impaired in PD patients, so one prediction is that PD patients will often switch away from explicit strategies even in tasks where a rule-based strategy is optimal. This phenomenon was observed in many of our simulations, where most responses from the simulated controls were produced by the hypothesis-testing system, but about half of the responses made by the simulated PD patients were produced by the procedural system. This is a qualitative prediction that should be tested empirically in the future.

7.3. Limitations and future work

While COVIS is successful at accounting for many behavioral phenomena observed in PD, it cannot yet account for at least three PD-related abnormalities. First, differential behavioral effects of dopaminergic medication have been observed in PD (e.g., Cools et al., 2006; Frank, Seeberger, & O’reilly, 2004; Gotham et al., 1988), and two of the PD models reviewed in Section 7.1 have proposed a computational account of PD medication effects (Frank, 2005; Moustafa & Gluck, 2010). We have not made a similar attempt with COVIS for two different reasons. First, Cools et al. (2006) report that different PD medications may have different behavioral effects. For instance, post hoc analyses suggest that only patients treated with pramipexole (a D3 agonist) were impaired in reversal learning. Bódi et al. (2009) found a similar but non-specific impairment in reversal learning for PD patients using a variety of D3 agonists. Most papers where PD patients are tested ON medication report which medications appear in their samples, but do not delineate the ON medication patients according to drug. Hence, it would be difficult to simulate the exact behavioral effects of different PD-related drugs within a particular sample of patients, especially considering that the affinity of D3 agonists is highest for D3 receptors (affinity for D2 and D4 receptors is lower), and that these receptors are mostly expressed in the ventral striatum (Foll et al., 2009). As mentioned earlier, this structure is not part of the COVIS model of categorization (Ashby et al., 1998, 2011). The issue of medication is further complicated by the observation that dopaminergic treatments have different effects depending on the progression of the disease and this interaction very well could be drug dependent. Second, a recent review of behavioral PD deficits posits that, because of the gradient of DA loss within the striatum, dopaminergic medication required to restore normal-like functionality can effectively “overdose” other regions of the striatum that are less afflicted (Price et al., 2009). The computational version of COVIS implemented herein has specific DA parameters for different regions in the striatum and prefrontal cortex, but the gradient effects of dopaminergic medication may exceed the spatial resolution of the COVIS DA parameters. However, it should be noted that the effect of the values given to the DA parameters on COVIS’ performance follows a U-shape function. As shown in this article, values that are too low result in poor performance (e.g., difficulty in rule switching and selection), but values that are too high will also yield poor performance (e.g., propensity to switch to or select a new rule on every trial). This could allow for a natural explanation for some PD deficits that are worsened by dopaminergic (over) medication (for a review, see Price et al., 2009). Thus, while the variable effects of medication on PD performance were not addressed by the current computational model, future work with COVIS could be devoted to adding the ventral striatum to the model and attempting to investigate the differential effects of PD medications when these become more reliably reported in published articles.

Second, attention has recently been devoted to understanding patterns of abnormal neuronal synchrony in a variety of disorders (Uhlhass & Singer, 2006). It is hypothesized that aberrant discharge rates evident in PD are related to motor deficits (e.g., tremor) and these observations are being considered to update models of normal/abnormal BG function accordingly (Hammond, Bergman, & Brown, 2007; Wichmann & DeLong, 1996). Although a COVIS implementation with spiking neurons has been proposed (e.g., Ashby et al., 2007; Ashby & Crossley, 2011), firing synchrony has not been explored. Such explorations could allow for a deeper investigation of abnormal neural synchrony exhibited in PD and its corresponding cognitive effects.

Finally, it has been hypothesized that schizophrenia may also be characterized by DA imbalances (e.g., Cohen & Servan-Schreiber, 1992). As such, the Monchi et al. (2000) and Moustafa and Gluck (2011) models of PD have also tried to address schizophrenia. In Monchi et al., schizophrenia is explained by problems with selecting working memory items due to a decrement of mesolimbic DA. In Mustafa and Gluck, schizophrenia is caused by damage to the hippocampus, which is used to pre-process the stimuli. COVIS does not include a detailed model of the hippocampus. As such, we would adopt an approach similar to other models that manipulate DA (e.g., Cohen & Servan-Schreiber, 1992; Monchi et al., 2000) to reflect the particular imbalance of DA in schizophrenic patients. For example, DA in the head of the caudate nucleus and the prefrontal cortex could be manipulated. Future work should allow us to determine whether these manipulations to DA parameters in COVIS could produce cognitive deficits similar to those observed in schizophrenia.