Skip to main content
PMC home page
Heredity logoLink to Heredity
. 2014 Apr 30;113(5):416–423. doi: 10.1038/hdy.2014.42

Segregation of a QTL cluster for home-cage activity using a new mapping method based on regression analysis of congenic mouse strains

S Kato 1,2, A Ishii 3,4, A Nishi 3,4, S Kuriki 1,2, T Koide 2,3,4,*
PMCID: PMC4220717  PMID: 24781804

Abstract

Recent genetic studies have shown that genetic loci with significant effects in whole-genome quantitative trait loci (QTL) analyses were lost or weakened in congenic strains. Characterisation of the genetic basis of this attenuated QTL effect is important to our understanding of the genetic mechanisms of complex traits. We previously found that a consomic strain, B6-Chr6CMSM, which carries chromosome 6 of a wild-derived strain MSM/Ms on the genetic background of C57BL/6J, exhibited lower home-cage activity than C57BL/6J. In the present study, we conducted a composite interval QTL analysis using the F2 mice derived from a cross between C57BL/6J and B6-Chr6CMSM. We found one QTL peak that spans 17.6 Mbp of chromosome 6. A subconsomic strain that covers the entire QTL region also showed lower home-cage activity at the same level as the consomic strain. We developed 15 congenic strains, each of which carries a shorter MSM/Ms-derived chromosomal segment from the subconsomic strain. Given that the results of home-cage activity tests on the congenic strains cannot be explained by a simple single-gene model, we applied regression analysis to segregate the multiple genetic loci. The results revealed three loci (loci 1–3) that have the effect of reducing home-cage activity and one locus (locus 4) that increases activity. We also found that the combination of loci 3 and 4 cancels out the effects of the congenic strains, which indicates the existence of a genetic mechanism related to the loss of QTLs.

Introduction

Quantitative trait loci (QTL) analysis of complex traits is one of the most important approaches available for understanding the genetic basis of common phenotypes. The identification of genes for QTLs mapped by genetic studies is making a substantial contribution to better understanding the mechanisms that underlie complex traits. However, many recent attempts to identify genes for QTLs have failed (Flint et al., 2005). Numerous studies showed that genetic loci that had significant effects in whole-genome QTL analyses turned out to be lost or weakened once congenic strains were established to show the effect of the QTL (Saad et al., 2008; Rapp and Joe, 2012; Stewart et al., 2012). Even after more than 2000 QTLs had been mapped, only 20 were identified as causative genes; this means that <1% of these applications of the QTL approach were successful (Flint et al., 2005). These problems have also been referred to as ‘missing heritability' although possible causes, such as a large number of genes with small effects, epistatic interaction among genes, gene–environment interactions and parent-of-origin effects have been proposed, the actual mechanism(s) responsible for the high level of failure remains unclear (Manolio et al., 2009; Eichler et al., 2010; Makowsky et al., 2011). It is therefore essential to address the genetic basis behind the loss of the QTL effect during the fine mapping of candidate genes.

Home-cage activity is a general activity that is influenced by the rhythm of an animal's spontaneous activity. We previously showed that the pattern of home-cage activity of a wild-derived mouse strain MSM/Ms (MSM) differs from that of C57BL/6J (B6), a commonly used laboratory strain (Nishi et al., 2010). To identify QTLs associated with the total amount of home-cage activity (total activity), we used consomic strains established from crosses between B6 and MSM. Given that each consomic strain has a particular chromosome derived from MSM, whereas the rest are from B6, the detection of a phenotypic difference from B6 enables efficient mapping of QTLs at the chromosomal level. As a result, we found that five consomic strains, for chromosomes 2T (telomere side), 3, 4, 13 and 14, showed significantly higher total activity than B6. In contrast, another five consomic strains, for chromosomes 6C (centromere side), 7T, 9, 11 and 15, were less active than B6. These results indicated that multigenic factors located on different chromosomes regulate the total activity. In order to address the genetic mechanism related to the difference in total activity, we chose chromosome 6, which was associated with one of the lowest scores of total activity, for further genetic analysis in the present study. By applying a two-step approach, namely QTL analysis followed by congenic analysis, we conducted high-resolution genetic analysis of loci related to the total activity. In the studies of a series of congenic strains, we found that the genetic effects behind the different level of total activity were lost in some of the congenic strains, which made it difficult to explain the genetic mechanism with a simple single-gene model. In order to characterise genetic factors related to the total activity in more detail, we used a regression model to reveal the existence of multigenic factors and to map them to different chromosomal regions. In this paper, we report the complex characteristics of the genetic basis for this quantitative trait.

Materials and methods

Animals

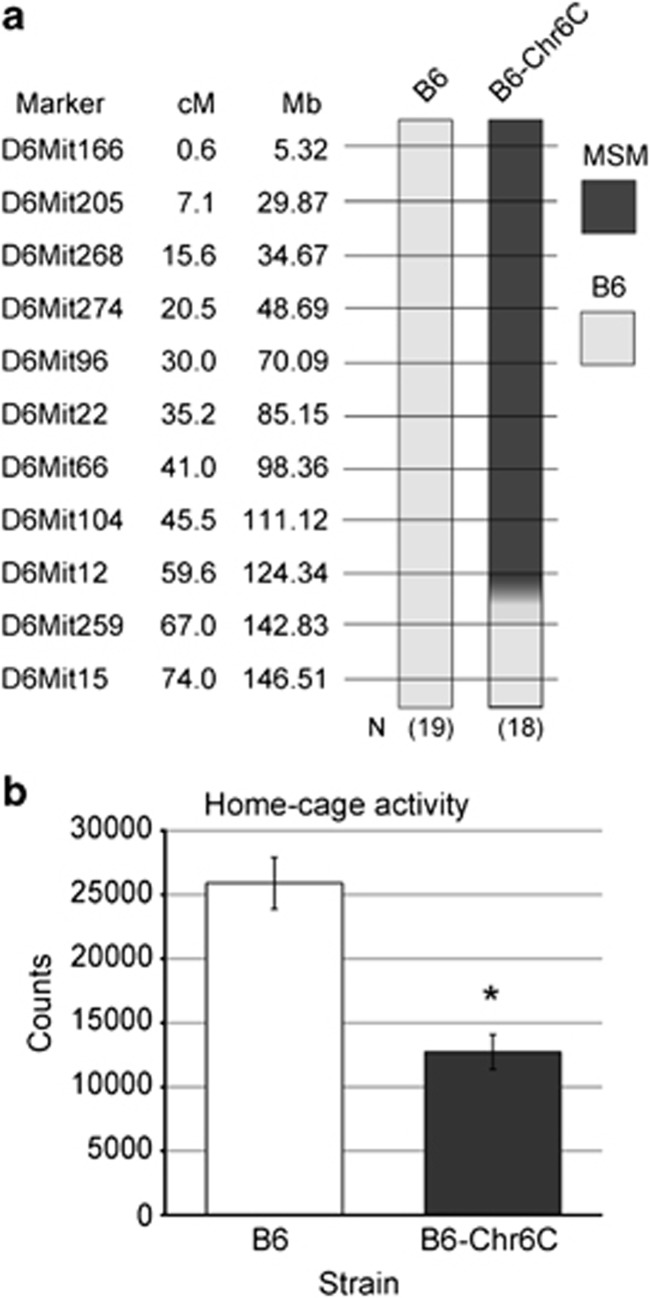
Mice of strains MSM/Ms (MSM), C57BL/6JJcl (B6), a consomic strain B6-Chr6CMSM (B6-Chr6C), a subconsomic strain B6.MSM-(D6Nig92.7-D6Mit374)/Ms (C7) and congenic strains were used in this study. MSM was established as an inbred strain from Japanese wild mice and maintained at the National Institute of Genetics, Mishima, Japan (Moriwaki et al., 2009). B6 mice were purchased from CLEA Japan, Inc. (Tokyo, Japan), and bred at the animal facility of the National Institute of Genetics. The consomic strain that carried a large segment of chromosome 6 was established by replacing chromosome 6 of B6 with that of MSM (Takada et al., 2008). As a consomic strain carrying the entirety of chromosome 6 was not successfully established, the proximal side of chromosome 6, a 59.6-cM chromosomal segment from the centromere to D6Mit12 derived from MSM, was used for a consomic strain, B6-Chr6C (Figure 1a). The subconsomic strain and all the congenic strains have the same genetic background as B6, except for a replaced chromosomal region of chromosome 6, derived from B6-Chr6C.

Figure 1.

Figure 1

Open in a new tab

Comparison of total activities between B6 and B6-Chr6C. (a) Genotypes of microsatellite markers on chromosome 6 are illustrated. The number of individuals used for each strain and the genotype of microsatellite markers on chromosome 6 are shown. The light grey box and filled box indicate the genotype of microsatellite markers of B6 and MSM, respectively. The gradated boxes indicate boundaries between two microsatellite markers in which recombination occurred. (b) Comparison of total activities between parental strains. Data are shown as the mean±s.e. An asterisk (*) indicates a significant difference according to the t-test at P<0.05.

All the animals were housed with their same-sex littermates until the time of home-cage activity testing in a plastic cage (measuring 19.5 × 29.5 × 15 cm) containing wood chips as the bedding material. The mice were maintained at a constant temperature of 23±2 °C and a 12-h light/dark cycle with lights on at 0600 h, with food and water available ad libitum. The home-cage activity of all male mice was tested at 9–12 weeks of age unless otherwise stated. The mice were maintained in accordance with National Institute of Genetics guidelines, and all procedures were carried out with the approval of our institutional animal care and use committee.

Behavioural testing

Male mice of B6, consomic, subconsomic and congenic strains were used for home-cage activity tests. Before these tests were conducted, the mice were kept individually for 1 day in their home cage to habituate them to isolation. The home-cage test involved the recording of individual spontaneous home-cage activity from 0600 h on the day after transfer for 3 days. An infrared sensor, Activity Sensor (Ohara Co. Ltd., Tokyo, Japan), was used to evaluate the spontaneous activity of each mouse in their home cage. This sensor was located above the lid (made of stainless steel wire) of each cage. The motion of the mouse inside the home cage was recorded as counts detected by the sensor. Using this apparatus, many kinds of activity, such as horizontal locomotion, climbing the cage lid, hanging on the lid and jumping could be detected efficiently as combined activity counts. However, grooming or foraging behaviour that occurred in one place was detected less efficiently. The test apparatus used can record activity in the home cage for 24 mice simultaneously. In each test session, we analysed up to 24 mice from several different strains at once. Four sets of analyses, namely QTL analysis, subconsomic analysis and two congenic analyses, constitute this study. These four sets of studies were conducted in different periods, with careful calibration of the test apparatus between all analyses. Mice of the control strain B6 were also separated into several groups and subjected to the same analyses as mice of the other strains. The activity in each 1-min bin was measured by accumulated counts if the animal was active in any area of the cage. The activity counts for 72 h were summed and the scores of total activity corresponded to the average counts for a 1-day period over the 3 days.

QTL analysis and genotyping of microsatellite polymorphisms

For QTL mapping analysis, F1 mice made by crossing B6 and B6-Chr6C were intercrossed to make F2 progeny. We performed the home-cage activity tests using 174 males of F2 progeny at 8–16 weeks of age. Genomic DNA was isolated from the tails using an automatic nucleic acid isolation system, the NA-2000 (Kurabo, Osaka, Japan). The genotype of each mouse at each of the microsatellite markers was determined. Information on the physical position and sequence information of each microsatellite marker and polymorphism between B6 and MSM for each microsatellite marker was obtained from the National Center for Biotechnology Information (http://www.ncbi.nlm.nih.gov/) and Mouse Microsatellite Database of Japan (http://www.shigen.nig.ac.jp/mouse/polymorphism/top/top.jsp). In addition to the available microsatellite markers, we designed new microsatellite markers as shown in Supplementary Table S1. Genomic DNA prepared from tails of F2 mice was amplified by PCR with primer sets of the above microsatellite markers. The amplified DNA fragments were separated on agarose gels by electrophoresis and stained with ethidium bromide.

To analyse the locations of the QTLs associated with total activity, composite interval mapping based on a multiple QTL model (Zeng, 1993, 1994) was conducted using Windows QTL Cartographer Version 2.5 software (Basten et al., 1997). For composite interval mapping, we used model 6 as a standard and a forward regression method with five control markers and 0.5-cM increments with a window size of 10 cM. The likelihood-ratio statistic is −2ln(L0/L1), where L0 and L1 are the maximum likelihoods under the null hypothesis H0 (there is no QTL at the test site) and alternative hypothesis H1 (there is a QTL at the test site), respectively. Next, the logarithm of odds scores were calculated as 4.605 likelihood ratio=1 logarithm of odds. To determine the 5% level of significance, 3000 replications of a permutation test were carried out.

Establishment of subconsomic and congenic strains

To analyse the effect of QTLs, we established a subconsomic strain from B6-Chr6C by introducing shorter chromosomal segments of MSM into B6. From the results of QTL analyses, we selected mice that carried an MSM-derived segment including the QTL region between D6Mit132 and D6Mit55, and made a subconsomic strain, B6.MSM-(D6Nig92.7-D6Mit374)/Ms (C7). Further recombinants were made by backcrossing C7 to B6. We made mice that have breakpoints by meiotic recombination at several different points between D6Nig92.7 and D6Mit374. The selected mice were crossed with B6 to obtain pairs of progeny that carried the recombined chromosomal segment. By intercrossing the mice, we obtained homozygotes of the MSM genotype for the loci of interest, and established a series of congenic strains. The genotypes of each microsatellite marker for the subconsomic and the congenic strains are shown in Figure 3.

Statistical analysis

Statistical analyses of behavioural test data were performed using the StatView software package (SAS Institute Inc., Cary, NC, USA). Analyses of variance were carried out for between- and within-group factors. One-way between-group analysis of variance (strain) was performed to compare the total activity of the B6 and congenic strains. In the case of significant F values, a t-test with Bonferroni correction (α=0.05/16 (number of test strains)) was conducted to compare B6 with each congenic strain.

Regression analysis using data of congenic strains

In order to identify chromosomal regions that influence the total activity and measure the levels of their influence, we used regression models. In these models, it is assumed that the response Yi (i=1,…,17) is the mean of the total activities of mice in congenic strain i, where i corresponds to one of the 17 different congenic strains established in the study. The regressors or dependent variables xi1,…, xi30, xi1 : xi2, xi2 : xi3,…, xi29 : xi30 consist of 30 genotypes of the microsatellite markers of the congenic strain i and 29 interactions between the adjacent markers. Here, the value of xij (j=1,…,30) is defined as 0 if the genotype of the jth marker of the mouse with the congenic strain i is the same as that of the mouse B6 and 1 if the genotype of the jth marker is the same as that of the mouse B6-Chr6C. The interaction between adjacent markers xij : xij+1 is defined as the product of the values of the two adjacent markers, namely, xij : xij+1=xij xij+1.

One technical problem arising from the regression analysis of these data was the so-called n<<p problem, which arises when the number of microsatellite markers exceeds the number of congenic strains. It is known that for such data there are no unique solutions to the estimating equation of the least squares linear regression model. To solve this problem, our regression analysis was conducted using the following two steps.

First, we performed model selection via the least absolute shrinkage and selection operator (lasso) (Tibshirani, 1996). In our setting, the lasso was applied as follows:

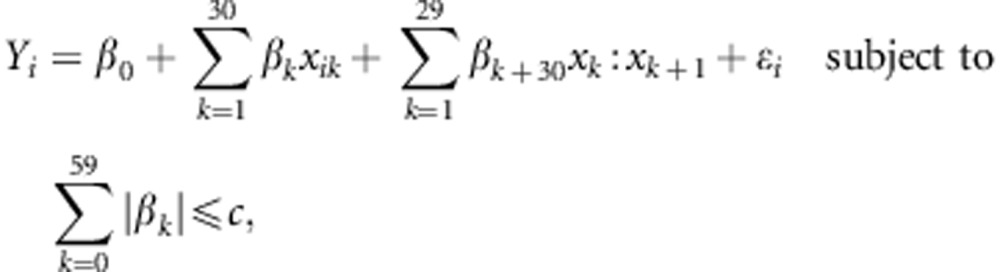graphic file with name hdy201442e1.jpg

where i=1,…,17, β0,…,β59 are the regression coefficients, ɛi's are independent and identically distributed as Gaussian distributions with mean 0 and variance σ2 and c is the tuning parameter. Before the lasso was fitted, the dimension of the regressors was reduced by identifying those variables that took the same values as the adjacent variables for all the strains as one variable. Next, the regression coefficients of the lasso were estimated by minimising the penalised least squares:

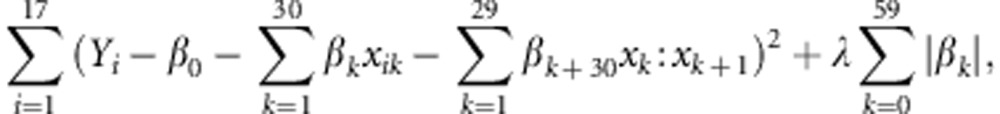graphic file with name hdy201442e2.jpg

for a given value of the tuning parameter, where λ is uniquely determined by the tuning parameter c. The tuning parameter λ was estimated using five-fold cross-validation. We generated 100 cross-validation samples and obtained the ultimate estimate of λ as the minimum mode of 100 estimates of λ.

Second, the least squares linear regression model was applied to the data whose number of dimensions of the regressors had become less than the number of congenic strains. In order to carry out further variable selection, we adopted all subsets based on the Akaike Information Criterion (Konishi and Kitagawa, 2008). The subset that minimised the Akaike Information Criterion value was selected as the model ultimately used for fitting. Using the theory of regression analysis (see, for example, McCullagh and Nelder, 1989), estimates of the regression coefficients and the corresponding P-values were obtained. The residual analysis was conducted to assess the goodness-of-fit of the model.

Regression analysis was performed by using the statistical software R. To estimate the regression coefficients and tuning parameter of the lasso, the R package ‘glmnet' was used. The generic function ‘lm' was used for estimation of the least squares linear regression model.

Results

Comparison of home-cage activity between the consomic strain and B6

In a previous study, we conducted a systematic analysis of home-cage activity using a series of consomic strains and found that five consomic strains including B6-Chr6C, a consomic strain for chromosome 6, showed significantly lower activity than B6 (Nishi et al., 2010). In the present study, we conducted home-cage activity tests and confirmed that B6-Chr6C showed lower total activity than B6 (P<0.0001) (Figure 1b).

QTL mapping of a locus for total activity on Chr 6

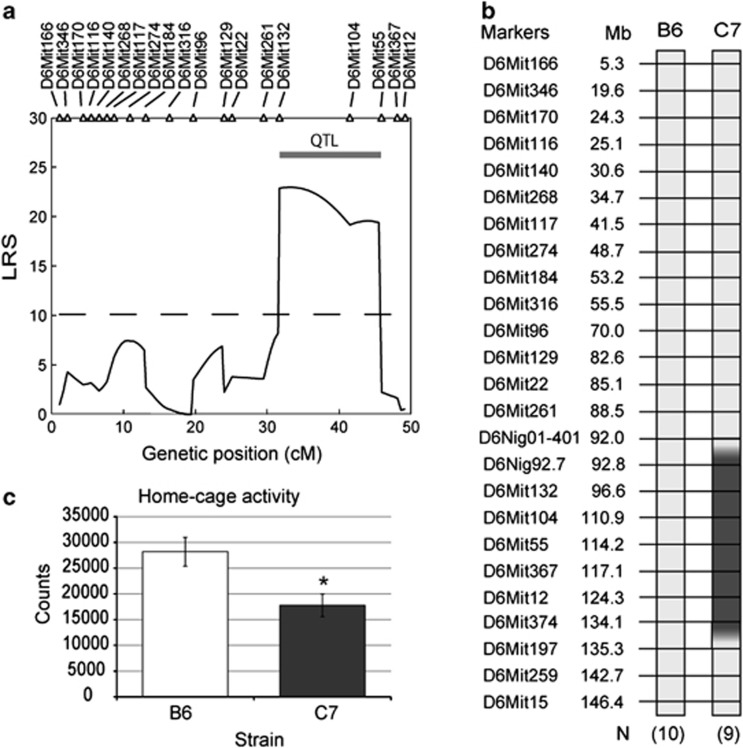
To map genetic loci related to total activity, we conducted QTL analysis with males of the F2 population made from an intercross of F1 mice between B6-Chr6C and B6. Figure 2a shows the results of the analysis by composite interval mapping for the total activity in which one QTL was mapped between D6Mit132 and D6Mit55 (17.6 Mbp). The logarithm of odds score of the QTL was 5.0.

Figure 2.

Figure 2

Open in a new tab

Mapping QTL for total activity. (a) Results of the QTL analysis for the total activity using composite interval mapping (CIM). The solid line indicates a QTL peak. The 5% significant threshold levels of the logarithm of odds (LODs) scores calculated by 3000 replications of a permutation test are indicated by a dotted line. Locations of QTLs are presented as bars that indicate a one LOD drop of confidence intervals from the LOD peaks. (b) Genotypes of microsatellite markers on chromosome 6 are illustrated. The light grey box and the filled box indicate the genotype of microsatellite markers of B6 and MSM, respectively. The gradated boxes indicate boundaries between two microsatellite markers in which recombination occurred. (c) Comparison of total activity using B6 and a subconsomic strain, C7. Data are shown as the mean±s.e. An asterisk (*) indicates a significant difference according to the t-test at P<0.05.

In order to show the effect of the QTL on the total activity directly, we made a subconsomic strain, C7, which has a chromosome fragment that spans the region between D6Nig92.7 and D6Mit374 (41.3 Mbp), including the QTL region between D6Mit132 and D6Mit55, derived from MSM (Figure 2b). The observation that C7 exhibited significantly lower total activity than B6 (P=0.0104) suggested the existence of a gene for the reduced total activity in the region between D6Mit132 and D6Mit55 (Figure 2c). Total activities of B6 and C7 were analysed with larger numbers of animals in the next experiment.

Analysis of total activity using congenic strains

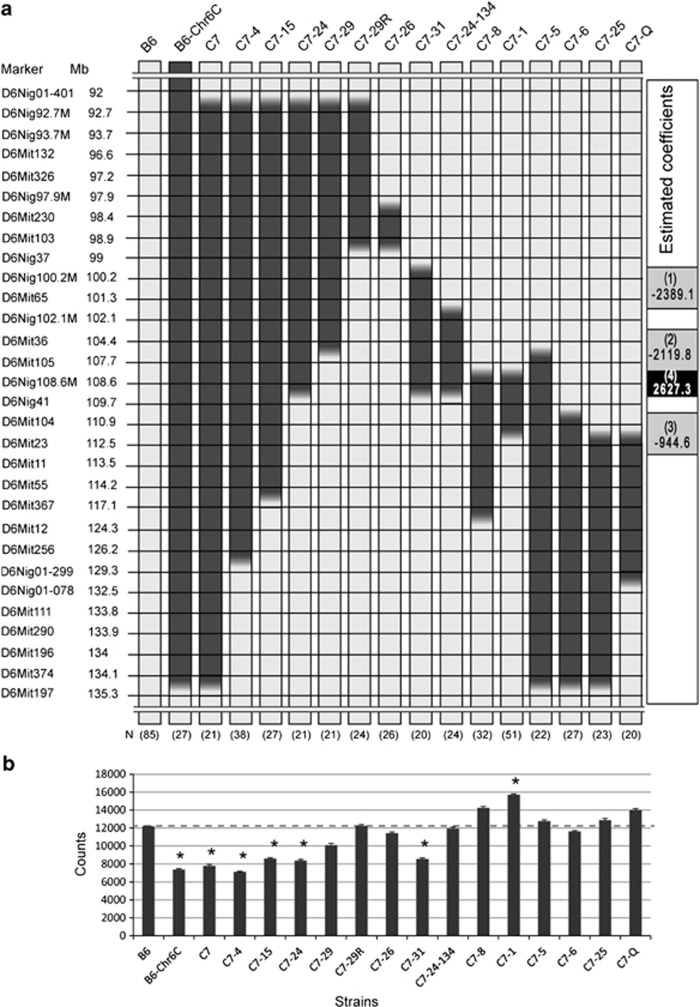
In order to map QTL related to total activity as precisely as possible, we made a series of congenic strains from C7 (Figure 3). Total activities of the congenic strains are shown in Figure 3. One-way analysis of variance showed a significant main effect of strain on the total home-cage activity (F(16,492)=15.97, P<0.0001). The results showed that four strains, C7-4, C7-15, C7-24 and C7-31, as well as parental strains B6-Chr6C and C7, exhibited significantly lower activities than B6 (P<0.05). In contrast, one strain, C7-1, showed significantly higher activity than B6, but another strain with a chromosome fragment that covered the entire region of C7-1, such as C7-5, did not. In the results, effects of both decreasing and increasing the total activity, as well as the offsetting of these effects, were observed among these congenic strains. These findings indicate that multiple loci exist in the chromosomal segment of the C7 region on chromosome 6. Given that the relationship of total activity and the regions specifically associated with each of the congenic strains varied among strains, it was difficult to map the QTL precisely using the currently available methods.

Figure 3.

Figure 3

Open in a new tab

Fine mapping of genetic loci for total activity using congenic strains. (a) The congenic strains used for the behavioural test, numbers of mice used for each strain and genotype of microsatellite markers on chromosome 6 are indicated. The light grey box and the filled box indicate the genotype of microsatellite markers of B6 and MSM, respectively. The gradated boxes indicate boundaries between two microsatellite markers in which recombination occurred. (b) Comparison of total activity in a series of congenic strains as well as parental strains. Data are shown as the mean±s.e. The dashed line indicates score of the control strain, B6. Asterisks (*) indicate significant differences in total activities compared with B6 according to the t-test with Bonferroni's correction at P<0.05. Significant estimates of the coefficients identified by the regression analysis and their positions are shown on the right side of the panel. The effects of the coefficients of decreasing the total activity are shown in grey cells and the effect of the coefficient of increasing the total activity is shown in the black cell with white text. The numbers shown in parentheses indicate the locus name.

Fine genetic mapping for total activity using regression analysis

To identify chromosomal regions that influence the total activity more precisely, we used a regression model in which the decreasing and increasing effects in the chromosome regions partitioned into different strains are summed over the entire strain. As a method of pretreatment, the variables in the regressors that took the same values as the adjacent variables for all the strains were grouped together as one variable. For example, the values of D6Nig92.7M, D6Nig93.7M and their interaction are the same for each strain; hence, we grouped these three variables together. This process is necessary because it is known in statistical theory that the estimates of those variables are not unique unless the variables are identified. This enabled us to reduce the dimensions of the regressors from 59 to 18 (Supplementary Table S2). We then applied the lasso for model selection and the least squares linear regression model for further variable selection and fitting.

First we discuss the results of the lasso. Table 1 displays non-zero estimates of the regression coefficients corresponding to the estimated tuning parameter λ=43.17. The lasso reduced the number of variables from 18 to 9. The average of the 100 mean cross-validated errors is 2 454 988. The average of 100 estimates of standard error based on the cross-validation samples is 749 904. The total amount of variance is 332 457.

Table 1. Estimates of the regression coefficients.

Regressors (Markers) Estimated coefficient
 P-value Locus
  Lasso All subsets    
Intercept (β0) 13176.1 12823.8 1.28 × 10−12  
D6Mit230—D6Mit103 −1035.4 −659.3 0.183  
D6Nig100.2M—D6Mit65 −2397.8 −2389.1 0.00312 Locus 1
D6Nig65 : D6Nig102.1M        
D6Mit36 : D6Mit105 −1573.9 −2119.8 0.0370 Locus 2
D6Mit105 −744.5 −1738.2 0.0669  
D6Mit105 : D6Nig108.6M        
D6Nig108.6M 700.1 2627.3 0.00123 Locus 4
D6Nig108.6M : D6Nig41 771.5 * *  
D6Nig41        
D6Nig41 : D6Mit104        
D6Mit104 : D6Mit23 −803.5 −944.6 0.0378 Locus 3
D6Mit367 : D6Mit12 −76.9 * *  
D6Mit12—D6Mit256        
D6Nig01-299 : D6Nig01-078 −253.6 * *  
D6Nig01-078—D6Mit374        
Open in a new tab

The ‘intercept' of the regressors denotes the regression coefficient β0 of the regression models. The notation ‘A:B' refers to the interaction between markers A and B, while ‘C—D' represents the chromosomal region ranging from C to D. Lasso: markers with estimated coefficients >0 are listed. Estimates of the regression coefficients and the corresponding P-values of the linear model. The P-values in bold type are significant (P<0.05).

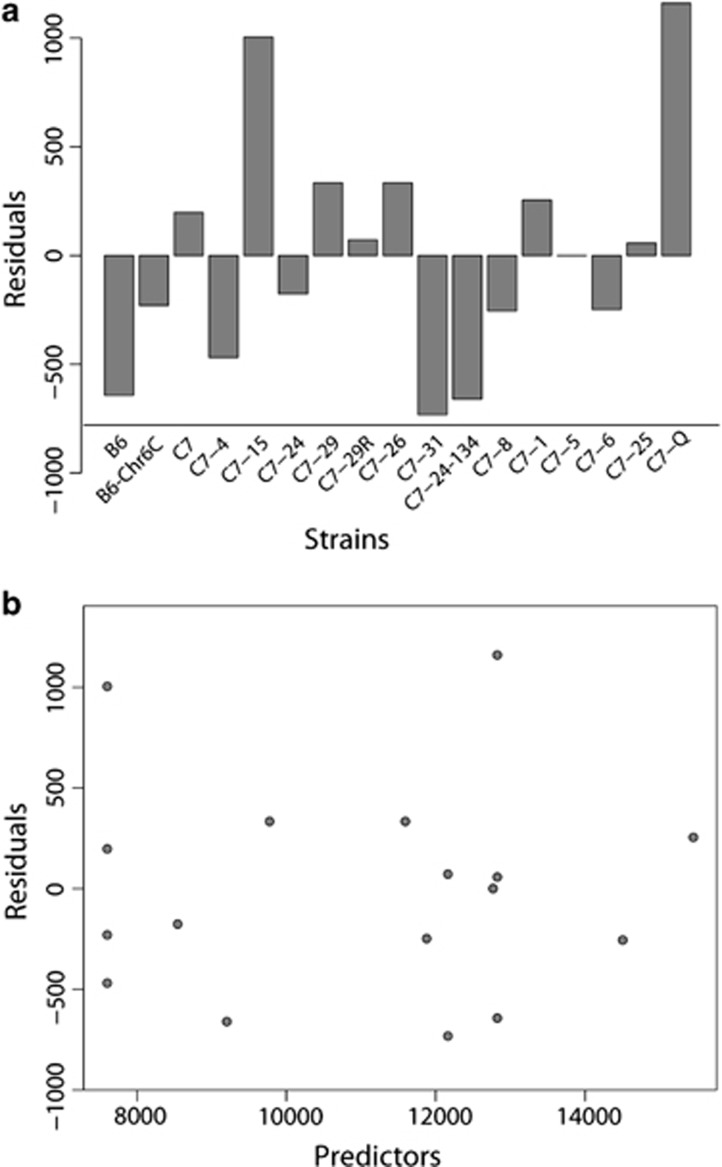
Second, the least squares linear regression model was fitted to data whose number of dimensions of the regressors was now less than the number of strains. Table 1 shows the estimates of the regression coefficients and the corresponding P-values of the selected regression model. The number of selected variables is 6 (out of 9). The maximum log-likelihood is −111.75 and the value of Akaike Information Criterion is 226.3. The total amount of variance is 265 183, which is ∼20% less than that of the estimated lasso. The results of the residual analysis are given in Figure 4a. These results suggest that the model generally fits well to the data. The maximum absolute value of the residuals is given for strain C7-Q as 1160.32, which is <10% of the total activity of the strain of 13 984.12. Figure 4b implies that there is no clear relationship between the values of the predictors and residuals. It seems from these observations that the fitted model provides a satisfactory fit to the data.

Figure 4.

Figure 4

Open in a new tab

(a) A barplot of the residuals of the estimated least squares linear regression model for each subconsomic strain, and (b) a plot of the residuals and predictors of the estimated least squares linear regression model.

From the results of our regression analysis, we mapped the QTL regions related to total activity. Table 1 implies that there are four chromosomal regions where the P-values are significant (P<0.05). The regression coefficients in those regions suggest that strain B6-Chr6C contains loci that decrease the total activity in the following chromosomal regions: adjacent to the marker D6Nig100.2M and/or between D6Nig100.2M and D6Nig102.1M (locus 1), between D6Mit36 and D6Mit105 (locus 2), and between D6Mit104 and D6Mit23 (locus 3). In addition, it is likely to be that there is a locus that increases the total activity in the region adjacent to the marker D6Nig108.6M (locus 4). The levels of influence of these chromosomal regions on total activity can be estimated from the values of the regression coefficients.

Loci for increasing home-cage activity and the suppressor

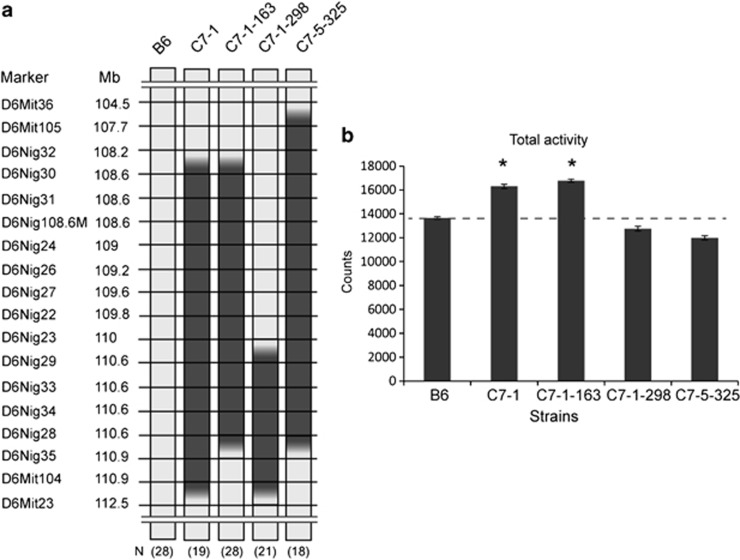
Among these four loci, locus 4, which has a positive effect, shows the opposite effect to the total cumulative effect on activity of B6-Chr6C, which covers a larger substituted region and is associated with lower home-cage activity. In order to confirm the positive effect of locus 4, we established further congenic strains and analysed their total activity (Figure 5). Two strains, C7-1-163 and C7-1-298, were established from C7-1, and a third strain, C7-5-325, was established from C7-5. One-way analysis of variance showed the significant main effect of strain on the total home-cage activity (F(4,109)=7.67, P<0.0001). C7-1-163 showed higher total activity than B6, at a level similar to that of C7-1, but C7-1-298 showed no significant increase, which indicated that the region between D6Nig32 and D6Nig29 has an effect of increasing total activity. However, when the region extends towards the proximal side up to 4.1 Mb in C7-5-325, the congenic strain does not exhibit increased total activity. These results suggest that the region between D6Mit36 and D6Nig30 has the effect of suppressing the increasing effect for total activity caused by a factor located in the region between D6Nig32 and D6Nig239. These results are consistent with the results of the regression analysis in that locus 4, which increases the total activity, is mapped around D6Nig108.6M, and locus 2, which decreases it, is mapped in the region between D6Mit36 and D6Mit105 (Figure 3a).

Figure 5.

Figure 5

Open in a new tab

Fine dissection of genetic loci for increased total activity and the suppressor using congenic strains. (a) The congenic strains used for the behavioural test, numbers of mice used for each strain and genotype of microsatellite markers on chromosome 6 are indicated. The light grey box and filled box indicate the genotype of microsatellite markers of B6 and MSM, respectively. The gradated boxes indicate boundaries between two microsatellite markers in which recombination occurred. (b) Comparison of total activity in the congenic strains and B6. Data are shown as the mean±s.e. The dashed line indicates the score of the control strain, B6. Asterisks (*) indicate significant differences in total activities compared with B6 according to the t-test with Bonferroni's correction at P<0.05.

Discussion

Home-cage activity will be influenced by many environmental factors, such as food intake, temperature, bedding materials and social conditions (Lightfoot et al., 2004). It is well known that interactions between the genetic apparatus and environment might have a substantial impact on the behavioural and physiological phenotype (Overall et al., 2013; Meek et al., 2014). We did not see significant difference in body weights between C7-31 and C7-1, which are strains that exhibit the extremes of the opposite deviations in total activity from B6. Thus, we do not have any data that suggest association of differences in physiological metabolism with the difference in home-cage activities between the strains. However, this point needs to be studied further to understand the mechanisms that underlie the differences in the home-cage activities in these congenic strains. In addition, it will be interesting to examine how changes in environmental factors affect the home-cage activities in these strains. Given that our current method for measuring home-cage activity depends on the infrared sensor located on the top of each mouse cage, we were unable to characterise the behaviour exhibited by the mouse in the home-cage in detail. Further studies to better characterise the quality of this behaviour will provide more in-depth understanding of the biological relevance of each genetic locus.

We previously conducted genetic analyses of behavioural traits using a panel of consomic strains established from MSM and B6 (Takahashi et al., 2008a, 2010; Nishi et al., 2010; Ishii et al., 2011). The results showed that there are many QTLs related to complex traits distributed over multiple chromosomes. The advantage of using consomic strains is that it makes it possible to focus on a particular chromosome that shows a significant effect on the phenotype under the same genetic background. In this case, further genetic mapping can be conducted under the assumption that a single gene associated with the trait of the consomic strain might exist on each mapped chromosome. Indeed, the result of the QTL analysis for total activity using the F2 population established using B6 and B6-Chr6C showed one significant QTL mapped to the telomere side of chromosome 6, although the QTL peak was relatively broad. In addition, the subconsomic strain C7, which included the QTL region spanning up to 43.3 Mb derived from MSM, showed lower activity, at a level similar to that of B6-Chr6C. However, the results of the regression analysis of the data from a series of congenic strains clearly mapped multiple loci that have effects of increasing activity, decreasing activity and suppression of the increase of activity separately within a small chromosomal region.

Several other studies using subconsomic or congenic strains showed the existence of multiple loci related to the phenotype associated with the substituted chromosome (Youngren, 2003; Shao et al., 2008; Takahashi et al., 2008b; Prevorsek et al., 2010; Parker et al., 2013). Complex regulation of the susceptibility to testicular germ cell tumours was reported using congenic strains derived from a consomic strain for chromosome 19, 129.MOLF-Chr19 (Youngren, 2003). In this previous study, it was indicated that susceptibility to such tumours is influenced by five genetic regions with additive and epistatic effects. These regions were found along the length of chromosome 19. Several other reports have shown that multiple genetic factors for various quantitative phenotypes are clustered in a small region (Christians and Keightley, 2004; Yalcin et al., 2004; Ashikari et al., 2005; Ashley-Koch et al., 2006; Christians et al., 2006; Ghazalpour et al., 2006; Yazbek et al., 2011; Rapp and Joe, 2012; Stewart et al., 2012). For example, a single QTL that affects body size appeared to be a cluster of at least four closely linked QTLs (Christians and Keightley, 2004; Christians et al., 2006). These multiple genetic factors might influence body size independently. In another case, two closely linked QTLs were suggested to influence the atherosclerotic phenotype by interacting with each other (Ghazalpour et al., 2006). In order to understand the biological functions of these clustered QTLs, it is important to characterise their molecular basis in more detail.

In the present study, we have mapped four loci: three (loci 1–3) that negatively regulate and one (locus 4) that positively regulates the total home-cage activity. Among these loci, locus 4, which is critical for increasing the total activity, has been mapped to a 1.4-Mb genomic region. It is noteworthy that both the low-activity strain C7-31 and the high-activity strain C7-1 carry locus 4. This result also indicates the complex nature of these multiple genetic loci for regulating home-cage activity. Locus 4 contains three annotated genes: Bhlhe40, Arl8b and Edem1. BHLHE40, also known as DEC1, is a member of the basic helix-loop-helix family and modulates the circadian phase expression of the Clock gene (Nakashima et al., 2008). ARL8B is an Arf-like GTPase that has a role in directing cargo traffic to lysosomes (Garg et al., 2011). EDEM1 is a type II endoplasmic reticulum transmembrane protein that is involved in the endoplasmic reticulum-associated protein degradation pathway to regulate the degradation of misfolded glycoproteins (Hosokawa et al., 2001). None of the functions of these genes is strongly suggestive of an association with home-cage activity; however, there is still a possibility of this in all cases. We conducted sequence analyses of these genes and found no non-synonymous polymorphisms between B6 and MSM. It is therefore possible that a different level of expression of one of these genes in the responsible tissue might affect the total activity, although further experiments are needed to clarify this.

Given that QTL analysis using a panel of congenic strains is one of the most powerful approaches to address multigenic factors behind complex traits, the method using a regression model should be very useful for numerous studies. The regression model used in the present study was the lasso, which is well known as a penalised regression model, that is, a regression model that imposes a certain relationship on unknown parameters. In addition to the lasso, there are several other penalised regression models, such as the ridge regression (Hoerl and Kennard, 1970) and elastic net (Zou and Hastie, 2005) models. Given that the purpose of the statistical analysis is to identify influential chromosomal regions, it seems that the lasso, which is commonly used for variable selection, is the most appropriate among the familiar penalised regression models.

The regression model applied in this study supposed that the effects of decreasing and increasing the home-cage activity in the chromosome regions partitioned into different strains are summed over the entire strain. Given that the residuals calculated in the congenic strains were <10% of the total activity of the strain, the current model fits well in this mapping study. In contrast, epistatic interaction between two loci that are not adjacent has a minor effect in the present case. Although we might need to consider the epistatic interaction between two distant loci in another mapping study, this would involve a heavy computational burden for the calculations. Therefore, this method for fine mapping with the regression model will not be applicable to mapping studies that require consideration of the epistatic interaction model.

In this study, we conducted high-resolution genetic mapping of home-cage activity using a series of congenic strains. This is a highly reliable approach because we can easily make multiple congenic strains from the consomic strains, and the phenotype data of each congenic strain can be collected from multiple mice, as noted previously (Nadeau et al., 2000). To identify genes associated with this phenotype, we are currently establishing more recombinants from the congenic strains carrying the shorter chromosomal segments. These further recombinant strains will aid in the identification of genes that increase or decrease home-cage activity in mice.

Data archiving

Data are deposited in the Dryad repository.

Acknowledgments

We are grateful to Drs Hironori Fujisawa for his useful comments on the regression analysis, Aki Takahashi for useful advice on this work, Juzoh Umemori for kind help with QTL analysis and Toshihiko Shiroishi for providing a consomic strain. This work was supported by JSPS KAKENHI (grant numbers 23650243 and 25116527), Yamada Science Foundation and the Research Organization of Information and Systems, Transdisciplinary Research Integration Center.

The authors declare no conflicts of interest.

Footnotes

Supplementary Information accompanies this paper on Heredity website (http://www.nature.com/hdy)

Supplementary Material

Supplementary Table S1
Click here for additional data file. (24KB, xls)
Supplementary Table S2
Click here for additional data file. (25KB, xls)

References

  1. Ashikari M, Sakakibara H, Lin S, Yamamoto T, Takashi T, Nishimura A, et al. Cytokinin oxidase regulates rice grain production. Science. 2005;309:741–745. doi: 10.1126/science.1113373. [DOI] [PubMed] [Google Scholar]
  2. Ashley-Koch AE, Mei H, Jaworski J, Ma DQ, Ritchie MD, Menold MM, et al. An analysis paradigm for investigating multi-locus effects in complex disease: examination of three GABA receptor subunit genes on 15q11-q13 as risk factors for autistic disorder. Ann Hum Genet. 2006;70:281–292. doi: 10.1111/j.1469-1809.2006.00253.x. [DOI] [PubMed] [Google Scholar]
  3. Basten CJ, Weir BS, Zeng ZB. QTL Cartographer: A Reference Manual and Tutorial for QTL Mapping. North Carolina State University: Raleigh, North Carolina; 1997. [Google Scholar]
  4. Christians JK, Hoeflich A, Keightley PD. PAPPA2, an enzyme that cleaves an insulin-like growth-factor-binding protein, is a candidate gene for a quantitative trait locus affecting body size in mice. Genetics. 2006;173:1547–1553. doi: 10.1534/genetics.106.057513. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Christians JK, Keightley PD. Fine mapping of a murine growth locus to a 1.4-cM region and resolution of linked QTL. Mamm Genome. 2004;15:482–491. doi: 10.1007/s00335-004-3046-0. [DOI] [PubMed] [Google Scholar]
  6. Eichler EE, Flint J, Gibson G, Kong A, Leal SM, Moore JH, et al. Missing heritability and strategies for finding the underlying causes of complex disease. Nat Rev Genet. 2010;11:446–450. doi: 10.1038/nrg2809. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Flint J, Valdar W, Shifman S, Mott R. Strategies for mapping and cloning quantitative trait genes in rodents. Nat Rev Genet. 2005;6:271–286. doi: 10.1038/nrg1576. [DOI] [PubMed] [Google Scholar]
  8. Garg S, Sharma M, Ung C, Tuli A, Barral DC, Hava DL, et al. Lysosomal trafficking, antigen presentation, and microbial killing are controlled by the Arf-like GTPase Arl8b. Immunity. 2011;35:182–193. doi: 10.1016/j.immuni.2011.06.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Ghazalpour A, Wang X, Lusis AJ, Mehrabian M. Complex inheritance of the 5-lipoxygenase locus influencing atherosclerosis in mice. Genetics. 2006;173:943–951. doi: 10.1534/genetics.106.057455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Hoerl AE, Kennard RW. Ridge regression: biased estimation for nonorthogonal problems. Technometrics. 1970;12:55–67. [Google Scholar]
  11. Hosokawa N, Wada I, Hasegawa K, Yorihuzi T, Tremblay LO, Herscovics A, et al. A novel ER alpha-mannosidase-like protein accelerates ER-associated degradation. EMBO Rep. 2001;2:415–422. doi: 10.1093/embo-reports/kve084. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ishii A, Koide T, Takahashi A, Shiroishi T, Hettinger TP, Frank ME, et al. B6-MSM consomic mouse strains reveal multiple loci for genetic variation in sucrose octaacetate aversion. Behav Genet. 2011;41:716–723. doi: 10.1007/s10519-011-9464-3. [DOI] [PubMed] [Google Scholar]
  13. Konishi S, Kitagawa G. Information Criteria and Statistical Modeling. Springer: New York; 2008. [Google Scholar]
  14. Lightfoot JT, Turner MJ, Daves M, Vordermark A, Kleeberger SR. Genetic influence on daily wheel running activity level. Physiol Genomics. 2004;19:270–276. doi: 10.1152/physiolgenomics.00125.2004. [DOI] [PubMed] [Google Scholar]
  15. Meek TH, Eisenmann JC, Keeney BK, Hannon RM, Dlugosz EM, Garland T., Jr Effects of early-life exposure to Western diet and wheel access on metabolic syndrome profiles in mice bred for high voluntary exercise. Genes Brain Behav. 2014;13:322–332. doi: 10.1111/gbb.12098. [DOI] [PubMed] [Google Scholar]
  16. McCullagh P, Nelder JA.1989Generalized Linear Models2nd edn.Chapman and Hall: London [Google Scholar]
  17. Makowsky R, Pajewski NM, Klimentidis YC, Vazquez AI, Duarte CW, Allison DB, et al. Beyond missing heritability: prediction of complex traits. PLoS Genet. 2011;7:e1002051. doi: 10.1371/journal.pgen.1002051. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, Hunter DJ, et al. Finding the missing heritability of complex diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Moriwaki K, Miyashita N, Mita A, Gotoh H, Tsuchiya K, Kato H, et al. Unique inbred strain MSM/Ms established from the Japanese wild mouse. Exp Anim. 2009;58:123–134. doi: 10.1538/expanim.58.123. [DOI] [PubMed] [Google Scholar]
  20. Nadeau JH, Singer JB, Matin A, Lander ES. Analysing complex genetic traits with chromosome substitution strains. Nat Genet. 2000;24:221–225. doi: 10.1038/73427. [DOI] [PubMed] [Google Scholar]
  21. Nakashima A, Kawamoto T, Honda KK, Ueshima T, Noshiro M, Iwata T, et al. DEC1 modulates the circadian phase of clock gene expression. Mol Cell Biol. 2008;28:4080–4092. doi: 10.1128/MCB.02168-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Nishi A, Ishii A, Takahashi A, Shiroishi T, Koide T. QTL analysis of measures of mouse home-cage activity using B6/MSM consomic strains. Mamm Genome. 2010;21:477–485. doi: 10.1007/s00335-010-9289-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Overall RW, Walker TL, Leiter O, Lenke S, Ruhwald S, Kempermann G. Delayed and transient increase of adult hippocampal neurogenesis by physical exercise in DBA/2 mice. PLoS ONE. 2013;8:e83797. doi: 10.1371/journal.pone.0083797. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Parker CC, Sokoloff G, Leung E, Kirkpatrick SL, Palmer AA. A large QTL for fear and anxiety mapped using an F cross can be dissected into multiple smaller QTLs. Genes Brain Behav. 2013;12:714–722. doi: 10.1111/gbb.12064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Prevorsek Z, Gorjanc G, Paigen B, Horvat S. Congenic and bioinformatics analyses resolved a major-effect Fob3b QTL on mouse Chr 15 into two closely linked loci. Mamm Genome. 2010;21:172–185. doi: 10.1007/s00335-010-9252-z. [DOI] [PubMed] [Google Scholar]
  26. Rapp JP, Joe B. Use of contiguous congenic strains in analyzing compound QTLs. Physiol Genomics. 2012;44:117–120. doi: 10.1152/physiolgenomics.00136.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Saad Y, Toland EJ, Yerga-Woolwine S, Farms P, Joe B. Congenic mapping of a blood pressure QTL region on rat chromosome 10 using the Dahl salt-sensitive rat with introgressed alleles from the Milan normotensive strain. Mamm Genome. 2008;19:85–91. doi: 10.1007/s00335-007-9084-7. [DOI] [PubMed] [Google Scholar]
  28. Shao H, Burrage LC, Sinasac DS, Hill AE, Ernest SR, O'Brien W, et al. Genetic architecture of complex traits: large phenotypic effects and pervasive epistasis. Proc Natl Acad Sci USA. 2008;105:19910–19914. doi: 10.1073/pnas.0810388105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Stewart TP, Mao X, Aqqad MN, Uffort D, Dillon KD, Saxton AM, et al. Subcongenic analysis of tabw2 obesity QTL on mouse chromosome 6. BMC Genet. 2012;13:81. doi: 10.1186/1471-2156-13-81. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Takada T, Mita A, Maeno A, Sakai T, Shitara H, Kikkawa Y, et al. Mouse inter-subspecific consomic strains for genetic dissection of quantitative complex traits. Genome Res. 2008;18:500–508. doi: 10.1101/gr.7175308. [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Takahashi A, Nishi A, Ishii A, Shiroishi T, Koide T. Systematic analysis of emotionality in consomic mouse strains established from C57BL/6J and wild-derived MSM/Ms. Genes Brain Behav. 2008;7:849–858. doi: 10.1111/j.1601-183X.2008.00419.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Takahashi A, Shiroishi T, Koide T. Multigenic factors associated with a hydrocephalus-like phenotype found in inter-subspecific consomic mouse strains. Mamm Genome. 2008;19:333–338. doi: 10.1007/s00335-008-9112-2. [DOI] [PubMed] [Google Scholar]
  33. Takahashi A, Tomihara K, Shiroishi T, Koide T. Genetic mapping of social interaction behavior in B6/MSM consomic mouse strains. Behav Genet. 2010;40:366–376. doi: 10.1007/s10519-009-9312-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Tibshirani R. Regression shrinkage and selection via the lasso. J R Stat Soc Ser B Stat Methodol. 1996;58:267–288. [Google Scholar]
  35. Yalcin B, Willis-Owen SA, Fullerton J, Meesaq A, Deacon RM, Rawlins JN, et al. Genetic dissection of a behavioral quantitative trait locus shows that Rgs2 modulates anxiety in mice. Nat Genet. 2004;36:1197–1202. doi: 10.1038/ng1450. [DOI] [PubMed] [Google Scholar]
  36. Yazbek SN, Buchner DA, Geisinger JM, Burrage LC, Spiezio SH, Zentner GE, et al. Deep congenic analysis identifies many strong, context-dependent QTLs, one of which, Slc35b4, regulates obesity and glucose homeostasis. Genome Res. 2011;21:1065–1073. doi: 10.1101/gr.120741.111. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Youngren KK. Testicular cancer susceptibility in the 129.MOLF-Chr19 mouse strain: additive effects, gene interactions and epigenetic modifications. Hum Mol Genet. 2003;12:389–398. doi: 10.1093/hmg/ddg036. [DOI] [PubMed] [Google Scholar]
  38. Zeng ZB. Theoretical basis for separation of multiple linked gene effects in mapping quantitative trait loci. Proc Natl Acad Sci USA. 1993;90:10972–10976. doi: 10.1073/pnas.90.23.10972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Zeng ZB. Precision mapping of quantitative trait loci. Genetics. 1994;136:1457–1468. doi: 10.1093/genetics/136.4.1457. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Zou H, Hastie T. Regularization and variable selection via the elastic net. J R Stat Soc Ser B Stat Methodol. 2005;67:301–320. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Table S1
Click here for additional data file. (24KB, xls)
Supplementary Table S2
Click here for additional data file. (25KB, xls)

Articles from Heredity are provided here courtesy of Nature Publishing Group

RESOURCES