Simultaneous Estimation of Bidirectional Particle Flow and Relative Flux using MUSIC-OCT: Phantom Studies

Abstract

In an optical coherence tomography (OCT) scan from a living tissue, red blood cells (RBCs) are the major source of backscattering signal from moving particles within microcirculatory system. Measuring the concentration and velocity of RBC particles allows assessment of RBC flux and flow, respectively, to assess tissue perfusion and oxygen/nutrition exchange rates within micro-structures. In this paper, we propose utilizing spectral estimation techniques to simultaneously quantify bi-directional particle flow and relative flux by spectral estimation of the received OCT signal from moving particles within capillary tubes embedded in tissue mimicking phantoms. The proposed method can be directly utilized for in vivo quantification of capillaries and microvessels. Compared to the existing methods in the literature that can either quantify flow direction or power, our proposed method allows simultaneous flow (velocity) direction and relative flux (power) estimation.

1. Introduction

The main role of microcirculatory system (including cardiovascular and lymphatic) is to transport oxygen, nutrition, fluid and necessary signaling molecules to the living cells via arteries/arterioles and collecting carbon dioxide and waste materials from the tissue cells. The exchange of oxygen and nutrition happens at capillary beds and then waste and carbon dioxide produced by the cells is diffused back into the capillaries and venules and sent back to the heart and respiratory system. Part of the waste in the interstitial fluid is also collected in the form of a protein-rich interstitial fluid (lymph) by lymphatic vessels [1]. Erythrocytes or red blood cells (RBCs), the most common type of blood cells, are the main carrier of oxygen and tissue fluid to the cells. RBCs are mainly composed of a protein called hemoglobin that binds to oxygen contained in a flexible plasma membrane

There are multiple sources in the literature that define blood flow, flux and flow rate interchangeably that sometimes causes ambiguity and confusion. In physics, flux is defined as a vector that has a direction and quantifies the flow rate of a property per unit area. In the neurovascular community, RBC flux is commonly referred to as the number of RBCs that pass through a single capillary vessel per unit time [2]. RBC flux measurement in the microcirculatory system allows for estimating the blood perfusion within tissue beds surrounding capillary beds, necessary for estimating metabolic activity of the tissue. RBC velocity should not be confused with RBC flux where the former quantifies average blood velocity within blood vessels and the latter quantifies the velocity and concentration of cells in the blood volume per unit area. Consequently, non-invasive measurement of RBC flux has an impact on studying and evaluating clinical applications related to vasculitis [3], angioneurosis [4], diabetes [5], cancer [6], cardiovascular [7], neurovascular [8] and retinal disease [9].

The most common non-invasive and label-free methods reported in the literature for measuring and imaging RBC flux within capillaries and small vessels are Laser Doppler Fluxmetry (LDF), laser Doppler imaging (LDI), photoacoustic microscopy (PAM) and optical microangiography (OMAG). LDF which is based on Doppler shift and broadening of monochromatic light due to moving particles within the tissue [10] has been widely used both in research and clinic to monitor subcutaneous microcirculatory flow in some disease such as Raynaud’s phenomenon [11]. In LDF, blood flux is defined as the product of the mean velocity and number (concentration) of RBCs, expressed in terms of arbitrary perfusion units [12]. Usually, LDF in a subcutaneous site is measured in response to an external stimulus such as pressure or temperature [13]. Laser Doppler imaging (LDI) is an expansion of LDF to provide perfusion map by scanning laser over a large area via a moving scanner mirror and analyzing the backscattered light signal, giving a two-dimensional image of blood flow perfusion. LDI has shown promising applications in dermatology such as assessment of burns [14,15], dermal inflammation [16] and cutaneous ulceration [17] and in rheumatology such as Raynaud’s phenomenon [18] and inflammatory joint disease [19]. Although widely used, the main disadvantages of LDF techniques are: (1) low spatial resolution (difficult to resolve single capillaries), (2) limited imaging depth (less than 0.5 mm) and (3) depth-integrated signal (cannot provide depth-resolved information).

Photoacoustic imaging (PAI) is performed by transmitting a sequence of short laser pulses into the sample tissue and ultrasound detection of the resulted thermo-elastic expansions of tissue cells [20]. Since hemoglobin is the main absorbing chromophore in the blood, PAM has been demonstrated in imaging vascular structures from macro-vessels down to individual capillaries. Using absorption properties of oxygenated-hemoglobin and high-frequency (25-Mhz) ultrasound microscopy, Jiang et al. [21] proposed a Doppler ultrasound and photoacoustic method of imaging blood oxygen flux in a single vessel where oxygen saturation and total hemoglobin concentration were estimated using PAM and mean flow velocity was estimated by ultrasound. Then, the blood oxygen flux (ml/min) was calculated as the volume of oxygen content transported from an area cross-section per unit time.

In contrast to PAI that is based on light absorption properties of the tissue, optical coherence tomography (OCT) is a non-contact technique based on light backscattering properties of the tissue structures [22, 23]. OCT is analogous to ultrasound imaging. Similar to ultrasound Doppler modes, OCT hemodynamic information can be acquired in addition to structure information. Compared to ultrasound imaging, OCT resolution is higher while the penetration and imaging depth is limited. Optical microangiography (OMAG) is a label-free non-invasive imaging and processing method to obtain 3-D blood perfusion map in microcirculatory tissue beds in vivo using Fourier-domain OCT [24, 25]. Conventional Doppler OCT (DOCT) or phase-resolved Doppler OCT (PRDOCT) utilizes the difference between phase information of adjacent A-lines acquired at the same spatial location to measure particle velocity within each voxel from the Doppler (phase) shift [26, 27]. It is commonly known that PRDOCT is mainly sensitive to the axial component of the flow (parallel to the beam). Due to the slow velocity of particles within capillary network (0.1–8 mm/s) and total imaging time limitation, PRDOCT is only practical for imaging blood flow perfusion within larger vessels (>30 μm diameter). Using PRDOCT, volumetric blood flow can be extracted by integrating the velocity profile over a vessel cross-section and taking other factors such as Doppler angle, tissue bulk motion and pulsation [28]. However, the limitation on this approach for measuring total blood flow is its sensitivity to the estimated Doppler angle as well as accurate estimation of vessel cross-section where some OCT image artifacts such as forward-scattering and phase-ambiguities below vessels can affect the accuracy of this approach [29]. In order to compensate for these artifacts, Srinivasan et al. suggested to use an en-face imaging technique that was originally developed in Doppler Ultrasound [30], in which the total blood flow is evaluated by integrating Doppler velocity profile over the en-face plane (xy plane) at each depth position instead of xz or yz planes [31]. Similar approach has been utilized to measure total volumetric blood flow in rodents [32] and human retina [33].

However, PRDOCT only measures the velocity of the particles passing through the probe beam and cannot quantify the concentration of particles or RBC flux. PRDOCT is analogous to color-Doppler ultrasound mode in which directional blood velocity (axial component) is quantified by measuring the center frequency of the Doppler shift. Due to its sensitivity to noise and tissue motion, color-Doppler mode is mainly used to measure large vessels and fast flow velocities and cannot measure blood velocity when ultrasound beam is perpendicular to the flow direction. Power-Doppler ultrasound can overcome some of the color-Doppler mode limitations by quantifying the amplitude peak in the shifted/broadened Doppler spectrum and is particularly useful for imaging small vessels and low-velocity flow [34]. It is known that under constant concentration condition, the Doppler spectrum is proportional to the number of RBCs while the Doppler peak value is sensitive to changes in concentration, shear rate and turbulence [35]. Also, some studies suggest that erythrocyte aggregation affects ultrasonic backscatter from RBCs and therefore shear-rate-dependent attenuation coefficient should be compensated for higher shear rates [36]. Given the similarities between ultrasound imaging and OCT, since color Doppler ultrasound is analogous to PRDOCT, we propose that there exists a similarity between ultrasound power Doppler and peak amplitude of the Doppler signal from moving particles such as RBCs. Therefore, we can infer that quantification of Doppler peak amplitude leads to measuring the number of RBCs moving through the probe beam (RBC flux).

Previously, some methods have been proposed in the OCT community based on signal decorrelation time [37,38] and amplitude peaks at capillary locations [39] to quantify RBC velocity and flux in single capillaries. The amplitude peak method only works in small capillaries with single RBC flowing through the vessel. In order to reproduce a high-resolution frequency estimate, the method based on signal decorrelation time required to capture a large amount of data set that made this method sensitive to possible tissue motion and vessel wall artifacts. Conventional spectral estimation techniques utilize Fast Fourier transform (FFT) of the autocorrelation function to estimate spectral information and the estimation resolution is very sensitive to the number of FFT points and number of autocorrelation lags. However, collecting large amount of data points (i. e. 1024) for each voxel makes such conventional methods extremely challenging for in vivo experiments because of motion artifacts and total imaging time. In order to mitigate these limitations, model-based spectral estimation techniques can be more favorable because the latter requires very fewer data points to estimate signal spectrum.

Model-based spectral analysis of time-domain color Doppler OCT have been investigated before [40]. Also, we have previously proposed a method to quantify blood flux within microcirculatory tissue beds of any size in vivo to overcome some of the mentioned challenges [41]. In this paper, we generalize the estimation technique to simultaneously quantify bidirectional particle flow and flux by spectral estimation of the received OCT signal from moving particles within capillaries and microvessels. We show the efficiency and performance of the proposed method in simulation and tissue-mimicking flow phantom. Compared to the existing methods that can either quantify flow direction or power, our proposed method allows simultaneous flow (velocity) direction and power (flux) estimation. Since, a super-resolution estimation technique is utilized, our method does not need a large data set to reconstruct power spectrum of the OCT signal. This method may be utilized to facilitate the evaluation of tissue oxygen/nutrition exchange and consumption by microstructures in biological tissues such as human/animal retina, skin and rodent brain.

2. Proposed Method

In the signal processing discipline, multiple signal classification (MUSIC) is a super-resolution spectral estimation method based on the principle of orthogonality [42]. The MUSIC estimation is based on the orthogonality property of noise and signal eigenvector subspaces. In contrast to the classical spectral estimation methods such as periodogram and correlogram [43] that use FFT, the frequency resolution of MUSIC is independent of the number of FFT points, which makes it a super-resolution method. We can model OCT signal measurement at each voxel as superposition of three independent components: tissue signal (stationary and slowly moving tissue structures), hemodynamic signal (mostly contribution from moving red blood cells) and noise (system noise and shot noise). Given the assumption that these components are independent, MUSIC has the capability to decompose the received OCT signal into orthogonal basis functions and therefore contributions from moving RBCs can be estimated and quantified.

The 3D OCT signal at each voxel given by a complex value x[n], where n corresponds to the temporal sampling at the voxel location, can be decomposed in terms of its exponential eigenfunctions given by

$$x[n]={\sum }_{i=1}^P{a}_i{e}^{j(n{\omega }_i+{\phi }_i)}+b_a[n]$$ (1)

where b_a[n] is a centered complex white noise of variance E{|b_a[n]|²} = σ² independent from a_i, a_i are random and independent variables of variance ${\sigma }_{a_i}^2$ that model field reflectivity, P is the total number of orthogonal components in the signal and a_i, φ_i and ω_i are the amplitude, phase and angular frequency of each component, respectively. Then, we can write the autocorrelation function of the observations as [44]:

$$r_{xx}[k,m,m^{\prime }]={\sum }_{i=1}^P{\sum }_{l=1}^{P}E\{a_i{a}_l^{\ast }\}{e}^{({\omega }_i-{\omega }_l)k}·e^{j(m{\omega }_i-m^{\prime }{\omega }_l)}+{\sigma }^2{\delta }_{m-m^{\prime }}$$ (2)

where δ_m−m′ is the Kronecker symbol and k = m−m′. If a_i are non-correlated, then x[n] is stationary and its correlation coefficients are:

$$r_{xx}[m-m^{\prime }]=r_{xx}[k]={\sum }_{i=1}^P{A}_i{e}^{jk{\omega }_i}+{\sigma }^2{\delta }_k$$ (3)

where $A_i=a_i^2$ and (|k| = 1,2,…, M) are autocorrelation lag values for M number of temporal samples. The M order correlation matrix is then given by

$$R_{xx}=\left[\begin{array}{ccc}{r}_{xx}[0]& \cdots & r_{xx}[-M-1]\\ ⋮& \ddots & ⋮\\ r_{xx}[M-1]& \cdots & r_{xx}[0]\end{array}\right]$$ (4)

If the temporal samples are larger than the number of orthogonal components (M > P), then Rank{R_xx} = min{M, P} = P. Since Rank{R_xx} = P, then R_xx can be represented by its first P eigenvalues/eigenvectors

$$R_{xx}={\sum }_{i=1}^M{\lambda }_i{u}_i{u}_i^H={\sum }_{i=1}^P{\lambda }_i{u}_i{u}_i^H={\sum }_{k=1}^P{A}_k{S}_k{S}_K^H={\mathit{SAS}}^H$$ (5)

where λ₁ ≥ λ₂ ≥ λ₃ ≥ ··· ≥ λ_M are eigenvalues and u₁, u₂, u₃, …, u_M are their corresponding normalized eigenvectors and λ_p+1 = λ_p+2 = ··· = λ_M = 0. The eigenvectors {u₁, u₂, …, u_P} are the principal eigenvectors of the autocorrelation matrix R_xx that spans the signal subspace. The autocorrelation matrix can also be written in the form of matrix eigenfunctions where S_M×P = [S₁, S₂ … S_P], S_i = [1 e^jω_i e^j2ω_i e^j3ω_i … e^j(M−1)ω_i]′, ω_i is one of the input’s principal frequency components and A = diag([A₁, A₂, A_P]). Here H is the matrix Hermitian (complex conjugate transpose) and diag([.]) is a diagonal matrix. The vector space S_M×P = {S₁, S₂, …, S_P} is called the signal subspace of {x[n]}.

Since we assume that the noise and signal subspaces are orthogonal to each other [51], a frequency estimator function can be developed to exhibit pseudo-spectrum plots with sharp peaks at signal frequency locations. In theory, the M−P noise subspace eigenvectors {u_P+1, u_P+2, …, u_M} of the autocorrelation matrix or any linear combination of them with an arbitrary weighting α_k given by

$${\sum }_{k=P+1}^M{\alpha }_k{\mid S^H(\omega )u_k\mid }^2=S^H(\omega ).({\sum }_{k=P+1}^M{\alpha }_k{u}_k{u}_k^H).S(\omega )$$ (6)

would be zero if evaluated at S(ω_i) = [1 e^jω_i e^j2ω_i …e^j(M−1)ω_i], where ω_i is the frequency component of the input signal. The MUSIC spectral estimator is defined by the function

$$P(\omega )=\frac{1}{{\sum }_{k=P+1}^M{(\mid S^H(\omega )u_k\mid )}^2}$$ (7)

and theoretically have an infinite value if evaluated at one of the signal’s frequency components (ω = ω_i). In practice, the MUSIC frequency estimation function is finite due to estimation error, but exhibits local maxima (peak) at those frequencies. Locating the peak value and its corresponding frequency will be an indicator of the blood flux and flow, respectively, at the voxel of interest. Accurate estimation of the blood velocity (ω_i) requires temporal sampling above the Nyquist rate [45]. However, the estimated peak value (P(ω_i) or flux) is less sensitive to that condition and frequency aliasing.

In practice, correlation matrix is not available and therefore an estimate of the correlation matrix is considered so that R̂_xx = {r̂_xx[m]} where

$${\widehat{r}}_{xx}[m]=\frac{1}{N}{\sum }_{n=\frac{N-1}{2}}^{\frac{N-1}{2}}x(n+m)x^{\ast }(n)$$ (8)

and N is supposed to be odd. This estimation of R_xx relies on the assumption that x[n] is ergodic. A spectral estimation method is called super-resolution when its asymptotic resolution is theoretically infinite in the sense that two signals with closely spaced frequency components can be separated, provided that the number of samples used for the estimation of the correlation matrix tends to infinity and the correlation estimate approaches the actual correlation matrix. To illustrate the concept of super-resolution in comparison to the classical Fourier analysis, we can rewrite the spectral estimators of the periodogram and correlogram, making the same sizes of observations M and N. Assuming N observations of x[k] partitioned in L adjacent sequences of M successive observations of x[k] partitioned in L adjacent sequences of M successive observations of x[k], the super-resolution periodogram is given by

$${\widehat{S}}_{xx}^{\mathit{per}}(f)=\frac{1}{L}{\sum }_{l=0}^{L-1}{\widehat{S}}_{xx}^{(l)}(f)=\frac{1}{L}{\sum }_{l=0}^{L-1}(\frac{1}{M}{\mid {\sum }_{m=0}^{M-1}x(lM+m)e^{-jm\omega }\mid }^2)$$ (9)

and the correlogram is given by

$${\widehat{S}}_{xx}^{\mathit{corr}}(f)={\sum }_{m=-\frac{M-1}{2}}^{\frac{M-1}{2}}{\widehat{r}}_{xx}(m).e^{-jm\omega }$$ (10)

where r̂_xx is given in Eq. (8). The super-resolution property of the sub-space based methods (periodogram) is based on the fact that at fixed M, it is enough to increase N so large that the method can distinguish two signals whose frequency components are closely-spaced. However, this is not the case for the periodogram (classical estimation techniques) methods because both M and N should increase at the same time to have this result.

The backscattered OCT signal has relatively higher signal-to-noise ratio (SNR) at stationary and non-moving tissue boundaries because the structure pattern is repeatable. However, the backscattered signal from moving scatters such as moving red blood cells inside patent vessels is typically weaker and temporally varying. Since the tissue component is always stronger than the hemodynamic component, their corresponding MUSIC eigenvalues will be in order so that the larger eigenvalue belongs to tissue signal subspace while smaller eigenvalue belongs to the hemodynamic signal subspace. Therefore, their corresponding subspaces can be separately estimated. In MUSIC estimation, the number of input signal components (P) is a user-defined input variable. By defining the number of input signal components to be P = 2, the largest peak in the MSUIC pseudo-spectrum of OMAG data corresponds to the stationary and non-moving tissue and the second largest peak corresponds to the moving RBCs. The value for P can be estimated with other techniques that we will cover at the discussion section. We can also approach this problem by first removing the stationary and non-moving tissue structural components (also known as clutter) from the input data, and then characterizing the remaining component which corresponds to the RBCs. This can be done using eigendecomposition-based clutter rejection filtering technique [46] or by simply subtracting A-lines acquired at the same location. The advantage of this approach is that after removing the clutter, a mask image based on the remaining flow information can be created and MUSIC is performed only on the voxels with high flow value, which would dramatically reduce the total processing time. In this paper, we define the MUSIC flux as the estimated velocity multiplied by the MUSIC peak value given by

$${\mathit{Flux}}_{\mathit{MUSIC}}=P({\omega }_i).{\omega }_i$$ (11)

3. System set up and experimental preparation

3.1 OCT system set up

We utilized an SD-OCT system to test and validate the proposed spectral estimation technique. In our SD-OCT system, the light source was a superluminescent diode (SLD, DenseLight, Singapore) with the center wavelength of 1310 nm and bandwidth of 65 nm (axial resolution of ~12 μm in the air). An optical circulator (OC) was used to couple the light from the SLD into fiber-based Michelson interferometer. In the reference arm of the interferometer, a stationary mirror was utilized after polarization controller. In the sample arm of the interferometer, a microscopy objective lens with 18-mm focal length was used to achieve ~5.8 μm lateral resolution. The backscattered light from the sample and the reflected light from the reference mirror were recombined at the 2 × 2 optical fiber coupler. A 633-nm laser diode was used as a guiding beam to locate the imaging position. The recombined light was then routed to a home-built high-speed spectrometer via the optical circulator (AC Photonics, USA). In the design of the spectrometer, a collimator with the focal length of 30 mm and a 14-bit, 1024-pixels InGaAs lines can camera (SUI, Goodrich Corp) were used. The camera speed was 47,000 lines per second. The spectral resolution of the designed spectrometer was ~0.141 nm that provided a detectable depth range of ~3.0 mm on each side of the zero-delay line. The system had a measured signal to noise ratio of ~105 dB with a light power on the sample at ~3 mW.

3.2 Scanning protocol

The scanning protocol utilized in this experiment was based on wide velocity range Doppler microangiography [47]. In this protocol, the beam is shifted to each spatial location and after the scanner is stabilized, multiple repeated A-scans per location are captured at a defined scan frequency (defined by Nyquist rate). Then, the probe beam is shifted to the adjacent spatial location and the same procedure continues until all the locations in the field of view on the tissue are covered. The advantage of this method is that temporal power spectral density broadening due to the moving scanner speed is minimized because the scanner is fully stabilized [31]. In this experiment, we acquired 25 A-lines repetition per location, 200 A-lines per B-frame and 200 frames for each 3D scan. Since the camera was triggered at 7 kHz (due to Nyquist rate), total scanning time for a 3D data set was ~140 seconds. The 7KHz scanning rate was chosen to meet the requirements for scanning blood perfusion in human skin. However, higher scanning rates should be utilized when scanning higher perfused tissues such as human retina or rodent brain.

4. Experimental Results

In order to show the performance of MUSIC method to estimate RBC velocity and flux, we made a series of experiments on a custom-made flow phantom. The phantom was made from 1% agar solution and 10% of low-fat milk (2% fat) to mimic heterogeneous tissue environment. A capillary tube with an inner diameter of ~400 μm was submerged and a diluted solution of milk (2% fat) and water was mixed to flow through the tube. A syringe pump (Fusion 100, Chemyx Inc.) was utilized to move the flowing particles from a syringe (5ml, Luer-Slip plastic, National Scientific, Germany) through the tube at a constant flow rate controlled by the pump. In order to simulate variable concentrations, three different diluted solutions of milk and water were utilized to model low, medium and high levels of concentration. The dilution portions of milk-to-water ratios were 0.5, 1 and 2 for low, medium and high concentration levels, respectively. For each solution, the syringe was pumped at controlled volumetric flow rates of [25, 50, 75, 100, 125, 150, 175, 200] μl/min. The OCT system and scanning protocol explained earlier were utilized to capture cross-sectional images. Instead of 3D data acquisition, 200 repeated B-frames consisting of 200 adjacent A lines per B-frame and 25 A-line repetitions at each spatial location when scanner was stable were captured and the estimated values were averaged. In order to minimize processing time, first the location of flow/tissue pixels was masked based on Eigen-decomposition clutter rejection filter [46]. Then, for each flowing voxel, MUSIC frequency (ω_s) and peak (P(ω_s)) were calculated. Total blood flow and flux within the tube were calculated by integrating estimated velocity and flux over all pixels within the tube.

Fig. 1(A) shows a cross-section of the phantom structure at the site of measurement. Fig 1(B) is the flow locations extracted using eigendecomposition clutter rejection and used as a mask to reduce processing time. Figs. 1(C,D) show the estimated velocities and flux, respectively, using MUSIC algorithm shown in the red-dotted square delineated in Fig. 1(B). It can be observed that the estimated MUSIC frequency (ω_s) is distributed based on laminar flow profile over the tube cross-section area and does not depend on the signal amplitude. On the other hand, MUSIC power peak (P(ω_s)) depends on the amplitude of the received signal and signal attenuation can influence the estimated peak. The estimated MUSIC flux also demonstrates a laminar profile across the tube. It should be noted that the inner diameter of the flow phantom utilized in this experiment was 400 μm which is relatively larger than most of the capillaries and small vessels in vivo. For instance, the diameter of arterioles in a young healthy wild-type mouse range between 10 μm to 50 μm and the diameter of venules are typically between 15 μm to 80 μm. Therefore, when estimating flow and flux in vivo, OCT signal attenuation within an arteriole/venule will be significantly less obvious.

Fig. 1.

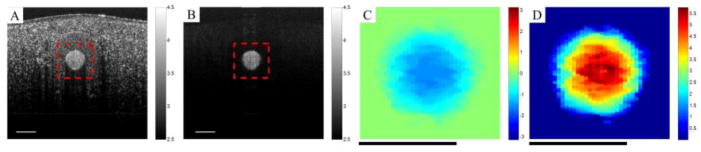
(A) A cross-section of the flow phantom structure. (B) Clutter rejected from structure measurements showing flowing particles (dB). (C) Estimated particle velocities (flow) based on MUSIC center frequency of the spectrum peak (shown from [−π π] in the rectangle area of Fig. 1(A). (D) Estimated moving particle flux based on MUSIC peak (dB). Color bars in dB.

Scale bar = 400 μm.

Total moving particle flow and flux within the phantom tube were calculated by integrating estimated MUSIC frequency (ω_s) and MUSIC flux (P(ω_s) × ω_s) over the flowing tube area. This method was utilized because we acquired only the repeated 2D scans for better statistics of the data and proof concept. Since the tube angle and imaging location were kept constant in between all measurements, the estimated total flow and flux can be comparable among these experimental conditions. When a 3D scan is acquired, the Doppler angle can be estimated and measurements should be compensated for that angle to account for total flow and flux.

Fig. 2(A) shows the total velocity (flow) that is the integration of estimated MUSIC velocities inside the tube. It can be observed that by increasing the flow rate in the syringe pump, total flow has increased linearly. As expected, changes in the number and concentration of flowing particles (flux) were not observed in the velocity map. Therefore, measuring total blood flow using integration of velocity map over a vessel cross-section (in any cross-section) cannot resolve flux information. However, blood flux can be assessed by estimating the peak of the MUSIC power spectrum, as shown in Fig. 2(B). For each concentration level, by increasing the flow rate of syringe pump, total MUSIC flux increased in an almost linear way. By increasing the concentration of flowing particles inside the tube, total MUSIC flux value significantly increased that was in agreement with the simulations. The only difference is that by increasing the flow rate on the syringe pump, total MUSIC flux leans towards a non-linear behavior that can be explained by photon multiple scattering effect and attenuation. This nonlinear effect of flux has been reported in the laser Doppler literature and similar measurements on flux (perfusion) as a function of particle velocity and concentration of moving particles has been presented [50]. Also, OCT signal attenuation and absorption should increase as particle concentration and velocity increases. Therefore, the detected signal SNR from deeper backscatters was lower and the estimated MUSIC peak was lower than expected.

Fig. 2.

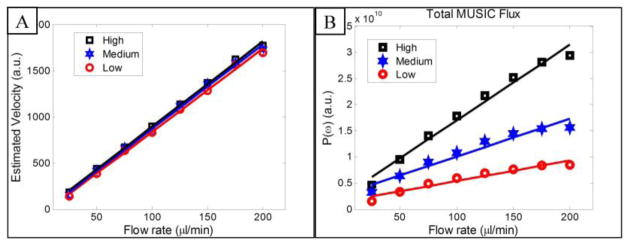
(A) Estimated flow rate by integrating total velocity of particles from the tube cross-section. The estimated flow follows a linear line as a function of syringe pump flow rate (r ≥ 0.99). (B) Estimated flux by integrating total MUSIC peak at the tube-cross section. The estimated flux is almost linear as a function of syringe pump flow rate (r ≥ 0.93).

In order to validate the results with actual flux values, exact measurement of particle concentration and size is required. However, in our case, we validated sensitivity of MUSIC flux estimation based on the linearity of total blood flux with respect to the density. Since all of the experimental conditions remain the same and only the solution concentration was altered, and total flux is linearly related to the solution concentration, we expect that by doubling the solution concentration, total flux would also double. Since the particle concentration of the low, medium and high conditions in Fig. 2 are linearly related, the slope of the fitted line to each curve can be a good measure to assess sensitivity of the MUSIC estimator to flux variations. A 1^st order polynomial was fitted to the total flux of each solution concentration data points as a function of syringe pump’s flow rate using the minimum least square error method with 95% confidence bounds and the fitting results are summarized in Table 1. Since R-square (goodness of the fit) for all of the cases is larger than 0.93, the data is fitted well to a linear first order polynomial model. It can be observed that the first coefficient of the fitted curves (P1) that shows the slope of the line is linearly related to the variations of the concentration. For instance the ratio of the coefficients can be calculated by $\frac{P1(4\%)}{P1(2\%)}=2.06\pm {\epsilon }_1$ and $\frac{P1(2\%)}{P1(1\%)}=1.85\pm {\epsilon }_2$ which are nearly a factor of two when the concentration is doubled. One reason that the ratios are not perfectly twice might be due to the impurities of the solution or other experimental and measurement errors.

Table 1.

Fitted parameters of the measured total blood flux using a minimum least square error to a first-order polynomial for different concentration of flowing particles. (R-sqaure is a measure of linearity)

Concentration	Fitted to a 1st order polynomial : f(x) = P1*x+P2
	P1/10^7	P2/10^8	R-square
High (4%)	11.62 ± 1.75	19.36 ± 22.14	0.97
Medium (2%)	5.64 ± 1.44	2.08 ± 18.19	0.94
Low (1%)	3.05 ± 0.81	8.46 ± 10.23	0.93

Flow and flux profiles within the tube are plotted in Fig. 3(A) and (B), respectively where x-axis is the spatial location at the tube cross-section. For each concentration, the syringe pump is driven by 125, 150, 175 and 200 μL/min flow rate. The velocity profile resembles parabolic shape. And regardless of the particle concentration, velocity profile remains the same. On the other hand, flux profile does not have a very smooth parabolic profile as explained earlier. Since MUSIC peak is sensitive to the amplitude of the received signal, surface reflection from the phantom and tube structures that were perpendicular to the beam can cause signal saturation or attenuation. Therefore, the flux profile does not follow a typical parabolic shape. However, changing in the concentration of moving particles can be differentiated on the flux profile and by increasing the concentration, flux profile appears larger.

Fig. 3.

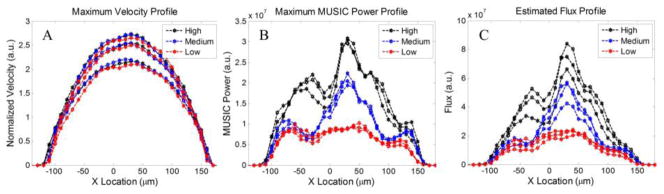
(A) Estimated velocity. Flow profiles of four syringe flow velocities (125, 150, 175 and 200 μL/min) along the tube with various concentration of particles. (B) Estimated MUSIC power peak for the profiles shown in Fig. 3(A). (C) Estimated MUSIC flux profile.

5. Discussions and conclusions

We compared the performance of MUSIC method in estimating total blood flow and flux with some of the existing techniques in the literature including phase-resolved color Doppler (PRCD) [27], speckle variance (SV) [52] and phase difference variance (PDV) [53]. We calculated total blood flow using each algorithm and presented the results similar to the approach explained in Fig. 3 and equations (19–20). The comparison between PRCD, PDV and SV for total flow measurements is shown in Fig. 5. It can be observed that PRCD is only sensitive to the velocity information, and the concentration of the flowing particles has a slight change in the estimated total blood flow. On the other hand, PDV and SV can encode the concentration information. However, the slopes of the fitted line for SV and PDV are not linearly dependent on the flowing particles’ concentration and the estimate is very biased. The ratio of the slopes of high to medium and medium to low concentrations are 1.06 and 1.10, respectively, which indicates that PDV cannot linearly encode the changes in the flowing particle concentrations and flux. The R-square measures of fitting a polynomial to the PDV data indicated that a second-order polynomial was a better fit to the data set, suggesting that PDV estimation of total blood flow may be linearly dependent on the square of the particle velocity. For the SV method, we noticed that the overall value of the estimated total blood flow was relatively larger for higher concentrations, while there was no linear relationship to the syringe pump’s increase of flow rate. Also, the ratios of the high/medium and medium/low slopes were 5.39 and 1.68, respectively, which deviates significantly from the ratio of the original concentration values. Similar to the PDV method, the R-square measures of goodness showed that SV data set is better fit with the second-order polynomial rather than a first-order. The fitting measures and quantities of PRCD, PDV and SV are given in Table 2.

Table 2.

Linearity of SV, PDV and PRCD methods to measure total flow.

Method	Concentration	R-square (1st order)	$\frac{\mathrm{P}1(\text{high})}{\mathrm{P}1(\text{medium})}$	$\frac{\mathrm{P}1(\text{medium})}{\mathrm{P}1(\text{low})}$
SV	High	0.76	5.39	1.68
	Medium	0.28
	Low	0.21
PDV	High	0.92	1.06	1.10
	Medium	0.93
	Low	0.95
PRCD	High	0.99	1.05	1.06
	Medium	0.99
	Low	0.99
MUSIC	High	0.97	2.06	1.85
	Medium	0.94
	Low	0.93

The relationship between the peak value of MUSIC estimator and particle flux can be explained in other words. By increasing the number of particles that are passing through a single voxel, the backscattered OCT signal-to-noise ratio would be stronger due to larger contribution from multiple cells. When estimating the spectrum using MUSIC, increased number of cells will eventually increase the estimation performance and the spectrum is asymptotically getting closer to the ideal case which is infinite value at the input signal frequency (assuming that the input signal is a single frequency exponential eigenfunction). In that case, no obvious change is observed in the estimated signal frequency and only the peak amplitude is increased.

Notwithstanding, MUSIC estimation also has some limitations. The computational complexity of the MUSIC method is in the order of M³ which is mainly because of searching the eigen-elements of the covariance matrix. Also, MUSIC is based on a precise modeling of the noise and assumes that the covariance matrix of the noise is known which may not be true for array processing. And other periodogram methods such as minimum variance should be utilized instead. One of the major limitations is that MUSIC method requires the knowledge about the number of complex sine waves before estimating their frequencies and the performance of the MUSIC estimation highly depends on accurate determination of the number of estimated complex sine waves. There are some techniques based on the likelihood function of the observation to determine the order of a model. Akaike information criterion (AIC) [54] consists of minimizing the quantity below in relation to the supposed number P of complex sine waves to determine the order of an autoregressive model:

$$\mathit{AIC}(P)=-\mathit{Nlog}(\frac{{\prod }_{i=p+1}^M{\widehat{\lambda }}_i}{{\left(\frac{1}{M-P}{\sum }_{i=p+1}^M{\widehat{\lambda }}_i\right)}^{M-p}})+p(2M-p)$$ (12)

where p is an estimate of P, N is the number of observations and λ̂_i are the eigenvalues of the covariance matrix R̂_xx arranged in descending order. The estimation of the noise variance is then given by the average of (M−P) smallest eigenvalues of the covariance matrix, that is

$${\widehat{\sigma }}^2(p)=\frac{1}{M-p}{\sum }_{i=p+1}^M{\widehat{\lambda }}_i.$$ (13)

Another criterion widely used to determine the order of a model is minimum description length (MDL) [55,56] which is slightly different from AIC:

$$\mathit{MDL}(p)=-\mathit{Nlog}(\frac{{\prod }_{i=p+1}^M{\widehat{\lambda }}_i}{{\left(\frac{1}{M-P}{\sum }_{i=p+1}^M{\widehat{\lambda }}_i\right)}^{M-p}})+\frac{1}{2}p(2M-p)\text{log}(N).$$ (14)

The MDL criterion is consistent and converges to the true value of P when N→∞. It is commonly known that the AIC criterion tends to overestimate while the MDL criterion underestimates the number of complex sine waves. Therefore, a hybrid technique based on both criterions may be utilized to determine the order of MUSIC.

Although widely used to measure Doppler velocity in Doppler OCT, it has recently been demonstrated that Kasai estimator [57] is statistically suboptimal as determined by the standard performance metrics of estimator bias, variance and efficiency [58]. The Kasai estimator is computationally simple and can be implemented for real-time applications. However, no prior knowledge or assumption is required about the noise statistics, meaning that the estimator is not optimal. It was suggested that maximum likelihood estimator (MLE) which is a parametric estimation technique based on the peak location of the power spectral density, can provide a consistent, asymptotically unbiased and asymptotically efficient estimation. In theory, the performance of an estimator is compared with Cramer-Rao lower bound (CRLB), which indicates the theoretical best performance of an unbiased estimator. It was shown that MLE estimator can achieve CRLB when SNR is higher than 36 dB and length of data is larger than 8. On the other hand, MUSIC algorithm estimates the spectral density of the received signal and finds peaks and their corresponding frequency locations on the spectrum which is similar to MLE and requires less knowledge of the model, except for the number of components in the signal. Stoica et al. [59] have shown that MUSIC estimator should asymptotically achieve CRB for uncorrelated signals and its error variance monotonically decreases by increasing samples. It was proved that MUSIC estimator is a large sample realization of the MLE if and only if the signal covariance matrix is diagonal (uncorrelated signal). In the correlated signal case, MUSIC error variance may occasionally increase. Therefore, MUSIC estimation can provide a promising estimate of the Doppler frequency (flow) and its corresponding peak (flux) and can asymptotically reach CRLB.

The proposed technique can be generalized to in vivo studies that require monitoring relative changes of blood flux with respect to physiological changes such as stroke models where a baseline and post-operation data are available for relative comparison. In that case, since 3D geometrical information about blood vessels can also be assessed to correct for Doppler angle and integration plane. Also, by making some assumptions about hematocrit level of the blood sample (assuming constant concentration), total blood flux can be measured similar to PAI [21]. Although we have shown flux measurement within a flow phantom with known flowing conditions, we would like to measure the flux within capillaries in vivo where a prior knowledge of the hematocrit condition is not available.

In laser Doppler perfusion and flux measurements, a baseline is collected and then changes relative to the baseline are measured. However, measurements of different subjects/sites may not be comparable in an absolute value and only relative values should be considered. That is the reason why most laser Doppler perfusions and flux measurements are given in auxiliary units. Most of the techniques in the OCT literature measure only the RBC velocity and total blood volume by integrating over a vessel cross-section. The angle-dependence measurements can be overcame with changing the integrating for total flow or flux over the XY plane instead of XZ cross-section planes. Also, MUSIC flux estimation can be normalized by the SNR value to consider depth-dependent attenuation [60]. In future, we would like to perform more experiments using whole blood samples and generate flow and flux curves to be able to provide calibrations based on the variation of RBC concentration, blood velocity and oxygen saturation. Given the calibration plots, we would be able to precisely measure total flow and flux within capillaries.

Fig. 4.

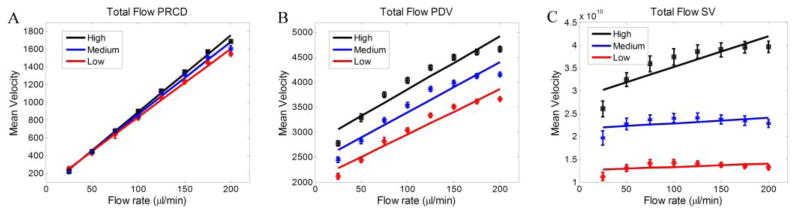
Comparison between PRCD(A), PDV(B) and SV(C) methods of measuring total flow.