Bayesian Mixed Hidden Markov Models: A Multi-Level Approach to Modeling Categorical Outcomes with Differential Misclassification

Abstract

Questionnaire-based health status outcomes are often prone to misclassification. When studying the effect of risk factors on such outcomes, ignoring any potential misclassification may lead to biased effect estimates. Analytical challenges posed by these misclassified outcomes are further complicated when simultaneously exploring factors for both the misclassification and health processes in a multi-level setting. To address these challenges, we propose a fully Bayesian Mixed Hidden Markov Model (BMHMM) for handling differential misclassification in categorical outcomes in a multi-level setting. The BMHMM generalizes the traditional Hidden Markov Model (HMM) by introducing random effects into three sets of HMM parameters for joint estimation of the prevalence, transition and misclassification probabilities. This formulation not only allows joint estimation of all three sets of parameters, but also accounts for cluster level heterogeneity based on a multi-level model structure. Using this novel approach, both the true health status prevalence and the transition probabilities between the health states during follow-up are modeled as functions of covariates. The observed, possibly misclassified, health states are related to the true, but unobserved, health states and covariates. Results from simulation studies are presented to validate the estimation procedure, to show the computational efficiency due to the Bayesian approach and also to illustrate the gains from the proposed method compared to existing methods that ignore outcome misclassification and cluster level heterogeneity. We apply the proposed method to examine the risk factors for both asthma transition and misclassification in the Southern California Children's Health Study (CHS).

1. Introduction

Understanding the relationship between explanatory variables and outcomes is one of the most fundamental tasks in statistical science. However, in practice, both explanatory variables and outcomes could be measured with error. In the case of categorical outcomes, an erroneous assignment of an attribute into a category other than that to which it should be assigned is referred to as misclassification. While measurement error models in general have received considerable attention in the literature for over 50 years [1-3], the issue of misclassification in categorical outcomes is gaining growing attention more recently [4-10]. To our knowledge, there has been no attention to methods exploring differential misclassification and determinants of the health process simultaneously in the context of multi-level design settings. To address this gap, we propose a new multi-level modeling technique to conduct inference in the presence of outcome misclassification.

The proposed technique was motivated by complications that arose when modeling questionnaire-based longitudinal information about children's asthma status that was subject to misclassification and simultaneously exploring risk factors for both the true health process and the misclassification probability. It has been long recognized that the Hidden Markov Model (HMM) provides a natural structure to model a stochastic process in which the true process is unobservable or immeasurable [11]. A general HMM consists of two processes: namely, the emission process and the transition process. The transition process is assumed to follow a Markovian structure, and the observed outcomes are assumed to be independent, conditional on the latent states [12, 13]. HMMs have been successfully applied in many fields such as speech recognition [14] and gene profiling and recognition [15]. However, most HMMs are developed for a single process. In 2007, Altman [16] introduced the concept of mixed hidden Markov models (MHMMs), which has a generalized HMM form that allows for multiple processes. In MHMMs, both fixed and random effects are incorporated into the transition process and the emission process, so that the assumption of having independent observations given the hidden states is relaxed. Altman [16] successfully applied this general approach to count data without considering the modeling of the prevalence probability.

In this article, we propose an approach called Bayesian Mixed Hidden Markov Model (BMHMM). The proposed method complements the framework of Altman [16] to model prevalence and transition probabilities simultaneously for categorical outcomes in the multi-level setting and take the differential misclassification into account. For example, in the Children's Health Study (CHS) data analysis discussed in Section 5, we consider multiple levels of aggregation at the temporal, subject and community levels. Because the Monte Carlo EM (MCEM) algorithm used by Altman [16] is computationally expensive in multi-level settings that have a rich random effect structure, we propose an alternative Bayesian method using Markov chain Monte Carlo (MCMC) for posterior computation.

The remainder of the article is organized as follows. In section 2 we specify the proposed Bayesian Mixed Hidden Markov Model. In section 3, we discuss the Bayesian inference framework. Results from simulation studies that we conducted to validate the estimation procedure, to show the computation efficiency and to make comparisons with models that ignore the outcome misclassification or cluster level heterogeneity are presented in section 4 in order to illustrate the gains from our methods. In section 5, we briefly describe the Southern California Children's Health Study, hereafter referred to as CHS which motivated this work and illustrate the results of the application of BMHMM to CHS data. Finally, Section 6 provides a summary and discussion for further extensions.

2. Bayesian Mixed Hidden Markov Models Formulation

The Bayesian Mixed Hidden Markov Model for categorical outcomes includes a prevalence probability model for the baseline latent true health states, a transition probability model for latent true health states during follow-up and a misclassification probability model (also referred to as emission process in general) for the observed health states, conditional on the latent true health states. For the prevalence and transition probability models, we assume that there are S₁ categories for the latent true health state variable indicated by $Y_{ij}^r$ for the i^th subject at a discrete time j;i=1⋯,N and j=1,⋯,T_i. Baseline health state prevalence probabilities, $P(Y_{i1}^r=k)$, and the transition probabilities, $P\left(Y_{ij}^r=k|Y_{ij-1}^r=l\right)$, are assumed to have a mixed-effect multinomial logit form and are modeled as functions of fixed effect covariates, $X_{ij}^{(1)}$ and random effects, $Z_{ij}^{(1)}$ with state specific coefficients; k,l=1,⋯S₁. Without loss of generality, we assume that the S₁^th state is the reference state. For simplicity of exposition, a first-order Markov process is assumed for the transition probability given the random effects:

$$P\left(Y_{i1}^r=k\right)=\frac{exp\left(a_{1k}+{\alpha }_{1k}^T\cdot X_{i1}^{(1)}+{\mathit{U}}_1^T\cdot Z_{i1}^{(1)}\right)}{1+{\sum }_{h=1\cdots S_1-1}exp\left(a_{1h}+{\alpha }_{1h}^T\cdot X_{i1}^{(1)}+{\mathit{U}}_1^T\cdot Z_{i1}^{(1)}\right)};$$ (1)

$$P\left(Y_{ij}^r=k|Y_{ij-1}^r=l\right)=\frac{exp\left(a_{2k}+a_{3kl}\cdot y_{i(j-1)l}^r+{\alpha }_{2k}^T\cdot X_{ij}^{(1)}+{\beta }_{kl}^T\cdot y_{i(j-1)l}^r\cdot X_{ij}^{(1)}+{\mathit{U}}_1^T\cdot Z_{ij}^{(1)}\right)}{1+{\sum }_{h=1\cdots S_1-1}exp\left(a_{2h}+a_{3hl}\cdot y_{i(j-1)l}^r+{\alpha }_{2h}^T\cdot X_{ij}^{(1)}+{\beta }_{hl}^T\cdot y_{i(j-1)l}^r\cdot X_{ij}^{(1)}+{\mathit{U}}_1^T\cdot Z_{ij}^{(1)}\right)},$$ (2)

where $y_{i(j-1)l}^r$ is the l^th entry in the dummy vector ${\mathit{y}}_{ij-1}^r={\left(y_{i(j-1)1}^r,\cdots ,y_{i(j-1)(S_1-1)}^r\right)}^t$ for latent health state $Y_{ij-1}^r$ and the cluster heterogeneity in the latent health process is captured by the random-effect vector U₁ (e.g., a vector representing the temporal, subject, and community levels as in CHS), typically assumed to follow a multivariate normal distribution (MVN) with mean 0 and unknown variance-covariance matrix Ψ₁ and be shared by both equation (1) and (2). We note that the assumption of normality for U₁ could be relaxed to allow other parametric and non-parametric alternatives. In equation (2), the term $a_{2k}+a_{3kl}\cdot y_{i(j-1)l}^r$ captures the probability for i^th subject's transition from the previous l^th true health state to the k^th true health state at time j. The parameter vector α_2k denotes the fixed effect of covariate $X_{ij}^{(1)}$ on the probability of being in the true k^th health state, given that the true state at the preceding time point is the reference state S₁. The effect of covariate $X_{ij}^{(1)}$ on the probability of transition to the k^th true health state from the previous l^th true state is captured via α_2k+β_kl. There is no time dependent parameter built into the model, and we assume that time dependence may only occur through time-varying covariates. In all terms dealing with the interaction of a covariate with the outcome (either at the previous time, or the latent outcome in the misclassification model), interpretation of the terms in the transition and misclassification models for the probability of transition or misclassification, respectively, are either at X_ij=0, or at an appropriately centered value.

Let $Y_{ij}^o$ represent the observed health state for i^th subject at a discrete time j, taking on values from a finite set {1,⋯,S₂}, where S₂ is a known positive integer not necessarily equal to S₁. Without loss of generality, the S₂^th state is again assumed to be the reference state. For the misclassification probability model, the conditional distributions of $Y_{ij}^o$ given $Y_{ij}^r$ are typically assumed to follow the multinomial distribution and the misclassification probabilities $P\left(Y_{ij}^o=m|Y_{ij}^r=n\right)$ are modeled as functions of fixed effect covariates $X_{ij}^{(2)}$ and random effectS $Z_{ij}^{(2)}$ using the following mixed-effects multinomial logit format:

$$P\left(Y_{ij}^o=m|Y_{ij}^r=n\right)=\frac{exp\left(b_{1m}+b_{2mn}\cdot y_{ijn}^r+{\gamma }_m^T\cdot X_{ij}^{(2)}+{\delta }_{mn}^T\cdot y_{ijn}^r\cdot X_{ij}^{(2)}+{\mathit{U}}_2^T\cdot Z_{ijnm}^{(2)}\right)}{1+{\sum }_{h=1\cdots S_2-1}exp\left(b_{1h}+b_{2hn}\cdot y_{ijn}^r+{\gamma }_h^T\cdot X_{ij}^{(2)}+{\delta }_{hn}^T\cdot y_{ijn}^r\cdot X_{ij}^{(2)}+{\mathit{U}}_2^T\cdot Z_{ijnm}^{(2)}\right)},$$ (3)

where U₂∼MVN(0,Ψ₂) with unknown variance-covariance matrix Ψ₂ and is assumed to be independent of the random effect U₁ in equations (1) and (2), n=1,⋯,S₁ and m=1,⋯,S₂. The term $b_{1m}+b_{2mn}\cdot y_{ijn}^r$ captures the probability of misclassifying the i^th subject from the n^th true health state to the m^th observed health state at time j. The parameter vector γ_m depicts the effect of covariate $X_{ij}^{(2)}$ on the probability of observing the m^th health state, given the true state is the reference state. The effect of covariate $X_{ij}^{(2)}$ on the probability of observing the m^th health state given the true state is the n^th one is given by γ_m+δ_mn.

There are several notable features in the proposed Bayesian Mixed Hidden Markov Model. First, the inclusion of covariates in the regression model for the observed health states allows for differential misclassification, i.e., differences in the misclassification probability for subgroups of subjects. Secondly, the random effects U₁ in the prevalence and transition probability models are used to capture the dependence between cluster-level heterogeneity at the subject and/or community levels and latent true health states. The corresponding random effects U₂ in the misclassification models are independent of the latent true health states and account for the heterogeneity in the misclassification probability. Thirdly, all random effects in this proposed method are assumed to follow the normal distribution. However, the model could be easily extended by assigning more robust distributions to random components such as the t-distribution – a case we will not consider in this paper. Fourthly, all the regression parameters are assumed to be time-independent, because this is a standard constraint in order to ensure identifiability of covariate effects [16]. This constraint is especially important in cases where the prevalence and transition probabilities of both observed and true health states depend on the same set of covariates [17]. The proposed method takes potential time dependence into account by including time-varying covariates in the models.

Based on the assumption of independence among subjects, given random effects, the observed-data likelihood for this model is

$$\begin{array}{l}L({\mathit{Y}}^o|\cdot )={{\displaystyle \iint }}^{}{\displaystyle \prod }_{i=1}^N\left\{{\displaystyle \sum }_{{\mathit{Y}}_i^r}P({\mathit{Y}}_i^o|{\mathit{Y}}_i^r,{\mathit{U}}_2)P({\mathit{Y}}_i^r|{\mathit{U}}_1)\right\}f({\mathit{U}}_1)f({\mathit{U}}_2)d{\mathit{U}}_{1}d{\mathit{U}}_2\hfill \\ ={\displaystyle \iint }{\displaystyle \prod }_{i=1}^N\left\{{\displaystyle \sum }_{{\mathit{Y}}_i^r}P(Y_{i1}^o|Y_{i1}^r,{\mathit{U}}_2)P(Y_{i1}^r|{\mathit{U}}_1){\displaystyle \prod }_{j=2}^{T_i}P(Y_{ij}^o|Y_{ij}^r,{\mathit{U}}_2)P(Y_{ij}^r|Y_{ij-1}^r,{\mathit{U}}_1)\right\}f({\mathit{U}}_1)f({\mathit{U}}_2)d{\mathit{U}}_{1}d{\mathit{U}}_2\hfill \end{array}$$

The proposed model is flexible enough to accommodate data with complicated multi-level structures. For example, for the binary case where the latent true health state could take one of two possible states, the transition probabilities of $P\left(Y_{ij}^r|Y_{ij-1}^r\right)$ are modeled as functions of subject-level random effect u_i and covariate x_ij with community-level random parameters α_c and β_c for main effect and interaction with $y_{ij-1}^r$, respectively:

$$P\left(Y_{ij}^r=1|Y_{ij-1}^r\right)=\frac{exp\left(a+{\alpha }_c\cdot x_{ij}+{\beta }_c\cdot y_{ij-1}^r\cdot x_{ij}+u_i\right)}{1+exp\left(a+{\alpha }_c\cdot x_{ij}+{\beta }_c\cdot y_{ij-1}^r\cdot x_{ij}+u_i\right)}.$$ (4)

The community-level random parameters α_c and β_c could be modeled as follows:

$${\alpha }_c=\alpha +{\varepsilon }_c,{\beta }_c=\beta +{\upsilon }_c,$$ (5)

where ε_c and υ_c are community-level random error terms, usually assumed to be mutually independent with each other and also with u_i. Note that, if we combine equations (4) and (5), we get the unified mixed-effect transition model (6) which is exactly the one given in equation (2):

$$\begin{array}{c}P\left(Y_{ij}^r=1|Y_{ij-1}^r\right)=\frac{exp\left(a+(\alpha +{\varepsilon }_c)\cdot x_{ij}+(\beta +{\nu }_c)\cdot y_{ij-1}^r\cdot x_{ij}+u_i\right)}{1+exp\left(a+(\alpha +{\varepsilon }_c)\cdot x_{ij}+(\beta +{\nu }_c)\cdot y_{ij-1}^r\cdot x_{ij}+u_i\right)}\\ \iff P\left(Y_{ij}^r=1|Y_{ij-1}^r\right)=\frac{exp\left(a+\alpha \cdot x_{ij}+\beta \cdot y_{ij-1}^r\cdot x_{ij}+{\varepsilon }_c\cdot x_{ij}+{\nu }_c\cdot y_{ij-1}^r\cdot x_{ij}+u_i\right)}{1+exp\left(a+\alpha \cdot x_{ij}+\beta \cdot y_{ij-1}^r\cdot x_{ij}+{\varepsilon }_c\cdot x_{ij}+{\nu }_c\cdot y_{ij-1}^r\cdot x_{ij}+u_i\right)}\end{array}$$ (6)

3. Bayesian Inference

The hierarchical characteristics of the proposed BMHMM model make a Bayesian approach attractive for estimation and inference. Altman [16] proposed a number of frequentist estimation methods for fitting MHMMs including one that uses the Monte Carlo EM algorithm (MCEM). Although the MCEM algorithm guarantees increments in the likelihood after each iteration and eventual convergence, several issues related to implementation arise as model complexity increases. First, the MCEM algorithm converges relatively slowly and hence may not be practical for dealing with complex models. Secondly, in some cases, the MCEM algorithm may get trapped in a local maximum without reaching the global maximum when dealing with mixture models. Thirdly, calculations of standard errors and confidence intervals are not usually straightforward [18]. Fourthly, the computational burden increases exponentially when the number of integrals becomes large. In fact, it has been pointed out that it is almost impossible to fit models including nonlinear functions of more than two latent variables using the EM algorithm under currently available computational capacity [19]. The Bayesian approach eliminates the need for numerical integration and enables interval estimation as a direct product of the estimation routine. Simulation based methods, such as the Markov chain Monte Carlo approach [20] including the Metropolis-Hasting algorithm [21, 22] and the Gibbs sampler [23], make the Bayesian approach relatively easily adaptable to complex latent variable models that are more difficult to fit in the frequentist setting.

The collection of all precision parameters in BMHMM is (Ψ₁,Ψ₂) and that of all regression parameters is Θ=(a₁, a₂, a₃, b₁,b₂, α₁,α₂, β, γ,δ). Following Garrett and Zeger [24], we assign a multivariate normal prior for Θ:

$$\mathbf{\Theta }\mathbf{~}\mathbf{\text{MVN}}(\mathbf{0}\mathbf{,}\frac{\mathbf{9}}{\mathbf{4}}\mathbf{I})$$

We also specify an Inverse-Wishart prior for the variance-covariance matrix of random effects with pre-specified hyper-parameters as follows:

$${\mathit{\psi }}_{\mathit{g}}~\mathbf{\text{Inv}}-\mathbf{\text{Wishart}}({\mathbf{\sum }}_{\mathit{g}},m_{\mathit{g}}),g=1,2,$$

where the dimension of Ψ_g is p_g. When p_g=1, Inv-Whishart prior distribution will reduce to Inv-Gamma distribution. In this case, the inverse of Ψ_g is assumed to follow a non-informative gamma prior distribution with shape parameter 0.01 and rate parameter 0.01.

The joint posterior distribution for all parameters and latent variables is

$$\begin{array}{l}f(\mathbf{\Theta }\mathbf{,}{\mathit{\psi }}_{\mathbf{1}}\mathbf{,}{\mathit{\psi }}_{\mathbf{2}}\mathbf{,}{\mathit{U}}_{\mathbf{1}}\mathbf{,}{\mathit{U}}_{\mathbf{2}}\mathbf{,}{\mathit{Y}}^r|{\mathit{Y}}^o)\propto f({\mathit{Y}}^o|\mathbf{\Theta }\mathbf{,}{\mathit{\psi }}_{\mathbf{1}}\mathbf{,}{\mathit{\psi }}_{\mathbf{2}}\mathbf{,}{\mathit{U}}_{\mathbf{1}}\mathbf{,}{\mathit{U}}_{\mathbf{2}}\mathbf{,}{\mathit{Y}}^r)f({\mathit{Y}}^r|{\mathit{U}}_{\mathbf{1}})f({\mathit{U}}_{\mathbf{1}})f({\mathit{U}}_{\mathbf{2}})f(\mathbf{\Theta })f({\mathit{\psi }}_{\mathbf{1}})f({\mathit{\psi }}_{\mathbf{2}})\hfill \\ \propto {\displaystyle \prod }_{i=1}^{N}P(Y_{i1}^o|Y_{i1}^r,{\mathit{U}}_1,{\mathit{U}}_2)P(Y_{i1}^r|{\mathit{U}}_1){\displaystyle \prod }_{j=2}^{T_i}P(Y_{ij}^o|Y_{ij}^r,{\mathit{U}}_1,{\mathit{U}}_2)P(Y_{ij}^r|Y_{ij-1}^r,{\mathit{U}}_1){\displaystyle \prod }_{g=1}^2\frac{1}{{|{\mathit{\psi }}_{\mathit{g}}|}^{0.5}}exp\left(-\frac{1}{2}{{\mathit{U}}^{\prime }}_{\mathit{g}}{{\mathit{\psi }}_{\mathit{g}}}^{\mathbf{-}\mathbf{1}}{\mathit{U}}_{\mathit{g}}\right)\hfill \\ \times exp\left(-\frac{9}{8}\mathbf{\Theta }\prime \mathbf{\Theta }\right){\displaystyle \prod }_{g=1}^2\frac{{|{\mathbf{\sum }}_{\mathit{g}}|}^{m_g/2}{|{\mathit{\psi }}_{\mathit{g}}|}^{-(m_g+p_g+1)/2}{e}^{-\mathit{\text{trace}}({\mathbf{\sum }}_{\mathit{g}}{{\mathit{\psi }}_{\mathit{g}}}^{-2})/2}}{2^{m_g{p}_g/2}{\Gamma }_{p_g}\left(m_g/2\right)}\hfill \end{array}$$

The unobserved latent true states are directly sampled from their conditional posterior distributions. The parameters in the models may be updated using a Metropolis-step or directly sampled from their posterior distributions. All of those computations can be implemented using WinBUGS [25]. Convergence of the MCMC algorithm is examined by using a convergence diagnostic statistic proposed by Gelman and Rubin [26]. In this approach, two parallel Markov chains with different starting values are used, and convergence is then said to be reached when the Gelman-Rubin statistic is close enough to 1. More details on the MCMC algorithm are given in the Appendix A.

Bayesian Mixed hidden Markov models are mixture models, where both observations and transitions are generated from mixture distributions. As is the case with Bayesian mixture models, the so-called label switching problem arises [27]. The label switching problem is caused due to the fact that the likelihood of a Bayesian mixture model could be invariant to permutations of the values, “labels”, of the discrete latent variable, such as $Y_{ij}^r$. This leads to non-identifiability of the labels of the latent discrete variable. Although various advanced strategies have been proposed for “relabeling” the MCMC output in an attempt to remove the label switching problem, we implement the most straightforward one called the Identifiability Constraints method which defines a restricted parameter space (such as $\mathit{\text{logit}}\left(P(Y_{ij}^o=1|Y_{ij}^r=1)\right)>\mathit{\text{logit}}\left(P(Y_{ij}^o=1|Y_{ij}^r=0)\right)$, when $Y_{ij}^o$ and $Y_{ij}^r$ are binary outcomes.) to ensure that there exists a unique permutation for component-specific parameters [27]. Here, the parameters in the random effects in the misclassification probability are fixed to ensure the identifiability of the regression parameters, without relying on informative prior distributions.

4. Simulation Study

A series of simulation studies were conducted to study the performance of our proposed modeling approach. In this section, we illustrated the performance of the new approach from the following aspects: 1) model validation; 2) computational efficiency of the MCMC based approach compared to the EM-based algorithms; 3) gains in terms of low bias and decreased MSE compared to the HMM that ignores cluster level heterogeneity; and 4) gains in terms of high average posterior coverage probabilities (APC), low bias and decreased mean square error (MSE) from BMHMM compared to longitudinal logistic regression model that ignores the misclassification. In all these simulations, we focused on the binary case, where both the latent and the observed health states have two categories in the simulated data structure. Even though an absorbing state is defined in some applications as a special true state in which the latent process will never leave it once it enters (e.g., death), no absorbing state in the true states is assumed in this simulation in order to allow for more general settings.

4.1 Model Validation

We conducted a simulation study to verify that our MCMC approach works properly. In each simulation replication, 400 subjects with 6 yearly binary observations were generated based on the following set of models:

Prevalence Probability Model

$$P(Y_{i1}^r=1)=\frac{exp(a_1+{\alpha }_1\cdot X{1}_{i1}+u_i)}{1+exp(a_1+{\alpha }_1\cdot X{1}_{i1}+u_i)},u_i~N(0,{\sigma }_1^2);$$ (7)

Transition Probability Model

$$P(Y_{ij}^r=1|Y_{ij-1}^r)=\frac{exp(a_2+a_3\cdot Y_{ij-1}^r+{\alpha }_2\cdot X{1}_{ij}+{\alpha }_3\cdot Y_{ij-1}^r\cdot X{1}_{ij}+u_i)}{1+exp(a_2+a_3\cdot Y_{ij-1}^r+{\alpha }_2\cdot X{1}_{ij}+{\alpha }_3\cdot Y_{ij-1}^r\cdot X{1}_{ij}+u_i)};$$ (8)

Misclassification Probability Model

$$P(Y_{ij}^o=1|Y_{ij}^r)=\frac{exp(b_1+b_2\cdot Y_{ij}^r+{\lambda }_1\cdot X{2}_i+{\lambda }_2\cdot Y_{ij}^r\cdot X{2}_i)}{1+exp(b_1+b_2\cdot Y_{ij}^r+{\lambda }_1\cdot X{2}_i+{\lambda }_2\cdot Y_{ij}^r\cdot X{2}_i)},$$ (9)

where covariate X1_ij for i^th subject at time j is a centered time-varying continuous variable associated with the latent process and X2_i is a time independent binary variable for i^th subject related to the misclassification model.

The MCMC algorithm was run with two chains on each simulated data set. We used the true values with a small perturbation as initial values. In each chain, the first 10000 iterations were discarded as a burn-in, and samples from every 10^th iteration in the next 10000 iterations were used to calculate the posterior summaries of parameters of interest. The Gelman-Rubin statistic was used to check for convergence [26]. The trace plots of the posterior samples versus iteration were also used to indicate that our posterior samples are indeed obtained from converged posterior distributions. For dealing with the label switching problem, we assume that parameter b₂>0 and b₂+λ₂>0 in order to satisfy the condition that $P(Y_{ij}^o=1|Y_{ij}^r=1)>P(Y_{ij}^o=1|Y_{ij}^r=0)$. This condition is a reasonable constraint for our applications because we believe that the sensitivity should be greater than the false positive rate when using a well designed questionnaire.

Table I summarized the results obtained based on 100 replications from the simulation process described above. The true values of all parameters in the simulated model are listed in the last column of Table I. Average bias and nominal 95% coverage were reported for all model parameters. The results showed that estimated posterior means for parameters of interest were close to the true values on average (Bias range = (0, 0.19)). About half of the median estimates were above the true parameter values. In addition, coverage rates of the estimated 95% credible intervals (CI) containing the true parameter values were at least 96%. Our simulation results confirmed that our estimation procedure performed well in terms of average bias and nominal coverage for both mean and variance parameters.

Table I. Simulation Results for Bayesian Mixed Hidden Markov Model.

	Coverage # (Total=100)	Average Mean	Average Median	Average SD	Mean Bias	Median Bias	True Value
Prevalence probability:
a1	100	-2.17	-2.17	0.26	0.03	0.03	-2.2
α1	98	0.08	0.08	0.17	0.02	0.02	0.1
Transition probability:
a2	100	-3.60	-3.60	0.20	0.00	0.00	-3.6
a3	100	5.56	5.56	0.30	0.16	0.16	5.4
α2	99	0.10	0.10	0.17	0.00	0.00	0.1
α3	100	0.18	0.19	0.26	0.02	0.01	0.2
Misclassification probability:
b1	96	-4.06	-4.06	0.17	0.14	0.14	-4.2
b2	97	5.31	5.31	0.19	0.19	0.19	5.5
λ1	100	-0.08	-0.08	0.24	0.02	0.02	-0.1
λ2	100	1.81	1.80	0.32	0.19	0.20	2
σ1	99	1.90	1.91	0.46	0.10	0.09	2

4.2 Computational Efficiency Compared to the EM-based Algorithms

To illustrate the computational efficiency of MCMC in the proposed BMHMM, we compared the computational time needed to fit the models specified via equations (7)-(9) by using our proposed MCMC algorithm and two widely used EM-based algorithms: MCEM and Stochastic EM (SEM). The MCMC algorithm procedure has been described in the subsection 4.1. Non-informative priors are used to ensure proper comparability with frequentist methods. For both EM algorithms, we first generated B samples of ${\mathit{Y}}_i^r$ and u_i for each subject from their conditional distributions on the observed data and parameter estimates at the p^th iteration via Gibbs sampling, and then approximated the expected value of the log likelihood function by calculating the average log likelihood over the B simulated samples in the E step. In the M step, we employed the quasi-Newton algorithm to get the updated parameter estimates which numerically maximize the expected log likelihood function in the E step. We repeated the E-step and M-step iteratively until convergence. The convergence is deemed to be reached when the sum of absolute changes of current estimated parameter values from their previous ones is less than 0.1. The size of simulated samples B is 2000 for MCEM algorithm. We note that the stochastic EM procedure is identical to that of MCEM but with only one simulation (B=1) conducted at each iteration.

Table II summarizes the estimates of all parameters from three algorithms and the computational time for each algorithm. The point estimates from all three algorithms performed properly except for the fact that a few estimates from the EM based algorithms might have been trapped at local maxima (such as the estimate of α₃ from the Stochastic EM algorithm). It took the MCMC algorithm less than one hour to reach the convergence, while several days were needed for the MCEM algorithm. The SEM algorithm converged much faster than MCEM algorithm and improved the computational speed by reducing the computing time to five hours, but was still significantly slower than our MCMC algorithm. All calculations were run using a dual core 2.83 GHz Intel processor and R package.

Table II.

Comparisons of Computational Efficiency MCMC and EM-based Algorithms with respect to Computational Times.

	MCMC	SEM	MCEM	True Value
Prevalence probability:
a1	-2.6	-1.9	-1.8	-2.2
α1	0.1	0.3	-0.2	0.1
Transition probability:
a2	-3.5	-3.3	-3.4	-3.6
a3	5.4	5.9	5.7	5.4
α2	0.2	-0.4	-0.1	0.1
α3	0.3	1.1	0.3	0.2
Misclassification probability:
b1	-4	-4.1	-4.2	-4.2
b2	5.3	5.3	5.5	5.5
λ1	-0.5	0.0	0.3	-0.1
λ2	2.4	1.8	2.2	2
σ1	2.5	1.0	1.9	2
Computation Time	<1 hr	5 hr	>2 Days

4.3 Gains from Accounting for the Cluster Level heterogeneity

To illustrate the gains from accounting for the cluster level heterogeneity, we fitted the traditional HMM using the data sets simulated from equations (7)-(9) in subsection 4.1. More specifically, we fitted models similar to equations (7)-(9) but without the random effect u_i. Under the same inference procedure, we calculated the estimates of parameters from 100 simulated data sets and compared them with the same true values used in the subsection 4.1 in terms of average bias and coverage rates of the estimated 95% CI containing the true values (Table III). We found that the estimates of main effect parameters a₁, a₂ and a₃ in both the prevalence and the transition probability models had a very poor coverage rate and large average bias (a₁: coverage rates=0%, bias=0.70; a₂: coverage rates=25%, bias=0.36; a₃: coverage rates=8%, bias=0.63). The estimates of parameters associated with the covariate X1_ij in both prevalence and transition probability models and parameters in the misclassification probability models were close to the true value on average (Bias range=(0,0.19)). The coverage rates of the estimated 95% CI for these parameters were at least 95%. The homogenous effect of the covariate X1_ij assumption in equations (7) and (8) is perhaps the main reason for good performances in parameters associated with the covariate X1_ij. Our simulation confirmed that ignoring the cluster level heterogeneity in HMM resulted in severe bias and poor coverage rates in the related parameter estimates.

Table III. Simulation Results for Bayesian Hidden Markov Model without Cluster-Effect.

	Coverage # (Total=100)	Average Mean	Average Median	Average SD	Mean Bias	Median Bias	True Value
Prevalence probability:
a1	0	-1.50	-1.50	0.13	0.70	0.70	-2.2
α1	96	0.06	0.06	0.13	0.04	0.04	0.1
Transition probability:
a2	25	-3.24	-3.24	0.13	0.36	0.36	-3.6
a3	8	6.03	6.03	0.23	0.63	0.63	5.4
α2	97	0.04	0.04	0.15	0.06	0.06	0.1
α3	100	0.14	0.14	0.23	0.06	0.06	0.2
Misclassification probability:
b1	95	-4.06	-4.05	0.17	0.14	0.15	-4.2
b2	95	5.32	5.32	0.19	0.18	0.18	5.5
λ1	100	-0.08	-0.08	0.24	0.02	0.02	-0.1
λ2	98	1.81	1.81	0.32	0.19	0.19	2

4.4 Gains from Accounting for Outcome Misclassification

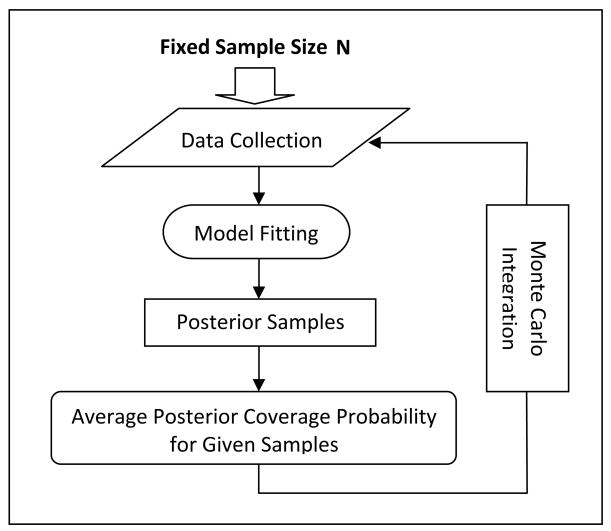
To illustrate the gains obtained from accounting for outcome misclassification, we first employed the simulation-based approach of Wang and Gelfand [28] to compare the average posterior coverage probabilities (APC) of symmetric intervals around the true value with varying interval lengths between the proposed modeling approach and the traditional longitudinal logistic model for a given sample size [28-30]. This generic Bayesian method provides an insight about how well the posterior samples from each given model clustered around the true values for a given sample size. Figure S.1 in the Appendix B provides a flow chart summarizing the steps in calculating APC.

For computational expediency, we simplified the above simulation process based on equation (9) and assumed that the misclassification probabilities in BMHMM are fixed with relatively high specificity (specificity=0.9) and sensitivity (sensitivity=0.9) and don't depend on any covariates. In each simulation replication (total 1000 replications), 100 subjects with six yearly observations were generated based on the following set of BMHMM models:

Prevalence Probability Model

$$\text{Pr}(Y_{i1}^r=1)=\frac{exp(a_1+{\alpha }_1\cdot X_{i1}+u_i)}{1+exp(a_1+{\alpha }_1\cdot X_{i1}+u_i)};$$ (10)

Transition Probability Model

$$Pr\left(Y_{ij}^r=1|Y_{ij-1}^r\right)=\frac{exp\left(a_2+{\alpha }_2\cdot X_{ij}+{\alpha }_3\cdot Y_{ij-1}^r+u_i\right)}{1+exp\left(a_2+{\alpha }_2\cdot X_{ij}+{\alpha }_3\cdot Y_{ij-1}^r+u_i\right)};$$ (11)

Misclassification Probability Model

$$\begin{array}{l}Pr(Y_{ij}^o=1|Y_{ij}^r=0)=1-\text{Specificity}=1-Pr(Y_{ij}^o=0|Y_{ij}^r=0)=0.1;\hfill \\ Pr(Y_{ij}^o=0|Y_{ij}^r=1)=1-\text{Sensitivity}=1-Pr(Y_{ij}^o=1|Y_{ij}^r=1)=0.1;\hfill \end{array}$$ (12)

The corresponding traditional longitudinal logistic regression method that ignores the misclassification and is used to fit the simulated data from equations (10)-(12) is defined as follows:

$$Pr(Y_{ij}^o=1)=\frac{exp(b+\beta \cdot X_{ij}+u_i)}{1+exp(b+\beta \cdot X_{ij}+u_i)}$$ (13)

To further simplify the comparison, we assumed that a₁=a₂=a=0.1, a₁=a₂=a=1.5 and u∼N(0,1) in (10) and (11). In other words, we assume that the intercept and covariate effects in the prevalence and transition models are identical. Note that if we assume that misclassification probabilities are such that $Pr(Y_{ij}^o=1|Y_{ij-1}^r=0)=0,Pr(Y_{ij}^o=0|Y_{ij-1}^r=1)=0$ and the transition effect α₃=0, BMHMM (10)-(12) is identical to the logistic regression (13). The coefficients α and β of covariate X_ij in the BMHMM (true model) and logistic regression model (misspecified model), respectively, measure the change of the log of odds per one unit change in covariate X_ij, describing the association between the outcome and covariate X_ij which is a continuous covariate simulated from standard normal distribution. We were interested in comparing the performance of effect estimations of parameters α and β associated with covariate X_ij from both models.

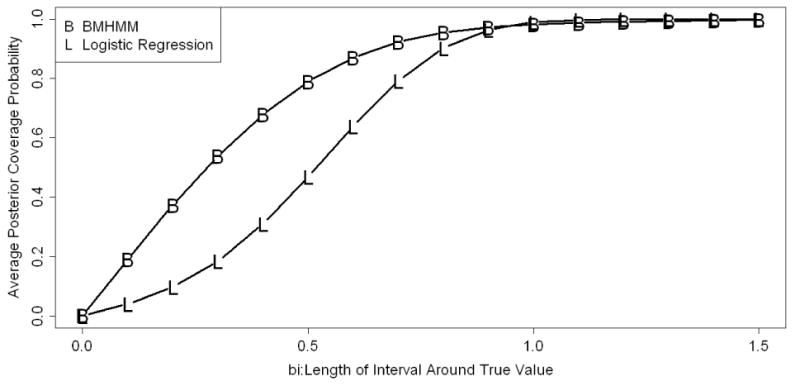
We computed the APC of a symmetric interval around the true value of the parameters associated with the covariate X_ij (True value=1.5) for the BMHMM and longitudinal logistic regression model described above and compared them for various lengths of symmetric intervals. The details of APC computation and the comparison procedure employed in this study are described in Appendix B. Figure 1 depicts the trends of APC against a series of increasing lengths of interval around the true value for two models. Both coverage probabilities increase monotonically and become identical as the length of the interval around the true value increases. The BMHMM had better coverage probability than the traditional longitudinal logistic regression in small lengths of intervals around the true value. These results indicated that the posterior distribution of the covariate effect from BMHMM is more likely to be clustered around the true value compared to those from traditional longitudinal logistic regression that ignores outcome misclassification.

Figure 1. Average Posterior Coverage Probability Curve Comparison between BMHMM and Logistic Model.

We also investigated the potential bias reduction in the estimation of the effect of covariate X_ij achieved by accounting for the misclassification under the same simulation setting. The histogram in the top panel of Figure 2 shows that in BMHMM, the estimated coefficients from 1000 simulated data sets are clustered around the true value of 1.5, with average bias of 0.06. However, the longitudinal logistic regression model that ignores the misclassification resulted in a severe downward bias of 0.51.

Figure 2.

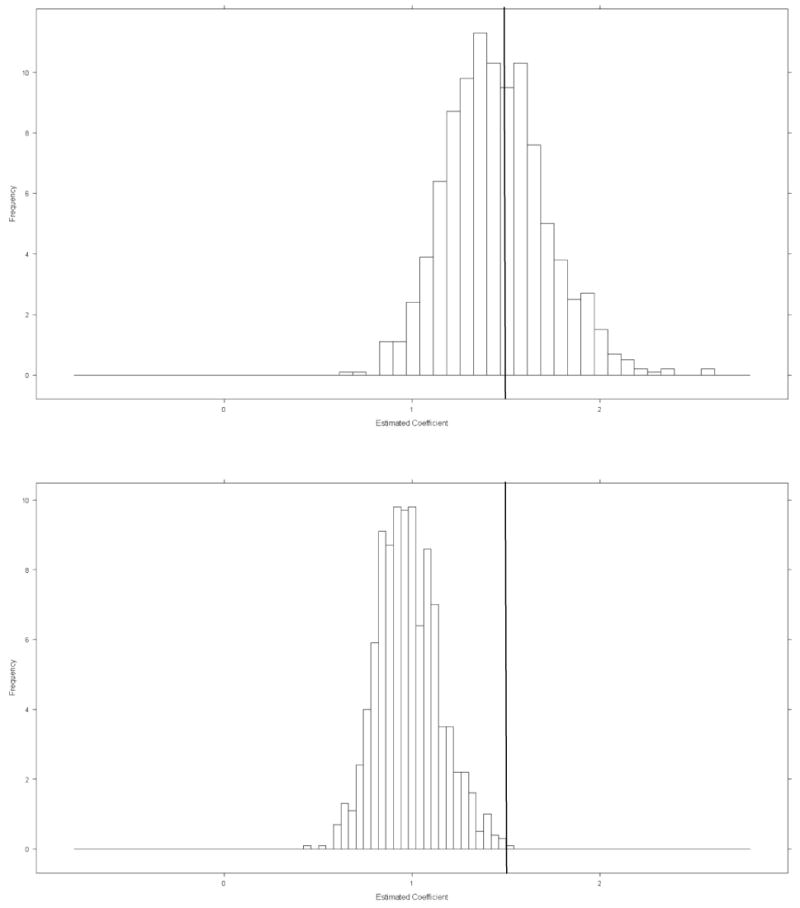
Top panel: Histogram of estimated effect of covariate Z for BMHMM which account for misclassification (True value is 1.5). Bottom panel: Histogram of estimated effect of covariate Z for Logistic Regression which didn't account for misclassification

In order to take the bias-variance tradeoff into account in our model comparisons, we further calculated the MSEs of the estimators of the effects of covariate X_ij from both traditional longitudinal logistic regression and BMHMM. We conducted these comparisons under three sensitivity/specificity settings, which represent no misclassification, low misclassification and high misclassification, respectively (Table IV). In all settings, our BMHMM method gives smaller MSE than logistic regression when the covariate X_ij is associated with the outcomes with effect size 1.5. The difference in MSE is particularly dramatic when the misclassification probability is high. When the covariate X is not associated with the outcomes, i.e. the effect size is set to zero, the MSE in our BMHMM is comparable to those from a traditional longitudinal logistic regression.

Table IV. Mean Square Error for the Estimation of the Effect of Covariate X in the Simulation Study with Various Misclassification Settings.

		Mean Square Error
Misclassification Settings*	True Effect of Covariate Xij	Logistic Regression (Frequentist)**	Logistic Regression (Bayesian)	BMHMM
1	1.5	0.05	0.04	0.04
2		0.29	0.28	0.08
3		1.15	1.12	0.23
1	0	0.02	0.02	0.02
2		0.02	0.02	0.03
3		0.02	0.02	0.01

^*1: Sensitivity=1.0, Specificity=1.0; 2: Sensitivity=0.9, Specificity=0.9; 3: Sensitivity=0.8, Specificity=0.6; These three sensitivity/specificity settings represent no misclassification, low misclassification and high misclassification, respectively.

^**glmer function in lme4 package in R program is used for this analysis.

5. Application in The Southern California Children'S Health Study

The proposed BMHMM model is illustrated by modeling potentially misclassified outcome data on self-reported asthma status (from a parent or the child) in the Southern California Children's Health Study (CHS). The CHS is a longitudinal study initiated in 1993 and it originally enrolled 3600 children from 12 Southern California communities [31]. A baseline questionnaire was completed by the primary caregiver of each child, covering residential history, current residential characteristics, personal risk factors, respiratory symptoms, and usual activities. An abbreviated yearly follow-up questionnaire was used to collect data on chronic respiratory symptoms and diseases and time-dependent covariates. When a parent or legal guardian answered “yes” to the question “Has a doctor diagnosed your child with asthma?” in the baseline questionnaire, or the child answered “yes” to the question “Has a doctor ever said you had asthma?” in the follow-up annual questionnaire at time of pulmonary function (PF) testing, the child was classified as having asthma [32, 33]. The main aim of our analysis was to properly handle the complications in modeling self-reported and questionnaire based information on physician diagnosed asthma which is observed with misclassification so that we can explore the risk factors for asthma prevalence, transition and misclassification processes in children simultaneously. Given that the CHS has a multi-level study design with measurements (and hence effects estimated) made at the temporal (over time), individual and community level, any proper modeling needs to be able handle the complex correlation structure due to the multi-level design. Hence, the BMHMM we have developed in Section 2, mainly motivated by the CHS, provides an ideal modeling approach for the CHS data structure. For purposes of illustration, the study cohort in this paper was restricted to 643 participants (308 girls and 335 boys) who have complete 4 year observations (1993-1996). In this analysis, self-reported asthma status was defined as a binary outcome; namely, “Non-asthma” or “Asthma”. The latent true asthma status was also defined as a binary outcome in the same manner. The “Asthma” state in the “unobserved” latent process was considered to be an absorbing state, i.e., once a child reported physician diagnosed asthma, he/she would stay in this latent asthmatic state afterwards. Note that this implicitly recognizes the conventional belief that a child remains asthmatic in the “true” sense (regardless of level of activity) once he/she is diagnosed with asthma, even though the “observed” asthma status may not necessarily be consistent about that. We also point out that our assumption of an “absorbing” state for the latent asthma status could be easily relaxed under our general modeling paradigm. Gender, age and race/ethnicity variables were default covariates in both the prevalence and transition probability models. Age was also forced into the misclassification model. In this application, residual within-subject correlation (above and beyond what could be accounted for via the multi-level random effect structure) was accounted for via a Markov first-order transition structure. A community-level random effect was included to account for community level heterogeneity. In the model fitting process, we ran two chains of 100,000 iterations, discarded the first 50,000 iterations for burn-in, and kept results from every 50^th iteration. The convergence of the model is then assessed by the Gelman-Rubin statistic [26].

The effect estimates (along with 95% CI) of the covariates entering into the final BMHMM for child reported asthma are summarized in Table V. In the prevalence probability model, we found that severe wheezing, as an important symptom of asthma, was significantly associated with asthma prevalence. Children with severe wheezing at baseline were more likely to have asthma at the same time (Severe Wheezing: OR (95% CI) = 5.2(1.7, 15.0)).

Table V. Parameter Estimates of Covariate for Children Reported Asthma in the CHS in BMHMM^{^}.

	Mean (95% CI)	OR (95% CI)
Prevalence probability:
Age	0.44 (-0.63,1.47)	1.55 (0.53,4.35)
Allergy	0.9 (-0.01,1.79)	2.46 (0.99,5.99)
Severe Wheeze	1.65 (0.52,2.71)*	5.21 (1.68,15.03)*
Transition probability:
Age	-0.76 (-1.59,-0.19)*	0.47 (0.20,0.83)*
Allergy	0.98 (0.18,1.69)*	2.66 (1.20,5.42)*
Current Wheeze	0.83 (-0.15,1.73)	2.29 (0.86,5.64)
Family History of Asthma	1.01 (0.23,1.85)*	2.75 (1.26,6.36)*
Misclassification probability:
AboveHS†
When Latent True Asthma=0	-0.16 (-1.08,0.74)	0.85 (0.34,2.10)
When Latent True Asthma=1	1.33 (0.04,2.57)*	3.78 (1.04,13.07)*
Current Wheeze	1.21 (0.38,2.06)*	3.35 (1.46,7.85)*

^{^}In the prevalence and transition probability models, we also adjusted for gender, and race/ethnicity. Medication use and Forced Expiratory Volume (FEV) were adjusted in prevalence models. Transition models were also adjusted for Ozone, number of sports and their interaction. In the misclassification probability models, we also adjusted for age and gender. Latent true asthma variable and its interaction with age were included in the misclassification model. Town-level random effect is included in the transition process.

^†AboveHS: An indicator variable of whether children come from families with education above the high school level.

Since we assumed that the true asthma status is an absorbing state, the transition probability model for asthma modeled the risk of developing asthma so that we can explore the risk factors associated with onset of physician diagnosed asthma. We found that Age, Family history of asthma and Allergy were risk factors significantly associated with asthma onset. More specifically, as age increased, children were less likely to become asthmatic, and for one additional year increase of age (from 10 years of age), the odds of new onset asthma decreases by 50% (Age: OR (95% CI) = 0.5 (0.2, 0.8)). During follow-up, children with allergy or family history of asthma were more likely to develop physician diagnosed asthma (Allergy: OR (95% CI) = 2.7 (1.2, 5.4); Family History of Asthma: OR (95% CI) = 2.7 (1.3, 6.4)). For comparison, we also fit traditional longitudinal logistic regression models to the same data set. All the covariates in the final prevalence and transition probability models in BMHMM were also included in the longitudinal logistic models. Both subject-level and community-level random effects were included for capturing the multi-level heterogeneity. In the logistic mixed effects regression models, neither Allergy nor Family History of Asthma were significantly associated with the onset of physician diagnosed asthma (Allergy: OR (95% CI)=4.4 (0.0, 2186.4); Family History of Asthma: OR (95% CI)= 1.9 (0.0, 749.9).

Besides the findings for both prevalence and transition probability models above, the BMHMM provides us with new insight by detecting factors associated with misclassification of asthma status. The covariate selection process in the misclassification model was based on the Deviance Information Criterion (DIC) [34]. In the final misclassification model, we found that children with current wheezing but without true latent asthma were more likely to misclassify themselves as having asthma (OR (95% CI) = 3.4 (1.5, 7.8)). Children from families with education above the high school level were more likely to provide accurate response when they indeed have physician diagnosed asthma, compared to those with high school education or less (OR (95% CI) = 3.8 (1.1, 13.1)). Table S.1, a complete version of Table V, in the Appendix C provides both reported and unreported parameter estimates as a reader's reference.

6. Summary and Discussion

In this article, we introduced a new latent variable approach called Bayesian Mixed Hidden Markov Model for modeling categorical outcomes with potential misclassification in the multi-level setting. The approach is useful when the outcome of interest is prone to being measured with error and the research interest is in simultaneously exploring the risk factors associated with the prevalence, transition and misclassification probabilities. We treat the true health state as a latent variable and we model the latent variables in both the baseline prevalence and transition probabilities during follow-up as functions of covariates and random effects. The strength of the proposed BMHMM lies in its ability to easily accommodate data from rich multi-level settings where several random effects are introduced to account for multiple levels of data aggregation, and allows for differential misclassification via regression of the observed health state on the latent true health state and covariates. We employ the fully Bayesian approach for improving computational efficiency. For illustrating the utility and benefits of this new method, we compared the average posterior coverage probabilities, bias and MSE associated with the estimation of parameters of interest from our BMHMM to those from the traditional longitudinal logistic regression method that ignores misclassification. This was done under various simulated misclassification settings. The proposed BMHMM was successfully applied to data from the CHS for modeling child-reported asthma that has been shown to be prone to misclassification. We found that parental education and children's wheezing status are two influential factors on the reliability of our observed outcomes.

In our application, we set the number of latent true health states as fixed and modeled self-reported asthma as a binary variable. However, the proposed method is general enough to allow any fixed number of health states. One potential future research area on this topic would be looking into how one could let the data themselves determine the number of latent classes. For example, one can put a prior distribution on the number of states and make the posterior inference based on the joint model. However, the computational intensity and the difficulty in interpretation of findings could prove to be big challenges. Another interesting research area is the implementation of forward-backward algorithm and Viterbi algorithm in the Bayesian inference so that we can have the ability to estimate the most possible latent true health state at any time and health state sequence for any subject. This potential research direction could provide medical practitioners with a useful predictive tool and may have a strong practical implication for clinical practice by allowing a more accurate prediction of children's asthma status instead of being solely dependent on questionnaire based response.

As is the case with all latent variable models, identifiability of regression parameters is always a concern. Our proposed models are mixture models and are fitted using a Bayesian MCMC algorithm. In such cases, one needs to deal with a well known identifiability problem, the “Label Switching Problem” [35]. In this paper, we used a relatively easy solution of putting Identifiability Constraints [36]. However, in some cases, it is hard to have adequate prior knowledge in setting reasonable parameter constraints. A more recent development in solving the label switching problem is the probabilistic relabeling algorithm proposed by Sperrin et al. [37], which has been successfully applied in simple mixture models. Unlike the deterministic relabeling algorithm, the probabilistic relabeling algorithm does not rely on a specified loss function, and allows the incorporation of uncertainty in the relabeling process. More research is needed in integrating such relatively more advanced algorithms into our Bayesian modeling process. In our application, the random effect in the misclassification model was dropped off for parsimony as we did not think it would be necessary for our data. Our rationale for including the random effects in the transition process is due to the multi-level characteristics of the data set. However, we don't have any priori reasons to consider the existence of cluster level heterogeneity during the misclassification model and prior knowledge to assign a reasonable informative prior distribution to the scale parameters in the misclassification in this application.

Appendix A. Details of the MCMC Algorithm

We describe the details of the MCMC algorithm used to sample from the joint posterior distribution in Section 3. Each parameter vector was updated by conditioning on all other parameters via Gibbs sampling. For simplicity of development, we denote the regression parameters in the prevalence, transition and misclassification probability models byΘ₁=(a₁,α₁), Θ₂=(a₂,a_3,α₂, β) and Θ₃=(b₁, b₂, γ, δ), respectively. The latent true health state for subject i is sampled directly from their full conditional distributions:

$$\begin{array}{l}p(Y_{i1}^r=k|{\mathbf{\Theta }}_{\mathbf{1}}\mathbf{,}{\mathbf{\Theta }}_{\mathbf{2}},{\mathbf{\Theta }}_{\mathbf{3}}\mathbf{,}{\mathit{U}}_{\mathit{1}}\mathbf{,}{\mathit{U}}_{\mathbf{2}}\mathbf{,}{\mathit{Y}}^o)\hfill \\ =\frac{p(Y_{i1}^r=k|{\mathbf{\Theta }}_{\mathbf{1}}\mathbf{,}{\mathit{U}}_{\mathbf{1}})\cdot p(Y_{i2}^r|Y_{i1}^r=k,{\mathbf{\Theta }}_{\mathbf{2}}\mathbf{,}{\mathit{U}}_{\mathbf{1}})\cdot p(Y_{i1}^o|Y_{i1}^r=k,{\mathbf{\Theta }}_{\mathbf{3}}\mathbf{,}{\mathit{U}}_{\mathbf{2}})}{{\sum }_{h=1\cdots S_1}p(Y_{i1}^r=h|{\mathbf{\Theta }}_{\mathbf{1}}\mathbf{,}{\mathit{U}}_{\mathbf{1}})\cdot p(Y_{i2}^r|Y_{i1}^r=h,{\mathbf{\Theta }}_{\mathbf{2}}\mathbf{,}{\mathit{U}}_{\mathbf{1}})\cdot p(Y_{i1}^o|Y_{i1}^r=h,{\mathbf{\Theta }}_{\mathbf{3}}\mathbf{,}{\mathit{U}}_{\mathit{2}})}\hfill \end{array}$$ (A1)

$$p(Y_{ij}^r=k|{\mathbf{\Theta }}_{\mathbf{1}}\mathbf{,}{\mathbf{\Theta }}_{\mathbf{2}}\mathbf{,}{\mathbf{\Theta }}_{\mathbf{3}}\mathbf{,}{\mathit{U}}_{\mathbf{1}}\mathbf{,}{\mathit{U}}_{\mathbf{2}}\mathbf{,}{\mathit{Y}}^o)=\frac{p\left(Y_{ij}^r=k|Y_{ij-1}^r,{\mathbf{\Theta }}_{\mathbf{2}},{\mathit{U}}_{\mathbf{1}}\right)\cdot p\left(Y_{ij+1}^r|Y_{ij}^r=k,{\mathbf{\Theta }}_{\mathbf{2}},{\mathit{U}}_{\mathbf{1}}\right)\cdot p(Y_{ij}^o|Y_{ij}^r=k,{\mathbf{\Theta }}_{\mathbf{3}},{\mathit{U}}_{\mathbf{2}})}{{\sum }_{h=1\cdots S_1}p\left(Y_{ij}^r=h|Y_{ij-1}^r,{\mathbf{\Theta }}_{\mathbf{2}},{\mathit{U}}_{\mathbf{1}}\right)\cdot p\left(Y_{ij+1}^r|Y_{ij}^r=h,{\mathbf{\Theta }}_{\mathbf{2}},{\mathit{U}}_{\mathbf{1}}\right)\cdot p(Y_{ij}^o|Y_{ij}^r=h,{\mathbf{\Theta }}_{\mathbf{3}},{\mathit{U}}_{\mathbf{2}})},\text{for}j=1,\dots ,T_i.$$ (A2)

The full conditional distribution of Θ₁ is

$$p({\mathbf{\Theta }}_{\mathbf{1}}|{\mathit{U}}_{\mathbf{1}},{\mathit{Y}}^r\text{)}\propto exp\left\{{\displaystyle \mathbf{\sum }}_{\mathit{i}}\mathit{\text{logp}}(Y_{i1}^r|{\mathbf{\Theta }}_{\mathbf{1}},{\mathit{U}}_{\mathbf{1}})\frac{9}{8}{\mathbf{\Theta }}_{\mathbf{1}}^{\mathbf{\prime }}{\mathbf{\Theta }}_{\mathbf{1}}\right\}.$$ (A3)

The full conditional distribution of Θ₂ is

$$p({\mathbf{\Theta }}_{\mathbf{2}}|{\mathbf{\Theta }}_{\mathbf{1}},{\mathit{U}}_{\mathbf{1}},{\mathit{Y}}^r)\propto exp\left\{{\displaystyle \mathbf{\sum }}_{\mathit{i}\mathbf{,}\mathit{j}\mathbf{=}\mathbf{2}}\mathit{\text{logp}}(Y_{ij}^r|{\mathbf{\Theta }}_{\mathbf{3}},{\mathit{U}}_{\mathbf{1}},Y_{ij-1}^r)-\frac{9}{8}{\mathbf{\Theta }}_{\mathbf{2}}^{\mathbf{\prime }}{\mathbf{\Theta }}_{\mathbf{2}}\right\}.$$ (A4)

The full conditional distribution of Θ₃ is

$$p({\mathbf{\Theta }}_{\mathbf{3}}|{\mathit{U}}_{\mathbf{2}},{\mathit{Y}}^r,{\mathit{Y}}^o)\propto exp\left\{{\displaystyle \mathbf{\sum }}_{\mathit{i},\mathit{j}}\mathit{\text{logp}}(Y_{ij}^o|{\mathbf{\Theta }}_{\mathbf{3}},{\mathit{U}}_{\mathbf{2}},{\mathit{Y}}^r)-\frac{9}{8}{\mathbf{\Theta }}_{\mathbf{3}}^{\mathbf{\prime }}{\mathbf{\Theta }}_{\mathbf{3}}\right\}.$$ (A5)

Since the full conditional distributions in (A3)-(A5) are not available in closed form, the posterior draws proceed via Metropolis algorithm [21].

Finally, the full conditional distribution ofψ_g is

$$p({\mathit{\psi }}_{\mathit{g}}|{\mathit{U}}_{\mathit{g}})\sim \mathbf{\text{Inv}}-\mathbf{\text{Wishart}}({\mathbf{\sum }}_{\mathit{g}}+\mathit{U}{\mathbf{\text{'}}}_{\mathit{g}}{\mathit{U}}_{\mathit{g}},m_g+d_g),$$ (A6)

where d_g is the dimension of random vector U_g;

Appendix B. Details of the Simulation-Based APC Comparison Procedure

The simulation-based APC comparison procedure consists of the following steps:

Step 1: Simulate one data set from the proposed BMHMM. With sample size N, the covariates are simulated from appropriate distributions. Based on generated covariates and assigned true values of parameters, the outcomes are then generated.

Step 2: Assign prior distributions to parameters and fit both the proposed BMHMM model and the traditional logistic regression model to the simulated data from Step 1 using the MCMC algorithm.

Step 3: After convergence is reached, the posterior samples for the coefficient of covariate Z from both BMHMM and logistic regression model are collected.

Step 4: For both BMHMM and the logistic regression model, the generated posterior samples from Step 3 are used to calculate the posterior coverage probability of a symmetric interval around the true value

$$Pr(|\alpha -\mathit{\text{true value}}|<b_i|\mathit{\text{data}})$$

for a series of increasing lengths of interval b_i(i=1,⋯,I), where α is the coefficient of covariate X_ij in the models. A Monte Carlo approximation to this probability is computed as the proportion of the posterior drawn samples that fall between true value-b_i and true value+b_i, namely $r=S^{-1}{\sum }_{s=1}^{S}I(|{\alpha }_s-\mathit{\text{true value}}|<b_i)$. In our simulation, we set I=16 and b_i=(i−1) 0.1.

Step 5: Go through Steps 1-4 for a large number times, say 1000 replications. Then, the average posterior coverage probability for each b_i,

$$P_i=E(Pr(|\alpha -\mathit{\text{true value}}|<b_i|\mathit{\text{data}})),$$

is approximated by the average of r's across 1000 simulated samples. Finally, the curves of P_i against b_i are drawn for both BMHMM and logistic regression models.

Appendix C. Complete Version of Table V with Full List of Parameter Estimates

Table S.1. Full List of Parameter Estimates of Covariate for Children Reported Asthma in the CHS in BMHMM.

	Mean	SD	2.5%	50%	97.5%	G-R^
Prevalence probability:
Intercept	-3.92	0.42	-4.81	-3.92	-3.13	1.00
Age	0.44	0.54	-0.63	0.45	1.47	1.00
Gender	-0.07	0.46	-0.97	-0.06	0.87	1.00
Ethnicity*: hispanic	-0.41	0.56	-1.56	-0.38	0.63	1.00
black	0.31	0.95	-1.74	0.34	1.98	1.00
asian	-0.87	1.06	-3.03	-0.82	1.00	1.00
others+mixed	-0.41	0.88	-2.23	-0.39	1.24	1.00
Medication Use	5.14	0.60	3.98	5.14	6.36	1.00
Allergy	0.90	0.47	-0.01	0.90	1.79	1.00
Severe Wheeze	1.65	0.56	0.52	1.67	2.71	1.00
FEV (log scale)	-0.61	1.06	-2.68	-0.59	1.45	1.00
Transition probability:
Intercept	-3.46	0.53	-4.50	-3.46	-2.36	1.00
Age	-0.76	0.38	-1.59	-0.71	-0.19	1.01
Gender	0.04	0.40	-0.71	0.02	0.86	1.00
Ethnicity: hispanic	0.15	0.45	-0.79	0.17	0.99	1.00
black	-0.23	1.00	-2.51	-0.09	1.46	1.00
asian	0.14	0.68	-1.33	0.18	1.32	1.00
others+mixed	-0.72	1.05	-3.03	-0.64	1.06	1.00
Allergy	0.98	0.39	0.18	0.98	1.69	1.00
Current wheeze	0.83	0.47	-0.15	0.82	1.73	1.01
Family History of Asthma	1.01	0.40	0.23	1.00	1.85	1.00
Ozone from 10 am to 6 pm	-0.03	0.02	-0.06	-0.03	0.00	1.00
Number of Sports	-0.54	0.73	-2.16	-0.48	0.72	1.00
Ozone*Number of Sports	0.97	1.08	-1.50	1.06	2.83	1.00
Misclassification probability:
Intercept	-4.31	0.42	-5.15	-4.31	-3.50	1.00
Latent True Asthma	5.34	0.71	4.01	5.32	6.77	1.00
Age	-0.16	0.25	-0.69	-0.14	0.28	1.00
Gender	0.11	0.42	-0.67	0.10	0.92	1.00
AboveHS†
When Latent True Asthma=0	-0.16	0.46	-1.08	-0.16	0.74	1.00
When Latent True Asthma=1	1.33	0.64	0.04	1.33	2.57	1.00
Current Wheeze	1.21	0.42	0.38	1.21	2.06	1.00
Age*Latent True Asthma	0.28	0.32	-0.33	0.27	0.93	1.00
Variance of Town Level Radom Effect	0.28	0.10	0.15	0.25	0.54	1.00

^{^}G-R: Gelman-Rubin Statistics.

^*The reference group is Non-Hispanic White group.

^†AboveHS: An indicator variable of whether children come from families with education above the high school level.

Figure S.1.

Flow Chart of Simulation-Based Average Posterior Coverage Probability Method