Abstract
The objective was to test how increasing fiber length above the critical length would influence mechanical properties and fracture crack propagation. Micromechanics considering fiber/matrix stress-transfer was used to evaluate the results in addition to a shear debonding volume percent correction term necessary for the final analysis. Fiber lengths of 0.5, 1.0, 2.0, 3.0, and 6.0 mm with 9 μm diameters were added into a photocure vinyl ester particulate-filled composite at a uniform 28.2 vol%. Mechanical flexural testing was performed using four-point fully articulated fixtures for samples measuring 2 × 2 × 50 mm3 across a 40 mm span. Fiber length correlated with improved mechanical properties for flexural strength, modulus, yield strength, strain, work of fracture, and strain energy release, p < 0.001. In addition, sample fracture depth significantly decreased with increasing fiber lengths, p < 0.00001. All mechanical properties correlated significantly as predictors for fracture failure, p < 0.000001, and as estimators for each other, p < 0.0001. The stress-transfer micromechanics for fiber length were improved upon for strength by including a simple correction factor to account for loss of fiber volume percent related to cracks deflecting around debonded fiber ends. In turn, the elastic property of modulus was shown to exhibit a tendency to follow stress-transfer micromechanics.
INTRODUCTION
Theoretical
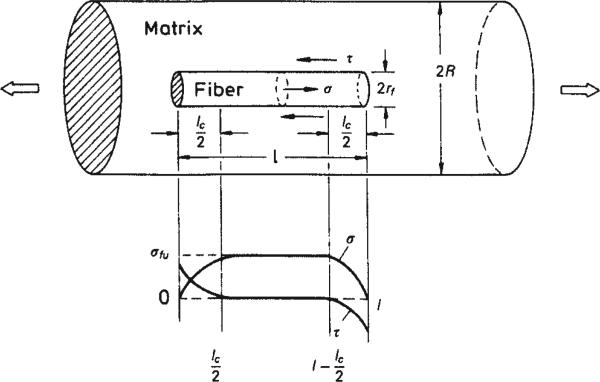
Aspects of the micromechanics for composites can be presented in classical terms by the rule of mixtures, which describes how concentrations and structures of the constituent geometry arrangements between fibers and polymer matrix influence material properties [1–3]. Primarily, mechanical properties for modulus and strength of composites are evaluated by the rule of mixtures through the dominant function of fiber volume percent using fiber modulus or fiber strength [1–3]. For any agreement with the rule of mixtures micromechanics, composite properties for modulus or strength must be tested in the longitudinal direction of the fiber reinforcement. Using fiber-length stress-transfer micromechanics as an extension of the rule-of-mixtures, a minimum fiber length is required so that stresses can transfer between fibers before strain-related polymer debonding occurs [1, 4, 5]. As an example, parallel shear strain bands that can develop during polymer/fiber composite tensile loading and initial debonding distortion are illustrated in Fig. 1, where the low modulus polymer strains are at a higher rate than the high modulus fiber [1, 6]. Stress-transfer micromechanics between the fiber and polymer is depicted in Fig. 2 showing the relationship between interfacial shear stress (τ) and the fiber stresses (σf) that develop in tension.
FIG. 1.

Composite strain field depicted between high modulus fiber and low modulus polymer in tension. Reproduced from “Composite Materials” by K. K. Chawla, Fig. 10.14 p. 335, copyright 1998, with permission from Springer Science and Business Media.
FIG. 2.
Stress-transfer between fiber and polymer includes a plot showing one-half the critical length at each fiber end in relation to tensile stress on the fiber and concurrent shear debonding. Reproduced from “Composite Materials” by K. K. Chawla, Fig. 10.15 p. 336, copyright 1998, with permission from Springer Science and Business Media.
During the research and development of discontinuous fiber-reinforced materials, it is particularly important to have a detailed understanding of the stress-transfer micromechanics between the matrix and the fibers. Consequently, by a force (F) balance equilibrium [1, 4, 5] between σf and τ, both with representative geometric areas (Aα and Aτ)
| (1) |
where the area distinguishes either the fiber cross section (Aσ = πr2 = πd2/4) or one side of the curved fiber surface cylinder area not including the extreme end diameter (Aτ = 2πrh = πdL/2). Also, r is the fiber radius, d is the fiber diameter, and L/2 the fiber length of potential debonding at one end as the polymer strains further beyond the high modulus fiber. Then
| (2) |
Simplifying gives
| (3) |
The fiber critical length (Lc) describes that the length of fiber with both ends can debond from the polymer to meet the stress equilibrium conditions whereby the stronger fiber will finally break (Fig. 2) such that
| (4) |
where that portion of the critical length from one fiber end equals Lc/2, which also equals 1 –Lc/2 at the opposite fiber end. The critical aspect ratio (Lc/d) or the debonding fiber length:fiber diameter ratio follows as a more descriptive functional relationship that accounts for increased shear effects associated with larger diameter fibers during uniaxial tension, or
| (5) |
In addition, the micromechanics for composite longitudinal strength (σcl) by the rule of mixtures can be obtained as
| (6) |
where σm is the matrix strength, Vf the fiber volume percent, and Vm is the matrix volume percent [1]. From the stress-fiber length diagram, Fig. 2, the average fiber stress equals the area under the graph divided by the fiber length. Fiber length can also be shown to influence the rule of mixtures through the micromechanics of stress-transfer as [1, 4, 5]
| (7) |
with β as a complex geometric stress-transfer factor across the fiber critical length, which equals 0.5 during linear plastic deformation (or average σf = σf [L – Lc+{2 × 0.5 × Lc/2}]/L from the area under the stress-fiber length diagram, Fig. 2), reasonably assumed at the fiber ends, so that
| (8) |
From a practical standpoint, composites do not appreciably increase mechanical strength until fibers reach critical length, since the matrix will fail first before fibers can break. Also, particulate filler is necessary to consolidate the resin to prevent void/porosity formation, so that Eqs. 6 and 8 were modified accordingly, where the particulate-filled composite matrix (σpc) replaces σm.
| (9) |
| (10) |
Photocure Applications and Other Discontinuous Fiber Polymer Matrix Composites
A photocure vinyl ester discontinuous fiber-reinforced composite is now under research and development to reduce micromotion with medical fixation devices during craniomaxillo-facial reconstruction, an alternative for acrylic cranioplastic material and as a replacement for current dental particulate-filled composites and amalgam restorative materials. The vinyl ester resin system was the culmination of over 30 years of chemistry development within the dental field to produce nonthermal ambient cure polymers. These studies started with tertiary amine redox couples for acrylic in Germany during the 1930s [7], the epoxy resin development concurrently by De Trey Freres in Switzerland [8], and the final breakthrough at the National Institute of Standards and Technology through the American Dental Association in the late 50s and early 60s [9]. Increased mechanical properties [10, 11] combined with improved handling that allows packing with a preimpregnated photocure composite similar to a conventional amalgam [12] are two of the major advantages for replacing photocure particulate-filled vinyl ester composites with molding compounds having fibers above critical length. Improved packing forces over particulate-filled composite by incorporating 3.0 mm discontinuous fibers also reduce voids through a consolidation process [12]. In addition, photocure fiber-reinforced molding compounds are being considered for structural adhesives, rapid field repair, and as a nonthermal means to provide tamper resistance and structural integrity for circuit boards.
Most recent studies related to discontinuous fiber-reinforced polymer matrix composites have involved matrices using vinyl ester resin, unsaturated polyester resin or various thermoplastics. Mechanical properties for strength and modulus with 3.0 mm quartz fiber lengths for a photocure composite independently evaluated and mechanically validated by the United States Department of Energy [10, 11] could further be compared with other discontinuous fiber-reinforced polymer matrix composites recently described in literature [13–27] (Table 1). The vinyl ester or unsaturated polyester silica-based fiber-reinforced composites, which included the quartz fiber photocure molding compound presented in this investigation, demonstrated mechanical properties by meta analysis that were generally much higher by comparison than most other types of discontinuous fiber-reinforced composites for both strength and modulus. In addition, the photocure composite used 3.0 mm discontinuous chopped fiber for a bulk moldable compound, whereas the other vinyl ester or unsaturated polyester composites incorporated much longer fibers ranging from 6.0 to 50.0 mm as mat or sheet molding compound that also included vacuum or thermal processing [13, 14, 16].
TABLE 1.
Mechanical properties for discontinuous PMCs (2000-2005).
| Polymer | Composite fiber type | Fiber lengths (mm) | Fiber diameter | vol% or wt% | Strength (MPa) | Modulus (GPa) |
|---|---|---|---|---|---|---|
| VE Photocure [10, 11] | Chopped quartz | 3.0 | 9.0 | 35 wt/32 vol | 227 FS | 19.8 FM |
| VE [13] | Glass mat | 6.0-9.0 | 38-43 vol | 108.5 ± 18.6 TS | 15.0 ± 2.39 TM | |
| VE [13] | Glass mat | ~25.0 | 38-43 vol | 193.4 ± 7.8 TS | 15.1 ± 1.3 TM | |
| UP [13] | Glass mat | 6.0-9.0 | 38-43 vol | 107.0 ± 15.6 TS | 16.1 ± 2.1 TM | |
| UP [13] | Glass mat | ~25.0 | 38-43 vol | 168.8 ± 21.0 TS | 14.9 ± 1.1 TM | |
| VE/EP [14] | Ceramic/glass mat | ≤50.0 | 9 and 11 | 70 wt | 145.3 ± 4.1 FS | 6.4 ± .01 FM |
| EP [15] | Carbon nanotubes | 2.0 wt | 63 FS | |||
| SMC resin [16] | Flax | 6-38 | 22 wt | 83-144 FS | 7-12 FM | |
| SMC resin [16] | Chopped glass | 25-50 | 70-160 FS | 7-11 FM | ||
| Acrylic [17] | Chopped Glass | 2.0 | 6.2 wt | 130 FS | 11.5 FM | |
| UP [18] | Chopped hard glass | 50.8 | 21 vol | 100a TS | ||
| UP [18] | Chopped soft glass | 50.8 | 21 vol | 85a TS | ||
| UP [18] | Chopped carbon | 50.8 | 21 vol | 50a TS | ||
| PP [19] | Milled glass | 0.209 | 13 | 8 vol | 52.4 ± 1.4 TS | |
| PP [19] | Milled flax | 0.860 | 36-450 | 13 vol | 17.9 ± 1.4 TS | |
| PP [20] | Milled basalt | 0.11 | 9.0 | 25 wt | 71.1 ± 1.7 FS | 3.1 ± 0.02 FM |
| PP [20] | Milled ceramic | 0.15 | 6.0 | 25 wt | 73.5 ± 2.5 FS | 3.0 ± 0.1 FM |
| PP [21] | Milled glass | 30 wt | 48.7 TS | 6.17 FM | ||
| PP/EPDM [22] | Chopped glass | 10-20 | 30 wt | 40.2 TS | 1.48 TM | |
| PE [23] | Glass mat | 452 TS | 1.2a TM | |||
| HDPE [24] | Glass mat | 5.0 | 13 | 20 vol | 20a TS | 1.8a TM |
| Nylon 6 [25] | Milled glass | 0.04-0.9 | 17 wt/8 vol | 115a TS | 4.8a TM | |
| Nylon 6 [25] | Milled glass | 0.04-0.9 | 17 wt/12 vol | 155a TS | 6.8a TM | |
| Nylon 6 [26] | Milled glass | 0.478 | 30 wt | 136.5 TS | 7.7 TM | |
| ABS [27] | Short glass | 13 | 30 wt | 78.0 ± 2.5 TS | 6.5 ± 3.5 TM |
VE, vinyl ester; SMC, sheet molding compound; UP, unsaturated polyester; EP, epoxy; PP, Polypropylene; EPDM, ethylene–propylene–diene terpolymer; PE, polyethylene; HDPE, high density polyethylene; ABS, acrylonitrile–butadiene–styrene; FS, flexural; TS, tensile; FM, flexural; TM, Tensile. All mechanical properties are the maximum reported values
approximated from chart.
Photocure technology provides an alternative system to thermal-type methods whereby fibers can be processed with a monomer resin for subsequent curing using photons as the energy to initiate polymerization [9, 28]. Accordingly, photocure by visible-light for small parts can be accomplished in relative short time-periods, measured in tens of seconds [9, 28]. In addition, photocure technology can reduce possible detrimental thermally induced internal shrinkage stresses that could influence structural relationships during mechanical deformation and fracture crack propagation [1, 28]. Thus, photocure energy was used as a process to minimize residual stresses that might be accentuated during mechanical testing between high modulus reinforcement and polymers with higher coefficients of thermal expansion [1]. Moreover, photon energy having a longer wavelength within the visible-light region has been shown to be more efficient than shorter wavelength ultraviolet light or UV energy for curing deeper parts associated with composite molding compounds [9]. Photocure times for visible-light measured in tens of seconds [9, 28] are much less compared to UV structural applications with curing times measured in minutes or thermal curing measured in hours [29]. Although UV-cured resins generally have lower mechanical properties than chemically or thermally cured composites [29], photocure visible-light vinyl ester composites can have comparable or enhanced mechanical properties (Table 1).
Basic fiber-length stress-transfer micromechanics predict increased mechanical properties with increasing fiber length and fiber volume percent [1, 4, 5]. On the other hand, the economics of manufacturing indicate that costs increase when comparing fiber-reinforced composites to particulate-filled materials. With regard to manufacturing in particular, viscosity increases are noted with higher fiber fractions and fiber aspect ratio lengths [30, 31]. Therefore, fiber length was investigated for research and development in relation to processing and mechanical properties. An advanced flexural test design system for small samples was used to reduce the influence probability of material defects [1] that included fully articulated fixtures to lower errors associated with sample parallelism [32], four-point rather than three-point to stress a larger portion of the material [32, 33], and a span to depth ratio of 20 so that the Euler-type bending would reduce shear stresses [34].
A statistical analysis examining fiber-length stress-transfer micromechanics was used to test the research and development hypothesis that increasing fiber lengths would increase composite mechanical properties, tested at α = 0.05. Also by increasing fiber lengths, fracture mechanic theories predicted that fracture depths will decrease, tested at α = 0.05. Significant differences between groups were determined by a t test with unequal variances, at α = 0.05
EXPERIMENTAL PROCEDURES
Materials
Quartz fibers (Saint Gobain, QPC Products, Lexington, KY), Table 2 [35], were 99.99% pure silica, thereby providing a hydrolytically stable inert material with low lattice impurities [36, 37]. Quartz fibers were silanated with 1.0 wt% 3-methacryloxypropyltrimethoxysilane (MPTMS) (DOW Chemical, Midland, MI) in 70% 2-propanol, dried overnight, and heated briefly at 120°C. The silanated quartz fibers were then impregnated with a photocure resin at 70 wt% fibers. The styrene-free bisphenyl A vinyl ester resin consisted of 2,2-bis [p-(2′hydroxy-3′- methacryloxypropoxyphenyl)] propane (BisGMA) (Esstech, PA) with 2.5 wt% triethylene glycol dimethacrylate (TEGDMA) monomer (Esstech, Essington, PA) to reduce viscosity. Resin systems were optimized to photocure by incorporating photo-oxidants camphorquinone (Aldrich, Milwaukee, WI) 0.6 wt% and Irgacure 819 (Ciba, Tarrytown, NY) 1.0 wt%, and photo-reductant 2-dimethylaminoethyl methacry-late (Aldrich, Milwaukee, WI) 1.0 wt%. Adhesion promoter SR9016 diacrylate (Sartomer, WestChester, PA) and MPTMS organosilane were added into the photocure resin as well at 2.0 and 1.0 wt%, respectively. Quartz fiber lengths of 0.5, 1.0, 2.0, 3.0, and 6.0 mm were preimpregnated using the photocure resin system.
TABLE 2.
Properties for quartz fibers.
| Mechanical properties | Strength (MPa) | Modulus (GPa) |
|---|---|---|
| Virgin filament | 6,000 (tensile) | 78 (tensile) |
| Yarn | 1,500 (tensile) | 78 (tensile) |
| Unidirectional composite | 1,200 (flexural) | 35 (flexural) |
Density 2.2 g/cm3; Fiber Diameter 9 μm.
The resultant quartz fiber-reinforced compounds were then thickened with 0.3 wt% zirconia silicate filler from 3M Corporation (St. Paul, MN). The zirconia silicate particulate had been milled into spheres by a proprietary process to provide a uniform particle distribution from 10 nm to 3.5 μm. Multimodal packing has been shown to reduce inter-particulate distances [38] to maximize secondary van der Waals forces of attraction [39]. The zirconia silicate particulate thus provides a hydrolytically stable thickener with high atomic numbers for radiographic purposes.
BisGMA vinyl ester and TEGDMA were then combined at 50:50 ratio in a similar photocure system for the addition of 84.5 wt% or 66 vol% 3M Corporation zirconia silicate particulate. The resultant paste with possible additional zirconia silicate was then used to incorporate all fiber length groups preimpregnated with photocure resin for final molding compounds with 30 wt% (uniform 28.2 Vf) fibers (Table 3).
TABLE 3.
Compound formulations volume percentages.
| Fiber lengths (mm) | Quartz fibers (Vf) | Zirconia silicate | Bis-GMA | TEGDMA |
|---|---|---|---|---|
| No fibers | 0.0 | 66.0 | 18.1 | 15.9 |
| 0.5 | 28.2 | 33.9 | 29.6 | 8.3 |
| 1.0 | 28.2 | 36.3 | 28.6 | 6.9 |
| 2.0 | 28.2 | 34.9 | 29.3 | 7.6 |
| 3.0 | 28.2 | 32.7 | 30.3 | 8.8 |
| 6.0 | 28.2 | 34.9 | 29.3 | 7.6 |
The Alert® fiber volume fraction is estimated at ~26 vol%. The density (g/cm3) for Quartz fibers is 2.2, Zirconia silicate is 3.10, Bis-GMA is 1.14, and for TEGDMA is 1.07.
A commercial photocure fiber-reinforced composite was used as a control for comparison purposes, Alert® (Jeneric Pentron, CT). Fibers in Alert® material were reported by the manufacturer directly as having an average fiber length of ~40 at 10 μm diameters. The manufacturer further indicated that fibers were added at ~1:2 ratio with glass particulate with high atomic number elements for a total fiber/filler concentration of 82 wt% (estimated 26 Vf).
Fully Articulated Flexural Test Specimen Preparation
Samples 2 × 2 × 50 mm3 meeting American National Standards Institute (ANSI)/American Dental Association (ADA) specification no. 27 but for a longer span at 40 mm rather than 20 mm were prepared with a split mould clamped between two glass plates. An Epilar 3000 (3M Corporation, St. Paul, MN) was used for the photocure initiation and monitored with a Demetron Radiometer daily to ensure intensities of concentrated light at a wavelength of 470 nm were above 500 mW/cm2. The Epilar had a 12 mm diameter light guide to photocure samples. Samples were irradiated by a small overlapping sequence for a total of 20 s on top and bottom, through the glass plates, 20 s on top and bottom after removing the glass plates, and from the sides for 1 min each with a focused 2-mm diameter beam. Excess material was removed from each sample followed by a sanding process down to 600 grit silicon carbide. Samples were then placed in a 37°C water bath for 24 h, primarily as a control for a uniform postcure before mechanical testing.
Mechanical Testing
Fully articulated four-point bend fixtures were supplied by MTS Systems Corporation (Minneapolis, MN) for advanced ceramics with a 40 mm span length using 1/4 point 20-mm spaced loading noses. A MTS inspection machine (858 MiniBionix) with a crosshead speed of 0.5 mm/min was used to mechanically test flexural properties. Sample size estimates were performed and 4 specimens from each fiber length group (0.0, 0.5, 1.0, 2.0, 3.0, and 6.0 mm) were tested.
| (11) |
| (12) |
Specifying F, maximum load; L, span length; b, sample width; d, sample depth; and M, slope of the tangent to the initial straight line on steepest part of the load-deflection curve.
Yield Strength was calculated from the flexural strength formula where the initial steep portion of the force-deflection curves started to deviate from linearity toward increased deflection. The yield strength magnitude also placed an upper limit check on determining the slope for flexural modulus.
| (13) |
Further denoting maximum strain r in the outer fibers at midspan on the tensile surface at maximum load and sample beam deflection D as digitally provided at maximum bend strength.
Fracture Toughness Analysis Using Simplified Energy Calculation Methods (kJ/m2)
Toughness stress-transfer micromechanics for fiber length was defined during static low strain rate specifically by sample cross-sectional area in terms of energy integrated under the load-deflection curve [40, 41] and further considered by measures of resilience, work of fracture (WOF), and strain energy release (SER). However, methods for determining energy are difficult to locate. Costly application software is available to integrate load-deflection data. Also, an ASTM method to integrate the energy area involves calibrating the load-deflection data graph chart paper, cutting out the curve and weighing the paper, although still considered time consuming and prone to some error [42]. A simplified method was considered by computer spreadsheet technology whereby energy values were calculated from summing successive complementary load-deflection data points using numerical integration with the trapezoidal rule [43], where
| (14) |
| (15) |
With fully articulated self-adjusting fixtures, deflections may reverse so that a negative trapezoidal area is balanced by a correspondingly larger positive area.
Resilience (kJ/m2)
Energy was integrated by numerical methods from the load-deflection curve in the elastic region up to yield point where the initial steep straight-line slope deviates toward increased deflection for cross-sectional sample area toughness.
Work of Fracture (kJ/m2)
Energy was integrated by numerical methods from the load-deflection curved out to a maximum of 5% deviation past the peak load for cross-sectional area toughness.
SERIC (kJ/m2)
The study of crack propagation can be investigated in relation to specimen deflection and the energy integrated beyond maximum peak or critical (C) load where unstable damage initially occurs as the critical strain energy release (SERc) for fiber-length stress-transfer micromechanics. SERc toughness values can then be associated with strain energy release rate (Gc), which is really not an energy rate but a true toughness value. Gc has been defined as the strain energy per unit increase in fracture surface area and related to both loading forces and reductions during crack propagation [44]. Although Gc is commonly measured as energy input per crack surface length, methods are presented here to measure a more conventional descriptive energy released following maximum load and continued strain with crack propagation over a fixed deflection as SERc. The process utilized data from the load versus deformation relationship with deformation taken from the testing machine fixture displacement rather than the specimen per se. Energy was integrated by numerical methods for area during Mode I (I) Euler tensile flexural bending under the load deflection curve from peak load to a maximum of 5% deflection past the highest force. SERIC toughness is then a function of energy relative to the material cross-sectional area. With small SERIC deflections less than 1% of the total for example when no fibers are added, judgment might be considered to look for deflection points that become lower due to rapid release of the platen load on the sample, such that a single load-deflection data set negatively impacting the total area could be discarded as indicated by analysis before summing all trapezoidal areas. When testing low strength materials, fracture noise could be eliminated using an appropriate scaled down load cell for better data resolution.
Percent Load Retained stress-transfer micromechanics for fiber length was characterized by dividing the load at a maximum 5% deflection past peak load by the maximum force. Fibers bridged cracks to prevent complete failure and accumulated damage away from the primary crack from observations so that testing normally did not result in complete failure at 5% deflection past maximum load even at low fiber fractions. The upper fixture attached to the MTS mechanical test machine was visually monitored from the digital output. Any retained load could be approximated at 5% deflection past the maximum flexural bending force and testing was then stopped so that fractures from the flexural tensile surface could be evaluated. Mechanical variables were then analyzed as potential predictors for fracture crack propagation.
Photocure Resin Polymer
A second fixture with 40 mm length support spans with a deepened well between support spans was fabricated so that large deflections experienced with unreinforced polymers were compared.
Fracture Analysis and Characterization
MicroVu Metrology with a calibrated accuracy to 0.1 μm along the x- and y-axes was used to measure primary surface fractures extending from the flexural tensile surface. Microscopy with a reflective Nikon system provided general fracture imaging of the fracture zone and fracture depth measurements at 20–30× magnification. Vertical fracture depths measured from the tensile failure side were normalized as a function of the sample thickness for evaluation with mechanical properties. Both lateral fracture sides were measured and averaged.
X-Rays
A General Electric Machine at 10 mA, 65 kVp, and 0.4 s was used to expose Kodak 7.7 × 5.7 mm2 film followed by developing with an automatic processor. Lateral view X-rays were taken for all samples from each fiber length group for general micromechanics analysis particularly with regard to diffuse crack propagation beyond the fracture surface that tended to extend toward the neutral axis during flexural testing [11]. Although X-rays supplied imaging of crack propagation within the internal regions of the composite, X-ray resolution, at ~20 lines/mm, was lower resolution than Nikon microscopy, which was used to measure the fracture depths at the surface.
Scanning Electron Microscope
Scanning electron microscope (SEM) has a large depth of field that is ideal for imaging deep fractures where high resolution provides excellent surface detail. Samples were viewed from the lateral surface to characterize the extent of material fracture depth-wise for each fiber length group. Before SEM imaging, samples were sputter-coated with gold/palladium.
In addition, samples selected from values surrounding the average flexural strength for each fiber length group were chosen for imaging and analysis including characterizing fiber orientation from each group for stress-transfer micromechanical comparisons. Samples were first sectioned distal to the primary fractures. Samples were then prepared by first inserting diamond blade saw cuts parallel to the top and bottom surfaces at each end to cleave material parallel to the general fiber direction down the long axis of the sample.
Statistical Analysis
The research and development hypothesis was that by increasing fiber length, composite mechanical properties would increase, when tested at α = 0.05. Also, by increasing composite fiber length, the fracture hypothesis predicted that fracture depths would decrease (α = 0.05).
Previous testing [10–12] allowed calculations for sample size estimates to compare differences between fiber length groups and especially with regard to alterations in the particulate-filled zirconia silicate composite after addition of 3.0 mm quartz fibers. The same sample size of four was used to test different fiber lengths. Significant differences between groups was established by a t test with unequal variances (α = 0.05). Correlation matrix analysis was applied to follow trends for mechanical properties as a function of fiber length, in addition to performing statistical analysis for correlations among mechanical interrelationships. Statistica including p-values and Microsoft Excel with Primer of Biostatistics were employed to confirm data transfer and test statistical significance.
RESULTS AND DISCUSSION
Mechanical Properties and Analyses
Increasing fiber length at 28.2 Vf from 0.5 to 6.0 mm into a particulate-filled vinyl ester photocure composite showed significant increases in all mechanical properties tested for flexural strength, modulus, yield strength, strain, resilience, WOF, and SERIC (Table 4). The property for percentage load retained at 5% deflection past peak load also increased. Although increases were not generally evident at a fiber length of 0.5 mm, the modulus significantly increased above the particulate-filled zirconia silicate composite by adding 0.5 mm fibers (p < 0.05). With the addition of 1.0 mm fibers, properties for modulus, maximum flexural strength, yield strength and WOF all significantly increased above the particulate-filled composite group (p < 0.05). By incorporating 2.0 mm fibers, all properties tested significantly increased above the particulate-filled composite group (p < 0.05). An ability of fibers to restrict crack propagation was particularly noted with SERIC using a fiber length of at least 2.0 mm, which increased up to as much as 67-fold. The percent load retained was another reinforcing property with a fiber length of at least 2.0 mm where values increased from 0.0 with complete brittle fracture up to 76% of the maximum force. Overall, by adding 28.2 Vf to a particulate-filled composite, mechanical properties increased with flexural strength about 3×, modulus almost 1.75×, yield strength over 3.5×, and strain capacity ~1.7×. Fracture toughness properties increased with resilience 6.5× and WOF 6.7×. The general impression of such mechanical improvements between the tested particulate-filled and fiber-reinforced composites might be similar to comparing a brittle stiffened polymer being transformed into a toughened ceramic.
TABLE 4.
Mechanical properties for different fiber lengthsa.
| Fiber length (mm) | Flexural strength (MPa) |
Modulus (GPa) |
Yield strength (MPa) |
Strain (10-2) |
Resilience (kJ/m2) |
WOF (kJ/m2) |
SERIC (kJ/m2) |
%Load retained |
|---|---|---|---|---|---|---|---|---|
| 0 (zirconia silicate) | 117.6(5.5) | 19.5 (1.3) | 95.4 (14.6) | 0.79 (0.18) | 3.03 (0.99) | 4.48 (0.42) | 0.036 (0.024) | 0 (0) |
| 0.5 | 113.8 (22.7) | 23.0 (1.4) | 92.8 (9.48) | 0.62 (0.09) | 2.35 (0.57) | 3.91 (1.46) | 0.075 (0.05) | 0 (0) |
| 1.0 | 173.6 (26.0) | 26.2 (0.8) | 126.1 (13.0) | 0.84 (0.11) | 3.84 (0.70) | 8.70 (3.13) | 0.097 (0.054) | 0 (0) |
| 2.0 | 373.9 (29.9) | 34.0 (2.9) | 329.8 (47.8) | 1.34 (0.21) | 19.71 (4.21) | 28.19 (3.17) | 1.882 (1.005) | 43.3 (15.8) |
| 3.0 | 374.9 (11.9) | 31.5 (1.2) | 343.5 (37.1) | 1.31 (0.04) | 23.31 (5.35) | 30.11 (1.51) | 2.400 (0.534) | 70.3 (16.0) |
| 6.0 | 332.6 (55.3) | 31.2 (1.2) | 252.8 (47.0) | 1.25 (0.14) | 13.04 (5.02) | 25.35 (4.96) | 2.047 (0.347) | 76.3 (12.3) |
| 0 (Alert) | 90.4 (19.4) | 17.6 (4.9) | 62.3 (12.2) | 0.69 (0.05) | 1.52(0.54) | 3.23 (0.70) | 0.034 (0.032) | 0 (0) |
| 0 (polymer) | 81.2(27.6) | 3.5 (0.3) | 53.2 (7.8) | 2.5 (0.63) | 9.53 (6.53) | 16.19 (10.47) | 0.262 (0.119) | 0 (0) |
Values in parentheses indicate standard deviations.
Flexural Strength
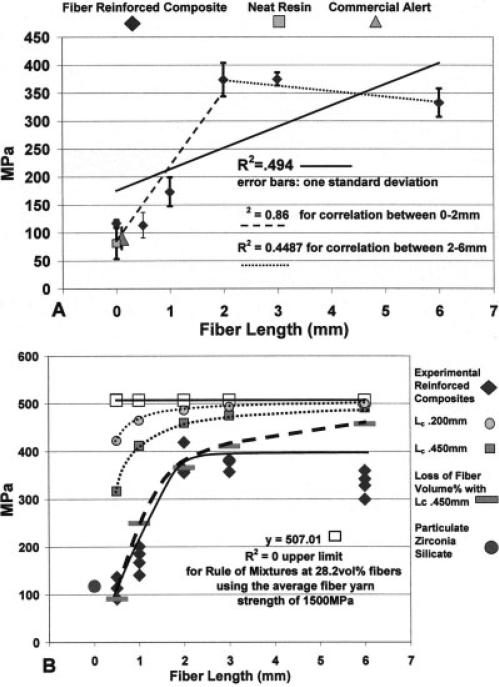
Increasing the fiber length to the particulate-filled composite increased average flexural strengths from ~118 MPa toward a 400 MPa plateau (Fig. 3A). When evaluating a regression equation, the coefficient of determination (R2) compares the scatter of X and Y data pairs to the mean for Y (total deviation) and the regression line distance to the mean for Y (explained deviation). R2 describes how strong the independent X values for the sample regression equation and the observed dependent values of Y follow a theoretical relationship using the linear equation, where in this case, X is represented by fiber length and Y by flexural strength. R2 then provides the magnitude of the explained sum of squares by the ratio of the total sum of squares, which in turn gives an indication of the amount of variation or percent explained by the regression [45]. The wide scatter of values represented by group means with standard deviations for flexural strength between 0 and 6 mm fiber length provided an R2 of 0.494, indicating that only about 49% of the variation in the flexural strength could be explained by a linear assumption for regression of fiber length. Two separate processes or relationships appeared to occur in the fiber length range from 0.0 to 2.0 mm and in the fiber length range from 2.0 to 6.0 mm. The limited interval for flexural strength data between the 0.0 to 2.0 mm fiber length had a computed R2 of .866 as a positive linear correlation. But, from the 2.0 to 6.0 mm fiber length interval, the computed flexural strength R2 had a value of 0.4487, but as a negative correlation for a linear relationship.
FIG. 3.
A: Group mean flexural strength for different fiber lengths. B: Strength results for different fiber lengths with rule of mixtures, stress-transfer critical length micromechanics, and volume percent correction term.
The rule of mixtures, Eq. 9, and stress-transfer micromechanics for fiber length, Eq. 10, were considered for explaining nonlinearity with strength in relation to fiber length. Plots were accordingly developed for comparisons of the experimental composites at each group mean fiber length for the same 28.2 Vf fiber fractions (Fig. 3B). All of the calculations for the rule of mixtures, Eq. 9, and stress-transfer micromechanics for fiber length with Lcs, Eq. 10, used an average fiber yarn strength of 1,500 MPa (Table 2) and average for the particulate-filled zirconia silicate composite of 118 MPa. Quartz fiber yarn strengths would then better reflect average defects present during flexural mechanical testing of macroscopic samples. The rule of mixtures by Eq. 9 calculation gave a uniform strength of 507 MPa for the quartz fiber composite tested, where Vf was expected to control composite properties (Fig. 3B).
For another comparison with experimental results, the stress-transfer micromechanics for fiber length predicted a loss of strength as Lc increased due to polymer/fiber debonding and also a plateau for increasing fiber strengths dependent on the Lc (according to Eq. 10). To account for polymer shear debonding from the shorter fibers when using Eq. 10, two Lcs were calculated to compare shifts in the plots at 200 and 450 μm. By using Eq. 10 and increasing Lc, the plots shifted progressively downward to lower values and provided better agreement with experimental data (Fig. 3B). Nonetheless, stress-transfer micromechanics for fiber length approximations were still well above the experimental results. With regard to differences for longer fibers between the micromechanics for the rule of mixtures and the stress-transfer micromechanics for fiber length predictions compared with experimental results, fiber misalignment and fiber–fiber interactions were considered [1, 46, 47]. Although comparisons between theoretical micromechanics and experimental results were greatly different for the shorter fibers, lower values have previously been predicted for shorter fibers under the assumption that fibers will not break but rather only pull out until 2Lc [48].
To better evaluate the experimental data by Eq. 10 for shorter fibers, a consensus value based on opinions reported through publications for critical aspect ratio was necessary to determine an average critical length using the 9 μm experimental quartz fibers with Eq. 5. First, a range of Lc/d ratios might be expected with a varying range of fiber strengths in addition to a range of interfacial shear bond strengths (τ). Table 5 presents literature Lc/d ratios for vinyl ester silica-based fiber-reinforced composites with values ranging from 46.3 to 65.1 [11, 49–51].
TABLE 5.
Vinyl ester and silica-based fiber Lc/d ratios.
| Fibers | τ (MPa) | Lc (μm) | Fiber diameter (μm) | Lc/d ratio |
|---|---|---|---|---|
| S2 glass [49] | 600 | 13 | 46.3 (2.7)a | |
| Eglass [50] | 22.3 | 958 | 14.71 (1.23)a | 65.1 |
| E glass [11, 51] | 33.8 (4)a | 800 | 16 | 50 |
Values in parentheses indicate standard deviations.
The average critical aspect ratio for the several silica-based fibers in a vinyl ester resin was 53.8 wherein a journal-based consensus critical length for the 9 μm diameter experimental composite quartz fibers in a vinyl ester resin was estimated to be about 484.2 μm. The plateau region for fiber length has further been proposed to exist at 4–5 Lc [52, 53] so that for the quartz fiber vinyl ester resin system with the experimental plateau starting near 2.0 mm, Lc should be approximately between 0.4 and 0.5 mm. Therefore, the critical length of 450 μm already plotted in Fig 3B appeared to be an acceptable approximation, although this value was unacceptable for explaining the large differences with experimental data.
As an extension to Eq. 10, an additional stress-transfer micromechanics for fiber length explanation could include partial loss of the effective 28.2 Vf during polymer debonding. Thereby, a percent of the fibers that have shear debonded could not participate as stress-transfer reinforcement when cracks exist around the fibers. A loss of working Vf was a particularly reasonable explanation at a higher rate for smaller fibers, since fracture crack propagation directed around debonding ends of the fibers would be expected to grow disproportionately as the number of fiber ends increases inversely with the fiber length. The fiber-length stress-transfer micromechanics only relies on Lc and the β load transfer function to account for loss of strength during shear debonding. To better predict values through stress-transfer micromechanics for fiber length, a correction term reducing the effective Vf during shear polymer/fiber debonding failure relying exclusively on Lc and L follows:
| (16) |
So that the rule of mixtures following the stress-transfer micromechanics for fiber length from Eq. 10 was further refined by L and Lc as
| (17) |
Combining two basic correction terms for a quasi-second-order equation for fiber length that better described a curve for shorter fibers to include an extended limit plateau for the longer fiber then gives
| (18) |
More precisely, a new function was established with a progressively increasing loss of strength as a smaller fiber length approached Lc. As fibers get much longer than Lc, a limiting plateau develops. Clearly, a linear regression R2 value of only 0.494 (Fig. 3A) did not sufficiently describe the experimental results. On the other hand, including a volume percent correction term accommodated both the loss of fiber stress-transfer during polymer/fiber shear debonding and crack propagation around debonding fiber ends for an improved micromechanics stress-transfer model. Eqs. 17 and 18 variables were obtained through an engineering literature meta analysis as a consensus value of 0.45 mm for Lc with the experimental 28.2 Vf and an average fiber yarn strength of 1,500 MPa. A plot by means of Eqs. 17 or 18 (Fig. 3B) demonstrated a close fit that coincides with experimental data for shorter fibers and brings the curves much closer for longer fibers. Fiber volume Vf reduction by the new correction term could account for fiber debonding related to crack propagation around fiber ends during fracture failure. The stress- transfer micromechanics by volume percent correction model also required a fiber length of 2Lc before strengths increased as previously predicted, where failure initially occurs by fiber pull-out below 2Lc [48]. Practically, at 1Lc, the entire fiber has already debonded and cannot participate in mechanical fracture. The volume percent correction term did not fully account for differences with longer fibers in the plateau (6.0 mm) region, which possibly presented with extra separate processes where fiber–fiber interactions, fiber misalignment, and void defects reduced the experimental results from the projected estimates [46, 47].
Strength for the polymer, particulate-filled zirconia silicate composite, Alert® particulate-filled composite with ~26 vol% microfibers, and zirconia silicate composite with 0.5 mm quartz fibers were not significantly different (Fig. 3A). Addition of 1.0 mm quartz fibers to the zirconia silicate composite significantly increased flexural strength above the polymer, zirconia silicate composite, Alert®, and zirconia silicate composite with 0.5 mm group mean fiber length (p < 0.05).
Modulus
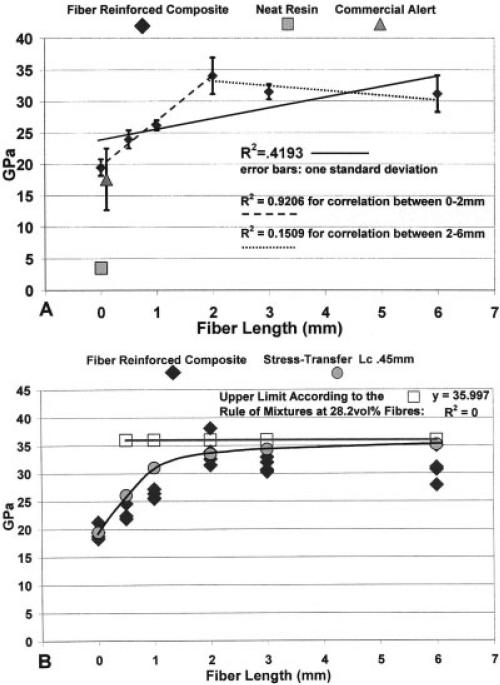
Increasing the fiber length from 0.0 to 6.0 mm at a constant 28.2 Vf for the same zirconia silicate particulate-filled composite increased modulus from 19.5 up to 34 GPa (Fig. 4A). However, fiber length could only explain about 42% of the variability for modulus by R2. Two separate processes appeared to occur as the group mean fiber length increased from 0.0 to 2.0 mm and as fiber length increased from 2.0 to 6.0 mm with R2s of 0.9206 as a positive correlation and 0.1509 as a negative correlation, respectively.
FIG. 4.
A: Group mean modulus for different fiber lengths. B: Modulus results for different fiber lengths with rule of mixtures and stress- transfer critical length micromechanics.
The rule-of-mixtures micromechanics for composite strength, Eq. 6 modified for particulate by Eq. 9, was applied for modulus (E) by the following equation [1–3]:
| (19) |
However, a plot for modulus by Eq. 19 using a fiber modulus of 78 GPa (Table 2) and particulate-filled composite matrix modulus of 19.5 GPa shows a uniform modulus of 36 GPa (Fig. 4B), which had very little resemblance to the experimental data. As a consequence, it was considered that a fiber-length stress-transfer micromechanics approach similar to composite strength by Eq. 10 might also be used to explain modulus increases with increasing fiber length according to the following equation:
| (20) |
A plot for modulus by Eq. 20 with Lc estimated once more at 0.45 mm using a fiber modulus of 78 GPa and average particulate-filled composite modulus of 19.5 GPa showed a similar agreement with the experimental data (Fig. 4B). Accordingly, the debonding effects during stress-transfer upon the modulus were sequentially minimized as fiber length increased relative to Lc. Consequently, a uniform increase in modulus occurred until 2.0 mm plotted by the stress-transfer micromechanics for fiber length and then continues as a slightly rising plateau where Lc becomes insignificant relative to longer fiber length. Agreement of the strength composite model from Eq. 17 would presume that deformation along the critical lengths for both fiber ends was plastic permanent yielding with regard to the β stress-transfer factor [1]. Modulus significantly increased immediately at a fiber length of 0.5 mm, or approximately the critical length estimated from literature, whereas strength was not expected to increase until about 2Lc [48]. As previously described, the plateau region was predicted to occur at 4–5×, the critical length for strength [52, 53], or ~2.0 mm, which was also seen experimentally for modulus. Initial elastic isostrain deformation defining the micromechanics related to modulus does not include manifestation of composite defects in the plastic region of the load-deflection curve so that crack propagation around fiber ends is not a confounding variable, which was seen with flexural strength. Predictions for modulus were thus broadened by the fiber-length stress-transfer theory as a classical extension of micromechanics for fiber volume percent.
Modulus for the polymer was considerably lower than all other groups, significantly increasing with the addition of zirconia silicate particulate filler and when compared to the Alert® particulate-filled composite with ~26 vol% microfibers (p < 0.05; Fig. 4A). The sequential increase of fiber length from 0.0 to 0.5 mm, 0.5 to 1.0 mm, and 1.0 to 2.0 mm significantly increased modulus at each level (p < 0.05).
Percent Load Retained
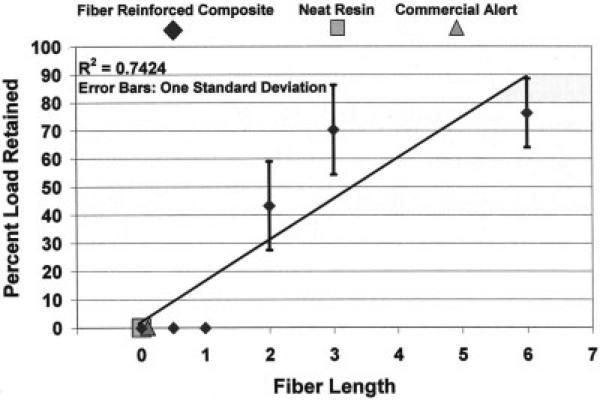
Extending quartz fiber length from 0 to 6 mm at a constant 28.2 Vf to the same particulate-filled composite increased the percent of load retained by the sample at 5% deflection past peak load, Fig. 5. No load was retained as fracture was immediately complete for the polymer, zirconia silicate particulate-filled composite, and the Alert® commercial composite with microfibers. Similarly, no load was retained for composites with fiber lengths of 0.5 and 1.0 mm, where it was considered that failure included fiber fracture with only fiber bridging available to hold samples together. However, with a fiber length at least 2.0 mm and above, fibers began to retain a substantial load beyond initial failure that progressively increased with longer fibers up to 6.0 mm. Fiber length could thus explain about 74% of the variability for percent load retained determined by R2 analysis. A plateau for improvement started at 3.0 mm rather than the 2.0 mm group mean fiber length with regard to percent load retained.
FIG. 5.
Group mean percent post load retained at 5% deflection past peak load for different fiber lengths.
Fracture Analysis
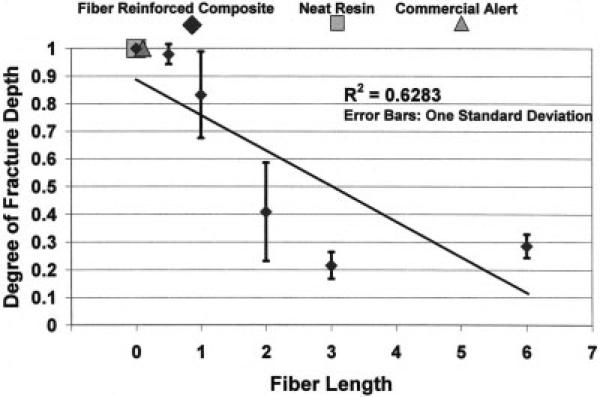
Increasing fiber length from 0.0 to 6.0 mm at a constant 28.2 Vf for similar particulate-filled composites showed a decrease in sample fracture depths as measured through reflective Nikon Microscopy (Fig. 6). Fractures were complete for all samples with the polymer, particulate-filled zirconia silicate composite, and the Alert® commercial composite with ~26 vol% microfibers. Following addition of 28.2 Vf 0.5 mm length quartz fibers to the zirconia silicate-particulate filled composite, complete fracture was not constant. As longer fibers were added, fracture depth decreased. Considering the results from R2 regression, about 63% of the total variation for fracture depth could be explained by fiber length. Instead of a plateau for improvements starting at 2.0 mm fiber length as seen with previous data, fracture depth reductions did not start to level off until 3.0 mm.
FIG. 6.
Group mean fracture depth level for different fiber lengths.
The correlation coefficient (R) is one measure of the influence for a linear relationship [45] for example between fiber length and a mechanical test variable. R then is the positive or negative square root of the coefficient of determination (R2) previously used for analysis. The magnitude of R can also be used to provide a test statistic based on a t test related to R, R2, and the sample size to determine a p-value regarding the probability of error when claiming the validity of a research and development hypothesis [45]. A correlation matrix (Table 6) was developed with both Pearson product correlation coefficients and p-values to examine relationships between fiber length and the mechanical properties, including percent load retained and degree of fracture depth, in addition to all other parameter interrelationships.
TABLE 6.
Correlation coefficient matrix analysis (p-values).
| Fiber length | Flexural strength (MPa) |
Modulus (GPa) |
WOF (kJ/m2) |
SERIC (kJ/m2) |
% Post load retained |
Degree fracture depth |
|
|---|---|---|---|---|---|---|---|
| Fiber length | 1.000000 | 0.702841 (0.001) | 0.647526 (0.001) | 0.706234 (0.001) | 0.718190 (0.001) | 0.861603 (0.000000) | − 0.792918 (0.00001) |
| Flexural strength | 0.702841 (0.001) | 1.000000 | 0.908969 (0.000000) | 0.992363 (0.000000) | 0.917640 (000000) | 0.846101 (000000) | −0.923731 (0.000000) |
| Modulus | 0.647526 (0.001) | 0.908969 (0.000000) | 1.000000 | 0.863642 (0.000000) | 0.801429 (0.00001) | 0.736831 (0.0001) | −0.833023 (0.000001) |
| WOF | 0.706234 (0.001) | 0.992363 (0.000000) | 0.863642 (0.000000) | 1.000000 | 0.933109 (0.000000) | 0.849621 (0.000000) | −0.916728 (0.000000) |
| SERIC | 0.718190 (0.001) | 0.917640 (000000) | 0.801429 (0.00001) | 0.933109 (0.000000) | 1.000000 | 0.890591 (0.000000) | −0.861417 (0.000000) |
| % Post load | 0.861603 (0.000000) | 0.846101 (000000) | 0.736831 (0.0001) | 0.849621 (0.000000) | 0.890591 (0.000000) | 1.000000 | −0.909908 (0.000000) |
| Fracture depth | −0.792918 (0.00001) | −0.923731 (0.000000) | −0.833023 (0.000001) | −0.916728 (0.000000) | −0.861417 (0.000000) | −0.909908 (0.000000) | 1.000000 |
All correlations with fiber length were significant (p < 0.001) and were positive with increasing values, except for the degree of crack depth values, which were negative and showed decreasing values with increasing fiber length (p < 0.00001). Fiber length had the highest linear relationship with percent load retained (R = 0.86), followed by degree of fracture depth (R = –0.79), then SERIC (R = 0.72), WOF (R = 0.71), flexural strength (R = 0.70), and modulus (R = 0.65). All mechanical parameters proved to correlate strongly with the degree of fracture depth in terms of final material failure analysis (p < 0.000001) and as estimators for each other (p < 0.0001). Failure measured by fracture depth was best predicted by flexural strength and WOF (R = –0.92). Other test estimators for fracture depth included percent load retained (R = –0.91), SERIC (R = –0.86), modulus (R = –0.83), and fiber length (R = –0.79). In terms of single estimators for other mechanical properties, flexural strength showed the best correlations with lowest probabilities of error when comparing the other parameters tested.
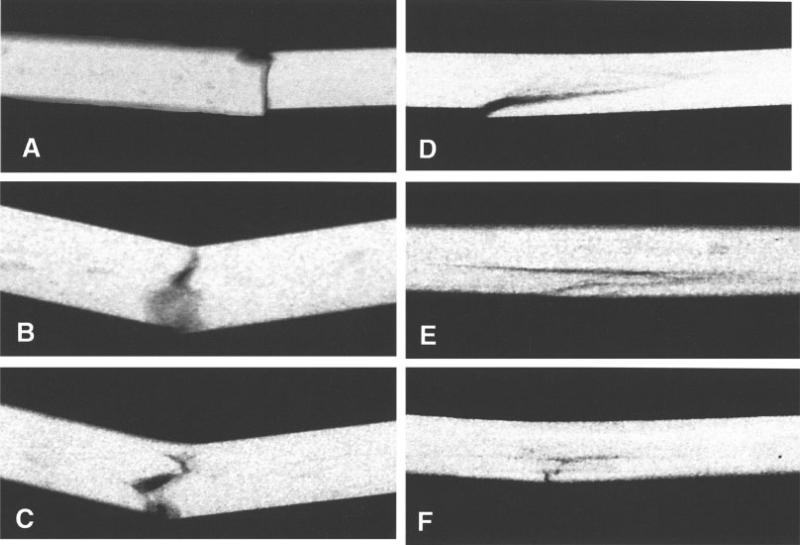
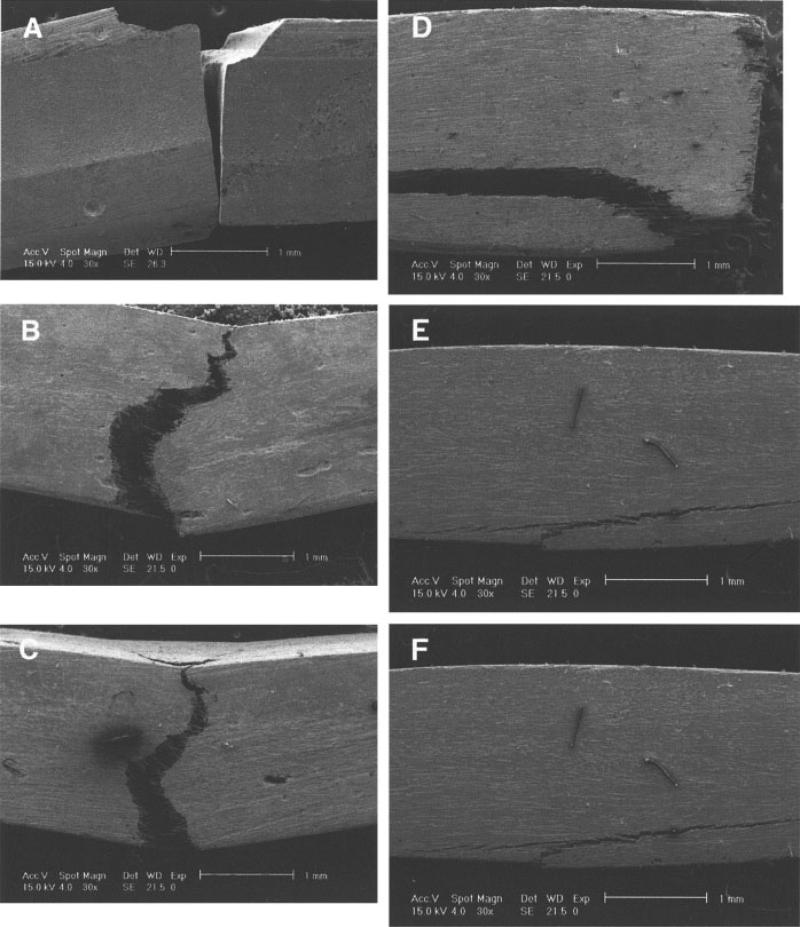
Representative X-rays in Fig. 7A–7F, and SEMs in Fig. 8A–8F, are presented for each fiber length. A progressive lessening of fracture depths from the tensile flexural surface was clearly evident with increasing fiber length. When compared to the unreinforced zirconia silicate particulate-filled composite with a smooth brittle vertical fracture surface (Figs. 7A and 8A), the addition of 0.5 mm fibers (Figs. 7B and 8B) immediately initiated noticeable lateral crack deflections that moved back and forth on the order of 0.25 to 0.5 mm into the sample. Cracks were further suppressed from extending in depth through the material as fiber length increased. Longer fibers also increased the degree of lateral crack deflections until at the 6.0 mm fiber length (Figs. 7F and 8F) where cracks began to diminish not only in depth but also in lateral deflection, as fibers apparently adsorbed more of the energy.
FIG. 7.
A–F: X-rays for different fiber length fracture surfaces A, no fibers; B, 0.5 mm fibers; C, 1.0 mm fibers; D, 2.0 mm fibers; E, 3.0 mm fibers; and F, 6.0 mm fibers.
FIG. 8.
A-F: SEMs for different fiber length fracture surfaces, 30×, scale bars 1.0 mm: A, no fibers; B, 0.5 mm fibers; C, 1.0 mm fibers; D, 2.0 mm fibers; E, 3.0 mm fibers; and F, 6.0 mm fibers.
Sample analysis by X-rays generally compared better with SEM imaging than reflective Nikon microscopy but showed slightly different crack propagation images. X-rays revealed diffuse cracks extending toward the neutral plane for 3.0 and 6.0 mm fibers (Fig. 7E and 7F), not evident from the SEM (Fig. 8E and 8F). A noticeable decrease in open fractures occurs by the 3.0 mm fiber length where damage accumulated in a more diffuse manner. When the neutral plane was penetrated, which generally occurred below the 2.0 mm fiber length group, mechanical properties declined drastically (Table 4) and was most notably evident with SERIC, dropping from 1.882 to 0.097 kJ/m2 when testing 1.0 mm fibers. The SEM imaging further provided examples where possible fiber fracture, fiber pull-out, and fiber bridging were occurring. Although fiber lengths of 0.5 and 1.0 mm were observed to generally prevent complete fracture, no load was retained after 5% deflection beyond maximum load capacity for fiber lengths of 0.5 and 1.0 mm, where failure included the fiber bridging as the mechanism to hold samples together. The SEM imaging for Alert® (not shown) from related wear studies displayed fibers much longer than the reported 40 μm, which has been previously imaged (54).
Cleavage planes parallel to the fiber axes of orientation were imaged by SEM from fiber- reinforced samples chosen from the average flexural strength for each fiber length group for a general characterization (Fig. 9A–9J). Each group was imaged at 30× and also at 200× toward the top edge. Fiber alignment was consistent for the most part when describing the micromechanics involved in debonding between the fiber and polymer. However, some extra mis-alignment was noted for the chosen sample closest to the mean strength with the 1.0 mm fiber length (Fig. 9C and 9D), which might be an indication that directional imperfections were related to lower experimental values plotted for strength and modulus when compared to theoretical predictions (Figs. 3 and 4). Conversely, improved alignment for longer fiber lengths at 3.0 and 6.0 mm may reflect the possibility of compressive shear deformation that might have lowered mechanical properties [34] in addition to flaws related to porosity or individual fiber interactions [46, 47].
FIG. 9.
A–J: SEMs for different fiber length split-planar views. A: SEM 30×, 0.5 mm fibers, scale bar 1.0 mm; B: SEM 200×, 0.5 mm fibers, scale bar 100 μm; C: SEM 30×, 1.0 mm fibers, scale bar 1.0 mm; D: SEM 200×, 1.0 mm fibers, scale bar 100 μm; E: SEM 30×, 2.0 mm fibers, scale bar 1.0 mm; F: SEM 200×, 2.0 mm fibers, scale bar 100 μm; G: SEM 30×, 3.0 mm fibers, scale bar 1.0 mm; H: SEM 200×, 3.0 mm fibers, scale bar 100 μm; I: SEM 30×, 6.0 mm fibers, scale bar 1.0 mm; and J: SEM 200×, 6.0 mm fibers, scale bar 100 μm.
With some misalignment considered in all samples and especially increasing toward shorter fibers, polymer toughness must be appreciated to counteract additional shearing forces. Indeed, with regard to strain and toughness, values for polymer strain, resilience, WOF, and SERIC exceeded the fiber length composite groups from 0.0 to 1.0 mm (Table 3). Also, the neat polymer strains were almost twice the strongest fiber-reinforced composites. Strain or toughness characteristics might then be considered important with regard to providing large deformations around the ends of high modulus fibers, especially as shearing forces are introduced with misaligned fibers. Plastic deformation shear yielding has previously been described regarding dissipation of fracture energy at a two-phase interface that was influenced by toughening complex crack paths [55]. Improving material toughness related to restricting crack propagation must then be appreciated with smaller, thinner parts commonly associated with medical/dental devices or during adhesive bonding. It should further be noted that all parallel cleavage planes seen with the 2.0, 3.0, and 6.0 mm length fibers (Fig. 9E, 9G, and 9I) did not develop on 0.5 and 1.0 mm fiber length composites that fractured with some brittle tendency (Fig. 9A and 9C).
Applications
Photocure vinyl ester discontinuous fiber-reinforced composites are now under research and development as bulk compound to improve contour adaptation and reduce micromotion with medical fixation devices during craniomaxillo-facial reconstruction. Photocure composites are also considered as an alternative for acrylic cranioplastic material [56, 57], especially when accompanied with mat or woven photocure materials. Nonthermal curing can be produced by pulsed photon light emission to prevent “burning” the underlying tissues during cranioplasty, experienced with current chemical cure acrylics [57]. Also, toxic acrylic methlymethacrylate monomers are eliminated. In addition, the surgeon has unlimited working time to place the material before applying the photocure visible-light source.
Manufacturing processes for particulate-filled composites should be adaptable to a fiber length between 1.0 to 2.0 mm toward an overall goal of replacing amalgam alloy for dental fillings. In addition to increased mechanical properties, fibers can be used to control handling of the material. As a result several clinical features may be improved that facilitate placement by the dentist [12]. When fully compounded with particulate-filled composites, fibers allow packing techniques similar to the amalgam alloy thereby minimizing the occurrence of large voids previously seen with particulate-filled dental composites[10–12]. Presently, the American Dental Association has not advocated the use of particulate-filled composite in “stress bearing” areas [58]. However, when noting strengths in the 400 MPa range, photocure fiber-reinforced composites may be a consideration for large losses of tooth structure, especially due to the adhesive stress-transfer nature of resin polymer matrix composites.
Wear is more than a surface property, where studies have shown that by increasing the underlying mechanical properties, wear may decrease [59, 60]. In addition, wear should decrease as the fiber length increases in length beyond any plowing grooves [60]. From literature and SEM composite imaging, it would appear in clinical use that quartz fibers would align parallel to the dental filling surface, and wear by thinning and then peal off so that smooth flat fiber wearing [60, 61] should not be excessive to the opposing enamel. Sheltering effects by the composite dispersed hardened phases [60] should reduce particulate loss by association with the fibers that should reduce third body particulate wear on opposing enamel wear, which still needs to be tested. If opposing enamel wear should increase with higher Vfs, these same high fiber concentrations should still be safely used to provide bulk mechanical strength below the masticatory surface and concurrently reduce surface wear at the lower surface fiber fractions, since incremental composite curing is reinforcing to adjacent material. If lower Vfs prevent composite wear, economics should improve commercialization of a product that should produce a profound effect on dentistry. In addition, by including the 2.0 mm fiber length, much stronger vinyl ester photocure composites could be provided, compared to previously known direct dental filling materials [62]. The vinyl ester photocure composites would also be adhesive to reinforce tooth structure and with increased mechanical strength, safety-factors allow combination of additives such as organic polymer compatible antimicrobials [63].
Nonthermal photocure processing is also feasible for high-tech structural encapsulants used in microelectronics. Photocure silica particulate-filled vinyl ester composites have previously been proposed to protect microelectronics [64]. Fibers then provide increased mechanical properties in addition to lower polymerization cure shrinkage stresses [65] that could damage fine electronic circuits.
Fibers are commonly used in adhesive films to control bond pressure and bondline thickness [66]. With regard to shorter fibers that may result in multiple fracture planes in a direction transverse to the primary crack failure direction, mechanical advantages may be produced along an adhesive XY-bond plane. By X-ray and SEM characterization, shorter fibers have the potential to deflect crack paths that occur out of the main fracture plane, which could include the adhesive surface bond plane of the material. Redirecting cracks could improve an adhesive bond zone by channeling energy into a cohesive material mode [67]. Planar fiber- reinforced films have also shown large improvements in shear bond toughness, by changing failure from adhesive to cohesive mainly through fiber bridging mechanisms [68]. In addition, those fibers that planarize along the bond plane as part of an adhesive resin system will further restrict stresses due to curing shrinkage [65]. By including the shorter 1.0 mm fiber length, to provide increased mechanical properties with some z-axis crack deflection away from the adhesive bond-plane, fiber-reinforced adhesives might then be better engineered to optimize adhesive/cohesive failure by design.
Although nonthermal photocure was employed as a means to reduce thermally induced cure stresses during micromechanical analysis, other broad applications for fiber-reinforced molding compounds or bonding adhesives with insufficient photocure visible-light access could also be cured by thermal or chemical means. Investigating fiber-reinforced composite micromechanics in the region above critical aspect ratio provides practical test results for applications specifically intended for smaller component devices. However, larger structural repairs combined by bonding fiber-reinforced molding compound with epoxy/carbon fiber composite stiffeners for example and photocure woven fabrics provide new avenues for material development. In addition, structural adhesive bonding with fiber-reinforced molding compound can further reduce use of strength-reducing fastener holes in large main frameworks [69, 70].
Summary
Adding quartz fibers with increasing lengths (0.5, 1.0, 2.0, 3.0, and 6.0 mm) at 28.2 Vf to a photocure vinyl ester particulate-filled composite, significantly correlated with increasing mechanical properties for maximum flexural strength, yield strength, modulus, strain, resilience, WOF, and SERIC (p < 0.001). Subsequent mechanical properties all correlated significantly with one another (p < 0.00001). Percent load retained following peak force also correlated significantly with increasing fiber length (p < 0.000000). Degree of fracture depth negatively correlated significantly as fiber length increased (p < 0.00001). Mechanical properties increased with flexural strength about 3×, modulus almost 1.75×, yield strength over 3.5× and strain capacity ~1.7×. Fracture toughness properties increased with resilience 6.5×, WOF 6.7× and SERIC 60×. A micromechanics for fiber length stress-transfer theory better explained strength by including a correction factor to account for any loss of Vf. The loss of effective Vf could be explained by crack propagation of the fracture zone during failure, which should proceed around the fiber when intersecting debonded fiber/polymer interfaces. A basic micromechanics for fiber length stress-transfer model was used to explain theoretical modulus with experimental results without considering the loss of Vf correction term. The Vf correction was not necessary for modulus, since it is considered that measurements were calculated from within the elastic isostrain region of the load-deflection curve before permanent deformation polymer/fiber debonding occurred.
CONCLUSIONS
The experimental outcome was different than expected, where fiber length and strength did not follow equations for either a simple linear regression or rule of mixtures or stress-transfer micromechanics for fiber length. An additional fracture-mechanics approach was necessary to explain loss of strength with loss of fiber volume percent during shear debonding. However, modulus, measured in the load-deflection elastic region, could be shown to follow the stress- transfer micromechanics equation for increasing fiber lengths. The theoretical rule-of-mixtures micromechanics for both modulus and strength were essentially validated by examining experimental discrepancies for fiber length just above critical length. The final encouraging results for a photocure composite were also surprising when compared to other engineered discontinuous fiber-reinforced materials from Table 1. The correlation matrix from Table 6 further provided significance statistically not only for fiber length with mechanical properties but also significant relationships for reductions in fracture depth and significant mechanical property interrelationships.
Photocure vinyl ester fiber-reinforced composites provided significant improvements with an increasing range of fiber lengths for several molding compounds intended later for medical and dental applications. A better appreciation for stress-transfer micromechanics particularly with shorter fibers will also help with the research and development of reinforced adhesives and structural encapsulants for microelectronics. Safety factors for mechanical properties became most evident for vast improvements that occurred with a plateau in the range of the 2.0 mm fiber length in the vinyl ester photocure polymer that can translate into incorporating possible new additive modifiers. In addition to increasing mechanical properties with longer fibers, fiber length variety should also allow development of different molding compounds with several consistencies to accommodate placement, packing, bonding, sealing, and bulk mechanical properties for the best possible material performances. The economics during equipment transition when incorporating fibers into isotropic materials should thus be much easier with an array of shorter fiber lengths.
ACKNOWLEDGMENTS
The investigation presented was originally derived from ongoing research and development of a photocure fiber-reinforced molding compound for medical/dental applications through the Department of Biomedical Engineering, School of Engineering, University of Alabama at Birmingham. Consultation for Micromechanics from Krishen K. Chawla, Department of Materials Science, School of Engineering, University of Alabama at Birmingham.SEM imaging by Vladimir M. Dusevich, Director, Electron Microscopy Laboratory, University of Missouri, Kansas City.
Contract grant sponsor: National Institutes of Health Research; contract grant number: T32DE14300.
NOMENCLATURE
- β
Geometric stress-transfer function
- C
Critical load or stress where fracture occurs. In mode I tension critical stress C is reached such that fracture occurs when C = IC
- E
Modulus
- I
Mode I tension
- Lc
Critical length
- Lc/d
Critical aspect ratio
- p
Probability of error when claiming a research hypothesis
- R
Pearson product correlation coefficient
- R2
Coefficient of determination
- σ
Tensile strength
- SEM
Scanning electron microscopy
- SER
Strain energy release (kJ/m2)
- τ
Shear strength
- Vf
Fiber volume percent
- WOF
Work of fracture (kJ/m2)
Contributor Information
Richard C. Petersen, Department of Biomedical Engineering, School of Engineering, University of Alabama at Birmingham, Birmingham, Alabama
Jack E. Lemons, Department of Biomedical Engineering, School of Engineering; Department of Surgery, School of Medicine; Division of Biomaterials, School of Dentistry, University of Alabama at Birmingham, Birmingham, Alabama
Michael S. McCracken, Division of Biomaterials, School of Dentistry, and Department of Biomedical Engineering, School of Engineering, University of Alabama at Birmingham, Birmingham, Alabama
REFERENCES
- 1.Chawla KK. Composite Materials. 2nd ed. Springer; New York: 1998. [Google Scholar]
- 2.Voigt W. Lehrbuch der Kristallphysik. Leipzig; Teubner: 1910. [Google Scholar]
- 3.Ratner BD, Hoffman AS, Shoen FJ, Lemons JE. Biomaterials Science. 2nd ed. Elsevier; New York: 2004. [Google Scholar]
- 4.Cox HL. Br. J. Appl. Phys. 1952;3:72. [Google Scholar]
- 5.Kelly A, Tyson WR. J. Mech. Phys. Solids. 1965;13:329. [Google Scholar]
- 6.Termonia Y. J. Mater. Sci. 1987;22:504. [Google Scholar]
- 7.Blumenthal LM. Recent Developments in the Field of Dental Resin. Office of Military Government for Germany (U.S.), Nat. Tech. Info. Serv.; 1947. Fiat final Report No. 1185 27, 1. [Google Scholar]
- 8.Lee H, Neville K. Handbook of Epoxy Resins. McGraw and Hill; New York: 1967. [Google Scholar]
- 9.Anusavice KJ. Science of Dental Materials. 11th ed. W. B. Saunders; Philadelphia: 2002. [Google Scholar]
- 10.Petersen RC, Wenski EF. Society for the Advancement of Materials and Process Engineering. 47th International SAMPE Symposium; Long Beach, California. 2002. [Google Scholar]
- 11.Petersen RC. J. Dent. Res. 2005;84:365. doi: 10.1177/154405910508400414. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Petersen RC. 2001 U.S. Patent 6,270,348.
- 13.Lindhagen JE, Berglund LA. Compos. Sci. Technol. 2000;60:885. [Google Scholar]
- 14.Szabo JS, Karger-Kocsis J, Gryshchuk O, Czigany T. Compos. Sci. Technol. 2004;64:1717. [Google Scholar]
- 15.Lau KT, Shi SQ, Zhou LM, Cheng HM. J. Compos. Mater. 2003;37:365. [Google Scholar]
- 16.van Voorn B, Smit HHG, Sinke RJ, de Klerk B. Compos: Part A. 2001;32:1271. [Google Scholar]
- 17.Puska MA, Narhi TO, Aho AJ, Yli-Urpo A, Vallittu PK. J. Mater. Sci.: Mater. Med. 2004;15:1037. doi: 10.1023/B:JMSM.0000042690.93328.e5. [DOI] [PubMed] [Google Scholar]
- 18.Boylan S, Castro JM. J. Appl. Polym. Sci. 2003;90:2557. [Google Scholar]
- 19.Biagiotti J, Fiori S, Torre L, Lopez-Manchado MA, Kenny JM. Polym. Compos. 2004;25:26. [Google Scholar]
- 20.Szabo JS, Czigany T. Polym. Testing. 2003;22:711. [Google Scholar]
- 21.Mader E, Pisanova E. Polym. Compos. 2000;21:361. [Google Scholar]
- 22.Wang W, Longxiang T, Qu B. Euro. Polym. J. 2003;39:2129. [Google Scholar]
- 23.Shonaike GO, Sugahara T, Murakami A. J. Appl. Polym. Sci. 2001;80:1395. [Google Scholar]
- 24.Kitano T, Haghani E, Tanegashima T, Saha P. Polym. Compos. 2000;21:493. [Google Scholar]
- 25.Ishiaku US, Hamada H, Mizoguchi M, Chow WS, Mohd Ishak ZA. Polym. Compos. 2005;26:52. [Google Scholar]
- 26.Yilmazer U, Cansever M. Polym. Compos. 2002;23:61. [Google Scholar]
- 27.Ozkoc G, Bayram G, Bayramli E. Polymer. 2004;45:8957. [Google Scholar]
- 28.Crivello JV, Dietliker K. Photoinitiators for Free Radical Cationic and Anionic Photopolymerisation. John Wiley and Sons; London: 1998. [Google Scholar]
- 29.Peck JA, Li G, Pang SS, Stubblefield MA. Compos. Struct. 2004;64:539. [Google Scholar]
- 30.Thomasset J, Carreau PJ, Sanschagrin B, Ausias G. J. Non-Newtonian Fluid Mech. 2005;125:25. [Google Scholar]
- 31.Cszrneck L, White JL. J. Appl. Polym. Sci. 1980;25:1217. [Google Scholar]
- 32.Baratta FI. Department of Defense, Approved for Public Release; Distribution unlimited, Nat. Tech. Info. Serv., ADA113937. 1982;21 [Google Scholar]
- 33.Quinn GD, Morrell R. J. Am. Ceram. Soc. 1991;74:2037. [Google Scholar]
- 34.ASTM D 6272–00 Test methods for flexural properties of unreinforced and reinforced plastics and electrical insulating materials.
- 35.Kossuth, Quartzel fused quartz textiles. Saint Gobain, Advanced Ceramic Division, Quartz Technology Department, 77793 Nemours Cedex, France, Paris, 2/1/002E (1998).
- 36.Charles RJ. J. Appl. Phys. 1958;29:1549. [Google Scholar]
- 37.Leinfelder K, Roberts TA. International State-of-the-art conference on Restorative Dental Materials. Vol. 1. National Institutes of Health; Bethesda, MD: 1986. [Google Scholar]
- 38.Milewski JV. Composites. 1973;4:258. [Google Scholar]
- 39.Atkins PW. Physical Chemistry. 5th ed. Vol. 763. W.H. Freeman and Company; New York: 1994. [Google Scholar]
- 40.Atkins AG, Mai YW. Elastic and Plastic Fracture. John Wiley and Sons; New York: 1988. [Google Scholar]
- 41.Callister WD. Materials Science and Engineering. 4th edn. John Wiley and Sons; New York: 1997. [Google Scholar]
- 42.ASTM D882–00 Test methods for tensile properties of thin plastic sheeting.
- 43.Greenspan HP, Benney DJ, Turner JE. Calculus. 2nd ed. Vol. 297. McGraw-Hill Ryerson; New York: 1986. [Google Scholar]
- 44.Tada H, Paris PC, Irwin GR. The Stress Analysis of Cracks Handbook. 3rd ed. Vol. 11. ASME Press; New York: 2000. [Google Scholar]
- 45.Daniel WW. Biostatistics. 7th ed. John Wiley and Sons; New York: 1999. [Google Scholar]
- 46.Phillips DC, Sambell RAJ, Bowen DH. J. Mater. Sci. 1972;7:1454. [Google Scholar]
- 47.Shia D, Hui CY, Phoenix SL. Compos. Sci. Technol. 2000;60:2107. [Google Scholar]
- 48.Chiang CR. Compos. Sci. Technol. 1994;50:479. [Google Scholar]
- 49.Palmese GR, Gan D, Chabra G. Proceedings 11th Technical Conf. Am. Soc. Compos.; Atlanta, Georgia. 1996. [Google Scholar]
- 50.Tripathi D, Turton T, Chen F, Jones FR. J. Mater. Sci. 1997;32:4759. [Google Scholar]
- 51.McDonough WG, Antonuucci JM, Dunkers JP. Dent. Mater. 2001;17:492. doi: 10.1016/s0109-5641(01)00008-2. [DOI] [PubMed] [Google Scholar]
- 52.Fu SY, Lauke B. Compos. Sci. Technol. 1996;56:1179. [Google Scholar]
- 53.Robinson IM, Robinson JM. J. Mater. Sci. 1994;29:4663. [Google Scholar]
- 54.Reis AF, Giannini M, Lovadino JR, Ambrosano GM. Dent. Mater. 2003;19:12. doi: 10.1016/s0109-5641(02)00014-3. [DOI] [PubMed] [Google Scholar]
- 55.Zheng S, Wang J, Guo O, Wei J, Li J. Polymer. 1996;37:4667. [Google Scholar]
- 56.McLone DG. Pediatric Surgery. W.B. Saunders; New York: 2001. [Google Scholar]
- 57.Albright AL, Pollack IG, Adelson PD. Operative Techniques in Pediatric Surgery. Thieme; New York: 2001. [Google Scholar]
- 58.American Dental Association Council on Scientific Affairs J. Am. Dent. Assoc. 1998;129:1627. doi: 10.14219/jada.archive.2012.0295. [DOI] [PubMed] [Google Scholar]
- 59.Giltrow JP. Composites. 1973;4(3):55. [Google Scholar]
- 60.Freidrich K. Advances in Composite Tribology. Elsevier; New York: 1993. [Google Scholar]
- 61.Friedrich K. Friction and Wear of Polymer Composites. Elsevier; New York: 1986. [Google Scholar]
- 62.O'Brien WJ. Dental Materials. 2nd ed. Quintessence; Chicago: 1997. [Google Scholar]
- 63.Petersen RC, Lemons JE, Reddy MS. Second Annual Southeast Workshop on Tissue Engineering and Biomaterials; Birmingham, Alabama. February 11–12.2005. [Google Scholar]
- 64.Baikerikar KK, Scranton AB. Polymer. 2001;42:431. [Google Scholar]
- 65.Cloud PJ, Wolverton MA. Plastic Technol. 1978;24(11):107. [Google Scholar]
- 66.Bolger JC. Adhesives in Manufacturing. Vol. 148. Marcel Dekker; New York: 1983. [Google Scholar]
- 67.Potter KD, Guild FJ, Harvey JJ, Wisnon MR, Adams RD. Int. J. Adhes. Adhesives. 2001;21:435. [Google Scholar]
- 68.Shetty SP, Spearing SM. Scripta Mater. 1997;37:787. [Google Scholar]
- 69.Baker AA. Composites. 1987;18:293. [Google Scholar]
- 70.Mario-Riga A, Xenos D, Vrettos C. Appl. Compos. Mater. 2004;11:191. [Google Scholar]