Assessing model fit in joint models of longitudinal and survival data with applications to cancer clinical trials

Abstract

Joint models for longitudinaland survival data now have along history of being used in clinical trials or other studies in which the goal is to assess a treatment effect while accounting for longitudinal assessments such as patient-reported outcomes or tumor response. Compared to using survival data alone,the joint modeling of survival and longitudinal data allows for estimation of direct and indirect treatment effects, thereby resulting in improved efficacy assessment. Although global fit indices such as AIC or BIC can be used to rank joint models, these measures do not provide separate assessments of each component of the joint model. In this paper, we develop a novel decomposition of AIC and BIC (i.e., AIC = AIC_Long + AIC_Surv|Long and BIC = BIC_Long + BIC_Surv|Long) that allows us to assess the fit of each component of the joint model, and in particular to assess the fit of the longitudinal component of the model and the survival component separately. Based on this decomposition, we then propose ΔAIC_Surv and ΔBIC_Surv to determine the importance and contribution of the longitudinal data to the model fit of the survival data. Moreover, this decomposition, along with ΔAIC_Surv and ΔBIC_Surv, is also quite useful in comparing, for example, trajectory-based joint models and shared parameter joint models and deciding which type of model best fits the survival data. We examine a detailed case study in mesothelioma to apply our proposed methodology along with an extensive set of simulation studies.

1. Introduction

Through the joint modeling of longitudinal and survival data, researchers may reduce bias in the estimates of the treatment effect and also increase the power to compare the efcacy of a new oncology treatment with the current standard of care [1, 2]. Although the joint analysis of longitudinal and time-to-event outcomes has been widely published in statistical journals, it has not yet been routinely applied to the analysis of patient-reported outcomes (PROs) for the purpose of evaluating the efcacy and tolerability of cancer treatment. One barrier to the implementation of these methods has been the lack of usable sofitware to guide the programming and evaluation of these joint models. Building on previous joint modeling work in a highly symptomatic and particularly fatal condition [malignant pleural mesothelioma (MPM)] [3, 4], we develop methods to evaluate model fit in order to identify proper model specification.

This work was motivated by the need to adequately assess the differential benefits of alternative medical treatments, particularly in oncology applications where the survival advantage between competing medications may be modest. In this setting, information from the patients’ perspectives can be useful in evaluating actual patients’ experiences on dimensions known to be important to them and also associated with treatment outcomes. Accordingly, the field of PROs has evolved and has reached a common understanding about good clinical practices for the use of PROs [5]. Additionally, the U.S. and European regulators have published guidance on the use of these measures to support PRO-based claims in pharmaceutical product labeling (European Medicines Agency, 2005; US Food and Drug Administration Guidance for Industry, 2009)[6]. Unfortunately, relatively little attention has been paid to similarly advancing the analysis of trial-based PRO data; the inclusion of PRO assessments is seldom done with the rigor used to specify and analyze traditional endpoints of survival and tumor response [7]. Hence, the benefits of good PRO practice standards and insightful regulatory guidance have not generally led to informative conclusions. Published results concerning the use of joint survival/PRO models should help inform decision makers about the impact of anticancer treatment on both survival and patient well-being [3, 4, 8]. Joint modeling of these endpoints can provide a comparative assessment of patient-reported changes in specifc symptoms or global measures (e.g., quality of life or functioning) that correspond to treatment-related changes in survival. Therefore, it could be shown that increased survival was accompanied by relatively better PRO scores or alternatively that extended progression-free or overall survival was experienced at the expense of well-being. To support this joint modeling, we show how to evaluate the distinct effects of longitudinal and time-to-event outcomes on the fit of the joint model, and we develop the necessary SAS code to facilitate use of these methods.

The literature on joint modeling of longitudinal and survival data has burgeoned to the point that it is impractical to make broad general conclusions based on a systematic review of the literature. It is, however, practical and useful to describe the two basic fundamental approaches in joint modeling of longitudinal and survival to achieve this goal. The first is the "trajectory model" (TM) approach, where the trajectory function (mean response) from the longitudinal model is substituted into the hazard function of the survival model, thereby serving as a time-varying covariate in the survival model. The second basic approach is the "shared parameter model" (SPM), where the longitudinal model and survival model share common random effects which then induces correlation between the longitudinal and survival components. Both modeling schemes have advantages and disadvantages. The TM advantage, compared to the SPM, is that it leads to a straight forward interpretation of the association between the longitudinal marker and survival time through the direct inclusion of the trajectory function in the hazard. For the SPM, the characterization of the association is much more complex and can only be analytically determined once the random effects have been integrated out, since the two components of the model are independent conditional on these random effects. Typically, this integration cannot be carried out in closed form, and even if it were, the resulting dependence structure would be very complicated involving lots of parameters and resulting in difcult interpretations.

There have been many papers in the statistical literature concerning these two basic approaches. The TM in joint modeling for cancer vaccine trials in malignant melanoma has been considered in [9, 10, 11, 12]. The TM models have been also used in quality-of-life studies [13, 14, 15, 16], and in AIDS studies [17, 18, 19, 20, 21, 22, 23]. The SPM models have been used in other types of biomedical applications [24, 25]. There has been much work on using the SPM in joint modeling of survival and longitudinal data focused on AIDS studies, and in particular, jointly modeling of survival data and univariate or multivariate longitudinal CD4 counts. These articles include [26, 27, 28]. Other researchers who have used SPM’s with a multivariate longitudinal response include [29, 30, 31, 32]. An excellent general review on joint modeling of longitudinal and survival data was given in [33]. Ibrahim, Chen, and Sinha ([34], Chapter 7) also gave an overview of joint modeling methods. Joint models for longitudinal and survival data in which the survival component of the model is a cure rate model were considered in [35, 10, 11], where the models focus on cancer clinical trials.

One important issue in the joint modeling of longitudinal and survival data concerns the separate contribution of the model components to the overall goodness-of-fit of the joint model. In this paper, we derive a novel decomposition of the AIC and BIC criteria into additive components that will allow us to assess the goodness of fit for each component of the joint model. More importantly, such a decomposition allows us to develop ΔAIC_Surv and ΔBIC_Surv to quantify the change of AIC and BIC in fitting the survival data with and without the longitudinal data. Thus, ΔAIC_Surv and ΔBIC_Surv can be used to determine the importance of the longitudinal data to the model fit of the survival data. In addition, ΔAIC_Surv and ΔBIC_Surv are also very useful in assessing whether a linear trajectory or quadratic trajectory is more suitable and in facilitating a direct comparison between TM’s and SPM’s. These proposed measures will help the data analyst in not only assessing each component of the joint model but also in determining the contribution of the longitudinal data to the fit of the survival data.

The rest of the paper is organized as follows. A detailed description of the longitudinal and survival data from a clinical trial is given in Section 2. The joint models, the time-varying covariates models, and the two-stage models are presented in Section 3 along with their properties. The proposed decomposition of AIC and BIC is developed in Section 4. An extensive simulation study is conducted in Section 5, and a comprehensive analysis of the longitudinal and survival data described in Section 2 is given in Section 6. We conclude the paper with a discussion including some proposed extensions to our research in Section 7.

2. The EMPHACIS Data

Our research was motivated by the large phase III multicenter, randomized, single-blind, EMPHACIS lung cancer clinical trial (Evaluation of MTA in Mesothelioma in a Phase 3 Study with Cisplatin). Although the details of this study have been published elsewhere [36], we provide the essential background information needed for contextual understanding of our proposed methodology. The study drug was pemetrexed (PEM), a multi-targeted antifolate (MTA), which was given in combination with cisplatin (Cis) (the PEM/Cis arm), and the active-treatment comparator was cisplatin alone (the Cis arm); respectively, 226 and 222 patients received at least one cycle of chemotherapy. The treatment for both arms was structured as six 21-day cycles of therapy; patients receiving treatment benefit could receive additional cycles based on investigator discretion.

Malignant pleural mesothelioma is characterized by rapid disease progression, high symptom burden, and a relatively short median survival of 12 months afiter diagnosis [37, 38]. Accordingly, patient-reported assessments are important for evaluation of disease progression and patients’ response to therapy. In oncology, the patients’ importance ratings on the magnitude of progression-free survival improvement has been shown to depend on the severity of disease-related symptoms [39]. We analyzed the disease-specifc patient-reported Lung Cancer Symptom Scales (LCSS) [40] to evaluate the patient-level association of five of the six instrument items (i.e., anorexia, cough, dyspnea, fatigue, and pain) with progression-free survival using the EMPHACIS trial data. The sixth LCSS symptom, hemoptysis, was not analyzed due to research suggesting that this phenomenon is not prevalent in MPM [41]. The three remaining LCSS items are global constructs (interference, quality of life, symptoms), and due to their non-specifcity, we also excluded these from our analysis. Each questionnaire item was assessed using l00-mm visual analogue scales (0=no symptoms, 100 = worst possible symptoms). There were two measurements at baseline. In our analysis, we took the average of the two baseline measurements of each longitudinal outcome as the baseline outcome and reset the measurement time so that the baseline measurement time is zero. Weekly measurements (at days 8 ± 1, 15 ± 1, l9) were taken in each 21-day therapy cycle. The LCSS was also assessed approximately every 3 months afiter the patient had received his or her last dose of treatment if the patient had not initiated subsequent therapy. Progression free survival time (PFS) is defined as the time from randomization to the time until documented progression or death from any cause. Beyond disease progression, very few LCSS assessments were available.

Previously, researchers have investigated the prognostic effect of baseline PRO outcomes on overall survival in patients with MPM [42]. We are, however, interested in the association between post-baseline PRO scores and PFS. The main goal of applying joint models in this study is to assess the association of each longitudinal LCSS symptom with PFS and the treatment effects on each LCSS item and PFS simultaneously. More importantly, with the novel decomposition of AIC and BIC, the longitudinal LCSS symptoms can be compared in terms of their contribution to the overall fit of the survival data.

Our cohort consists of 425 patients with at least one post-baseline value for each longitudinal outcome. The covariates we consider in this study include race/ethnicity, gender, age, Karnofsky status, baseline stage of disease, vitamin supplementation, and treatment assignment. Table 1 shows the baseline characteristics of the patients in each treatment group and the four descriptive statistics (minimum, median, maximum and mean) for PFS.

Table 1.

Baseline characteristics of patients and summary of PFS in each treatment group

		Pemetrexed/Cisplatin n=208 (%)	Cisplatin n=217 (%)
Covariates	Race: White	189 (91%)	202 (93%)
	Gender: Male	169 (81%)	177 (82%)
	Age: ≥ 65	80 (38%)	83 (38%)
	Karnofsky: High (90-100)	112 (54%)	124 (57%)
	Stage: I/II	48 (23%)	46 (21%)
	Vitamin Supplement: Full	156 (75%)	158 (73%)
PFS (in months)	Minimum	0.4	0
	Median	6.1	3.6
	Maximum	27.1	21.8
	Mean	7.0	4.8

3. The Models

Suppose that there are n subjects. For the ith subject, let Y_i(t) denote the longitudinal outcome, which is observed at time t ∈{a_i1, a_i2,...., a_imi}, where a_i1 = 0 <a_i2 < ... <a_imi and m_i > 1. Note that Y_i(0) corresponds to the baseline value. Let t_i denote the failure time, which may be right-censored, and let δ_i be the censoring indicator such that δ_i = 1 if t_i is a failure time and 0 if t_i is right-censored for the ith subject. Also let z_i be the treatment indicator such that z_i = 1 for the treatment and z_i = 0 for the control. We further let x_i denote the p-dimensional vector of covariates. We first consider the joint model for (Y_i, t_i), which consists of the longitudinal component and survival component presented in Subsections 3.1 and 3.2. We also consider a time-varying covariates (TVC) model for t_i, where Y_i(t) is treated as a time-varying covariate in Subsection 3.3.

3.1. Longitudinal Component of the Joint Model

For the ith subject, we assume a mixed effects regression model for the longitudinal outcome Y_i(t), which is given by

$$Y_i\left(a_{ij}\right)={\theta }_i^{\prime }g\left(a_{ij}\right)+{\gamma }_1{z}_i+{\gamma }_2^{\prime }{x}_i+{∊}_i\left(a_{ij}\right),$$ (3.1)

where $g\left(a_{ij}\right)={(1,a_{ij},a_{ij}^2,\dots ,a_{ij}^q)}^{\prime }$ is a polynomial vector of order q for j = 1,..., m_i, θ_i is a (q+1)-dimensional vector of random effects, and γ₂ is a p-dimensional vector of regression coefficients. In (3.1), we further assume θ_i ~ N(θ, Σ), where θ is the (q+l)-dimensional vector of overall effects, Σ is a (q+1)×(q+1) positive definite covariance matrix with lower triangle consisting of {Σ₀₀, Σ₁₀, Σ₁₁,..., Σ_qq}, ε_i(a_ij) ~ N(0, σ²), and θ_i and ε_i(a_ij) are independent. We note that in (3.1), if q = 1, g(a_ij) = (1,a_ij)′ and ${\theta }_i^{\prime }g\left(a_{ij}\right)$ yields a linear trajectory, and if q = 2, $g\left(a_{ij}\right)={(1,a_{ij},a_{ij}^2)}^{\prime }$ and ${\theta }_i^{\prime }g\left(a_{ij}\right)$ leads to a quadratic trajectory.

3.2. Survival Component of the Joint Model

For failure time t_i, we assume the hazard function is of the general form

$$\lambda (t\mid {\lambda }_0,\beta ,\alpha ,{\theta }_i,g\left(t\right),\gamma ,z_i,x_i)={\lambda }_0\left(t\right)\exp \{h(\beta ,{\theta }_i,g\left(t\right),{\gamma }_1{z}_i,{\gamma }_2^{\prime }{x}_i)+{\alpha }_1{z}_i+{\alpha }_2^{\prime }{x}_i\},$$ (3.2)

where λ₀(t) is the baseline hazard function, h(·) is a linear function of θ_i, g(t), γ₁z_i, and ${\gamma }_2^{\prime }{x}_i$ with β being a vector of the corresponding regression coefcients, $\gamma ={({\gamma }_1,{\gamma }_2^{\prime })}^{\prime }$, and $\alpha ={({\alpha }_1,{\alpha }_2^{\prime })}^{\prime }$. Note that in (3.2), θ_i, g(t), γ₁, and γ₂ are the parameters or the functions from the longitudinal component of the joint model in (3.1), and λ₀, β, α₁ and α₂ are the only parameters pertaining to the survival component. When

$$h(\beta ,{\theta }_i,g\left(t\right),{\gamma }_1{z}_i,{\gamma }_2^{\prime }{x}_i)=h^{\ast }(\beta ,{\theta }_i^{\prime }g\left(t\right),,{\gamma }_1{z}_i,{\gamma }_2^{\prime }{x}_i),$$ (3.3)

where h^*(·) is a linear function of ${\theta }_i^{\prime }g\left(t\right)$, γ₁z_i, and ${\gamma }_2^{\prime }{x}_i$, (3.2) leads to the TM. In this case, the hazard function depends on θ_i and g only through ${\theta }_i^{\prime }g$. When h does not depend on g(t), that is,

$$h(\beta ,{\theta }_i,g\left(t\right),{\gamma }_1{z}_i,{\gamma }_2^{\prime }{x}_i)=h^{\ast }(\beta ,{\theta }_i,{\gamma }_1{z}_i,{\gamma }_2^{\prime }{x}_i)$$

where h^*(·) is a linear function of ${\theta }_i^{\prime }$, γ₁z_i, and ${\gamma }_2^{\prime }{x}_i$, (3.2) reduces to the SPM.

In (3.2), we further assume a piecewise constant hazard model for λ₀(t). Specifcally, we first construct a finite partition of the time axis, 0 = s₀ < s₁ < s₂ < ... < s_K−1 < s_K = ∞. Thus, we have K intervals (0,s₁], (s₁,s₂], ... , (s_K−1,s_K]. Then, we assume a constant baseline hazard within each of the K intervals, that is,

$${\lambda }_0\left(t\right)={\lambda }_k,t∊(s_{k-1},s_k]\text{for}k=1,...,K.$$ (3.4)

Finally, we write λ = (λ₁,...,λ_K)′. Using (3.4), the complete-data likelihood function for the survival component for the ith subject can be written as

$$L(\lambda ,\beta ,\alpha \mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\gamma )={\left[\lambda (t_i\mid {\lambda }_0,\beta ,\alpha ,{\theta }_i,g\left(t_i\right),\gamma ,z_i,x_i)\right]}^{{\delta }_i}\times \exp \left\{-{\int }_0^{t_i}\lambda (u\mid {\lambda }_0,\beta ,\alpha ,{\theta }_i,g\left(u\right),\gamma ,z_i,x_i)du\right\},$$ (3.5)

where λ(t|λ₀, β, α, θ_i, g(t), γ,z_i, x_i) is given in (3.2).

Remark 3.1 In (3.2), when β = 0, $h(\beta ,{\theta }_i,g\left(t\right),{\gamma }_1{z}_i,{\gamma }_2^{\prime }{x}_i)\equiv 0$ and the hazard function reduces to $\lambda (t\mid {\lambda }_0,\beta =0,\alpha ,{\theta }_i,g\left(t\right),\gamma ,z_i,x_i)={\lambda }_0\left(t\right)\exp ({\alpha }_1{z}_i+{\alpha }_2^{\prime }{x}_i)$. In this case, we fit the survival data alone (without the longitudinal data) and the likelihood function in (3.5) for the ith subject reduces to

$$L_0(\lambda ,\alpha \mid t_i,{\delta }_i,z_i,x_i)=\left\{{\lambda }_0\left(t_i\right)\exp {({\alpha }_1{z}_i+{\alpha }_2^{\prime }{x}_i)}^{{\delta }_i}\right\}\exp \left[-\exp ({\alpha }_1{z}_i+{\alpha }_2^{\prime }{x}_i)\left\{{\int }_0^{t_i}{\lambda }_0\left(u\right)du\right\}\right].$$ (3.6)

3.3. The Time-Varying Covariates (TVC) Model

If t_i is of primary interest, the time-varying covariates model (see, for example, [43, 44]) can be used to model the failure time t_i, in which Y_i(t) can be considered as a time-varying covariate. Under the TVC model, the hazard function is assumed to be

$$\lambda (t\mid {\lambda }_0,\beta ,\alpha ,z_i,x_i,Y_i\left(t\right))={\lambda }_0\left(t\right)\exp \left\{\beta Y_i\left(t\right)+{\alpha }_1{z}_i+{\alpha }_2^{\prime }{x}_i\right\},$$ (3.7)

where λ₀(t) is the baseline hazard function. Since the longitudinal outcome Y_i(t) is observed only at each of a_i1, ... , a_imi, we let Y_i(t) = Y_i(a_ij) for a_ij ≤ t <a_i,j+1 for j = 1, ... , m_i, where a_i,mi+1 = ∞. Similar to (3.2), a piecewise constant hazard model in (3.4) is assumed for λ₀(t) in (3.7). Finally, we notice that in the TVC model (3.7), Y_i(t) is a one-dimensional covariate and therefore, β is one-dimensional as well.

3.4. The Two-Stage (TS) Model

Instead of directly using the longitudinal outcome Y_i(t) as a covariate in (3.7), (i) we first fit (3.1) to the longitudinal data alone, obtain the estimates of θ_i, γ₁, and γ₂, denoted by ${\widehat{\theta }}_i$, ${\widehat{\gamma }}_1$ and ${\widehat{\gamma }}_2$; and compute ${\widehat{Y}}_i\left(t\right)={{\widehat{\theta }}_i}^{\prime }g\left(t\right)+{\widehat{\gamma }}_1{z}_i+{\widehat{\gamma }}_2^{\prime }{x}_i$; and (ii) we then use ${\widehat{Y}}_i\left(t\right)$ as a time-varying covariate in the survival model, in which the hazard function is defined as $\lambda (t\mid {\lambda }_0,\beta ,\alpha ,z_i,x_i,{\widehat{Y}}_i\left(t\right))={\lambda }_0\left(t\right)\exp \left\{\beta {\widehat{Y}}_i\left(t\right)+{\alpha }_1{z}_i+{\alpha }_2^{\prime }{x}_i\right\}$. At first, it appears that the above hazard function is similar to (3.7). However, there is a substantial difference between Y_i(t) and ${\widehat{Y}}_i\left(t\right)$. The longitudinal outcome Y_i(t) is observed only at each of the time points a_i1, ..., a_imi while ${\widehat{Y}}_i\left(t\right)$ is defined at any time t. In addition, ${\widehat{Y}}_i\left(t\right)$ is much less variable than Y_i(t) since ${\widehat{Y}}_i\left(t\right)$ is a smooth function of t and Y_i(t) is random. The model defined here is known as the two-stage (TS) model [33].

4. Assessing the Contribution of Longitudinal Data When Modeling the Survival Data

For the joint model discussed in the previous section, we develop a new method to assess the contribution of the longitudinal data when fitting the survival data. We first introduce some notation. We rewrite (3.1) as follows: $Y_i=W_i{({\theta }_i^{\prime },{\gamma }^{\prime })}^{\prime }+{∊}_i$ where Y _i =(Y_i(a_i1),...,Y_i(a_imi))' , W_i is a m_i by (p + q + 2) matrix whose ith row is $(1,a_{ij},\dots ,a_{ij}^q,z_i,x_i^{\prime })$, and ε_i =(ε_i(a_i1),...,ε_i(a_imi))’ ~ N(0,σ²I_mi). The complete-data likelihood function of the longitudinal outcomes for the ith subject is given by

$$L(\gamma ,{\sigma }^2\mid Y_i,W_i,{\theta }_i)\propto {\sigma }^{-m_i}\exp \left\{-\frac{1}{2{\sigma }^2}{(Y_i-W_i{({\theta }_i^{\prime },{\gamma }^{\prime })}^{\prime })}^{\prime }(Y_i-W_i{({{\theta }^{\prime }}_i,{\gamma }^{\prime })}^{\prime })\right\},$$ (4.1)

for i = 1,...,n. Note that the density of θ_i is given by

$$f({\theta }_i\mid \theta ,\sum )=\frac{\mid \sum {\mid }^{-\frac{1}{2}}}{{\left(2\pi \right)}^{\frac{q+1}{2}}}\exp \left\{-\frac{1}{2}{({\theta }_i-\theta )}^{\prime }{\sum }^{-1}({\theta }_i-\theta )\right\}.$$ (4.2)

Let φ = (λ, β, α, γ,σ², θ, Σ). Using (3.5), (4.1), and (4.2), the observed-data likelihood function for (Y_i,t_i,δ_i) for the ith subject is given by

$$L(\phi \mid Y_i,t_i,{\delta }_i,z_i,x_i,W_i)=\int L(\lambda ,\beta ,\alpha \mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\gamma )L(\gamma ,{\sigma }^2\mid Y_i,W_i,{\theta }_i)f({\theta }_i\mid \theta ,\sum )d{\theta }_i,$$ (4.3)

for i = 1,..., n. Let $\widehat{\phi }$ denote the maximum likelihood estimate (MLE) of φ from the joint model. Using (4.3), the Akaike Information Criterion (AIC) [45] for the joint model is given by

$$\mathrm{AIC}=-2\sum _{i=1}^n\log L(\widehat{\phi }\mid Y_i,t_i,{\delta }_i,z_i,x_i,W_i)+2\dim \left(\phi \right)$$ (4.4)

and the Bayesian Information Criterion (BIC) [46] is defined as

$$\mathrm{BIC}=-2\sum _{i=1}^n\log L(\widehat{\phi }\mid Y_i,t_i,{\delta }_i,z_i,x_i,W_i)+\dim \left(\phi \right)\log n.$$ (4.5)

4.1. AIC and BIC Decomposition

To assess the contribution of longitudinal data to the fit of the survival data, we need to decompose AIC in (4.4) into two parts: one part for the longitudinal data and the other part for the survival data conditional on the longitudinal data. Write φ₁ =(γ,σ², θ, Σ) and φ₂ =(λ, β, α). We are led to the following theorem.

Theorem 4.1 Let f(θ_i|Y _i,W_i, φ₁) be the conditional density of the random effects θ_i given Y _i, and also let $L({\phi }_1\mid Y_i,W_i)=\int L(\gamma ,{\sigma }^2\mid Y_i,W_i,{\theta }_i)f({\theta }_i\mid \theta ,\Sigma )d{\theta }_i$, which is the likelihood function corresponding to the marginal distribution of Y_i. Then AIC in (4.4) has the following decomposition:

$$\mathrm{AIC}={\mathrm{AIC}}_{\mathrm{Long}}+{\mathrm{AIC}}_{\mathrm{Surv}\mid \mathrm{Long}},$$ (4.6)

where ${\mathrm{AIC}}_{\mathrm{Long}}=-2{\sum }_{i=1}^n\log L({\widehat{\phi }}_1\mid Y_i,W_i)+2\dim \left({\phi }_1\right)$, ${\mathrm{AIC}}_{\mathrm{Surv}\mid \mathrm{Long}}=-2{\sum }_{i=1}^n\log \int L({\widehat{\phi }}_2\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\widehat{\gamma })f({\theta }_i\mid Y_i,W_i,{\widehat{\phi }}_1)d{\theta }_i+2\dim \left({\phi }_2\right)$, and ${\widehat{\phi }}_1$ and ${\widehat{\phi }}_2$ are the MLEs of ${\phi }_1$ and ${\phi }_2$.

The proof of Theorem 4.1 is given in the Appendix. BIC in (4.5) has a similar decomposition as in (4.6); this result is stated in the following corollary, and the proof of this corollary directly follows that of Theorem 4.1.

Corollary 4.1 BIC in (4.5) can be decomposed as BIC = BIC_Long + BIC_Surv|Long, where BIC_Long = AIC_Long + dim(φ₁)(log n − 2), and BIC_Surv|Long = AIC_Surv|Long + dim(φ₂)(log n − 2).

Remark 4.1 We note that the AIC decomposition in (4.6) and the BIC decomposition in Corollary 4.1 hold for general longitudinal data models, which may not be normal. However, for normally distributed longitudinal data, f(θ_i|Y_i,W_i, φ₁) and L(φ₁|Y_i,W_i) in Theorem 4.1 are available in closed form. It is easy to see that

$$E\left(Y_i\right)=E\left[E(Y_i\mid {\theta }_i)\right]=W_i{({\theta }^{\prime },{\gamma }^{\prime })}^{\prime },$$

and

$$Var\left(Y_i\right)=E\left[Var(Y_i\mid {\theta }_i)\right]+Var\left[E(Y_i\mid {\theta }_i)\right]={\sigma }^2{I}_{mi}+W_i\left(\begin{array}{cc}\hfill \Sigma \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right){W^{\prime }}_i.$$

Thus, the observed-data likelihood function of the longitudinal data takes the form:

$$L({\phi }_1\mid Y_i,W_i)=\frac{{\mid {\sigma }^2{I}_{mi}+W_i\left(\begin{array}{cc}\hfill \Sigma \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)W_i^{\prime }\mid }^{-\frac{1}{2}}}{\left(2\pi \right)\frac{m_i}{2}}\exp \left\{-\frac{1}{2}{(Y_i-W_i{({\theta }^{\prime },{\gamma }^{\prime })}^{\prime })}^{\prime }\times {\left({\sigma }^2{I}_{mi}+W_i\left(\begin{array}{cc}\hfill \Sigma \hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill \end{array}\right)W_i^{\prime }\right)}^{-1}(Y_i-W_i{({\theta }^{\prime },{\gamma }^{\prime })}^{\prime })\right\}.$$ (4.7)

After some algebra, we also obtain the conditional distribution of the random effects θ_i given the longitudinal data, which is given by

$${\theta }_i\mid Y_i,W_i,{\phi }_1~N\left({\left({\Sigma }^{-1}+\frac{1}{{\sigma }^2}\left(I_{q+1}0\right)W_i^{\prime }{W}_i\left(\begin{array}{c}\hfill I_{q+1}\hfill \\ \hfill 0\hfill \end{array}\right)\right)}^{-1}\left[\frac{1}{{\sigma }^2}\left(I_{q+1}0\right){W_i}^{\prime }\left(Y_i-W_i\left(\begin{array}{c}\hfill 0\hfill \\ \hfill I_{p+1}\hfill \end{array}\right)\gamma \right)+{\Sigma }^{-1}\theta \right]{\left({\Sigma }^{-1}+\frac{1}{{\sigma }^2}\left(I_{q+1}0\right){W_i}^{\prime }{W}_i\left(\begin{array}{c}\hfill I_{q+1}\hfill \\ \hfill 0\hfill \end{array}\right)\right)}^{-1}\right).$$

Remark 4.2 SPM and TM discussed in Section 3 can be implemented in SAS via PROC NLMIXED. The NLMIXED procedure calculates ${\widehat{\phi }}_1$, ${\widehat{\phi }}_2$, and the overall AIC using adaptive Gaussian quadrature to approximate (4.3). For normally distributed longitudinal data, AIC_Long can be computed using (4.7) and ${\widehat{\phi }}_1$, which may be implemented in SAS via PROC IML. Subsequently, AIC–AIC_Long gives AIC_Surv|Long. Alternatively, given ${\widehat{\phi }}_1$ and ${\widehat{\phi }}_2$, we may use a Monte Carlo (MC) method to compute AIC_Surv|Long using (4.6) and an MC sample generated from $f({\theta }_i\mid Y_i,W_i,{\widehat{\phi }}_1)$. This alternative approach can be used to validate the total AIC obtained from PROC NLMIXED.

4.2. ΔAIC_Surv and ΔBIC_Surv

AIC_Long (BIC_Long) measures the contribution to the total AIC (BIC) due to the longitudinal data while AIC_Surv|Long (BIC_Surv|Long) quantifes the contribution to the total AIC (BIC) due to the survival data with the additional information from the longitudinal data. Let

$$\begin{array}{cc}\hfill {\mathrm{AIC}}_{\mathrm{Surv},0}& =-2{\Sigma }_{i=1}^n\log L_0(\widehat{\lambda },\widehat{\alpha }\mid t_i,{\delta }_i,z_i,x_i)+2\dim (\lambda ,\alpha ),\hfill \\ \hfill {\mathrm{BIC}}_{\mathrm{Surv},0}& =-2{\Sigma }_{i=1}^n\log L_0(\widehat{\lambda },\widehat{\alpha }\mid t_i,{\delta }_i,z_i,x_i)+\dim (\lambda ,\alpha )\log n,\hfill \end{array}$$ (4.8)

where L₀(λ, α|t_i,δ_i,z_i, x_i) is defined by (3.6). We now propose the following two model assessment criteria:

$$\begin{array}{cc}\hfill \Delta {\mathrm{AIC}}_{\mathrm{Surv}}& ={\mathrm{AIC}}_{\mathrm{Surv},0}-{\mathrm{AIC}}_{\mathrm{Surv}\mid \mathrm{Long}},\hfill \\ \hfill & \Delta {\mathrm{BIC}}_{\mathrm{Surv}}={\mathrm{BIC}}_{\mathrm{Surv},0}-{\mathrm{BIC}}_{\mathrm{Surv}\mid \mathrm{Long}}.\hfill \end{array}$$ (4.9)

Both ΔAIC_Surv and ΔBIC_Surv measure the gain of the fit in the survival component due to the longitudinal data with a penalty for the additional parameters in the survival component of the joint model. The model with a large value of ΔAIC_Surv (ΔBIC_Surv) is more preferred. To address an important practical issue of how ΔAIC_Surv and ΔBIC_Surv are related to the magnitude of the longitudinal outcomes, we establish a useful result, which is formally stated in the following theorem.

Theorem 4.2 The criteria ΔAIC_Surv and ΔBIC_Surv are invariant to location and scale transformations of the longitudinal outcomes. Specifcally, consider a linear transformation: ${Y_i}^{\ast }\left(a_{ij}\right)=\frac{Y_i\left(a_{ij}\right)-b}{c}$ for j =1,...,m_i and i = 1,...,n, where b and c > 0 are two known constants. The resulting criteria corresponding to the transformed longitudinal outcomes $Y_i^{\ast }\left(a_{ij}\right)$'s are denoted by ΔAIC_Surv(b, c) and ΔBIC_Surv(b, c). Then, we have ΔAIC_Surv(b, c)= ΔAIC_Surv and ΔBIC_Surv(b, c) = ΔBIC_Surv for all −∞ <b< ∞ and c > 0.

The proof of Theorem 4.2 is given in the Appendix. We note that if $b=\stackrel{‒}{Y}$ and c = S, where $\stackrel{‒}{Y}=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}{Y}_i\left(a_{ij}\right)}{{\sum }_{i=1}^n{m}_i}$ and $S^2=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^{m_i}{(Y_i\left(a_{ij}\right)-\stackrel{‒}{Y})}^2}{{\sum }_{i=1}^n{m}_i-1}$, then the $Y_i^{\ast }\left(a_{ij}\right)$'s are the standardized longitudinal outcomes. This linear transformation invariant property of ΔAIC_Surv and ΔBIC_Surv allows us to standardize the longitudinal outcomes to improve numerical stability in fitting the joint model of the longitudinal and survival data as well as computing ΔAIC_Surv and ΔBIC_Surv using existing statistical sofitware such as SAS.

5. Simulation Studies

In this section, we conduct extensive simulation studies to examine the empirical performance of ΔAIC_Surv and ΔBIC_Surv in model comparison as well as in the determination of the contribution of the longitudinal data to the goodness-of-fit of the survival model. In the simulation studies, we consider four types of models, namely, SPM, TM, TS and TVC models. Although the definitions of ΔAIC_Surv and ΔBIC_Surv are based on the joint model, they can be extended to the TS and TVC models as well. Specifcally, for the TVC model, AIC is given by

$${\mathrm{AIC}}_{\mathrm{Surv}\mid }Y=-2\sum _{i=1}^n\log L(\widehat{\lambda },\widehat{\beta },\widehat{\alpha }\mid t_i,{\delta }_i,z_i,x_i,Y_i)+2\dim (\lambda ,\beta ,\alpha ),$$ (5.1)

where $L(\lambda ,\beta ,\alpha \mid t_i,{\delta }_i,z_i,x_i,Y_i)={\left[\lambda (t_i\mid {\lambda }_0,\beta ,\alpha ,z_i,x_i,Y_i\left(t_i\right))\right]}^{{\delta }_i}\exp \{-{\int }_0^{t_i}\lambda (u\mid {\lambda }_0,\beta ,\alpha ,z_i,x_i,Y_i\left(u\right))du\}$ and λ(t|λ₀, β, α,z_i, x_i, Y_i(t)) is given in (3.7). We define ΔAIC_Surv as follows: ΔAIC = AIC_Surv,0 − AIC_Surv|Y, where AIC_Surv,0 is given by (4.8). ΔBIC_Surv can be defined in a similar fashion. Replacing Y by $\widehat{Y}$ in (5.1), ΔAIC_Surv and ΔBIC_Surv can be defined for the TS model.

Three simulation studies are considered (i) to examine the performance of ΔAIC_Surv and ΔBIC_Surv in selecting the true model (Simulations I and II) and determining the true longitudinal outcome that is most related to the survival model (Simulation III); (ii) to investigate the empirical properties of the maximum likelihood estimates of the parameters in the joint model (Simulations I and II); and (iii) to test the robustness of the computational procedure to the dimension of the model parameters (Simulation II). In all three simulation studies, we independently generate 500 simulated datasets, and in each dataset there are n = 400 subjects. The treatment indicator z_i is generated from a Bernoulli(0.5) distribution. The time points a_ij’s at which the longitudinal outcomes are taken are fxed at (0, 21, 42, 63, 84, 105, 126)/30.4375, where 30.4375 is the average number of days in each month and is obtained by 365.25/12. Other data generation details are given as follows.

Simulation I: The true model is SPM with linear trajectory denoted by SPML. Specifcally, the longitudinal data is simulated from a N(μ_i(a_ij),σ²) distribution, where μ_i(a_ij) = θ0_i + θ_1iaij + γz_i, and t_i^* is generated from [−λexp{β₁(θ_0i + γz_i)+ β₂θ_1i + αz_i}]⁻¹log(1 − U), where U ~ U(0, 1). The design values of the parameters are given in Table 2. The censoring time C_i is generated from an exponential distribution with mean 100. The right censoring percentage is roughly 8% which mimics the real data analysis. The failure time and censoring indicator are calculated as $t_i=\min \{t_i^{\ast },C_i\}$ δ_i and $t_i^{\ast }\le C_i$ and 0 otherwise.

Table 2.

Parameter estimates of SPML and SPMQ in Simulations I and II

Simulation	Param.	True	EST	SE	SD	RMSE	CP
I	α	−0.4	−0.399	0.105	0.104	0.104	0.956
	γ	0.05	0.050	0.087	0.088	0.088	0.950
	β 1	0.3	0.301	0.067	0.066	0.066	0.960
	β 2	1.2	1.211	0.246	0.234	0.234	0.958
	σ	0.5	0.500	0.008	0.008	0.008	0.954
	logλ	−1.7	−1.700	0.076	0.076	0.076	0.964
	θ 0	−0.01	−0.007	0.063	0.063	0.063	0.944
	θ 1	0.08	0.079	0.014	0.014	0.014	0.934
	Σ 00	0.7	0.698	0.058	0.058	0.058	0.936
	Σ 10	−0.03	−0.030	0.013	0.013	0.013	0.944
	Σ 11	0.06	0.059	0.006	0.006	0.006	0.930
II	α	−0.4	−0.411	0.113	0.116	0.116	0.946
	γ	0.03	0.033	0.088	0.086	0.086	0.956
	β 1	0.3	0.307	0.075	0.076	0.077	0.946
	β 2	1	0.994	0.142	0.146	0.146	0.938
	β 3	5	4.989	0.209	0.211	0.211	0.942
	σ	0.5	0.499	0.009	0.009	0.009	0.952
	logλ	−1.7	−1.690	0.082	0.081	0.082	0.942
	θ 0	−0.02	−0.022	0.065	0.067	0.067	0.936
	θ 1	0.1	0.097	0.037	0.038	0.038	0.950
	θ 2	−0.1	0.099	0.017	0.017	0.017	0.944
	Σ 00	0.7	0.700	0.063	0.062	0.062	0.954
	Σ 10	−0.08	−0.080	0.037	0.038	0.038	0.952
	Σ 11	0.3	0.298	0.039	0.038	0.038	0.968
	Σ 20	0.01	0.009	0.016	0.016	0.016	0.942
	Σ 21	−0.05	−0.049	0.014	0.013	0.013	0.946
	Σ 22	0.1	0.099	0.008	0.008	0.008	0.936

Simulation II: The true model is SPM with quadratic trajectory denoted by SPMQ. The data generation process follows the same steps as in Simulation I. The design values of the parameters are shown in Table 2.

Simulation III: The same setting as in Simulation I is used to generate the longitudinal data and survival times under the true model SPML. This dataset is denoted by D_Long. We also generate three additional sets of longitudinal data, which are associated with the one generated in Simulation I. These additional longitudinal trajectories are simulated from ${\mu }_{li}\left(a_{ij}\right)=({\theta }_{0i}+{\tau }_{l0i})+{({\theta }_{1i}+{\tau }_{l1i})}_{aij}+\gamma z_i$, where ${({\tau }_{l0i},{\tau }_{l1i})}^{\prime }~N(0,{{\sigma }_l}^2{I}_2)$, and then the longitudinal data are generated from N(μ_li(a_ij), 0.5²) for l =1, 2, 3, where σ1 = 0.1, σ2 = 0.5, and σ3 = 1. These three sets of longitudinal data each are coupled with the same survival times as in D_Long to form four additional datasets. These resulting datasets are denoted by D_Long1,...,D_Long3.

In Simulation I, we fit SPML, TML (TM with linear trajectory and $h^{\ast }(\beta ,{\theta }_i^{\prime }g\left(t\right),{\gamma }_1{z}_i,{\gamma }_2^{\prime }{x}_i)=\beta ({\theta }_i^{\prime }g\left(t\right)+{\gamma }_1{z}_i)$ in (3.3)), the TS model with linear trajectory, and the TVC model (all with K = 1, where K is defined in (3.4)) to each simulated dataset. In Simulation II, we fit SPML, SPMQ, TML, TMQ (TM with quadratic trajectory), the TS model, and the TVC model to each simulated dataset. In Simulation III, we fit SPML to each of the datasets D_Long, D_Long1, D_Long2, D_Long3 and the corresponding results are labeled as Long, Longl, Long2, and Long3.

In both Simulations I and II, we compute the estimates of the parameters under the true models. Let η denote a parameter in the true model. Also let ${\widehat{\eta }}_b$ and $\mathrm{se}\left({\widehat{\eta }}_b\right)$ be the MLEs of η and the standard error of ${\widehat{\eta }}_b$ from the b^th simulated dataset for b =1, 2,..., 500. We define the simulation estimate (EST) and the standard error (SE) to be $\stackrel{‒}{\eta }=\frac{1}{500}{\sum }_{i=1}^{500}{\widehat{\eta }}_b$ and $\frac{1}{500}{\sum }_{i=1}^{500}\mathrm{se}\left({\widehat{\eta }}_b\right)$. We also define the simulation standard deviation (SD) and the root of the mean squared error (RMSE) as ${\left[\frac{1}{500-1}{\sum }_{b=1}^{500}{({\widehat{\eta }}_b-\stackrel{‒}{\eta })}^2\right]}^{1∕2}$ and ${\left[\frac{1}{500}{\sum }_{b=1}^{500}{({\widehat{\eta }}_b-{\eta }^{\ast })}^2\right]}^{1∕2}$, where η^*is the true value of η. Finally, we define the coverage probability (CP) of the 95% confidence intervals as $\frac{1}{500}{\sum }_{b=1}^{500}1\left\{L_b<{\eta }^{\ast }<U_b\right\}$, where Lb and Ub are the 95% lower and upper limits in the b^th simulation. The ESTs, SEs, SDs, RMSEs, and CPs for the parameters in SPML and SPMQ are reported in Table 2. From this table, we see that for all parameters, the ESTs are very close to the corresponding true values, the SEs are very close to the SDs, and the CPs are always around 95% under both SPML and SPMQ.

Suppose we compare a total of J candidate models. Let ΔAIC_Surv,jb and ΔBIC_Surv,jb denote the values of ΔAIC_Surv and ΔBIC_Surv from the b^th simulated dataset. Then, the frequency of ranking Model j as the best according to ΔAIC_Surv criterion is defined as ${\sum }_{b=1}^{500}1\{\Delta {\mathrm{AIC}}_{\mathrm{Surv},jb}w\Delta {\mathrm{AIC}}_{\mathrm{Surv},lb}\mathrm{for}\mathrm{all}l\ne j\}$ A similar frequency can be defined for the ΔBICSurv criterion or the other criteria. If Model l is the true model, the average misspecification rate according to ΔAIC_Surv is given by $1-\frac{1}{500}{\sum }_{b=1}^{500}1\{\Delta {\mathrm{AIC}}_{\mathrm{Surv},1b}>\Delta {\mathrm{AIC}}_{\mathrm{Surv},lb}\mathrm{for}\mathrm{all}l\ge 2\}$.

Table 3 shows the means of ΔAIC_Surv and ΔBIC_Surv as well as the frequencies of ranking each model as best based on ΔAIC_Surv and ΔBIC_Surv for 500 simulated datasets for all three simulations. In Simulations I and III, the true model is SPML with K = 1 while the true model is SPMQ with K = 1 in Simulation II. In all three simulations, the true model always has the largest mean of either ΔAIC_Surv or ΔBIC_Surv and the highest frequency of ranking the true model as best based on either ΔAIC_Surv or ΔBIC_Surv. The average misspecification rates according to ΔAIC_Surv and ΔBIC_Surv in Simulation I, II, and III are 0.24 and 0.538, 0.058 and 0.272, 0.136 and 0.136, respectively. We also see from Table 3 that the differences in the means of ΔAIC_Surv between SPML and TML or SPMQ and TMQ are greater than the differences in the means of ΔBIC_Surv. These results are expected since TML and TMQ have fewer regression coefcients than SPML and SPMQ, and BIC penalizes the dimension of the parameters more than AIC. Similar results are observed based on the frequency of ranking each model as best. Thus, the performance of ΔAIC_Surv is slightly better than ΔBIC_Surv in correctly identifying the true model. It is interesting to note that although neither TM nor the TS model is the true model, TM outperforms the TS model in both Simulations I and II. In Simulations I and II, the TVC model fits the data the most poorly based on both ΔAIC_Surv and ΔBIC_Surv.

Table 3.

Mean of ΔAIC_Surv (ΔBIC_Surv) and frequency of ranking each model as best based on ΔAIC_Surv (ΔBIC_Surv)

		ΔAICSurv		ΔBICSurv
Simulation	Model	Mean	Frequency	Mean	Frequency
I	SPML	42.55	380	34.57	231
	TML	38.38	76	34.39	181
	TS	38.16	32	34.17	70
	TVC	30.70	12	26.71	18
II	SPML	588.66	29	580.68	136
	SPMQ	596.68	471	584.70	364
	TML	419.99	0	416.00	0
	TMQ	419.52	0	415.53	0
	TS	418.56	0	414.57	0
	TVC	399.51	0	395.52	0
III	Long	42.55	432
	Long1	38.37	67
	Long2	15.64	1
	Long3	6.46	0

In Simulation III, the true longitudinal outcome is Long, and Longl is obtained by adding random errors to both the random intercept and slope of the linear trajectory in Long for l = 1,..., 3. Longl to Long3 become gradually further apart from Long since the standard deviation of the random errors increases from 0.1 to l. Since we fit the same model to each of these five datasets, the differences between ΔAIC_Surv and ΔBIC_Surv are the same for Long, Longl, ... , Long3. Thus, only the results based on ΔAIC_Surv are reported in Table 3. We see from this table that Long has the largest mean of ΔAIC_Surv and the highest frequency of ranking Long as best, and the mean and frequency corresponding to Longl decrease as l increases. The results for Long and Long1 are very close, which is expected since Longl is obtained by adding a very small amount of noise to Long.

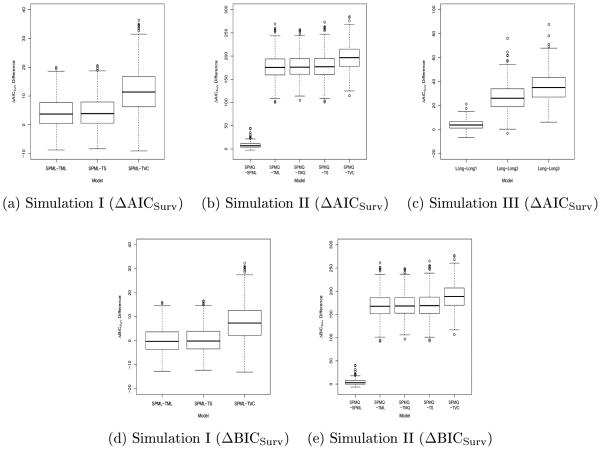
In addition, Figure 1 shows the boxplots of the ΔAIC_Surv and ΔBIC_Surv differences between the true model and the competing models, respectively. From Figure 1 (a), (b), and (c), we see that most of these boxes are above zero, which indicates that the true model does fit the data much better than the competing models based on ΔAIC_Surv. All boxes for ΔBIC_Surv differences in Figure 1 (e) are also above O. However, the medians of the ΔBIC differences between SPML and TML or between SPML and TS shown in Figure 1 (d) are very close to O. These results are consistent with those based on the means of ΔAIC_Surv and ΔBIC_Surv and the frequencies of ranking each model as best.

Figure 1.

Boxplots of the ΔAIC_Surv differences ((a), (b), and (c)) and the ΔBIC_Surv differences ((d) and (e)) between the true and competing models.

6. Analysis of the EMPHACIS Data

In this section, we carry out a detailed analysis of the EMPHACIS data using the models discussed in Section 3 and the ΔAIC_Surv and ΔBIC_Surv criteria proposed in Section 4. As stated in Section 2, data from n = 425 patients are used, and the longitudinal and survival data we consider are one of five patient-reported LCSS outcomes corresponding to anorexia, cough, dyspnea, fatigue, and pain along with progression free survival time in months. The treatment indicator z_i = 1 if the ith patient received pemetrexed/cisplatin and z_i = 0 if the ith patient received cisplatin alone, and the covariates (Table l) include race (x_i1), gender (x_i2), age (x_i3), Karnofsky status (x_i4), baseline stage of disease (x_i5), and vitamin supplementation (x_i6). All six covariates (p = 6) are binary, each taking a value of 0 or 1. Specifcally, x_i1 = 1 if white, x_i2 = 1 if male, x_i3 = 1 if age ≥ 65, x_i4 = 1 if Karnofsky status is high, x_i5 = 1 if stage I/II, and x_i6 = 1 if full vitamin supplementation. In all calculations, we standardized all five patient-reported LCSS outcomes. The LCSS original-scaled item means (standard deviations) were 30.79 (27.19), 11.48 (17.93), 31.41 (26.33), 39.38 (27.06), and 24.64 (24.90) for anorexia, cough, dyspnea, fatigue, and pain, respectively. The total numbers of completed longitudinal assessments (i.e., ${\sum }_{i=1}^n{m}_i$) including the baseline measurements were 5504, 5544, 5553, 5530, and 5546 for anorexia, cough, dyspnea, fatigue, and pain.

We fit the SPML, SPMQ, TML, TMQ, TS and TVC models, where SPML, SPMQ, TML, and TMQ are defined in Section 5, to the PFS data paired with one of the five LCSS longitudinal outcomes corresponding to anorexia, cough, dyspnea, fatigue, and pain. As suggested by an anonymous referee, we also considered the joint model with a quadratic trajectory in the longitudinal component and only a linear trajectory in the the survival component, where the models corresponding to SPMQ and TMQ are denoted by SPMQL and TMQL. The six covariates (x_i’s) and the treatment indicator were included in all the models we estimated. As shown in Table 1, the maximum values of PFS were 27.1 and 21.8 months for the pemetrexed/cisplatin arm and the cisplatin alone arm, respectively. For all the models, we used the piecewise constant hazard model given in (3.4) for the baseline hazard, and the partition intervals were constructed based on the percentiles such as the first (Q₁), second (Q₂), and third (Q₃) quartiles of the PFS times.

We used the ΔAIC_Surv and ΔBIC_Surv criteria as well as the AIC_Surv|Long and BIC_Surv|Long criteria to determine the number of intervals (K) in (3.4). We first fit the PFS data alone using (3.6). The values of AIC_Surv,0 and BIC_Surv,0 defined by (4.8) were 2225.80 and 2258.22 for K = 1, 2206.29 and 2242.76 for K = 2, and 2209.71 and 2254.28 for K = 4. We considered two methods for constructing the three intervals: inserting two intervals within the first interval or the second interval using the piecewise constant hazard model with K = 2. The resulting piecewise constant hazard models with (s₀ = 0, s₁ = Q₁, s₂ = Q₂) and (s₀ = 0, s₁ = Q₂, s₂ = Q₃) are denoted by K = 3⁽¹⁾ and K = 3⁽²⁾. Similarly, we constructed the partitions for K > 3. This approach is desirable when more events occur early in the follow-up. Another advantage of this approach is that the resulting partitions are nested and, hence, the log-likelihood of the joint model increases in K when the longitudinal component remains fxed. The values of AIC_Surv,0 and BIC_Surv,0 were 2208.27 and 2248.79 for K = 3⁽¹⁾ and 2207.73 and 2248.25 for K = 3⁽²⁾. These results indicate that when we fit the PFS data alone, the piecewise constant hazard model with K = 2 fits best according to both AIC_Surv,0 and BIC_Surv,0. We then fit the PFS data and the LCSS longitudinal data jointly. For ease of presentation, we discuss the case for the longitudinal outcomes corresponding to pain only since the results were similar for anorexia, cough, dyspnea, and fatigue. Figure 2 shows the MLEs of λ and the values of AIC_Surv|Long and BIC_Surv|Long for K = 1, 2, 3, and 4 under SPML. From Figure 2, we see that AIC_Surv|Long and BIC_Surv|Long were 2199.30 and 2239.82 for K = 1; 2161.84 and 2206.42 for K = 2; 2l63.01 and 2211.64 for K =3⁽¹⁾; 2163.84 and 2212.47 for K = 3⁽²⁾; and 2164.98 and 2217.66 for K = 4, respectively. Clearly, the best values of AIC_Surv|Long and BIC_Surv|Long were obtained under SPML with K = 2. Thus, according to AIC_Surv|Long and BIC_Surv|Long, SPML with K = 2 fits the PFS data the best. We also see from Figure 2 that for K = 2, λ₂ =0.276 is much larger than λ1 = 0.138, indicating that the exponential model (i.e., K = 1) did not fit the PFS data well. All of the above results suggest that it is sufcient to choose K = 2 in fitting the PFS data. We note that the issue of interval choice has also been discussed in [47], [48], and [49].

Figure 2.

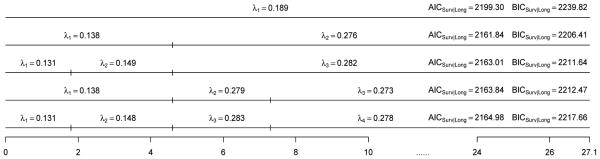
The diagrams of the MLEs of λ, AIC_Surv|Long and BIC_Surv|Long with various values of K under SPML for pain.

Table 4 shows AIC, AIC_Long, ΔAIC_Surv, BIC, BIC_Long, and ΔBIC_Surv for SPML, SPMQ, SPMQL, TML, TMQ, and TMQL and ΔAIC_Surv and ΔBIC_Surv for the TVC and TS models. The ΔAIC_Surv’s and ΔBIC_Surv’s are plotted in Figure 3. We see from Table 4 that pain had the largest values of ΔAIC_Surv and ΔBIC_Surv under SPML, SPMQ, SPMQL, TML, TMQ, TVC, and TS; fatigue had the largest values of ΔAIC_Surv and ΔBIC_Surv under TMQL and the second largest values of ΔAIC_Surv and ΔBIC_Surv under the other seven models; and cough had the smallest values of ΔAIC_Surv and ΔBIC_Surv. These results indicate that pain led to the most gain in fitting the PFS data while cough had the least contribution to the fit of the PFS data. However, AIC and BIC were not able to determine the contribution of the longitudinal data in fitting the survival data for these five sets of LCSS longitudinal outcomes under the joint modeling framework. We observe from Table 4 that the smallest values of AIC and BIC were attained by dyspnea under SPML, SPMQ, TML, and TMQ. Afiter examining AIC Long and BICLong, we found that dyspnea had the smallest values of AICLong and BICLong. Thus, AIC_Long and BIC_Long were the main contributions to the smallest values of AIC and BIC for dyspnea. From Table 4, we also see that (i) the values of ΔAIC_Surv under SPMQ are greater than those under SPMQL for anorexia, cough, dyspnea, and pain while the value of ΔAIC_Surv under SPMQ is very similar to the one under SPMQL for fatigue; and (ii) the values of ΔBIC_Surv under SPMQL are greater than those under SPMQ for anorexia, cough, dyspnea, and fatigue due to the extra parameter in the survival component under SPMQ. However, the values of ΔAIC_Surv and ΔBIC_Surv under TMQ are consistently higher than those under TMQL since under the TM, both TMQ and TMQL share the same number of parameters in the survival component. We note that on the one hand, ΔAIC_Surv and ΔBIC_Surv are defined primarily based on the likelihood function of the survival data; on the other hand, AIC and BIC are constructed using the likelihood function of both the longitudinal and survival data. Thus, since the total number of longitudinal outcomes were different among these five symptoms, AIC and BIC were indeed not comparable among them. Within each of these five symptoms, AIC and BIC selected SPMQ over SPML and TMQ over TML, due to the fact that AIC _Long and BIC _Long were in favor of quadratic trajectories over linear trajectories. These results indicate that the quadratic trajectories fit the longitudinal data better.

Table 4.

AICs and BICs for models with K = 2

Model		Anorexia	Cough	Dyspnea	Fatigue	Pain
SPML	AIC	14205.13	14451.48	12101.25	13184.26	13030.39
	AICLong	12017.95	12248.34	9912.26	11005.53	10868.55
	ΔAICSurv	19.11	3.15	17.30	27.56	44.46
	BIC	14302.38	14548.73	12198.50	13281.51	13127.64
	BICLong	12070.63	12301.02	9964.94	11058.20	10921.23
	ΔBICSurv	11.01	−4.95	9.20	19.45	36.35
SPMQ	AIC	14123.05	14250.06	11908.13	13058.18	12778.41
	AICLong	11933.53	12046.68	9714.28	10873.93	10610.07
	ΔAICSurv	16.77	2.91	12.44	22.04	37.95
	BIC	14240.57	14367.57	12025.64	13175.69	12895.92
	BICLong	12002.42	12115.56	9783.17	10942.82	10678.96
	ΔBICSurv	4.62	−9.25	0.29	9.89	25.80
SPMQL	AIC	14124.36	14251.34	11911.54	13057.48	12788.89
	AICLong	11933.24	12046.45	9713.94	10873.82	10609.26
	ΔAICSurv	15.17	1.40	8.70	22.63	26.67
	BIC	14237.82	14364.80	12025.00	13170.94	12902.35
	BICLong	12002.12	12115.34	9782.83	10942.70	10678.15
	ΔBICSurv	7.06	−6.70	0.60	14.53	18.56
TML	AIC	14204.92	14449.26	12106.26	13185.81	13038.62
	AICLong	12017.75	12248.29	9911.77	11005.07	10867.68
	ΔAICSurv	19.12	5.32	11.81	25.56	35.35
	BIC	14298.12	14542.46	12199.45	13279.01	13131.82
	BICLong	12070.43	12300.97	9964.45	11057.75	10920.36
	ΔBICSurv	15.07	1.27	7.76	21.50	31.30
TMQ	AIC	14118.40	14244.30	11904.94	13049.48	12773.67
	AICLong	11933.39	12046.50	9713.94	10873.95	10609.29
	ΔAICSurv	21.29	8.50	15.29	30.77	41.92
	BIC	14227.80	14353.70	12014.34	13158.89	12883.07
	BICLong	12002.27	12115.39	9782.82	10942.84	10678.17
	ΔBICSurv	17.23	4.45	11.24	26.72	37.86
TMQL	AIC	14128.97	14254.40	11916.77	13067.97	12805.13
	AICLong	11933.74	12046.45	9713.94	10874.12	10609.33
	ΔAICSurv	11.07	−1.65	3.47	12.45	10.49
	BIC	14238.38	14363.81	12026.18	13177.38	12914.54
	BICLong	12002.63	12115.34	9782.83	10943.01	10678.21
	ΔBICSurv	7.02	−5.70	−0.58	8.40	6.44
TS	ΔAICSurv	18.45	5.17	11.55	24.77	34.32
	ΔBICSurv	14.40	1.11	7.50	20.72	30.27
TVC	ΔAICSurv	19.52	4.25	15.04	27.76	48.60
	ΔBICSurv	15.47	0.20	10.99	23.71	44.54

Figure 3.

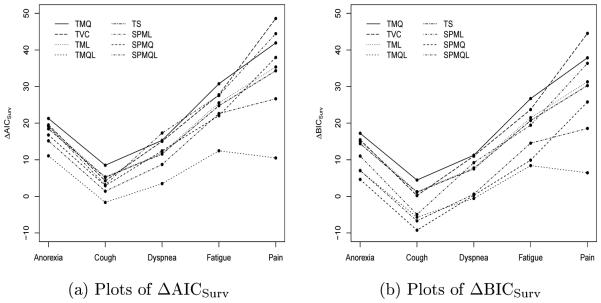
Plots of ΔAIC_Surv (a) and ΔBIC_Surv (b) under the SPML, SPMQ, SPMQL, TML, TMQ, TMQL, TVC, and TS models with K = 2.

Tables 5 and 6 show the hazard ratios (HR’s, the exponentiated parameters) and p-values of the direct treatment effect on PFS (α), the overall treatment effect (α^* = α₁ + β₁γ₁ or α^* = α₁ + βγ₁), and the regression coefficients β associated with random trajectories under SPML, SPMQ, SPMQL, TML, TMQ, and TMQL. From these two tables, we see that except for cough and dyspnea, the HR’s for the overall treatment effect on PFS that ranged from 0.620 to 0.645 for the joint model were smaller than the HR of 0.647 when we fit the PFS data alone. It is interesting to mention that under TML and TMQ, the order in the magnitude of the HR’s for β is consistent with the values of ΔAIC_Surv and ΔBIC_Surv. For example, pain had the largest HR’s, namely, 1.464 and 1.5O4 under TML and TMQ, while cough had the smallest HR’s, namely, 1.194, 1.237, and 1.019 under TML, TMQ and TMQL.

Table 5.

Estimates for the survival components of SPMs with K = 2

	Longitudinal Symptom	α*		α 1		β 1		β 2		β 3
Model		HR	P-value	HR	P-value	HR	P-value	HR	P-value	HR	P-value
SPML	Anorexia	0.628	<.0001	0.604	<.0001	1.403	<.0001	2.850	0.0024
	Cough	0.646	<.0001	0.643	<.0001	1.209	0.0080	1.722	0.0892
	Dyspnea	0.654	<.0001	0.666	0.0001	1.218	0.0043	3.560	<.0001
	Fatigue	0.635	<.0001	0.632	<.0001	1.418	<.0001	3.539	0.0003
	Pain	0.645	<.0001	0.669	0.0002	1.380	<.0001	5.331	<.0001
SPMQ	Anorexia	0.622	<.0001	0.597	<.0001	1.512	<.0001	3.087	0.0439	152.189	0.1499
	Cough	0.638	<.0001	0.632	<.0001	1.271	0.0054	1.811	0.0940	12.470	0.1317
	Dyspnea	0.646	<.0001	0.661	<.0001	1.228	0.0053	2.896	0.0093	44.221	0.0688
	Fatigue	0.620	<.0001	0.619	<.0001	1.446	<.0001	2.275	0.0873	9.179	0.4013
	Pain	0.645	<.0001	0.662	<.0001	1.403	<.0001	4.293	<.0001	144.619	0.0035
SPMQL	Anorexia	0.618	<.0001	0.599	<.0001	1.382	0.0001	1.382	0.0378
	Cough	0.632	<.0001	0.628	<.0001	1.178	0.0193	1.087	0.4370
	Dyspnea	0.637	<.0001	0.649	<.0001	1.176	0.0203	1.416	0.0058
	Fatigue	0.614	<.0001	0.612	<.0001	1.407	<.0001	1.542	0.0018
	Pain	0.638	<.0001	0.652	<.0001	1.308	0.0001	1.618	<.0001

When fitting the PFS data alone using (3.6), the HR for the treatment effect is 0.647 with p-value <.0001.

Table 6.

Estimates for the survival components of TMs with K = 2

	Longitudinal Symptom	α*		α 1		β
Model		HR	P-value	HR	P-value	HR	P-value
TML	Anorexia	0.631	<.0001	0.609	<.0001	1.365	<.0001
	Cough	0.650	<.0001	0.647	<.0001	1.194	0.0056
	Dyspnea	0.642	<.0001	0.655	<.0001	1.255	0.0002
	Fatigue	0.630	<.0001	0.627	<.0001	1.417	<.0001
	Pain	0.628	<.0001	0.655	<.0001	1.464	<.0001
TMQ	Anorexia	0.629	<.0001	0.607	<.0001	1.409	<.0001
	Cough	0.647	<.0001	0.642	<.0001	1.237	0.0010
	Dyspnea	0.640	<.0001	0.657	<.0001	1.291	<.0001
	Fatigue	0.628	<.0001	0.626	<.0001	1.486	<.0001
	Pain	0.635	<.0001	0.655	<.0001	1.504	<.0001
TMQL	Anorexia	0.630	<.0001	0.621	<.0001	1.164	0.0008
	Cough	0.650	<.0001	0.650	<.0001	1.019	0.5561
	Dyspnea	0.640	<.0001	0.645	<.0001	1.089	0.0220
	Fatigue	0.629	<.0001	0.628	<.0001	1.161	0.0003
	Pain	0.642	<.0001	0.649	<.0001	1.135	0.0007

7. Discussion

We have proposed novel decompositions of AIC and BIC to individually assess the contributions of each component in joint models of longitudinal and survival data, and we use ΔAIC_Surv and ΔBIC_Surv to determine the contribution of the longitudinal data to the fit of the survival data. We conducted extensive simulation studies to examine the empirical performance of ΔAIC_Surv and ΔBIC_Surv and demonstrated our proposed methodology on a detailed case study in mesothelioma. The proposed methodology is quite useful in also comparing and choosing between a trajectory-based model or a shared parameter model, which is important, since these two classes of models are often used and the choice of which one to use is not always clear. Our proposed criteria also help in the assessment of the survival model, in determining how many intervals to choose, for example, in the piecewise constant hazard model.

All computations in Section 5 and 6 were done in SAS. PROC NLMIXED was used to obtain the MLEs and AIC, and PROC IML was used to compute AIC_Long. The Riemann integral was used to compute the cumulative hazard function in (3.5) for the trajectory models. The Monte Carlo (MC) method for estimating AIC_Surv|Long discussed in Remark 4.2 was also implemented in PROC IML. As an illustration, for anorexia, cough, dyspnea, fatigue, and pain under TML with K = 1, the AIC_Surv|Long’s computed from AIC−AIC_Long using PROC NLMIXED were 2210.94, 2223.57, 2217.17, 2205.12, and 2200.94, while those obtained by the Monte Carlo method with an MC sample of size 10,000 were 2211.00, 2223.58, 2217.17, 2205.09, and 2200.93, respectively, which empirically validates the AIC obtained from PROC NLMIXED. Due to the nature of the joint model, there are more random effects in SPMQ than SPML, and hence, the computations for SPMQ are much more intensive than that for SPML. When the patients were followed much longer for the survival times than for the longitudinal outcomes, we used a constant extrapolation afiter the time of the last observed longitudinal outcome for the trajectory ${\theta }_i^{\prime }g\left(t\right)$ to adjust the hazard functions for all TM’s and TS. The results shown in Table 2 empirically confrm that the NLMIXED procedure is quite reliable in computing the MLEs of the parameters in the joint model and they are robust with respect to the dimension of the model parameters. Finally, we note that each simulation with 500 simulated datasets took about l hour on a Dell PC with an Intel i5 processor, 2.40 GHz CPU, and 6 GB of memory. The SAS macros are available from the authors upon request.

In our simulation study, we observed that ΔAIC_Surv and ΔBIC_Surv correctly identify the true survival component in the joint model. In the analysis of the EMPHACIS data, we showed that the survival model with K = 2 fit the data the best along with SPML and TMQ. There are several potential extensions of the proposed method. The proposed methodology would be quite useful in situations where we wish to simultaneously jointly model a multivariate longitudinal marker, such as several PRO outcomes, with a time-to-event outcome, such as PFS. The proposed ΔAIC_Surv and ΔBIC_Surv can be very useful in this context as they can tell us about the overall contribution of the multivariate longitudinal marker to the fit of the survival data. The proposed methodology is also useful for multivariate survival data, such as PFS and OS for example, and then ΔAIC_Surv and ΔBIC_Surv can be used in assessing the contribution of the longitudinal data to the fit of the multivariate survival data. Finally, ΔAIC_Surv and ΔBIC_Surv can also be used in joint models for multivariate longitudinal and multivariate survival data and hence identify the combinations of longitudinal outcomes that are most highly associated with a multivariate time-to-event. These extensions are currently under investigation.

Appendix: Proofs of Theorems

Proof of Theorem 4.1

Let D_obs = {(Y_i,t_i,δ_i,z_i, x_i), i =1,…,n} denote the observed data. We frst observe that

$$L(\gamma ,{\sigma }^2\mid Y_i,W_i,{\theta }_i)f({\theta }_i\mid \theta ,\Sigma )=f({\theta }_i\mid Y_i,W_i,{\phi }_1)L({\phi }_1\mid Y_i,W_i).$$ (A.1)

Using (4.3) and (A.1), the joint likelihood for all subjects is given by

$$\begin{array}{cc}\hfill L(\phi \mid g,D_{obs})& =\prod _{i=1}^n\int L({\phi }_2\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\gamma )L(\gamma ,{\sigma }^2\mid Y_i,W_i,{\theta }_i)f({\theta }_i\mid \theta ,\Sigma )d{\theta }_i\hfill \\ \hfill & =\prod _{i=1}^n\int L({\phi }_2\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\gamma )f({\theta }_i\mid Y_i,W_i,{\phi }_1)L({\phi }_1\mid Y_i,W_i)d{\theta }_i\hfill \\ \hfill & =\prod _{i=1}^{n}L({\phi }_i\mid Y_i,W_i)\prod _{i=1}^n\int L({\phi }_2\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\gamma )f({\theta }_i\mid Y_i,W_i,{\phi }_1)d{\theta }_i.\hfill \end{array}$$ (A.2)

Taking -2log of (A.2) yields

$$-2\log L(\phi \mid g,D_{obs})=-2\sum _{i=1}^n\log L({\phi }_1\mid Y_i,W_i)-2\sum _{i=1}^n\log \int L({\phi }_2\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\gamma )f({\theta }_i\mid Y_i,W_i,{\phi }_1)d{\theta }_i.$$ (A.3)

The AIC decomposition in (4.6) directly follows from (4.4) and (A.3), which completes the proof.

Proof of Theorem 4.2

Since AIC_Surv,0 depends on the survival data alone and BIC_Surv|Long = AIC_Surv|Long + dim(φ₂)(log n − 2), it is sufcient to show

$${\mathrm{AIC}}_{\mathrm{Surv}\mid \mathrm{Long}}(b,c)={\mathrm{AIC}}_{\mathrm{Surv}\mid \mathrm{Long}}.$$

Let Y_i =(Y_i(a_i1),…,Y_i(a_imi))′ and $Y_i^{\ast }={(Y_i^{\ast }\left(a_{i1}\right),\dots ,Y_i^{\ast }\left(a_{i{m}_i}\right))}^{\prime }$ denote the original and transformed longitudinal outcomes, respectively. Then we have $Y_i^{\ast }=\frac{1}{c}{Y}_i-\frac{b}{c}{1}_{m_i}$, where $1_{m_i}={(1,\dots ,1^{\prime })}_{m_i\times 1}$. Write $W_i=\left(W_{i1}{W}_{i2}\right)$, where W_i1 is a m_i × (q + 1) matrix and W_i2 is a m_i × (p + 1) matrix. The conditional density of Y_i is given by

$$Y_i\mid W_i,{\theta }_i,\gamma ,{\sigma }^2~N\left(W_i\left(\begin{array}{c}\hfill {\theta }_i\hfill \\ \hfill \gamma \hfill \end{array}\right),{\sigma }^2{I}_{m_i}\right)=N(W_{i1}{\theta }_i+W_{i2\gamma },{\sigma }^2{I}_{m_i}),$$

where I_mi is the m_i × m_i identity matrix. We then obtain

$$Y_i^{\ast }\mid W_i,{\theta }_i,\gamma ,{\sigma }^2~N((W_{i1}{\theta }_i+W_{i2\gamma },-b{1}_{mi})∕c,{(\sigma ∕c)}^2{I}_{mi}).$$

Write ${\theta }_i={({\theta }_{i0},{\theta }_{i1},\dots ,{\theta }_{iq})}^{\prime }$, ${\theta }_{iq}={({\theta }_{i1},\dots ,{\theta }_{iq})}^{\prime }$, $\theta ={({\theta }_0,{\theta }_1,\dots ,{\theta }_q)}^{\prime }$ and ${\theta }_q={({\theta }_1,\dots ,{\theta }_q)}^{\prime }$. Let ${\theta }_i^{\ast }=\left(\begin{array}{c}\hfill ({\theta }_{i0}-b)∕c\hfill \\ \hfill {\theta }_{iq}∕c\hfill \end{array}\right)=\frac{1}{c}{\theta }_i-\frac{1}{c}\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right)$, ${\theta }^{\ast }=\left(\begin{array}{c}\hfill ({\theta }_0-b)∕c\hfill \\ \hfill {\theta }_q∕c\hfill \end{array}\right)=\frac{1}{c}\theta -\frac{1}{c}\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right)$, ${\gamma }^{\ast }=\gamma ∕c,{\sigma }^{\ast }=\sigma ∕c$ and ${\Sigma }^{\ast }=\Sigma ∕c^2$. Since θ_i ~ N (θ, ∑), we have

$$Y_i^{\ast }\mid W_i,{\theta }_i^{\ast },{\gamma }^{\ast },{\left({\sigma }^{\ast }\right)}^2~N(W_{i1}{\theta }_i^{\ast }+W_{i2}{\gamma }^{\ast },{\left({\sigma }^{\ast }\right)}^2{I}_{m_i}),\text{and}{\theta }_i^{\ast }~N({\theta }^{\ast },{\Sigma }^{\ast }).$$ (A.4)

Similar to (3.2), we write the hazard function corresponding to Y_^{i ;* _^} as

$$\lambda (t\mid {\lambda }_0^{\ast },{\beta }^{\ast },{\alpha }^{\ast },{\theta }_i^{\ast },g\left(t\right),{\gamma }^{\ast },z_i,x_i)={\lambda }_0^{\ast }\left(t\right)\exp \{h({\beta }^{\ast },{\theta }_i^{\ast },g\left(t\right),{\gamma }_1^{\ast }{z}_i,{\left({\gamma }_2^{\prime }\right)}^{\prime }{x}_i)+{\alpha }_1^{\ast }{z}_i+\left({{\alpha }_2^{\prime }}^{\prime }\right)x_i\},$$ (A.5)

where λ₀^*(t) is the baseline hazard function, which is assumed to take the same form as λ₀(t) given by (3.4). Then complete-data likelihood function for the survival component in (3.5) under the transformed longitudinal data becomes

$$\begin{array}{cc}\hfill L^{\ast }({\lambda }^{\ast },{\beta }^{\ast },{\alpha }^{\ast }\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i^{\ast },g,{\gamma }^{\ast })& ={\left[\lambda (t_i\mid {\lambda }_0^{\ast },{\beta }^{\ast },{\alpha }^{\ast },{\theta }_i^{\ast },g\left(t_i\right),{\gamma }^{\ast },z_i,x_i)\right]}^{{\delta }_i}\hfill \\ \hfill & \times \exp \left\{-{\int }_0^{t_i}\lambda (u\mid {\lambda }_0^{\ast },{\beta }^{\ast },{\alpha }^{\ast },{\theta }_i^{\ast },g\left(u\right),{\gamma }^{\ast },z_i,x_i)du\right\}.\hfill \end{array}$$ (A.6)

By comparing (A.4) and (A.5) to (4.1), (4.2), and (3.2), we obtain that ${\lambda }^{\ast }=\lambda \exp \left({\widehat{\beta }}_{1}b\right)$ for SPM, ${\lambda }^{\ast }=\lambda \exp \left(\widehat{\beta }b\right)$ for TM, β^* = cβ, and α^* = α.

Let $\widehat{\phi }$ and ${\widehat{\phi }}^{\ast }=({\widehat{\theta }}^{\ast },{\widehat{\gamma }}^{\ast },{\widehat{\sigma }}^{\ast },{\widehat{\Sigma }}^{\ast },{\widehat{\lambda }}^{\ast },{\widehat{\beta }}^{\ast },{\widehat{\alpha }}^{\ast })$ denote the MLEs of the model parameters under the original longitudinal data and the transformed longitudinal data coupled with the same survival data, respectively. Using the transformation invariance principle of MLE, we have ${\widehat{\theta }}^{\ast }=\left(\begin{array}{c}\hfill ({\widehat{\theta }}_0-b)∕c\hfill \\ \hfill {\widehat{\theta }}_q∕c\hfill \end{array}\right)=\frac{1}{c}\widehat{\theta }-\frac{1}{c}\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right)$, ${\widehat{\gamma }}^{\ast }=\widehat{\gamma }∕c$, ${\widehat{\sigma }}^{\ast }=\widehat{\sigma }∕c$, ${\widehat{\Sigma }}^{\ast }=\widehat{\Sigma }∕c^2$, ${\widehat{\lambda }}^{\ast }=\widehat{\lambda }\exp \left({\widehat{\beta }}_{1}b\right)$ for SPM, ${\widehat{\lambda }}^{\ast }=\widehat{\lambda }\exp \left(\widehat{\beta }b\right)$ for TM, ${\widehat{\beta }}^{\ast }=c\widehat{\beta }$ and ${\widehat{\alpha }}^{\ast }=\widehat{\alpha }$.

Corresponding to ${\phi }_1=(\gamma ,{\sigma }^2,\theta ,\Sigma )$ and ${\phi }_2=(\lambda ,\beta ,\alpha )$, we write ${\phi }_1^{\ast }=({\gamma }^{\ast }{\left({\sigma }^{\ast }\right)}^2,{\theta }^{\ast },{\Sigma }^{\ast })$ and ${\phi }_2^{\ast }=({\lambda }^{\ast },{\beta }^{\ast },{\alpha }^{\ast })$. Write $\widehat{\phi }=({\widehat{\phi }}_1,{\widehat{\phi }}_2)$ and ${\widehat{\phi }}^{\ast }=({\widehat{\phi }}_1^{\ast },{\widehat{\phi }}_2^{\ast })$. Let ${\Sigma }_r={({\Sigma }^{-1}+\frac{1}{{\sigma }^2}{W}_{i1}^{\prime }{W}_{i1})}^{-1}$ and ${{\Sigma }_r}^{\ast }={\Sigma }_r∕c^2$. The conditional distribution of the random effects θ_i given the original longitudinal data takes the form

$${\theta }_i\mid Y_i,W_i,{\phi }_1~N\left({\Sigma }_r\left[\frac{1}{{\sigma }^2}{W}_{i1}^{\prime }(Y_i-W_{i2\gamma })+{\Sigma }^{-1}\theta \right],{\Sigma }_r\right),$$ (A.7)

and the corresponding density is given by

$$f({\theta }_i\mid Y_i,W_i,{\phi }_i)=\frac{1}{{\left(2\pi \right)}^{(q+1)∕2}\mid {\Sigma }_r{\mid }^{1∕2}}\exp \left\{-\frac{1}{2}{\left({\theta }_i-{\Sigma }_r\left[\frac{1}{{\sigma }^2}{W_{i1}}^{\prime }(Y_i-W_{i2}\gamma )+{\Sigma }^{-1}\theta \right]\right)}^{\prime }\times {{\Sigma }_r}^{-1}\left({\theta }_i-{\Sigma }_r\left[\frac{1}{{\sigma }^2}{W}_{i1}^{\prime }(Y_i-W_{i2}\gamma ){\Sigma }^{-1}\theta \right]\right)\right\}.$$ (A.8)

Note that ${({\Sigma }^{-1}+\frac{1}{{\sigma }^2}{W}_{i1}^{\prime }{W}_{i1})}^{-1}=\Sigma -\frac{1}{{\sigma }^2}\Sigma {W_{i1}}^{\prime }(I+\frac{1}{{\sigma }^2}{W}_{i1}\Sigma {W_{i1}^{\prime }}^{-1})W_{i1}\Sigma$ and $W_{i1}=\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right)=b{1}_{m_i}$. Replacing the original data and parameters with the transformed ones in (A.7) yields

$${\theta }_i^{\ast }\mid Y_i^{\ast },W_i,{\phi }_1^{\ast }~N\left({{\Sigma }_r}^{\ast }\left[\frac{1}{\left({{\sigma }^{\ast }}^2\right)}{W_{i1}}^{\prime }(Y_i^{\ast }-W_{i2}{\gamma }^{\ast })+{\left({\Sigma }^{\ast }\right)}^{-1}{\theta }^{\ast }\right],{{\Sigma }_r}^{\ast }\right),$$ (A.9)

and the conditional density of θ^*_i is given by

$$f^{\ast }({\theta }_i^{\ast }\mid Y_i^{\ast },W_i,{\phi }_1^{\ast })=\frac{1}{{\left(2\pi \right)}^{(q+1)∕2}\mid {\Sigma }_r^{\ast }{\mid }^{1∕2}}=\exp \left\{-\frac{1}{2}{\left({\theta }_i^{\ast }-{\Sigma }_r^{\ast }\left[\frac{1}{\left({{\sigma }^{\ast }}^2\right)}{W}_{i1}^{\prime }(Y_i^{\ast }-W_{i2}{\gamma }^{\ast })+{\left({\Sigma }^{\ast }\right)}^{-1}{\theta }^{\ast }\right]\right)}^{\prime }\times {\left({{\Sigma }_r}^{\ast }\right)}^{-1}\left({\theta }_i^{\ast }-{{\Sigma }_r}^{\ast }\left[\frac{1}{{\left({\sigma }^{\ast }\right)}^2}{W}_{i1}^{\prime }(Y_i^{\ast }-W_{i2}{\gamma }^{\ast })+{\left({\Sigma }^{\ast }\right)}^{-1}{\theta }^{\ast }\right]\right)\right\}.$$ (A.10)

Using (A.6), (A.8), and (A.10) and after some algebra, we can show that

$$L^{\ast }\left({\widehat{\phi }}_2^{\ast }\mid t_i,{\delta }_i,z_i,x_i,\frac{1}{c}{\theta }_i-\frac{1}{c}\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right),g,{\widehat{\gamma }}^{\ast }\right)=L({\widehat{\phi }}_2\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\widehat{\gamma })$$ (A.11)

and

$$f^{\ast }\left(\frac{1}{c}{\theta }_i-\frac{1}{c}\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right)\mid Y_i^{\ast },W_i,{\widehat{\phi }}_1^{\ast }\right)=cf({\theta }_i\mid Y_i,W_i,{\widehat{\phi }}_1).$$ (A.12)

Using (A.11) and (A.12), we have AIC_Surv|Long (b, c)

$$\begin{array}{cc}\hfill & =-2\sum _{i=1}^n\log \int L^{\ast }({\widehat{\phi }}_2^{\ast }\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i^{\ast },g,{\widehat{\gamma }}^{\ast })f^{\ast }({\theta }_i^{\ast }\mid Y_i^{\ast },W_i,{\widehat{\phi }}_1^{\ast })d{\theta }_i^{\ast }+2\text{dim}\left({\phi }_2^{\ast }\right)\hfill \\ \hfill & =-2\sum _{i=1}^n\log \int L^{\ast }\left({\widehat{\phi }}_2^{\ast }\mid t_i,{\delta }_i,z_i,x_i,\frac{1}{c}{\theta }_i-\frac{1}{c}\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right),g,{\widehat{\gamma }}^{\ast }\right)f^{\ast }\left(\frac{1}{c}{\theta }_i-\frac{1}{c}\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right)\mid Y_i^{\ast },W_i,{\widehat{\phi }}_1^{\ast }\right)d\left[\frac{1}{c}{\theta }_i-\frac{1}{c}\left(\begin{array}{c}\hfill b\hfill \\ \hfill 0\hfill \end{array}\right)\right]+2\dim \left({\phi }_2^{\ast }\right)\hfill \\ \hfill & =-2\sum _{i=1}^n\log \int L({\widehat{\phi }}_2\mid t_i,{\delta }_i,z_i,x_i,{\theta }_i,g,\widehat{\gamma })f({\theta }_i\mid Y_i,W_i,{\widehat{\phi }}_1)d{\theta }_i+2\text{dim}\left({\phi }_2\right)\hfill \\ \hfill & ={\mathrm{AIC}}_{\mathrm{Surv}\mid \mathrm{Long}},\hfill \end{array}$$

which completes the proof.