Fully Automated Assessment of the Severity of Parkinson’s Disease from Speech

Abstract

For several decades now, there has been sporadic interest in automatically characterizing the speech impairment due to Parkinson’s disease (PD). Most early studies were confined to quantifying a few speech features that were easy to compute. More recent studies have adopted a machine learning approach where a large number of potential features are extracted and the models are learned automatically from the data. In the same vein, here we characterize the disease using a relatively large cohort of 168 subjects, collected from multiple (three) clinics. We elicited speech using three tasks – the sustained phonation task, the diadochokinetic task and a reading task, all within a time budget of 4 minutes, prompted by a portable device. From these recordings, we extracted 1582 features for each subject using openSMILE, a standard feature extraction tool. We compared the effectiveness of three strategies for learning a regularized regression and find that ridge regression performs better than lasso and support vector regression for our task. We refine the feature extraction to capture pitch-related cues, including jitter and shimmer, more accurately using a time-varying harmonic model of speech. Our results show that the severity of the disease can be inferred from speech with a mean absolute error of about 5.5, explaining 61% of the variance and consistently well-above chance across all clinics. Of the three speech elicitation tasks, we find that the reading task is significantly better at capturing cues than diadochokinetic or sustained phonation task. In all, we have demonstrated that the data collection and inference can be fully automated, and the results show that speech-based assessment has promising practical application in PD. The techniques reported here are more widely applicable to other paralinguistic tasks in clinical domain.

1. Introduction and Motivation

Parkinson’s disease (PD), which is characterized by tremors and impaired muscular co-ordinations, currently has no cure and hence screening for early detection and monitoring its progression are important tools for managing the disease in the growing population of the elderly. The disease is associated with low levels of dopamine in the brain and the symptoms are managed by artificially increasing amounts of dopamine with drugs (e.g., L-dopa) and in severe cases by electrically stimulating specific regions in the mid-brain. The severity of the disease is typically assessed in a clinic with a battery of tests – the Unified Parkinson’s Disease Rating Scale (UPDRS) – consisting of clinician-scored motor evaluations and self evaluation of the activities of daily life including speech, swallowing, handwriting, dressing, hygiene, falling, salivating, turning in bed, walking, and cutting food. The UPDRS scores range from 0 to 176, with 0 corresponding to a healthy state and 176 to a severe affliction [22]. The assessment is time-consuming and is performed by trained medical personnel, which becomes burdensome when, for example, frequent re-assessment is required to fine-tune dosage of drugs or the parameters of the electrical pulse train in deep brain stimulations. Not surprisingly, there has been a growing interest in creating tools and methods for alternative home-based assessments of this disease. Easier methods of assessment can play a crucial role in screening for early detection of PD, the second most common neurodegenerative disease in US.

Since speech production involves complex motor coordination, the disease exhibits tell tale symptoms which are well-known to speech pathologists, although the exact pathophysiological cause remains unclear. For several decades now, researchers have been interested in measuring these symptoms in speech more objectively with the hope of augmenting or simplifying the assessment. Speech tasks can be administered remotely, avoiding the need for driving to the clinic, which can be challenging for those with severe PD-related motor tremors. Speech can be elicited, recorded and analyzed automatically relatively easily at much lower cost than in-person clinical assessment. Furthermore, speech-based assessment can monitor changes objectively over time more accurately.

While there has been considerable interest in analyzing speech in PD, spanning about five decades, only recently it has attracted the attention of computational speech researchers. Early studies, reported in clinical journals, employed relatively simple analysis of speech samples. Here, we set the context of this work by reviewing a sampling of previous work in Section 2. As evident from this review, previous studies have several limitations. With a few exceptions, most studies have been conducted on relatively smaller cohorts, recruited from a single clinic and often narrowly focused on characterizing pathology related to production of vowels. Data collected from a single clinic can suffer from bias due to the subjective nature of clinical assessments.

In this article, we investigate the accuracy of automatically inferring the severity of PD from speech samples in a relatively large cohort collected from multiple clinics. The data collection is described in detail in Section 3. One of the aims of this paper is to investigate the utility of current speech processing and machine learning techniques with publicly available tools for inferring the severity of Parkinson’s disease. In Section 4, we extract a number of potential speech features using standard speech processing algorithms and apply several machine learning algorithms to predict the clinical ratings from the speech features. Standard pitch detection algorithms do not have the necessary time-frequency resolution to capture the fine tremors observed in PD. We recently developed a pitch estimation algorithm that addresses this problem, which incidentally won the 2013 Interspeech Challenge on detecting and diagnosing Autism Spectral Disorders [20]. We describe our method and our evaluation on PD in Section 5. Finally, we summarize the contributions of this paper.

2. Brief Review of Speech in PD

The earliest work on measuring speech abnormalities objectively in PD can be traced back to Canter’s dissertation. Taking advantage of then newly available instruments to measure pitch using a direct-writing oscilloscope (Sanborn, Model 450) and vocal intensity using a high-speed level recorder (Bruel and Kjaer, Model 2304), Canter compared speech from 17 patients, who were off medication for 48 hours, with 17 age-matched controls [4, 5, 6]. PD subjects exhibited higher median pitch and lower range than the controls. They lacked the necessary control to generate soft sounds. At the other end of the scale, they had lower intensity of maximal loudness. They were able to sustain phonation for markedly shorter duration, about 50% of the control. In articulation, PD subjects were slower and plosives lacked precision, often confused with fricatives. Canter also noted that the rate of speech and intelligibility were significantly different from the controls. Most of his conclusions, even though deduced from manual measurements from plots, have been subsequently confirmed by measurements with more sophisticated instruments, although with small number of subjects [32, 7]. One exceptionally large sample study collected speech from about 200 PD subjects [19]. They confirmed Canters findings and in addition observed characteristic types of misarticulations (e.g., back-of-tongue, tongue tip, lips). The above mentioned studies were conducted by clinical researchers who compiled the features with manual measurements and perceptual ratings.

There have been very few studies on employing automatic speech processing to classify PD subjects from controls or inferring the severity of the diseases. Here we describe a few representative studies. Guerra and Lovely attempted to emulate the ratings of speech pathologists [14]. Specifically, they created a linear regression with automatically extracted features but whose coefficients were manually set to emulate perceptual measures such as harsh voice, breathy voice and audible inspirations. While their approach was meant to facilitate easy clinical adoption, their method was ad hoc and they were only able to map a few perceptual measures. Little and his colleagues focused their attention on relatively simple analysis of phonation of a single vowel, collected from 42 subjects, including 10 controls [33]. They evaluated the efficacy of their algorithm using cross validation and reported a mean absolute error (MAE) of 6.6 in inferring the severity of PD. Their results are overly optimistic because their test and training sets have significant overlap, with same speakers contributing large number of samples to both. They erroneously assumed speech frames from each sessions were independent. So, they model not just the difference between speakers due to PD but also due to normal variations in speaker traits. More recently, Bocklet and colleagues applied a more rigorous machine learning approach to classify 23 PD subjects from 23 control subjects [2]. They extracted 292 prosodic features, adapted a 128 component Gaussian mixture model or universal background model using maximum a posteriori criterion and found that they were able to perform the classification with good accuracy. However, their task was classification, not assessing the degree of severity which is more relevant in a monitoring application such as the one we are interested in.

Taken together, there has been continuous interest spanning several decades in characterizing the speech abnormalities in PD. However, early studies were focused on measuring group differences of speech features and recent studies have been performed on small samples.

3. Data Collection and the Corpus

Speech data for this work was collected as a part of a larger study whose goal is to develop an objective measure of severity for Parkinson’s disease. As a clinical reference, the severity of subjects’ condition were measured by clinicians using the UPDRS. In this study, we focused on motor sub-scale (mUPDRS), which spans from 0 for healthy individual to 108 for extreme disability. The data was collected from multiple (three) clinics to alleviate potential bias due to clinic-specific practices. The objective measures were collected using a battery of tests administered on a portable platform developed by Intel, the Kinetics Foundation and a consortium of neurologists [13]. The platform measured fine motor control of hands and foot (via a foot-tapper) and recorded speech via a close-talking microphone. Subjects were prompted to respond to different motor and speech tasks in a prearranged sequence. The tasks were administered by trained PD clinicians who were familiar with the device. Note, the key motivation for developing the portable platform was to create a home-based assessment platform and for that purpose the data collection was fully automated.

The battery of speech tasks, listed below, were compiled to measure different aspects of speech production. The tasks were chosen so that they can be administered automatically and performed within a short time budget of 4 minutes.

1. Sustained phonation task: Subjects were instructed to phonate the vowel /ah/ for about 10 seconds, keeping their voice as steady as possible at a comfortable, constant vocal frequency. Speech pathologists often rate voice quality during this task.

2. Diadochokinetic (DDK) task: Subjects were asked to repeat the sequence of syllables /pa/, /ta/ and /ka/ continuously for about 10 seconds as fast and as clearly as they possibly could. This task is often employed by speech pathologists to judge articulatory precision, control and speed.

3. Reading task: Subjects were asked to read 3 standard passages, which are referred to in the literature as “The North Wind and The Sun”, “The Rainbow Passage”, and “The Grandfather Passage”. For example, the first story begins as – The North Wind and the Sun were disputing which was the stronger, when a traveler came along wrapped in a warm cloak. This reading task allows measurement of vocal intensity, voice quality, and speaking rate including the number of pauses, the length of pauses, the length of phrases, the duration of spoken syllables, the voice onset times (VOT), and the sentence durations.

The empirical evaluations in this paper were performed with data from 168 subjects, all of whom were diagnosed with PD. Thus, this corpus has more subjects than previous studies on automated assessments – 42 PD subjects and 10 controls [33], 23 PD subjects and 23 controls [2]. The severity of the disease in our subjects ranged from 0 (control) to 55 on the UPDRS scale in our subjects, with a mean of 22.9 and standard deviation of 9.3. Our subject pool exhibits slightly higher mean and range of severity of the disease than the most closely related previous work by Bocklet and colleagues whose PD subjects had a mean UPDRS score of 17.5 and a standard deviation of 7.3. As we shall later see in Section 8, the diversity of subjects influences how well the automated assessment can generalize, for example, across clinics.

4. Comparison of Learning Strategies

In this section, we describe our baseline system and investigate how the accuracy of inferring the severity of PD depends on different learning strategies.

The larger goal of the project is to assess and to monitor the severity of PD using both motor and verbal responses and our task is to focus on the latter. Specifically, to learn a regression on the features extracted from the elicited speech. Let the speech data collected from a subject be x⁽ⁱ⁾ and y his or her clinical rating (UPDRS score). Thus, we need to learn a regression function f (x; β), parametrized by β, that approximates the UDPRS scores from the available training data D = {(xⁱ, yⁱ); i = 1, …, n}.

$$y=f(\mathbf{x};\mathit{\beta })+\epsilon$$ (1)

Assuming an independent identically distributed regression error ε, the optimal function can be learned by minimizing the average loss.

$${\mathit{\beta }}_{\mathit{\text{opt}}}=\underset{\mathit{\beta }}{\text{argmin}}\sum _{i=1}^n\ell (y^i,f({\mathbf{x}}^i;\mathit{\beta }))$$ (2)

The learned parameters will depend on the choice of the loss function ℓ, which may be absolute loss, squared loss and hinge loss. The simplest regression function is a constant and that would correspond to guessing the same severity (chance) for all subjects. For absolute and squared loss, the optimal guess would be the median and mean UPDRS respectively. In most literature on this topic, the performance is reported in terms of mean absolute error (MAE). On our data set, the median UPDRS score is 21 and the mean absolute error of 7.5.

The most popular regression function is a linear function, where the parameters {β_i; i = 0, …, d} are regression coefficients and d is the dimension of features x_i extracted from x.

$$f(\mathbf{x};\mathit{\beta })={\beta }_0+\sum _{i=1}^d{x}_i{\beta }_i$$ (3)

The number of potential speech features that can be extracted from the speech samples elicited through the four tasks can be large, much larger than the number of subjects in the study. In such a scenario, the learning task, in Equation (2), is an ill-posed problem without a unique solution for the linear function. The simplest solution to this problem is to augment the cost function with a regularization term r(β) that penalizes large values of the regression coefficients, driving them to zero when they are not useful.

$${\mathit{\beta }}_{\mathit{\text{opt}}}=\underset{\mathit{\beta }}{\text{argmin}}\sum _{i=1}^n\ell (y^i,f({\mathbf{x}}^i;\mathit{\beta }))+\lambda r(\mathit{\beta })$$ (4)

The trade-off between accurate inference of the severity of PD and discarding irrelevant features is controlled by the regularization weight λ, which is often picked using cross-validation [31].

4.1. Speech Features

Before delving into our experiments on different modeling strategies, we briefly describe the features extracted for this task. Classic perceptual characteristics associated with PD are reduced loudness; monotonous pitch; monotonous loudness; reduced stress; breathy, hoarse voice quality; imprecise articulation; and short rushes of speech. In general, we can divide the aforementioned problems into three major categories: loudness related problems, pitch related problems and articulatory related problem. In our experiment, we used a diverse set of features to capture cues associated with these categories. For our baseline system, we adopted the baseline features defined in INTERSPEECH 2010 Paralinguistic Challenge [25] using openSMILE toolkit [11].

The features, comprised of 1582 components, can be broadly categorized into three groups: 1) loudness related features such as RMS energy and PCM loudness, 2) voicing related features like pitch frequency, jitter, and shimmer, and 3) articulatory related features such as mel-frequency cepstral coefficients and line spectral frequencies. The above configuration provides 38 features along with their derivatives to form the frame-level acoustic features. The derivatives allow us to capture local dynamics of pitch and other features. The features computed at the frame-level were summarized into a global feature vector of fixed dimension for each recording using 21 standard statistical functions including min, max, mean, skewness, quartiles and percentile.

4.2. Learning Strategies

We investigated three forms of regularization, L2-norm in ridge regression, L1-norm in lasso, and hinge loss function in support vector machine. We describe them briefly here and more details can be found in standard textbooks [16].

Ridge Regression In ridge regression, the loss function ℓ() and the regularizer r() are the squared loss and the L2-norm, respectively.

$$\ell (y^i,f({\mathbf{x}}^i;\mathit{\beta }))={(y^i-f({\mathbf{x}}^i;\mathit{\beta }))}^2,r(\mathit{\beta })={\Vert \mathit{\beta }\Vert }_2^2$$

Lasso Regression In lasso regression, the loss function is again the squared loss but the regularizer is the L1-norm. The L1-norm is well-known for finding sparse solution, assigning zero values to useless regression coefficients [31].

$$\ell (y^i,f({\mathbf{x}}^i;\mathit{\beta }))={(y^i-f({\mathbf{x}}^i;\mathit{\beta }))}^2,r(\mathit{\beta })={\Vert \mathit{\beta }\Vert }_1$$

Linear Support Vector Regression Support vector regression uses the ε-insensitive loss function and the L2-norm for regularization.

$$\ell (y^i,f({\mathbf{x}}^i;\mathit{\beta }))=\text{max}(0,{\Vert y^i-f({\mathbf{x}}^i;\mathit{\beta })-\epsilon \Vert }_1),r(\mathit{\beta })={\Vert \mathit{\beta }\Vert }_2^2$$

These three learning strategies were evaluated on our data set using leave-one-out cross-validation with the scikit-learn toolkit [24] and the performances are shown in Table 1. The ridge regression and the support vector regression are significantly better than chance with a p-value of less than 0.001, according to cross-validated paired t-test [9], and is denoted by (^†) in the table. Ridge regression is much faster to learn than the support vector regression.

Table 1.

Comparison of performance of different regressions for inferring the severity of PD, where † denotes statistically significant results.

	Mean Absolute Error
Chance	7.5
Lasso	6.9
Ridge	5.9†
Linear SVR	5.9†

5. Improved Pitch-Related Features

The tremors observed in Parkinson’s disease can be as low as ten hertz [32]. Even though there are a large number of pitch estimators in the literature [30, 3, 8, 17, 28, 10, 18], most of them are not well-suited for measuring the small tremors in PD. The key issue is that resolutions as low as 10Hz can be obtained only using large time windows. But speech, unlike for example elephant vocalizations, is highly non-stationary and violates the stationarity assumption when long windows are considered. The autocorrelation based methods wrongly assume the pitch is constant over the duration of the frame [30, 3, 8]. Methods that locate peaks in frequency domain, power spectrum or cepstral domain also suffer from similar drawbacks [17, 28, 10, 18]. For example, at 16KHz sampling, a 25 millisecond frame would correspond to 400 sample points and a frequency resolution of about twenty hertz or more. Increasing the resolution with longer frames runs afoul of the stationarity assumption as the frame includes sounds corresponding to different phones. The pitch estimator needs to measure tremors of the order of 10 hertz using standard 25 millisecond time frames, which most current methods cannot do.

One notable exception is the harmonic model of speech where the harmonic coefficients are allowed to vary in time within the frame. This model takes into account the harmonic nature of voiced speech and can be formulated to estimate pitch candidates with maximum likelihood criterion [1].

5.1. Harmonic Model

The popular source-channel model of voiced speech considers glottal pulses as a source of periodic waveforms which is being modified by the shape of the mouth assumed to be a linear channel. Thus, the resulting speech is rich in harmonics of the glottal pulse period. The harmonic model is a special case of a sinusoidal model where all the sinusoidal components are assumed to be harmonically related, that is, the frequencies of the sinusoids are multiples of the fundamental frequency [27]. The observed voiced signal is represented in terms of a harmonic component and a non-periodic component related to noise.

Let y = [y(t₁), y(t₂), …, y(t_N)]^T denote the speech samples in a voiced frame, measured at times t₁, t₂, …, t_T. The samples can be represented with a harmonic model with an additive noise n = [n(t₁), n(t₂), …, n(t_N)]^T as follow:

$$s(t)=a_0+\sum _{h=1}^H{a}_h\text{cos}(2\pi f_{0}ht)+b_h\text{sin}(2\pi f_{0}ht)y(t)=s(t)+n(t)$$ (5)

where H denotes the number of harmonics and 2π f₀ stands for the fundamental angular frequency. The harmonic coefficients a_h and b_h in this equation are assumed to be constant for each frame, but this assumption is relaxed while computing jitter and shimmer, as described later in Section 5.6. The harmonic signal can be factored into coefficients of basis functions, α, β, and the harmonic components which are determined solely by the given angular frequency 2π f₀.

$$s(t)=[1A_c(t)A_s(t)]\left[\begin{array}{c}\hfill a_0\hfill \\ \hfill \alpha \hfill \\ \hfill \beta \hfill \end{array}\right]A_c(t)=[\text{cos}(2\pi f_{0}t)\cdots \text{cos}(2\pi f_{0}Ht)]A_s(t)=[\text{sin}(2\pi f_{0}t)\cdots \text{sin}(2\pi f_{0}Ht)]\alpha ={[a_1\cdots a_H]}^T\beta ={[b_1\cdots b_H]}^T$$ (6)

Stacking rows of [1 A_c(t) A_s(t)] at t = 1, ⋯, T into a matrix A, equation (2) can be compactly represented in matrix notation as:

$$\mathbf{y}=\mathbf{A}\mathbf{m}+\mathbf{n}$$ (7)

where y = A m corresponds to an expansion of the harmonic part of the voiced frame in terms of windowed sinusoidal components, and $\mathrm{\Theta }=[f_0,\mathbf{b},{\sigma }_n^2,H]$ is the set of unknown parameters.

5.2. Pitch Estimation

Assuming the noise samples n are independent and identically distributed random variables with zero-mean Gaussian distribution, the likelihood function of the observed vector, y, given the model parameters can be formulated as the following equation. The parameters of the vector m can then be estimated by maximum likelihood (ML) approach.

$$\mathbf{L}(\mathrm{\Theta })=-\frac{D}{2}\text{log}(2\pi {\sigma }_n^2)-\frac{1}{2{\sigma }_n^2}{\Vert \mathbf{y}-\mathbf{A}\mathbf{b}\Vert }^2{\mathbf{m̂}}_{ML}={({\mathbf{A}}^T\mathbf{A})}^{-1}{\mathbf{A}}^T\mathbf{y}$$ (8)

Under the harmonic model, the reconstructed signal ŝ is given by ŝ = A m. The pitch can be estimated by maximizing the energy of the reconstructed signal over the pre-determined grid of discrete f₀ values ranging from f_{0 min} to f_{0 max}.

$${\mathrm{f̂}}_{0ML}=\underset{f_0}{\text{arg max}}{\mathbf{ŝ}}^T\mathbf{ŝ}$$ (9)

5.3. Segmental Pitch Tracking

The frame-based pitch estimation does not prevent pitch from varying drastically from one frame to the next. In natural speech, however, pitch often varies smoothly across frames. This smoothness constraint can be enforced using a first order Markov dependency between pitch estimates of successive frames. Adopting the popular hidden Markov model framework, the estimation of pitch over utterances can be formulated as follows.

The observation probabilities are assumed to be independent given the hidden states or candidate pitch frequencies here. A zero-mean Gaussian distribution defined over the pitch difference between two successive frames is a reasonable approximation for the first order Markov transition probabilities [29], $P(f_0^{(i)}|f_0^{(i-1)})=𝒩(f_0^{(i)},{\sigma }_t^2)$. Putting all this together and substituting the likelihood from the Equation 9, the pitch over an utterance can be estimated as follows.

$${\mathbf{F̂}}_0=\underset{{\mathbf{F}}_0}{\text{argmax}}[\sum _{i=0}^M{{\mathbf{ŝ}}_{\mathbf{i}}}^T{\mathbf{ŝ}}_{\mathbf{i}}|f_0^{(i)}+\text{log}𝒩(f_0^{(i)},{\sigma }_t^2)]$$ (10)

Thus, the estimation of pitch over an utterance can be formulated as an HMM decoding problem and can be efficiently solved using Viterbi algorithm.

5.4. Pitch Halving and Doubling

Like in other pitch detection algorithms, pitch doubling and halving are the most common errors in harmonic models too. The harmonics of f₀/2 (halving) include all the harmonics of f₀. Similarly, the harmonics of 2f₀ (doubling) are also the harmonics of f₀. The true pitch f₀ may be confused with f₀/2 and 2f₀ depending on the number of harmonics considered and the noise.

In many conventional algorithms, the errors due to halving and doubling are minimized by heuristics such as limiting the range of allowable f₀ over a segment or an utterance. This requires prior knowledge about the gender and age of the speakers. Alternatives include median filtering and constraints in Viterbi search [30], which remain unsatisfactory.

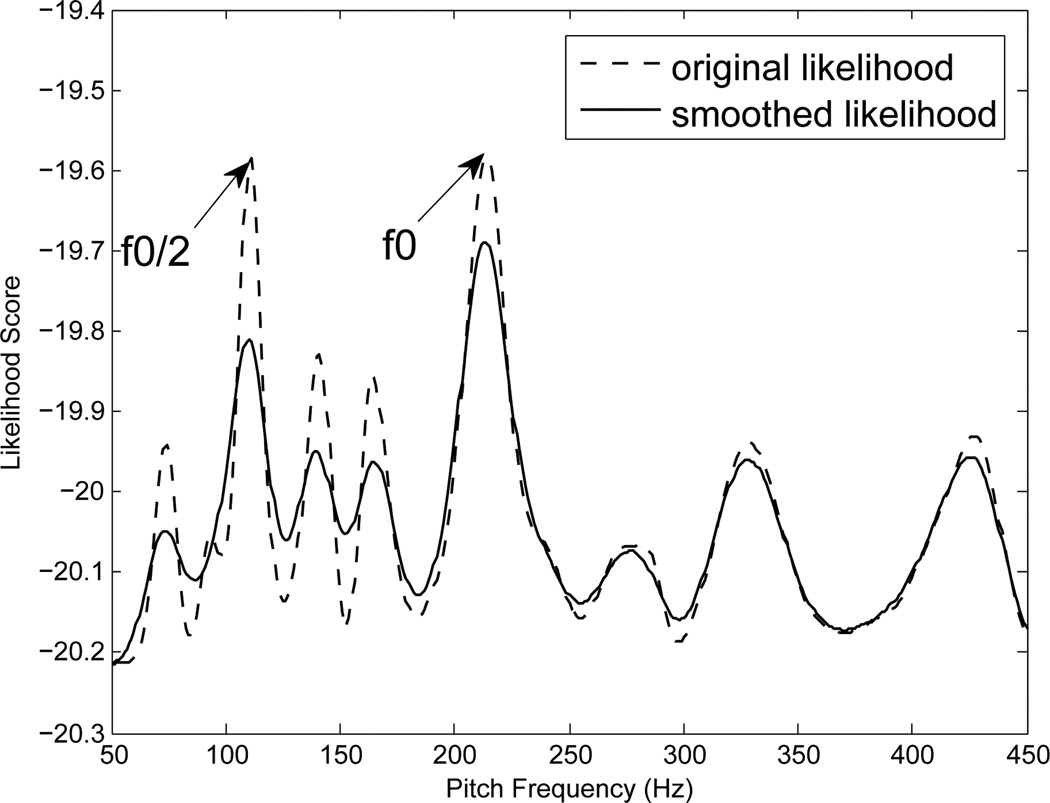
We propose a method to capture the probability mass in the neighborhood of the candidate pitch frequency. The likelihood of the observed frames falls more rapidly near candidates at halving f₀/2 and doubling 2f₀ than at the true pitch frequency f₀. This probability mass in the neighborhood can be captured by convolving the likelihood function with an appropriate window. Figure 1 illustrates the problem of halving and demonstrates our solution for it. The dotted line shows the energy of the reconstructed signal ŝ for a frame. A maximum of this function will erroneously pick the candidate f₀/2 as the most likely pitch candidate for this frame. However, notice that the function has a broader peak at f₀ than at f₀/2. The solid line shows the result of convolving the energy of the reconstructed signal with a hamming window. In our experiments, we employed a hamming window with the length of f_0−min/2 where f_0−min is the minimum pitch frequency. The locally smoothed likelihood shows a relatively high peak at the true pitch frequency f₀ compared to f₀/2, thus overcoming the problem of halving.

Figure 1.

This figure illustates an example frame where both f₀ and f₀/2 are equally likely pitch candidates according to maximum likelihood criterion. However, when the likelihood is smoothed, as described above, the problem of halving is solved.

5.5. Model Selection

Another problem with the harmonic model is the need to specify the number of harmonics considered. This is typically not known a priori and the optimal value can be different in different noise conditions. Davy proposed a sampling-based method for estimating the number of harmonics [12]. Their approach is based on Monte Carlo sampling and requires computationally expensive numerical approximations. Mahadevan employs the Akaike information criteria (AIC) for tackling the problem of model order selection [21]. Here, we follow a Bayesian approach trying to maximize the likelihood function given by:

$$Ĥ=\underset{H}{\text{arg max}}p(\mathbf{y},{\mathrm{\Theta }}_H)$$ (11)

where Θ_H denotes the model constructed by H harmonics. The likelihood function increases as a function of increasing model order and often leads to the overfitting problem. We adopt the Bayesian information criterion (BIC) as a model selection criterion, where the increase in the likelihood is penalized by a term that depends on the model complexity or the number of model parameters. For the harmonic model, we include a term that depends on the number of data points in the analysis window N.

$$BIC(H)=-2\text{log}p(\mathbf{y},{\mathrm{\Theta }}_H)+H\text{log}N$$ (12)

Thus, in our proposed model selection scheme, we compute the average frame-level BIC for different model orders, ranging from H = 2, ⋯, H_max. For a given task or noise condition, we choose the number of harmonic that minimizes the average frame-level BIC.

5.6. Jitter and Shimmer

Speech pathologists often measure cycle-to-cycle variations in glottal pulse to characterize abnormalities in voice production [32]. In early work, the cycle-to-cycle variation in fundamental time period T_i and amplitude A_i were measured manually and computed using a variant of the equation below.

$$J=\frac{1/(N-1){\sum }_{i=1}^{N-1}|T_i-T_{i+1}|}{1/N{\sum }_{i=1}^N{T}_i}$$ (13)

$$S=1/(N-1)\sum _{i=1}^{N-1}|\text{log}(A_{i+1}/A_i)|$$ (14)

Automatic measurement of time period and amplitude of each cycle is prone to errors due to noise. Most automated methods sidestep this problem by measuring the variation across frames using the average time period and amplitude per frame [23, 15, 26]. However, this approach ignores variations within frame.

The harmonic model allows an alternate method to measure jitter and shimmer that is less sensitive to noise and can also capture variation within a frame. The key idea of our approach is to reconstruct two versions of the input waveform in each frame – a version where the amplitudes of the harmonics are constant, as in Equation 6, and another without that assumption. Both reconstructions are estimated to minimize the effect of noise.

The model for the voiced speech that allows harmonic amplitude to vary with time can be represented as follows (HM-VA) [12].

$$s(t)=a_0(t)+\sum _{h=1}^H[a_h(t)\text{cos}(2\pi f_{0}ht)]+\sum _{h=1}^H[b_h(t)\text{sin}(2\pi f_{0}ht)]$$ (15)

Note, the previous model defined by Equation 5, here the harmonic coefficients a_h(t) and b_h(t) are allowed to vary with time within a frame. Thus, this model is capable of capturing cycle-to-cycle variations within a frame. The cycle-to-cycle variations in harmonic amplitudes cannot be arbitrary and can be constrained by imposing smoothness constraints to improve the robustness of their estimation. One easy method for imposing smoothness is to represent the harmonic coefficients as a superposition of small number of basis functions ψ_i as in equation 16 [12].

$$a_h(t)=\sum _{i=1}^I{\alpha }_{i,h}{\psi }_i(t),b_h(t)=\sum _{i=1}^I{\beta }_{i,h}{\psi }_i(t)$$ (16)

We represent this smoothness constraints within a frame using four (I = 4) Hanning windows as basis functions. For a frame of length M, the windows are centered at 0, M/3, 2M/3, and M. Each basis function is 2M/3 samples long and has an overlap of M/3 with immediate adjacent window. The parameters of this model can be expressed, once again, as a linear model, similar to Equation 7, but this time the A and m have dimensions four times the original dimensions. Given the fundamental frequency from Equation 10, we compute a_h(t) and b_h(t) using a maximum likelihood framework.

Now, the cycle-to-cycle variation associated with jitter and shimmer can be computed from the estimated parameters of the two models, with constant amplitudes, a_h and b_h, and the time-varying amplitudes, a_h(t) and b_h(t), of the harmonics. Shimmer can be considered as a function f(t) that scales the amplitudes of all the harmonics in the time-varying model.

$$c_h(t)=c_{h}f(t)+e(t),t=1,\dots ,T,h=1,\dots ,H$$ (17)

where $c_h=\sqrt{{\sum }_{h=1}^H{a}_h^2+b_h^2}$ denotes the constant amplitude of the harmonic components in the harmonic model and c_h(t) is the counterpart where the amplitudes vary within a frame. Once again, assuming uncorrelated noise, f(t) can be estimated using maximum likelihood criterion.

$$\mathrm{f̂}(t)=\frac{{\sum }_{h=1}^H{c}_h{c}_h(t)}{{\sum }_{h=1}^H{c}_h^2}$$ (18)

The larger the tremor in voice, the larger the variation in f(t). Hence, we use the standard deviation of f(t) as a summary statistics to quantify the shimmer per frame.

For computing jitter, we first create a matched filter by excising a one pitch period long segment from the signal estimated with the constant-amplitude harmonic model from the center of the frame. This matched filter is then convolved with the estimated signal from the time-varying harmonic model and the distance between the maxima defines the pitch periods in the frame. The perturbation in period is normalized with respect to the given pitch period and its standard deviation is an estimate of jitter.

5.7. Harmonic-to-noise ratio (HNR)

Researchers have used HNR in the acoustic studies for the evaluation of voice disorders. Given the reconstructed signal as the harmonic source of vocal tract, the noisy part is obtained by subtracting the reconstructed signal from the original speech signal. The noisy part encompasses everything in the signal that is not described by harmonic components including fricatives. In our model, HNR and the ratio of energy in first and second harmonics (H_1/2) can be computed from the HM-VA as follows.

$$c_h(t)=\sqrt{\sum _{i=1}^I{a}_h{(t)}^2+b_h{(t)}^2}HNR=\text{log}\sum _{t=1}^N\sum _{h=1}^H{c}_h{(t)}^2-\text{log}\sum _{t=1}^N{(y(t)-s(t))}^2{H}_{1/2}=\text{log}\sum _{t=1}^N{c}_1{(t)}^2-\text{log}\sum _{t=1}^N{c}_2{(t)}^2$$ (19)

Thus, we compute jitter, shimmer, harmonic-to-noise ratio and the ratio of energy in first and second harmonics using reconstructed signal that is less prone to noise related errors. The effectiveness of these two measures are evaluated in the experiments below.

5.8. Experimental Results

Using our new features, we compared the performance of the ridge regression for inferring the severity of PD. The results are reported in Table 2 for the leave-one-out cross-validations. Using the harmonic model we estimated the pitch, then applied the time-varying harmonic model to compute the jitter and shimmer. Together with other pitch related features and MFCC computed with openSMILE, 925 features were extracted for each subject, far fewer than the 1582 features computed using openSMILE in the baseline system. Both standard speech features and those extracted using harmonic models perform significantly better than chance with p-value of less than 0.001. The features from the harmonic model perform better than standard features, but the improvement is not statistically significant in this corpus. Combining the two sets of features does not result in any additional gain. The explained variance for the regression using features extracted from the harmonic model is about 61% when averaged across the cross-validation folds.

Table 2.

Comparison of performance of ridge regressions for inferring severity of PD using feature extracted from openSMILE, the proposed model, and a combination of both, where † denotes statistically significant results.

Features	Mean Absolute Error
Chance	8.0
OpenSMILE	5.9†
Harmonic Model	5.5†
Hybrid	5.7†

6. Effectiveness of Speech Elicitation Tasks

As mentioned in Section 3 under Data Collection and Corpus, speech was elicited from subjects by administering three tasks – sustained phonation task, diadochokinetic task and the reading task. They exercise different aspects of the speech production system and can reveal different deficiencies, for example, tremors in pitch, poor articulatory control and large variations in speaking rate respectively. For large scale screening and in poor noise conditions, one may want to scale back the data collection to administer only the sustained phonation task, as in the widely publicized Parkinson’s Voice Initiative. In phonation task, there are fewer speech features to extract from speech and they can be extracted more robustly. We examined the benefits of the additional tasks in inferring the severity from speech and report our results in the Table 3. The sustained phonation task by itself is not particularly effective at this task. In contrast, the diadochokinetic task is a simple task and the speech features extracted from it are better at assessing the severity of the disease. The features extracted from the reading task are most effective at this task. The performance of regressions with features from DDK and reading tasks are statistically better than chance, while the regression with features from phonation task is not. Combining the features does not result any further improvements.

Table 3.

Comparison of regressions using features extracted from speech, elicited by different tasks, for inferring severity of PD, where † denotes statistically significant results.

	Elicitation Tasks	Mean of Absolute Errors
	Chance	8.0
a)	Phonation Task	7.1
b)	DDK Task	6.1†
c)	Reading Task	5.6†
d)	All (a+b+c)	5.5†

7. Influence of Control

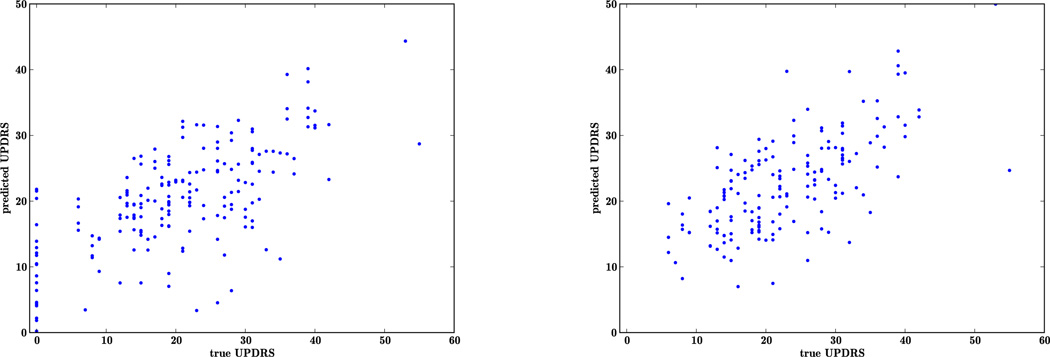
Apart from data described in the corpus, speech recordings were obtained from 21 controls from one clinic, where they were assigned a UPDRS motor score of zero without assessments. Thus the scale has a discontinuity close to zero which makes it difficult to learn a good fit for the controls. We investigate this effect by learning two different regressions, with and without the controls. The results for leave-one-out cross-validation are reported in Table 4 for ridge regression using features from harmonic model. The mean absolute error for chance or the best guess increases to 9.0 when the controls are included. The ridge regression improves the inferred severity in both cases. In Figure 2, we illustrate the correlation between the inferred severity and the clinical reference. The overall correlation in both cases is about the same, at 0.66. However, there is a large variance in inferred severity for the controls, as represented by the points on the y-axis.

Table 4.

Effect of including controls in the training data when learning regressions for inferring severity of PD, where † denotes statistically significant results.

Subjects	Chance	MAE
PD	8.0	5.5†
PD + Control	9.3	6.6†

Figure 2.

Plot of reference UPDRS vs. predicted UPDRS to illustrate how controls (assigned a reference UPDRS score of zero) skew the performance of the inference of severity of PD.

8. Clinic-Specific Influence

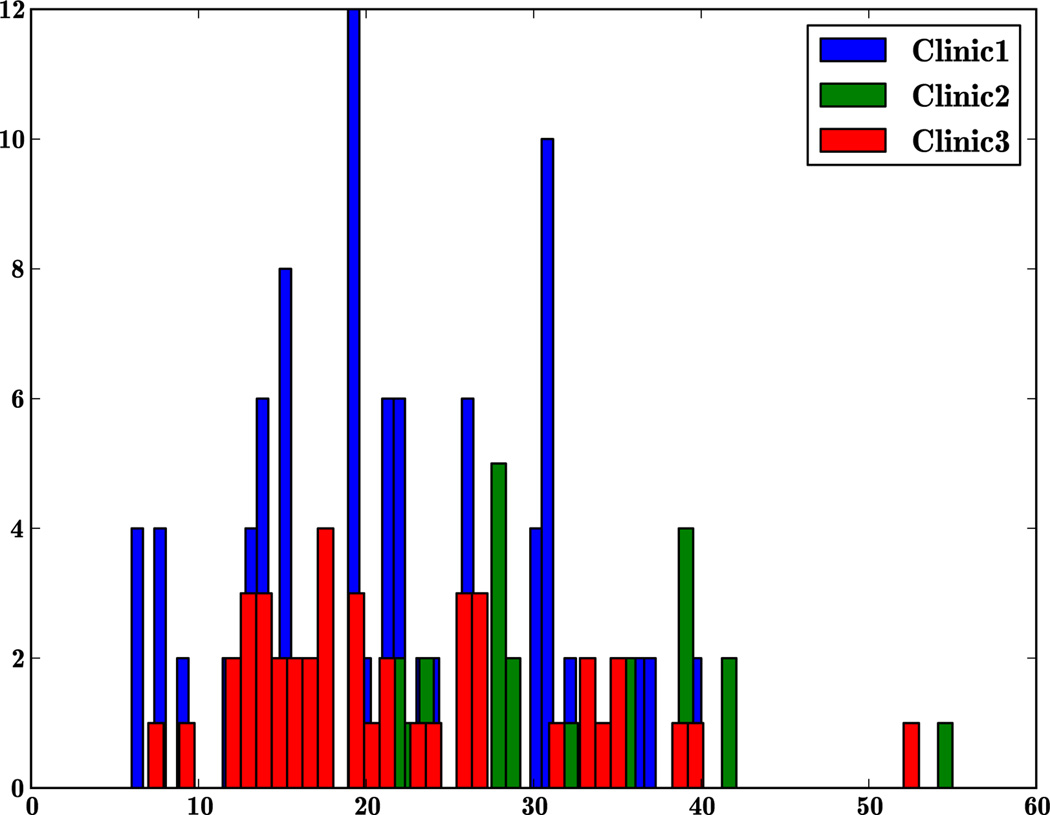
One problem with clinical studies where the gold standard itself has a subjective component is the bias introduced by the data collected in each clinic. The bias could be due to numerous factors including the severity of the disease in the patient population or the training of those administering the assessments. Our multisite study affords an opportunity to check this variability. We separated the data from the three clinics and Figure 3 illustrates the difference in distribution of severity of PD patients observed in the three clinics. The patients seen at clinic 1 have a wider distribution of severity of the disease than the other two clinics. Incidentally, more patients (99) were seen at clinic 1 than in the other two clinics (43 and 26). The median UPDRS motor score per clinic ranged from 6.9 to 7.4.

Figure 3.

Plot illustrates the difference in the frequency (y-axis) of severity of PD across the three clinics in terms of UPDRS motor scale (x-axis).

For understanding how well our models can generalize across clinics, we learned a separate model for each clinic and evaluated the model on the data from the other two clinics. Our results based on the features from our proposed harmonic model are reported in Table 5. The regression learned on clinic 1, which has the most diverse as well as the most number of patients, generalizes better than those trained on the other two clinics. While this is not a surprising result, it underlines the need for samples that are more diverse in severity and larger in number than in previous studies [33, 2].

Table 5.

Comparison of the performance of the regressions learned using data from one clinic and evaluated on the data from the other two clinics, where † denotes statistically significant results.

Training Data	N	Chance	MAE
Clinic 1	99	6.9	4.6†
Clinic 2	26	7.4	6.1
Clinic 3	43	7.3	5.7
All	168	8.0	5.5†

9. Conclusions & Discussion

In summary, we have reported our experiments on inferring the severity of PD from speech recorded from a relatively large sample of 168 subjects, from multiple clinics, using three elicitation tasks – the sustained phonation task, the diadochokinetic task and the reading task. These tasks can be administered automatically remotely and our results show that the severity can be inferred with a mean absolute error of 5.5, explaining 61% of the variance and consistently well-above chance across all clinics. In the framework described in this paper, the errors will be lower in applications where the progression of the disease needs to be monitored over time and there is an opportunity to learn the regression for each subject via better priors. We found that our pitch related features are consistently better than alternative features across different test conditions. Our analysis of the results show that the phonation task is a poor predictor of the severity. Diadokinetic and reading tasks are better predictors and the combination of all three tasks gives the best results.

Considerable work still remains to be performed for improving the accuracy of inference. The perceptual characteristics of PD such as imprecise articulation, short rushes of speech and language impairment are still not modeled in the literature on this topic. Further work is required to present information to clinicians and speech pathologists in a manner that will be useful for them to interpret the results of automated analysis, perhaps, by mapping them to perceptual quantities they are familiar with. Last but not least, the current gold standard for measuring severity (UPDRS) neglects the effects on speech and needs to be updated to capture them better. Automated assessment of speech impairment in PD can potentially fill this gap in UPDRS and better characterize the disease and its progression.

This paper investigates the problem of automatically inferring the severity of Parkinson's disease from speech.

The key contributions of the paper are:

1. Development of better models for extraction of features related to pitch, jitter and shimmer;

2. Analysis of the effectiveness of different tasks for eliciting speech;

3. Demonstration of the feasibility of administering a battery of PD tests on a portable platform and automating the analysis of elicited speech.