Electron tunneling pathways in respiratory complex I. The role of the internal water between the enzyme subunits

Abstract

Recently, the atomistic details of the electronic wiring of seven Fe/S clusters (N3, N1b, N4, N5, N6a, N6b, N2) of respiratory complex I, along which electrons are injected into the electron transport chain, have been revealed; the tunneling pathways between the clusters and the contributing key residues were identified [1]. In this study, the sensitivity of the electron tunneling pathways to the internal water at the protein subunit boundaries is investigated by simulating tunneling pathways of N3→N1b and N6b→N2 with and without the internal water. It is found that the hydrogen bonding networks formed along the internal water can provide efficient tunneling pathways. In N3→N1b, the tunneling pathway with the internal water is drastically different with significantly shorter (3.4 Å) total tunneling distance along the trajectory. In N6b→N2, the internal water contributes to the tunneling as a bridge between N6b and ₉Ile⁹⁹ with two shorter through-space jumps instead of one longer jump. The resulting enhancement of the rates of the individual electron tunneling process is two to three orders of magnitude. This study demonstrates that the tunneling pathways and tunneling rates are sensitive to the internal water, which suggests that the tunneling pathways can change dynamically due to the diffusion of the internal water, and that the efficient electron tunneling occurs at some specific optimal positions of the internal water.

1. Introduction

NADH:ubiquinone oxidoreductase (complex I) is a large L-shaped membrane bound enzyme involved in cellular respiration which catalyzes the oxidation of NADH and the reduction of ubiquinone in mitochondria and respirating bacteria [2-4] This reaction involves the transfer of electrons over approximately 90 Å along seven iron-sulfur (Fe/S) clusters (N3, N1b, N4, N5, N6a, N6b, N2) from NADH bound to the hydrophilic domain to ubiquinone in or near the hydrophobic membrane bound domain of complex I [5]. The reaction provides the driving force for the transport of 4 protons from the mitochondrial matrix to the intermembrane space thus generating, in part, the proton gradient necessary for ATP production [2]. Complex I defects are the cause of several neurodegenerative diseases including Parkinson's disease , Alzheimer's disease and Huntington's disease [6].

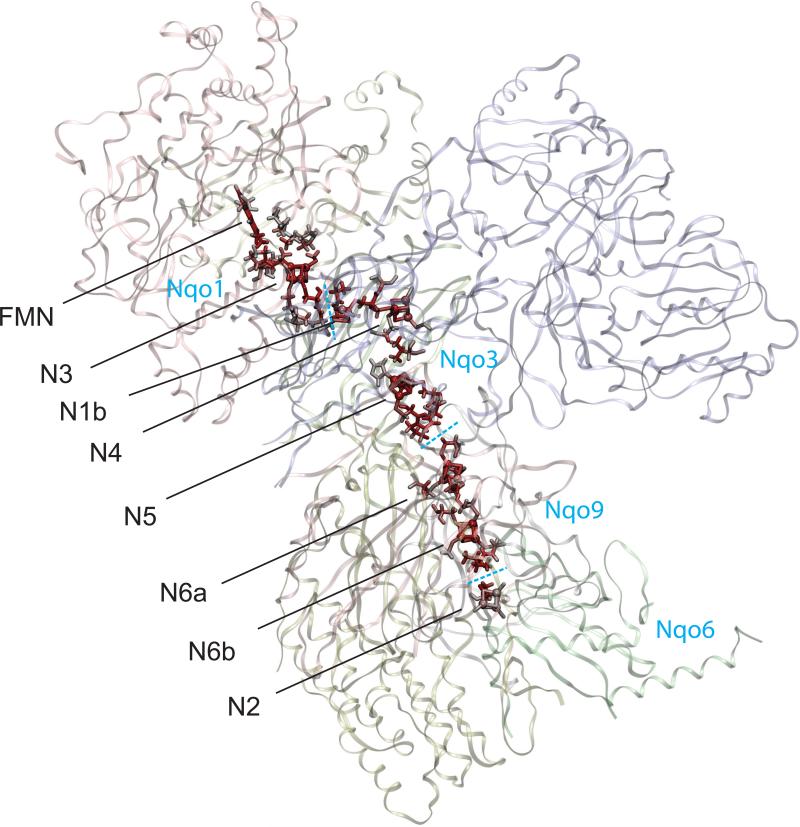
The crystal structure of hydrophilic domain of complex I from Thermus thermophilus was reported in 2006 [7], and the whole architecture of the enzyme has just been revealed in 2010 [8]. Recently we have identified the atomistic details of the electron tunneling from flavin mononucleotide (FMN) and along the seven Fe/S clusters in complex I (Figure 1). Distinct electron tunneling pathways between neighboring Fe/S clusters are identified; the pathways primarily consist of two cysteine ligands and one additional key residue. The internal water between protein subunits of complex I is identified as an essential mediator to achieve the efficient overall transfer rate observed experimentally in the range of 170 ~ 10⁴ s⁻¹. However, the tunneling pathways between the Fe/S cluster pair in different protein subunits can fluctuate due to the thermal diffusion of the internal water at the subunit boundary. To investigate the sensitivity of the tunneling pathways to the internal water molecules, here we focus on the electron tunneling processes of N3→N1b and N6b→N2, where the donors and acceptors are located in different subunits, simulating the tunneling pathways with and without the internal water.

Figure 1.

Calculated complete electron tunneling pathway from FMN to N2 of respiratory complex I from Thermus thermophilus [7] from FMN and along seven Fe/S clusters. The atoms with significant electron tunneling probability are highlighted with red color intensity corresponding to their total current densities (Eq. (6)). The blue dashed lines indicate the protein subunit boundaries.

2. Theoretical Basis and Computational Technique

The simulations of electron transfer between redox centers are based on the tunneling current theory [9-10], which had been successfully applied to several systems previously. The theory treats many-electron wavefunctions explicitly by incorporating both the tunneling electron orbitals and the induced polarization of core electrons. Assuming single Slater determinant many-electron wave functions of the donor and acceptor diabatic states, the donor and acceptor tunneling orbitals which carry the tu nneling electron are obtained as biorthogonal donor and acceptor orbitals with the smallest overlap [9, 11]. The rest of the orbitals undergoing induced polarization in the tunneling transition give rise to the electronic Frank-Condon factor [10-11]. The calculations focus on the evaluation of the transition flux between donor | D > and acceptor | A > electronic states,

$$\overrightarrow{J}\left(r\right)=-i\langle A\mid \vec{\widehat{j}}\left(r\right)\mid D\rangle$$ (1)

where $\widehat{j}$ is the quantum flux operator. The coarse-graining of the flux results in so-called interatomic currents J_ab which describe the tunneling flux at the atomic level [10]. The total current through a given atom is proportional to the probability that the tunneling electron passes through it in the tunneling jump from donor to acceptor. Tunneling matrix element T_DA is calculated by using the tunneling flux theorem as the total flux across the dividing plane ∂Ω between the donor and acceptor [9-10],

$$T_{DA}=-\hslash {\int }_{\partial \Omega }(d\overrightarrow{s}\cdot \overrightarrow{J}).$$ (2)

When the donor and acceptor states are represented by single Slater determinant many-electron wave functions, a set of biorthogonal (corresponding) orbitals is obtained by appropriate rotations of the canonical MO's of both states:

$$\begin{array}{cc}\hfill \mid {\Psi }_D\rangle =& \mid {\phi }_{1\alpha }^D\cdots {\phi }_{m\alpha }^D{\phi }_{1\beta }^D\cdots {\phi }_{n\beta }^D\rangle \hfill \\ \hfill \mid {\Psi }_A\rangle =& \mid {\phi }_{1\alpha }^A\cdots {\phi }_{m\alpha }^A{\phi }_{1\beta }^A\cdots {\phi }_{n\beta }^A\rangle \hfill \end{array}$$ (3)

where the overlap matrix of |Ψ_D〉 and is |Ψ_A〉 is diagonal: $\langle {\phi }_{i\sigma }^A\mid {\phi }_{j\sigma }^D\rangle ={\delta }_{ij}{s}_i^{\sigma }$ [12-16].

For proteins the one-electron tunneling (OTE) approximation holds [11], which means that a single pair of the corresponding orbitals with the smallest overlap ($\mid {\phi }_{1\alpha }^A\rangle$ and $\mid {\phi }_{1\alpha }^D\rangle$ when an α-electron tunnels) gives the largest and dominant contribution to the tunneling current, whereas the rest (core orbitals) undergo induced polarization and participate as an electronic Franck–Condon factor [17]. By introducing the atomic basis set, the interatomic currents J_ab employed in this study has the form [11, 18],

$$J_{ab}=\prod _{i\ne 0}{s}_i^{\alpha }\prod _i{s}_i^{\beta }\sum _{\nu \in a}\sum _{\mu \in b}(h_{\nu \mu }-E_0{S}_{\nu \mu })(A_{\mu }{D}_{\nu }-D_{\mu }{A}_{\nu }).$$ (4)

Here v and u are the atomic orbitals of atom a and b ; D_μ and A_v are the expansion coefficients of the donor and aceptor tunneling orbitals, respectively; _vμ are core Hamiltonia and overlap matrix, and E₀ is a tunneling orbital energy defined by

$$E_0=\sum _{\lambda ,\rho }{D}_{\lambda }{\overline{F}}_{\lambda \rho }{D}_{\rho }=\sum _{\lambda ,\rho }{A}_{\lambda }{\overline{F}}_{\lambda \rho }{A}_{\rho }$$ (5)

where F̄_λρ is the Fock matrix. The second equality in Eq. (5) corresponds to the resonance of the donor and acceptor redox potentials, and is achieved by applying a static electric field mimicking the solvation and the protonation of the protein residues in in vivo environment. The total atomic current through an atom a is expressed as

$$J_a^{tot}\equiv \frac{1}{2}\sum _b\mid J_{a,b}\mid$$ (6)

The dynamical average of the tunneling matrix element [19] <T_DA² > is calculated by the statistical renormalization procedure described in Ref. [1] . The electron transfer rates are calculated by using Marcus’ theory [20];

$$k_{ET}=\frac{2\pi }{\hslash }\frac{\langle {T_{DA}}^2\rangle }{\sqrt{4\pi \lambda k_{B}T}}\exp [-\frac{{(\Delta G^0+\lambda )}^2}{4\lambda k_{B}T}],$$ (7)

with a generic reorganization energy λ = 0.5 eV [21-22] and the driving force ΔG = 0 eV [23-24].

To simplify computationally intensive all-electron calculations, a protein pruning procedure was performed for each pair of neighboring Fe/S clusters as describe in Ref. [25]. The resulting pruned systems of N3→N1b and N6b→N2 contain 232 and 214 atoms, respectively. The subsequent BS-ZINDO calculations were performed using Gaussian 03 program [26] as described in [1].

3. Results and Discussion

Clusters N3 and N1b, located in subunit Nqo1 and Nqo3, respectively, have a center-to-center distance of 14.0 Å. Two cysteine ligands (₁Cys³⁵⁶ and ¹Cys³⁵⁹: the prefix indicates subunit number) of N3 are connected by neighboring ₁Thr³⁵⁷ and ₁Pro³⁵⁸ to make a backbone loop (N3-₁Cys³⁵⁶₋₁Thr³⁵⁷₋₁Pro³⁵⁸₋₁Cys³⁵⁹-N3), with ₁Cys³⁵⁶, ₁Thr³⁵⁷ and ₁Pro³⁵⁸ exposed to the subunit boundary of Nqo1 and Nqo3. N1b complex has ₃Cys⁶⁴ cysteine ligand oriented toward N3, of which the amide C=O group together with neighboring ₃Ala⁶³ and ₃Arg⁶⁵ is facing the subunit boundary.

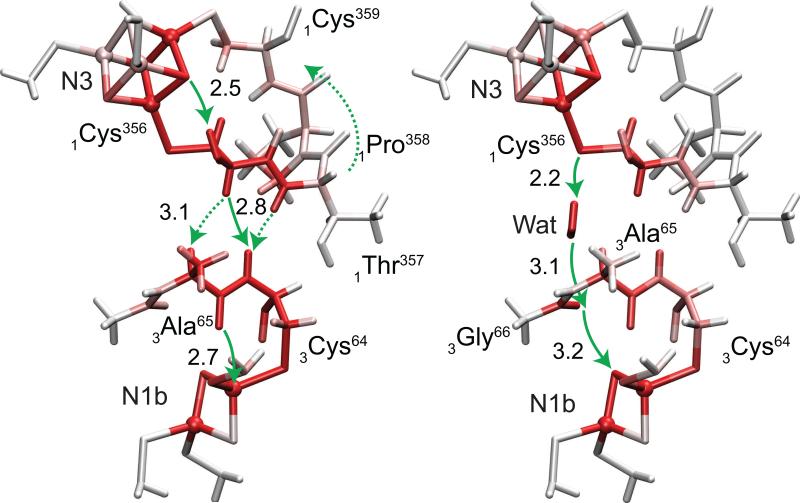
The simulated electron tunneling pathways of N3→N1b with and without the internal water at the subunit boundary are shown in Figure 2. In the system without water, the tunneling current flows from N3 along the backbone loop of ₁Cys³⁵⁶→₁Thr³⁵⁷→₁₁Pro³⁵⁸→₁Cys³⁵⁹ back to N3. A part of the loop current is transmitted from ₁Cys³⁵⁶ and ₁Thr³⁵⁷ to ₃Ala⁶³₋₃Cys₆₄ wire aligned in parallel across the subunit boundary. The main pathway from N3 to N1b is through ₁Cys³⁵⁶ and ₃Cys⁶⁴ with a 2.8 Å through-space jump. When the internal water molecule is present, the tunneling occurs along a new pathway through the water. The electron tunnels from the sulfur atom of ₁Cys³⁵⁶ to the amide oxygen between ₃Ala⁶⁵ and ₃Gly⁶⁶ along the hydrogen bonding network formed with the internal water where two through-space jumps of 2.2 and 3.1 Å are involved. The tunneling electron makes another 3.2 Å through-space jump to reach the sulfur of N1b.

Figure 2.

Electron tunneling pathways of N3→N1b with and without the internal water (left and right panels, respectively). Total atomic currents proportional to probability that the tunneling electron will pass through a given atom (Eq. (6)) is indicated by red color intensity. Through-space jumps are indicated by green arrows with distances in Å.

The total tunneling distance along the trajectory defined as the sum of the bond lengths along the primary path connecting the two gateway atoms of the donor and acceptor [1], the through-space jump distances, and the electron tunneling rate are summarized in Table 1. While the both two tunneling pathways with and without the internal water involve three through-space jumps, the jump distances are slightly longer in the pathway with water with the longest of 3.2 Å instead of 2.8 Å. The tunneling distance along the trajectory of the system with water (11.6 Å) is dramatically shorter than that without water (15.0 Å). The tunneling electron thus prefers to take the pathway of 3.4 Å shorter tunneling distance in expense of a longer distances of through-space jumps (0.4 Å in maximum) when the internal water is present. The drastic enhancement of the tunneling rate due to the internal water (2.2×10³) can be ascribed mainly to the decrease of the total tunneling distance along the trajectory.

Table 1.

Total tunneling distance, through-space jump distances and tunneling rate constant of the processes N3→N1b and N6b→N2 with and without the internal water (Dry and Wet, respectively).

Pair		Tunneling Distance [Å]	Through-Space Jump Distances [Å]			kET [s−1]
N3→N1b	Dry	15.0	2.5	2.8	2.7	1.3×103
	Wet	11.6	2.2	3.1	3.2	2.9×106
N6b→N2	Dry	13.0	3.2	-	2.5	1.9×104
	Wet	13.2	2.2	1.7	2.5	1.8×106

Clusters N6b and N2, located in subunits Nqo9 and Nqo6, respectively, have a distance 13.7 Å. While ₆Cys¹⁴⁰ ligand of N2 is pointing toward N6b being the optimal electronic wire, there is no cystein ligand of N6b pointing to N2. ₉Ile⁹⁹ located in the middle of the donor and acceptor has the optimal Y-shape sec-butyl side chain as a mediator residue [1] with γ-methyl and δ-methyl groups oriented toward N6b and ₆Cys¹⁴⁰, respectively. The internal water at the subunit boundary between Nqo9 and Nqo6 is expected to access close to N6b in sufficiently large space surrounded by N6b, ₉Ile⁹⁹ and basic ₉Arg⁹⁷.

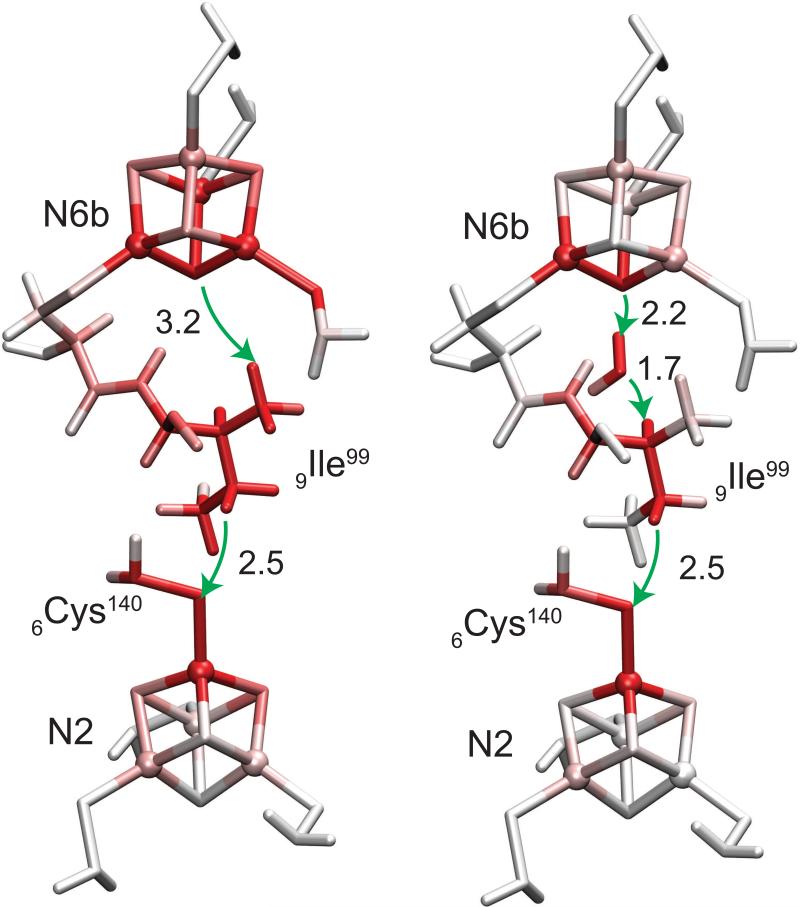
The simulated electron tunneling pathways of N6b→N2 with and without the internal water at the subunit boundary are shown in Figure 3. In the system without the internal water, the tunneling electron first makes a 3.2 Å through-space jump from S2 of N6b to γ-methyl hydrogen of ₉Ile⁹⁹. The electron then follows the alkyl chain of ₉Ile⁹⁹ to the γ-methylene group and makes the second 2.5 Å through-space jump to ₆Cys¹⁴⁰ ligand of N2. In the system with the internal water, the electron tunnels along the hydrogen bonding network formed through the internal water (S2...H-OH...H-C ). Although it requires two through-space jumps for the tunneling electron to reach ₉Ile⁹⁹ residue instead of one without water, the distance of each jump (2.2 and 1.7 Å) is significantly shorter than the distance from S2 to ₉Ile⁹⁹ of 3.2 Å in the system without water. The resulting total tunneling distance along the trajectory of the system with water (13.2 Å) is slightly longer than the system without water (13.0 Å). Overall it is suggested that the tunneling electron prefers to take the pathway with 3 shorter through-space jumps instead of 2 longer through-space jumps even in expense of slightly longer total tunneling distance along the trajectory when the internal water is present. The resulting enhancement of the tunneling rate due to the internal water is about 0.95×10², which can be ascribed to the distance decrease of each through-space jump.

Figure 3.

Electron tunneling pathways of N6b→N2 with and without the internal water (left and right panels, respectively). Total atomic currents proportional to probability that the tunneling electron will pass through a given atom (Eq. (6)) is indicated by red color intensity. Through-space jumps are indicated by green arrows with distances in Å.

4. Conclusions

This study demonstrates that the hydrogen bonding networks formed through the internal water at the protein subunit boundaries can provide efficient electron tunneling pathways of respiratory complex I. The internal water can contribute as a bridge to create a new direct path with significantly shorter total tunneling distance along the trajectory, while without water the tunneling electrons are forced to take detours to avoid large gaps between the boundaries. The internal water can also bridge a gap at subunit boundaries to result in two shorter through-space jumps instead of one longer jump without affecting significantly the total tunneling distance. The resulting enhancement of the rates of the individual electron tunneling process is found drastic by two to three orders of magnitude. It is indicated that the tunneling pathways can change dynamically due to the diffusion of the internal water, and that efficient electron tunneling is driven in optimal positions of the internal water.