Mechanism of long-range proton translocation along biological membranes

Abstract

Recent experiments suggest that protons can travel along biological membranes up to tens of micrometers, but the mechanism of transport is unknown. To explain such a long-range proton translocation we describe a model that takes into account the coupled bulk diffusion that accompanies the migration of protons on the surface. We show that protons diffusing at or near the surface before equilibrating with the bulk desorb and re-adsorb at the surface thousands of times, giving rise to a power-law desorption kinetics. As a result, the decay of the surface protons occurs very slowly, allowing for establishing local gradient and local exchange, as was envisioned in the early local models of biological energy transduction.

Introduction

Proton exchange between proton pumps and ATP synthase plays a key role in biological energy transduction. Despite a half-century-long history of chemiosmotic theory, the exact mechanism of proton transport in the membrane proton circuits still remains a subject of intense debate, rendering the celebrated theory incomplete. The debated issue is the mode of exchange – global or local – as presented by several competing models [1-6].

In the model proposed by Mitchell [1-2], the protons released on the outer side of the membrane by proton pumps equilibrate with the bulk, and it is the equilibrium difference in pH on the two sides of the membrane, along with the membrane potential generated by the proton gradient common for the whole organelle, that act on the ATP synthase. However, as was originally pointed out by Williams [3-4], this mechanism is not most efficient because protons released to the bulk irreversibly lose part of their free energy. In Williams' model, protons always remain inside the membrane, providing for local exchange and ensuring maximum efficiency of energy transduction. However, it was not clear what would keep protons inside the membrane (see Supplementary Material for additional comments). Kell [5] developed an alternative view of local coupling by introducing an interphase, which assumes a barrier between the membrane and the bulk solution and also special pathways of efficient proton lateral movement via chains of “structured” water molecules. Skulachev [6] argued that if the local coupling were true, ATP synthesis would be possible in open systems, which had never been observed. Instead, he combined Mitchell's delocalized mechanism with a local contribution due to highly curved structure of the inner mitochondrial membrane where proton generators and consumers are closely spaced on different sides of cristae. While this type of local coupling may indeed be an essential part to the driving force, Skulachev's argument cannot be used to dismiss the Williams/Kell coupling type, for in open systems the opposite sides of the membrane are not isolated from each other, hence protons can leak between them around the edge [7-8] on the same time-scale or faster than ATP synthase turnover. The easiest way to prevent this is to use a closed membrane isolating inside and outside, as in the original chemiosmotic theory; however, the closed surface by itself does not mean that the coupling is global via equilibrated protons.

Numerous studies of the past two decades [7-24] indicate that the local model is more likely to be realized in real cells. The experiments, while often not unambiguous [23-26], did reveal however a puzzling property of protons migrating along the membrane surface – they appear to remain on the surface for too long, making surface transport surprisingly long-distant, up to tens of micrometers. This long apparent surface dwell-time – up to hundreds of milliseconds – calls for an unusually deep potential well that would keep protons at the surface. A simple estimate by the transition-state theory (TST) gives the potential barrier of about 30 RT for the dwell-time observed. The mechanism of such significant proton affinity to the surface is hard to rationalize. Moreover, as was recently reported [9], the retention time does not appear to depend on the properties of the surface charged groups that could potentially retain the protons, adding to the puzzle. (For further estimates of the barrier and discussion of proton retention at the interface, see Supplementary Material.)

Here we show that the puzzling observations of proton migration on the micrometer scale along the membranes and the retention time up to a second can be explained by taking into account the coupled bulk diffusion which accompanies migration of protons on the surface [14-15]. The apparent long-time retention of protons at the interface surface is not due to a deep potential well or high-pK_a ionized groups, but rather due to compensation of the surface depletion by return of the released protons and their re-adsorption by the surface. This back reaction results in a power-law decay kinetics of the surface protons and explains both their long apparent dwell-time on the surface and corresponding long-distance lateral migration, and their high apparent surface diffusivity.

Results and Discussion

If a surface attracts and retains protons, whatever the microscopic mechanism is, its proton affinity can be characterized by the equilibrium condition

$${\mathrm{\sigma }}_{\text{eq}}=L_0{n}_{\text{eq}},$$ (1)

where σ_eq and n_eq = 10^−pH are equilibrium surface and bulk concentrations and L₀ is the equilibrium constant with dimension of length. As we will see, this is the distance over which surface and bulk protons are coupled. The equilibrium surface concentration can be expressed by equation

$${\mathrm{\sigma }}_{\text{eq}}=n_{\text{eq}}exp(U/RT)d,$$ (2)

where d is the width of the interfacial water layer where the protons are retained and U is the well depth that represents the difference in proton free energies between the bulk and the surface layer (no barrier from the bulk side is assumed). Equation (2) expresses the fact that attraction of protons to surface increases acidity (decreases pH) of the interfacial layer [17]. Combining Eqs. (1) and (2), we derive a formula for the equilibrium constant,

$$L_0=dexp(U/RT).$$ (3)

Assuming d = 1 nm and U = 12 RT, we obtain L₀ = 160 μm. This is the key point where the dimension of micrometer size appears. If the surface retains protons due to ionized groups, then L₀ is expressed in terms of their surface density and pK_a [27-28]; a similar estimate, L₀ = 170 μm, was given [27] for un-buffered solutions. As will be seen below, it is diffusion over this long distance in the bulk that sets the relevant time-scale for proton escape from the surface.

In the above estimates, we used an order-of-magnitude value for d and a median U value of those cited in the Supplementary Material. If we use the lowest barrier, U = 5 RT, and a thinner interfacial layer, d = 0.6 nm, corresponding to two hydrogen bonds, we obtain L₀ = 0.1 μm, which is still macroscopically long and is compatible with experimental data of Heberle et al. [7] and Alexiev et al. [8], where proton diffusion was observed at purple membrane sheets of 0.6 and 0.25 μm, respectively.

The kinetic model is formulated as follows. We consider a typical experimental setup: Excess protons are released on the surface at time t = 0 by a source of finite size r₀ and are observed at a spot on the surface at distance r≫r₀. In order to understand how the excess protons are distributed over the surface and in the bulk, and how this distribution is changing with time, one needs to solve coupled surface and bulk diffusion equations [15] for σ(r,t) and n(r,z,t) (see Methods). The analysis shows that there are two types of long-time decay kinetics of the excess protons on the surface: exponential and power-law, depending on a single parameter ν, see Eq. (6), which is a combination of L₀, the bulk diffusion coefficient D_b, and the desorption rate constant k_off. The two limiting cases are referred to as slow and fast exchange between the surface and bulk protons [27-28]. In these two regimes, the mechanisms of proton transfer along the surface are fundamentally different. Below, we discuss these two limiting cases separately, using simplified models, which demonstrate explicitly the essential points and accurately follow the exact solution [15].

Two populations of excess protons are considered: total surface population p_s(t), i.e. population of the interfacial layer, and total bulk population p_b(t). The interfacial layer has width d, as above. The bulk part can be also considered as a layer whose width is increasing with time owing to diffusion normal to the surface, $L_b(t)\propto \sqrt{D_{b}t}$. The exact analysis shows that $L_b(t)=\sqrt{\pi D_{b}t}$.

The rate with which protons are exchanged between the surface and the bulk can be fast or slow with respect to diffusion. In the fast-exchange regime, thermal equilibrium is established between the two layers at every moment of time (it will be clear later that this is the most realistic case). The two populations are normalized as

$$1=p_s+p_b=p_s+p_s{e}^{-U/RT}(L_b/d),$$ (4)

hence, the total surface population is approximately given by

$$p_s(t)={[1+(L_b(t)/L_0)]}^{-1},$$ (5)

which differs insignificantly from a rigorous equation [15]. The relation between p_s and p_b used in Eq. (4) is determined by the relative energy of the layers, U, and by the number of sub-states in each layer, which is proportional to its size, i.e. d for the surface layer and L_b for the bulk layer. The second term in brackets of Eq. (5) leads to depletion of the surface population with time because of diffusion normal to the surface and resulting increase of L_b. It is clear that the surface population p_s will be half-depleted over the time interval equal to that of diffusion in the bulk over distance L_b = L₀; that is, the effective dwell time will be of the order of $t_0=L_0^2/D_b$. This time is quite long because of large L₀. Obviously, the key here is the fast exchange, i.e. fast forward and back reactions, between layers s and b, compared to the diffusion equilibration time t₀. This condition is equivalent to (see Methods and ref [28])

$$\mathrm{\nu }\equiv k_{\text{off}}{t}_0\gg 1.$$ (6)

Here, we use diffusion coefficient D_b assuming that diffusion normal to surface at the surface layer is of the same order as in the bulk; in fact, there may be some small variations of this parameter [29-30], however, it cannot change the qualitative picture. If we assume diffusion-controlled escape from the surface (the Kramers limit of TST), then the proton hopping time is simply the time d²/D_b needed for a proton to diffuse across the interfacial layer. Multiplying the corresponding rate by the Boltzmann factor and using Eq. (3), we obtain k_off = D_b/L₀d, which results in an approximate estimate (based on D_b = 9.3×10⁻⁵cm²/s and L₀ = 160 μm) $k_{\text{off}}^{-1}=10\mathrm{\mu }\mathrm{s}$ or shorter. A similar estimate is obtained when the protons are retained at the surface by ionized groups [15,27]. We see that, since d≪L₀ by a factor exp(U/RT), the condition of fast equilibrium, Eq. (6), is indeed satisfied with a large margin: For U = 12 and 5 RT used above, we obtain ν ∼ 10⁵ and 10², respectively. Thus, the fast exchange case considered above is most realistic and directly applicable to the membrane systems studied in refs. [7-9].

In the case opposite to Eq. (6), when diffusion is fast and the exchange with the surface is slow, the population of the surface layer mainly decays exponentially with the desorption rate constant k_off,

$$p_s(t)=exp(-k_{\text{off}}t),$$ (7)

no back reaction occurs, and the dwell time is simply $k_{\text{off}}^{-1}$. At very long times, however, the decay asymptotically turns back to the power-law, Eq. (5), see Methods. The exact condition for this exponential decay is ν ≪1. A proton, once left the surface, escapes to the bulk, without returning back to the surface, and hence the surface diffusion decouples from the bulk diffusion. The distance traveled by a proton on the surface during its dwell time $k_{\text{off}}^{-1}$ estimated [15] for unbuffered solutions is $L_s\equiv \sqrt{D_s/k_{\text{off}}}=7-200\text{nm}$. Distance L_s was also estimated [31] to be only a few nanometers, even smaller than this estimate. Thus, the distance traveled by a proton along the surface during its single dwell-time $k_{\text{off}}^{-1}$ is much smaller than that observed in refs. [7-9]. (Moreover, it is even smaller than the size of the initial acid droplet in the Antonenko and Pohl experiments [10], which means that the exponential kinetics could not be observed at all.) As already argued, this limiting case with exponential decay is not applicable to the systems studied in refs. [7-9].

In the fast-exchange regime, quasi-equilibrium between the surface and the adjacent bulk layer is quickly established at every moment of time at each surface point, similar to true equilibrium, Eq. (1),

$$\mathrm{\sigma }(r,t)\equiv L_{0}n(r,0,t).$$ (8)

Now, the surface population decays very slowly, see Eq. (5), with a typical characteristic time constant t₀ = 1 s. This is much longer time than $k_{\text{off}}^{-1}=10\mathrm{\mu }\mathrm{s}$, which means the proton effectively stays on the surface much longer than the single life-time $k_{\text{off}}^{-1}$, and therefore it can travel along the surface much longer distance r than L_s and r₀. However, this mode of transport is not simple diffusion along the surface, because in this case the proton desorbs and returns back to the surface repeatedly. The number of such returns is given by Eq. (6) and is very high. Given our estimate $k_{\text{off}}^{-1}=10\mathrm{\mu }\mathrm{s}$ and t₀ = 1 s (U = 12 RT), we find ν ∼ 10⁵, while for the lower estimate of U = 5 RT, ν ∼ 10². For further discussion of the fast-exchange limit, see Supplementary Material.

The difference between the exponential population decay under slow exchange and power law under fast exchange is illustrated by Fig. 1, which shows the probability p_s(t) to find a proton at the surface in these two regimes. The exact solution of the coupled surface and bulk diffusion equations is shown, which differs insignificantly from the approximate formulas, Eqs. (5) and (7). In the slow-exchange regime, it is simple exponential with a high decay rate constant k_off, whereas in the fast-exchange regime it decays very slowly, according to Eq. (5), illustrating our point that protons can travel much longer distance, on the order of L₀, along the surface via combined surface and bulk diffusion.

Figure 1.

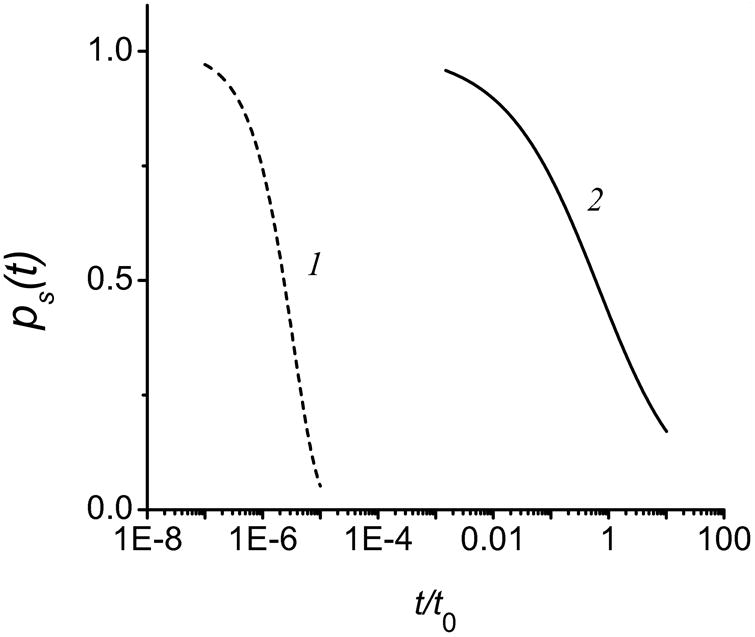
Probability of retention of excess proton at surface. The probability p_s (t) was calculated by the exact equations [15] in the slow (1) and fast (2) exchange regimes (the weak-and strong-coupling cases, respectively). In the slow-exchange regime, protons escape the surface without return, therefore, the decay is exponential and rapid. In the fast-exchange regime, the decay is retarded owing to a high probability of returns.

The actual distribution of the excess protons on the surface and in the bulk can be found by solving coupled bulk-surface diffusion equations [15]. In general, the solution is quite cumbersome, but it can be expressed analytically in the case of equal surface and bulk diffusivities, D_s=D_b, which is useful for present discussion. For the surface proton density, it reads

$$\mathrm{\sigma }(r,t)=\frac{A}{\pi (4D_{s}t+r_0^2)}exp(-\frac{r^2}{4D_{s}t+r_0^2})p_s(t),$$ (9)

where A is normalization constant and p_s(t) is given by Eqs. (5) or (7) for the fast- and slow-exchange regimes, respectively. The bulk excess proton density n(r,z,t) can be found numerically. The predictions of Eq. (9) for the kinetics to be observed are reviewed in Supplementary Material.

The numerical solution n(r,z,t) of the coupled surface and bulk diffusion equations demonstrates the behavior shown in Fig. 2 for the fast-exchange case. In the figure, full lines are bulk proton concentrations at three observation points located near the surface (line 1) and deeply in the bulk (lines 4 and 5), at distances $\mathrm{\rho }\equiv \sqrt{r^2+z^2}=0.25L_0$ away from the acid-injection point (i.e. inside the L₀ area). It is seen that the signal maximum arrives at the three points nearly simultaneously (the different arrival times are possible when D_s ≠ D_b). For comparison, two limiting forms of the signal at surface (r = 0.25L₀, z = 0) are shown: One corresponds to L₀ → ∞ (line 2, the 2D diffusion at all times), the other to L₀→0 (line 3, the 3D diffusion at all times). Before and near the maximum, which occurs at t < t₀, the signal has the 2D shape, both on the surface and in the bulk, but acquires the 3D shape at t > t₀.

Figure 2.

The time dependence of excess bulk proton concentration. The concentration n(r,z,t) was calculated at three observation points r,z at equal distances ρ = 0.25L₀ from acid-injection point. The strong-coupling case with equal diffusion coefficients, D_s = D_b was assumed. Solid line 1, r = ρ, z = 0; dotted line 2 and dashed line 3, the 2D and 3D limiting forms of line 1, respectively; solid lines 4 and 5, r = z = ρ/√2 and r = 0, z = ρ, respectively. All curves are normalized to a given number of protons injected at t = 0 inside a hemisphere of radius r₀=1μm around the coordinate origin. The signals at three observation points (solid lines) all have the 2D shape (line 2) at t < t₀, and they all approach the 3D shape (line 3) at t > t₀. The surface proton concentration σ(r,t) is given by Eq. (8).

On the other hand, if the observation point is located outside the L₀ area, the signal has the 3D shape, independently of whether it is observed in the bulk or on the surface.

In general, the surface diffusivity is expected to be smaller than the bulk one in unbuffered solutions, D_s < D_b, because of restrictions imposed by surface on proton movement. The model of coupled surface-bulk diffusion predicts complicated kinetics [14-15] with an apparent surface diffusivity intermediate between the surface and the bulk because protons move alternatively along the surface and through the bulk. Thus, the model predicts high apparent diffusivity in lateral direction even when the generic surface diffusivity is low.

The effect of pH buffer and further implications for theory and experiment are briefly discussed in Supplementary Information. It is also instructive to contrast our model with the theoretical treatment by Agmon and Gutman [13] of the kinetic data of Springer et al. [9], which assumed the exponential kinetics but with very small effective rate constant k₁ ∼1 s^-1; the smallness of k₁ assumes a deep potential well near the surface of unknown nature. We find the data can be well fit with the power-law kinetics of the present theory (see Supplementary Material) without invoking deep potential well at interface required in the exponential kinetics model.

Summarizing, our analysis shows that the kinetics of proton desorption from the interface surface is not exponential but rather is a slow power law. This explains both the apparent long dwell-time and related long-distance translocation along the surface with high diffusivity observed in refs. [7-9].

The implications for bioenergetics are significant: If average distance between the source and the drain, i.e. proton pumps and ATP synthase, is less than L₀, which is obviously the case given the density of respiratory components in mitochondrial and bacterial membranes [2], the protons may not necessarily equilibrate with the bulk during their circulation in the membrane respiratory system simply because equilibration time t₀ is too long – of the order of a second; instead, near the surface a stationary distribution of protons develops, so that the local pH near the surface can be much lower than that in the bulk. As a result, more protons are available at the membrane surface. The membrane protons, and those in the surface layer L_b, can directly be transferred from the source to the drain, conserving part of their free energy that would be lost should the protons be equilibrated with the bulk. The actual parameters of this non-equilibrium stationary distribution would be interesting to elucidate in the future investigations.

The above conclusion is directly related to the “Pacific Ocean” argument of Williams in the historic discussion of local vs global modes of the coupling [3]. His point was that part of the energy is lost in equilibration, hence local coupling is preferred. We can now see that in reality the equilibration does not occur on the time scale of ATP synthesis because the full equilibration time t₀ is immensely long. We estimated it to be about 1 s in both unbuffered and buffered solutions [15].

The key that explains the relatively slow process of proton equilibration - and resulting long-distance proton migration – is 1D nature of the diffusive equilibration process: Protons can only move in one dimension, normal to the surface, to get away from it, but the diffusion in one dimension is slow. The density of desorbed protons falls off with time in the equilibration process only as t^−1/2, instead of much faster 3D version t^−3/2, or exponentially, as was assumed previously. This slow, restricted-dimensionality equilibration keeps the protons near the surface for very long time, preventing loss of their free energy (due to entropy increase upon equilibration), and thereby increasing the efficiency of energy transduction upon their back-flow through ATP synthase, as was envisioned in the early Williams [3-4] and Kell [5] local versions of chemiosmotic theory.

Methods

The model is specified by two diffusion equations for bulk and surface proton number densities, n(x,y,z,t) and σ(x,y,t), respectively,

$$\frac{\partial n}{\partial t}=D_b(\frac{{\partial }^{2}n}{\partial x^2}+\frac{{\partial }^{2}n}{\partial y^2}+\frac{{\partial }^{2}n}{\partial z^2}),z>0,$$ (10)

$$\frac{\partial \mathrm{\sigma }}{\partial t}=D_s(\frac{{\partial }^2\mathrm{\sigma }}{\partial x^2}+\frac{{\partial }^2\mathrm{\sigma }}{\partial y^2})+k_{\text{off}}(L_{0}n-\mathrm{\sigma }),z=0,$$ (11)

where x,y are coordinates at surface and z is the one normal to it, D_b and D_s are diffusion coefficients, k_off and k_offL₀ are constants of proton dissociation and association. At t = 0, acid droplet in the form of Gaussian hemisphere with effective radius r₀ is injected at the coordinate origin, and the signal is observed at a point r,z, where r is distance from the proton source at the surface. Owing to cylindrical symmetry, the proton densities are written as n(r,z,t) and σ(r,t). These functions are shown in Eq. (9) and Fig. 2.

The transition between the exponential population decay, Eq. (7), and the power law, Eq. (5), can be explicitly derived by solving the 1D diffusion equation with back reaction [32], which follows from Eq. (11) integrated over the membrane plane,

$${\dot{p}}_s(t)=-k_{\text{off}}{p}_s(t)+k_{\text{off}}{L}_0{P}_b(0,t),$$ (12)

where p_s(t) and P_b(z,t) are integrated densities. The exact solution can be obtained by the Laplace transform; however, it is more revealing to use an approximation. If we assume that the number of bulk protons near the surface is proportional to the number of protons released [32], and that it is diluted by the width of the bulk layer, then

$$P_b(0,t)=\frac{1-p_s(t)}{L_b(t)}.$$ (13)

Inserting this into Eq. (12) gives a closed equation easy to solve. The solution critically depends on parameter ν, Eq. (6). The population decays exponentially at short times and by a power law at long times; the power law dominates practically at all times in the fast-exchange regime ν ≫1 whereas the exponential law dominates in the opposite regime, ν ≤ 1.

Highlights.

• Long-range lateral proton translocation is due to accompanying bulk diffusion.

• Protons diffuse alternatively along surface and in bulk.

• Protons desorb and re-adsorb at surface many times before equilibrating with bulk.

• Surface depletion is compensated by return of the released protons.

• Surface protons decay very slowly, allowing for local coupling.

Abbreviations

TST

transition-state theory