The relationship of leaf photosynthetic traits – V_cmax and J_max – to leaf nitrogen, leaf phosphorus, and specific leaf area: a meta-analysis and modeling study

Abstract

Great uncertainty exists in the global exchange of carbon between the atmosphere and the terrestrial biosphere. An important source of this uncertainty lies in the dependency of photosynthesis on the maximum rate of carboxylation (V_cmax) and the maximum rate of electron transport (J_max). Understanding and making accurate prediction of C fluxes thus requires accurate characterization of these rates and their relationship with plant nutrient status over large geographic scales. Plant nutrient status is indicated by the traits: leaf nitrogen (N), leaf phosphorus (P), and specific leaf area (SLA). Correlations between V_cmax and J_max and leaf nitrogen (N) are typically derived from local to global scales, while correlations with leaf phosphorus (P) and specific leaf area (SLA) have typically been derived at a local scale. Thus, there is no global-scale relationship between V_cmax and J_max and P or SLA limiting the ability of global-scale carbon flux models do not account for P or SLA. We gathered published data from 24 studies to reveal global relationships of V_cmax and J_max with leaf N, P, and SLA. V_cmax was strongly related to leaf N, and increasing leaf P substantially increased the sensitivity of V_cmax to leaf N. J_max was strongly related to V_cmax, and neither leaf N, P, or SLA had a substantial impact on the relationship. Although more data are needed to expand the applicability of the relationship, we show leaf P is a globally important determinant of photosynthetic rates. In a model of photosynthesis, we showed that at high leaf N (3 gm⁻²), increasing leaf P from 0.05 to 0.22 gm⁻² nearly doubled assimilation rates. Finally, we show that plants may employ a conservative strategy of J_max to V_cmax coordination that restricts photoinhibition when carboxylation is limiting at the expense of maximizing photosynthetic rates when light is limiting.

Introduction

Photosynthesis is the proximal driver of the carbon cycle (Canadell et al. 2007; Cadule et al. 2010) and is thus a core driver of carbon flux and central to carbon cycle models (e.g., Woodward et al. 1995; Cox 2001; Sitch et al. 2003; Zaehle and Friend 2010; Bonan et al. 2011). Enzyme kinetic models of leaf photosynthesis (Farquhar et al. 1980; described below) are typically embedded in global carbon cycle models to mechanistically reflect plant physiological responses to atmospheric CO₂. The Farquhar et al. (1980) photosynthetic submodel and its subsequent variants (Von Caemmerer and Farquhar 1981; Farquhar and Wong 1984; Collatz et al. 1991; Harley et al. 1992) are at the heart of almost all land surface models of carbon flux, several ecosystem dynamic models, and dynamic global vegetation models. We hereafter refer to these global land surface, ecosystem, and vegetation models as terrestrial biosphere models (TBMs).

Simulated photosynthetic rates in TBMs are highly sensitive to V_cmax and J_max (Zaehle et al. 2005; Bonan et al. 2011; Verheijen et al. 2012), the maximum rate parameters of enzyme kinetic processes driving photosynthesis. Accuracy in these parameters is central to an effective photosynthetic submodel in the TBMs. Theory and empirical data suggest that these photosynthetic rates scale with leaf nitrogen (N) via the large amount of leaf N invested in the ribulose 1-5-bisphosphate oxygenase/carboxylase (RuBisCO) protein, and phosphorus (P) availability influences many aspects of plant physiology central to photosynthesis, including membrane solubility, ATP, and NADPH production (Marschner 1995; Taiz and Zeiger 2010). V_cmax and J_max have also been linked to structural leaf traits via specific leaf area (SLA). Theory and data (Kattge et al. 2009; Domingues et al. 2010; Cernusak et al. 2011) clearly suggest mechanistic links between V_cmax, J_max, and several functional plant traits that correlate with photosynthetic biochemistry.

Accurate simulation of plant physiological responses to atmospheric CO₂ in TBMs thus requires data on how V_cmax and J_max scale with plant traits N, P, and SLA accounting for the immense species-specific and regional variation in availability of N and P and subsequent variation in leaf N, P, and SLA.

Here, we provide a global assessment of the relationship between V_cmax and J_max and leaf N, P, and SLA, drawing on estimates made on 356 species around the world.

When do V_cmax and J_max variation matter?

TBMs typically assign a single, fixed V_cmax or J_max parameter value (Rogers 2014) to each plant functional type (PFT). Scaling from plant to ecosystem or globe is achieved via PFT distribution maps. Recently, however, the predictive performance of such models has improved by allowing parameter values to vary. For example, at sites of the FLUXNET network where high-resolution data exist on all parameters and rates, predictive performance improved when V_cmax and J_max were allowed to vary interannually (Groenendijk et al. 2011). Additionally, some TBMs improve prediction by simulating leaf nitrogen as part of the model and specify a linear relationship between V_cmax and leaf N (e.g., Woodward et al. 1995), defined for each PFT (Kattge et al. 2009). Finally, Mercado et al. (2011) demonstrated considerable improvements to model predictions of carbon fluxes in the Amazon when leaf P was taken into account.

Empirically, there is also a strong relationship between J_max and V_cmax (Wullschleger 1993; Beerling and Quick 1995), and most TBMs simulate J_max as a linear function of V_cmax. However, this assumption could be erroneous because the correlation between J_max and V_cmax is likely to be influenced by leaf N, P, and SLA. The coordination hypothesis of photosynthetic resource allocation (Chen et al. 1993) states that the Calvin–Benson cycle limited rate of assimilation (W_c, see below) equals the electron transport-limited rate of assimilation (W_j). The relationship between J_max and V_cmax affects the relationship between W_c and W_j and may reflect coordination of these two rate-limiting biochemical cycles. When carboxylation is limiting photosynthesis, high investment in J_max relative to V_cmax would lead to electron transport not used in photosynthesis requiring dissipation of that energy to avoid photoinhibition (Powles 1984; Krause et al. 2012). However, when light is limiting photosynthesis, high investment in J_max relative to V_cmax would maximize photosynthetic rates. Therefore, a trade-off exists in high investment in J_max relative to V_cmax whereby the marginal benefit to photosynthetic rates when light is limiting is offset by the cost of energy dissipation when carboxylation is limiting.

Moving forward: global variation in V_cmax and J_max as a function of N, P, and SLA

As noted above, we make here a global assessment of the relationship between V_cmax and J_max and leaf N, P, and SLA, drawing on estimates made on 356 species by treatment combinations around the world from 24 different studies. We used these data to test several hypotheses. First, we hypothesized that leaf P will modify the relationship of V_cmax to leaf N. Second, we hypothesized that leaf P will modify the relationship of J_max to V_cmax. Third, drawing on the coordination hypothesis of photosynthetic resource allocation, we predict that the relationship between J_max and V_cmax results from efficient resource investment in J_max reflecting the trade-off between photosynthetic gain and costs of energy dissipation.

To test our hypotheses, we combine a global meta-analysis of the relationships of V_cmax and J_max with N, P, and SLA and then examine the consequences of these patterns in a leaf photosynthesis model. Combined, our effort offers a global-scale definition of V_cmax and J_max variation in relation to leaf-trait variation and provides an empirical alternative to single value PFT scaling or the type of tuned relationships presented above in global TBMs. Our empirical representation of V_cmax and J_max should lead to improved simulation of carbon fluxes across multiple scales.

Materials and Methods

Literature review & data collection

In September 2012, we searched the Thompson Reuters Web of Science database for “photosynthesis” or “carboxylation” and either “N,” “P,” or “SLA” and similar related search terms. The aim was to find papers that had simultaneously measured as many of the following leaf traits: V_cmax, J_max, leaf N, leaf P, and specific leaf area (SLA) or leaf mass-to-area ratio (LMA). Data were copied from tables or digitized from graphics using Grab It! (Datatrend Software 2008). Minimum requirements for inclusion in this study were that either V_cmax or J_max were calculated from A/C_i curves along with two of the other three leaf traits, yielding data from 24 papers and 135 species x location combinations, distributed globally (Tables 1 and S1). Some of these data were collected on plants in their natural environment and subject to natural environmental variation, while other data were collected on laboratory-grown plants (mostly tree species) subjected to experimental treatments. The majority of the species used in the greenhouses and laboratories were native to the area of the research center. Either species means or treatment means were collected leading to a dataset of 356 species/treatment combinations. The data can be downloaded from the ORNL DAAC (http://dx.doi.org/10.3334/ORNLDAAC/1224).

Table 1.

Sources of data collected for the meta-analysis and associated information including location, number of species and any experimental treatment

Reference	Number of species	PFT*	Longitude (°E)	Latitude (°N)	Elevation (m)	Location	Country	Experiment	N	P
Aranda et al. (2005)	1	Temp Ev Bl	−3.43	39.23	650	Alburquerque	Spain	Light*water	Y	N
Bauer et al. (2001)	6	Temp Dc Bl and Ev Nl	−71.03	42.21	40	Havard forest	USA	CO2*N	Y	N
Bown et al. (2007)	1	Temp Ev Nl	176.13	−38.26	600	Purokohukohu Experimental Basin	NZ	N*P	Y	Y
Brück and Guo (2006)	1	Temp legume crop	10.08	54.19	40	Kiel	Germany	NH4 vs. NO3	Y	N
Calfapietra (2005)	1	Temp Dc Bl	11.48	42.22	150	Viterbo	Italy	CO2*N canopy level	Y	N
Carswell et al. (2005)	4	Temp Dc Bl and Ev Nl	170.3	−43.2	90	Okarito	NZ	N*P	Y	Y
Cernusak et al. (2011)	2	Trop Ev Bl	139.56	−22.59	150	Boulia	Australia	None	Y	Y
Cernusak et al. (2011)	2	“	133.19	−17.07	230	Sturt plains	Australia	None	Y	Y
Cernusak et al. (2011)	2	“	132.22	−15.15	170	Dry creek	Australia	None	Y	Y
Cernusak et al. (2011)	2	“	131.23	−14.09	70	Daly river	Australia	None	Y	Y
Cernusak et al. (2011)	2	“	131.07	−13.04	80	Adelaide river	Australia	None	Y	Y
Cernusak et al. (2011)	2	“	131.08	−12.29	40	Howard springs	Australia	None	Y	Y
Deng (2004)	2	Sub-trop forb	113.17	23.08	10	Guanzhou	China	None	Y	N
Domingues et al. (2010)	3	Trop Dc Bl	−1.5	15.34	280–300	Hombori	Mali	None	Y	Y
Domingues et al. (2010)	7	“	−1.17	12.73	250	Bissiga	Burkina Faso	None	Y	Y
Domingues et al. (2010)	8	“	−3.15	10.94	300	Dano	Burkina Faso	None	Y	Y
Domingues et al. (2010)	5	“	−1.86	9.3	370	Mole	Ghana	None	Y	Y
Domingues et al. (2010)	8	“	−1.18	7.3	170	Kogye	Ghana	None	Y	Y
Domingues et al. (2010)	21	Trop Dc Bl and Ev Bl	−1.7	7.72	200	Boabeng Fiame	Ghana	None	Y	Y
Domingues et al. (2010)	4	“	−2.45	7.14	25	Asukese	Ghana	None	Y	Y
Grassi (2002)	1	Sub-trop Ev Bl	149.07	−35.18	600	Canberra	Australia	N	Y	N
Han et al. (2008)	1	Temp Ev Nl	138.8	35.45	1030	Canberra	Australia	N	Y	N
Katahata et al. (2007)	1	Ev shrub	138.4	36.51	900	Niigata	Japan	Light*leaf age	Y	N
Kubiske (2002)	2	Temp Bl Dc	−84.04	45.33	215	Pellston	USA	N* CO2*light	Y	N
Manter (2005)	1	Temp Ev Nl	−122.4	45.31	75	Portland	USA	N	Y	N
Merilo et al. (2006)	2	Temp Ev Nl	26.55	58.42	65	Saare	Estonia	Light	Y	N
Midgley et al. (1999)	4	Temp Ev shrub	20	−34.5	120	Cape Agulhas	SA	CO2*N&P	Y	N
Porte and Lousteau (1998)	1	Temp Ev Nl	−0.46	44.42	60	Bordeaux	France	Leaf age*canopy level	Y	Y
Rodriguez-Calcerrada et al. (2008)	2	Temp Dc Bl	−3.3	41.07	50	Madrid	Spain	Light	Y	N
Sholtis (2004)	1	Temp Dc Bl	−84.2	35.54	230	Oak Ridge	USA	CO2*canopy level	Y	N
Tissue et al. (2005)	3	Temp Ev Nl and Bl Dc	170.3	−43.2	50	Okarito forest south Westland	NZ	Canopy level	Y	Y
Turnbull et al. (2007)	1	Temp Ev Bl	142.05	−37.03	470	Ballarat	Australia	Defoliation	Y	Y
Warren (2004)	1	Temp Ev Bl	143.53	−37.25	450	Creswick	Australia	N	Y	N
Watanabe et al. (2011)	1	Temp Dc Nl	141	43	180	Asapporo	Japan	CO2*N	Y	Y
Wohlfahrt et al. (1999a)	28	Temp C3 grass and forb	11.01	46.01	1540–1900	Monte Bondone	Estern Alps	None	Y	N
Zhang and Dang (2006)	1	Temp Dc Bl	89.14	48.22	200	Ontario	Canada	CO2*age	N	Y
Additional datasets
TRY – Kattge et al. (2011)	1048
Wullschleger (1993)	110

^*PFT abbreviations: Temp, temperate; Trop, tropical; Ev, evergreen; Dc, deciduous; Nl, needleleaf tree; Bl, broadleaf tree.

V_cmax and J_max are calculated by fitting equations 1 and 2, or 1,3, and 4 to sections of the A/C_i curve (Von Caemmerer and Farquhar 1981; Sharkey et al. 2007), and these calculations are sensitive to the kinetic parameters, K_c and K_o and to Γ_*, used in the fitting process (Medlyn et al. 2002). Using a method (detailed in Appendix S1) similar to Kattge and Knorr (2007), we removed the variation in V_cmax and J_max across studies caused by different parametric assumptions by standardizing V_cmax and J_max to a common set of kinetic parameters (derived by Bernacchi et al. 2001). We also corrected V_cmax and J_max to a common measurement temperature of 25°C and to the O₂ partial pressure at the measurement elevation. Errors introduced by the standardization were well within the measurement error of A/C_i curves (Appendix S2). Standardizing for the kinetic parameters had a substantial impact on V_cmax and to a lesser extent J_max (Figure S1), as observed by Kattge et al. (2009). Standardization for O₂ partial pressure decreases with altitude had a small impact on values taken from plants growing at altitudes up to 2000 m (Figure S2).

We related J_max and V_cmax such that:

(1)

where b_jv is the slope of the relationship and a_jv the intercept. Gu et al. (2010) demonstrated a method-specific bias on b_jv (on non-log-transformed variables) caused by predetermination of the limitation state of points on the A/C_i. However, most authors in this meta-analysis used a fitting procedure which removed points that were potentially either limitation state (Wullschleger 1993; Sharkey et al. 2007) which minimizes potential biases in b_jv.

Where LMA was reported, we converted to SLA by taking the reciprocal of LMA. While this introduced some error (the reciprocal of the mean of a set of values does not equal the mean of the reciprocals of that set), the error was distributed across the whole range of SLA so was unlikely to have biased the effect of SLA. To compare the J_max to V_cmax relationship from our dataset, we also used V_cmax and J_max data from Wullschleger (1993) and the TRY database (Kattge et al. 2011; data from Atkin et al. 1997; Kattge et al. 2009). V_cmax and J_max are measured on a leaf area basis, and in models of photosynthesis, area-based measurement integrates these parameters with light capture. Therefore, we restricted our analysis to leaf-area-based measurements.

Statistical analysis

To assess the importance of P and SLA as covariates with leaf N in determining V_cmax and J_max, we developed multiple regressions of V_cmax or J_max as the dependent variable and leaf N, leaf P, and SLA as the independent variables. To increase sample size and increase the range of each variable, we also developed multiple regressions of V_cmax or J_max against leaf N and either SLA or leaf P. In the analysis of J_max, we also included V_cmax as an independent variable based on our hypothesis that W_c and W_j are coordinated via the J_max to V_cmax relationship. We used linear mixed-model regression framework with leaf traits as fixed effects and the author of the paper from which the data were collected as the random effect (Ordonez et al. 2009). Including the study author as a random effect in the regression model accounted for the nonindependence of data within a study. We were unable to account for differential accuracy between studies, often measured by sampling variance or sample size in meta-analysis, and therefore did not weight the data. All variables were natural-log-transformed to ensure normality of residuals.

Similar to all meta-analyses (Gurevitch and Hedges 1999), there is likely to be some error introduced by the different methods used by the different research groups, but the standardization method and the mixed-model analysis with study group as the random effect will have minimized this error.

All statistical analyses were carried out using the open-source software package R, version 2.13.0 (R Core Development Team 2011). We employed a backward, stepwise, AIC-based model simplification process. Our maximal models contained 3-way interactions for V_cmax (and all 2-way interactions in the models with two independent variables) and J_max and were fit with the “lme” function of the “nlme” library (Pinheiro et al. 2011). Models were then simplified using the “dropterm” function of the “MASS” library to conserve marginality (see Venables and Ripley 2002). Model selection aimed to find the minimum adequate model – the model explaining the most variation in the dependent variable with minimum necessary parameters. Model selection was based on the model with the lowest corrected Akaike information criterion (AICc) and with a significance level of each model term of P < 0.1, subject to conservation of marginality. The AIC is a relative measure of competing models' likelihood penalized by the number of parameters fit by the model, and the AICc is the AIC when corrected for finite sample size (Burnham and Anderson 2002). Given a set of competing models, the model with the lowest AICc can be considered the preferred model (the minimum adequate model).

We report the likelihood ratio test (LRT) statistic between a model and an intercept only (i.e., only random effects) null model and calculated model significance P-values using the chi-square distribution. As there is no mixed-model method to estimate variance in the dependent variable explained by the model, we report the proportional decrease in the residual variance in the minimum adequate model compared with the null, random effects only, model as a metric of explained variance (Xu 2003).

Models were checked for violation of the assumptions of mixed-model linear regression (homoscedasticity of residuals; normal distribution of residuals within the random groups and that observed values of the dependent variable bore a linear relationship to model fitted values), and all minimum adequate models satisfied these checks (a comparison of model assumptions when using nontransformed and transformed data are presented in Appendix S3).

Modeling carbon assimilation

After Medlyn et al. (2002) and Kattge and Knorr (2007), carbon assimilation was modeled using the Farquhar et al. (1980) biochemical model for perfectly coupled electron transport and the Calvin–Benson cycle, as reported in Medlyn et al. (2002). Enzyme kinetic models of photosynthesis (Farquhar et al. 1980) simulate net CO₂ assimilation (A) as the minimum of the RuBisCO-limited gross carboxylation rate (W_c) and the electron transport-limited gross carboxylation rate (W_j), scaled to account for photorespiration, minus mitochondrial (dark) respiration (R_d). The net assimilation function takes the form:

(2)

where Γ_* is the CO₂ compensation point (Pa), the C_i at which the carboxylation rate is balanced by CO₂ release from oxygenation. Both W_c and W_j are modeled as functions of the intercellular CO₂ partial pressure (C_i − Pa). W_c follows a Michaelis–Menten function of C_i in which V_cmax (μmol CO₂ m⁻²·s⁻¹) determines the asymptote:

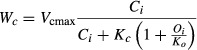(3)

where O_i is the intercellular O₂ partial pressure (kPa); K_c and K_o are the Michaelis–Menten constants of RuBisCO for CO₂ (Pa) and for O₂ (kPa). The light-limited gross carboxylation rate (W_j) is a function of the electron transport rate (J - μmol·e·m⁻²·s⁻¹) following a similar function of C_i where the asymptote is proportional to J:

J is a function of incident photosynthetically active radiation (I – μmol photons m⁻²·s⁻¹) that saturates at the maximum rate of electron transport (J_max), formulated by Harley et al. (1992) following Smith (1937), though other formulations exist:

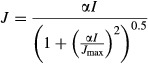where α is the apparent quantum yield of electron transport (assumed to be 0.24 mol electrons mol⁻¹ photons by Harley et al. (1992) although α is not invariant in nature) and is the result of multiplying the true quantum yield and light absorption by the leaf. By determining the asymptotes of the two rate-limiting cycles of photosynthesis, it is clear from the above set of equations that carbon assimilation is highly sensitive to V_cmax and J_max.

Temperature sensitivities of V_cmax and J_max were simulated using the modified Arrhenius equation of Johnson et al. (1942), see Medlyn et al. (2002). For consistency with the temperature sensitivity functions of V_cmax and J_max (see Medlyn et al. 2002), the temperature sensitivities of the kinetic properties of RuBisCO and the CO₂ compensation point in the absence of dark respiration were modeled after Bernacchi et al. (2001). See Appendix S4 for further details.

Coefficients of the equations relating V_cmax to leaf N and J_max to V_cmax were taken from the models presented in Table 3. The impact of P and SLA on assimilation was simulated by predicting V_cmax using the 5th and 95th percentile of either P (0.05 and 0.22 mg·g⁻¹) or SLA (adjusted to provide realistic combinations of SLA and leaf N 0.01 m²·g⁻¹ and 0.025 m²·g⁻¹) from our database. The biophysical space over which carbon assimilation was simulated was PAR ranging from 0 to 1500 μmol·m⁻²·s⁻¹, internal CO₂ partial pressure of 30 Pa, at two levels of leaf N (0.5 and 3 g·m⁻²) and at a temperature of 25°C.

Table 3.

Details of the recommended minimum adequate models (MAM) explaining V_cmax and J_max. All traits were expressed on an area basis and were natural-log-transformed. The LRT was the likelihood ratio test statistic of the model against the null (intercept only) model, and the residual variance reduction was the proportional reduction in residual variance when compared to the null model. A colon represents the interaction between two variables. Using the example of model 1, the equation describing V_cmax would take the form: ln(V_cmax) = 1.993 + 2.555ln(N) − 0.372ln(SLA) + 0.422ln(N)ln(SLA)

	Response trait	Explanatory traits of the maximal model1	Explanatory variables of the MAM	Coefficient	SE	df	Student's t-test	P	N obs	N groups	Residual variance reduction (%)	LRT	P-value
Model 1	Vcmax	N, P	Intercept	3.946	0.229	99	17.26	<0.001	110	8	19.5	25.5	<0.001
			N	0.921	0.301	99	3.06	0.003
			P	0.121	0.085	99	1.42	0.156
			N:P	0.282	0.145	99	1.95	0.054
Model 2	Vcmax	N, SLA	Intercept	1.993	0.410	237	4.86	<0.001	260	20	36.6	99.1	<0.001
			N	2.555	0.522	237	4.89	<0.001
			SLA	-0.372	0.093	237	-4.00	<0.001
			N:SLA	0.422	0.115	237	3.67	<0.001
Model 3	Jmax	Vcmax, N, P	Intercept	1.246	0.233	96	5.33	<0.001	105	7	83.5	189.1	<0.001
			Vcmax	0.886	0.043	96	20.60	<0.001
			P	0.089	0.041	96	2.20	0.033
Model 4	Jmax	Vcmax, N, SLA	Intercept	1.197	0.115	215	10.45	<0.001	235	17	84.2	416.1	<0.001
			Vcmax	0.847	0.025	215	34.23	<0.001

¹Including all combinations of interactions between each trait.

To simulate the sensitivity of carbon assimilation to the J_max to V_cmax slope, the model was driven with a full range of photosynthetically active radiation (PAR, 0–1500 μmol·m⁻²·s⁻¹) and three levels of V_cmax (25, 50 & 90 μmol·m⁻²·s⁻¹). For simplicity, we only simulated the sensitivity at 25°C, acknowledging that temperature is also an important factor determining the sensitivity of assimilation to the J_max to V_cmax slope.

Results

V_cmax and J_max in relation to leaf N, leaf P, and SLA

The most likely model, that is, the minimum adequate model, when V_cmax was regressed on all three leaf traits together (leaf N, P, and SLA) was the model with SLA as the only explanatory variable (see Table S2). However, there were less data available for this analysis (n = 90, over 50% of which came from a single study), and as a consequence, the range of leaf N and SLA values were restricted compared with their range in the trivariate models discussed below. For this reason, we present no further discussion of V_cmax regressed on leaf N, leaf P, and SLA. For J_max regressed on V_cmax, leaf N, leaf P, and SLA, the minimum adequate model was of J_max regressed only on V_cmax and leaf P with no interaction (see Table S2). With increased range in the explanatory variables, we focus on the models with one less explanatory variable.

For V_cmax regressed against leaf N and either leaf P or SLA, the minimum adequate models were also the maximal models – those with both traits and their interaction (Table 2; models 1 and 2). Models of V_cmax regressed on leaf N and either SLA or leaf P were both highly significantly different from the null (intercept and random effects only) model (P < 0.001).

Table 2.

Model selection table for multiple regressions of V_cmax and J_max regressed against leaf N, or leaf N and V_cmax respectively, and in combination with either leaf P or SLA. The minimum adequate model (MAM) was the model with the lowest AICc. All traits were expressed on a leaf area basis and were natural-log-transformed

Response trait	Model	Model explanatory variables1	Residual variance reduction (%)	AICc
Vcmax	Maximal model, MAM – Model 1	N, P, N:P	19.5	44.2
		N, P	16.6	45.8
		N	13.5	47.7
		P	6.5	56.9
Vcmax	Maximal model, MAM – Model 2	N, SLA, N:SLA	36.6	174.6
		N, SLA	32.5	185.7
		N	30.2	187.8
		SLA	12.3	248.4
Jmax	Maximal model	Vcmax, N, P, all 2-way interactions, 3-way interaction	83.6	−115.6
		Vcmax, N, P, all 2-way interactions	83.6	−117.9
		Vcmax, N, P, Vcmax:N, N:P	83.4	−118.9
		Vcmax, N, P, Vcmax:N	83.4	−120.1
		Vcmax, N, P	83.4	−121.4
	MAM – Model 3	Vcmax, P	83.5	−123.2
		Vcmax, P, Vcmax:P	83.5	−121.2
		Vcmax	82.9	−120.8
		N	10.4	49.3
		P	12.5	46.2
Jmax	Maximal model	Vcmax, N, SLA, all 2-way interactions, 3-way interaction	85.1	−196.2
		Vcmax, N, SLA, all 2-way interactions	84.7	−193.7
		Vcmax, N, SLA, Vcmax:N, Vcmax:SLA	84.7	−195.3
		Vcmax, N, SLA, Vcmax:SLA	84.6	−194.5
		Vcmax, SLA, Vcmax:SLA	84.5	−196.4
		Vcmax, SLA	84.3	−196.4
	MAM – Model 4	Vcmax	84.2	−196.0
		Vcmax, N, Vcmax:N	84.2	−193.0
		Vcmax, N	84.2	−194.0

¹All models include an intercept term.

For V_cmax against leaf N and P (model 1), leaf N was a significant explanatory variable (P = 0.003), as was the interaction between leaf P and leaf N (P = 0.054), although just outside the 95% confidence level (Table 3). The AICc model selection procedure indicates that the P x N interaction was important and the response surface of V_cmax to leaf N and leaf P (Fig. 1) also shows the importance of leaf P in determining V_cmax. Leaf P modified the relationship of V_cmax to leaf N such that as leaf P increased, the sensitivity of V_cmax to leaf N increased (Fig. 1), that is, the coefficient of the interaction term was positive (Table 3). The term for leaf P alone was not significant, but was retained in the minimum adequate model to preserve marginality (see Venables and Ripley 2002).

Figure 1.

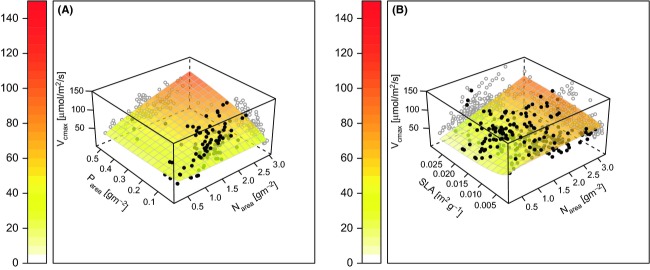
The derived relationships between V_cmax and leaf nitrogen (Table 3), as modified by leaf P (A – Table 3, model 1) and SLA (B – Table 3, model 2).

For V_cmax against leaf N and P (model 2), increasing SLA increased the sensitivity of V_cmax to leaf N; however, the magnitude of the effect was smaller than the effect of increasing leaf P (Fig. 1). In contrast to the effect of leaf P, the effect of SLA alone was significant and was contradictory to its effect in interaction – increasing SLA decreased V_cmax although this effect was only clearly visible at low levels of SLA and leaf N (Fig. 1B). There were few data points at low SLA and low leaf N because as SLA decreases, leaf N concentrations would have to be extremely low to allow low values of leaf N when expressed on an area basis, again suggesting that the effect of SLA on V_cmax was not substantial.

Leaf P had a larger effect on the V_cmax to leaf N relationship than did SLA (compare Fig. 1A and B), by contrast SLA was more significant in model 2 than was leaf P in model 1. The contrast arises from the reduced sample size of the leaf P regressions (110 observations in eight groups) compared with the SLA regressions (260 in 20 groups). While the effect of leaf P was greater, statistical confidence in the effect was lower and more data are needed to improve our confidence in the statistical model.

For the multiple regressions of J_max against V_cmax, N, and P, the minimum adequate model was that of V_cmax and P, with no interaction term, explaining 84% of the residual variance compared with the null model (Table 2; model 3). For J_max regressed against V_cmax, N, and SLA, the minimum adequate model was that with V_cmax alone, explaining 84% of the residual variance when compared to the null model (Table 2; model 4). Both models were highly significantly different from the null model (P < 0.001 – Table 3). While model 4 had a slightly higher AICc than the model with V_cmax, SLA and their interaction as model terms (Table 2), SLA and the V_cmax x SLA interaction were not significant model terms (P > 0.1; results not shown). This was also the case for the model with V_cmax and SLA and this led to the selection of model 4 (J_max against V_cmax alone; Tables 2 and 3) as the minimum adequate model. The inclusion of V_cmax in the regressions of J_max meant that the traits leaf N, leaf P, and SLA were tested for their effect on J_max that were orthogonal to their effect already implicitly considered via their effect on V_cmax. The leaf traits were considered as modifiers of the J_max to V_cmax relationship, not as direct determinates of J_max.

The effect of leaf P was significant in model 3; however, variation in leaf P had little effect on calculated values of J_max (Fig. 2). The effect of V_cmax was the most important in determining J_max demonstrating the tight coupling between the two maximum rate parameters. A regression of J_max on V_cmax alone yielded 301 observations, with a b_jv of 0.89 ± 0.02 (Table 4). In the first analysis to our knowledge of the in vivo relationship between J_max and V_cmax, Wullschleger (1993) described a slope coefficient (b_jv) of 1.64 for untransformed data. For comparison with our dataset, we natural-log-transformed J_max and V_cmax from the Wullschleger (1993) dataset and re-analyzed them with a linear regression. Regression assumptions were not violated by the transformation and b_jv was 0.84 with an R² of 0.87 (Table 4). In an analysis of natural-log-transformed J_max against V_cmax from the TRY database (Kattge et al. 2011), J_max scaled against V_cmax with a b_jv of 0.75 (and R² of 0.79). All three datasets have similar slope parameters for the log-transformed relationship ranging from 0.75 for the TRY data to 0.89 for our dataset (Fig. 3).

Figure 2.

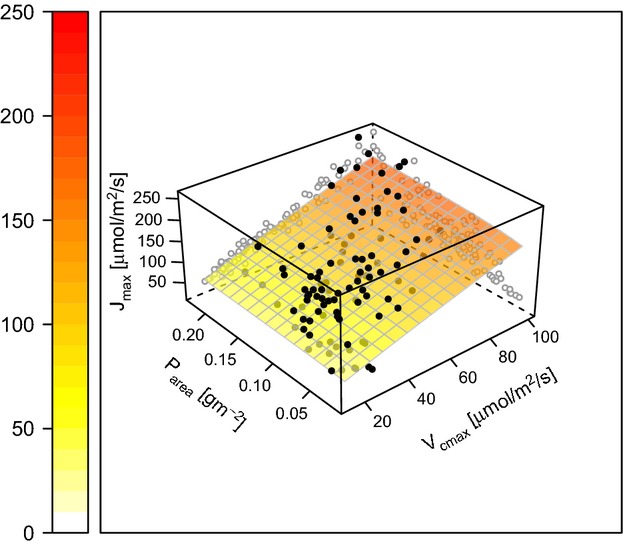
The relationship between J_max and V_cmax as modified by leaf P (Table 3, model 3).

Table 4.

Slope coefficients from linear regressions of log-transformed J_max on V_cmax from the data collected in this study, from the TRY database and from Wullschleger (1993). The data collected in this study were analyzed using a mixed-effects model with the author as the random effect, while data from the other two studies were analyzed using a fixed-effects model

	N	Model term	Coefficient	SE	Reduction in residual variance (%)	P-value*
This study	301	Intercept	1.010	0.097	86.7	<0.001
		Slope	0.890	0.021
TRY/Kattge	1048	Intercept	1.668	0.048	78.9	<0.001
		Slope	0.750	0.012
Wullschleger	110	Intercept	1.425	0.128	87.2	<0.001
		Slope	0.837	0.031

^*For this study's dataset, the P-value is based on the LRT statistic, and for Kattge and Wullschleger, it is based on the F statistic.

Figure 3.

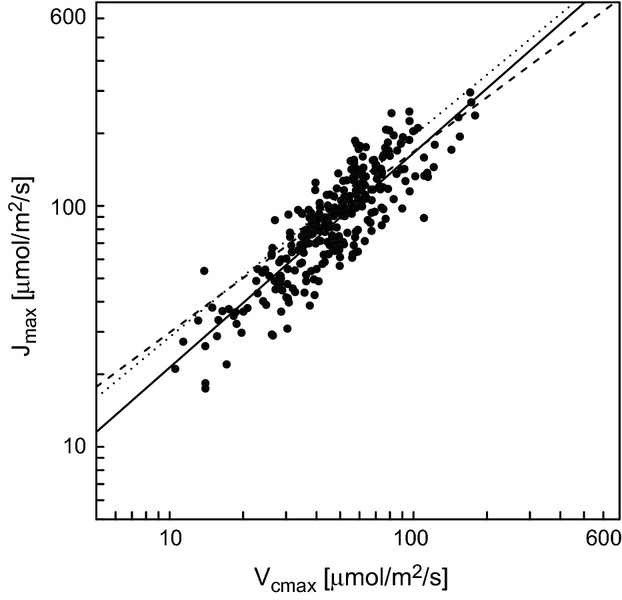
The relationship between J_max and V_cmax collected in this study (black circles and solid line) and compared against the regressions based on the Kattge et al. (2009) dataset (dotted line) and the Wullschleger (1993) dataset (dashed line). Log-scaled axes.

Variation in carboxylation rates caused by variation in P and SLA

The sensitivity of simulated carboxylation rates to variation in V_cmax and J_max caused by variation in leaf P or SLA (based on the minimum adequate models presented in Table 3) is shown in Fig. 4). At high leaf N (3 gm⁻²), increasing leaf P from the 5^th to the 95^th percentile (0.05 gm⁻² to 0.22 gm⁻²) almost doubled carboxylation rates at high PAR (Fig. 4), while at low leaf N (0.5 gm⁻²), assimilation was little affected by changes in leaf P. The increase in assimilation caused by increased leaf P at moderate-to-high leaf N, but not at low N, was because leaf P was important only in interaction with N. At low leaf P (0.05 gm⁻²), increasing leaf N from 0.5 to 3 gm⁻² resulted in a slight increase in carboxylation rates (compare solid lines in Fig. 4A and B). The effect of leaf P on J_max was so small (Table 3 and Fig. 2) in comparison with the effect of V_cmax that there was very little effect on carboxylation rates caused by variation in J_max resulting from variation in leaf P (results not shown).

Figure 4.

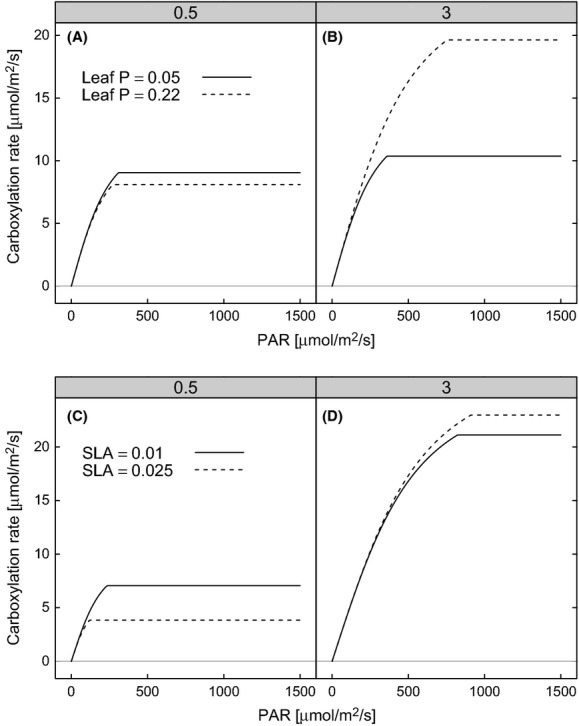
Simulated variation in gross carboxylation light-response curves as a result of variation in leaf P (A–B) or SLA (C–D) used in the minimum adequate models presented in Table 3. Light responses were simulated at two levels of leaf N, 0.5 gm⁻² (A & C) and 3 gm⁻² (B & D).

At high leaf N, increasing SLA from 0.01 m²·g⁻¹ to 0.025 m²·g⁻¹ had little effect on simulated carboxylation rates. At low leaf N (0.5 gm⁻²), carboxylation rates were decreased as SLA increased. Assimilation was reduced at low leaf N because the effect of SLA alone (which has a negative relationship to V_cmax) was larger than the effect of SLA in interaction with low levels of leaf N. At higher leaf N, the effect of SLA alone was canceled by the effect of SLA in interaction with leaf N, and therefore, there was little overall effect of SLA on V_cmax and hence carboxylation rates (Fig. 4).

The consequence of variation in b_jv on carbon assimilation

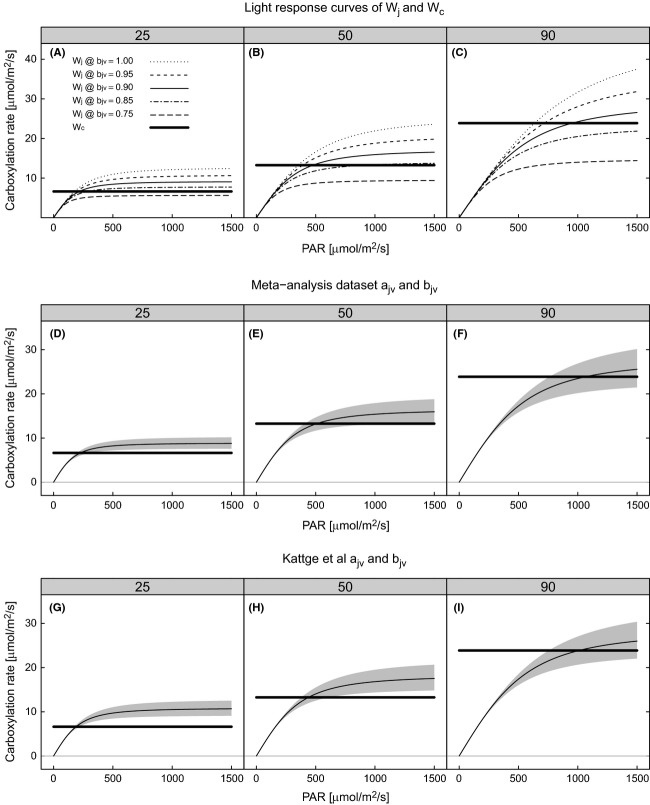
To analyze the relationship of J_max to V_cmax in more depth, we investigated the effect of the slope parameter (b_jv) on the modeled light response of carbon assimilation at three levels of V_cmax (25, 50, and 90 μmol·m⁻²·s⁻¹). Figure 5A–C shows the light-response curves of the W_c and W_j gross carboxylation rates. Obviously, W_c is insensitive to variation in irradiance, and W_j shows the typical saturating response at high light. Increasing b_jv increases the asymptote of W_j, which affects the transition point between W_c and W_j limitation. The light level at the transition where W_c and W_j are colimiting increases as b_jv decreases (Fig. 5A–C).

Figure 5.

Simulated light-response curves of W_j and W_c in response to b_jv variation (A–C), using a_jv and b_jv calculated from the dataset compiled in this study (D–F) and using a_jv and b_jv calculated from the dataset of Kattge et al. (2009) (G–I). All curves calculated at three levels of V_cmax 25 (A, D & G), 50 (B, E & H), and 90 (C, F, & I) μmol·m⁻²·s⁻¹. On panels D–I, the black line within the gray-shaded area represents W_j using the calculated coefficients and the gray-shaded area 95% confidence interval of W_j.

The relationship of the colimiting light level to b_jv allows us to categorize values of b_jv into two types: (1) intermediate values of b_jv where the point of colimitation occurs between the linear phase and the asymptote of the light response; and (2) low values at which there is no colimitation point, that is, electron transport is always limiting. Within the first category, the light level of colimitation is highly sensitive to b_jv. At the upper end of these intermediate b_jv values, the colimitation point occurs while assimilation is still in the linear phase of the light response and thus maximizes quantum yield (the differential of the curve), while W_j limits photosynthesis (Fig. 5A–C). At levels of irradiance above the colimitation point, high values of b_jv cause W_j to be substantially higher than W_c representing “spare” electron transport capacity. As b_jv increases, quantum yield decreases and the W_j asymptote approaches the W_c rate of carboxylation. In the second category of b_jv values, the light–response curve asymptotes below the value of W_c, that is, assimilation is light limited at all light levels, there is no colimitation, and quantum yield is very low (see Fig. 5c). It is also possible at high values of b_jv for the colimitation point to occur at a fixed level of irradiance, independent of b_jv although these are at values of b_jv > 1 (see Fig. 5A), substantially higher than observed (Table 4).

The J_max to V_cmax relationship of the data collected in this study, and those from the TRY database (Table 4), both have values of b_jv within the first category (Fig. 5D–I). The transition is highly dependent on b_jv, and the W_c rate of assimilation is generally within the uncertainty of the potential W_j carboxylation rate at saturating light. For the coefficients derived from the data collected in this study, quantum yield is not maximized, that is, the colimitation point is never in the linear phase of the light response. When V_cmax was 50 μmol·m⁻²·s⁻¹ and over, at light levels above those at the colimitation point, W_j was similar but slightly higher than W_c. At low photosynthetic capacity (i.e., V_cmax = 25 μmol·m⁻²·s⁻¹) across the whole range of uncertainty, electron transport capacity above that necessary for carboxylation is apparent when W_c is limiting (Fig. 5D and G).

Discussion

Our goal in this study was to derive relationships of V_cmax and J_max in relation to leaf N, P, and SLA. Using a meta-analytic approach to assess patterns among 356 species drawn from 24 different studies around the world, in agreement with many previous studies, we found that V_cmax increased in relation to leaf N (Wohlfahrt et al. 1999b; Aranda et al. 2006; Bown et al. 2007; Kattge et al. 2009; Domingues et al. 2010) and that both leaf P and SLA increased the sensitivity of V_cmax to leaf N. We also found that the relationship between J_max and V_cmax was not substantially affected by leaf N, leaf P, or SLA (Table 2). Our efforts and in particular the statistical models provide a formal template on which to improve the parameterization of terrestrial ecosystem and biosphere models (TBMs; Tables 3 and 4). We demonstrated the impact of these variable rate parameters in a simple model of photosynthesis.

Evaluating the three hypotheses

In analyzing the data, we had three a priori hypotheses: (1) leaf P will modify the relationship of V_cmax to leaf N, (2) leaf P will modify the relationship of J_max to V_cmax, (3) the relationship between J_max and V_cmax results from a trade-off between photosynthetic gain and costs of energy dissipation.

In support of our first hypothesis, we found that leaf P was an important factor modifying the V_cmax to leaf N relationship. For V_cmax, we recommend the use in TBMs of coefficients and terms of model 1 and model 2 presented in Table 3. For those models, such as CABLE and CLM-CNP, that prognostically simulate, or explicitly parameterize leaf N and leaf P, we recommend the use of model 1 to simulate V_cmax (Table 3) and we suggest that incorporation of variation in leaf P is necessary for accurate scaling of V_cmax. Many models do not prognostically simulate SLA, and we have demonstrated that while significant, the effect size of SLA on V_cmax was small and we suggest it is not a priority for inclusion in TBMs for accurate parameterization of V_cmax. However, depending on model structure, SLA is indirectly important for scaling leaf N concentrations to area-based values of leaf N.

In contrast, and with reference to hypothesis two, we find that leaf P had little effect on the J_max to V_cmax relationship. For J_max, we recommend the use in TBMs and related tools of the model presented in Table 4 of J_max regressed on V_cmax alone. Although the minimum adequate model of J_max regressed on V_cmax, leaf N and P included leaf P as an explanatory variable, the small coefficients (Table 3) suggested that the additional impact of leaf P on J_max was minimal as demonstrated in Fig. 3.

The observed relationship between J_max and V_cmax run through a chloroplast-level photosynthesis model showed that the W_c rate of assimilation is generally within the uncertainty of the potential W_j carboxylation rate at saturating light and that quantum yield is not maximized. In terms of hypothesis three, the results suggest that the costs of energy dissipation and potential for photoinhibition outweigh the marginal benefits to photosynthetic gain.

The impact of leaf P

The empirical functions we present can be applied in TBMs with a phosphorus cycle and would allow scaling of V_cmax and J_max that will be more in tune with nutrient cycling than using a single parameter value for a particular plant functional type (PFT). The use of the empirical function we developed (model 1, Table 3) will reduce simulated carbon assimilation and productivity by TBMs in regions where leaf P is low and leaf N is high, and should help to improve these simulations (Mercado et al. 2011; Yang et al. 2013). Our finding for leaf P was similar to that of Reich et al. (2009) who found that, in a global analysis, increased leaf P increased the sensitivity of A_max to leaf N. Reich et al. (2009) showed this modification of the relationship between A_max and leaf N by leaf P to hold true across biomes with different N/P ratios.

The analysis of V_cmax and J_max by Domingues et al. (2010) concluded that leaf N and leaf P were best considered in terms of limiting factors, that is, that V_cmax was determined by either leaf N or leaf P, as often the interaction term between leaf N and P was not significant. Although within the mixed-model framework we were not able to test the limiting factor hypothesis of Domingues et al. (2010), our results suggest that aggregated across diverse sites and species, there is likely to be some colimitation between N and P.

We also aimed to ascertain whether the effect of leaf P held true across multiple biomes and whether this may be a reason for the different V_cmax to N sensitivities. There was some suggestion that there was an interaction of biome with the V_cmax relationship to N and P (results not shown), but the majority of leaf P data were gathered from within the tropical zone (Table 2) and the datasets when divided by biome were dominated by individual studies, reducing the power of the meta-analysis. In data gathered primarily within tropical latitudes, we have shown that leaf P substantially impacts the V_cmax to leaf N relationship.

Kattge et al. (2009) demonstrated variability in the V_cmax to leaf N relationship across biomes, indicating that in tropical biomes where P was expected to be more limiting, V_cmax was less sensitive to leaf N. Our analysis shows that across a range of predominantly tropical biomes, the sensitivity of V_cmax to N was reduced by low leaf P and the derived relationship may help to move forward from PFT-/biome-based parameterizations in TBMs toward a trait correlation approach.

We demonstrated that variation in V_cmax related to variation in leaf P had a large impact on carboxylation rates. Increasing leaf P from 0.05 gm⁻² to 0.22 gm⁻² approximately doubled modeled gross carboxylation rates under high N levels (Fig. 4). Some of the latest generation of TBMs now includes a P cycle (Wang et al. 2010; Goll et al. 2012; Yang et al. 2013), and Mercado et al. (2011) demonstrated the importance of considering P when simulating carbon fluxes in the Amazon. In addition, anthropogenic N and P pollution has had profound effects on global ecosystems (Penuelas et al. 2012). Evidence suggests that N is more limiting than P in temperate and boreal zones (Elser et al. 2007), which may preclude the measurement of P in these zones or that studies measured P but the effects were not significant so were left out of publications. Despite a comprehensive survey of the literature, assessment of the variation in V_cmax in relation to the leaf N, leaf P, and SLA remains data limited. To fully quantify the effect of leaf P on the V_cmax to N relationship, we need more data from all ecosystems, but especially temperate and boreal ecosystems. We appeal to the leaf gas exchange research community to measure leaf P in conjunction with leaf gas exchange across all biomes.

The impact of SLA

Our results show that the relationship of V_cmax to leaf N was affected by SLA, albeit a small effect, at low values of leaf N (Fig. 1). Both similar and contrasting effects (Wright et al. 2004; Aranda et al. 2006) in the literature suggest that the effect of SLA on V_cmax is complex. SLA responds to multiple environmental and ecological factors and leaf density and leaf thickness strongly correlate with leaf N (Niinemets 1999; Poorter et al. 2009). In a previous meta-analysis, the components of SLA – leaf thickness and leaf density – showed different relationships to A_max (Niinemets 1999), indicating that SLA may not have a consistent effect on photosynthesis. For example, leaf thickness and leaf density are likely to have different effects on internal CO₂ conductance (g_i) and the N allocation ratio between RuBisCO and leaf structural components (Poorter et al. 2009). Unfortunately, with this dataset, we were unable to assess the effect of mesophyll conductance (g_i) on the V_cmax to N relationship. SLA is likely to affect g_i (Flexas et al. 2008), and the effects of SLA on the V_cmax to N relationship will be best assessed once when variation in g_i can be accounted for.

Resource allocation between J_max and V_cmax

The J_max and V_cmax relationship represents resource allocation between the two photosynthetic cycles – electron transport and the Calvin–Benson cycle. Coordination of resource investment in photosynthetic capacity is reflected by the strong relationship between V_cmax and J_max. Given the tight coupling of J_max with V_cmax across growth environments and species (Fig. 5), we suggest, as noted in many previous studies (Wullschleger 1993; Beerling and Quick 1995; Harley and Baldocchi 1995; Leuning 1997; Medlyn et al. 2002; Kattge and Knorr 2007), that their coupling may be a fundamental feature of plant photosynthetic trait relationships.

Traditionally, J_max has been related to V_cmax based on the assumption that optimization of resource allocation to photosynthesis would maintain a close relationship between these two parameters, an assumption verified by analysis of empirical data (e.g., Wullschleger 1993; Beerling and Quick 1995). The similarity in the regression model parameters between our dataset, the TRY dataset, and that of Wullschleger (1993) was remarkable considering the differences between these datasets (Table 4 & Fig. 3). The Wullschleger (1993) dataset comprised mainly grass and crop species as well as some temperate trees, while our dataset predominantly consists of tropical and temperate tree species.

While the general relationship between J_max and V_cmax is preserved across datasets (Fig. 3), there is substantial variation of individual species data from this relationship (Fig. 3). Some of this variation may arise due to the measurement error. V_cmax and J_max are differentially sensitive to temperature (Medlyn et al. 2002; Kattge and Knorr 2007), and their temperature sensitivity varies across species (Wohlfahrt et al. 1999b). For most species, this temperature sensitivity is not known, and while necessary, the correction of V_cmax and J_max to 25°C with non-species-specific sensitivity parameters may add variation into the J_max to V_cmax relationship. V_cmax is more sensitive to mesophyll conductance than J_max (Sun et al. 2013) and it may be that some of the variation in the relationship may be attributable to variation in g_i; however, it was not possible to determine the effect of g_i with this dataset. We present our results assuming infinite g_i because assuming infinite g_i is currently standard practice in TBMs and was the assumption made by most of the studies used in our meta-analysis. By analyzing the general relationship between J_max and V_cmax, we aim to provide a framework that can be applied to explain J_max to V_cmax relationships and consequences of variation in the relationship.

Maire et al. (2012) demonstrated that plants adjust leaf N investment to coordinate W_c and W_j (Chen et al. 1993) for environmental conditions over the previous month (the lifetime of RuBisCO). Scaling between J_max and V_cmax, represented by the slope parameter b_jv, affects the light (and CO₂, Von Caemmerer and Farquhar 1981) transition point at which carbon assimilation switches between W_c and W_j, that is, the light level where W_c and W_j are colimiting. We hypothesized that b_jv may also coordinate instantaneous W_c and W_j when W_c is limiting as investment in J_max that would support rates of W_j higher than W_c, when W_c is limiting, represents investment in unused resources. At the assumed leaf absorptance and at 25°C, simulations show that potential W_j rates at high light and W_c rates are similar (Fig. 5D–I), when the probable range in b_jv values from our dataset (Table 4) are used. Generally, quantum yield is not maximized. Synthesized across multiple species and environments, the presented relationship suggests that J_max is related to V_cmax to coordinate W_j with W_c and hedge against photoinhibition, when RuBisCO carboxylation is limiting. Aggregated across the different species and environments, support for co-ordination at light saturation is a very general assertion. The degree of control that plants have over the relationship between J_max and V_cmax needs to be tested in controlled environments at a range of temperature and light levels (Wohlfahrt et al. 1999a) and giving consideration to mesophyll conductance and leaf absorptance.

Maire et al. (2012) show that coordination occurs over monthly timescales, while our simulations (Fig. 5) are on instantaneous timescales. The timescale over which coordination is considered is important, and given the huge diurnal variability in incident light, W_c and W_j cannot always be coordinated on subdaily timescales. The relationship that we derived between J_max and V_cmax appears to coordinate, within uncertainty bounds, the W_c and W_j rates of photosynthesis at high light levels (Fig. 5D–I). However, there is some variability and the derived relationship has high W_j at low photosynthetic capacity (Fig. 5D and G), and W_j higher than W_c when W_c is limiting indicates unused electron transport capacity at high light. Unused electron transport capacity could produce reducing power not used in carbon reduction and which could be used in biochemical pathways other than the Calvin–Benson cycle (Buckley and Adams 2011) such as the reduction of nitrite to ammonium that occurs in the chloroplast (Anderson and Done 1978; Searles and Bloom 2003) and the production of isoprene (Morfopoulos et al. 2013).

Conclusion

For the first time, we assess the sensitivity of carbon assimilation to the J_max to V_cmax relationship, and results from the meta-analysis suggest that plants may employ a conservative strategy of J_max to V_cmax coordination to avoid photoinhibition. Work is needed to extend this analysis with the consideration of mesophyll conductance and species-specific temperature effects.

We also present for the first time the significance of P and SLA on the relationship of V_cmax to nitrogen and of J_max to V_cmax in a globally extensive meta-analysis. Modeling demonstrates that variation in leaf P has large consequences for carbon assimilation. The relationships presented in this study can be used to parameterize V_cmax and J_max in a rigorous fashion based on data-derived relationships, moving parameterization away from methods with limited variation or limited grounding in the literature. To fully understand variability in the relationship of V_cmax and J_max to leaf N, leaf P, and SLA, work is needed to extend the geographic range of data, particularly into temperate and boreal regions.

Conflict of Interest

None declared.

Supporting Information

Additional Supporting Information may be found in the online version of this article: