Quantifying spatio-temporal dynamics of biomarker pre-concentration and depletion in microfluidic systems by intensity threshold analysis

Abstract

Microfluidic systems are commonly applied towards pre-concentration of biomarkers for enhancing detection sensitivity. Quantitative information on the spatial and temporal dynamics of pre-concentration, such as its position, extent, and time evolution are essential towards sensor design for coupling pre-concentration to detection. Current quantification methodologies are based on the time evolution of fluorescence signals from biomarkers within a statically defined region of interest, which does not offer information on the spatial dynamics of pre-concentration and leads to significant errors when the pre-concentration zone is delocalized or exhibits wide variations in size, shape, and position over time under the force field. We present a dynamic methodology for quantifying the region of interest by using a statistical description of particle distribution across the device geometry to determine the intensity thresholds for particle pre-concentration. This method is applied to study the delocalized pre-concentration dynamics under an electrokinetic force balance driven by negative dielectrophoresis, for aligning the pre-concentration and detection regions of neuropeptide Y, and for quantifying the polarizability dispersion of silica nano-colloids with frequency of the force field. We envision the application of this automated methodology on data from 2D images and 3D Z-stacks for quantifying pre-concentration dynamics over delocalized regions as a function of the force field.

I. INTRODUCTION

Sensitivity gains from the scale-down of various sensor paradigms can be realized only if the ensuing mass transport limitations are alleviated,¹ since the slow analyte settling and binding kinetics at the sensor surface can substantially delay signal onset at micro/nanosensors.² Micro/nanofluidic device methodologies are routinely applied towards enabling analyte pre-concentration within physiologically relevant media^3–5 for reducing target diffusion time towards the sensor⁶ and thereby enhancing detection sensitivity.⁷ Selective pre-concentration also enables analyte enrichment over interfering proteins and small molecules,⁸ which is especially relevant given the wide concentration range of proteomic biomarkers within typical biofluids (mg/ml–pg/ml).⁹ In order to capitalize on the reduced diffusion lengths towards the sensor upon analyte pre-concentration within microfluidic and nanochannel geometries, there is a need to effectively overlap the pre-concentration and detection regions for ensuring enhanced target binding kinetics at the sensor. We describe herein a methodology for quantifying the spatio-temporal dynamics of biomarker preconcentration within microfluidic systems to ensure effective alignment of the sensor to pre-concentration within the microfluidic device, for guiding device fabrication.

A variety of force fields are utilized within microfluidics to realize varying degrees of pre-concentration, including electrokinetic, chemical, diffusional, inertial, and magnetic methods.^10,11 The degree of pre-concentration is quantified by following the time evolution of fluorescence signals from labeled analyte biomarkers as a function of the force field driving the enrichment.^12,13 Quantification of the spatio-temporal dynamics of pre-concentration has usually been accomplished by monitoring fluorescence alterations over time inside a particular region of interest (ROI), as specified by discrete points,^14,15 or along a representative line axis,^16–18 or a statically defined box,^19,20 to identify the time and location of the peak intensity. All these prior methods for quantifying pre-concentration have been based on the application of a static ROI. One drawback of utilizing such passive methodologies to follow pre-concentration dynamics is the error that can be introduced due to exclusion of the full extent of pre-concentration or inclusion of the background intensity, thereby leading to underestimation or overestimation of the pre-concentration degree over time. Furthermore, static ROIs cannot capture the spatial dynamics of the pre-concentration zone, such as its extent or rate of growth. Finally, while such passive ROIs may be adequate in situations where pre-concentration is highly localized, they are not well suited for cases where pre-concentration has a more diffuse or delocalized nature, such as is common under a balance of opposing force fields.

Dielectrophoresis (DEP) enables the frequency-selective translation of polarized particles under a spatially non-uniform electric field^21,22 and is routinely applied towards pre-concentration of biomolecules.^23–25 Positive DEP (pDEP) or particle translation towards localized regions of high field causes rapid pre-concentration. Quantification of pre-concentration dynamics under pDEP, as presented within prior work,^26–31 is relatively straightforward due to the spatially localized nature of the pre-concentration region. Negative DEP (nDEP) or particle translation away from localized high field points can also cause rapid pre-concentration when it is applied in conjunction with electro-osmosis or electrophoresis.³² However, since pre-concentration under the ensuing electrokinetic force balance is spatially delocalized, there is a need to develop methodologies that are based on the pixels over the entire extent of the pre-concentration zone, rather than utilizing methods based on pixels within a limited ROI, such as point, line, or boxed areas. Furthermore, given the wide variations in pre-concentration extent with force fields, there is a need for methodologies to dynamically define the ROI for characterizing the pre-concentration dynamics. Finally, since pre-concentration occurs chiefly due to the high spatial non-uniformities of the electrokinetic force fields, there is a need for criteria to weight each pixel within the pre-concentration zone based on its geometric location from the high field points that drive this force field, for accurately quantifying the relative particle polarizability and force dispersion dynamics.

Herein, we present a dynamic methodology for quantifying the pre-concentration dynamics of particles under an electrokinetic force balance, driven by nDEP away from insulating constriction tips, which causes a highly delocalized pre-concentration zone. This automated methodology for quantifying pre-concentration is based on defining a threshold intensity level for dynamic determination of the ROI, through a statistical description of particle distribution across the device geometry to enable the quantification of pre-concentration and depletion signals over the background level. We illustrate the need for such a method by utilizing it within two distinct applications: (a) for optimizing placement of the sensor electrode within a nanochannel device for overlapping the pre-concentration and sensor regions during the electrochemical detection of neuropeptide Y (NPY), a biomarker for stress; and (b) for quantifying the polarizability dispersion of silica nano-colloids by accounting for the field non-uniformities across the pre-concentration zone through weighting pixels in the ROI based on their geometric location from the force field driving the pre-concentration. In this manner, we are able to quantify the pre-concentration dynamics and the DEP force dispersion under both, positive and negative DEP. Given the ability of this image analysis methodology for automation, with no dependence on the pre-concentration position, profile, or extent, we envision its universal utility in quantifying pre-concentration dynamics over 2D images, as well as from 3D Z-stack data acquired by confocal microscopy.

II. METHODS

A. Device geometry for pre-concentration

Dielectrophoresis was conducted within an electrode-less device geometry, with external Pt electrodes (Alfa Aesar) that were driven using a function generator (Agilent 33220 A) and a voltage amplifier³³ for generating applied fields of ∼300 V_pp/cm over a 10 kHz to 5 MHz frequency range, with sharp dielectric constrictions to create localized high field points for enabling DEP pre-concentration of polarized particles at the constriction tips by pDEP or away from constriction tips by nDEP. In this manner, fluorescently labeled NPY biomarkers (Phoenix) were pre-concentrated in PBS media (150 mM NaCl and 2 mM NaN₃) at pH 7.2 and σ_m ∼ 1.6 S/m, using AC fields in the 1–3 MHz range within a quartz nanochannel (200 nm depth) away from constrictions (30 μm to 30 nm over 3 μm extent). Silica nano-colloids (Corpuscular Inc., Cold Spring, NY; 80 nm sized) were pre-concentrated in 0.1× PBS media (σ_m ∼ 0.1 S/m) in the 100 kHz–2 MHz range using constrictions (1 mm to 1 μm over a 10 μm length extent) patterned on PDMS (poly-di-methyl-siloxane) channels (7 μm depth). The micro/nanofabricated device was bonded onto cover slip glass for imaging using an inverted microscope (Zeiss Observer A1) and an EMCCD (Electron Multiplying Charge Coupled Device) camera (Hamamatsu). For the electrochemical detection of NPY, graphene-modified glassy carbon electrodes were patterned on the cover slip and bonded to the channel after alignment to the pre-concentration region,⁸ based on procedures described herein to quantify pre-concentration dynamics. To enhance particle accumulation under nDEP, a small DC offset (0.5–1 V/cm) was applied to the AC field (300 V_pp/cm). As per the schematic in Figure 1, electro-osmosis (EO) under the DC field dominates at all points within the device except in the vicinity of the constriction, where nDEP dominates. Upon the balancing of EO with nDEP, particle accumulation occurs on one side of the constriction, with no accumulation on the other side, since nDEP and EO are in the same direction. The degree of pre-concentration of biomarkers is quantified by ratio of intensity enhancement over the background level.

FIG. 1.

(a) Force balance under EO versus negative dielectrophoresis at the insulator constriction (nDEP) causes pre-concentration of particles over a delocalized region of the microfluidic device geometry. The position of the inner arc, i.e., (i) vs. (ii) is determined by the force balance of nDEP and EO, with higher nDEP pushing the arc further from the constriction tip. The position of the outer arc is determined by the flux balance that includes diffusion. Fluorescence images of pre-concentration (greyscale) overlayed with equi-field lines (red lines) shows pre-concentration over a spread of field lines (one order of magnitude variation) under nDEP with EO (b), while the pre-concentration is tightly distributed over field lines (<20% variation) under pDEP (c).

B. Correlating fluorescence measurements to the force field for pre-concentration

Spatio-temporal quantification of the force field driving the pre-concentration can be carried out by correlating the rate of change in fluorescence intensity ($\dot{F}$) to the rate of change in number of particles entering that particular region ($n$), for particle concentration ($c$) in the region imaged by the pixel, assuming a uniform initial particle concentration in the pre-concentration region, as described by the Fokker-Planck equation (FPE)^22,30

$$\dot{F}\hspace{0.17em}\propto \hspace{0.17em}\frac{\partial n}{\partial t}\propto \frac{\partial c}{\partial t}=-\nabla .{\mathit{J}}_{\mathit{Total}}.$$ (1)

Here, ${\mathit{J}}_{\mathit{Total}}$ is the total flux of particles due to the net force field. In the case of nDEP driven pre-concentration with a DC field offset, the force field occurs due to the balance of nDEP, electrophoresis (EP), EO and diffusion (Diff). Neglecting particle-particle interactions, the total particle flux J can be written as the summation of particle fluxes caused by each of these forces:

$${\mathit{J}}_{\mathit{Total}}={\mathit{J}}_{\mathit{DEP}}+{\mathit{J}}_{\mathit{Diff}}+{\mathit{J}}_{\mathit{EP}}+{\mathit{J}}_{\mathit{EO}}.$$ (2)

The concentration of particles $\hspace{0.17em}c=c(\mathit{r},t)$, $\mathit{r}=x,y,z,$ can then be related to the particle flux J, as follows:

$$\frac{\partial c}{\partial t}=-\nabla .J=-\frac{1}{f}\nabla .\left(c\frac{\alpha \left({\omega }_1\right)}{2}\nabla {\left|E\right|}^2\right)+\nabla .D\nabla c+\nabla .\left(c\frac{\epsilon \zeta }{\eta }E\right)+\nabla .(c.v_{\mathit{F}\mathit{l}\mathit{u}\mathit{i}\mathit{d}}).$$ (3)

Here, α is the real part of the frequency dependent effective polarizability of the particle under DEP, E is the RMS value of electric field, ∇ is the gradient operator, $\zeta$ is zeta potential of particles, $\eta$ is fluid viscosity, and D = k_BT/f is the diffusion constant, where f is the particle friction factor (6πηa). This can be related to the rate of change in florescent intensity as

$$\dot{F}\hspace{0.17em}\propto -\nabla .J=-\frac{1}{f}\nabla .\left(c\frac{\alpha \left({\omega }_1\right)}{2}\nabla {\left|E\right|}^2\right)+\nabla .D\nabla c+\nabla .\left(c\frac{\epsilon \zeta }{\eta }E\right)+\nabla .(c.v_{\mathit{F}\mathit{l}\mathit{u}\mathit{i}\mathit{d}}).$$ (4)

Based on this relationship on the rate of change in florescence intensity under pre-concentration to the divergence of flux of the particles (Eq. (4)), we explore the following simplifications. First, for purposes of calculating the force dispersion, i.e., variation of force field at various frequencies, we can assume that particle polarizability is the only significant parameter that causes the DEP force to vary with frequency, since while EO and EP influence particle pre-concentration, their effect is invariant with frequency of the field. It is noteworthy that the influence of frequency dependent nonlinear AC electroosmotic flow is neglected, since the constrictions bending the field lines within our device are composed of highly insulating quartz or dense PDMS materials, rather than conducting granules or nearly insulating materials, which can cause vortices as per prior work.^34–36 Second, by focusing only at the early time points for pre-concentration (t→0), we can eliminate diffusional effects on the net flux. Hence, the rate of change in florescence intensity of a pixel in the pre-concentration region under a pre-dominantly DEP force field, at frequency ${\omega }_1$ versus $\hspace{0.17em}{\omega }_2$, is quantitatively described by the relative DEP forces on the particle at these two frequencies, thereby allowing a quantitative computation of force dispersion as per the ratio

$$\frac{\dot{F}(0,{\omega }_1)}{\dot{F}(0,{\omega }_2)}=\frac{F_{\mathit{D}\mathit{E}\mathit{P}}\left({\omega }_1\right)}{F_{\mathit{D}\mathit{E}\mathit{P}}\left({\omega }_2\right)}=\frac{\frac{1}{f}\left(c\frac{\alpha \left({\omega }_1\right)}{2}\nabla {\left|E\right|}^2\right)}{\frac{1}{f}\left(c\frac{\alpha \left({\omega }_2\right)}{2}\nabla {\left|E\right|}^2\right)}.$$ (5)

Under pDEP, the ratio in Eq. (5) is equal to ratio of polarizabilities at the respective frequencies as per prior work,^29–31 since pre-concentration is driven solely towards the highest field point (Figure 1(c)), thereby making differences in the $\nabla {\left|E\right|}^2$ term to be insignificant. However, under nDEP, since the pre-concentration occurs over a spread of field values (at least an order of magnitude as per Figure 1(b)), the different $\nabla {\left|E\right|}^2$ values need to be accounted through appropriately weighting the pixels, for quantifying the relative polarizability variations.

C. Computing relative polarizability from particle collection rate data

The rate of change in florescence intensity for particle pre-concentration under conditions of varying frequency or particle type can be utilized to compute the relative particle polarizability and DEP force dispersion, by utilizing the collection rate data at the earliest time points where DEP dominates. To ensure a sufficient number of data points at the initial time values, an analytical equation fitting the data at the earliest time points is utilized.^28,30 A linear approximation for the fluorescence rate is the easiest method to measure collection rate

$$F(t)=mt+n.$$ (6)

Herein, $F$ is the average pixel intensity in the ROI, $m$ is the slope of the linear fit, $t$ is time, and $n$ is the y-axis intercept of the function. The rate of change in florescence at the earliest time ($\dot{F}(0)$) may then be calculated from the slope of this function

$$\dot{F}(t\to 0)=m.$$ (7)

However, since diffusion will cause pre-concentration to saturate over time, a linear fit will only be valid within a limited concentration enrichment interval. In situations of extremely fast pre-concentration kinetics, a single or double exponential function will be a more accurate description, as per the following function:

$$F(t)=a\hspace{0.17em}\text{exp}\hspace{0.17em}(-b(t-t_0))+c\hspace{0.17em}\text{exp}(-d(t-t_0))+e.$$ (8)

By differentiating this analytical function with respect to time, at $\hspace{0.17em}t=0$, the rate of change in florescence may be determined as

$$\dot{F}(t\to 0)=-(ab+cd).$$ (9)

In this manner, using either the linear or exponential approximation, the initial collection rate can be correlated to the rate of change in florescence (Eqs. (7) and (9)) to calculate the relative alterations in particle polarizability under various experimental conditions, as per Eq. (5).

III. RESULTS

A. Image analysis method for quantifying pre-concentration dynamics

We present an automated image analysis methodology for quantifying the pre-concentration dynamics in situations where the pre-concentration is highly delocalized and driven by spatially non-uniform force fields. As shown within the schematic of Figure 1(a) and fluorescence image overlayed with equi-field lines in Figure 1(b), the pre-concentration of silica nano-colloids occurs over a wide spatial extent on one side of the insulator constriction due to the force balance of nDEP, which sharply depends on field: ∇E² (the product of field and field gradient) versus EO, which depends linearly on field: E. In fact, while the pre-concentration under nDEP (at 100 kHz) is delocalized over field lines spread over an order of magnitude (Figure 1(b)), the pre-concentration under pDEP (at 2 MHz) is highly localized (Figure 1(c)), since all particles are driven to the maximum field point (E_max), with a minimal spread of field lines (0.8–1 E_max). As per Figure 1(a), the pre-concentration profile consists of an inner arc neighboring the constriction tip, which occurs at the location where nDEP exactly equals EO, whereas the outer arc occurs at the location where the sum of nDEP and diffusion flux exactly equal that under EO. As a result, while polarizability variations with frequency of the applied field can be easily computed from pre-concentration dynamics under pDEP, without accounting for the field non-uniformities within the ratio in Eq. (5), the same is more involved under nDEP due to the delocalization of pre-concentration over a spread of field values. Hence, characterizing the polarizability dispersion requires that each pixel be weighted by its field non-uniformity—as characterized by its geometric location from the constriction tip—to ensure, for instance, that the pre-concentration level represented by a profile (Figure 1(a)) with the inner arc (i) (solid line) is different from that with the inner arc (ii) (dashed line), since the nDEP force is higher for the case (ii) versus (i), even if the raw pixel intensity levels do not always exhibit this difference. This wide spatial extent for pre-concentration requires the means to dynamically define the ROI for pre-concentration based on threshold fluorescence signal levels that are determined by particle distribution statistics, for computing the normalized intensity enhancement over the background in the pre-concentration region.

1. Dynamic determination of the region of interest

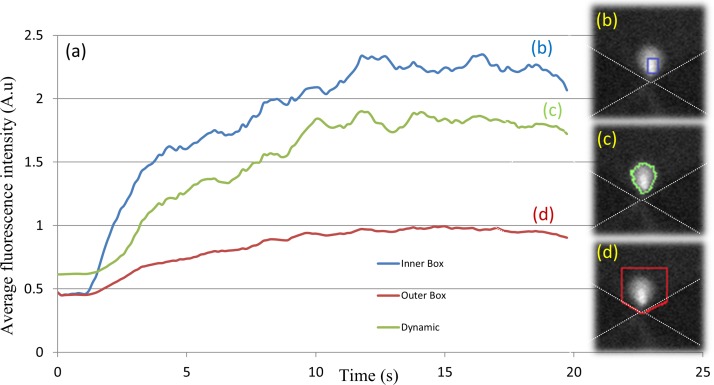
Prior methods for quantifying pre-concentration dynamics were based on monitoring the time evolution of the cumulative or averaged florescence intensity of each pixel within a pre-defined ROI. This ROI, which is usually centered on the region with the highest pre-concentration, remains static irrespective of the time point of the image or alterations to the force field that cause the pre-concentration. The passive nature of this ROI determination method can cause errors in determination of the pre-concentration level, due to either signal underestimation caused by exclusion of the full extent of pre-concentration or overestimation caused by inclusion of background intensity levels from regions that do not experience pre-concentration. Figure 2 highlights this issue by presenting two cases: (i) an ROI chosen to cover the pre-concentration zone, including all of the collected time points (large ROI as in Figure 2(d)); and (ii) an ROI that is centered only on the region at a particular time point with the highest sample enrichment (small ROI as in Figure 2(b)). Since the pre-concentration zone tends to begin within a small region and gradually expand over time, the application of the large ROI of method (i) to measure enrichment level based on average pixel intensity within the ROI will lead to underestimation of the pre-concentration level and rate at the early time points, due to inclusion of pixels from regions not experiencing pre-concentration. On the other hand, if the pre-concentration level is quantified by summing the pixel intensities over the ROI, then the large ROI of method (i) will lead to overestimation of pre-concentration level at the early time points, due to inclusion of pixel intensity from the background regions that do not experience pre-concentration. While this problem can be mitigated by using a background removal step to zero out the pixel intensity within the regions lacking pre-concentration, such an operation would make it difficult to detect particle depletion. Similarly, the small ROI of method (ii) will lead to overestimation of the pre-concentration level if the signal averaging method is used, whereas it will lead to underestimation of pre-concentration level if the cumulative signal method is used, due to exclusion of some regions from the total signal. In situations with localized pre-concentration as in Figure 1(c), the error from using static ROI methods to monitor the pre-concentration dynamics may be acceptable, but in situations with delocalized pre-concentration, as is the case under a balance of force fields in Figure 1(b), the errors caused by static ROI methods can be substantial. Furthermore, as will be explored subsequently, the quantitative comparison of relative force fields for pre-concentration requires that each pixel in the pre-concentration zone be weighted to account for the spatial non-uniformities of the force field. For such applications, a static ROI method can induce substantial errors due to the inclusion of background intensities or exclusion of pre-concentration signals in the weighting process. Hence, we choose to dynamically determine the ROI based on a threshold signal level determined by particle distribution statistics.

FIG. 2.

(a) Comparing static methods for determination of ROI with dynamic methods for quantifying the pre-concentration from fluorescence signal levels. ROI based on the blue box inside the pre-concentration zone (b) versus the red box that surrounds the entire possible pre-concentration zone (d) is compared to the green curve that dynamically detects the boundaries of the pre-concentration region versus the background (c).

2. Particle distribution statistics to determine signal and background thresholds

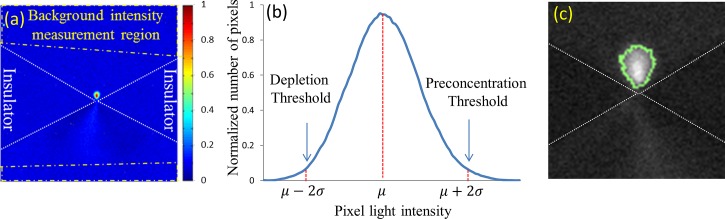
The criteria for setting the minimum and maximum threshold pixel intensity levels for determining sample pre-concentration and depletion, respectively, are described here. Since typical experiments to optimize pre-concentration levels are often performed under differing initial conditions—such as the starting particle concentration level, fluorescent labels of differing quantum efficiency, and variations in the intensity of the light source used for excitation, the threshold levels may need to be redefined for each experiment. Hence, we begin by delineating the background measured in a background region of interest (BROI), wherein the concentration of sample particles is uniform and not affected by pre-concentration or depletion, as shown in Figure 3(a) for our particular device geometry. The background intensity distribution will either be measured initially and remain constant through the duration of the pre-concentration experiment or be continuously computed for each time point and/or varying force field. Accurate measurement of the background intensity can be challenging within some microfluidic device geometries, such as due to delocalized pre-concentration zones or overlapping pre-concentration and depletion regions, which can introduce substantial errors. In such situations, an ideal BROI is chosen to be in a region that is far enough from the pre-concentration zone, so that it is not affected by particle enrichment. In this background region, we can assume that particles are uniformly distributed in the media and consequently the light intensity distribution follows a normal distribution for which the mean intensity is defined as μ and the standard deviation is defined as σ. In such regions, only 2% of pixels should have intensity levels higher than two times the standard deviations above the mean intensity level: μ + 2σ. If more than 2% of pixels in the BROI have intensity levels greater than μ + 2σ or lower than μ-2σ, then it indicates that some portion of this BROI is experiencing either depletion or pre-concentration. Hence, the size of BROI is reduced row-by-row or column-by-column, starting from the side of the BROI that is closest to the likely pre-concentration region. After each reduction in size, the pixel intensity distribution is again measured and the process is repeated until the above criterion is satisfied. In this manner, the background region can be unequivocally assigned in an automated manner for each pre-concentration time point and force field variation. Once the background distribution has been delineated, it may be used to define threshold intensities for depletion and enrichment (Figure 3(b)). Again, assuming that the background light intensity distribution follows a normal distribution, there is a 98% chance that pixels with intensity levels greater than μ + 2σ are experiencing particle enrichment, thereby delineating the threshold level for pre-concentration. In order to prevent false positives, our image analysis method labels a particular pixel as undergoing pre-concentration, only if one or more of its neighboring pixels are also above the threshold level. Similarly, since only 2% of pixels have intensity levels lower than twice the standard deviation below the mean intensity: μ-2σ, we delineate this as the threshold level for depletion. Using these thresholds, we can quantify the degree of pre-concentration or depletion of each pixel through intensity measurements.

FIG. 3.

(a) Defining the BROI for measuring background intensity. (b) Normalized pixel intensity distribution in BROI and criterion for setting intensity threshold levels to detect pixels undergoing pre-concentration or depletion to determine the net pixel intensity distribution. (c) Dynamic determination of region of interest for quantifying pre-concentration. Light intensities are converted from a 16 bit scale to a scale of: 0–1.

3. Computation of pre-concentration over 2D areas and 3D stacks

Based on these threshold levels, an ROI of similar shape and extent as the pre-concentration zone can be dynamically defined (Figure 3(c)). Unlike the static ROI used in prior work, the dynamic ROI can adapt its shape, position, and extent based upon alterations in the pre-concentration zone at different time points or under varying force fields, thereby enabling a more accurate computation of the cumulative and average pixel intensity at each time point of the pre-concentration. This dynamic method also allows for spatially characterizing the pre-concentration and depletion zones for computation of the rate of growth, direction of growth, and deviations from the previously defined ROI. Furthermore, it provides information on the statistics of particle distribution within the pre-concentration zone, which can be applied towards the design for localization of the sensor for particle detection. The threshold levels can also be defined based on sensitivity levels of a particular detection scheme to couple pre-concentration with detection. This dynamic method also enables accurate quantification of pre-concentration over a three dimensional volume. Images collected from a set of 3D z-stack images can be analyzed individually, each with its unique ROI, thereby allowing for accurate analysis of variations in the z direction. This would not be possible with a static ROI, since the varying shape, position, and extent of the pre-concentration over the Z-stacks would lead to substantial error.

4. Application towards aligning pre-concentration and detection regions

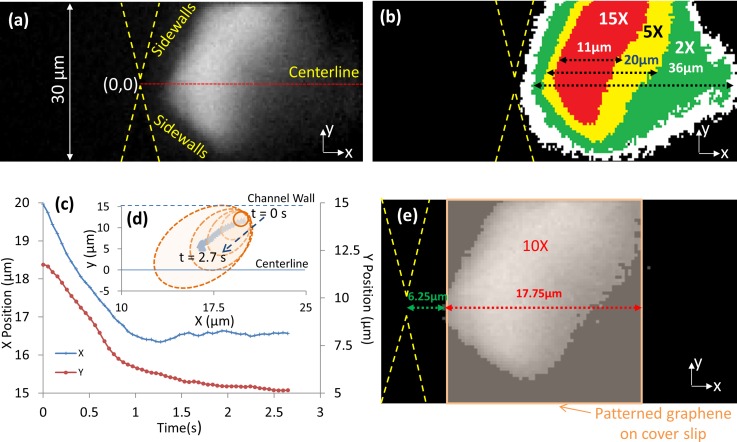
We illustrate the relevance of this image analysis methodology for quantifying pre-concentration dynamics, by utilizing it to ensure optimal alignment of the electrochemical detection electrode for NPY biomarkers to its pre-concentration region under the nDEP force balance, which exhibits significant changes in shape and position over time. Figure 4(a) shows the highly delocalized pre-concentration profile of positively charged NPY biomarkers under the electrokinetic force balance. The image analysis methodology is utilized to quantify the position and shape of the regions that exhibit intensity enhancements up to 15× over the background. In fact, as per the time evolution of the intensity profiles in Figures 4(c) and 4(d), the highest intensity region changes significantly in position and shape over the pre-concentration time, beginning close to the channel walls and evolving gradually towards the device centerline. In this manner, the edge position and width of graphene-modified glassy carbon electrodes patterned on the cover slip can be aligned to the constriction tip of the microfluidic channel prior to device bonding. This ensures effective coupling of NPY pre-concentration to electrochemical detection, as per Figure 4(e), for covering the region with at least 10× intensity enhancements. Significant deviations in electrode alignment from this optimized position would reduce the binding kinetics of pre-concentrated NPY biomarkers on the sensor, thereby lowering signal from electroactive tyrosine groups, while the electrode area outside the pre-concentration region contributes to capacitive background without signal enhancement. In this manner, by utilizing this methodology to determine alignment of detection electrodes within the nanochannel of a constriction device, we have demonstrated the detection of neuropeptides at picomolar levels within a few seconds.⁸

FIG. 4.

Alignment of the graphene-modified electrode in the nanochannel based on spatio-temporal dynamics of NPY pre-concentration: (a) fluorescence image of NPY pre-concentration; (b) spatial spread of intensity enhancements over the active device region; (c) and (d) time evolution of pre-concentration region; (e) alignment of sensor electrode over the pre-concentration region for reducing diffusion lengths of pre-concentrated analytes.

B. Quantifying the force dispersion from fluorescence images

Quantification of the driving force for particle pre-concentration is necessary for optimizing the degree of enrichment, since force analysis can offer important information on the dielectric properties of the particle^28,30 and the microfluidic device design parameters to enhance pre-concentration. While prior work has utilized particle tracking methods to correlate the force field to velocity profiles of the pre-concentrated particles,^37,38 similar direct measurements are not possible for nano-colloids or molecular biomarkers due to sizes that are well below the diffraction limit. A possible indirect method for force measurement is through its correlation to the rate of change in measured florescence intensity within the pre-concentration zone. As per Eq. (5) (Sec. II), the relative DEP force causing particle pre-concentration at various frequency levels of the electric field is determined by the rate of change in florescence intensities of the pixels in the pre-concentration region. Hence, the average pixel intensity in the ROI can be measured at each time point to compute the rate of change at the initial time points by using linear or exponential fit methods. In previous studies,³⁰ this correlation has been applied to determine the force dispersion within electrode-based pDEP enrichment devices by computing the relative pDEP force versus frequency of the applied electric field. However, these methods cannot be applied within situations of delocalized concentration profiles, as present within nDEP pre-concentration using insulator-based constriction devices. Under pDEP pre-concentration, the rate of change of fluorescence intensity at different frequencies or for different particle-types directly indicates the relative polarizability differences of the particles under the respective conditions, since the locations within the device geometry showing high pixel intensity are localized only at the high field regions, as per Figure 1(c). On the other hand, under nDEP conditions, the pixel intensities are delocalized over a region of wide extent, with substantial spatial non-uniformities in the field at each of these pixel locations, as illustrated in Figure 1(b). Hence, comparisons of relative polarizabilities of the particles under conditions of different frequencies or particle-types, which can substantially alter the shape, position, and extent of the pre-concentration region, can be obtained only by normalizing the rate of change in fluorescence intensity for the field non-uniformities that occur over the extent of the pre-concentration region. Herein, we account for these field non-uniformities in the nDEP pre-concentration profile by multiplying each pixel intensity level with a weighting function at that location: $f(\nabla E^2,r)$. This function representing the normalized force field depends on $\nabla E^2$ at each location across the device geometry ($\nabla E^2(r)$) versus the maximum $\nabla E^2$ in the device

$$f\left(\nabla E^2,r\right)=\frac{Max(\nabla E^2)}{\nabla E^2\left(r\right)}.$$ (10)

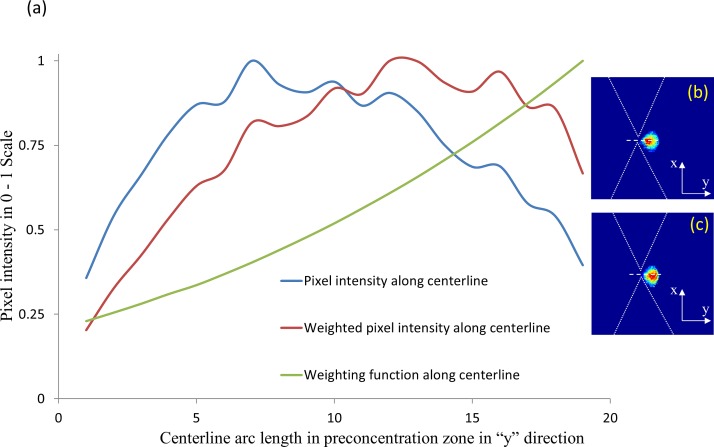
Based on a CAD file of the device geometry, COMSOL Multiphysics field simulation software is used to compute $\nabla E^2(r)$ and the maximum $\nabla E^2$ in the device geometry. A 2D matrix of the ($\nabla E^2$) distribution is imported into MATLAB to generate the weighting function overlay. Following this, image registration techniques are used to map the weighting function onto each frame of the experimentally captured images. Figure 5 shows an example of how the raw intensity distribution of pixels across a particular direction is altered upon force field normalization using this weighting function. Assuming a threshold intensity scale of 0.75 for significant level of pre-concentration, it is apparent that the normalized intensity distribution after weighting the pixels is more evenly spread out than the original raw image.

FIG. 5.

(a) Weighting the pixels of the pre-concentration region to account for the spatial field non-uniformities for applying pixels in the ROI towards quantitative comparisons of relative polarizability differences between experiments. Blue curve shows the original normalized pixel light intensity over centerline. Red curve shows normalized weighted pixel intensity for DEP measurements. Green curve shows the normalized signal along centerline after applying the weighting function. Intensity distribution before (b) and after (c) the application of the weighting function is shown.

C. Quantifying nDEP force dispersion on SiO₂ nano-colloids using collection rate

The quantitative fluorescence collection rate data determined using the dynamic ROI method as per Sec. III A can be applied in conjunction with the weighting function described in Sec. III B, to compute the alterations in relative particle polarizability and force dispersion for varying frequencies (as per Eq. (5)), thereby leading to a more quantitative understanding of the polarization mechanism. For this purpose, the collection rate data of silica nano-colloids under nDEP at various frequencies (Figure 6) is fit at the early time points to the linear (Eq. (7)) or exponential functions (Eq. (9)), to compute the rate of change in fluorescence (Eq. (5)), after normalizing with the weighting function for the particular device geometry (Eq. (10)). Since the images were acquired at 10 fps (frame per second) for the analysis of data from the first 5 frames (a time period of just 0.5 s), we judge that transport under nDEP dominates over diffusion for the timeframe of our analysis. Results of the fitting parameters based on the linear and exponential functions are shown in Table I, and the relative alterations in polarizability of SiO₂ nano-colloids with frequency of the field is shown in Table II. The nDEP behavior of nano-colloids at sub-MHz frequencies has been attributed to concentration polarization of ions in the diffuse layer around the colloid.^39,40 The inverse RC time constant of the diffuse layer around nano-colloids can be calculated as⁴¹

$${\omega }_{\mathit{R}\mathit{C}}=\frac{D}{\lambda a}.$$ (11)

Here, D is diffusion coefficient of ions in the media, λ is the thickness of the electrical double layer around the colloid, and a is the hydrodynamic radius of the colloid. For silica nano-colloids of a = 40 nm in 0.1× PBS media, the inverse RC time constant can be calculated as: ∼ 1 MHz. Hence, at greater time intervals than this RC time constant (i.e. for lower frequencies of applied field), the nDEP level is greater due to the availability of greater time for build-up of charges within the diffuse layer of the nano-colloid. However, for time intervals approaching the RC time constant (i.e., for higher field frequencies approaching 1 MHz), the nDEP is gradually lowered due to the lack of time for build-up of charges within the diffuse layer of the nano-colloid. This explains the results of Figure 6(a) and Table II that show a maximum level of nDEP for SiO₂ nano-colloids at 100 kHz, with a 20% drop at 150 kHz, ∼ 55% drop at 400 kHz, and 85% drop at 800 kHz. Hence, through weighting the pixel intensities for delocalized nDEP pre-concentration with the field non-uniformities (over one order of magnitude, as per Figure 1(b)) using Eq. (10), the exponential fits of the collection rate at each frequency can be utilized to derive a quantitative polarizability dispersion of the nano-colloid, as per Figure 6(f). Through fitting this dispersion to a single-shell model, we are able to draw quantitative inferences on the polarization mechanism. This suggests that while the surface conductance at sub-μs time-scales (>MHz frequencies) results in a mild level of pDEP (Figure 1(c)), this interfacial polarization mechanism can be reversed at sub-MHz frequencies to cause nDEP, likely due to the availability of sufficient time (μs-ms) for causing concentration polarization of ions in the diffuse layer around the nano-colloid (outer shell in Figure 6(g)). Hence, the quantitative force dispersion computed through the image analysis method described here can provide quantitative information on particle polarization mechanisms under nDEP and pDEP.

FIG. 6.

(a) The pre-concentration dynamics of silica nano-colloids under nDEP at different frequencies ((b) 100 KHz, (c) 150 KHz, (d) 400KHz, (e) 800 kHz), with opposing EO, is quantified using the dynamic ROI method and fit at early time points (Table I) to compare relative polarizability differences with frequency in (f) (details in Table II), to quantify the polarizability dispersion as per the shell model in (g).

TABLE I.

Fitting parameters for pre-concentration dynamics at early time points using the linear and exponential functions (refer to Eqs. (7) and (9) for details).

Frequency	a	b	c	d	${\mathit{F}}_{\mathit{Exp}}^{·}(0)$	m	n	${\mathit{F}}_{\mathit{lin}}^{·}(0)$
100 KHz	5.132	−0.009398	−4.166	−0.3795	1.5328	0.138	1.08	0.138
150 KHz	5.603	−0.02778	−4.68	−0.2696	1.2101	0.109	0.99	0.109
400 KHz	1.858	−0.00786	−1.402	−0.514	0.7060	0.06	0.99	0.05897
800 KHz	0.2806	0.755	0.02074	0.1882	0.2158	0.018	0.98	0.018

TABLE II.

Quantifying relative alterations in polarizability of SiO₂ nano-colloids with frequency.

Frequency	${\mathit{F}}_{\mathit{Exp}}^{·}(0)$	$\frac{{\mathit{F}}_{\mathit{Exp}}^{·}(0)}{{\mathit{F}}_{\mathit{Exp}100\mathit{KHz}}^{·}(0)}$	${\mathit{F}}_{\mathit{lin}}^{·}(0)$	$\frac{{\mathit{F}}_{\mathit{lin}}^{·}(0)}{{\mathit{F}}_{\mathit{lin}100\mathit{KHz}}^{·}(0)}$
100 KHz	1.5328	1	0.138	1
150 KHz	1.2101	0.79	0.109	0.79
400 KHz	0.7060	0.46	0.06	0.43
800 KHz	0.21	0.14	0.018	0.13

IV. CONCLUSIONS

We present a dynamic methodology for defining the region of interest towards quantifying the pre-concentration dynamics of fluorescently labeled biomarkers over delocalized zones, as obtained under a balance of varying force fields. Unlike prior methods based on a statically defined region of interest, our method uses a statistical description of particle distribution across the device geometry to determine threshold intensity levels for pre-concentration and depletion, thereby dynamically defining the region of interest. This automated methodology is applied to study the pre-concentration dynamics of Neuropeptide Y biomarkers and silica nano-colloids under an electrokinetic force balance, driven by negative dielectrophoresis from insulating constriction tips, which causes a highly delocalized pre-concentration zone. The spatio-temporal evolution of the preconcentration dynamics is used to optimize alignment of the electrochemical detection electrode to the region with a threshold preconcentration level, to enhance analyte binding kinetics to the sensor. In order to quantitatively characterize the polarizability dispersion of pre-concentrated particles, the pixels are weighted to account for the spatial non-uniformities in the force field driving the pre-concentration. This methodology is applied to quantify the force dispersion of silica nano-colloids, thereby leading to quantitative inferences on the time evolution of the polarization mechanism.