Dynamics of chronic myeloid leukemia response to dasatinib, nilotinib, and high-dose imatinib

Abstract

Treatment with the tyrosine kinase inhibitor imatinib is the standard of care for newly diagnosed patients with chronic myeloid leukemia. In recent years, several second-generation inhibitors – such as dasatinib and nilotinib – have become available: these promise to overcome some of the mutations associated with acquired resistance to imatinib. Despite eliciting similar clinical responses, the molecular effects of these agents on different subpopulations of leukemic cells remain incompletely understood. Furthermore, the consequences of using high-dose imatinib therapy have not been investigated in detail. Here we utilized clinical data from patients treated with dasatinib, nilotinib, or high-dose imatinib, together with a statistical data analysis and mathematical modeling approach, to investigate the molecular treatment response of leukemic cells to these agents. We found that these drugs elicit very similar responses if administered front-line. However, patients display significantly different kinetics when treated second-line, both in terms of differences between front-line and second-line treatment for the same drug, and among agents when used as second-line. We then utilized a mathematical framework describing the behavior of four differentiation levels of leukemic cells during therapy to predict the treatment response kinetics for the different cohorts of patients. The dynamics of BCR-ABL1 clearance observed in our study suggest that the use of standard or high-dose imatinib or a second-generation tyrosine kinase inhibitor such as nilotinib or dasatinib elicits similar responses when administered as front-line therapy for patients with chronic myeloid leukemia in chronic phase.

Introduction

The tyrosine kinase inhibitor imatinib (STI571, Gleevec; Novartis), administered at 400 mg daily, is the standard front-line therapy for patients with chronic myeloid leukemia (CML) in chronic phase.^1–3 This molecularly targeted therapy leads to a dramatic clinical response: the International Randomized Study of Interferon Versus STI571 (IRIS) trial showed that 82% of patients achieved a complete cytogenetic response.⁴ However, a substantial fraction of patients develops acquired resistance to imatinib.^5–7 In order to improve the outcome of patients with early chronic-phase CML, several phase II clinical trials were conducted at the MD Anderson Cancer Center to investigate the treatment effects of new strategies: front-line treatment with high-dose imatinib (800 mg daily) as well as with the second-generation tyrosine kinase inhibitors dasatinib and nilotinib.^8,9 Results from these studies suggested the superiority of the use of dasatinib and nilotinib over standard imatinib therapy as front-line treatment. Both dasatinib and nilotinib induced a 98% complete cytogenetic response rate in patients treated for at least 3 months, with nearly 90% of patients achieving complete cytogenetic response by 3 months of therapy.^4,8,9 Furthermore, randomized phase III trials have demonstrated improved response rates and decreased rates of transformation in patients treated with nilotinib or dasatinib compared to the rates in patients treated with imatinib.^10–12 In addition, these tyrosine kinase inhibitors are more potent as inhibitors of the kinase activity of BCR-ABL1 and overcome the resistance imposed by most BCR-ABL1 mutants identified in patients with CML in whom imatinib therapy fails. When nilotinib or dasatinib is used after failure of imatinib therapy, these agents induce complete cytogenetic responses in approximately 50% of patients.^13–16

Despite the demonstrated superiority of the second-generation tyrosine kinase inhibitors as front-line therapy, several critical questions remain. For instance, the differential effects of dasatinib, nilotinib and high-dose imatinib on different subpopulations of CML cells are incompletely understood. We have previously addressed this question utilizing data from patients treated front-line with low-dose imatinib.^17,18 Furthermore, the ability of these agents to eliminate minimal residual disease remains to be demonstrated. Here we utilized datasets of patients with CML treated in several phase II studies to discern potential differences in the dynamics of molecular responses to second-generation tyrosine kinase inhibitors or high-dose imatinib in the context of front-line and post-imatinib failure settings. Our efforts include the development of a statistical model that gives a good, low-dimensional representation of the time courses and a mathematical model that estimates biologically interesting parameters. The parameters of these models were then compared between treatments strategies. This approach is useful for understanding the effects of different tyrosine kinase inhibitors on individual cell populations and can also be applied to other cancer types treated with targeted agents.

Methods

Study population and data collection

A total of 290 patients with CML treated front-line or second-line with tyrosine kinase inhibitors were investigated. These patients comprised 92 treated with dasatinib, 75 treated with nilotinib, and 123 treated with high-dose imatinib. All imatinib-treated patients were treated front-line, i.e. immediately after diagnosis of the disease, while 23 dasatinib–treated and 24 nilotinib-treated patients were administered the respective drug as second-line therapy after progression of disease. All patients received these agents in phase II studies^8,9 at the MD Anderson Cancer Center. Fourteen of the 243 patients treated front-line and 16 of the 47 treated second-line had accelerated phase disease based exclusively on the presence of clonal evolution; the remaining patients were in chronic phase. The assignment of treatment was not done in a randomized fashion; the studies with imatinib and high-dose imatinib were conducted in a sequential fashion. Subsequently, both phase II studies using either nilotinib or dasatinib as front-line therapy were conducted in parallel and superseded the study with high-dose imatinib. While patients were not assigned to the latter phase 2 studies in a randomized fashion, they were distributed between both studies so as to sustain a similar rate of accrual.

The levels of BCR-ABL1 transcripts in peripheral blood samples were measured by quantitative real-time polymerase chain reaction. The ratio of BCR-ABL1 to the control gene ABL1 was determined. BCR-ABL1/ABL1 ratios are expressed in accordance with the International Scale. Patients’ samples were obtained to determine the BCR-ABL1/ABL1 ratio ideally at 0, 3, 6, 9, 12, 18, and 24 months after initiation of therapy. All 290 patients had measurements at the first five time points. Overall, 32 (11%) patients had five measurements, 41 (14%) patients had six measurements, and 217 (75%) patients had all seven measurements.

A second set of 13 patients treated with standard-dose imatinib (400 mg daily) from the IRIS trial was included as a control and analysed using the same methodology. We utilized only measurements made at 0, 3, 6, 9, 12, 18, and 24 months after initiation of therapy for this analysis. The 15- and 21-month measurements as well as measurements after the 24^th month (if any) were neglected to make the data sets comparable. Importantly, only patients with measurements at the first five time points were included.

Data were analyzed using two types of models. The first was a statistical model described in the following part of the manuscript. The second was a mathematical model described partly after the statistical model and partly in the Online Supplement. All analyses were conducted in R. Statistical tests with corresponding P values less than 0.05 were considered significant.

Results

To investigate the time courses of BCR-ABL1 transcript levels, we first designed a statistical model with the primary goal of finding the best fit to the data with minimal assumptions. We chose a low-dimensional model in our statistical approach because we sought to obtain simple summaries of the time courses. In addition, since there were at most seven measurements per patient, the data supported only a low-dimensional model. As a first step, we used the natural logarithm to transform our data, since the measurements were on vastly different scales. We added 1 to the observed data before transformation since some of the measured transcript levels were 0. Our initial model on the transformed data was bi-exponential, which is the sum of two scaled exponentials, and is traditional for modeling exponentially-decaying data.¹⁹ Such a model contains four parameters per subject, which were considered to be too many. As shown in Online Supplementary Figure S1, we found that one of the exponentials could be replaced with a constant, which saved a parameter with little reduction in goodness of fit. To save additional degrees of freedom, we examined models that represented aspects of the times courses that were common across subjects. Our resulting model for the i^th subject at time t was given by y_it = α_0i + α_1i exp[-βt] + ε_it, where α_0i was the subject-specific intercept, α_1i was the subject-specific slope, β was the population-based shape parameter and εit were independent, identically distributed mean 0 errors. In other words, α_0i was the patient-specific amount by which the exponential curve was offset from 0, α_1i was the patient-specific magnitude by which the exponential curve was multiplied, and β was the common value across all patients that determined the shape of the exponential curve, with larger values implying faster decreases. We did not consider patient-specific β values because we wanted a low-dimensional model and because trying to estimate them would have introduced identifiability issues. We then developed an iterative procedure to fit the model to the data. We obtained an initial estimate of β after merging all data from all subjects using non-linear least squares. With β fixed, we then estimated the subject-specific parameters (α_0i and α_1i) using traditional least squares. We iterated between estimating the population parameter and the subject-specific parameters until convergence. A z-test was used to test differences in the population parameters between treatment groups.

Estimates of α_0i and α₁ for subjects were treated as data for further analysis. These estimates were correlated with each other, so joint modeling was necessary. Specifically, multivariate analysis of variance (MANOVA),²⁰ an extension of univariate analysis of variance (ANOVA), was used with treatment drug, front-line or second-line status of the drug, and stage as independent variables and α₀ and α₁ as dependent variables. Significance was assessed using the Wilks test. Because the dependent variables were not jointly Gaussian, inference was based on 10,000 permutations of the independent variables. The variable that was permuted (treatment, line, or stage) corresponded to the variable on which inference was made.

Once we had decided on our model, the primary analysis tested whether the subject-specific parameters were equal, first three-way and then pairwise. Subsequent analyses compared front-line to second-line treatment and chronic to accelerated phase within the dasatinib and nilotinib cohorts and the whole set of hypotheses on only the set of typical curves.

We fitted the exponential model described above to the transcript levels of 290 CML patients. The means for the ratios for time points 0, 3, 6, 9, 12, 18, and 24 months after initiation of therapy were 28.4, 4.3, 2.1, 0.7, 2.6, 1.8, and 0.8. We first fitted the model separately for patients treated with dasatinib, nilotinib or high-dose imatinib. Note that this investigation utilizes data of patients treated first-line as well as patients treated second-line; we present the analysis for subcohorts later. We estimated the population parameter β as 0.69 for dasatinib-treated patients, 0.65 for nilotinib-treated patients and 0.62 for the patients treated with high-dose imatinib. Recall that β represents the common value that determined the shape of the exponential curve, with larger values implying faster decreases. These parameter estimates were not significantly different in any pairwise comparison between the treatment groups (P=0.84 for high-dose imatinib versus nilotinib; P=0.58 for high-dose imatinib versus dasatinib; P=0.85 nilotinib versus dasatinib). Therefore, we concluded that a single population parameter β, which represents the rate of exponential depletion of BCR-ABL1 values over time, could accurately represent the curves across treatment groups. To estimate this single β, we combined all data across groups and fitted the exponential model again. The resulting β was 0.65. The model fitted the data well for all three treatment groups, with a median R² of 0.96 for each. The fits, shown in Figures 1–3, were the basis for further analyses. There are cases shown in Figure 3 that do not follow our exponential model; the repetition of the analysis without such cases is discussed later.

Figure 1.

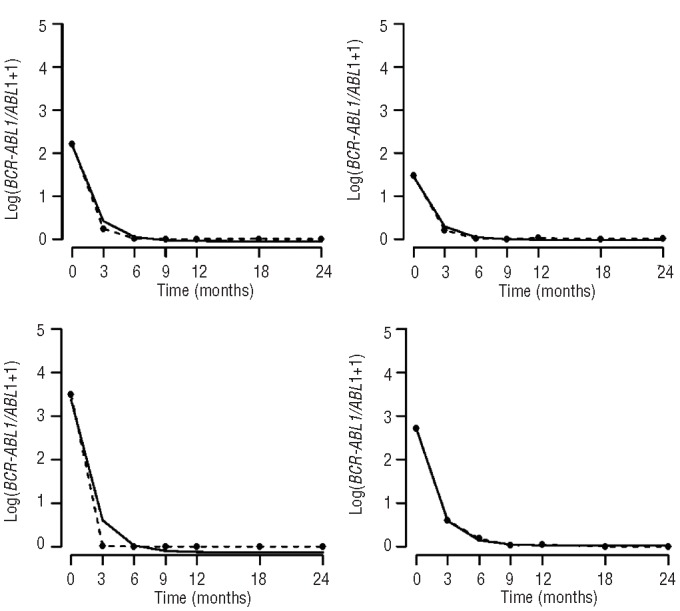
The high-dose imatinib cohort. The figure shows data from four representative patients from the high-dose imatinib cohort, displaying the ratio of BCR-ABL1 to ABL1 plus one over time measured in months (broken line) as well as the exponential model (solid line).

Figure 3.

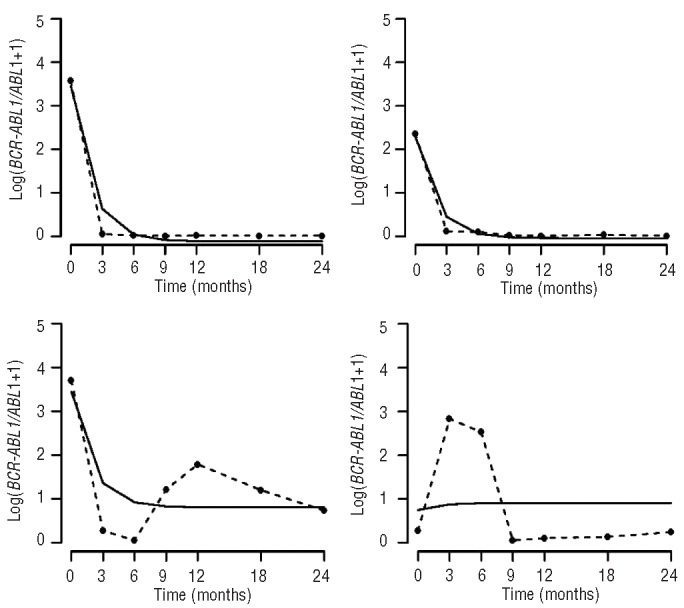
The dasatinib cohort. The figure shows data from four representative patients from the dasatinib cohort, displaying the ratio of BCR-ABL1 to ABL1 plus one over time measured in months (broken line) as well as the exponential model (solid line).

Figure 2.

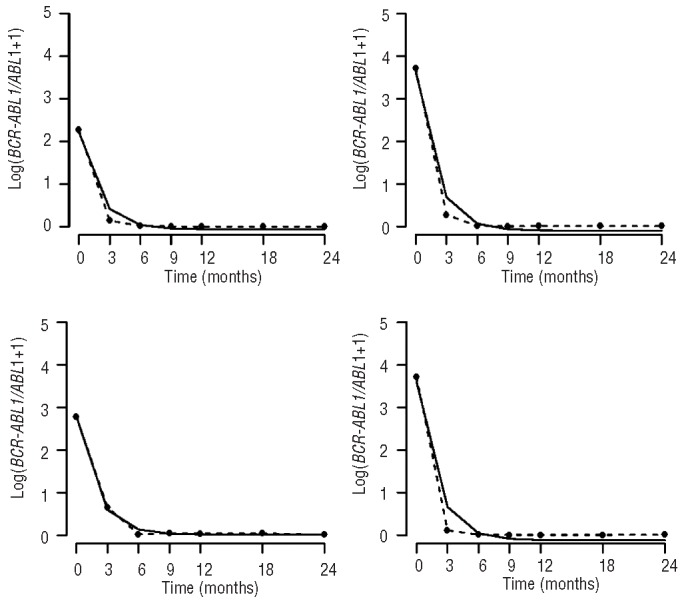
The nilotinib cohort. The figure shows data from four representative patients from the nilotinib cohort, displaying the ratio of BCR-ABL1 to ABL1 plus one over time measured in months (broken line) as well as the exponential model (solid line).

The subject-specific intercept (α₀) and slope (α₁) values from the combined fit were dependent variables in MANOVA models; these models examined whether there were independent variables with which the dependent variables were associated. Results are displayed in Table 1. Recall that α_0i represents the patient-specific amount by which the exponential curve was offset from 0, and α_1i was the patient-specific magnitude by which the exponential curve was multiplied. A three-way comparison among the treatment groups was significant (P=0.004), so the hypothesis that the subject-specific parameters were the same across groups was rejected. Pairwise comparisons between treatment groups showed no significant difference between high-dose imatinib and dasatinib (P=0.14). However, they did show a significant difference between imatinib and nilotinib (P=0.001) and between nilotinib and dasatinib (P<0.001). The average intercept for nilotinib-treated patients was higher (0.52 versus 0.29) and the average slope was lower (2.34 versus 2.51) relative to those for the dasatinib-treated patients. Note that these results were obtained when analyzing patients treated front-line or second-line. When analyzing only the patients treated front-line, the three-way comparison among treatments was not significant (P=0.72). However, front-line versus second-line status led to significantly different results (P<0.001). Here patients treated front-line had a lower average intercept (0.14 versus 1.04) and a higher average slope (2.70 versus 1.44) than patients given the tyrosine kinase inhibitor as second-line treatment. Within the dasatinib and nilotinib cohorts, front-line was significantly different than second-line (P<0.001 for both). The directions of slope and intercept were the same as in the merged front-line and second-line groups.

Table 1.

Comparison of intercepts α₀ and slopes α₁ in the statistical model for treatment groups, front-line versus second-line, as well as CML stages.

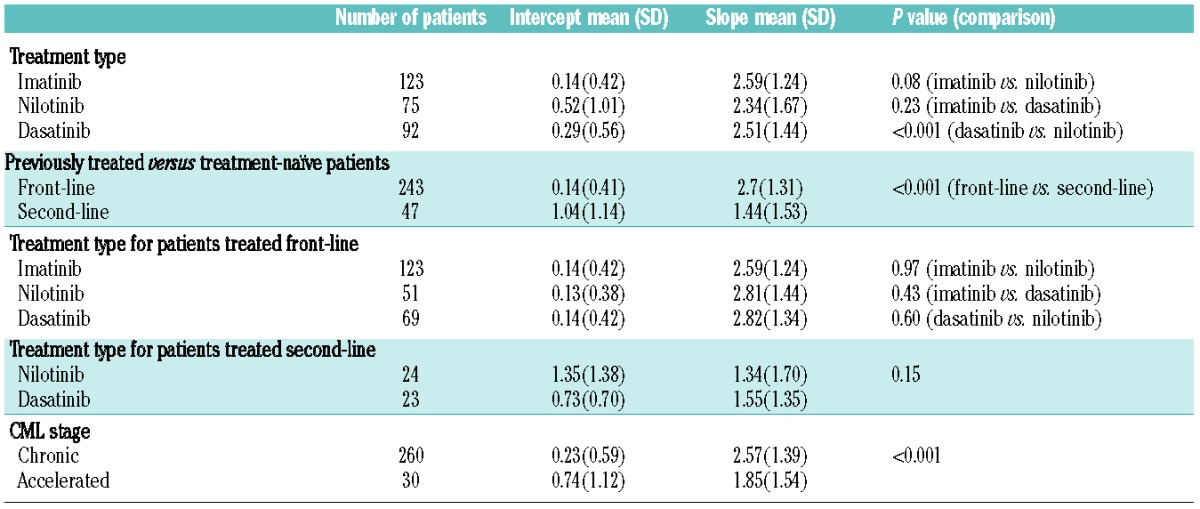
Overall, there were no significant pairwise differences between treatment groups within the front-line or within the second-line cohorts. While there was a significant difference between chronic and accelerated phase (P<0.001), there was no significant difference between stages when analyzing only patients treated front-line. A bivariate model with both treatment and front-line status was significant for both variables, indicating treatment and front-line status were independent prognostic factors.

Based on the preceding analysis, we drew a few conclusions. First, the shape of the curves was similar across treatment groups. Second, the driver of the difference between curves was front-line versus second-line status. The front-line curves tended to have lower intercepts but higher scale factors. Third, after taking into account front-line versus second-line status, there was still an impact of treatment.

We also conducted a similar analysis on the cohort of patients treated with 400 mg imatinib. Here the population parameter β was taken from the earlier three-group analysis and the subject-specific parameters were compared. The four-way comparison among groups was again statistically significant (P<0.001). Pairwise comparisons between each of the three groups and standard-dose imatinib were all statistically significant.

We next explored the robustness of our modeling. There were two main ways in which a subset of curves differed from the typical exponential pattern. Some curves increased over a portion of the time interval, rather than decreasing or staying level. Other curves showed low values throughout. To identify the increasing curves, we used the heuristic of two measurements in the log-transformed data that were more than one unit above the previously observed minimum. The reason for choosing this criterion was that small increases were possible due to random variation in small values. In addition, occasional faulty measurements were possible. There were 22 (7.6%) such increasing curves. The percentages by treatment groups were 3.3% for the patients treated with high-dose imatinib, 8.7% for those treated with nilotinib, and 13.3% for the patients treated with dasatinib. Pairwise, the only significant difference in percentages was between high-dose imatinib- and dasatinib-treated patients (P=0.01). Among the patients treated front-line, 3.3% had increasing values, while among the patients treated second-line, 29.8% had increasing values. This difference was statistically significant (P<0.001).

Low value curves were those with maximum values less than one in the log-transformed data. There were 22 samples (7.6%) of this type. The percentages were 6.5% for imatinib-, 8.0% for nilotinib-, and 8.7% for dasatinib-treated patients. None of these percentages was significantly different from each other by pairwise comparison. These percentages were 7.4% for front-line treatment and 8.5% for second-line treatment, which were again not significantly different.

The analyses above were repeated on just the patients treated at the MD Anderson Cancer Center with the increasing and low value curves eliminated. This approach left 246 out of the original 290 patients. The population parameter β was again not significantly different among treatment groups based on pairwise comparison, so a single model was fitted to all curves. For the MANOVA model, the three-way comparison among the treatment groups was only borderline significant (P=0.06). Pairwise differences this time were all not significant. The three-way comparison for just the patients treated front-line was again not significant (P=0.38). Front-line versus second-line status was again significant when comparing all patients or only within nilotinib- or dasatinib-treated patients (P<0.001 for all three). The bivariate model with both treatment and front-line status was again significant for both variables, indicating that treatment and front-line status were independent prognostic factors. Overall, the results were robust to inclusion or exclusion of atypical curves.

We then utilized a previously designed mathematical model describing the differentiation hierarchy of hematopoietic cells^17,18 to analyze the data. This model was created to relate the available data on BCR-ABL1 transcript levels in peripheral blood to the kinetics of other, unobservable levels of differentiation of leukemic cells. Through this model, we thus aimed to investigate the underlying mechanism of treatment response by studying the different response kinetics of separate leukemic subpopulations. In the context of this model, stem cells on top of the hierarchy give rise to progenitor cells, which produce differentiated cells, which in turn produce terminally differentiated cells. This differentiation hierarchy applies to normal and leukemic cells. The model assumes that the BCR-ABL1 oncogene increases the rate at which progenitors and differentiated cells are being produced. Molecularly targeted therapy counteracts the effects of BCR-ABL1 by reducing the differentiation rates and possibly reducing the growth rate of leukemic stem cells. The basic model together with a description of the parameters is provided in Online Supplementary Table S1.

This model represents the four kinetically dominant subpopulations in the hematopoietic differentiation hierarchy; in reality, this hierarchy includes a larger number of distinct differentiation levels. However, for the purposes of explaining the dynamics of response to tyrosine kinase inhibitors, only four populations need to be included in a mathematical model since they are the kinetically dominant populations. Similarly, if each subpopulation consists of many clones of the same differentiation stage, which may have distinct growth, differentiation, and death kinetics, then the predictions of the model with regard to the question addressed in this paper does not change. The model then describes the dominant clone within the respective subpopulation at any given time.

To investigate the parameters of the mathematical model, we again utilized the data of newly diagnosed patients who were treated with front-line dasatinib, nilotinib or imatinib (800 mg or 400 mg daily) outlined above. Any value of zero, i.e. any value below the detection baseline of the polymerase chain reaction assay, was replaced with 0.00001. The replacement value of 0.00001 was chosen because the minimum value in the data was 0.00004. This replacement was needed for the logarithmic transformation and is consistent with the previous use of this model.¹⁸ We later conducted sensitivity analyses on the choice of this replacement value using 0.00002 and 0.000005 and obtained consistent conclusions. For each treatment cohort, we investigated two models and selected the one that best fitted the data using R² and a permutation test. The two models analyzed were: (i) an exponential model, which predicts that the leukemic cell burden declines at a single exponential rate; and (ii) a bi-phasic exponential model, which predicts that the BCR-ABL1/ABL1 ratio declines according to two exponential slopes with a turning point.^17,18 The estimated slopes were then incorporated into our mathematical framework to predict the dynamics of treatment responses in the four cohorts. Note that the model fitting and R² calculation used the logarithmically transformed data (Online Supplementary Information). Once we decided on our model, the primary analysis tested whether the estimated slopes were equal, first three-way and then pairwise.

When applying this approach to our cohorts of CML patients, we found that the bi-phasic exponential model was the better fitting of our two models for all four cohorts (Online Supplementary Table S2). Besides the analysis of the entire cohort, we also performed individual model fitting to compare, for each individual patient, the fit of the single-phasic and bi-phasic exponential models. Based on the permutation test procedure (using the join-point software, http://surveillance.cancer.gov/joinpoint/), we obtained a better fit of the bi-phasic model for 35 out of the 69 patients in the dasatinib cohort, 26 out of the 51 patients in the nilotinib cohort, 54 out of the 123 patients in the high-dose imatinib cohort, and for all 13 patients in the standard-dose imatinib cohort (Online Supplementary Table S3). The first and second slopes of depletion as well as the turning point for the bi-phasic patients in the four cohorts are summarized in Table 2.

Table 2.

Summary statistics of slopes and turning points in all four cohorts of patients. The table displays the first (β₁) and second (β₂) slopes as well as the turning points (τ) for all patients in all four cohorts whose treatment response data displayed a bi-phasic trend and whose first and second slopes were negative. The unit for slopes is BCR-ABL1/ABL1% per day and the unit for the turning point is months.

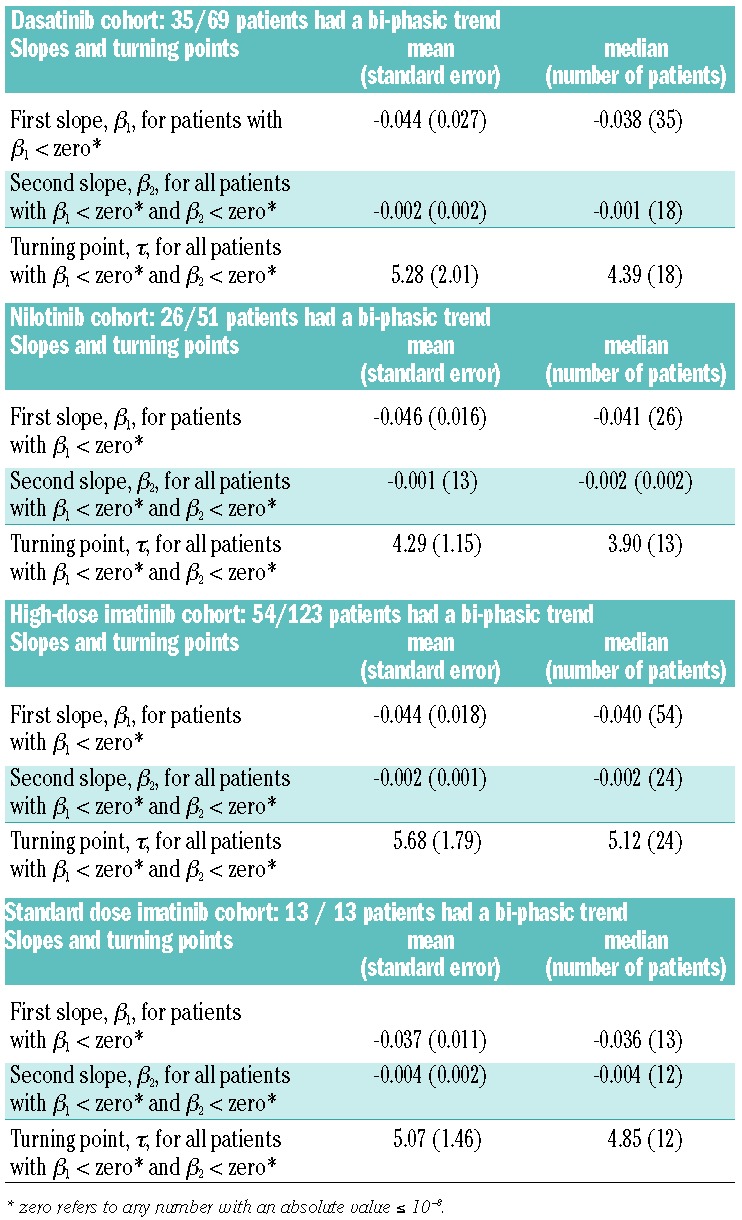
There was no significant difference in the number of patients exhibiting single-phasic versus bi-phasic trends among the dasatinib, nilotinib and high-dose imatinib cohorts (Fisher exact test, P=0.55 for the three-way comparison, P values for pairwise comparisons were 1, 0.37, and 0.41, respectively) (Online Supplementary Table S3). The differences in the trend were significant for pairwise comparison of the low-dose imatinib cohort with the dasatinib, nilotinib and high-dose imatinib cohorts (Fisher exact test, P=5×10⁻⁴, P=9×10⁻⁴, P=5×10⁻⁵, respectively).

For patients with the bi-phasic model as better fitting in the dasatinib, nilotinib and 800 mg imatinib cohorts, there was no significant difference in the number of positive/negative/zero second slopes (Fisher exact test, P=0.85 for the three-way comparison, P values for the pairwise comparisons were 0.79, 0.58, and 0.94 respectively) (Online Supplementary Table S3). The differences were significant when performing pairwise comparisons between the cohorts treated with 400 mg imatinib or dasatinib, and between the cohorts treated with nilotinib or 800 mg imatinib (Fisher exact test, P=0.025, P=0.028, and P=0.009, respectively).

There were 35 patients in the dasatinib cohort, 26 in the nilotinib cohort, 54 in the high-dose imatinib cohort and 13 patients in the low-dose imatinib cohort in whom the bi-phasic model was the better fitting model and for whom the first slopes were negative (Online Supplementary Table S3). There was no significant difference in the first slope among the four cohorts when applying the Wilcoxon test in a pairwise manner. Regarding the second slopes, the number of bi-phasic patients with both negative first and second slopes was 18 for the dasatinib cohort, 13 for the nilotinib cohort, 24 for the high-dose imatinib cohort and 12 for the 400 mg imatinib cohort (Online Supplementary Table S3). For the three cohorts (dasatinib, nilotinib and 800 mg imatinib) from MD Anderson, there was no significant difference in the second slope among them. However, there was a significant difference in second slopes between the 400 mg imatinib cohort and all three other cohorts. There was a significant difference in turning points only between the nilotinib cohort and the 800 mg imatinib cohort.

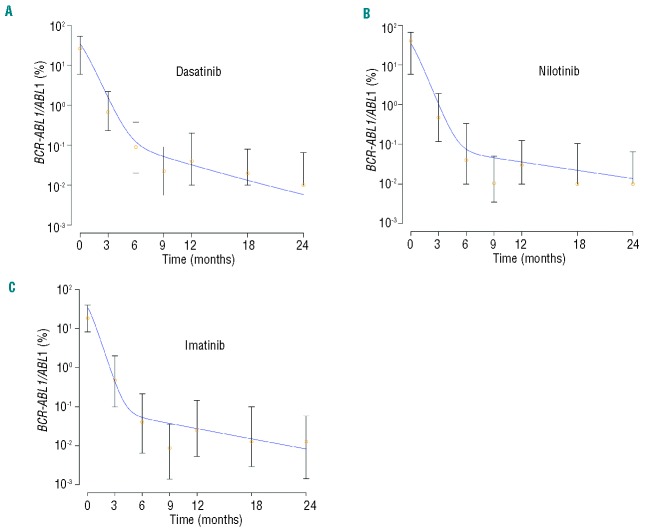
We then incorporated the estimated first and second slopes into our mathematical framework to investigate the dynamics of treatment responses of the four cohorts. We found that the framework accurately predicted the dynamics of treatment responses of all cohorts (Figure 4). These findings suggest that a model based on four distinct subpopulations of cells within the differentiation hierarchy can accurately explain the treatment responses not only to first-line, low-dose imatinib, but also to second-line treatment as well as therapy with second-generation tyrosine kinase inhibitors. This model will be useful for analyzing long-term treatment responses as more data become available.

Figure 4.

A mathematical framework accurately predicts the dynamics of treatment responses of cohorts of patients treated with dasatinib, nilotinib and high-dose imatinib separately. The panels display the median (orange circles) and quartiles of the dasatinib, nilotinib and high-dose imatinib response data together with the results of the mathematical framework (blue curves, see Online Supplementary Table S1). (A) Median plots and results of the mathematical framework for the dasatinib response data. (B) Median plots and results of the mathematical framework for the nilotinib response data. (C) Median plots and results of the mathematical framework for the high-dose imatinib response data. Based on the model presented in the Online Supplement, the mathematical model prediction is given by y₃/(2x₃+ y₃). Here x₃ and y₃ denote the abundance of normal and leukemic terminally differentiated cells. Parameter values are d₀ = 0.0005, d₃ = 1, r_x = 0.008, r_y = 0.01, p_x = 1.5×10⁻⁵, p_y = 1.9×10⁻6, a_x = 0.35, b_x = 5.5, c_x = 100, a_y = 2a_x, b_y = 1.5*b_x, c_y = c_x, c′_y = c_y, r′_y = r_y/15. For the dasatinib cohort, d₁ = 0.0053, d₂ = 0.0394, a′_y = a_y/200, b′_y = b_y/300; for the nilotinib cohort d₁ = 0.0028, d₂ = 0.0442, a′_y = a_y/400, b′_y = b_y/600; for the high-dose imatinib cohort, d₁ = 0.0035, d₂ = 0.055, a′_y = a_y/400, b′_y = b_y/600. Apart from the dimension-less parameters, all values are given in units per day. Note that these parameter choices represent only one example that can recapitulate the dynamics of the treatment response seen in the clinic; other choices are possible.

Discussion

We have presented a quantitative approach to model the time course of BCR-ABL1 transcripts in patients with CML. We first designed a statistical model using minimal assumptions to provide maximal generalizability and information retrieval from the data. This model provided information on the shape of the treatment response curves as well as differences between and among cohorts of patients. We then utilized a mathematical model emphasizing the biological interpretability of the parameters. This model considers four distinct cell populations within the differentiation hierarchy of the leukemia and can be used to predict the treatment response for different cohorts of patients.

Our approach demonstrated that dasatinib, nilotinib and high-dose imatinib elicit very similar treatment responses in patients treated first-line with these tyrosine kinase inhibitors. These patterns include decreases in BCR-ABL1 transcripts in two phases during short-term treatment. The main result from the statistical model was a difference between dasatinib and nilotinib only when including front-line and second-line patients. When comparing the 400 mg imatinib cohort from the IRIS trial with the three cohorts from the MD Anderson Cancer Center in a pairwise manner, there were significant differences in phase trends and second slopes.

However, there were a number of limitations to our study. The set of data from the IRIS trial was much smaller than the datasets obtained from the MD Anderson patients and the data were generated at different geographical sites. Furthermore, with the exception of the nilotinib and dasatinib datasets, which were derived from two parallel phase II clinical trials, the data were not contemporaneous with each other nor were they obtained from a randomized study. In addition, the low-dose imatinib cohort contained a small number of patients who tolerated the treatment for up to 10 years, which might lead to the analysis of a very selected subgroup of patients. For the MD Anderson patients, there was not a significant difference among treatment groups by age (P=0.53; Kruskal-Wallis test) or by percentage in chronic phase (P=0.09; Fisher exact test). Another limitation of the analysis was the limited number of data points (between 5 and 7) for each individual subject. A final limitation was that multiple analyses were performed. The nature of these analyses (some of them were multiple treatment comparisons and some were subset analyses) makes it difficult to control the family-wise error rate. However, even in randomized trials it is rare to see an adjustment for subgroup analyses, so we believe that our approach is valid.

These caveats notwithstanding, and in concert with the results herein reported, in the setting of front-line therapy, treatment with the second-generation tyrosine kinase inhibitors nilotinib and dasatinib has been shown in randomized phase III studies (i.e. the ENESTnd and DASISION studies) to produce remarkably better response rates than standard-dose imatinib.^10–12 However, results from the TOPS study, a phase III randomized study comparing the efficacy of high-dose imatinib and standard-dose imatinib, resulted in similar outcomes in both arms of the study.²¹ A potential explanation for this discrepancy is the fact that in the TOPS study, a higher proportion of patients receiving high-dose imatinib had to discontinue therapy with such an approach due to toxicity, whereas in the ENESTnd and DASISION studies, the toxicity profiles of nilotinib and dasatinib were similar to (if not better than) that of imatinib and the dropout rates from the study favored the use of the second-generation tyrosine kinase inhibitors.^10–12 It is also worth emphasizing that in the TOPS study, patients treated with high-dose imatinib achieved complete cytogenetic responses and major molecular responses considerably earlier than those receiving standard-dose imatinib (6-month complete cytogenetic response 57% versus 45% with standard dose; P=0.01) and those receiving high-dose imatinib capable of maintaining adequate dose intensity had improved outcomes. A recent study showed higher major molecular response rates at 12 months among patients receiving high-dose imatinib than among those receiving standard-dose imatinib (59% versus 44%, P<0.001) and improved rates of complete molecular responses by 3 years (57% versus 46%, respectively).²² These results are important given the favorable prognostic impact of achieving early deep molecular responses shown by different independent studies.^23–25 In contrast to these findings, the dynamics of BCR-ABL1 clearance observed in our study suggest that the use of standard or high-dose imatinib or a second-generation tyrosine kinase inhibitor such as nilotinib or dasatinib elicits similar responses when administered as front-line therapy for patients with CML in chronic phase. The discrepancy between our results and previous findings might stem from differences in the selection of patients, an absence of randomization in the study protocol leading to biases in the MD Anderson cohorts, and the use of different statistical methods designed to analyze the shape of the treatment response curves in detail. In particular, the standard-dose imatinib cohort was part of the Australasian arm of the IRIS trial and represents a very selected subgroup of patients – those that tolerated imatinib for a prolonged period (up to 10 years) without developing resistance or progression of disease. They might thus be examples of the best possible response kinetics that standard-dose imatinib can elicit. Furthermore, the blood samples of these patients were not analyzed at MD Anderson, unlike the samples from the remainder of the patients included in our study. Nevertheless, our results do not provide evidence against using second-generation tyrosine kinase inhibitors as front-line treatment for patients with chronic phase CML.