On the Selection of Sampling Points for Myocardial T₁ Mapping

Abstract

Purpose

To provide a method for the optimal selection of sampling points for myocardial T₁ mapping, and to evaluate how this selection affects the precision.

Theory

The Cramér-Rao lower bound on the variance of the unbiased estimator was derived for the sampling of the longitudinal magnetization curve, as a function of T₁, signal-to-noise ratio (SNR) and noise mean. The bound was then minimized numerically over a search space of possible sampling points to find the optimal selection of sampling points.

Methods

Numerical simulations were carried out for a saturation recovery based T₁ mapping sequence, comparing the proposed point selection method to a uniform distribution of sampling points along the recovery curve for various T₁ ranges of interest, as well as number of sampling points. Phantom imaging was performed to replicate the scenarios in numerical simulations. Invivo imaging for myocardial T₁ mapping was also performed in healthy subjects.

Results

Numerical simulations show that the precision can be improved by 13-25% by selecting the sampling points according to the target T₁ values of interest. Results of the phantom imaging were not significantly different than the theoretical predictions for different sampling strategies, SNR and number of sampling points. In-vivo imaging showed precision can be improved in myocardial T₁ mapping by using the proposed point selection method as predicted by theory.

Conclusion

The framework presented can be used to select the sampling points in order to improve the precision without penalties on accuracy or scan time.

Introduction

Quantitative mapping of various MR parameters, such as longitudinal (T₁) or transverse (T₂) relaxation times may provide diagnostic information beyond conventional contrast-weighted images (1). These quantitative techniques have found a range of applications in neurological (2,3), oncologic (4,5) and cardiac (6,7) applications. In particular, recently, myocardial T₁ mapping (8-12) has been shown to provide a technique for assessment of interstitial diffuse fibrosis (13). Furthermore, if myocardial T₁ maps are acquired both prior to and following contrast injection, they can further be used to measure the extracellular volume fraction (14), which has shown utility for detection of diffuse myocardial fibrosis (6).

Quantitative mapping approaches rely on acquiring multiple images of the same anatomy with different contrast weightings, achieved by varying one or more imaging parameter(s). These parameters may include flip angles (15), echo times (16) and/or inversion/saturation times (17). Then a closed-form expression, which characterizes how the magnetization evolves, as a function of the unknown parameters of interest and the known parameter(s) that is being varied, is voxel-wise fitted to these series of images. Clearly, the number of images in this series has to be greater than or equal to the number of unknown parameters of interest. Thus, multiple images are acquired in the series with different contrasts, which correspond to different sampling points on the magnetization curve that is parameterized by the unknown quantities.

To achieve a sufficient level of precision in the estimation, a high number of images are acquired with different choices of sampling points (18), typically with a uniform distribution along the curve (10,19), resulting in a long acquisition time. However, there is a degree of freedom on the selection of the location and the number of the sampling points on the parametric curve, which is controlled by the sequence designer. Furthermore, in myocardial parameter mapping, the respiratory motion has to be compensated for. In myocardial T₁ mapping, this is commonly achieved by performing breath-holds, typically ranging from 11 to 17 heartbeats (8,10,11,20). Thus it is critical to improve the precision of the sequence with this constraint on the total scan time.

The precision of the T₁ estimation process can be characterized by the Cramér-Rao Bound, which (CRB) provides a lower bound on the variance of an unbiased estimator of a deterministic parameter (21). Furthermore it characterizes when an estimator that achieves this lower bound exists. CRB has been used in a number of MRI applications, including diffusion kurtosis imaging (22,23) and parameter mapping (24-26). By considering a parametric model involving the gradient vector directions, as well as the diffusion and kurtosis tensors, an estimation theoretic approach was used to optimize the direction and b-value of the diffusion weighting gradients (23). It was shown that the optimal selection was different than the conventionally used set of standard gradient settings, and this selection lead to improvements in precision. In parameter mapping, an approach for determining experimental parameters were proposed in (24) for rapid simultaneous T₁ and T₂ measurement. This CRB-based technique was used in (25) for characterizing optimal sampling times to determine the T₂ relaxation time. The optimal scheme yielded a distribution concentrated at certain points related to the T₂ value, unlike the traditional uniform distribution utilized in other studies. Most similar to our current work is that of (26), which derived the CRB for T₁ mapping. This was then used to characterize the selection strategies for certain ordered sampling schemes, which lead to tractable analytical expressions.

Because the search space in (26) was limited to these ordered sampling schemes, the resulting sampling schemes were not similar to that of (25) in T₂ mapping, which exhibited concentrations at certain areas of the parametric curve. Furthermore, only numerical simulations were used in (26), with no validation for phantom or in-vivo data.

In this work, we sought to use an estimation theoretic framework for bounding the precision of a given myocardial T₁ mapping sequence in the presence of noise. We extend the bounding approach of (26) to accommodate a wide range of T₁ values of interest, by providing a Bayesian lower bound on the precision of the T₁ estimator, defined as the standard deviation of error for a given noise level. We then propose to determine the optimal selection of sampling points by numerically minimizing this bound. To test the theory in practice, we choose a saturation-based T₁ mapping sequence, and minimize the corresponding closed form expression for the lower bound over a large search space of sampling points to select an improved distribution of sampling points for a given range of T₁ values of interest. Numerical experiments, phantom and in-vivo imaging are performed to evaluate the proposed sampling point strategy versus a uniform distribution of sampling points along the curve.

Theory

Cramér-Rao Lower Bound for Parameter Mapping

For completeness, we describe the signal model and derive the CRB for T₁ mapping, which is similar to the derivation of (26). In myocardial T₁ mapping, at each sampled image voxel, we observe

$$y_k=M(x_k;a,b,T_1)+n_k,$$ [1]

for k ∈ {1, ..., K} representing images with different contrast weightings along the longitudinal magnetization curve. n_k is measurement noise. Furthermore,

$$M(x_k;a,b,T_1)=a(1-b\exp (-x_k∕T_1)),$$ [2]

is the magnetization at x_k on the magnetization curve, parameterized by a, the signal-to-noise ratio of the image with fully recovered magnetization (with appropriate normalization for the noise variable n_k); b, which captures the saturation/inversion efficiency, the effects of imaging pulses on the magnetization recovery (10) and the mean of noise in the magnitude images (27), and T₁, the longitudinal relaxation time.

For the K observations, we let Y = {y₁, y₂, ..., y_K}. Based on the noise distribution, the probability density function p(Y|a,b,T₁) can be determined. This in turn can be used to find the Fisher information matrix (21), whose info (i,j)^th entry is given by:

$${\left[\mathbf{I}\right]}_{ij}=-E\left[\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\log p(\mathbf{Y}\mid \theta )\right],$$ [3]

where, for ease of notation, θ₁ = a, θ₂ = b, θ₃ = T₁. Then the CRB states, if p(Y|a,b,T₁) satisfies certain regularity conditions (21), the estimator of T₁, denoted by $T_1^{est}$, has variance bounded by

$$\mathrm{var}\left(T_1^{est}\right)\ge {\left[{\mathbf{I}}^{-1}\right]}_{3,3}.$$ [4]

Since the Rician noise in the magnitude images is well-approximated as Gaussian noise with sufficient baseline SNR (27), and since the maximum-likelihood estimate for Gaussian noise corresponds to the least-squares estimator that is commonly used in the context of MR parameter estimation (2,8), we restrict ourselves to a Gaussian noise model. Without loss of generality, we consider unit-variance zero-mean Gaussian noise, since the non-zero mean can be captured using the parameters, a and b in the T₁ mapping model. In this setting,

$$\log p(\mathbf{Y}\mid \theta )=C-\frac{1}{2}\sum _{k=1}^K{\mid y_k-M(x_k;\theta )\mid }^2,$$ [5]

where C is a constant. We also note that the maximum-likelihood estimator is unbiased and attains this lower bound for this log-likelihood function (21).

Optimization of Sampling Point Selection

The model described by Equations [1] and [5] leads to:

$${\mathbf{I}}_{ij}=-E\left[\frac{{\partial }^2}{\partial {\theta }_i\partial {\theta }_j}\log p(\mathbf{Y}\mid \theta )\right]=\sum _{k=1}^K\frac{\partial M(x_k;\theta )}{\partial {\theta }_i}\frac{\partial M(x_k;\theta )}{\partial {\theta }_j},$$ [6]

Thus the Fisher information matrix for the T₁ mapping model of [6] is

$$\mathbf{I}=\left[\begin{array}{ccc}\hfill \sum _{k=1}^K{\left(1-b{e}^{\frac{-x_k}{T_1}}\right)}^2\hfill & \hfill \sum _{k=1}^K\left(-a{e}^{\frac{-x_k}{T_1}}\right)\left(1-b{e}^{\frac{-x_k}{T_1}}\right)\hfill & \hfill \sum _{k=1}^K-ab\frac{x_k}{T_1^2}{e}^{\frac{-x_k}{T_1}}\left(1-b{e}^{\frac{-x_k}{T_1}}\right)\hfill \\ \hfill \sum _{k=1}^K\left(-a{e}^{\frac{-x_k}{T_1}}\right)\left(1-b{e}^{\frac{-x_k}{T_1}}\right)\hfill & \hfill \sum _{k=1}^K{\left(-a{e}^{\frac{-x_k}{T_1}}\right)}^2\hfill & \hfill \sum _{k=1}^K{a}^{2}b\frac{x_k}{T_1^2}{e}^{\frac{-2x_k}{T_1}}\hfill \\ \hfill \sum _{k=1}^K-ab\frac{x_k}{T_1^2}{e}^{\frac{-x_k}{T_1}}\left(1-b{e}^{\frac{-x_k}{T_1}}\right)\hfill & \hfill \sum _{k=1}^K{a}^{2}b\frac{x_k}{T_1^2}{e}^{\frac{-2x_k}{T}}\hfill & \hfill \sum _{k=1}^K{\left(ab{e}^{\frac{-x_k}{T_1}}\frac{x_k}{T_1^2}\right)}^2\hfill \end{array}\right],$$ [7]

The goal of the optimization procedure is to minimize the variance of the estimator of T₁. From Equation [4], $\mathrm{var}\left(T_1^{est}\right)\ge {\lfloor {\mathbf{I}}^{-1}\rfloor }_{3,3}$, where

$$J(a,b,T_1,\left\{x_k\right\})={\left[{\mathbf{I}}^{-1}\right]}_{3,3}=\frac{{\mathbf{I}}_{11}{\mathbf{I}}_{22}-{\mathbf{I}}_{12}^2}{{\mathbf{I}}_{11}({\mathbf{I}}_{22}{\mathbf{I}}_{33}-{\mathbf{I}}_{23}^2)-{\mathbf{I}}_{12}({\mathbf{I}}_{33}{\mathbf{I}}_{12}-{\mathbf{I}}_{23}{\mathbf{I}}_{13})+{\mathbf{I}}_{13}({\mathbf{I}}_{12}{\mathbf{I}}_{23}-{\mathbf{I}}_{22}{\mathbf{I}}_{13})}.$$ [8]

We minimize $J(a,b,T_1,\left\{x_k\right\})$ as a surrogate for minimizing $\mathrm{var}\left(T_1^{est}\right)$. While this is a closed form expression in terms of {x_k} given the values of [a, b, T₁] that we are interested in, the analytical minimization of the objective function is not tractable. Thus we propose to solve

$$\left\{x_k^{samp}\right\}=\arg \underset{\left\{x_k\right\}}{\min }J(a,b,T_1,\left\{x_k\right\})$$ [9]

numerically over a grid of values for {x_k} for the desired values of a, b, T₁. Furthermore, in Appendix A, we show that

$$J(a,b,T_1,\left\{x_k\right\})=\frac{1}{{\left(ab\right)}^2}J(1,1,T_1,\left\{x_k\right\}).$$ [10]

Thus the values of a, b only scales the lower bound itself, and the minimization over the grid of values for {x_k} is independent of a, b, and only depends on the T₁ value of interest.

Methods

All imaging was performed on a 1.5T Philips Achieva (Philips Healthcare, Best, The Netherlands) system. Phantom imaging was performed with a body coil, and in-vivo imaging was performed with a 32-channel cardiac phased-array receiver coil. For this HIPAA-compliant study, the imaging protocol was approved by our institutional review board, and written informed consent was obtained from all participants.

Saturation and inversion recovery are the most commonly employed techniques for sampling of the longitudinal magnetization recovery. Currently, there are no myocardial T₁ mapping sequences that sample an unperturbed inversion recovery (IR) curve in a single breath-hold, though there are Look-Locker based variants (8,9). Hence, we concentrate on the saturation recovery (SR) curve. We choose a SR-based T₁ mapping sequence, SASHA (10), for validation in this study. This sequence is electrocardiogram-triggered, and applies a saturation pulse at every heart beat, followed by imaging after a recovery time of x_k. The first heart beat is acquired without magnetization preparation, corresponding to an infinite SR time. Since different SR times can be selected for each heart beat in this sequence, this increases the degrees of freedom for the selection of the optimal sampling points.

Numerical Simulations

Simulation Setup

We note from Equation [8], $J(a,b,T_1,\left\{x_k\right\})$ depends directly on 1/a², i.e. the lower bound on the variance of the estimator scales inversely with the square of the SNR. Thus the choice of a does not affect the evaluation of the function, only changing the scaling. Hence a = 40 was arbitrarily chosen as the baseline SNR for the simulations. b = 0.9 was used for the simulations, selected from the typical experimental range of b values for SASHA between 0.9 and 1.1 (10). A trigger delay of 780 ms at 60 bpm and an acquisition window of 190 ms were used. Including the duration of the saturation pulse and the duration of the read-outs to the k-space center (with the assumption of a linear profile order), the allowable saturation times ranged between T_min = 140 ms and T_max = 760 ms.

Experiments

Two sets of experiments were performed. In Numerical Experiment A, the bound was evaluated for various T₁ values of interest for K = 11 sampling points: i) 1250 ms (myocardium pre-contrast), ii) 450 ms (myocardium post-contrast), iii) 950 – 1250 ms (pre-contrast T₁ range), iv) 400 – 600 ms (post-contrast T₁ range), v) 450 & 1250 ms (myocardium pre- and post-contrast). In Numerical Experiment B, the bound was evaluated for various K values of {5, 7, 9, 11, 13, 15} for T₁ values of interest from 950 to 1250 ms.

Additional experiments, the effects of changing T_max, and allowing for multiple sampling of the point at infinity were performed, and are included in Appendix B.

Numerical Optimization

The K sampling points {x_k} were selected numerically as follows: The search space was generated as all the possible saturation times from T_min to T_max with a step size of 10 ms, and a saturation time at infinity, corresponding to sampling without any magnetization preparation. Every possible ordered samplings of length K, allowing repetitions, was generated from the search space. The point at infinity was only allowed to be included once in any sampling, since any imaging pulse performed during acquisition disturbs the magnetization at this point. Thus, to sample the same point at infinity requires multiple rest periods for the longitudinal magnetization to re-grow, which decreases efficiency, especially considering the constraints on scan duration with the breath-hold acquisition. For every ordered sampling, $J(a,b,T_1,\left\{x_k\right\})$ was evaluated for the given [a, b, T₁].

For the T₁ values in a continuous range, a Bayesian CRB variant was used (28), where

$$J_B({\theta }_1,{\theta }_2,\left\{x_k\right\})=\frac{1}{T_1^{\max }-T_1^{\min }}{\int }_{T_1^{\min }}^{T_1^{\max }}J({\theta }_1,{\theta }_2,{\theta }_3,\left\{x_k\right\})d{\theta }_3$$ [11]

was evaluated instead. The integral was performed numerically with a step size of 5 ms, while making sure the (nearly)-uniform distribution on T₁ was 0 at the boundary points as required in (28). For the bi-modal T₁ value of optimization (v), the procedure was evaluated with both equal weights and weights proportional to 1/T₁² for the variances associated with the two T₁ values.

The CRB on precision, defined as the square root of $J(a,b,T_1,\left\{x_k\right\})$ and denoted by CRB_prec, was evaluated for the points selected by the optimization procedure, and compared to a uniform distribution of sampling points, where K – 1 sampling points are uniformly spread in the range T_min to T_max, and a point at infinity as in (10).

Phantom Imaging

Imaging Setup

To characterize the effect of the choice of sampling points on the precision of the T₁ estimates, phantom imaging was performed using 14 NiCl₂ doped agarose vials (29), whose T₁ and T₂ values spanned the ranges of values found in the blood and myocardium pre- and post- contrast. A single-shot steady-state free precession (SSFP) sequence with the following parameters was used: 2D single-slice, FOV = 210×170 mm², in-plane resolution = 1.9×2.5 mm², slice-thickness = 8 mm, TR/TE = 2.7 ms/1.35 ms, flip angle = 70°, 10 ramp-up pulses, acquisition window = 190 ms, linear k-space ordering. All scans were repeated 5 times to average out random variations.

Experiments

The first set of experiments compared different sets of sampling points for K = 11. The sets of sampling points tested were the ones chosen from the numerical simulations for T₁ values of interest varying from 950 to 1250 ms, from 400 to 600 ms, and 450 and 1250 ms. For comparison, acquisitions with saturation times uniformly distributed in the range T_min to T_max, plus a point at infinity (referred to as “uniform”) were performed. Each scan was acquired with number of signal averages (NSA) = 5 for sufficient baseline SNR.

The second set of experiments evaluated the precision of the uniform and proposed point selection techniques for T₁ values of interest varying from 950 to 1250 ms, for different number of sampling points, K = {5, 7, 9, 11, 13, 15}. NSA = 5 was used for these scans as well.

The third set of experiments was performed to validate the inverse linear dependence of precision to baseline SNR. The sequence was designed to last for K = 11 heartbeats, and the scans were acquired with NSA = {1, 3, 5, 10}. The uniform point selection and the proposed point selection for T₁ values of interest varying from 950 to 1250 ms were utilized.

In-vivo Imaging

Myocardial T₁ maps were acquired in 5 healthy adult subjects (4 women, 23.4 ± 3.3 years) without a contrast injection. Images were acquired in the short-axis of the heart. The SASHA sequence was used with a single-shot acquisition and an SSFP readout with the following parameters: 2D single-slice, FOV = 300×300 mm², in-plane resolution = 1.9×2.5 mm², slice-thickness = 8 mm, TR/TE = 3.1 ms/1.55 ms, flip angle = 70°, 10 ramp-up pulses, SENSE rate = 2, acquisition window = 190 ms, linear k-space ordering. The sequence duration was 11 heartbeats, and it was performed during breath-hold. Acquisitions were performed using a uniformly distributed point selection and the proposed selection of points for T₁ values between 950 and 1250 ms. For each point selection strategy, the acquisition was repeated 5 times to average out random variations.

Image Analysis

T₁ estimation was performed offline using MATLAB (v7.6, MathWorks, Natick, MA) using the 3-point model (10) of Equation [2]. Any point acquired without a saturation preparation was assumed to be sampled at an infinite (∞) saturation time. Multiple points acquired at the same point on the magnetization recovery curve were used individually for fitting, instead of averaging prior to fitting.

For T₁ measurements, a region-of-interest (ROI) analysis was performed for both phantom and in-vivo imaging. The mean value and standard deviation in the ROI was recorded for each acquisition. The estimated T₁ value, T₁^est, is reported as an average ± standard deviation of the mean values in the ROI (over the 5 acquisitions for each sampling strategy), which is a surrogate for accuracy and the inter-scan reproducibility. Under the assumption that the T₁ values are homogenous in the small ROI (11), the precision, prec(T₁^est), is reported as the average ± standard deviation of the spatial standard deviation of the T₁ values in the ROI (over 5 acquisitions for each sampling strategy).

For phantom imaging, circular ROIs were drawn across each of the 14 vials, starting from the center of the vial and containing ~300 voxels. The ratios of the mean prec(T₁^est) for the two sampling strategies were then compared to the ratios predicted by the theoretical model for different K and T₁ values in the union of the ranges of optimization using paired t-test. For the SNR experiment, the correlation between prec(T₁^est) for different NSAs were compared to 1/NSA² using Pearson's linear correlation coefficient for both sampling strategies. For in-vivo imaging, ROIs were manually drawn, by two independent experienced readers, in the left ventricle (LV) myocardium and the blood pool. T₁^est and prec(T₁^est) were calculated for both strategies.

Results

Numerical Simulations

Point selection for different T₁ values of interest

The 11 sampling points selected by the proposed method for the first 4 different cases of T₁ values of interest, and the associated CRB_prec are depicted in Table 1 for SNR = 40, along with the corresponding CRB_prec for a uniform distribution of sampling points. The proposed choice of sampling points yields a tri-modal distribution: 1 point at ∞, 3-4 points at T_min and 6-7 points close to the T₁ value(s) of interest. The proposed selection leads to a reduction in CRB_prec in all cases (13%, 26%, 24%, 12.1% reduction for T₁ values of interest of 450 ms, 1250 ms, 950 – 1250 ms, 400 – 600 ms respectively) compared to the uniform selection.

Table 1.

Results of the proposed optimization procedure for sampling point selection for various T₁ values of interest and 11 sampling points. The saturation recovery times are chosen between T_min = 140 ms and T_max = 760 ms (and possibly one point at ∞, representing an acquisition with no preparation). The associated Cramér-Rao lower bound (CRB) on the standard deviation (std) of the T1 estimator (CRB_prec) when using the proposed strategy and a strategy selecting uniformly separated points are also depicted. The results indicate that the optimization procedure favors selection of multiple points at the same locations, with multiple points at T_min, as well as multiple points close to the T₁ value of interest (or the closest to it if these values are greater than T_max). In all cases, the optimized procedure has a lower CRB associated with the variance and standard deviation of the T₁ estimator, when compared to a uniform distribution of sampling points.

T1 values of interest (ms)	Sampling Point Selection Strategy	Saturation Recovery Sampling Points (ms)	CRBprec (ms)
1250	proposed	(140, 140, 140, 140, 760, 760, 760, 760, 760, 760, ∞)	82.6
	uniformly distributed	(140, 209, 278, 347, 416, 485, 554, 623, 692, 760, ∞)	111.3
450	proposed	(140, 140, 140, 480, 480, 480, 480, 480, 480, 480, ∞)	33.9
	uniformly distributed	(140, 209, 278, 347, 416, 485, 554, 623, 692, 760, ∞)	39.1
950 - 1250	proposed	(140, 140, 140, 140, 760, 760, 760, 760, 760, 760, ∞)	71.8
	uniformly distributed	(140, 209, 278, 347, 416, 485, 554, 623, 692, 760, ∞)	94.0
400 - 600	proposed	(140, 140, 140, 510, 510, 510, 510, 510, 510, 510, ∞)	36.9
	uniformly distributed	(140, 209, 278, 347, 416, 485, 554, 623, 692, 760, ∞)	42.0

For the fifth case of T₁ values, the optimization with equal weights yielded 4 points at 140 ms, 6 at 760 ms and 1 at ∞. In this case, CRB_prec associated with the T₁ = 450 ms estimation was 42.3 ms, whereas CRB_prec for T₁ = 1250 ms was of 82.6 ms, where the former is worse than for uniform selection. Note that for equal weights, the variance of the higher T₁ value dominates the optimization procedure, yielding the same choice of points as for just T₁ = 1250 ms. When weights of 1/T₁² are used to capture the percentage variation in estimation, the optimal selection becomes 4 points at 140 ms, 4 at 570 ms, 2 at 760 ms and 1 at ∞, resulting in reductions in CRB_prec of 5% and 18% (for T₁ of 450 and 1250 ms respectively) compared to uniform selection. This latter selection of points is used in subsequent imaging for these T₁ values of interest.

Effect of changing the number of sampling points

Table 2 depicts the results of the proposed point selection strategy and CRB_prec for both point selection strategies for T₁ values of interest of 950-1250 ms for various numbers of sampling points, K. The trend for the optimization strategy is to select one point at ∞, floor(K/2)-1 or floor(K/2) points at T_min, and floor(K/2) or floor(K/2)+1 points at T_max (since T₁ > T_max). The reduction in CRB_prec compared to uniform sampling is 18.7%, 24.4%, 25.6%, 25.8%, 25.7%, 24.9% for K = 5, 7, 9, 11, 13, 15 points respectively.

Table 2.

The variation of the selected points for different number of sampling points, K, as well as the associated CRB on the standard deviation of the T₁ estimator (CRB_prec) when using the proposed strategy and a strategy selecting uniformly separated points. The range of T1 values of interest was from 950 ms to 1250 ms, with T_min = 140 ms and T_max = 760 ms. The proposed selection procedure again favors a bi-modal distribution of points among Tmin and Tmax, which results in an improvement over the CRB for variance and std of the T1 estimator with respect to a uniform distribution of selection points for all K.

# sampling points, K	Point Selection Strategy	Saturation Recovery Sampling Points (ms)	CRBprec (ms)
5	proposed	(140, 140, 760, 760, ∞)	117.7
	uniform	(140, 347, 554, 760, ∞)	144.8
7	proposed	(140, 140, 760, 760, 760, 760, ∞)	98.6
	uniform	(140, 264, 388, 512, 636, 760, ∞)	130.4
9	proposed	(140, 140, 140, 760, 760, 760, 760, 760, ∞)	88.8
	uniform	(140, 229, 318, 407, 496, 585, 674, 760, ∞)	119.4
11	proposed	(140, 140, 140, 140, 760, 760, 760, 760, 760, 760, ∞)	82.6
	uniform	(140, 209, 278, 347, 416, 485, 554, 623, 692, 760, ∞)	111.3
13	proposed	(140, 140, 140, 140, 140, 760, 760, 760, 760, 760, 760, 760, ∞)	78.2
	uniform	(140, 196, 252, 308, 364, 420, 476, 532, 588, 644, 700, 760, ∞)	105.2
15	proposed	(140, 140, 140, 140, 140, 760, 760, 760, 760, 760, 760, 760, 760, 760, ∞)	74.8
	uniform	(140, 188, 236, 284, 332, 380, 428, 476, 524, 572, 620, 668, 716, 760, ∞)	99.6

Phantom Imaging

Precision for different sampling point selections

Table 3 depicts the results of the phantom measurements over all 14 vials with different T₁ values for various sampling strategies with NSA = 5 for each acquisition and K = 11. The estimated T₁ values for different sampling strategies for each vial are in good agreement with theory, even though there are variations between the 5 acquisitions due to noise (reflected as the standard deviation in the T₁^est). The ratio of prec(T₁^est) for each proposed sampling strategy and that of the uniform sampling strategy is reported as “precision (prec) with respect to (wrt) uniform.” The points optimized for T₁ values from 950 to 1250 ms show consistent improvement (as a ratio < 1) in this range with respect to the uniform strategy. Similarly, the points optimized for T₁ values from 400 to 600 ms show consistent improvement for smaller T₁ values < 1150 ms. The points optimized for two T₁ values of 450 and 1250 ms show improvement in standard deviation of the estimator for all T₁ values. Theoretical prediction for the ratios of prec(T₁^est) with respect to that of the uniform strategy is also reported for all selection of points. These are not statistically different than the experimental ratios (P = 0.26, P = 0.09, P = 0.05 for T₁ values of 950 – 1250 ms, 400 – 600 ms, 450 & 1250 ms respectively) for vials with T₁ values in the union of the ranges of optimization.

Table 3.

Results of the phantom imaging over all 14 vials with different T₁ values for various sampling strategies, where each acquisition was repeated 5 times and K = 11. The ratio of the standard deviation of the T₁ estimator for each proposed sampling strategy and that of the uniform sampling strategy is reported as “precision (prec) with respect to (wrt) uniform.” The points from numerical experiment #3, #4 and #5 show improvement on the standard deviation of the uniform sampling strategy for T₁ values > 600 ms, T₁ values < 1150 ms and all T₁ values, respectively. The theoretical prediction corresponding to the ratios of standard deviations are also reported for each sampling strategy, which are in good agreement with the experimental ratios (P = 0.26, P = 0.09, P = 0.05 for the point selections of different T₁ values of interest respectively) for vials with T1 values in the union of the ranges of optimization.

	uniformly distributed points		points optimized for T = 950 - 1250 ms				po i n t s o pt i mized for T1 = 400 - 600 ms				po i nts o pt imized for T1 = 450 & 1250 ms
Vial	(T1est (ms)	prec (T1est) (ms)	T1est (ms)	prec (T1est) (ms)	prec wrt. uniform	theory prec wrt. uniform	T1est (ms)	prec T1est (ms)	prec wrt. uniform	theory prec wrt. uniform	T1est (ms)	prec (T1est) (ms)	prec wrt. uniform	theory prec wrt. uniform
1	1457 ± 7.7	69.2 ± 6.3	1456 ± 7.4	48.1 ± 5.2	0.70	0.71	1432 ± 12.7	72.0 ± 5.2	1.04	1.01	1450 ± 26.5	48.8 ± 4.4	0.71	0.81
2	1144 ± 14.5	55.7 ± 6.7	1130 ± 7.1	41.0 ± 2.5	0.74	0.76	1127 ± 6.8	54.1 ± 2.7	0.97	0.98	1125 ± 12.9	44.7 ± 2.3	0.80	0.82
3	1151 ± 11.5	53.2 ± 3.8	1155 ± 8.6	43.1 ± 1.4	0.81	0.76	1146 ± 12.2	54.0 ± 6.7	1.02	0.98	1147 ± 20.3	45.3 ± 1.9	0.85	0.82
4	274 ± 5.0	15.3 ± 1.2	275 ± 6.8	23.2 ± 2.5	1.51	1.71	271 ± 7.7	14.7 ± 0.8	0.96	0.99	269 ± 4.5	15.0 ± 0.9	0.98	1.17
5	429 ± 6.6	17.3 ± 1.1	431 ± 2.3	18.8 ± 1.5	1.09	1.11	426 ± 6.8	14.1 ± 1.0	0.81	0.87	426 ± 5.9	15.2 ± 1.0	0.88	0.96
6	729 ± 10.3	31.3 ± 1.2	724 ± 2.1	26.1 ± 3.3	0.83	0.86	724 ± 4.6	29.0 ± 2.6	0.93	0.91	727 ± 13.9	27.7 ± 1.6	0.88	0.87
7	595 ± 6.6	20.0 ± 1.6	599 ± 6.0	18.8 ± 1.6	0.94	0.94	590 ± 11.3	17.8 ± 1.9	0.89	0.89	588 ± 11.8	16.6 ± 1.2	0.83	0.89
8	597 ± 5.0	25.9 ± 0.9	597 ± 5.0	23.3 ± 3.0	0.90	0.94	592 ± 5.3	22.8 ± 1.3	0.88	0.89	594 ± 11.8	23.1 ± 0.3	0.89	0.89
9	980 ± 11.2	34.6 ± 1.2	981 ± 10.4	25.2 ± 0.6	0.73	0.78	971 ± 8.5	29.0 ± 2.5	0.84	0.96	983 ± 13.5	24.2 ± 1.0	0.70	0.84
10	823 ± 13.3	29.8 ± 2.1	822 ± 7.7	24.2 ± 2.0	0.81	0.83	816 ± 8.3	29.0 ± 2.4	0.97	0.93	816 ± 15.0	22.1 ± 1.3	0.74	0.86
11	1148 ± 18.4	52.6 ± 6.4	1144 ± 8.3	37.8 ± 1.5	0.72	0.76	1129 ± 15.5	45.9 ± 2.4	0.87	0.98	1151 ± 18.7	42.0 ± 2.8	0.80	0.82
12	341 ± 4.1	19.4 ± 1.7	342 ± 5.8	22.6 ± 2.4	1.17	1.29	337 ± 7.0	16.3 ± 1.0	0.84	0.89	335 ± 8.7	17.3 ± 0.3	0.89	1.01
13	963 ± 13.8	49.8 ± 3.4	962 ± 6.2	35.4 ± 2.2	0.71	0.79	956 ± 3.7	47.1 ± 5.4	0.95	0.95	964 ± 8.6	37.9 ± 4.1	0.76	0.83
14	1130 ± 10.6	55.8 ± 5.6	1137 ± 10.5	45.0 ± 3.9	0.81	0.76	1121 ± 4.5	52.9 ± 2.2	0.95	0.98	1139 ± 15.8	45.0 ± 1.7	0.81	0.82

Precision versus number of sampling points

Table 4 shows phantom results evaluating how prec(T₁^est) varies with number of sampling points, K. The ratio of prec(T₁^est) between the proposed and uniform point selections are depicted for K = {5, 7, 9, 11, 13, 15} for the vials, whose T₁ values are between 950 and 1250 ms. Corresponding ratios predicted by theory for these vials are also reported. The experimental and theoretical ratios are in good agreement across all vials considered (P = 0.97).

Table 4.

The results of phantom imaging for various values of number of sampling points, K, depicting the precision values, the ratio of the standard deviation of the proposed point selection for T1 values ranging from 950 ms to 1250 ms and that of the uniformly distributed point selection, as well as the ratio predicted by theory. The ratios are in good agreement across all vials considered (P = 0.97).

Vial #	Evaluation Metric	K = 5	K = 7	K = 9	K = 11	K = 13	K = 15
2	uniform - prec(T1est) (ms)	70	59	58	56	50	47
	proposed - prec (T1est) (ms)	53	45	44	41	39	35
	std ratio proposed vs. uniform	0.76	0.77	0.73	0.73	0.80	0.76
	theoretical ratio	0.83	0.77	0.76	0.76	0.76	0.77
3	uniform - prec(T1est) (ms)	62	56	55	53	50	47
	proposed - prec(T1est) (ms)	53	45	44	43	40	37
	std ratio proposed vs. uniform	0.86	0.81	0.79	0.81	0.79	0.77
	theoretical ratio	0.82	0.76	0.75	0.75	0.76	0.77
9	uniform - prec(T1est) (ms)	43	36	35	34	34	30
	proposed - prec(T1est) (ms)	35	28	28	25	24	25
	std ratio proposed vs. uniform	0.81	0.78	0.81	0.73	0.70	0.85
	theoretical ratio	0.85	0.79	0.78	0.79	0.79	0.80
11	uniform - prec(T1est) (ms)	59	54	52	53	45	45
	proposed - prec(T1est) (ms)	49	39	41	37	35	34
	std ratio proposed vs. uniform	0.84	0.73	0.80	0.71	0.79	0.76
	theoretical ratio	0.82	0.76	0.75	0.75	0.76	0.76
13	uniform - prec(T1est) (ms)	53	49	48	49	44	40
	proposed - prec(T1est) (ms)	45	41	37	35	34	33
	std ratio proposed vs. uniform	0.85	0.84	0.78	0.71	0.78	0.82
	theoretical ratio	0.85	0.79	0.79	0.79	0.80	0.80
14	uniform - prec(T1est) (ms)	63	62	58	56	50	48
	proposed - prec(T1est) (ms)	53	44	45	45	39	36
	std ratio proposed vs. uniform	0.84	0.70	0.79	0.81	0.77	0.75
	theoretical ratio	0.82	0.77	0.76	0.76	0.76	0.77

Precision versus baseline SNR

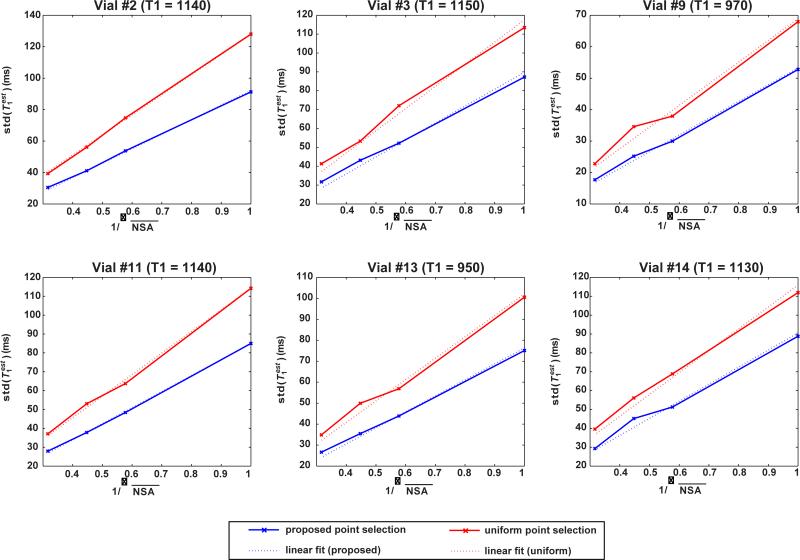
Figure 1 depicts prec(T₁^est) with changing NSA (equivalently √SNR) for all vials with T₁ values between 950 and 1250 ms and for both point selection strategies. The best linear fits (y = ax) are also shown (dashed lines) as a function of changing NSA. As predicted by Equation [8], these are in good agreement with the experimentally measured prec(T₁^est) in all cases, with Pearson correlation coefficients >0.99 for all vials and for both point selection strategies. The baseline SNR was 29.2 ± 2.3 for the case of full longitudinal recovery (i.e. with SR time of ∞) image with NSA = 1.

Figure 1.

Standard deviation of the T₁ estimator as a function of varying NSA (or equivalently √SNR) for the proposed point selection for T₁ values ranging from 950 to 1250 ms and the uniformly distributed point selection. The experimental results are in good agreement with the best linear fit of the form y = ax (dashed lines) with Pearson coefficients > 0.99 for all cases.

In-vivo Imaging

Table 5 depicts the results of in-vivo T₁ measurements for the five healthy subjects using the proposed and uniform sampling strategies. The reduction in prec(T₁^est) as measured by reader 1 were 13.9% and 20.1% for the myocardium and blood respectively, with the proposed approach compared to the uniform selection strategy. The corresponding reductions measured by reader 2 were 20.2% and 26.6% for the myocardium and blood respectively. Overall, there was a 17.0% and 23.5% reduction in the prec(T₁^est) in the myocardium and blood respectively using the proposed approach compared to the uniform selection.

Table 5.

The results of in-vivo imaging on five healthy subjects using the proposed and uniform sampling strategies, where each acquisition was repeated 5 times, as measured by two independent readers. T₁^est is reported as the mean ± std of the spatial average T1 values in the ROI across 5 scans, as a surrogate for accuracy and inter-scan reproducibility. prec(T₁^est) is reported as the mean ± std of the spatial std of the T1 values in the ROI across 5 scans, as a surrogate for the precision within the scan. Std wrt. uniform is the ratio of the mean values of prec(T₁^est) using the proposed and uniform point selection, characterizing the percentage gain in precision. prec(T₁^est) in the myocardium and blood was reduced by 17.0% and 23.5% respectively using the proposed approach.

				uniform point selection		proposed point selection
	subject	heart rate (bpm)	anatomy	T1est (ms)	prec (T1est) (ms)	T1est (ms)	prec (T1est) (ms)	std wrt.uniform
Reader #1	1	65	myocardium	1163 ± 24.2	104.9 ± 15.6	1155 ± 33.3	103.7 ± 11.3	0.99
			blood	1926 ± 17.2	162.5 ± 15.3	1897 ± 26.8	114.7 ± 10.2	0.71
	2	75	myocardium	1350 ± 19.6	177.9 ± 11.5	1348 ± 30.0	103.7 ± 11.3	0.89
			blood	1751 ± 46.4	187.6 ± 30.3	1766 ± 59.6	149.0 ± 5.8	0.79
	3	70	myocardium	1242 ± 40.7	153.4 ± 21.1	1255 ± 15.6	124.5 ± 14.5	0.81
			blood	1799 ± 9.5	189.0 ± 20.7	1811.2 ± 36.5	155.0 ± 12.0	0.82
	4	68	myocardium	1200 ± 33.9	110.9 ± 11.5	1193 ± 13.6	93.7 ± 9.9	0.84
			blood	1733 ± 44.2	140.8 ± 14.8	1754 ± 16.1	128.1 ± 17.8	0.91
	5	58	myocardium	1135 ± 77.9	105.1 ± 18.9	1185 ± 16.5	81.8 ± 10.3	0.78
			blood	1757 ± 52.1	150.2 ± 15.1	1751 ± 15.1	116.8 ± 9.6	0.78
Reader #2	1	65	myocardium	1188 ± 15.6	115.7 ± 16.2	1194 ± 15.3	91.7 ± 11.0	0.79
			blood	1925 ± 25.1	166.7 ± 16.5	1903 ± 19.2	111.8 ± 7.7	0.67
	2	75	myocardium	1314 ± 25.4	174.4 ± 28.6	1307 ± 21.5	150.1 ± 21.2	0.86
			blood	1772 ± 24.1	205.0 ± 32.3	1755 ± 20.8	148.2 ± 7.2	0.72
	3	70	myocardium	1204 ± 70.2	117.0 ± 16.7	1218 ± 37.8	83.0 ± 13.5	0.71
			blood	1787 ± 37.3	179.7 ± 26.5	1809 ± 35.4	138.1 ± 14.9	0.77
	4	68	myocardium	1213 ± 49.5	107.3 ± 16.7	1207 ± 31.7	85.0 ± 5.3	0.79
			blood	1755 ± 34.7	161.4 ± 16.7	1780 ± 19.2	131.4 ± 12.8	0.81
	5	58	myocardium	1168 ± 54.3	95.3 ± 6.8	1187 ± 14.8	76.6 ± 5.0	0.80
			blood	1772 ± 47.8	164.7 ± 18.9	1761 ± 20.8	114.2 ± 10.4	0.69

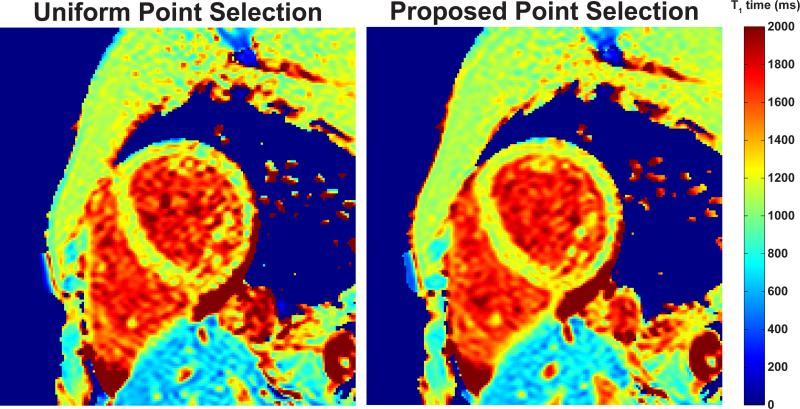
Figure 2 shows example myocardial T₁ maps from a healthy subject (subject #5), acquired using the proposed and uniform point selection strategies at a heart rate of 60 bpm. Homogeneity of the T₁ maps is visibly improved in the blood pools, where the T₁ value is higher compared to the myocardium. prec(T₁^est) in the myocardium averaged over the 5 acquisitions showed 22% and 20% improvement with the proposed selection as measured by readers 1 and 2 respectively. Similarly, prec(T₁^est) for the blood pool showed 22% and 31% improvement as measured by readers 1 and 2 respectively. In comparison, the theory predicts reductions of 24.6% and 30.3% for CRB_prec of the myocardium and blood respectively.

Figure 2.

T₁ maps from a healthy subject (subject #5), acquired using the proposed and uniform point selection strategies. The T₁ map generated using the proposed point selection is more homogenous, as visible in the blood pool. prec(T₁^est) averaged over the 5 acquisitions were 105.1 ± 18.9 ms and 81.8 ± 10.3 ms for the myocardium as measured by reader 1, and 95.3 ± 6.8 ms and 76.6 ± 5.0 ms as measured by reader 2 for uniform and proposed selection strategies respectively. prec(T₁^est) for the blood pool were 150.2 ± 15.1 ms and 116.8 ± 9.6 ms as measured by reader 1, and 164.7 ± 18.9 ms and 114.2 ± 10.4 ms as observed by reader 2 for uniform and proposed selection strategies respectively.

Discussion

In this study, we used an estimation theoretic framework for evaluating the precision of myocardial T₁ mapping techniques to devise a sampling point selection strategy. This was achieved by minimizing the CRB on the variance of the estimators over the search space of possible sampling points. Subsequently, we evaluated this point selection strategy in a saturation-recovery based T₁ mapping sequence, and compared it to a uniform distribution of sampling points along the SR curve. The improvements in precision in phantom and in-vivo imaging matched those from the numerical simulations derived from the theory.

The proposed optimized selection procedure yielded sampling points that are concentrated in 3 areas of the T₁ relaxation curve: one at a low saturation (or inversion) recovery time (T_min), one with a saturation time near (or due to sequence limitations, T_max, the closest possible value to) the T₁ value of interest, and the third point at ∞. The multiplicity of the points at these locations varies with the total number of points, as well as the sequence being simulated (e.g. taking multiple points at ∞ may not be feasible in cardiac MR). In all cases, these lead to an improved precision with respect to a uniform distribution of the points along the T₁ relaxation curve. Thus, from a theoretical perspective it is better to improve the SNR at specific well-chosen points along the magnetization recovery curve by sampling multiple times at these locations than to distribute the sampling points along the curve. We note that this choice of points tends to be different than another existing hypothesis that points on the curve with higher magnitude derivatives with respect to time are more influential on the final estimate (30).

The CRB for T₁ mapping was also derived previously in (26). This was then used to select a new set of sampling points, however the search space was only limited to ordered (linear, quadratic, cubic) sampling schemes due to the analytical tractability of these expressions. Thus, the tri-modal distribution resulting from our numerical optimization scheme with a more extensive search space, was not observed in (26). We note that the tri-modal distribution of optimal points presented here is similar to the bi-modal distribution observed in T₂ mapping where a 2-parameter model was utilized (25). Apart from the differences in search spaces, which lead to substantially different selection of optimal sampling points, there are other differences between our work and (26). In particular, only numerical simulations were provided in (26), while we have also provided phantom and in-vivo data to validate the precision gains of our point selection approach directly. Furthermore, we have also evaluated our selection strategy using a Bayesian CRB to accommodate a wide range of T₁ values of interest.

From both the theoretical and experimental perspectives it is observed that the standard deviation of the estimator increases with increasing T₁ values, which is reflected in the choice of sampling points when a range of T₁ values are of interest. This is also reflected in the corresponding gains of the optimized point selection versus uniformly distributed point selection, with more substantial gains in the precision for higher T₁ values. Conversely, for shorter T₁ values, both the percentage and the absolute reduction in the standard deviation of the estimator were smaller when using the optimized point selection.

Optimization of the sampling points for one range of T₁ values does not guarantee a systematic improvement in precision across all T₁ values. This is consistent with previous studies in parameter mapping (25,26). This was further validated in phantom imaging, where the sampling points optimized for T₁ values from 950 to 1250 ms, did worse than uniform distribution in terms of precision for low T₁ values < 400 ms. Optimizing for a larger spread of values also requires careful consideration as to how the final variance should be weighted. For instance, equal weights for T₁ values of interest of 450 and 1250 ms yielded the same distribution as just optimizing for 1250 ms, since the variance of the estimator is dominated by the larger T₁ value. However, by switching to weights scaling as 1/T₁², thus characterizing the weighted error as a percentage of the T₁ values, an optimal point selection that systematically outperformed the uniform sampling point distribution in numerical and phantom experiments was obtained.

The point selection procedure is not dependent on the SNR of the fully-recovered image, a or saturation/inversion efficiency, b, as shown in Appendix A. However, the standard deviation of the T₁ estimator scales inverse-linearly with a, and with b. Thus, the percentage gain in precision between optimal point selection and uniform point distribution is constant for varying SNR, but the numerical difference becomes small for high values of a. Hence, for high SNR sequences, the gains from the proposed point selection may not be noticeable. Since b also inverse-linearly scales the standard deviation, the dynamic range acquired by doing an inversion recovery T₁ mapping doubles the precision with respect to SR, assuming accurate flip angles and ignoring effects of imaging pulses until the acquisition of central k-space.

The effects of increasing K versus improving the SNR are different based on the constraints on what points on the curve can be sampled with a given sequence. In a practical myocardial T₁ mapping scenario, where an infinite SR time can be imaged only once, going from K = 5 to 15 lead to an improvement in the standard deviation of the T₁ estimator that was worse than the corresponding improvement achieved by increasing the SNR by √3. However, in an ideal scenario, where any point can be sampled multiple times (in Appendix B), going from K = 5 to 10 was better for improving the precision than increasing the SNR by √2. Thus, based on the constraints on the sampling points and the sequence, the designer can perform the numerical simulations based on the theory and conclude whether to improve the SNR or increase K for improved precision in estimation.

The general estimation theoretic framework for evaluation of variance lower bounds can be used for a wide range of sequences and applications (22-26). Since the differences predicted by the theory for different sampling point selection schemes matches experimental values well, the bounds themselves may be useful in comparing multiple sequences in terms of their precision theoretically in a quantitative manner. Alternatively this can also be studied with Monte-Carlo simulations (31), although this does not lead to closed form expressions, and thus does not allow for a computationally tractable method of optimizing point selection.

In this study, we have arbitrarily chosen a SR approach utilized in myocardial T₁ mapping for validation. This sequence has certain limitations, most notably the need to apply the saturation pulse and imaging during the same R-R interval. This limits the maximum possible saturation time to T_max, which decreases as the heart rate increases. Thus, for higher heart rates (or larger acquisition windows), the optimal selection at T_max will shift to smaller values, reducing the precision of the sequence for the same number of sampling points. Furthermore, the results in Appendix B indicate that the precision can be improved if T_max is higher than the T₁ value of interest. Thus, precision may be improved by applying the preparation pulse(s) in one R-R interval and imaging in the consequent one, which was explored in other works (32,33).

The accuracy of the T₁ estimation using SASHA sequence with respect to a gold standard inversion recovery spin echo sequence using phantom measurements were not evaluated, as this has already been reported (10), and further studied elsewhere (12,34). Our focus is on the choice of sampling points and how this can reduce the variance of the estimator, i.e. the precision, as evaluated by signal homogeneity in an ROI where T₁ is expected to be homogenous. We do note that the CRB theory presented here is for unbiased estimators, which is an assumption satisfied by the SASHA sequence with sufficient SNR and the 3-point T₁ fitting of Equation [2] (10). The theory of CRB can be extended to biased estimators, provided that the bias term can be characterized in terms of the parameters that are being estimated (28). An interesting implication of the CRB for biased estimators is that a biased estimator does not necessarily have worse precision than an unbiased estimator, and this extension may be appropriate for alternative myocardial T₁ mapping sequences based on Look-Locker experiments (8,9,35).

We have based the probabilistic model in our CRB derivation on least squares estimation, the most commonly used T₁ curve fitting procedure (8-12). This has one-to-one correspondence with a Gaussian noise model in the images. However, the noise in the magnitude images is Rician. Thus, there is an underlying assumption that the noise in the magnitude images can be well-approximated by Gaussian noise, which is true with sufficient SNR (27). However, this assumption may not hold for images acquired close to the saturation pulse in the SASHA sequence. This, in turn, may translate to an apparent bias in the T₁ estimates if sufficiently many of the acquired images have low SNR. For instance, such cases may happen when the heart-rate of the subject is high, thus T_max is low, which was discussed in (10). In our case, this was observed in phantom experiments for vials with high T₁ values, when sampling points were selected for low T₁ values, but were used to image vials with high T₁ values. Thus, the unbiased nature of SASHA should be considered, when using the optimal selection procedure for one range of T₁ values, but imaging another higher range of T₁ values.

Our study has several limitations. We have provided a general theory for evaluating the variance of estimators in myocardial parameter mapping, but we have only evaluated this approach in saturation-recovery based myocardial T₁ mapping, the choice of which was arbitrary. Further studies for confirming the theoretical results for other parameter mapping techniques are warranted. The in-vivo data presented was acquired using breath-hold, but respiratory drift may be present among subsequent contrast-weighted images (corresponding to different sampling points along the SR curve), which can corrupt the estimated T₁ maps and their homogeneity. In the in-vivo data, in-flow and off-resonance effects (36) may also increase signal inhomogeneity, affecting the final reported mean and precision of the T₁ values.

Conclusion

We have used an estimation theoretic framework to evaluating the precision of a T₁ mapping technique in the presence of noise, and to choose the location and number of sampling points on the parametric magnetization curve to achieve a given level of precision. The point selection can be optimized for different values of interest of a given parameter to achieve higher levels of precision in estimation without increasing the scan time.

Appendix A

Equation [8] states

$$J(a,b,T_1,\left\{x_k\right\})={\left[{\mathbf{I}}^{-1}\right]}_{3,3}=\frac{{\mathbf{I}}_{11}{\mathbf{I}}_{22}-{\mathbf{I}}_{12}^2}{{\mathbf{I}}_{11}({\mathbf{I}}_{22}{\mathbf{I}}_{33}-{\mathbf{I}}_{23}^2)-{\mathbf{I}}_{12}({\mathbf{I}}_{33}{\mathbf{I}}_{12}-{\mathbf{I}}_{23}{\mathbf{I}}_{13})+{\mathbf{I}}_{13}({\mathbf{I}}_{12}{\mathbf{I}}_{23}-{\mathbf{I}}_{22}{\mathbf{I}}_{13})}.$$ [A1]

We let

$${\gamma }_k=e^{\frac{-x_k}{T_1}}\text{and}{\beta }_k=\frac{x_k}{T_1^2}.$$ [A2]

Thus, the numerator of [A1] becomes

$$\begin{array}{cc}\hfill {\mathbf{I}}_{11}{\mathbf{I}}_{22}-{\mathbf{I}}_{12}^2=& \sum _{k-1}^K{(1-b{\gamma }_k)}^2\sum _{l-1}^K{(-a{\gamma }_l)}^2-\sum _{k-1}^K(-a{\gamma }_k)(1-b{\gamma }_k)\sum _{l-1}^K(-a{\gamma }_l)(1-b{\gamma }_l)\hfill \\ \hfill =& a^2\sum _{k-1}^K(1-b{\gamma }_k)\sum _{l=1}^K{\gamma }_l({\gamma }_l-{\gamma }_k)\hfill \\ \hfill =& a^2\sum _{k=1}^K\sum _{l=1}^K{\gamma }_l({\gamma }_l-{\gamma }_k)-a^{2}b\left(\sum _{k=1}^K\sum _{l=1}^K{\gamma }_k{\gamma }_l^2-\sum _{k=1}^K\sum _{l=1}^K{\gamma }_k^2{\gamma }_l\right)\hfill \\ \hfill =& a^2\sum _{k=1}^K\sum _{l=1}^K{\gamma }_l({\gamma }_l-{\gamma }_k)\hfill \end{array}$$ [A3]

since ${\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_k{\gamma }_l^2={\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_k^2{\gamma }_l$ with a simple change of indices. Similarly, the denominator of [A1] is given by

$$\begin{array}{cc}\hfill {\mathbf{I}}_{11}({\mathbf{I}}_{22}{\mathbf{I}}_{33}-{\mathbf{I}}_{23}^2)-{\mathbf{I}}_{12}({\mathbf{I}}_{33}{\mathbf{I}}_{12}-{\mathbf{I}}_{23}{\mathbf{I}}_{13})+{\mathbf{I}}_{13}({\mathbf{I}}_{12}{\mathbf{I}}_{23}-{\mathbf{I}}_{22}{\mathbf{I}}_{13})=& a^4{b}^2\sum _{j=1}^K(1-b{\gamma }_j)\sum _{k=1}^K\sum _{l=1}^K\left\{{\gamma }_k^2{\gamma }_l^2{\beta }_l({\beta }_l-{\beta }_k)+{\gamma }_j{\gamma }_k{\gamma }_l{\beta }_l({\gamma }_k{\beta }_k-{\gamma }_l{\beta }_l)+{\gamma }_j{\gamma }_k{\gamma }_l{\beta }_j{\beta }_l({\gamma }_l-{\gamma }_k)\right\}\hfill \\ \hfill =& a^4{b}^2\sum _{j=1}^K\sum _{k=1}^K\sum _{l=1}^K\left\{{\gamma }_k^2{\gamma }_l^2{\beta }_l({\beta }_l-{\beta }_k)+{\gamma }_j{\gamma }_k{\gamma }_l{\beta }_l({\gamma }_k{\beta }_k-{\gamma }_l{\beta }_l)+{\gamma }_j{\gamma }_k{\gamma }_l{\beta }_j{\beta }_l({\gamma }_l-{\gamma }_k)\right\}-a^4{b}^3\sum _{j=1}^K\sum _{k=1}^K\sum _{l=1}^K\left\{{\gamma }_k^2{\gamma }_l^2{\beta }_l({\beta }_l-{\beta }_k)+{\gamma }_j^2{\gamma }_k{\gamma }_l{\beta }_l({\gamma }_k{\beta }_k-{\gamma }_l{\beta }_l)+{\gamma }_j^2{\gamma }_k{\gamma }_l{\beta }_j{\beta }_l({\gamma }_l-{\gamma }_k)\right\}\hfill \\ \hfill =& a^4{b}^2\sum _{j=1}^K\sum _{k=1}^K\sum _{l=1}^K\left\{{\gamma }_k^2{\gamma }_l^2{\beta }_l-({\beta }_l-{\beta }_k)+{\gamma }_j{\gamma }_k{\gamma }_l{\beta }_l({\gamma }_k{\beta }_k-{\gamma }_l{\beta }_l)+{\gamma }_j{\gamma }_k{\gamma }_l{\beta }_j{\beta }_l({\gamma }_l-{\gamma }_k)\right\}\hfill \end{array}$$ [A4]

since ${\sum }_{j=l}^K{\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_k^2{\gamma }_l^2{\gamma }_j{\beta }_l^2={\sum }_{j=l}^K{\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_j^2{\gamma }_k{\gamma }_l^2{\beta }_l^2,{\sum }_{j=l}^K{\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_k^2{\gamma }_l^2{\gamma }_j{\beta }_l{\beta }_k={\sum }_{j=l}^K{\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_l^2{\gamma }_k{\gamma }_l^2{\beta }_j{\beta }_l$, and ${\sum }_{j=l}^K{\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_j^2{\gamma }_k^2{\gamma }_l{\beta }_l{\beta }_k={\sum }_{j=l}^K{\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_j^2{\gamma }_k^2{\gamma }_l{\beta }_j{\beta }_l$ after change of indices.

From these expressions we have

$$J(a,b,T_1,\left\{x_k\right\})=\frac{1}{a^2{b}^2}\frac{{\sum }_{k=1}^K{\sum }_{l=1}^K{\gamma }_l({\gamma }_l-{\gamma }_k)}{{\sum }_{j=l}^K{\sum }_{k=1}^K{\sum }_{l=1}^K\left\{{\gamma }_k^2{\gamma }_l^2{\beta }_l({\beta }_l-{\beta }_k)+{\gamma }_j{\gamma }_k{\gamma }_l{\beta }_l({\gamma }_k{\beta }_k-{\gamma }_l{\beta }_l)+{\gamma }_j{\gamma }_k{\gamma }_l{\beta }_j{\beta }_l({\gamma }_l-{\gamma }_k)\right\}}.$$ [A5]

Since γ_k and β_k are functions of {x_k} and T₁ only, this shows $J(a,b,T_1,\left\{x_k\right\})$ is inversely proportional to a²b². In particular,

$$J(a,b,T_1,\left\{x_k\right\})=\frac{1}{a^2{b}^2}J(1,1,T_1,\left\{x_k\right\}).$$ [A6]

Appendix B

Two additional numerical simulations of theoretical interest were performed. First, for the T₁ value of 1250 ms with K = 11, T_max was set to 1300 ms, which is higher than the trigger delay time, and the optimization procedure was repeated. Second, to compare the effects of increasing SNR versus increasing K under the assumption that any sampling point can be selected multiple times, we simulated the sequence with K = 5 and K = 10 for T₁ values of interest varying from 950 to 1250 ms, allowing for multiple sampling of all points, including the point at infinity.

For the set of experiments, where T_max = 1300 ms, the proposed selection of points yielded (140, 140, 140, 1060, 1060, 1060, 1060, 1060, 1060, 1060, ∞), whereas the uniform distribution resulted in (140, 269, 398, 527, 656, 785, 914, 1043, 1172, 1300, ∞). These lead to CRB_prec of 77.2 ms vs. 89.1 ms respectively (13.4% reduction). The distribution of points using the proposed method shows the trend of the optimization procedure to select 1 point at ∞, 3 points at T_min, and the remaining 7 points at 1060 ms.

For the second set of experiments, where any sampling point can be selected multiple times, the optimization for the sequence with K = 5 yielded (140, 1265, 1265, ∞, ∞) for a CRB_prec of 86.7 ms, whereas K = 10 yielded (140, 140, 1220, 1220, 1220, 1220, 1220, ∞, ∞, ∞) for a CRB_prec of 60.1 ms. We note that the point selection still favors choosing points in a concentrated region, favoring multiplicities of the points with higher signal content. It is also worth noting that going from 5 to 10 points yields an improvement of 31% in the variance, which is better than acquiring the K = 5 points twice for double the SNR (29%), although the difference is not large.