Detecting and Removing Data Artifacts in Hadamard Transform Ion Mobility-Mass Spectrometry Measurements

Abstract

Applying Hadamard transform multiplexing to ion mobility separations (IMS) can significantly improve the signal-to-noise ratio and throughput for IMS coupled mass spectrometry (MS) measurements by increasing the ion utilization efficiency. However, it has been determined that fluctuations in ion intensity as well as spatial shifts in the multiplexed data lower the signal-to-noise ratios and appear as noise in downstream processing of the data. To address this problem, we have developed a novel algorithm that discovers and eliminates data artifacts. The algorithm employs an analytical approach to identify and remove artifacts from the data, decreasing the likelihood of false identifications in subsequent data processing. Following application of the algorithm, IMS-MS measurement sensitivity is greatly increased and artifacts that previously limited the utility of applying the Hadamard transform to IMS are avoided.

Introduction

Hadamard multiplexing is a widely researched technique used in a variety of scientific instruments to multiplex incoming spectra and thereby improve the signal to noise ratio (SNR) [1-5]. Hadamard multiplexing has been investigated for some time with time-of-flight (TOF) mass spectrometers, where it is used to increase the duty cycle and resolution of the platform by multiplexing the m/z domain [2, 6]. The SNR improvement often observed is known as Fellgett’s advantage [7], and is witnessed when taking multiplexed measurements. The principle technique to deconvolve the multiplexed (i.e., phased) spectrum into a single signal is the Fourier transform. The Hadamard transform is also in the class of generalized Fourier transforms and uses a pseudo random sequence (PRS) to encode the multiplexed data. The pseudorandom nature of multiplexing allows elimination of systematic noise, making it a popular choice for scientific instrumentation, e.g., capillary electrophoresis[1, 8], TOF-MS [2], ion mobility spectrometry [9], spectroscopy [10], and interferometry [3].

In instruments that make measurements in pulsed modes, such as ion mobility separations (IMS) coupled to TOF-MS, the continuous ion source leads to a loss of potential sensitivity because of the limited measurement duty cycle, since only a portion of the ions can be utilized [9, 11, 12]. IMS distinguishes ions based on the speed at which they move through a buffer gas under the influence of a weak electric field. IMS measurements can provide potential benefits in speed and/or sensitivity compared with other approaches, and has been important in various applications ranging from biomolecule structural characterization to detection of trace substances such as toxins or explosives [13]. Traditionally, in a single IMS cycle, ions are injected into the IMS drift tube as a single packet and no additional packets are introduced until the preceding ion populations exit the drift tube. Because of this pulsing nature, IMS suffers from a low duty cycle with continuous ionization sources, which can only be partially addressed by the accumulation of ions prior to injection into the drift cell due to space charge limits upon the extent of ion accumulation [9, 11, 12]. To overcome this problem and to increase the sensitivity of IMS measurements, the drift time dimension can be multiplexed to allow multiple ion packets to be concurrently resident in the drift tube, increasing the duty cycle up to ~50% [9, 14-16]. As the multiple packets traverse the drift cell, fast moving ions from one packet overlap with slow moving ions from a previous packet and the information for all packets is recorded by the detector in one raw data file. The multiplexed raw data is demultiplexed using a Simplex matrix, which is based on the gating of the ions and the pseudo random sequence.

Real world data often contain slight imperfections between the packets of multiplexed data. At a minimum, these deviations can be attributed to ion source fluctuations, drift in electronics, and ion optic imperfections, all of which are particularly evident when dealing with the low signal levels often observed in low concentration ions. Since the Hadamard transform is designed to work on data that is perfectly encoded, the mathematical deconvolution of imperfect data elicits defects, which create pervasive noise artifacts in the post Hadamard transformed (demultiplexed) data. The properties of the artifacts have been known for some time. Gao et al. [17] observed artifacts in the demultiplexed data, described as having both positive and negative echoes arising from imperfections in the electronics that encode the multiplexing sequence. Zeppenfeld et al. [18] further examined the contributions to artifacts and noted negative systematic artifacts. To avoid these artifacts, approaches have generally focused on improving instrumentation rather than mathematical solutions [19, 20]. One specific mathematical approach to resolve artifacts is spectral methods, which has been successfully applied to TOF-MS data [21]. Other areas, such as spectroscopy and imaging where opaque masks are used to multiplex light or radiation, have artifacts that are more difficult to fit since they are attributed to faulty mask manufacturing and errors in mask alignment[10]. A separate MS approach, Fourier transform ion cyclotron resonance, also noted the presence of artifacts in transformed data, witnessed as peaks with negative intensity [17]. As with other applications of Hadamard multiplexing, the demultiplexed data obtained from the IMS-MS platform contains some artifacts, which are distinct from measurement noise. Here we explore the source of a select class of these artifacts, present the general mathematical solution for their removal, and demonstrate the effects of the algorithm on real multiplexed data obtained by the IMS-MS platform.

Methods

Instrumentation

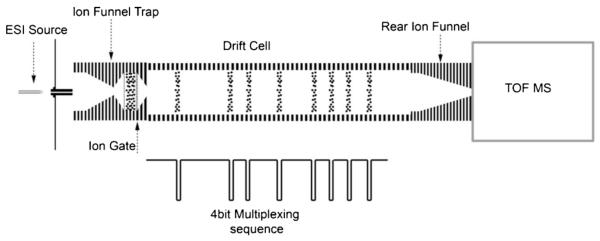
The IMS-MS instrument used in this study has been previously described [5, 9, 11]. Figure 1 illustrates a schematic of the instrumental setup during multiplexed IMS data acquisition. Briefly, molecules exiting the RPLC column are ionized in positive mode by ESI. Ions are transferred from atmospheric pressure through a stainless steel capillary heated to 120°C into a vacuum chamber that houses an ion funnel trap [22]. The expanded ion plume from the inlet capillary is focused in the converging section and then transferred into the trap section [22]. Based on a timing sequence, ions are allowed to enter the trap by lowering the voltage of an entrance grid and are then accumulated inside the trap by increasing the voltage on the ion gate. Once ions enter the trap, the entrance grid is closed to the incoming ion stream. This allows precise control of the ion population inside the trap. To release ions from the trap, the voltage of the ion gate is lowered for several hundred μs and then raised again. Ions exiting the trap are focused and released into the drift tube filled with 4 Torr nitrogen gas, where they drift under the influence of a weak electric field of ~18 V/cm (~14 Td, 1 Td=10⁻¹⁷ V.cm²). Based on the collision cross section of each ion, different ion species travel through the drift tube with different velocities. Ions of high mobilities (e.g., smaller size) travel faster than larger ions with lower mobilities. Ion packets moving through the drift cell experience radial diffusion as well as axial diffusion. To efficiently capture the diffused ion packet at the end of the drift cell, an ion funnel focuses the packet through a 2.5 mm orifice. The focused ion beam exits the rear funnel and travels through two differentially-pumped rf-only quadrupoles before entering the TOF MS (6224; Agilent Technologies, Santa Clara, CA, USA). The signal from the MCP detector is fed into an analog-to-digital (ADC) converter (Acqiris, Geneva, Switzerland) and TOF mass spectra are collected sequentially as ions elute from the drift tube.

Figure 1.

A schematic of the ion mobility drift tube is shown with eight ion packets simultaneously being measured. Ions are collected in an ion funnel trap and ion packets are injected into the drift tube according to the multiplexed sequence, shown below the drift cell as a square function. As ions exit the drift tube, they are focused by the rear ion funnel and analyzed by time-of-flight mass spectrometry

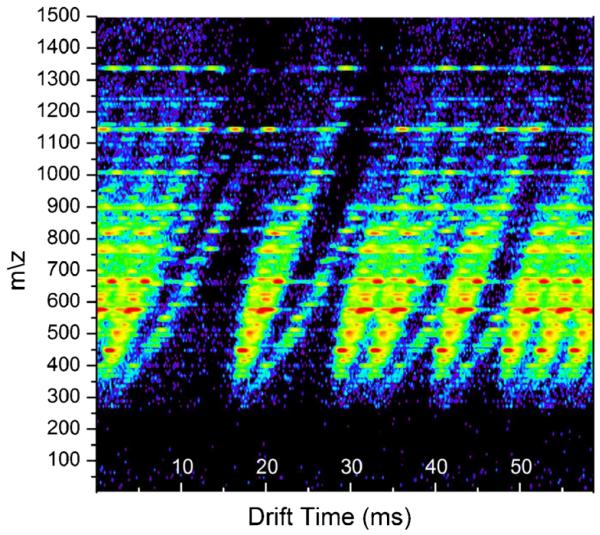
In the present platform, individual TOF pusher pulses are collected sequentially, forming an IMS drift time spectrum. Each TOF pusher pulse generates a mass spectrum, which we term an IMS scan. To improve ion statistics, IMS drift time spectra are accumulated over multiple seconds to form an IMS-MS “frame.” The quantity and temporal spacing of multiplexed ion packets injected into the drift cell are defined by a four-bit pseudo-random sequence (PRS). The length and pressure of the drift cell limits the maximum PRS to five bits. Above five bits, the ion plumes are spaced too closely to demultiplex with an appreciable gain in SNR. Figure 2 exemplifies a typical distribution of ion packets through the drift region according to the PRS. The four-bit multiplexing sequence utilized for the experiments in this manuscript corresponds to a PRS length of 2⁴–1, or 15, and the exact PRS used in this instrument setup is “100110101111000.” Each “1” in the PRS corresponds to the injection of ions into the drift cell and each “0” represents gating the ions, which prevents the injection of ions into the drift cell. The 15 segments of the PRS have spatial oversampling equivalent to 24 IMS scans, thereby defining a total drift dimension of 360 IMS scans (15 * 24). Since each scan is the result of a 162 μs pusher pulse a 58.32 ms (360 * 162) time period is utilized for all IMS drift time spectra in this manuscript.

Figure 2.

IMS- MS frame. An LC frame showing IMS-MS data of a tryptic digest of human serum. This data is the raw instrument data and, therefore, still multiplexed. The data contains 360 IMS scans with eight packets of ions distributed throughout the drift region according to the pseudorandom sequence (PRS) of the 4-bit Hadamard multiplexing scheme

Demultiplexing Using the Hadamard Transform

The Hadamard Transform is a standard mathematical function. The abbreviated description provided here is used to show how the transform applies to the specific instrument setup used in this work. In performing the Hadamard transform, a single m/z value is measured over time and stored in an array where the index corresponds to the IMS scan number .

The steps of the Hadamard transform require that the data array is first split into segments. The segments contain values that are not contiguous in drift time, but instead correspond to the periodicity of the encoding PRS. The following formula defines the set of indices that comprise a segment:

$${\left(u_k\right)}^m,u_k=c+u_{nk}$$ (1)

where m is the length of the segment u (which is also the length of the PRS), k is the index of the segment, cε[0, n–1] that defines the start of the segment, and n is the number of segments for a given TOF bin. In our setup, m=15 and n=24. Table 1 is an example segment where c is 0. This segment is then demultiplexed using the inverse scaled simplex matrix. Finally, demultiplexed values are reassigned into the full array according to their original indices.

Table 1.

Segment for c=0

Index	PRS	Multiplexed	Demultiplexed
0	1	3910	0
24	0	0	0
48	0	0	0
72	0	0	0
96	1	3910	31280
120	0	0	0
144	0	0	0
168	1	3910	0
192	1	3910	0
216	0	0	0
240	1	3910	0
264	0	0	0
288	1	3910	0
312	1	3910	0
336	1	3910	0

Columns are as follows: index is the IMS scan number, PRS is the pseudorandom sequence used for injecting ions into the drift tube, the multiplexed and demultiplexed data correspond to data from Fig. 3a and c, respectively.

Algorithm Description

The purpose of this algorithm is to validate each value in the demultiplexed segment after Hadamard transformation. The validation process may discover zero, one, or many true values and only preserves true signal; it does not adjust or alter the abundance values. At a high level, the algorithm validates signals by requiring them to contain a periodicity corresponding to the pseudorandom sequence for injection of ions, meaning that if a true signal were present after injection into the drift tube, we would expect it to show up every time the PRS dictated an injection (corresponding to a 1 value in the PRS), as shown in Table 1.

The algorithm begins by creating segments from the input as is normally done in the Hadamard transform. Each segment contains the intensities from a single TOF bin in an IMS-MS frame. Algorithm 1 in the Supplemental Algorithm Details is the pseudocode used to implement the segmentation (see also Equation 1). Segment creation is then followed by the application of the Hadamard transform. Both the original multiplexed segment and the Hadamard demultiplexed data are the input into an algorithm that validates the demultiplexed values. Algorithm 2 in the Supplemental Algorithm Details is the pseudocode used to implement the validation routine. It validates or invalidates demultiplexed data by examining specific properties of the demultiplexed and multiplexed segments. Prior to scoring each segment, a series of analytical tests are applied to quickly verify the existence of a true signal. These analytical tests rely on the existence of only one true signal per segment. The primary analytical test conducted is to take the sum of the demultiplexed segment. If only one value exists that equals the sum, then this is the value of the true signal and it is preserved. If there are multiple values that equal the sum (or its negative), then the entire segment is invalid and no true signal exists. If, however, there are no values that equal the sum of the segment, then it is possible that more than one true signal exists in that segment, and the scoring portion of the algorithm must be applied to verify the existence or absence of true signal(s). To validate segments with greater than one signal, scoring is employed. Each of the positive values in the demultiplexed segment is scored using the pseudorandom sequence to find the value associated with the strongest score. If the strongest score is above 0, then the associated demultiplexed value is validated and retained. The scoring process repeats until no more valid demultiplexed values are found (i.e., all score ≤0). When this occurs, the remaining demultiplexed values are all removed. Each value validated by Algorithm 2 is then unpacked and placed back into the original data array. Supplemental File 1 presents a detailed description of the algorithm.

Results and Discussion

We previously showed that multiplexing the drift time dimension of an ion mobility separation significantly increases the duty cycle and ion utilization, as well as improves the signal-to-noise ratio of IMS measurements [12]. As with other uses of Hadamard multiplexing, the demultiplexed data contains artifacts, most easily noticed as negative intensities. In this work, we explore the cause of such artifacts and computational solutions to remove them, thus dramatically improving the signal quality.

Investigations of Artifacts

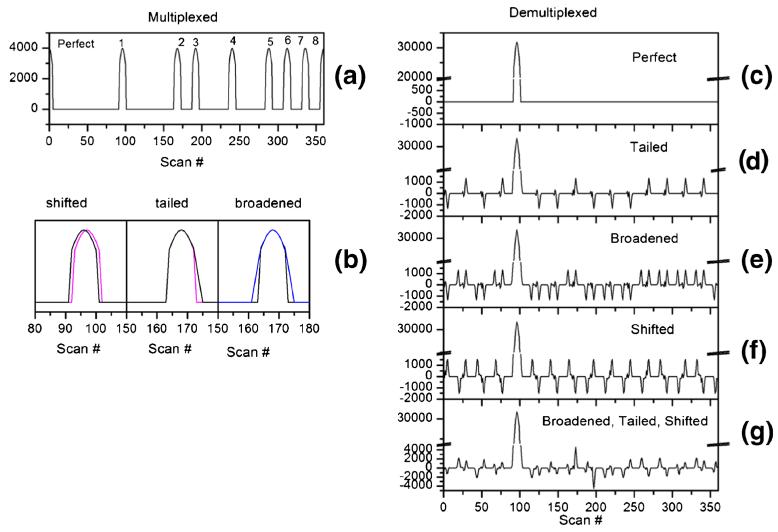
The data investigated in this manuscript were generated on an IMS-MS by multiplexing the ions into the drift tube (Figs. 1 and 2). Specifically, we utilized the Hadamard pseudorandom sequence (PRS) and injected ions into the drift cell where there is a “1” in the PRS, and otherwise gated the ions (see Methods and Table 1). As the Hadamard transform is designed to work on perfectly encoded data, it is expected that any deviation would result in artifacts and degrade the signal. To investigate these effects, a set of synthetically generated spectra were created with various perturbations in spatial location to members of the multiplexed series (Fig. 3). The synthetic data are eight Gaussian peaks with slight modifications to one or more of the peaks (Fig. 3a, b). When the synthetic data are demultiplexed, artifacts occur that do not represent the true signal. Figure 3 shows data resulting from the demultiplexing of spectra where one of the eight peaks contains a slight tailing, symmetric widening, peak shifting, or all three modifications. Artifacts are present in the data that alternate between positive and negative values for all perturbations. As more modulations to the data are introduced, the artifacts created become more complex and it becomes difficult to distinguish between artifacts and true signal, especially for low abundance peaks.

Figure 3.

Effects of perturbations on the multiplexed series. Examples of how different modulations of multiplexed data affect the resulting demultiplexed data. Top left is the raw multiplexed signal that would result from a gating/injection timed from the pseudorandom sequence (PRS). In this top frame, all Gaussian peaks are identical and perfectly spaced according to the PRS. Thus, it yields a perfect demultiplexed signal. The middle left panel shows perturbations to the multiplexed signal, e.g., a single member of the multiplexed series is tailed. On the right are graphs of the effects of the perturbations: tailing a single Gaussian peak, symmetric widening of a single Gaussian peak, shifting a single Gaussian peak, and the combination of all three modulations. In each case, any perturbation to a single member of the multiplexed series creates positive and negative data artifacts

We have formalized an algorithm that identifies and removes signal artifacts in demultiplexed data. In its simplest form, the algorithm checks data points to see if they have the periodicity expected from the multiplexed injection timing. The pseudorandom sequence (PRS) used to gate and release ions should be reflected in ion intensities during the IMS drift time spectrum. Thus, the algorithm traces out data for a single m/z value over all drift times and tests for this consistency (see Methods and Supplemental Algorithm Details). The synthetic dataset above illustrates how a single aberrant data point can cause the artifacts shown in Fig. 3b. Looking specifically at the tailed perturbation, there is a non-zero value at scan 172. Relying on the pseudorandom sequence that produced the multiplexed data, the expected periodicity is 24 scans (see Methods). This periodicity of ion injection implies that we would expect to see the same intensity value at scan 172+24, etc. However, when such a set of indices is examined from the tailed example, only index 172 has a non-zero value, as all other Gaussians do not contain the tail (Supplemental Table 1). If this set of indices is naively transformed through the Hadamard equations (see Methods), it creates the positive and negative artifacts seen in Fig. 3d. Full details of the new algorithm and how it identifies data points that are not consistent with the PRS gating/injection timing can be found in the Supplemental Algorithm Details. Although this simple example shows only a single true signal, the algorithmic approach is designed to identify multiple signals per m/z slice. The mathematics used in the algorithm are not confined to a single signal per m/z slice. As we show in the next section, multiple true signals are detected and preserved.

Application of Algorithm on Real Data

The purpose of using Hadamard multiplexing is to repeat the signal in a predefined manner and, therefore, facilitate the identification of measurement noise. Previous research has shown that Hadamard multiplexing does indeed significantly improve data quality [12]. However, as shown in the synthetic data, any non-uniformity in the members of a multiplexed series creates data artifacts (characterized by both positive and negative intensities in the demultiplexed data). Slight alterations attributable to changes to peak shape and/or signal intensities are common during liquid chromatography and electrospray ionization, and mass spectrometry measurements in general. Furthermore, in the multiplexed signal in Fig. 2, chemical and detector noise are present in the data. All of these would cause data artifacts.

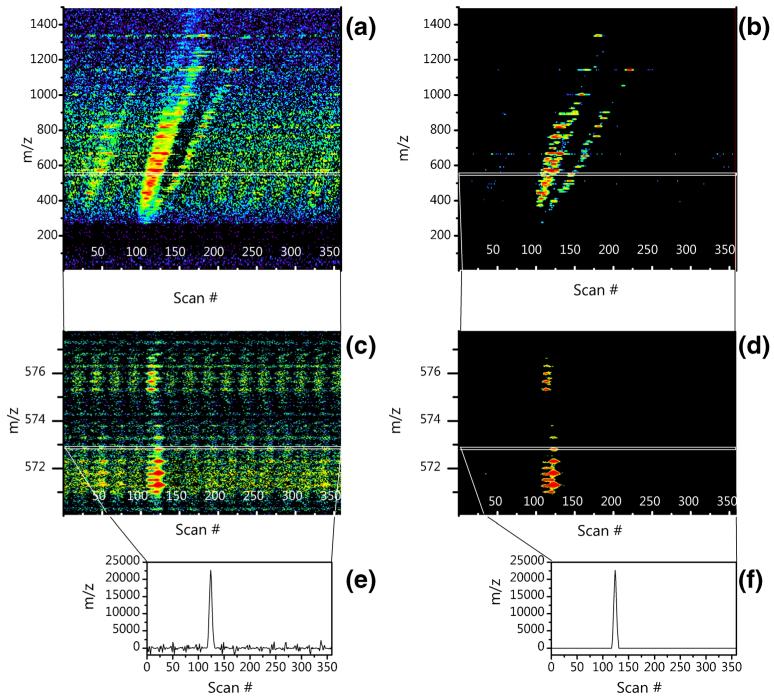
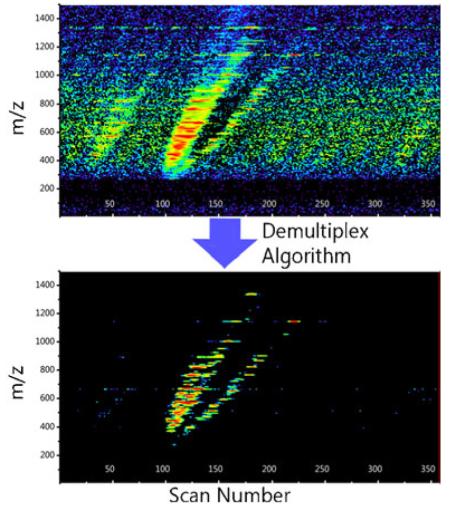
Figure 2 shows the raw multiplexed data from an IMS-MS frame. Figure 4 shows the same frame after demultiplexing. The left side of Fig. 4 is the demultiplexed frame immediately after the Hadamard transform is applied and the right side illustrates the demultiplexed data after the algorithm is applied. Both Fig. 4c and d zoom into the spectra to highlight isotopic profiles, and Fig. 4e and f show a single slice of m/z space to indicate the nature of the artifacts produced. Figure 4e and f illustrate a typical scenario where there exists a primary true peak and nothing else, and all negative values are artifacts from the transform as they are both physically impossible and did not exist in the original data. When looking at the entire IMS frame in Fig. 4a, it is clear that the aggregation of data artifacts present within each m/z slice produce a pervasive artifact scatter. Figure 4c shows a tighter m/z range and demonstrates that the artifacts persist down to individual m/z bins. The present algorithm dramatically cleans the spectrum and improves data quality. However, it should be noted that artifacts still remain after the execution of the algorithm. Some of these artifacts can be seen as scattered data points in Fig. 4b. These artifacts remain because the algorithm is designed to be as close to 100% inclusive of true signal as possible. If a data point cannot be determined to be false with a 100% certainty, it is not removed.

Figure 4.

Performance of the Algorithm. The data from Fig. 2 demultiplexed immediately after the Hadamard transform (left) and following application of the algorithm (right). The entire IMS-MS frame is illustrated in (a) and (b), whereas (c) and (d) zoom into the spectra to highlight isotopic profiles, and (e) and (f) further zoom in to show ~0.016641m/z or a single TOF bin to indicate the nature of the artifacts produced

In general, the effectiveness of the algorithm to detect and remove artifacts does not diminish if there are multiple true signals. Figure 5 shows an example of an m/z slice with three m/z isobars overlapping signals, and illustrates the effective removal of the artifacts. As the algorithm independently validates each data point in the m/z slice over all drift times, it is unaffected by the presence of multiple true signals. Using a scoring metric based on signal intensities of the multiplexed segment, the algorithm systematically tests the hypothesis that an index might be the true signal. After each true signal is found, it is subtracted out and other peaks continue to be tested. There are some cases where two true signals are spaced so as to mimic the PRS, and thus their artifacts cannot be definitively falsified. However, such cases are rare. For example, in the IMS frame data from Fig. 4, only 20m/z slices out of 100,000 (0.02%) have data remaining that is likely to be an artifact. Moreover, these remaining scattered artifacts are typically removed through deisotoping and, therefore, do not confound downstream analysis.

Figure 5.

Multiple signals. A single m/z slice is shown where three isobars are present in the drift time dimension. The original data is shown in its multiplexed, demultiplexed, and new algorithm form. The three signals are not baseline resolved in the demultiplexed data prior to the algorithm due to the presence of artifacts, but are easily resolved when the new algorithm is employed

Conclusions

A novel algorithm to improve Hadamard transformed data has been presented. We demonstrated that this algorithm is able to effectively remove artifacts from IMS-MS data of various complexities. Where there exists only a single signal in a given m/z slice, validation tends to be straight forward due to the properties of the demultiplexed segment and the property of the true signal value in the segment. For multisignal segments, the validation requires knowledge of the multiplexed signal in order to remove signals attributable to mathematical artifacts. The algorithm is demonstrably superior to a naïve SNR threshold or cutoff, as such a threshold would remove real signal, while potentially preserving the high intensity artifacts. Thus, sensitivity for the IMS-MS platform is increased because of the retention of low intensity true signal peaks, coupled with the removal of high intensity artifacts. The algorithm is mathematically general and will work for any bit-order multiplexing. However, as the number of bits increases, the signal intensity of the true signal no longer competes with the intensity of artifacts in the spectra. Therefore, it may be possible that the algorithm is not necessary to process Hadamard transformed data utilizing a large number of bits. The algorithm is platform-independent and can be used with instruments that have varying PRS bit lengths. However, we have not yet proved efficacy of this algorithm with other instruments that utilize the Hadamard transform, but such investigations are planned.