For comparison of three or more independent groups, Kruskal-Wallis test which is comparable to one-way ANOVA is used. Also for analysis of correlated data with three or more occasions or conditions, Friedman test, comparable to repeated measures one-way ANOVA, is used as a nonparametric method.
1. Kruskal-Wallis test
The Kruskal-Wallis test, an extension of the Wilcoxon rank-sum test, may be applied to data of independent three or more groups whose outcome measurements are at least ordinal. The null hypothesis is that three sets of samples came from the same population and they do not differ systematically.
1st step: Transform observed data into ranks. Tied values get average ranks.
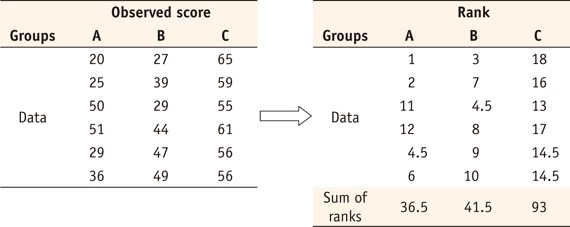
2nd step: Calculation of rank sum for each group (Tg).
T1 = 36.5, T2 = 41.5, T3 = 93.
3rd step: Calculate H value
![]()
![]()
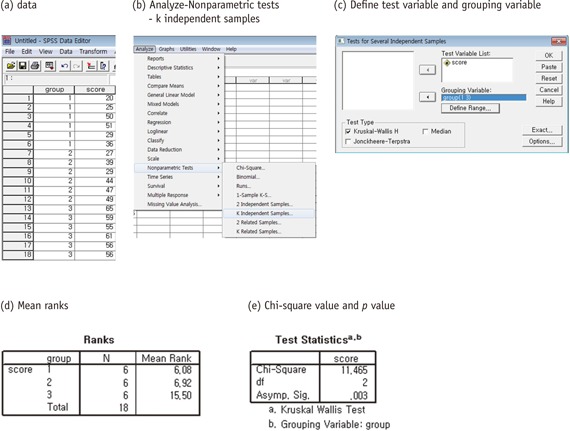
4th step: Compare with the chi-square distribution with degree of freedom (number of groups-1). Reject null hypothesis if the calculated H value is greater than the critical chi-square value. The calculated H value 11.4 is larger than the critical value, χ2(d.f. = 2, p = 0.05) = 5.99. Therefore the null hypothesis is rejected, and it is concluded that at least distribution of one group is different from other groups.
5th step: If the group difference is statistically significant, a post-hoc paired comparison is implemented using the nonparametric two group comparison method with adjusting Bonferroni-corrected alpha level.
1) Post-hoc paired comparison may be done using the Wilcoxon rank-sum test
2) Bonferroni-corrected alpha level is an alpha level divided by the number of comparisons. For example, if three groups were compared by three different pair-wise comparisons, an alpha level divided by 3 should be applied, e.g., 0.05/3 = 0.0167.
The Krusal-Wallis test using the SPSS statistical package is according to the following procedures:
2. Friedman test
The Friedman test, an extension of the Wilcoxon signed rank test, is used for within-subject design. It is used for data with three or more correlated or repeated outcomes whose distribution is not normal. The null hypothesis is that the distribution is the same across repeated measures.
1st step: Transform observed data into ranks within the subjects
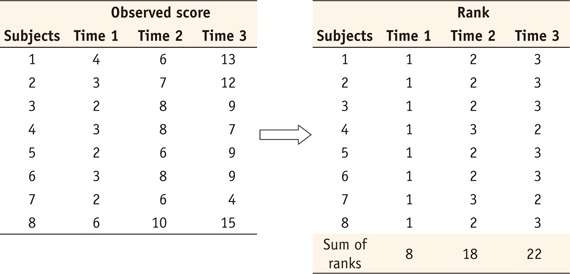
2nd step: Calculation of rank sum for each time point (Ri).
R1 = 8, R2 = 18, R3 = 22.
3rd step: Calculate Fr value
![]()
![]()
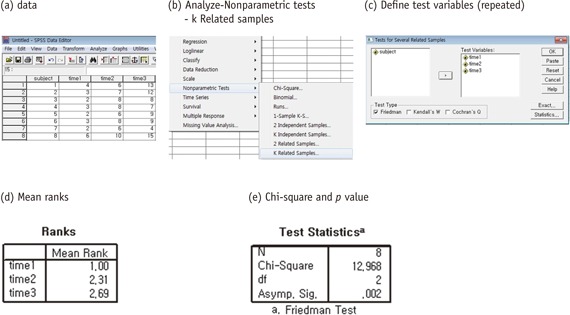
4th step: Compare with the chi-square distribution with degree of freedom (number of repetitions-1). Reject null hypothesis if the calculated Fr value is greater than the critical chi-square value. The calculated Fr value 13 is larger than the critical value, χ2(d.f. = 2, p = 0.05) = 5.99. Therefore, the null hypothesis was rejected and it is concluded that at least distribution of one occasion is different from other time points.
5th step: If the difference is statistically significant, a post-hoc paired comparison is implemented using the nonparametric two related sample comparison method with adjusting Bonferroni-corrected alpha level.
1) Post-hoc paired comparison may be done using the Wilcoxon signed rank test
2) Bonferroni-corrected alpha level should be applied for each comparison, e.g., 0.05/3 = 0.0167 for three pairwise comparisons.
The Friedman test using the SPSS statistical package is according to the following procedures:
References
- 1.McDonald JH. Handbook of biological statistics. Baltimore, Maryland: Sparky House Publishing; 2008. pp. 153–160. [Google Scholar]


