Modeling K,ATP-Dependent Excitability in Pancreatic Islets

Abstract

In pancreatic β-cells, K,ATP channels respond to changes in glucose to regulate cell excitability and insulin release. Confirming a high sensitivity of electrical activity to K,ATP activity, mutations that cause gain of K,ATP function cause neonatal diabetes. Our aim was to quantitatively assess the contribution of K,ATP current to the regulation of glucose-dependent bursting by reproducing experimentally observed changes in excitability when K,ATP conductance is altered by genetic manipulation. A recent detailed computational model of single cell pancreatic β-cell excitability reproduces the β-cell response to varying glucose concentrations. However, initial simulations showed that the model underrepresents the significance of K,ATP activity and was unable to reproduce K,ATP conductance-dependent changes in excitability. By altering the ATP and glucose dependence of the L-type Ca²⁺ channel and the Na-K ATPase to better fit experiment, appropriate dependence of excitability on K,ATP conductance was reproduced. Because experiments were conducted in islets, which contain cell-to-cell variability, we extended the model from a single cell to a three-dimensional model (10×10×10 cell) islet with 1000 cells. For each cell, the conductance of the major currents was allowed to vary as was the gap junction conductance between cells. This showed that single cell glucose-dependent behavior was then highly variable, but was uniform in coupled islets. The study highlights the importance of parameterization of detailed models of β-cell excitability and suggests future experiments that will lead to improved characterization of β-cell excitability and the control of insulin secretion.

Introduction

In pancreatic islets, insulin secretion is linked to glucose concentration by β-cell excitability. Critically, the ATP-sensitive K⁺ current (IK,ATP) links the β-cell metabolic response to bursts of electrical activity and hence to oscillatory increases of intracellular Ca²⁺ concentration, [Ca²⁺]_i, which in turn stimulate insulin release. [Ca²⁺]_i oscillations that arise from electrical bursting are optically detectable using Ca²⁺-sensitive fluorophores that are loaded into the cells. Nominally, mouse islets typically show [Ca²⁺]_i oscillations at glucose concentrations of ∼8 mM or higher. In β-cells, four Kir6.2 subunits assemble to form the ion-conducting pore of the K,ATP channel, surrounded by four additional SUR1 subunits. In mice with heterozygous knockout (KO) of Kir6.2 or SUR1 subunits, the K,ATP conductance of isolated β-cells is reduced by ∼50%, resulting in elevated excitability, with oscillations of islet [Ca²⁺]_i, and insulin secretion seen at glucose concentrations of ∼6 mM (1). In mice expressing dominant-negative Kir6.2[AAA] subunits, K,ATP is lost completely from ∼50 to 60% of the cells, but the transgene is not expressed in the remaining cells, which therefore exhibit normal K,ATP conductance (2).

In these islets, the average K,ATP conductance is thus approximately the same as that in heterozygous knockout islets, but the distribution is very different. Nevertheless, the effect on islet activity is essentially the same as in heterozygous knockouts, with oscillations of islet [Ca²⁺]_i, and insulin secretion at glucose concentrations beginning at ∼6 mM (3). Thus, we conclude that electrical coupling between β-cells is sufficient to maintain syncytial behavior, such that the K,ATP conductance is essentially averaged across all cells. Complete knockout of K,ATP, as in Kir6.2 KO or SUR1 KO mice, results in essentially glucose-independent bursting (4,5), with oscillations of islet [Ca²⁺]_i even at very low glucose (6). Conversely, mice with gain-of-function (GOF) mutations in Kir6.2 or SUR1 display greatly reduced β-cell excitability, indicating the very prominent role of IK,ATP in controlling β-cell activity (7–9), first recognized 25 years ago (10).

The first mathematical models of pancreatic β-cell electrical activity were developed 30 years ago, and showed how slow rhythmic electrical burst-interburst events can be generated by the interaction between Ca²⁺ channel-driven excitation and slow changes in cytosolic factors. These were originally proposed to be accumulation of intracellular Ca²⁺, driving activation of Ca²⁺-activated K⁺ channels (11,12) or Ca²⁺-dependent inactivation of ICa_V (13); or by changes of intracellular nucleotides ([ATP], [ADP]) driving changes in (I,KATP) (14). More comprehensive models have since been developed in an attempt to describe the details of glucose-dependent electrical activity, including the glucose-dependence of metabolism (15–18), as well as descriptions of other membrane currents and the associated changes in intracellular ion concentrations (19–22). The Cha-Noma model, recently developed by Cha et al. (23,24) reproduces an appropriate glucose-dependence of excitability in wild-type (WT) cells. In our study, we sought to further develop this model, and given the significant constraints provided by the multiple animal models with genetically altered K,ATP levels and properties, to test the ability of the model to reproduce the K,ATP-dependence of excitability.

Methods

Islet model

The single cell model from Cha et al. (24) was implemented in the software C++ using the original VISUAL BASIC code (http://www.vbcode.com/) as a reference. Islet simulations were accomplished by linking multiple cells together in a three-dimensional cube—4×4×4 for initial simulations and 10×10×10 for production runs.

Cell-cell coupling in the intact islet was simulated, as previously, by introducing a gap junction current between each β-cell (25). The gap junction conductance depended on a normal distribution centered at 0.215 nS with a standard deviation (SD) of 0.11 (25–27). To model cell-to-cell variability of the conductances of major currents including IK,ATP, the voltage-sensitive Ca²⁺ current (ICa_V), the nonspecific background current (IB_Nsc), the delayed rectifier K⁺ current (IK_Dr), the transient outward K⁺ current (IK_to), and the Ca²⁺-activated K⁺ current (IK,SK) were also allowed to vary with an SD equal to 20% of the average.

Modeling Kir6.2 [AAA] K,ATP conductance

In the Kir6.2[AAA] mouse, islet β-cells are distributed in clusters that either have wild-type K,ATP current levels or complete loss of K,ATP currents, reflecting mosaicism of transgene expression (2,3). To mimic this distribution in the model islet, 100 progenitor cells were randomly distributed throughout the 10×10×10 cube with 50% containing normal gK,ATP and 50% containing zero gK,ATP. The islet was then grown by allowing each progenitor cell to impart its phenotype to a single, randomly chosen, neighboring slot corresponding to the six sides of a cube, in random order. If the neighboring slot was already occupied, or the edge of the cube representing the islet was detected, nothing was changed. This growth step was repeated until all 1000 slots were assigned a β-cell with normal or zero gK,ATP.

Numerical methods

Random numbers were generated by a Mersenne Twister pseudo-random number generator implemented in the software C++ (28). Sequences of numbers were randomized in conjunction with this generator using Durstenfeld’s Fisher Yates shuffle. Differential equations were integrated with a Forward Euler solver and a fixed timestep of 0.05 ms. Solvers that are more complicated, with adaptive time stepping, were avoided due to added complexity in synchronizing the time stepped in each individual β-cell, which adds to the computational overhead. The output was sampled and written to disk after every 50 steps.

Computation

All code was implemented in the software C++, compiled with the Intel C++ compiler (Intel Corporation, Santa Clara, CA) and run on a cluster with dual six-core Xeon E5 processors (Intel Corporation). For large-scale three-dimensional simulations, parallelization was accomplished using the software OPENMP (http://openmp.org/wp/). An eightfold increase in speed was achieved by parallelizing the loop that cycled through each cell to update its differential equations. Thirty minutes of wall-clock time was required to simulate an islet of 1000 cells for 350 s.

Adjustment of model from Cha et al. (24)

Two ATP-sensitive model components were adjusted to achieve an appropriate K,ATP dependence of cellular activity.

The first component was the glucose dependence of the Na-K ATPase, which was originally adapted from Oka et al. (29). For this formulation, glucose more potently inhibited the ATPase, F_Glc = 0.3 + 0.7 ⋅ e^−G/2, so that the NaK pump was now more active at low glucose concentrations (30).

The second component was the voltage-dependent Ca²⁺ current (ICa,v). The ATP sensitivity was initially described by

$$\frac{1}{1+{\left(\frac{1.4}{{\text{ATP}}_i}\right)}^3}.$$

This was changed to

$$0.5+0.5\times \frac{1}{1+{\left(\frac{0.4}{{\text{ATP}}_i}\right)}^3}$$

to introduce a component of ICa_V that is insensitive to elimination of ATP (31) (see Fig. S1 in the Supporting Material for comparison). The half-maximal activatory Ca²⁺ concentration of the plasma membrane Ca²⁺ pump was increased from 0.00014 to 0.00018 mM. Finally, the mean permeability of the background Na⁺ current was reduced from 3.96 to 3.00 pA/mM and the background K⁺ permeability was increased from 2.525× to 6× that of Na⁺.

Experimental procedures

Beta-cell isolation for patch-clamp and fluorescence-activated cell sorting (FACS) experiments were carried out as previously described in Remedi et al. (8). Patch-clamp experiments were carried out on isolated membrane patches as described in Remedi et al. (8). Cells were sorted using a FACSAriaII-2 (BD Biosciences, San Jose, CA) with the 505LP dichroic filter and a bandpass filter of 550 ± 15 nm. Presorting gates (side scatter versus forward scatter, related to cell size) were set to exclude noncellular debris. Cells were sorted at a rate of 1000 events per s using Normal Recovery mode.

Results

Three-dimensional multicellular islet model

Electrical activity of single islet β-cells is notoriously variable, probably intrinsically so, yet the integrated activity of the islet is very reproducible. Our first objective was to examine the consequences of single cell parameter variability and to extend the single cell model of Cha et al. (24) to three dimensions, in part to examine how single cell variability could be integrated in the intact islet. To reduce simulation time for these initial simulations, the islet size was a minimal 4×4×4 cube. Fig. 1 A shows uncoupled (i.e., single) β-cells in this cube with the SD for each current component set to 20% of the mean current (see Methods). At 8 mM glucose, even this relatively small variability of individual currents results in extensive variability in the bursting pattern in these uncoupled, isolated cells. The duration of the burst and the interburst interval are highly variable, with several cells stable at ∼−56 mV and not bursting at all. Coupling cells with experimentally suggested parameters (Fig. 1 B) results in synchronous bursting throughout the simulated islet, with characteristics very similar to those of the isolated cell without parameter variability. However, although the voltage magnitude across all cells is maintained, the variability in ICa,V results in significant differences in the magnitude of the [Ca²⁺]_i oscillations (Fig. 1 C and see Fig. S2).

Figure 1.

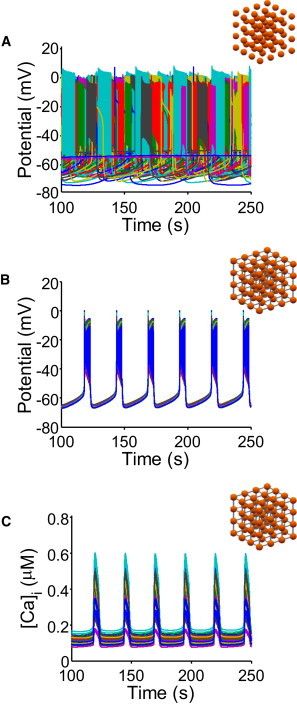
Coupling of β-cells synchronizes bursting. 4×4×4 cubes of β-cells were simulated at 8 mM glucose and data from all 64 cells is plotted simultaneously. (A) Uncoupled β-cells with variation in the major currents display varied bursting behavior, including quiescent cells. (B) Introducing coupling between cells results in synchronized bursting behavior throughout the simulated tissue. (C) [Ca²⁺]_i oscillations are also synchronized, but magnitude differs because of the variability of the ionic conductances.

Incorporating K,ATP-dependence of islet activity

When coupled together in a 10×10×10 islet, WT islet simulations show appropriate electrical bursting (Fig. 2 A) and [Ca²⁺]_i oscillations (Fig. 2 B) as glucose crosses a threshold at 8 mM with longer bursts at higher concentrations, as expected from the published Cha-Noma single cell model (blue traces). However, when gK,ATP is reduced to zero, to mimic the Kir6.2 or SUR1 KO mouse behavior, electrical activity remains strongly glucose-dependent, such that there is no excitability at low glucose (Fig. 2, red traces), in contrast to what is experimentally observed. This failure to demonstrate electrical activity and elevated [Ca²⁺]_i at low glucose indicates that the model underrepresents the prominence of gK,ATP in the physiological glucose response.

Figure 2.

Cha-Noma model does not recapitulate K,ATP dependence. Glucose dependence of (A) electrical activity and (B) [Ca²⁺]_i in the original model from Cha et al. (24) was simulated with cells coupled in a 4×4×4 cube as in Fig. 1. (Blue lines) WT model [Ca²⁺]_i averaged over all 64 cells, which shows appropriate bursting beginning at 8 mM glucose. (Red lines) Response with zero K,ATP conductance (as in SUR1 KO). Bursting below 8 mM glucose, as would be expected based on experiment, is not observed.

Only a few components of the model are directly dependent on intracellular ATP. These are ICa,V INaK, and IK,ATP. Accordingly, we reviewed the experimental evidence for the ATP-dependence of these components. In the original model, INaK is inhibited at low glucose on the assumption that glucose itself regulates INaK activity. However, we noted that glucose per se should inhibit pump activity through regulation of the channel by protein kinase C (30), but at low glucose levels, lower ATP levels will also inhibit pump activity. We increased the fraction of channels that can be maximally inhibited at high glucose (through the first mechanism) and increased the steepness of the inhibition (see Methods). Although not necessary to reproduce bursting at low glucose, the increased inhibition improved the behavior of the model in absence of gK,ATP at higher levels of glucose.

The original model implies zero ICa,V in the absence of ATP. Data representing the actual ATP-dependence of β-cell ICa,V are unavailable, but experiments clearly show an ATP-insensitive component of the current (31). In the revised model, this was accounted for by adding an ATP-independent component to the equation describing the ATP-dependence (see Methods). The point at which significant reduction in ICa,V occurs was also shifted to lower concentrations.

The glucose dependence of the modified WT model is shown in Fig. 3 (blue lines). Similar to experiments, electrical bursting and [Ca²⁺]_i oscillations begin at 8 mM glucose and the duration of the bursts increases at higher glucose concentrations. Now, however, the prominence of K,ATP in glucose dependence is appropriately reproduced. Reducing K,ATP conductance to 50% shifts the threshold for bursting to 6 mM glucose (Fig. 3, green lines), as in the Kir6.2^+/− or SUR1^+/− mouse, but moreover, with zero K,ATP (as in the Kir6.2 or SUR1 KO mouse), oscillations are now observed even at the lowest glucose concentrations (2 mM, Fig. 3, red lines).

Figure 3.

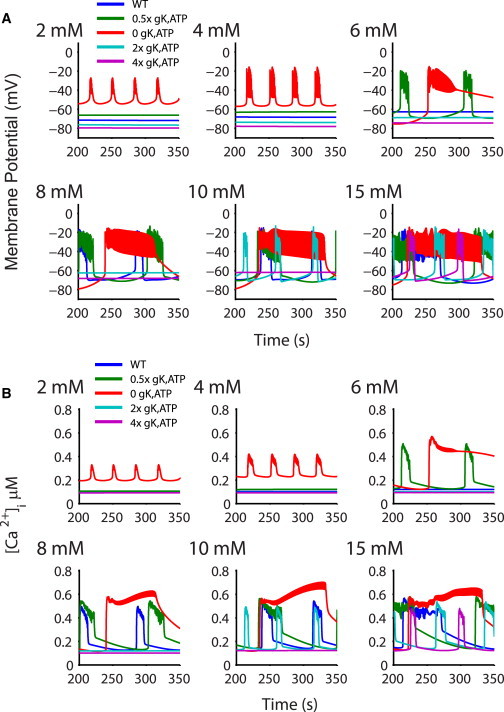
Glucose dependence of islets with varying gK,ATP. (A) Glucose dependence of the membrane potential with the updated model in a 10×10×10 cube. (Blue lines) WT model, showing appropriate bursting beginning at 8 mM glucose. (Green lines) Simulations with a 50% gK,ATP to mimic Kir6.2^+/− resulting in appropriate bursting at 6 mM glucose. (Red lines) Islet with zero K,ATP as in the SUR1 KO and bursting at very low (2 mM) glucose. Increasing gK,ATP causes proportionally reduced bursting (2× gK,ATP in cyan and 4× pink). (B) Traces as in panel A, showing intracellular [Ca]_i averaged over all 1000 cells.

The ability of the model to now appropriately simulate the effect of lowering gK,ATP on the glucose-dependence of excitability also allows us to predict the potential consequences of elevating gK,ATP. Increasing gK,ATP by a factor of 2× or 4× shifts the initiation of bursting to 10 and 15 mM glucose, respectively (Fig. 3, cyan and pink traces). The continuum of the simulated β-cell response indicates that the magnitude of gK,ATP will set the bursting threshold.

Accounting for mosaicism of K,ATP channel density

In addition to the well-studied Kir6.2- and SUR1-KO mice, we have generated a series of transgenic animals expressing either dominant-negative Kir6.2[AAA] or GOF Kir6.2[ΔN30] or Kir6.2[ΔN30,K185Q] mutations (2,7,8). The Kir6.2[AAA] transgene is strongly expressed in only a subset of β-cells (2). Approximately 50% of cells express the transgene, and have no measurable gK,ATP, but there is no obvious expression in the other cells, which have normal gK,ATP. The Kir6.2[AAA] transgene carries a GFP-tag, and FACS-sorting of β-cells from Kir6.2[AAA] islets (see Fig. 4 A) confirms this essentially binary expression, with a very clear separation of GFP-expressing (green box) and nonexpressing cells. Confocal imaging (Fig. 4 A, below) shows that the distribution of the transgene-expressing cells is essentially random, resulting in different patterns between individual islets. Despite this, experimental analysis of islet [Ca²⁺]_i activity demonstrates uniform [Ca²⁺]_i responses in both GFP-expressing and nonexpressing cells, indicating that there is sufficient gap-junctional coupling to overcome individual cellular responses (3). One advantage of the three-dimensional multicellular model is that mosaic distributions of K,ATP conductances, such as those observed in the Kir6.2 [AAA] mouse, can be assessed. The behavior of two 10×10×10 cube models each with randomly generated [AAA] distributions (see Methods) are shown in Fig. 5 A. The bursting behavior is essentially indistinguishable between the two, indicating that the gap junction coupling in the model is sufficient to maintain syncytial behavior, independent of the cellular patterning. Simulations of both distributions show bursting that begins at 4 mM glucose, decreasing the dependence of bursting on glucose, as in experiment.

Figure 4.

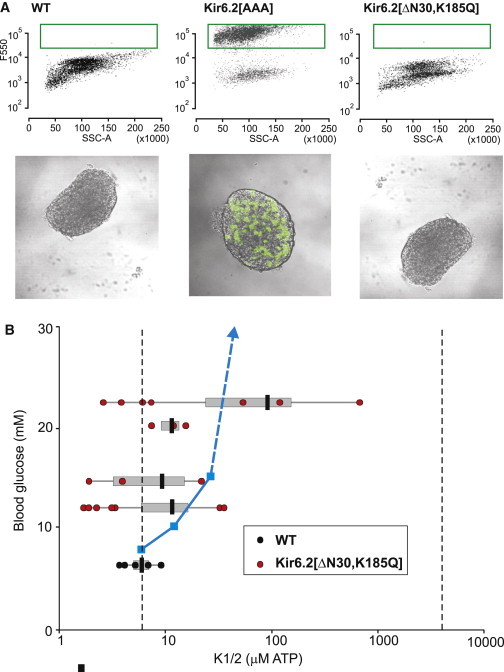
Experimental sensitivity of blood glucose to gK,ATP. (A) FACS-sorting of wild-type β-cells (above) results in a uniform population, but Kir6.2 [AAA] β-cells generate two distinct populations, one of which shows high 550-nm fluorescence (green box), reflecting high level of expression of the GFP-tagged (Kir6.2[AAA] transgene (further evident in confocal images, below). In contrast, even when blood glucose has risen to 23 mM in a Kir6.2[ΔN30,K185Q] mouse (in which GFP is coexpressed with the transgene), GFP fluorescence is minimal in isolated islets or β-cells. (B) K1/2 was estimated for individual membrane patches from WT and Kir6.2[ΔN30,K185Q] β-cells and plotted versus blood glucose in the mouse at the time of isolation (each set of horizontally grouped values are from one mouse). (Gray bars) 1 SD from the mean (black bar). (Dashed vertical lines) Predicted K1/2,ATP for homomeric WT Kir6.2+SUR1 channels (8 μM) and for homomeric Kir6.2[ΔN30,K185Q] channels (4 mM). (Blue line) Shift in glucose threshold for excitation versus K1/2,ATP predicted for the modeled islet (see Fig. 6A).

Figure 5.

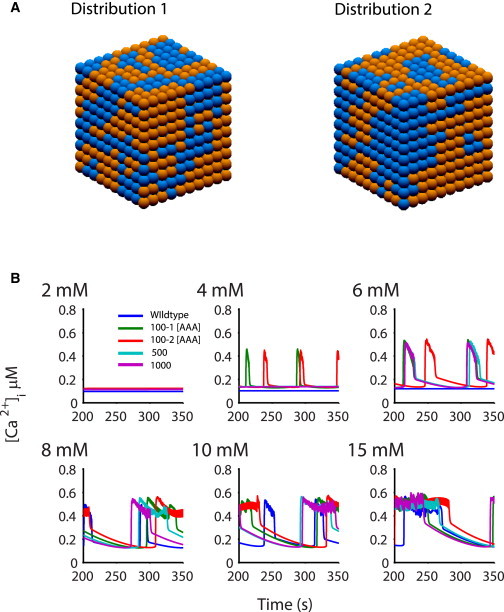
Glucose dependence of the Kir6.2 [AAA] islet. 10×10×10 Kir6.2 [AAA] islets were simulated with 50% of the cells set to gK,ATP = 0, whereas the others had WT levels. Islets were populated from 100 progenitor cells, randomly assigned to contain either normal or zero gK,ATP. (A) Two randomly generated distributions (distributions 1 and 2) of β-cells with 0 K,ATP (blue) and WT K,ATP (orange). (B) The two distributions (marked 100-1, 100-2) in panel A show weak bursting behavior at 4 mM glucose, consistent with the decreased glucose sensitivity shown in experiment. Increasing the number of progenitor cells to 500 (blue) and 1000 (pink) resulted in bursting at higher (6 mM) glucose, indicating a role for the proximity of cells with similar phenotype.

The two expression distributions shown in Fig. 5 A were generated by assigning 100 progenitor cells a random phenotype (see Methods). To further probe the effect of the degree of clustering, we also created distributions with 500 and 1000 progenitors, increasing the randomness of the distribution. As can be seen in Fig. 5 B, increased randomness shifts bursting to higher glucose concentrations (6 mM, blue and purple) due to the reduced proximity of cells with similar phenotypes.

Accounting for K,ATP channel overactivity

Highlighting the prominent role of K,ATP in controlling insulin secretion, transgenic mice expressing GOF Kir6.2[ΔN30] or Kir6.2[ΔN30,K185Q] mutations (which generate K,ATP channels with reduced sensitivity to ATP (32)) develop a profound neonatal diabetes, predicting and modeling human neonatal diabetes mellitus (NDM) (33). This diabetes results from loss of β-cell electrical activity and hence of the oscillations of [Ca²⁺]_i that trigger insulin secretion (34–37). The shift in ATP sensitivity found in NDM-causing mutations can be relatively small (less than fivefold increase) (37), and even a very small shift (less than twofold increase) of ATP-sensitivity generated by the common human Kir6.2[E23K] polymorphism results in predisposition to type-2 diabetes (38–42). This indicates an exquisite sensitivity of electrical activity and insulin secretion to the available gK,ATP (10). We have attempted to correlate the degree of change of ATP sensitivity of β-cell K,ATP channels with blood glucose at the onset of disease. The [ATP] causing half-maximal inhibition of channel activity of WT Kir6.2 (+SUR1) channels is ∼8 μM, but for homomeric mutant Kir6.2[ΔN30,K185Q] (+SUR1) channels this is greatly shifted to ∼4 mM (7). As shown in Fig. 4 B, blood glucose rises very rapidly after onset of induction of expression of ATP-insensitive Kir6.2[ΔN30,K185Q] transgenes in β-cells (8), even though the mean change in ATP-sensitivity of expressed K,ATP channels is only minimally shifted. Only once blood glucose has risen >20 mM are channels with K1/2 > 100 μM observed, and no patches even approach the ATP-sensitivity that would be expected for homomeric Kir6.2[ΔN30,K185Q] channels, implying that very few mutant subunits have been incorporated into functional channels at this stage. Consistent with this conclusion, GFP is coexpressed with the transgene (8) but green fluorescence in islets at this stage is minimal (Fig. 4 A, right). These results confirm the exquisite sensitivity of electrical activity and insulin secretion (and hence the resulting blood glucose levels) to the available gK,ATP.

We have quantitatively assessed the model sensitivity to loss of ATP sensitivity, by increasing the binding constant for ATP in the K,ATP formulation (Fig. 6 A). With no other changes to the model parameters, we find that even a small (2×) reduction of ATP affinity weakens the glucose-dependence of excitability, with reduced electrical burst durations and a shift of threshold from 8 to 10 mM. At only 5× reduction of ATP affinity (modeling weak NDM mutations), the glucose-dependence of bursting is dramatically shifted from a threshold of 8 mM to 15 mM glucose, and at 10×, no bursting is observed at 15 mM glucose and even at 40 mM (not shown).

Figure 6.

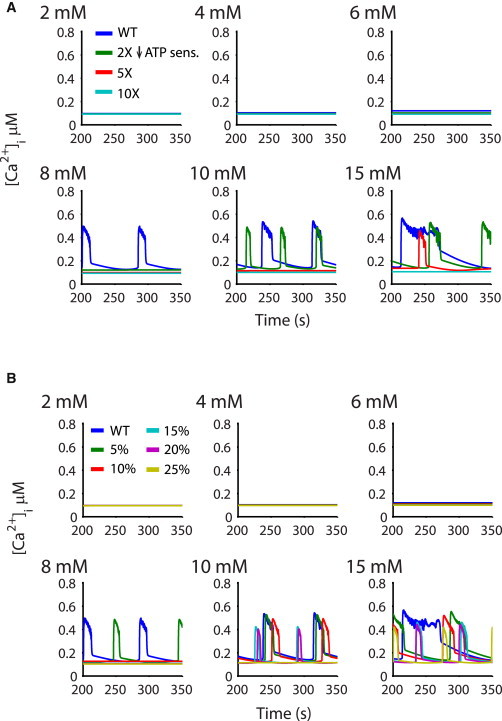
Glucose dependence with reduced K,ATP sensitivity to ATP. (A) Progressive reduction of sensitivity to ATP markedly right-shifted the glucose threshold. The simulated islet shows decreased responsiveness to glucose as sensitivity is decreased from 2× to 10×, where no bursting is observed even at high (15 mM) glucose concentrations. (B) A small percentage of cells were altered such that their sensitivity to ATP was reduced 100-fold. As the percentage increased from 10 to 25%, glucose-dependence was gradually abolished. With 25% of cells 100-fold less sensitive to ATP, oscillatory behavior was absent up to 10 mM glucose, and only weakly present at 15 mM glucose.

Because of the strong gap junctional coupling between β-cells, even a few cells expressing ATP-insensitive channels could have a profound effect on excitability, and we have shown that even with only <10% of cells expressing visibly detectable levels of GFP-tagged ATP-insensitive Kir6.2[ΔN30] subunits, there is marked reduction of insulin secretion (32). Fig. 6 B shows the effects of increasing the percentage of ATP-insensitive (100-fold decrease of ATP insensitivity) β-cells (randomly assigned as in the Kir6.2[AAA] simulation, Fig. 5). With only 10% of cells expressing the ATP-insensitive conductance, bursting is abolished at 8 mM glucose. With 25% of the cells carrying this severe phenotype, only occasional bursting is observed at 15 mM glucose. This result demonstrates that, in the coupled islet, the presence of a few cells with ATP-insensitive channels can control the behavior of the majority of cells with normal K,ATP channels.

Discussion

Development of realistic models of islet excitability

In a highly complex, nonlinear system, such as the pancreatic islet, models that integrate the kinetics of molecular components can inform the mechanistic basis of behavior at the cellular and tissue level. Recapitulation of tissue-level experimental data provides critical validation of the model and its physiological relevance. Previous models of pancreatic β-cell electrical activity have shown that rhythmic electrical burst-interburst events can be generated by the interaction between Ca²⁺ channel-driven excitation and slow changes in Ca-activated K⁺ channel activity (11,12), or Ca-dependent inactivation of ICa,v (13), driven by accumulation of intracellular Ca during the burst. Subsequent models have emphasized the potential of changes of intracellular nucleotides ([ATP], [ADP]) driving changes in (I,KATP), in generating burst-interburst events (14), as well as slowly activating Ca-activated K⁺ channels underlying very fast Ca oscillations, increases in the ATP/ADP ratio and endoplasmic reticulum calcium concentration underlying fast bursts and cytoplasmic Ca oscillations, and cyclical cytoplasmic Na changes underlying slow Ca oscillations (43). In general, the glucose-dependence of activity has not been the primary focus of most such modeling efforts. Our goal was to explore this question specifically, without focusing on the details of bursting patterns. The model developed by Cha et al. (23,24) is attractive in this regard, because it reproduces an appropriate glucose dependence of wild-type electrical activity and so, in this study, we focused on examination of the ability of the model to reproduce appropriate glucose responsivity when the K,ATP conductance is modified genetically.

With modification of INaK and ICa,v, to more closely match experimental data, the model is able to reproduce the key experimental findings from genetic modification of K,ATP conductance. However, although much experimental data are available, not all measurements required to fully parameterize the models have been performed. For ICa,v, where the major molecular components that generate the current are not clearly specified, the data are particularly sparse, and [ATP] dependence is only reported at zero and physiological levels (30). While the half-maximal ATP-dependence of ICa,v reported in guinea-pig ventricular myocytes was used in the Cha-Noma model, the ATP dependence of ICa,v in the β-cell has not been assessed. Therefore a critical system component, which regulates the bursting behavior and initiates insulin release, has not been quantitatively characterized. The INaK pump model is highly detailed and represents one of the most sophisticated kinetic models of any membrane protein (29,44). However, the glucose regulation relies on a phenomenological description that reduces pump activity at high glucose. Given the critical role such regulation can play in the physiological response of the model, inclusion of more experimental details regarding the interaction of protein kinase C with INaK would likely lead to more accurate reproduction of β-cell electrophysiology.

As modified, the model was successful in accounting for the role of gap junctions in overcoming mosaicism and in generating appropriate left-shift in glucose responsiveness in Kir6.2[AAA] transgenic mice. A previous analysis using a simpler model was also able to reproduce appropriate shift, in this case, by compensating for reduced K,ATP density by increasing open probability because of elevated Ca (45). Although this may be reasonable, such a model may not then reproduce the paradoxically dramatic right-shift in glucose-dependence that results from K,ATP GOF (Figs. 4 and 6), because the same mechanism would be limiting (i.e., reduced Ca would then compensate for reduced ATP-sensitivity by inhibiting channels). Previous models (25,27) have used experimental results from dissociated pairs of β-cells to find a lower limit of β-cell coupling (26). More recent experiments have estimated values of 0.14 nS (46) to 0.17 nS (47), which is near the value (0.215 nS) that we chose. However, a confounding factor may be the number of connections between β-cells. To generate a three-dimensional islet, we assume a cubic form factor that forces a set number of six connections. Native β-cells are not cubes and the number of couplings between cells may be much more variable than modeled.

The role of gK,ATP in controlling islet activity

A primary advance made by this study is to introduce adjustments to the Cha-Noma model to reproduce the gK,ATP dependence of the glucose response. Multiple lines of mice with genetically modified K,ATP conductances have been generated and characterized in terms of properties, levels, and distribution of K,ATP, as well as glucose-dependence of [Ca²⁺]_i, and insulin secretion. These studies highlight the very prominent role of IK,ATP in control of β-cell excitability and insulin secretion. Complete knockout of either Kir6.2 or SUR1 results in elevation of islet [Ca²⁺]_i even at extremely low glucose (4,6). Heterozygous knockout of either Kir6.2 or SUR1 subunits essentially halves the K,ATP conductance of isolated β-cells, and this results in the threshold for [Ca²⁺]_i oscillations decreasing from ∼8 to ∼6 mM glucose (2,3). A similar overall decrease in K,ATP conductance is present in islets from mice expressing dominant-negative Kir6.2[AAA] subunits, but this results from strong expression of the transgene in only ∼50% of the cells and no expression in the remainder, such that gK,ATP is absent from ∼50% of the cells and normal in the remainder. Thus, in these islets, the average K,ATP conductance is similar to that in heterozygous knockout islets, but the distribution is very different. However, the effect on glucose-dependence of activity is essentially the same in Kir6.2[AAA] islets as in heterozygous knockouts As shown in Fig. 5, this experimental finding is well reproduced by the model, highlighting how the gap junction coupling is sufficient to overcome any effect of distribution of transgene.

Perspective and conclusion

The Cha-Noma model attempts a realistic model of β-cell electrical activity, incorporating major ion conductances, carriers, and metabolic components. With suitable adjustments, and incorporation of appropriate gap junctional conductances, we now show that the model can be expanded to a 1000-cell islet. It can reproduce the glucose-dependence of electrical activity for wild-type islets, and islets with both reduced gK,ATP or enhanced g,KATP. This modeling highlights several components of the model that are critical to reproducing the islet response—in particular, the K,ATP current, ICa_V, and INaK. The paucity of relevant experimental data for fully parameterizing these components is an issue. One limitation of the model is that it still does not show a decrease in the interburst interval in response to increases in glucose, as is observed experimentally, a phenomenon that was reproduced in earlier β-cell models (11,12). The model shows bursting behavior at very low glucose. Strong suppression of K,ATP activity with sulfonylureas typically results in permanent firing of individual β-cells without burst termination (e.g., (48,49)). However, variability of firing patterns and clear evidence of oscillations of firing and [Ca²⁺]_i have been reported in SUR1 KO islets (6,50). More or less continuous elevation of [Ca²⁺]_i over a relatively short time frame has been reported in Kir6.2 KO β-cells (4), but the details of electrical activity and Ca oscillatory patterns in the truly steady state in the absence of Kir6.2 may not yet have been well characterized.

Both the original Cha-Noma model and our revised model predict that the active-phase and silent-phase durations increase with glucose. In experiments, the silent phase typically decreases with glucose. Moreover, the model does not account for slow oscillations (period 3–10 min), which are likely to underlie whole-body pulsatile insulin secretion. Given its attempt to comprehensively consider underlying conductances, the Cha-Noma model remains attractive for further consideration. However, to fully constrain and accurately reproduce the relevant behavior with the level of detail required in the model, both further modeling and experimental efforts will be required.