Competing risks analyses: objectives and approaches

Abstract

Studies in cardiology often record the time to multiple disease events such as death, myocardial infarction, or hospitalization. Competing risks methods allow for the analysis of the time to the first observed event and the type of the first event. They are also relevant if the time to a specific event is of primary interest but competing events may preclude its occurrence or greatly alter the chances to observe it. We give a non-technical overview of competing risks concepts for descriptive and regression analyses. For descriptive statistics, the cumulative incidence function is the most important tool. For regression modelling, we introduce regression models for the cumulative incidence function and the cause-specific hazard function, respectively. We stress the importance of choosing statistical methods that are appropriate if competing risks are present. We also clarify the role of competing risks for the analysis of composite endpoints.

Introduction

Many cardiovascular studies use the time to some disease events as their primary outcome and hence, statistical methods developed for survival data are usually applied. However, in some instances, the time to a specific event is of primary interest but competing events may preclude its occurrence or greatly alter the chances to observe it. In other situations, different types of events may all be relevant and the analysis may focus on both the time and the type of the first event. In both situations, competing risks methods, an extension of survival analysis methods, are required for a correct analysis. In data sets, competing risks outcomes are usually recorded as a multi-component endpoint of two variables: one variable describes the time to the first observed event and the second the type of the first event (either the ‘event of interest’ or a ‘competing event’).

As an example, the prediction of coronary heart disease (CHD) in elderly subjects is complicated by the fact that a substantial proportion of them may die from causes other than CHD prior to CHD onset and the outcome would be recorded as the time to CHD or death from other causes, whichever occurs first, and the event type (CHD or prior death).¹ As another example, randomized controlled trials (RCTs) in cardiology frequently use composite endpoints, such as the time to myocardial infarction or death, to provide an overall estimate of the effect of an intervention.² Survival analysis can be used to analyse the composite endpoint, but competing risks methodology may provide further insights into the effect of interventions on the separate endpoint components.

In most studies, there will be subjects for whom the follow-up ends before any event can be observed. Such observations will be right-censored at their last follow-up visit to indicate that the exact (future) time and event type are unknown. All statistical methods which will be presented can account for right-censoring but, as in survival analysis, they are only valid if censoring is independent of the outcome which means that subjects who are censored at a given time point would have had the same future prognosis (i.e. they are neither ‘sicker’ nor ‘healthier’) as those who remained in the study beyond that time point.^3,4

This article gives a non-technical overview of competing risks concepts assuming that the reader is familiar with the basic concepts of survival analysis.^3,4 For simplicity, we discuss the situation of two different event types only, but the methodology generalizes seamlessly to more than two types.

Example data set

We use data from a published study of subjects with implantable cardioverter-defibrillators (ICDs) from the ICD registry of the Department of Cardiology, University Hospital Basel, Switzerland for illustration.⁵ In brief, the study included 442 subjects with ischaemic or dilated cardiomyopathy with an ICD implanted for primary (n = 182) or secondary prevention (n = 260), a median age of 63.4 years, and a median follow-up duration of 3.3 years. The study aimed to quantify the benefit of ICD implantation in an unselected routine-care population by analysing the time from ICD implantation to the first appropriate ICD therapy or death without prior appropriate ICD therapy. Implantable cardioverter-defibrillator therapy that failed to save the patient's life at the time of the arrhythmia was classified as death, not as appropriate ICD therapy. A total of 180 patients experienced an appropriate ICD therapy (and hence benefited from implantation), 29 died without prior appropriate ICD therapy (and hence did not benefit from implantation by termination of a life-threatening arrhythmia event), and the remaining 233 subjects were censored at their last follow-up visit.

Description of competing risks data

Descriptive statistics are the first step of every data analysis. We discuss methods for competing risks that describe the occurrence of different event types over time and can be applied to the entire population or to subgroups defined by, e.g. treatment assignment or age group.

The cumulative incidence function

The primary interest in describing competing risks data is often to estimate the absolute risk of the occurrence of an event of interest up to a follow-up time point t. This risk is formalized by the cumulative incidence function (CIF) which is defined for each event type separately and increases with time: the CIF at time t is defined as the probability that an event of that type occurs at any time point between baseline and time t. If the data do not contain any censored individuals, the CIF at time t can be estimated as the ratio of the number of subjects who experienced that event type until time t divided by the total number of subjects in the data set. As time increases, the CIF increases from zero to the total proportion of events of that type in the data.

If the data set contains censored observations, i.e. not all subjects are observed to experience an event, this simple estimate must be modified to correctly account for censoring. We omit the details here as they are not essential for a qualitative understanding of the CIF and have been described in many publications.⁶

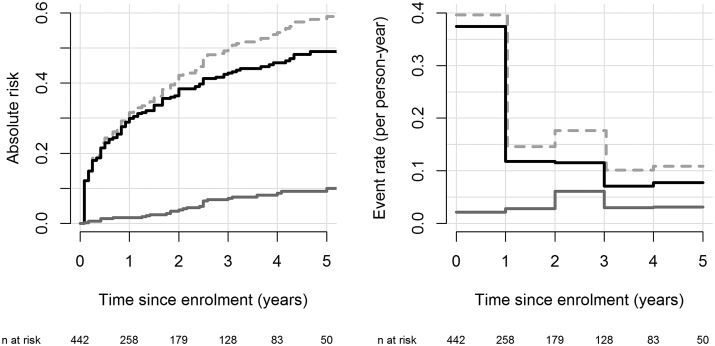
The CIFs for the ICD data set are displayed in the left panel of Figure 1. The estimated probability of having an appropriate ICD therapy is 30% during the first year and 49% during the first 5 years after ICD implantation. The estimated 5-year probability of death without any prior ICD therapy is 10%.

Figure 1.

Descriptive statistics for the implantable cardioverter-defibrillator data: estimated cumulative incidence functions (left panel) and yearly cause-specific incidence rates (right panel). Black lines correspond to events of type ‘first appropriate ICD-therapy’, solid grey line to ‘death without prior ICD-therapy’. The dashed grey line is the sum of the two cumulative incidence functions or cause-specific failure rates and denotes the total cumulative incidence function or event rate, respectively. Numbers at the bottom of the graph are the number of subjects who are still at risk, i.e. under follow-up and free of any event, at each time point.

Kaplan–Meier estimation and the cumulative incidence function

The total CIF of any first event occurring over time can be estimated with the Kaplan–Meier estimator of the time to the first event (i.e. using survival analysis and ignoring the event type).^3,4 Alternatively, one could estimate this quantity as the sum of the CIFs of all different event types and, indeed, it can be shown that this gives the same result as the Kaplan–Meier estimator.⁶

It is tempting to also estimate the CIF of a specific event of interest with the Kaplan–Meier method instead of using the estimator described in the previous section. For this naive Kaplan–Meier estimator, subjects experiencing competing events would be treated as censored observations at the time of the competing event occurrence. While frequently used, it is important to note that the logic of this modified estimator is flawed. Treating subjects as censored indicates that they have not yet had the event of interest up to the censoring time but could experience that event at a future unobserved time point. However, we do know that these subjects experienced the competing event and thus will never experience the event of interest as a first event. It can be shown that this inappropriate treatment of competing events causes the Kaplan–Meier estimator to over-estimate the CIF in the presence of competing risks and that the risk over-estimation is particularly severe if the competing event is frequent.⁶

For the ICD example, the Kaplan–Meier ‘estimate’ of the 5-year risk of having a first appropriate ICD therapy is 51% and the corresponding risk of death without prior ICD therapy is 16%. The latter substantially overestimates the correct CIF estimate of 10%. For this reason the Kaplan–Meier method should not be used in the presence of competing risks.

Some have interpreted the naive Kaplan–Meier estimate as corresponding to a world, where the competing event does not exist. For example, the 51% provided earlier would be interpreted as the risk of an appropriate ICD therapy within 5 years in a hypothetical world where no subject would experience the competing event, i.e. nobody would die prior to having their first appropriate ICD therapy. The value of statements referring to such a hypothetical world has been hotly debated in the clinical discussion on heart valve replacement.⁷ Clearly, quantities such as the CIF which refer to absolute risks in the real-world where competing events do occur seem more important for medical decision-making. Moreover, we mentioned earlier that the validity of all presented methods depends on the assumption of independent censoring. Since this approach treats subjects experiencing competing events as censored, it implicitly assumes that the different competing risks are independent of each other, i.e. that subjects experiencing a competing event would neither have a lower nor a higher future event rate of the event of interest than subjects without any prior event who were followed-up beyond that time point. The validity of this independence assumption cannot be statistically verified and is often clinically implausible. Specifically, in the ICD example, older subjects are more likely to die prior to an appropriate ICD therapy, i.e. they are ‘sicker’ than those who remain under follow-up, as we will show in the regression section below.

The cause-specific hazard function

While the CIF evaluates the cumulative probability of the occurrence of an event at any time between baseline and a specific time point t, the cause-specific hazard function measures the instantaneous potential per unit time for a specific event type to occur at time t among subject without any prior event.³ The cause-specific hazard function is defined for each event type separately and is a function of time: at time t, it is determined as the rate (i.e. probability per unit time) of experiencing a specific event type during a short time-period after time t among all subjects who have not experienced any prior event. The rate of a specific event type can be interpreted as the momentary ‘force’ at time t for subjects without a prior event to experience that event type. All cause-specific event rates jointly provide a dynamic description of the forces that draw subjects towards the different event types as the competing risks process evolves over time.

Different methods to estimate the cause-specific hazard function exist and we will explain the simplest one which requires first dividing the time scale into distinct time intervals and assuming that the cause-specific hazard is constant in each interval. The cause-specific hazard function can then be estimated by the observed incidence rate in each time interval. The incidence rate of an event of interest for a particular time interval is defined as the number of events of interest occurring during that time interval divided by the total observation time in that same interval. A subject contributes observation time to a time interval if they are still free of any event and under follow-up at the beginning of the time interval.

The yearly incidence rates for the ICD example are given in the right panel of Figure 1. The rate of first appropriate ICD therapies is the highest in the first year following implantation and then decreases sharply. The rate of death without prior appropriate ICD therapy remains roughly constant over time at ∼0.03 deaths per person-year of follow-up.

To illustrate the calculation of the incidence rate for the ICD example during Year 2 of follow-up, note that 258 subjects were at risk (i.e. event-free and under follow-up) at the beginning of Year 2; 25 of them had an appropriate ICD therapy and 6 of them died without prior ICD therapy during Year 2. The total observation time in Year 2 was 212 person-years based on 179 subjects contributing a full year and 79 subjects contributing an average of 0.42 years until their event or loss to follow-up. The resulting incidence rate in Year 2 was 25/212 = 0.12 for an appropriate ICD therapy and 6/212 = 0.03 for death without prior ICD-therapy.

Cause-specific hazard functions are more difficult to interpret than the CIF and less frequently used for descriptive purposes. However, they do play an important role in regression modelling.

Regression models for competing risks

Regression models assess the association between baseline covariates such as treatment assignment or age with outcome. In the competing risks context, two different approaches to regression modelling exist: the first approach models the dependence of the cause-specific hazard function on covariates, and the second models the dependence of the CIF on covariates. Both approaches are valid and the choice of the appropriate approach depends on the research question as we show below.

Relation between cause-specific hazard functions and the cumulative incidence function

We first discuss the impact of a single binary covariate such as a treatment assignment (intervention vs. control) on the event of interest and the competing event. As an example, let the event of interest be fatal CHD and the competing event death from non-coronary causes. Assume that a specific intervention reduced the rate (i.e. the cause-specific hazard function) of fatal CHD but did not affect the rate of death from non-coronary causes. Clearly, we would expect such an intervention to reduce the absolute risk of fatal CHD, but this reduced risk would leave more subjects vulnerable to the force that draws them towards non-coronary death. Thus, although the intervention does not affect the rate of non-coronary deaths, we would expect to observe an increase in the absolute risk of non-coronary deaths associated with the intervention. Similarly, if an intervention reduced the rate of fatal CHD only moderately but simultaneously reduced the rate of non-coronary deaths dramatically it could be that the absolute risk of fatal CHD events increased solely because the lowered event rate of non-coronary death left more subjects at risk and evaluable for experiencing fatal CHD. This could over-compensate and therefore conceal the moderate rate reduction of fatal CHD events associated with the intervention.

Thus, in the situation of competing risks, a research question relevant for clinical decision-making (‘Does the intervention lower the absolute risk of the event of interest?’) and an aetiological research question (‘Does the intervention cause a decrease in the rate of the event of interest amongst subjects without a prior event?’) may have different answers. This is in contrast to survival analysis without competing risks where there is a one-to-one association between a decrease in the event rate and a decrease in the absolute risk of the event. This discrepancy has been identified as a major difficulty in the interpretation of competing risks and interferes with a traditional understanding of disease.^8,9

Regression on the cause-specific hazard rates and regression on the cumulative incidence function

We have seen that the effects of covariates on the CIF and the cause-specific hazard function of the event of interest, respectively, may differ. This implies that we have to decide which of these two quantities to target with our regression analysis. For the purposes of prognosis and medical decision-making, the primary interest is in the absolute risks of the event of interest and the CIF should thus be the target of statistical inference.¹⁰ However, our example illustrated that to understand why an intervention affects the CIF of the event of interest in a certain way we need to look at its effect on both cause-specific hazard functions. Thus, to answer aetiological research questions regression models for cause-specific hazard functions are of primary importance because they directly model the covariate effect on event rates among subjects at risk.^8–10 As one type of analysis does not preclude the other, a deeper understanding of competing risks data can be gained by performing both regression on the CIFs and regression on the cause-specific hazard functions and this approach has been recommended by some authors.^9,11

Regression on the cause-specific hazard function can be performed with a Cox proportional cause-specific hazards regression model. This model assumes the same functional relationship between the cause-specific hazard function and covariates as the popular Cox model for survival data without competing risks does for the relationship between the overall hazard and covariates.^3,6 Technically, a cause-specific hazards model for an event of interest can be fitted using standard statistical software for Cox regression if competing events are treated as censored observations and, importantly, this approach is valid regardless whether different event types are independent of each other or not.^6,9 The effect measure for each covariate is a cause-specific hazard ratio (HR) which measures how strongly the rate is affected by that covariate. An HR = 1 implies no association between the covariate and the cause-specific hazard function, an HR > 1 implies that an increase of the covariate value is associated with an increased rate, whereas an HR < 1 implies that an increase in the covariate value is associated with a reduced rate. Moreover, the further away the HR is from 1, the larger the estimated effect per unit increase in that covariate.

Several models for regression on the CIF have been proposed and the most popular model is the Fine-Gray model^6,12 which has also been implemented in major statistical software packages including R, STATA, and SAS.^13,14 The resulting effect measure for each covariate is a so-called subdistribution hazard ratio (sHR). While the numerical interpretation of sHR is not straightforward, a sHR = 1 implies no association between the covariate and the corresponding CIF, a sHR > 1 implies that an increase of the covariate value is associated with an increased risk, whereas a sHR < 1 implies the opposite. Moreover, the further away the sHR is from 1, the larger the estimated effect size on the CIF.

Results of multivariable regression models for the cause-specific hazards and the CIFs of the ICD example are displayed in Table 1. If one is primarily interested in the aetiological question of how the covariates affect the rates of appropriate ICD therapy and prior death, respectively, at each time point after implantation, the cause-specific hazards models would be most appropriate. They show that an advanced age (HR = 1.23) and an ICD implantation for secondary prevention (HR = 2.29) both significantly increase the rate of appropriate shocks, but only advanced age (HR = 1.63) is significantly associated with a higher event rate of death without prior ICD therapy.

Table 1.

Multivariable regression models for competing risks endpoints and for the composite endpoint of the implantable cardioverter-defibrillator data

	Regression on the cause-specific hazard functiona [HR (95% CI); P-value]	Regression on the CIFb [sHR (95% CI); P-value]
Event: first appropriate ICD therapy
Covariates
Age (for each 10-year increase)	1.23 (1.07–1.41); P = 0.003	1.19 (1.05–1.36); P = 0.006
Secondary prevention (compared with primary)	2.29 (1.60–3.27); P < 0.001	2.23 (1.58–3.14); P < 0.0001
Event: death without prior ICD therapy
Covariates
Age (for each 10-year increase)	1.63 (1.11–2.39); P = 0.01	1.40 (0.92–2.13); P = 0.12
Secondary prevention (compared with primary)	1.25 (0.54–2.89); P = 0.60	0.92 (0.39–2.15); P = 0.85
Composite endpoint: first appropriate ICD therapy or prior death
Covariates
Age (for each 10-year increase)	1.28 (1.12–1.45); P < 0.001	1.28 (1.12–1.45); P < 0.001
Secondary prevention (compared with primary)	2.11 (1.52–2.93); P < 0.001	2.11 (1.52–2.93); P < 0.001

Note that the effect on the hazard function and the CIF is identical for the composite endpoint for which no competing risks are present.

HR, (cause-specific) hazard ratio; sHR, ratio of the subdistribution hazards; CI, confidence interval.

^aCox proportional hazards models for cause-specific hazards for competing risks endpoints. Cox proportional hazards model for the composite endpoint.

^bFine-Gray regression for competing risks endpoints. Cox proportional hazards model for the composite endpoint.

If one is interested in predicting which patients benefit most from ICD implantation, i.e. which patients have a high predicted risk of receiving an appropriate (and potentially life-saving) ICD therapy and a low risk of death without prior ICD therapy, the regression on the CIFs would be most relevant. Both higher age (sHR = 1.19) and an ICD implantation for secondary prevention (sHR = 2.23) are associated with an increased risk of an appropriate ICD therapy. There is no evidence of an association between a secondary prevention and an increased risk of prior death. The effect of age does also not reach conventional significance and the estimated effect (sHR = 1.40) is smaller than the corresponding age effect on the rate (HR = 1.63). This may be explained by the effect of older age on the cause-specific event rate of the more frequent endpoint of first appropriate ICD therapy which reduces the pool (risk set) of older subjects evaluable for experiencing prior deaths over time.

We conclude our discussion of regression modelling by noting that as in survival analysis³ modelling of competing risks data requires a careful evaluation of underlying model assumptions which we have not discussed here.

Composite endpoints and competing risks

According to a systematic review, 37% of published RCTs in cardiology used a composite primary endpoint.² Often, this composite endpoint is the time to the first of several events such as death, myocardial infarction, or hospitalization and the primary analysis is a standard survival analysis which ignores the event type. The merits and disadvantages of composite endpoints have been discussed in many publications^15,16 and we restrict our discussion to the contribution of competing risks analyses in this setting.

Competing risks analyses allow disentangling the contribution of an intervention (or other covariates) on each event type separately. Results for the ICD example both for the composite endpoint and for individual components are displayed in Table 1. For the composite endpoint, the standard survival analysis without competing risks is appropriate, and the effect estimates of covariates on the hazard function and the CIF are identical. The analysis shows that both advanced age and an ICD implantation for secondary prevention show a highly significant association with an increased rate (and risk) of the combined outcome of prior ICD therapy or death.

However, it is important to note that competing risks analyses applied to composite endpoints may not always be useful and can even be misleading. First, RCTs are frequently not powered to detect an effect of the intervention on individual components and competing risks analysis might have a low chance of detecting a true effect. Indeed, the fact that sample size requirements for an RCT powered to the most severe events would be prohibitively large is often the main reason for using composite endpoints.¹⁶ Second, recent discussions on composite endpoints stress the clinical importance of analyses that are not restricted to the first event but include repeated events of the same type (e.g. hospitalizations) as well as more severe events after the first event (e.g. deaths after a prior stroke).¹⁷ Competing risks analyses focus on the first event and to analyse repeated events or transitions between multiple event types, more complex multi-state modelling would be required.⁶

Final remarks

This article presents an overview of competing risks concepts and stresses the importance of using appropriate statistical methods if competing risks are present. Key messages are summarized in Box 1.

Box 1.

Competing risks: five key points

Item	Description
1	Competing risks occur if the time to a specific event is of interest but other types of events may preclude the occurrence of that event. More generally, competing risks methods can be used if different types of events are studied and the focus is on the time and type of the first event.
2	The basic descriptive statistic for competing risks data is the cumulative incidence function (CIF) which describes the absolute risk of an event of interest over time. The Kaplan–Meier method should not be used in the presence of competing events as it over-estimates the true absolute risk.
3	A complication of competing risks is that covariates can affect the absolute risk and the rate of an event of interest differently. Regression models based on the CIF (e.g. Fine-Gray models) explore the association between covariates and the absolute risk and are therefore essential for medical decision-making and prognostic research questions. Cause specific models for event rates (e.g. Cox proportional cause-specific hazards models) on the other hand are to be preferred for answering aetiological research questions.
4	A complete description of competing risks data should include the modelling of all event types and not only of the event of main interest.
5	Competing risks models can assess the effect of an intervention on individual components of a composite endpoint.

Funding

M.W. is supported by the Wellcome Trust. The research of V.S.S., K.J.J., K.L., and G.H. leading to these results has received funding from the European Community's Seventh Framework Programme under grant agreement number HEALTH-F2-2009-241544 (SysKID). Funding to pay the Open Access publication charges for this article was provided by the Wellcome Trust.

Conflict of interest: none declared.