Light-activated self-propelled colloids

Abstract

Light-activated self-propelled colloids are synthesized and their active motion is studied using optical microscopy. We propose a versatile route using different photoactive materials, and demonstrate a multiwavelength activation and propulsion. Thanks to the photoelectrochemical properties of two semiconductor materials (α-Fe₂O₃ and TiO₂), a light with an energy higher than the bandgap triggers the reaction of decomposition of hydrogen peroxide and produces a chemical cloud around the particle. It induces a phoretic attraction with neighbouring colloids as well as an osmotic self-propulsion of the particle on the substrate. We use these mechanisms to form colloidal cargos as well as self-propelled particles where the light-activated component is embedded into a dielectric sphere. The particles are self-propelled along a direction otherwise randomized by thermal fluctuations, and exhibit a persistent random walk. For sufficient surface density, the particles spontaneously form ‘living crystals’ which are mobile, break apart and reform. Steering the particle with an external magnetic field, we show that the formation of the dense phase results from the collisions heads-on of the particles. This effect is intrinsically non-equilibrium and a novel principle of organization for systems without detailed balance. Engineering families of particles self-propelled by different wavelength demonstrate a good understanding of both the physics and the chemistry behind the system and points to a general route for designing new families of self-propelled particles.

1. Introduction

Shrinking people down to the micrometre is a classical science-fiction premise in which the agents could manipulate tiny objects as in a microscopic factory. Ultimately, they may be injected in the body and repair dysfunctional organs or carry drugs to the appropriate cells. Beyond the limitless imagination of writers, this points towards a challenging question for the scientific community: how can we design populations of artificial microagents capable of moving autonomously in a controlled fashion while performing complex tasks? Recently, this question has fuelled a great effort towards the fabrication and the development of the first generation of synthetic micro- and nano-robots [1–3].

In living matter, the energy is extracted from the hydrolysis of ATP into ADP, which constitutes the ‘quantum’ of intracellular energy transfer. Similarly, artificial systems need to harvest the free energy from the environment and convert it into mechanical work. Numerous experimental realizations of such systems have been performed in recent years, many of them taking advantage of phoretic mechanisms [4–11], which interfacial origin provides a driving force robust to downsizing. Collections of active micro-particles thereafter constitute a controlled realization of active matter, in which self-driven units convert an energy source into useful motion and work, and provide a formidable playground for the study of phenomena in internally driven systems. Active matter exhibits a wealth of non-equilibrium effects observed in nature as well as synthetic systems: pattern formation [12,13], enhanced mixing [14,15] or sensing and interaction with the environment. For example, Escherichia coli bacteria were shown to concentrate owing to the presence of microfluidic funnels [16], rotate microscopic gears [17,18] or self-propelled nanorods are captured by passive spheres, stressing the importance of activity-driven interactions [19]. From a fundamental standpoint, they allow for the development of a theoretical framework for non-equilibrium statistical mechanics [20].

In this paper, we focus on recent developments on light-activated self-propelled colloids using the photocatalytic decomposition of hydrogen peroxide as a source of free energy. We present various realizations of self-propelled colloids using different photocatalytic materials, titanium oxide and haematite, which can be activated by the adequate wavelength. The activation induces interfacial flows leading to an osmotic self-propulsion of the particles and a phoretic attraction between them. We harness these mechanisms to use them as colloidal dockers to target and transport passive objects at the microscale. Finally, we discuss the collective properties of a dense suspension of these spherical active particles. They form ‘living crystals’ which form, break apart, heal and reform. We reproduce these crystals using simple numerical simulations of self-propelled hard disks coupled by a phoretic attraction. We show that the collisions are required to account for the observed effect, stressing the role of self-trapping as an organization principle in non-equilibrium systems.

2. Photo-activated colloids

(a). Photocatalytic materials

The particles considered in this paper are micrometre-sized particles containing a photoactive materials, immersed in a fuel solution containing hydrogen peroxide. Because hydrogen peroxide is metastable at ambient temperature, the reaction of decomposition, 2H₂O₂=2H₂O+O₂, is thermodynamically favourable but kinetically limited. The energy barrier is overcome by providing external energy such as UV-light or heat or by the presence of a catalyst lowering the energy barrier. Although the mechanism for the photocatalytic decomposition of hydrogen peroxide is not well understood, we infer that the effect originates in the reaction of the hydrogen peroxide in solution with the electron–hole pairs generated by the absorption of ultraband gap energy photons in the semiconductor (SC) [21]. The reaction produces radicals that cause the rapid degradation and bleaching of fluorescent dyes present in solution. A similar effect is observed by Soler et al. [22], who used Fenton reactions over Fe–Pt nanorods to degrade rhodamine 6G in a solution of hydrogen peroxide.

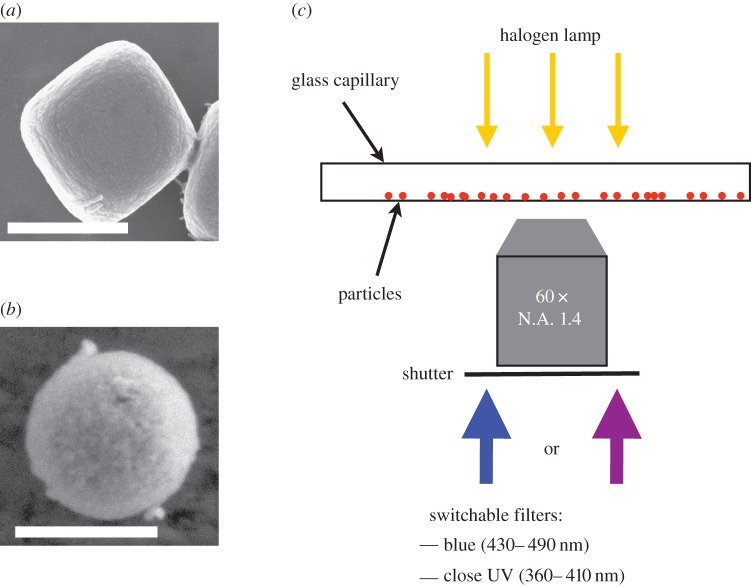
In this paper, we present particles with two different SC as photoactive materials. We use an iron oxide, (α-Fe₂O₃), named haematite (figure 1a), with a band gap of about 2.2 eV, corresponding to a visible wavelength λ_Fe2O3∼560 nm [23] and previously studied in [24,25]. We moreover present a new colloidal particle taking advantage of an alternate photoactive material: titania (TiO₂) in the anatase phase (figure 1b), with a bandgap of 3.1 eV, corresponding to the wavelength λ_TiO2=400 nm [26]. The particles are conveniently observed with an inverted optical microscope equipped with high magnification objectives, typically 60× or 100× and a conventional bright-field diascopic illumination. The microscope is equipped with filters to combine the bright field illumination with various wavelength bands from an episcopic fluorescent lamp (ultra-high-pressure 130 W mercury lamp, Nikon Intensilight), filtered and focused on the sample through the observation objective. We use interchangeable bandpass filters to select the windows of wavelength of the excitations λ_E. In the experiment, we use bandpass filters with an excitation E₁, in the blue (λ_E1∈ (430–490 nm), Semrock, FF01-460/60-25), or E₂, UVA-violet, (λ_E2∈ (370–410 nm), Semrock, LF405/LP-B). We can manually swap the filters during the experiment. A mechanical shutter on the lamp allows to turn on an off the excitation light providing a wireless and reversible activation of the system (figure 1c).

Figure 1.

(a) Scanning electronic microscopy (SEM) picture of a photoactive haematite cube. Scale bar is 500 nm. (b) SEM picture of a photoactive titania particle. Scale bar is 500 nm. (c) Experimental set-up. A capillary is filled with the solution of particles and observed in an inverted microscope. The excitation light comes from a filtered UV-light source through a large magnification objective. The excitation wavelength can be changed manually with bandpass filters. Here, we use blue (430–490 nm) light or UVA-violet (370–410 nm). A mechanical shutter allows for an external and wireless actuation of the system. (Online version in colour.)

(b). Chemical gradients and diffusiophoresis

(i). Chemical gradient

The photocatalytic material is immersed in a solution of hydrogen peroxide fuel H₂O₂. Under activation by light, it decomposes the hydrogen peroxide fuel and the concentration profile of hydrogen peroxide, [H₂O₂]_(r,t), is given by the solution of the diffusion–reaction equation

2.1

where t is the time, D^⋆ is the self-diffusion constant of hydrogen peroxide and α, the reaction rate of decomposition of hydrogen peroxide on the considered photocatalytic surface, at position r=0.

At steady state, equation (2.1) simplifies to the Laplace equation, 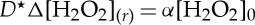. The solution of this equation in three dimensions, for an infinity large reservoir of hydrogen peroxide, in the diffusion-limited regime is

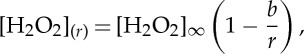2.2

where 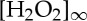is the bulk concentration of hydrogen peroxide and b is the half size of the catalytic site. The photocatalytic material acts as a sink for the hydrogen peroxide and a source of oxygen O₂, which dissolves in the solution (figure 2a,b). Following the stoichiometry of the decomposition reaction, equation (2.2) gives the concentration of oxygen in the solution: .

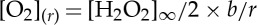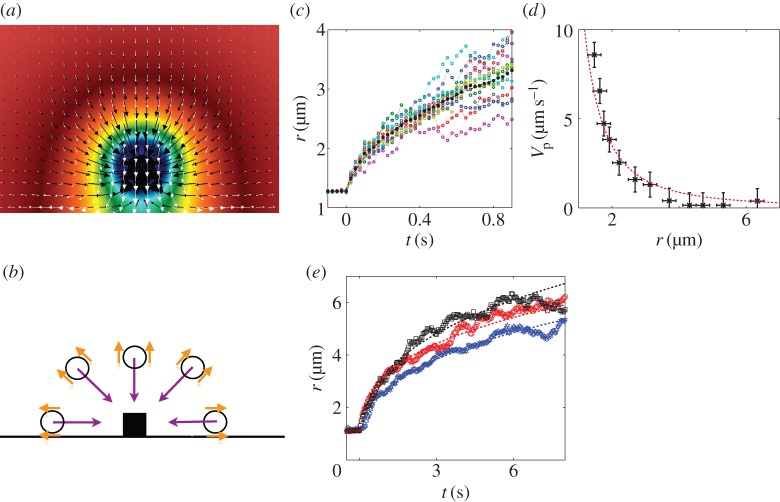
Figure 2.

(a) Three-dimensional simulations of the experiment of a photoactive particle on a surface. The colour map represents the concentration of fuel, here H₂O₂ (linear scale). It follows a ∝1/r decay. The white arrows represent the osmotic pumping flow along the substrate induced by the particle. The black arrows is the velocity of a phoretic particle in the solution, thus a superimposition of the phoretic migration of the particle and the advection by the osmotic flow. The phoretic migration dominates the osmotic contribution for particles not strictly restricted to the very close vicinity of the wall. The length of the arrows represents the intensity of the flow. Simulations realized by the group of A. Donev (Courant Institute, NYU). (b) Sketch of the experiment. The particles in solution sense the chemical gradients. They exhibit an interfacial flow (orange arrows) resulting in a diffusiophoretic migration (purple arrows) towards the photoactive material. The attraction is isotropic, particles come from every direction, discarding the possibility of an hydrodynamic flow of an incompressible fluid. (c) Timelapse displacement of different 1.5 μm TPM colloids in a concentration gradients (coloured symbols). The trajectories are averaged out to suppress the thermal random component of the displacement (black full symbol) and extract the phoretic drift. (d) The migration velocity V _p(r) (black symbols) is extracted by differentiation of the average displacement in (c). For a diffusiophoretic migration, we expect a migration velocity proportional to the gradient of the concentration, hence ∝1/r² (red dashed line), showing a good agreement with the experimental data. (e) Phoretic migration for tracers of ∼1.5 μm size made of different materials: silica (blue symbols), TPM (red symbols) and PS (black symbols). The experimental data are fit by r(t)=At^1/3, prescribed by a diffusiophoretic mechanism. The diffusiophoretic mobility depends on the material and ranges within a factor of two for the considered materials. (Online version in colour.)

(ii). Effect of the chemical gradient: diffusiophoresis

In order to study the effect of the chemical gradient, a haematite particle is attached to the bottom surface of a glass capillary and immersed in a solution of hydrogen peroxide containing the fuel (hydrogen peroxide) and tetramethylammonium hydroxide (TMAH), at pH∼8.5. The haematite particle is immobilized and conveniently observed under an optical light microscope.

In the absence of activation by light, the colloidal tracers diffuse in the solution, at equilibrium with the solvent. Under light activation (blue or UVA-violet for the haematite, or UVA- violet for the titania particles), the colloids in the solution are attracted towards the photoactive materials, for all the material we tested (various polymeric colloids or silica). The attraction comes from every direction, thus discarding the possibility of a flow which would exhibit recirculation by incompressibility of the fluid (figure 2b). Additional experiments with a haematite cube sedimenting through a solution of colloids also shows an isotropic attraction, ultimately leading to the formation of raspberry-like particle, with the photoactive material at the core.

The colloidal particles are migrating in response to the chemical gradients, oxygen (O₂) or hydrogen peroxide (H₂O₂). The motion of colloids induced by a solute gradient is called diffusiophoresis. It is an interfacial physical mechanism which belongs to the more general class of surface-driven phoretic phenomena [4,5]. It results from an unbalanced osmotic pressure occurring within the diffuse layer in the close vicinity of a solid surface (typically of the order of a few nanometres), which thereby plays the role of the semipermeable membrane in the classical osmosis. This induces an interfacial flow along the surface, leading to the motion of the particle in the surrounding medium [27,28]. Diffusiophoresis is therefore material- and pH-dependent, because it originates from the interaction between the solute and the solid surface.

We gather the results of the migration of 1.5 μm colloids made out of 3-methacryloxypropyl trimethoxysilane (TPM), a polymer material, to a haematite photoactive cube (figure 2c). We record the displacement of an ensemble of particles (typically 10) towards the haematite particle under light activation by blue light, excitation E₁. The different trajectories are averaged out in order to extract the diffusiophoretic drift R(t) from the random Brownian noise (figure 2c, black filled symbols). We differentiate the experimental curve to compute the phoretic velocity, V _p(r), at a distance r from the centre of the cube to the centre of the sphere. We measure a good agreement between the experimental measurement V (r) and the diffusiophoretic velocity in a solute gradient C(r), for which V _DP∝∇C(r)∝1/r² (figure 2d, red dashed line).

Reproducing the experiment with spheres of different materials (TPM, polystyrene (PS) or silica), we observe dependence of the attraction with respect to the material (figure 2e). However, for the different materials tested, the attraction strength is of the same order of magnitude and we measure diffusiophoretic mobilities within a factor of 2.

In our experiments, we did not find any material which did not present attraction towards the haematite at the considered pH∼8.5: TPM, PS, silica, PDMS, quartz, etc. However, the diffusiophoretic migration is reversed for TPM and PS if we lower the pH to 6.5 by suppressing the TMAH in solution: the colloidal particles are repelled away from the photoactive material.

(iii). Self-propelled osmotic surfers

We now consider the situation of a photoactive material (haematite or titania) dispersed in a solution of fuel with hydrogen peroxide and pH∼8.5. The particles are heavy and reside near the bottom surface. In the absence of any photoexcitation, those are Brownian particles, diffusing near the bottom surface. If we shine the appropriate excitation light, it triggers the chemical reaction of decomposition and the particle establishes a chemical cloud C(r) in its surrounding, following (2.2). In the same way, a free colloidal particle migrates in a gradient by phoresis, a fixed surface of the same material induces an osmotic flow in opposite direction when exposed to a gradient [4]. The glass substrate of the capillary is exposed to the concentration gradient generated by the active particle, and induces an osmotic pumping flow, attracting the particles to the surface (figure 2a, white arrows). The surrounding chemical cloud is, in principle, symmetric and the particle should sit there. However, we observe experimentally that a significant portion of the particles starts propelling on the substrate (electronic supplementary material, movie S1).

We envision two different scenarii to account for this effect: (i) the particles are not perfectly symmetric, one side is more chemically active than the other, thus breaking the symmetry. This could originate in ‘imperfections’ from the synthesis, or intrinsic anisotropic properties of the particles. For example, it is known that the particles surface has an intrinsic chemical anisotropy owing to the fine grained structure of the haematite [29]. Unfortunately, the size of the particles—typically 600 nm—challenges the optical resolution of the microscope, and it is difficult to resolve experimentally the facets of the cube making this hypothesis difficult to test in a direct observation. However, we observe that an increase of the roughness of the particles by a strong acid treatment (1 M hydrochloric acid) favours the propulsion of particles. This points towards the importance of roughness and chemical anisotropy in the system.

An alternative scenario (ii) is a spontaneous symmetry-breaking mechanism. In a nutshell, the particle sits in a symmetric gradient, until a fluctuation pushes it on one direction, the chemical gradient is steepened on this side and smoothened on the other side, breaking the symmetry and the particle follows the direction of the fluctuation. Such spontaneous autophoretic propulsion of isotropic phoretic particles has been discussed numerically by Michelin et al. [30]. The authors show there that isotropic particles can exhibit spontaneous self-diffusiophoretic propulsion and spontaneous symmetry-breaking as a result of an instability driven by the Peclet number Pe of the system (the Peclet number compares the role of advection and diffusion in the transport of the solute: Pe=R×V _prop/D). Our experiments are typically at very low Peclet: the diffusion is too fast to allow any significant deformation of the chemical cloud owing to the propulsion of the particle. As a consequence, we do not expect this effect to be predominant in the experiment.

As a remark, one could argue that the experiments presented on (figure 2b,c), with a haematite cube attached to a glass substrate, should exhibit the superimposition of the osmotic flow along the substrate with the phoretic attraction, whereas our earlier interpretation only discusses the role of phoresis (figure 2d). Additional numerical simulations of these experiments were performed in the group of A. Donev (Courant Institute, NYU) to test the effect of the presence of an osmotic flow on the measurement. An immersed-boundary method [31] is used to solve the concentration distribution in the solution (figure 2a, colour map). The steady Stokes equation is solved numerically with a slip boundary condition on the bottom wall proportional to the gradient of concentration to obtain the osmotic flow velocity [32] (figure 2a, white arrows). It exhibits a fast decay from the wall and the simulation shows that, at the exception of a very narrow layer near the wall, the phoretic migration totally overcomes the opposite osmotic flow (figure 2a, black arrows). This legitimates our measurement in the previous section and stresses the difficulty to measure experimentally the osmotic flow: small colloids will not be restrained by gravity to the close vicinity of the wall while large colloids migration will be dominated by phoresis. One solution is to use phoretically neutral particles. One way to obtain them is to use ‘hairy’ colloids for which the viscous drag in a dense interfacial polymer forest zeroes the interfacial flow and the phoretic mobility. Further work is conducted along this line to obtain the colloids and measure the osmotic flow.

(iv). Multiwavelength activation

The particles are activated using a commercial fluorescent lamp equipped with bandpass filters. Using an excitation wavelength below the bandgap has no effect on the dynamics of the particles: TiO₂ particles, for example, remain at equilibrium and exhibit a thermal diffusive motion when exposed to the blue light of excitation spectrum E₁: the energy of the blue photons is below the energy bandgap of the material. However, they start propelling once exposed to the UV-violet light E₂ in the presence of hydrogen peroxide (electronic supplementary material, movie S2). According to previous reports [33], titania particles self-propel in pure water under strong UV-light owing to the reaction of water-splitting, but we do not observe this effect, in our experimental conditions probably because of the low light intensity and longer wavelengths.

Haematite composites are activated by both the excitation E₁ and E₂. Both violet (or UVA) and blue light are above the energy bandgap of the haematite and the particles exhibit self-propulsion (electronic supplementary material, movie S2).

By turning off the excitation light, the system goes back to equilibrium in a few tens of milliseconds and the particles recover a thermal Brownian motion. The ability to turn on and off the activity and self-propulsion is an asset of our experimental system, and allows us to discriminate non-equilibrium effects from colloidal aggregation and instability owing to the chemical reaction. The multiwavelength activation is unique and allows to design separate families of active particles.

(c). Composite colloids

(i). Colloidal cargos

Here, we harness both the phoretic attraction and the osmotic self-propulsion to form composite particles and colloidal cargos. Here, we use a mixed system of colloidal particles, typically PS or TPM polymer particles of 1 μm radius, and light-activated colloids, haematite or titania. In the absence of any excitation light, the system is at equilibrium and the particle diffuses. Under activation by light, the light-activated particles generate a chemical cloud which can be sensed by a ‘passive’ colloid, then migrating phoretically towards the photoactive particle. Once docked, the composite system propels as a whole, the photoactive part heading (electronic supplementary material, movies S1 and S3). The magnetic properties of haematite can furthermore be used to steer and direct remotely the colloidal cargo, as discussed in [25] (figure 3a and electronic supplementary material, movie S3). One limit of this composite system is that a single passive colloid can couple with many active patches or alternatively one active patch with many passive colloids leading to a complicated and uncontrolled mix of self-assembled particles, some of them exhibiting self-propulsion, some of them inactivated by symmetry, for example, one active patch surrounded by four spheres, as theoretically discussed in a recent paper ([34] and electronic supplementary material, movie S1).

Figure 3.

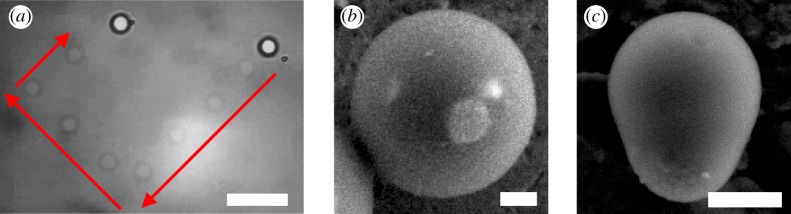
(a) Colloidal cargos: timelapse of the trajectory of a colloidal cargo, light spheres are positions every 1 s, showing the initial and final positions. A haematite particle is activated by (blue) light, phoretically attracts a 5 μm TPM sphere, docks it, forming a self-propelling colloidal cargo. The system self-propels as a whole, directed with an external uniform magnetic field (red arrows). Scale bar is 20 μm. (b) SEM picture of photoactive haematite particle embedded in a polymer spherical shell. (c) SEM picture of photoactive titania particle embedded in a polymer TPM shell. Scale bar is 500 nm. (Online version in colour.)

In order to overcome this limitation, we design component particles in which the active patch (haematite or titania) is embedded into a dielectric shell, protruding outside (figure 3b,c). These particles are synthesized in bulk, in a controlled manner.

(d). Colloidal surfers

Composite colloids or colloidal surfers are prepared. They consist of photoactive materials (haematite or titania) partially protruding outside a shell of TPM. The synthesis of these composites is described in details in the Materials and methods section. In a nutshell, we trap solid inorganic colloids at the interface of an oil-in-water emulsion droplets of TPM [35].

The haematite iron oxide can be synthesized and obtained in various sizes and shapes (cubes, peanuts or ellipsoids). Seeded growth of TPM on these particles result in various particles as presented in a recent paper by Sacanna et al. [36]. In this paper, for an observation with optical microscopy, relatively large (greater than 500 nm) haematite cubes or ellipsoidal particles are encapsulated as shown in (figure 4a,b).

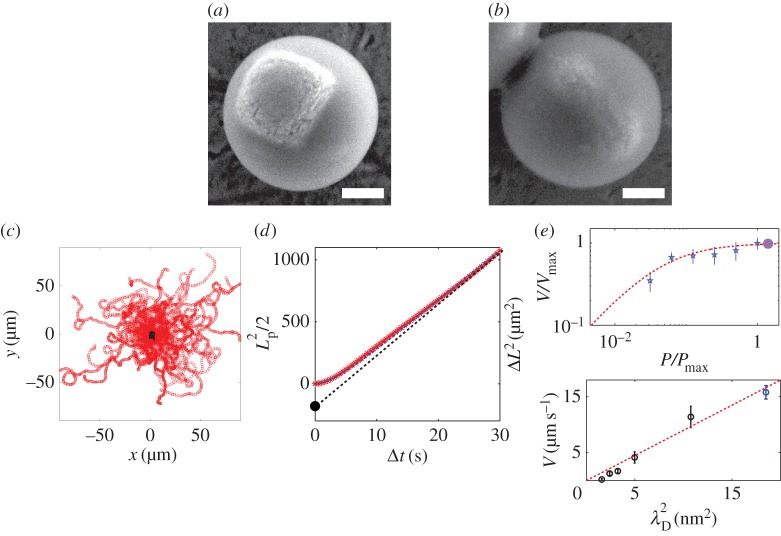
Figure 4.

(a,b) A diverse family of colloidal surfers. (a) SEM picture of large haematite cube embedded in a spherical TPM shell. (b) SEM picture of ellipsoid haematite embedded in a TPM shell. (c) Superimposition of many trajectories of the colloidal surfers light off (black) and light on (red). The trajectories are started at position (0, 0). The self-propulsion is isotropic and the dynamics is a persistent random walk. The particles self-propel at a given velocity V which direction is randomized by thermal fluctuations, over a timescale τ_r. (d) Mean square displacement (MSD) ΔL² averaged for a dozen particles (red symbols). The MSD is well described by a persistent random-walk dynamics (equation (2.3), blue dashed line). For short times, t≪τ_r, the trajectory is ballistic and ΔL²∝Δt². The self-propelled particles exhibit an enhanced effective diffusion at long times ΔL²∝4D_effΔt. The extrapolation of the enhanced diffusion regime allows an alternate determination of the persistent length of the motion (equation (2.4), black dashed line). (e) Self-propulsion velocity of haematite composite surfers as a function of the light intensity. Blue symbols for activation by blue (430–490 nm) light, and full violet circle for activation by the UVA-violet (370–410 nm) light. The red dashed line is a fit of the experimental data by a Michaelis–Menten kinetics, typical of enzyme catalysis. (f) Self-propulsion velocity as a function of the Debye length of the solution, varied by addition of sodium chloride salt (black symbols) and withdrawing of the SDS surfactant in the solution (blue symbol). The experimental results agree with 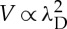(red dashed line), expected for phoretic interfacial transport, stressing the role of electrostatics in the system. (Online version in colour.)

Haematite is a canted anti-ferromagnetic iron oxide with a permanent magnetic moment μ, scaling as the volume of the haematite component of the particle. Composite particles with large haematite components interact magnetically and self-assemble in equilibrium dipolar structures [37]. In the experiment, we limit the size of the haematite component to a typical volume of 0.2 μm³ to avoid magnetic interactions between the particles. The magnetic moment is, however, large enough to interact with a weak and uniform external magnetic field B₀∼1 mT, tilting the orientation of the cube and allowing to steer the particles externally, as discussed in the previous section.

The composite particles are mixed with the regular fuel solution, in a basic solution (pH∼8.5) containing hydrogen peroxide (0.1–3% w/w) and 5 mM TMAH in deionized water. The colloids sediment under gravity and reside near the surface of a clean glass capillary. Under normal bright field illumination, the particles are at equilibrium with their solvent and exhibit a thermal Brownian diffusion. The rotational diffusion of the particle is visible, thanks to the optical contrast provided by the photoactive part. Under light-activation above the bandgap of the material, the composite particle generates a chemical gradient, inducing an osmotic flow along the substrate, which forces the particle to rotate and the active part to face the substrate. The particles do not self-propel in bulk and only propel at the substrate. It is usually at the bottom substrate of the cell but it is not restricted to it by gravity. Particles can climb up the lateral walls of the capillary, the photocatalytic material facing the substrate, as well as propelling upside down on the top surface (electronic supplementary material, movie S4). Turning off the light, the propulsion stops and the particles sediment towards the bottom surface.

We can activate the titania and haematite particles simultaneously using UVA-violet light or only the haematite composite particles shining the blue light on the sample (electronic supplementary material, movie S5). The possibility to use different wavelength to activate independently different populations of active particles is unique. Engineering families of particles activated by different wavelength, using different photoactive materials, demonstrates a good understanding of the system and points to a general route for designing new families of self-propelled particles.

The mode of self-propulsion is unusual. Defining a north–south axis along the asymmetry of the particle, the direction of the propulsion is along the equatorial direction. Janus particles generate a gradient along the asymmetry ‘pole’ axis and subsequently self-propel along this axis [38,39]. Here, the particles generate the gradient, thanks to their photoactive component and harvest the free energy from their environment, but the actual engine for the propulsion is localized on the substrate through the osmotic flow. Grafting a polymer brush to the wall suppresses the osmotic flow at the substrate and therefore the self-propulsion. Alternatively, we observe a ∼35% increase of the propulsion velocity of the particles in experiments where the glass capillary are plasma cleaned and immediately used. Plasma treatments are known to enhance the charge of glass substrates thus increasing the interfacial transport along it. After 2 h, the velocity returns to its original value.

This peculiar mode of propulsion makes the particles very sensitive to the detailed properties and alterations of the substrate. They follow shallow cracks or atomic steps on a cleaved mica, as well as a nanotexture imprinted in a PDMS substrate, which would be otherwise ignored by thermal diffusion.

(i). Individual dynamics

The dynamics of individual active colloids is investigated measuring the two-dimensional (x,y) motion of the colloids with a camera (Lumenera Infinity X32 or Edmund Optics-1312M) at a frame rate between 1 and 50 Hz. The position and trajectories of the particle are extracted and reconstructed with a single particle tracking algorithm using a Matlab routine adapted from Crocker & Grier [40]. We use a circular Hough transform and circular shape recognition to determine the position of the centre of the particles, and avoid the inaccurate determination of the centre otherwise induced by the contrast of the composite particles containing black and white components.

The trajectories are then extracted. The mean square displacement (MSD) of the colloids is obtained as ΔL²(Δt)=〈(R(t+Δt)−R(t))²〉, where R(t) is the (two dimensions) instantaneous colloid position and the average is performed over time for each individual trajectory and then over an ensemble of trajectories (typically 15). For the activated colloids, the MSD differs drastically from the equilibrium diffusive dynamics. The colloid exhibits ballistic motion at short times, ΔL²(t)∼V ²Δt², whereas at longer times a diffusive regime, ΔL²(t)∼4D_effΔt, is recovered with an effective diffusion coefficient D_eff much larger than the equilibrium coefficient D₀. As discussed in [7,10], the active colloids are expected to perform a persistent random walk, owing to a competition between ballistic motion under the locomotive power (with a constant swimming velocity V), and angular randomization of the direction over a persistence time τ_r. In the experiment, we measure a persistent time τ_r consistent with the thermal Brownian rotational diffusion of the particles at a given radius R. The transition between the two regimes occurs at the rotational diffusion time τ_r of the colloids. The characteristic ballistic length scale is accordingly L_p=V ×τ_r. For timescales long compared with τ_r, the active colloids therefore perform a random walk with an effective diffusion D_eff=D₀+V ²τ_r/4. The full expression of the MSD at any time for a purely two-dimensional motion is obtained as [7,10]

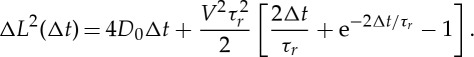2.3

We can accurately fit the experimental data (figure 4d, red symbols) with the persistent random walk dynamics (equation (2.3)) (figure 4d, blue dashed line). The measured persistence time is in line with the equilibrium Stokes–Einstein rotational diffusion. We measure, for example, τ_r=8.0±1.5 s for composite particles with a radius R=1 μm. Note that the Stokes—Einstein rotational time exhibits a cubic dependence on the particle size τ_r∝R³, making it sensitive to the size of the polymer sphere embedding the photoactive material. This can be finely tuned through the synthesis during the growth step and provides an additional source of control in the experiment.

The persistence length, L_p, of the motion can be extracted from the MSD (equation (2.3)), as the extrapolation of the enhanced diffusion regime at t=0 (figure 4d, black dashed line). For t≫τ_r, equation (2.3) rewrites

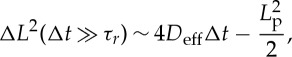2.4

where L_p=V τ_r is the persistence length.

The propulsion can be tuned with external parameters: reducing the intensity of the activation light reduces the velocity (figure 4e), following a Michaelis–Menten kinetics typical of enzyme catalysis [41]. Shining the violet light (E₂) on composite haematite particles has no effect on the propulsion velocity of the particles in line with the assumption of diffusion-limited regime describing the experiment (see equation (2.2) and figure 2d).

Finally, the propulsion is altered by the ionic strength: the addition of salt reduces the velocity. Osmotic flows generically exhibit a velocity dependence V ∝L², owing to a balance between a driving force ∝L acting over the interfacial layer of thickness L and the viscous drag ∝1/L in this layer. The scaling is expected to be modified in the regions where the interfacial layer thickness is comparable to the roughness of the surface, as observed for example for electro-osmotic flows [42]. Our experimental results are in good agreement with a velocity 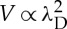, λ_D being the Debye length, defining the range of the electrostatic screening around a charged colloid (figure 4f). This stresses the role of electrostatics in the system thus discarding neutral diffusiophoresis/osmosis as the main transport mechanism in our system. The importance of electrostatic contributions in the propulsion mechanism of platinum-coated Janus particles has been recently pointed and thoroughly discussed in [43,44].

3. Emergence of collective effects and living crystals

(a). Living crystals

For dilute sample of composite particles, we observe a ‘gas phase’: the particles self-propel with a persistent random walk and collide each other sometime (electronic supplementary material, movie S6). The collisions are isotropic, and the behaviour of the particles shows no significant difference with the individual behaviour. Increasing the surface density Φ_s of the particles in the experiment, we observe the emergence of ‘living crystals’ (electronic supplementary material, movie S7). This state is qualitatively very different from the gas phase, particles spontaneously assemble in mobile crystalline structure, mobile, which exchange particles, collide, break apart and reform. This phase is observed for surface fraction, as low as Φ_s>7–10%. Following a collision, two crystals rearrange, ‘heal’ and suppress the existence of a grain boundary (electronic supplementary material, movie S7).

In order to see if our understanding of the main components of the system accounts for these observations, we developed a simple code in Matlab of (i) self-propelled hard disks with a persistent random walk dynamics with (ii) a phoretic attraction between pairs of disks as observed in the experiment.

(b). Numerical simulations and algorithm

(i). Dynamics

We consider a numerical model in which the self-propelled colloids are represented by hard disks propelled with a constant velocity V ₀ along a direction, diffusing on a circle over a timescale τ_r governed by rotational Brownian diffusion. It is implemented in the simulations as a random Gaussian noise to the propulsion angle. The variance of the Gaussian noise controls the the persistence time τ_r of the motion (figure 5a).

Figure 5.

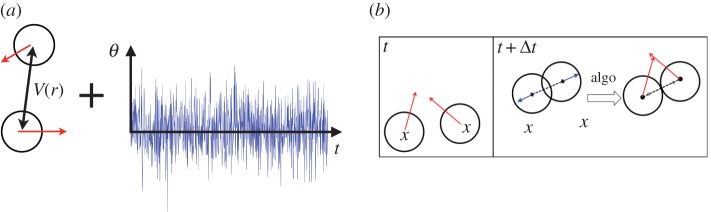
Numerical simulations. (a) We consider two-dimensional simulations of hard disks propelled at a constant velocity V ₀ (red arrows) with a fluctuating direction of propulsion and an attraction interaction V (r) (black arrow). The noise on the direction is a Gaussian noise, which amplitude is set by thermal rotational diffusion. (b) Event-driven algorithm for the collisions. If two particles overlap after a displacement, they are separated by moving each one of them half of the overlap distance along their centre-to-centre axis. This algorithm does not introduce correlations in the propulsion direction nor collisions and motion. (Online version in colour.)

(ii). Interaction between particles

We model the phoretic attraction between the particles as a pairwise attractive interaction. For each time step Δt, the particle i undergoes a displacement ΔR_i resulting from its own self-propulsion and the attraction by the neighbours, for j≠i:ΔR_i=V ₀Δt+Σ_j≠iV _att(r_i,j)Δt, with r_i,j being the distance between particle i and j. The pairwise attraction follows the phoretic attraction 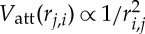, measured experimentally. The hard-sphere repulsion between particles is event-driven: if a displacement makes two particles overlap, they are separated by moving each one of them half of the overlap distance along their centre-to-centre axis (figure 5b). The displacement perpendicular to the line of centres is preserved. This is an appropriate procedure for low Reynolds number propulsion. It shares forces and hence velocities along the line of centres and preserves tangential velocities. It does not correlate steric effects and motion. Rather it is similar to introducing a sharp repulsive potential between particle surfaces in the very low Reynolds number limit.

 Limits of this model. The model assumes pairwise interactions between the particles. The actual attraction should result from the concentration field induced by the resolution of the coupled diffusion–reaction equation around each particles. Solving the diffusion–reaction equation of a collection of self-propelled sinks of hydrogen peroxide is a complex problem beyond the scope of this paper. Moreover, the interaction here considered results in an effective potential E(r)∝1/r analogous to an unscreened gravitational interaction. The bigger the cluster, the more attractive, eventually leading to a ‘gravitational collapse’. We observe such phenomena, for which the simulations break down and we therefore imposed in the simulations a threshold for the interaction range of three particles diameters. This is in line with experimental results where particles do not seem to interact above this distance, but remains questionable in the frame of our model. Our physical picture for the cut-off is that the concentration profile inside the crystal is uniform and flat and that only the particles at the edge of the crystal contributes to the attraction. This phenomenon is not taken into account summing pairwise interactions.

(iii). Numerical parameters

The simulations are made dimensionless setting the diameter 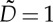and the velocity 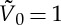of the self-propelled disks to unity. This defines a spatial and temporal time step for the simulations. The parameters in the simulation are fixed in the following range, according to the experimental value

• — diameter of the particles:

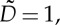
• — rotational diffusion time: 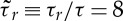–50,

• — pairwise attraction: .

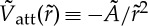The simulations run with N=1–1000 particles in a box of typical size 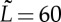with periodic boundary conditions with various surface fractions Φ_s of active particles. The time step for updating particle positions is 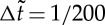, and particle–particle pairwise attractions are cut-off for interparticle distances greater than 3.

(c). Results and discussion

At low density of particles, the simulations show self-propelled disks with a persistent random-walk dynamics. Increasing the surface density of the particle, they form crystals and reproduce qualitatively well the experiment (electronic supplementary material, movie S8). Following recent experimental [45] and theoretical [46] works, we measured the number fluctuations in the system and showed a transition from normal to giant fluctuations for a critical surface coverage of particles 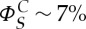[24]. This quantitative agreement between the experimental and the numerical results stresses that a simple model of self-propelled particles with a persistence length and attraction between the particles capture the essential ingredients at stake in the experiment.

However, one can still envision two scenarii for the emergence of dense structures in this system. First, it could arise from the light-activated phoretic attraction between the colloids. If the attraction overcomes the loss of entropy in the dense phase, an equilibrium system spontaneously phases separates into a dense liquid and a solid. It is therefore expected that suspensions of attractive colloids form clusters at equilibrium.

Furthermore, the situation of self-propelled particles coupled by chemical attraction has been studied extensively in biology for bacteria with chemical chemotactic sensing since the pioneering work by Keller & Segel [47]. The so-called Keller–Segel (KS) equation is a mean field description taking into account the diffusion of bacteria, a drift induced by chemical sensing, and the production and diffusion of a chemoattractant. An interesting feature of the KS description is that it exhibits singular solutions and a ‘chemotactic collapse’ of the structure into a single or many dense aggregates, above a threshold, the Chandrasekhar number N_C [48]. This description was used to discuss the emergence of clustering in a collection of Janus particles coupled by diffusiophoretic chemical attraction and performed by others [49].

Alternatively, it has been pointed out that self-propelled particles lacking an alignment rule exhibit collective behaviour and form dense dynamical clusters in equilibrium with a gas phase. This behaviour arises from a self-trapping mechanism: self-propelled particles with a persistent time and colliding head on, arrest each other owing to the persistence of their orientation (figure 6a). Increasing the surface fraction of particles, this simple mechanism leads to a dynamic phase transition from a gas phase of hot colloids [10] to a dense state, resulting from the ‘traffic jam’ of the persistent self-propelled particles [46,50–57]. The emergence of arrested phase owing to density-dependent mobility has been discussed theoretically in the context of bacteria by Tailleur & Cates [58]. The role of the self-trapping mechanism for the emergence of clustering was shown in the recent and remarkable experiments by Buttinoni et al. [59], where they used ‘large’ 4 μm self-propelled carbon-coated Janus colloids, which self-propel under illumination in a near-critical water–lutidine mixture [60], and for which the caps can be optically resolved, indicating the direction of self-propulsion. They showed that the particles in a clusters are arrested, heads-on.

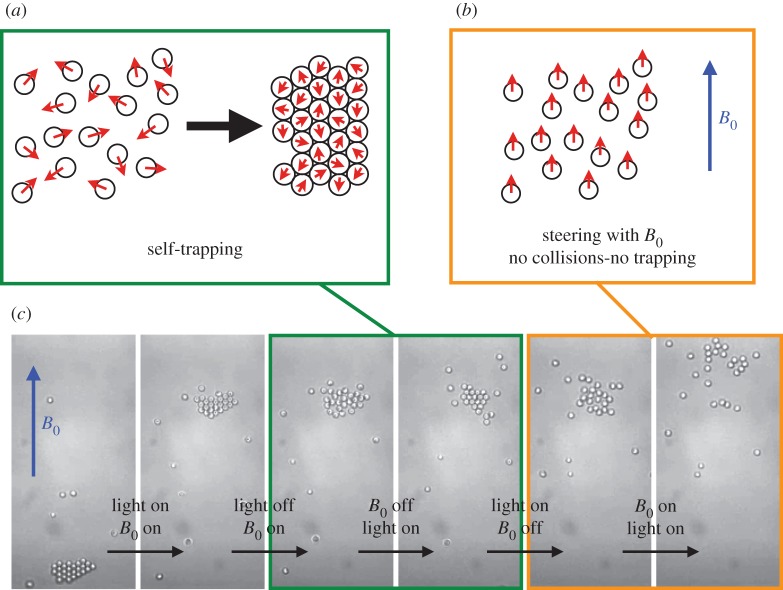
Figure 6.

(a) Self-trapping mechanism self-propelled particles with a persistent length spontaneously exhibit a dynamic phase transition and form dense clusters. They collide head on, arrest each other owing to the persistence of their orientation leading to self-trapping. (b) Using an external magnetic field to direct the haematite colloidal surfers, the particles all go in the same direction, they do not collide, self-trapping is suppressed. (c) In the experiment, the light activation induces attraction and persistent self-propulsion, thus entangling the role of attraction and self-trapping in the formation of the crystals. A magnetic field is used to suppress the collisions and shows the importance of the collisions in the system to form the crystals. A crystal is first formed and steered using a uniform magnetic field B₀∼1 mT. The light is turned off, the magnetic field being on, the system is at equilibrium and the crystal melts. The magnetic field is turned off, and the light is activated. The particles self-propel, collide and reform the crystal. The light is turned off as well as the magnetic field, the crystal melts. Now, the magnetic field is on before the light is activated. The particles self-propel in the same direction, they do not collide, the crystal does not reform. This shows that the collisions are important to observe in the timescale of the experiment, the emergence of the crystals in the system. (Online version in colour.)

In our experiments, however, the light activation induces both (i) an attraction as well as (ii) the persistent self-propulsion entangling the importance of an equilibrium-like crystallization with a non-equilibrium dynamic phase transition. In order to disentangle the two contributions, we take advantage of the magnetic properties of the haematite to steer the particles. Forcing the particles to all go in the same direction, we suppress the collisions between the particles thus testing the importance of the self-trapping in the formation of our living crystals (figure 6b).

We start with a crystal of self-propelled particles formed along a wall, because collisions are favourable along the one-dimensional system defined by the wall. We steer it away from the wall using a uniform magnetic field B₀∼1 mT. Turning off the light as well as the magnetic field, the crystal melts, the particles diffusing away. Turning on the light, the magnetic field remaining off, the individual particles self-propel in every direction, collide and reform the crystal. The light is turned off, and the crystal melts again. Now, the magnetic field B₀ is actuated before the light is turned on again. The particles all propel all along the same line, the direction of B₀, they do not collide and do not form the crystals. This shows that within the time scale of the experiment, the phoretic attraction is not sufficient to account for the formation of the living crystals (figure 6c).

To summarize, the collisions and self-trapping make the system phase-separate and form aggregates. The presence of the attraction orders these aggregates into two-dimensional crystals and shifts the threshold for the dynamical transition to a low surface density of particles Φ_s∼7–10%, in line with the numerical results by Redner et al. [61]. In the absence of attraction between particles, the dense state develops for larger surface fractions, typically approximately 30–40% for self-propelled hard disks with no alignment as discussed theoretically by Fily & Marchetti [46], and confirmed experimentally and numerically by [59].

(d). Living crystals versus swarming and flocks behaviour

We do not observe experimentally or numerically the swarming behaviour predicted theoretically by many authors [62–65] for nematic self-propelled particles similar in spirit to the Vicsek model [66]: transition to a flocking behaviour with coherent groups of particles moving in the same direction, swarming or formation of travelling bands otherwise recently observed experimentally by the group of Bausch [67] or more recently the large-scale vortices observed by Sumino et al. [68] or by the group of Bartolo with self-propelled rollers colloids [69], or active nematics [70]. In all those works, the self-propelled particles are polar with nematic interactions, i.e. they align their velocity vectors in direction, as prescribed by ‘Vicsek’s rule’. The role of the nematic alignment owing to the collisions of rod-like microtubules have recently been pointed by [68] to explain the emergence of long-range interactions and vortices at high density (or in an granular context by Deseigne et al. [71]). In our experiment, owing to the isotropic shape of the particles we do not observe any nematic interaction of the self-propelled particles, thus defining a different class of systems and non-equilibrium phases than the Vicsek model.

To the best of our knowledge, the transition from dynamic clusters emerging from a self-trapping mechanisms, for particles without alignment, to flocking behaviour, for active nematic, has not been studied theoretically. It would be interesting to see how altering the alignment mechanism, e.g. altering the shapes of the self-propelled particles, can induce a transition from one class of collective behaviour to another.

4. Conclusion

In the paper, we showed how we could harness the photo properties of haematite and titania semiconductors to design self-propelled colloids in a solution of hydrogen peroxide fuel. The photocatalytic decomposition of hydrogen peroxide is triggered by a light with a wavelength above the bandgap of the material. It generates a chemical gradient around the particles, which induces an osmotic self-propulsion of the particle along the substrate and a phoretic attraction between the particles. We demonstrate here, for the first time, a wavelength-dependent activation in a mixture of different types of self-propelled particles. The engineering of such colloids provides a general route for designing new families of self-propelled particles.

We show that a collection of these particles spontaneously assemble in living crystals, mobile which form, heal, break apart and reform, and could reproduce this with numerical simulations of a simple model. Using a magnetic field to direct the particles with an iron oxide, haematite, component, we show that the collisions are central in the observed formation of the crystals. This self-trapping mechanism is a non-equilibrium effect and points towards the emergence of novel organization principles in non-equilibrium systems. The transition from self-trapping to flocks is a open question, which could be addressed, for example, changing the shape of the self-propelled particles.

5. Material and methods

(a). Synthesis of the active colloids

(i). Haematite cubes

Haematite (α-Fe₂O₃) cubic colloids were prepared following the method described by Sugimoto et al. in [72]. Briefly, a ferric hydroxide gel was prepared by mixing 100 ml of aqueous NaOH (6 M) with 100 ml of FeCl₃×6H₂O (2 M) and aged in a sealed Pyrex bottle at 100^°C. After 8 days, the gel changed into a thick reddish sediment which was repeatedly washed in deionized water to reveal the colloidal cubes. From electron microscopy pictures, we measured an average particle size of 600 nm with a typical polydispersity of 3%.

(ii). Titania microspheres

Titania (TiO₂) colloids were prepared by hydrolysis and condensation reaction of titanium isopropoxide (TTIP) with dodecylamine (DDA) as a catalyst in a co-solvent of methanol/acetonitrile [73]. In a typical synthesis, 0.384 ml of water was added to a solution consisting of 103 ml of methanol and 32 ml of acetonitrile. Then, 0.7 g of DDA was dissolved in the mixture, followed by 1.07 ml of TTIP. The mixture was left under stirring for 12 h. The resulting titania suspension was centrifuged at 1500 r.p.m. for 10 min, and the sediments were washed three times with methanol. The particles were finally dried and calcinated at 500^°C for 5 h.

(iii). Encapsulation of haematite or titania

To embed the haematite or titania component into larger spherical particles, we added 25 μl of NH₃ 28% to a 30 ml aqueous suspension of haematite particles (≈2% wt) followed by 100 μl of 3-methacryloxypropyl trimethoxysilane (TPM, ≥98% from Sigma-Aldrich). The reaction mixture was kept under vigorous stirring and sampled every 15 min to monitor the particles’ growth. The reactor is fed with more TPM (100 μl of TPM for each addition) at intervals of approximately 1 h until the particles reached the desired size. Finally, 0.5 mg of 2,2′-azo-bis-isobutyrylnitrile (Sigma-Aldrich) were added and the mixture heated to 80^°C for 3 h to harden the particles. After the synthesis, the particles were cleaned and separated from secondary nucleation by sedimentation and were finally resuspended in deionized water. The surface zeta potential in water at a pH of 9 was measured to be −70 mV.

Funding statement

This work was supported by the Materials Research Science and Engineering Centers programme of the NSF under award number DMR-0820341 and by the US Army Research Office under grant award no. W911NF-10-1-0518. We acknowledge partial support from the NASA under grant award NNX08AK04G. G.R.Y. and S.H.K. acknowledges support from Korean NRF grant (no. 2010-0029409) and Human Resources Development Programme (no. 20124010203270) of KETEP. J.P. and P.M.C. acknowledges support from the Moore Foundation.