Photosymbiotic giant clams are transformers of solar flux

Abstract

‘Giant’ tridacnid clams have evolved a three-dimensional, spatially efficient, photodamage-preventing system for photosymbiosis. We discovered that the mantle tissue of giant clams, which harbours symbiotic nutrition-providing microalgae, contains a layer of iridescent cells called iridocytes that serve to distribute photosynthetically productive wavelengths by lateral and forward-scattering of light into the tissue while back-reflecting non-productive wavelengths with a Bragg mirror. The wavelength- and angle-dependent scattering from the iridocytes is geometrically coupled to the vertically pillared microalgae, resulting in an even re-distribution of the incoming light along the sides of the pillars, thus enabling photosynthesis deep in the tissue. There is a physical analogy between the evolved function of the clam system and an electric transformer, which changes energy flux per area in a system while conserving total energy. At incident light levels found on shallow coral reefs, this arrangement may allow algae within the clam system to both efficiently use all incident solar energy and avoid the photodamage and efficiency losses due to non-photochemical quenching that occur in the reef-building coral photosymbiosis. Both intra-tissue radiometry and multiscale optical modelling support our interpretation of the system's photophysics. This highly evolved ‘three-dimensional’ biophotonic system suggests a strategy for more efficient, damage-resistant photovoltaic materials and more spatially efficient solar production of algal biofuels, foods and chemicals.

1. Introduction

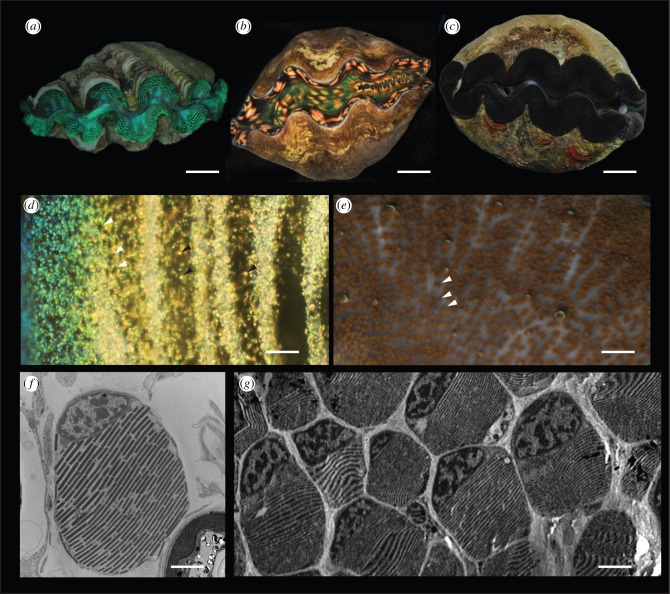
‘Giant’ clams, (family Tridacnidae), native to coral reefs of the western tropical Pacific, reach their large sizes in part due to a photosymbiosis with brown, single-cell algae of the genus Symbiodinium [1]. As part of this photosymbiotic lifestyle, these clams have evolved a weighted shell hinge and/or boring behaviour, ensuring that the shell gape always points upward to the sky, thus exposing the animal's mantle tissues to sunlight [2]. The surface of the mantle tissue is covered with a layer of clam cells called iridocytes, which impart the clams’ famously sparkly, colourful appearance (figure 1a,b,d). The mantle tissue lines the exposed inner surfaces of the shell and is several millimetres thick. Under the colourful iridocytes concentrated at the surface of the tissue, there are high densities of photosynthesizing Symbiodinium (figure 2a). The rare clam without iridocytes appears dark-coloured due to these high densities of algae (figure 1c,e).

Figure 1.

Overview of tridacnid ‘giant’ clams. (a) Photograph of Tridacna crocea with prominent green iridocytes. Scale bar, 2 cm. (b) Tridacna derasa specimen with yellow iridocytes. Scale bar, 10 cm. (c) Tridacna crocea with almost no iridocytes. Scale bar, 5 cm. (d) Darkfield micrograph showing example iridocyte cells (black arrowheads) and tips of algal micropillars emerging from underneath the superficial layer of iridocytes (white arrowheads). Scale bar, 100 μm. (e) Darkfield micrograph of T. crocea with nearly no iridocytes. Tips of algal micropillars are more visible in the absence of superficial iridocytes (white arrowheads). Scale bar, 200 μm. (f) Single clam iridocyte in TEM. Scale bar, 2 μm. (g) TEM of iridocyte-bearing tissue showing orientation of platelets between iridocytes, and that the iridocyte layer is closely packed. Scale bar, 4 μm.

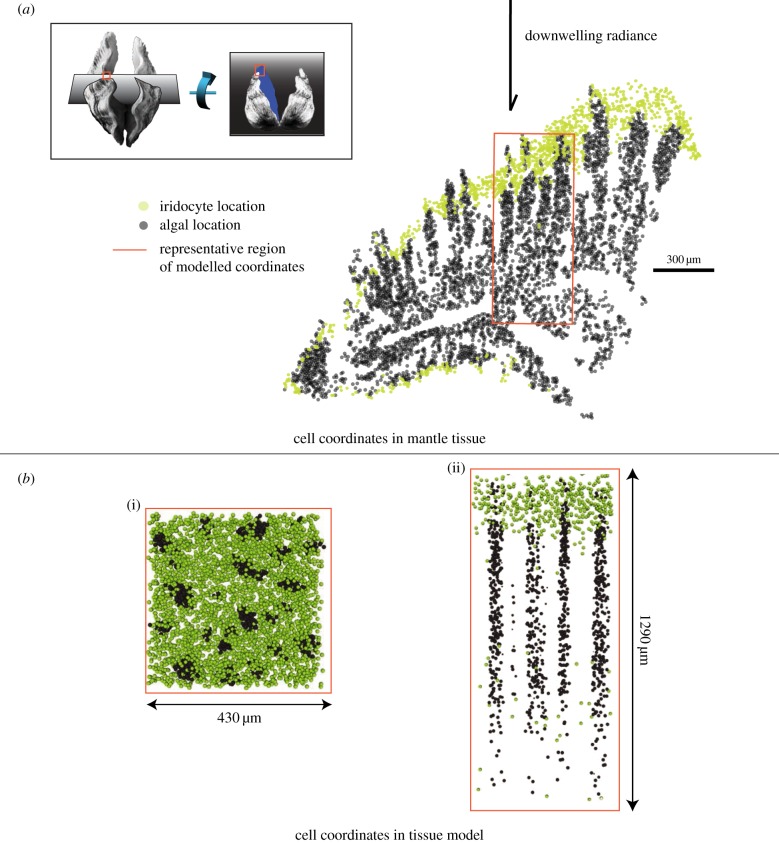
Figure 2.

Generation of three-dimensional cell coordinates. (a) Locations of algae (grey dots) and iridocytes (yellow dots) in a single histological section. The approximate direction of downwelling radiance in the ocean relative to this epithelial tissue section is shown with a black arrow. Inset: cartoon showing orientation of the clam shells visible in figure 1 relative to tissue section in this figure. Grey planes show sectioning planes used for histology in figure 2 relative to the clam shell. Red box shows approximate region of the histological section used in the rest of figure 2a. (b) Modelled tissue section; two-dimensional projection of top surface of model tissue (i) and two-dimensional lateral slice of model tissue (ii).

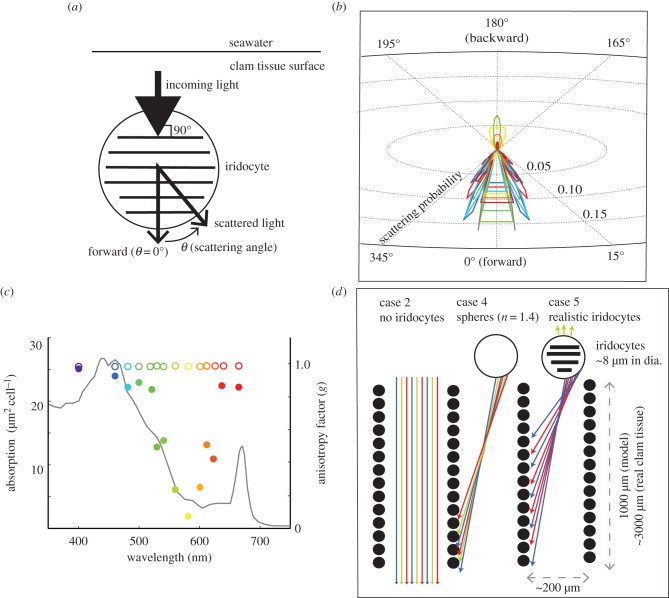
The clam's iridocyte cells have a curious structure with respect to visible light. The individual iridocyte cells are spherical, with a diameter of approximately 8 µm, making them sufficiently larger than the wavelength of visible light (400–750 nm) to be lens-like with respect to these wavelengths. However, superimposed within this 8-µm sphere is a visible-wavelength-resonant Bragg reflector consisting of alternating layers of transparent high-index, protein-filled, membrane-bound platelets (index approx. 1.55) separated by layers of transparent low-index extracellular space or cytoplasm (index approx. 1.33), both with average thicknesses of approximately 100 nm (figure 1f,g) [3,4]. We measured that these layers in all iridocytes are oriented roughly parallel to the surface of the tissue and perpendicular to incoming sunlight.

This combination of significant supra- and sub-wavelength structure puts predictions of the optical behaviour of these cells beyond the reach of simple geometric optics, so it is difficult to predict a priori how they will scatter light. For this reason, the presence of structured, iridescent cells in these species has until now eluded simple explanation. Because these animals are completely sessile, they do not exhibit either of the two major optical behaviours usually associated with structural colour: conspecific display (for communication or signalling; e.g. [5,6]), or crypsis (e.g. [7,8]). The original ultrastructural descriptions of clam iridocytes suggested that because these cells are somewhat reflective, they may play a photoprotective role in the animal's photosymbiosis [3,4]. At odds with this hypothesis, our data show that back-scattering from iridocytes is typically strongest in the green to yellow portion of the visible spectrum, where absorption by Symbiodinium is minimal, as these algae more efficiently use red and blue visible light for photosynthesis. The yellow and green light predominantly backscattered by iridocytes is absorbed at only one-sixth the rate of red and blue wavelengths [9,10]. Even for inefficiently used yellow and green wavelengths, only approximately 20% of incident light is backscattered by iridocytes (electronic supplementary material, figure S1b), so any direct photoprotective effect to Symbiodinium due to backscattered light would be minimal.

The algae are approximately 10 µm spheres and are located underneath the superficial layer of iridocytes. These cells are not arranged randomly in the tissue space. Instead, they are arranged into vertical columns that are roughly parallel to the direction of incident solar photons, as a result of their confinement within thin membranous tubules that originate during development from the clam's stomach (figure 2) [11,12]. When looking straight down at the surface of the mantle tissue, the tips of these algal pillars can be seen emerging from the layer of iridocytes (figure 1d) and are more conspicuous in the clams that do not have iridocytes (figure 1e). The algae and the iridocytes in the clam mantle therefore present an optical system consisting of two types of spherical cells, one scattering (iridocytes) and the other strongly absorbing and scattering (algae), which are organized in a complex, three-dimensional geometric arrangement. The organization of algae into micropillars rather than a close-packed sheet within the mantle tissue of the clam effectively increases the bulk surface area of algae available for photosynthesis. However, this reorganization also reorients the major planar surfaces of the bulk system from horizontal (the surface of the tissue) to vertical (the surfaces of the algal micropillars). As downwelling light is roughly perpendicular to the surface of the clam tissue, this increased surface area by itself will have little or no effect on solar energy harvesting if there is no corresponding mechanism for redistributing the flux of incoming solar photons passing through the horizontal plane (travelling perpendicular to the surface of the clam tissue) to vertical planes (travelling perpendicular to the sides of the vertical micropillars).

We hypothesized that in the context of the clam's photosymbiosis, it is the forward-scattering from the iridocytes, rather than the visually conspicuous back-scattering, that is the optical parameter driving the evolution of these photonically unique cells. We investigated this hypothesis using intra-tissue radiometry and an optical model. We show here that giant clam iridocytes function to spatially redistribute downwelling light evenly over the large vertical surface area of the algal micropillars. The effects of this redistribution are: (i) all algae within the system operate at the same flux (photons per surface area), which is lower than incoming solar flux, while efficiently using all incident solar energy and (ii) in the context of extremely high solar radiances on coral reefs, the majority of algae in the system operate below the light threshold at which photodamage and inefficiencies due to non-photochemical quenching occur. We suggest that these two effects acting together mean that the clam harvests more solar energy more efficiently and with less photodamage to the symbiotic microalgae given the system's environmental radiance. Further, the incoming light redistribution brought about by iridocytes is wavelength specific, directing efficient red and blue wavelengths to the algae, while photosynthetically inefficient green wavelengths are selectively rejected from the system.

2. Results

2.1. Tissue architecture

Within the epithelial tissue of the three species that we examined (Tridacna crocea, Tridacna maxima and Tridacna derasa), algae are densely organized within quasi-ordered vertical micropillars, with the long axis of these pillars parallel to downwelling light, as described above (figure 2). We find that these pillars are approximately 50–100 µm in diameter, a few millimetres in length, and spaced approximately 200 µm apart. Given the reconstructed three-dimensional coordinates of algal cell locations, the surface area of imaginary cylinders containing these algae is approximately 10 times greater than the top surface area of the mantle tissue containing them (figure 3a). Iridocytes are organized in the tissue in a diffuse layer over the tops of these pillars of algae (figure 2; electronic supplementary material, figure S3) and are distributed to a depth in the mantle tissue of approximately one quarter of the length of an algal pillar. Although iridocyte spatial distribution varies to some extent within and between species, the preponderance of clams we examined have a majority of iridocytes that are blue-green to yellow in appearance, consistent with the measured broad peak of backscattered light between 500 and 600 nm (electronic supplementary material, figure S1b). The most reflective clam we measured showed 10–30% backscatter relative to the Lambertian reflector Spectralon at the peak back-scattering wavelength; typically measured values were lower than this (electronic supplementary material, figure S1b).

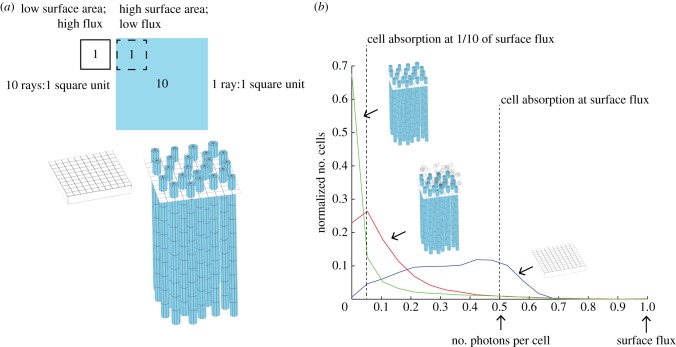
Figure 3.

Geometric redistribution of light flux from the mantle surface to the surface area of micropillars. (a) Schematic showing relative areas of mantle surface to micropillars (containing Symbiodinium) given realistic measurements of the micropillars in the clam tissue. An increase in vertical surface area is of no use to a photosynthesizing system if there is not a corresponding redistribution of photons over the increased area. In an idealized system, a 10-fold increase in surface area (presented by the algal pillars) would lead to light levels of one-tenth of those at the surface if the light were evenly redistributed. (b) Normalized histograms of the number of photons per algal cell for a close-packed sheet of algae with volumetric density equal to cell density in the micropillars (blue curve) and with a thickness equal to the average radius of one micropillar of algae (approx. 20 µm), cells re-templated into micropillars (green curve) and cells re-templated into micropillars with iridocytes present (red curve). Only in the case of pillars with iridocytes is the number of photons per cell relatively constant, and approximately one-tenth that of the algal cells in the close-packed sheet scenario.

2.2. Intra-tissue radiometry

To measure the light environment internal to clam tissue, we conducted intra-tissue radiometry measurements on live clam tissue in Koror, Palau, where several species of Tridacna are readily accessible from aquaculture facilities and from the natural environment.

For these experiments, we constructed 60 µm-diameter fibre optic probes (electronic supplementary material, figure S2a) (adapted from [13,14]). We measured both scalar irradiance (light intersecting at a point from all directions) and downwelling radiance (light directed straight downward on a plane) continuously throughout the depth of living clam tissue. For measuring downwelling light, we constructed tapered optical fibres with a blunt termination; for measuring scalar irradiance, we added a light-collecting sphere made from a viscous UV-curing epoxy mixed with titanium dioxide to the end of a tapered fibre. With 0° defined as the direction of incoming radiance, the downwelling probe accepted only angles from approximately −10° to 10°, while the scalar irradiance probe accepted incoming light from approximately −160° to 160° (electronic supplementary material, figure S2b). We used a halogen lamp to provide downwelling light for all tissue radiometry experiments. Algal pillars and densities of iridocytes were similar in the individuals we studied from both species we measured (T. crocea and T. derasa). Rarely, individual specimens of T. crocea are found with a negligible number of iridocytes but with the same arrangement of pillared algae with tips equidistant from the tissue surface (figure 1c,e); this natural variation allowed us to compare intra-tissue radiance measurements made in the presence and absence of the surficial iridocyte layer. All mantle tissue had an extremely tough, transparent cuticle covering the surface that our approximately 50 µm probe tips were unable to penetrate without breaking. Therefore, we were unable to measure light at positions extremely close to the true tissue surface. We estimate that we reached to within approximately 100 µm of the surface of the tissue before our probes broke.

Individual algae can absorb around 50% of light at red and blue photosynthetically productive wavelengths, while little light is absorbed in intermediate green and yellow wavelengths [9,10]. Therefore, as would be expected for the strongly absorbing algae-dense medium, when we measured downwelling radiance as a function of depth within the clam tissue (light incident on an imaginary horizontal plane) within all clams, red and blue wavelengths were found to attenuate quickly with distance below the tissue surface (electronic supplementary material, figure S1a). By contrast, in clams with iridocytes, within-tissue scalar irradiance (light intersecting an imaginary point) was an appreciable fraction of surface scalar irradiance at many visible wavelengths throughout the depth of the tissue (figures 4a and 5). In these clams, scalar irradiance decreased gradually from the surface and reached a constant asymptote at around 5% of surface scalar irradiance, depending on wavelength (figures 4a and 5a,b). This was not the case in clams without iridocytes, however; in no-iridocyte clams, scalar irradiance, like downwelling radiance, also attenuated quickly below the tissue surface to levels that were too low to measure (figures 4a and 5a,b). Although iridocyte patterns can vary in all species of Tridacna we have observed, in our experience, T. crocea is the only species that occasionally produces individuals with few or no iridocytes. For these radiometry experiments, we selected iridocyte-bearing clams with uninterrupted layers of iridocytes, and few-iridocyte individuals from T. crocea.

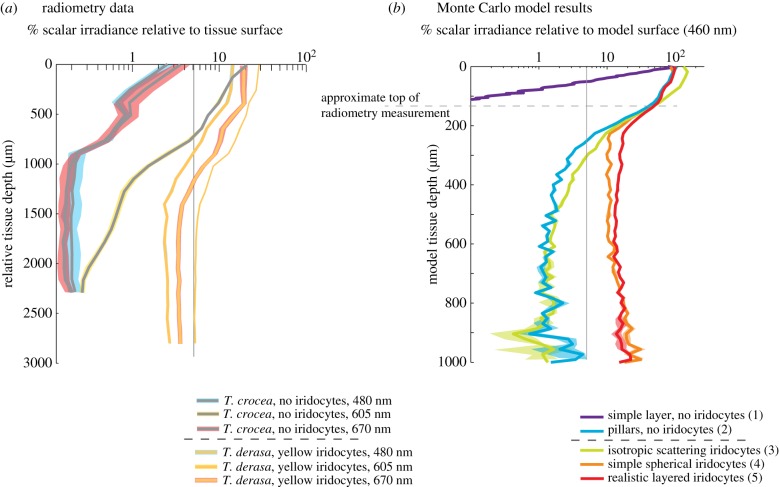
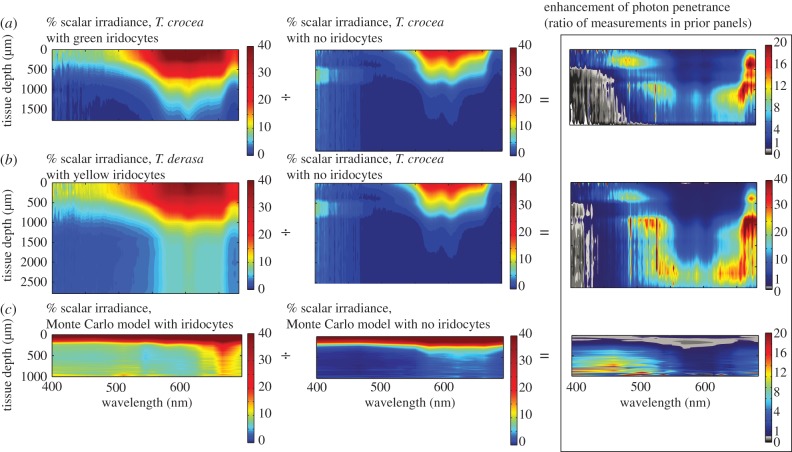
Figure 4.

Direct comparison of tissue radiometry results and Monte Carlo radiative transfer model results. (a) Log plot of radiometry results for T. derasa with yellow iridocytes and T. crocea with no iridocytes. Traces show per cent scalar irradiance (light reaching the detector from all directions) in the tissue relative to the position closest to the surface measured (approx. 100 µm away from emerging); translucent traces show measurement error estimated as the standard deviation of a 10-pixel sliding window of the spectrometer output. Scalar irradiance is greater for all wavelengths and depths in T. derasa with yellow iridocytes than in a specimen of T. crocea with no iridocytes but the same arrangement of algal pillars and is in good agreement with radiative transfer results in the right panel. All measurements had low enough error to justify comparison through ratio. For reference, grey line shows the location of 5% of surface irradiance. (b) Log plot of Monte Carlo radiative transfer model results, shown as average scalar irradiance versus simulated tissue depth for 460 nm. Traces show mean irradiance in three runs of our model, translucent overlays show error estimated as standard deviations of these results. Legend shows description of each model with case number according to table 1 in parentheses. Scattering from the realistic, layered iridocyte structure results in greater absorbance deeper within the tissue than in the other cases. In addition, intermediate values of absorbance are most probable in the DDA-scattering case, with fewer cells absorbing at very high or very low rates, in comparison to the other cases considered. For reference, vertical grey line shows the location of 5% of surface irradiance, and horizontal grey line shows approximate position of surface-most measurement in the experiment relative to the ‘true’ surface obtained in the model.

Figure 5.

Experimental tissue radiometry results. Ratio of scalar irradiance (total light intersecting an imaginary point from all directions) in the presence versus absence of iridocytes as a function of wavelength and depth within the mantle tissue. (a) Raw scalar irradiance as a percentage of the signal in a blank gelatin sample in green-iridocyte-bearing T. crocea; raw scalar irradiance as a percentage of a blank in a no-iridocyte T. crocea; and the ratio of these two measurements shown as fold-enhancement. In the right-most ratio plot, red means high enhancement of scalar irradiance, blue means lower enhancement. A greyscale colour bar is used to indicate regions where the ratio between the two measurements was less than one—in general, these portions of the measurement suffered from low signal-to-noise ratio. The data show enhanced penetration of light into tissue in wavelength bands centred near 530 and 670 nm (coinciding with spectral photosynthetic efficiency in Symbiodinium) down to the bottom of the clam tissue. Tissue depth in these figures shows the total depth of the samples and model, with the top measurement of the tissue aligned in all cases. (b) Comparison between T. derasa with yellow iridocytes and T. crocea with no iridocytes; other parameters are the same as panel (a). (c) Monte Carlo radiative transfer model of scalar irradiance in simulated yellow-iridocyte-bearing clam tissue, simulated no-iridocyte clam tissue, and the ratio between the two models. The same degree of enhancement is seen in the model (bottom right) and in the radiometry data (top right and centre right) in two wavelength bands centred near 500 and 670 nm.

To further understand the possible influence of iridocytes on the distribution of light within the tissue, we calculated the ratio of measured scalar irradiance as a function of wavelength and tissue depth in clams with iridocytes relative to that in clams without iridocytes. We found a many-fold increase in relative scalar irradiance in clams with iridocytes at all wavelengths (figure 5a,b). This relative increase was greatest in the red and blue wavelengths that are most efficient for photosynthesis (figure 5). We then integrated our measurements of relative scalar irradiance over wavelength and throughout the total clam tissue depth. This integration shows that there were approximately fivefold more photons available for algal photosynthesis within the volume of clam tissue with iridocytes compared with clam tissue without iridocytes.

2.3. Discrete dipole approximation of a single iridocyte

To investigate the mechanism by which iridocytes alter the spatial distribution of flux within the mantle tissue, we calculated light scattering from a single iridocyte cell using the discrete dipole approximation (DDA) [15]. This technique calculates the scattering and absorption of electromagnetic waves by a target object of arbitrary structure and was judged to be the most relevant optical modelling technique available due to the iridocytes’ unusual combination of a micrometre-scale sphere (which by itself could be approximated using Mie theory) and a distributed Bragg stack (if the stack were infinite in the plane of the surface of the tissue, the structure could be approximated using multilayer theory). A priori, we might expect iridocytes to have some forward-scattering characteristics as predicted by Mie theory for spheres of this size, and some back-scattering characteristics as predicted for a Bragg stack with the observed spacing.

We used an optimized version of the DDA code for scattering from objects that are large compared with the wavelength of incident light, such as the iridocytes observed in these clams [16]. As mentioned above, our histology shows that the 100-nm-thick platelets in the iridocytes (responsible for the clams’ coloured appearance from backscatter) are oriented approximately parallel to the surface of the clam tissue (the mean angle between the long axis of the platelets and the surface of the mantle tissue was 5° with s.d. of 30°), and thus approximately perpendicular to the direction of downwelling solar radiance at noon. Therefore, for our DDA calculation, we simulated a single iridocyte by building a grid of one million dipoles into 50 alternating high-index (n = 1.55, densely packed protein) and low-index (n = 1.33, water) layers, each 100 nm thick, with less than 1% variance, within a 5-µm sphere (figures 1f,g and 6a; electronic supplementary material, figure S4). The most accurately measured values of the high-refractive index platelets in protein-based iridocytes vary from 1.44 to 1.55 [17–19]. We chose the high end of this possible index range due to the extremely densely packed protein platelets we observed in TEM. Because no measurements of the wavelength dependence of refractive index for clam iridocyte proteins are available, we did not consider dispersion in these calculations; however, change in refractive index in the visible wavelength range for dense protein materials is small (approx. 1% change in n between 450 and 700 nm) [20]. Our DDA model then calculated the phase function (angular distribution of light intensity scattered by a particle as a function of wavelength) of the simulated iridocyte structure for unpolarized light incident along the axis perpendicular to the surface of the intracellular platelets and the surface of the clam tissue, for 14 wavelengths between 400 and 700 nm (figure 6; electronic supplementary material, figure S4).

Figure 6.

DDA of iridocyte structure. (a) Schematic showing orientation of incoming light and scattered light from an iridocyte cell relative to the internal platelets as modelled by DDA. (b) DDA-predicted phase function on radial coordinates, showing forward-cone scattering behaviour predicted for iridocytes. The data show significant back-scattering for yellow light, but only forward-scattering in red and blue. In panels (b,c,d), colours are assigned according to the approximate perceived colour of the wavelength described, e.g. data for 480 nm is blue, 550 nm is green and 700 nm is red. (c) Sum of the scattering intensity for cosine of the angle (called the scattering anisotropy factor, g), shown for iridocytes (closed circles); for a Mie-scattering sphere of the same radius (open circles) and compared to the single-cell photosynthetic efficiency for algae (black line). (d) Schematic illustrating scattering between algal pillars for the case without iridocytes (no scattering of downwelling light entering clam tissue); and the case of a realistic iridocyte evenly scattering mostly red and blue light along the sides of the pillars.

2.4. Iridocyte phase function (light scattered per solid angle)

Our DDA calculation predicted an unusual scattering behaviour for iridocytes. These cells were predicted to scatter downwelling red and blue light, most efficiently used for photosynthesis, into a cone approximately 15° wide in the forward direction (figure 6b,c), while photosynthetically inefficient yellow and green light was equally scattered forward and backward, consistent with the typical iridescent yellow or green appearance of the clams. By contrast, Mie theory shows that if the cells were simple lens-like spheres of the same size and average refractive index, most of the energy at all visible wavelengths would scatter forward at approximately 0°. A simple metric of scattering geometry from a complex structure is the scattering anisotropy factor, ‘g’. This factor is the mean cosine of the angles of scattering intensity from a structure, with any back-scattering at 90–270° from the incident beam at 0° contributing negative values to g (see figure 6a for orientation). Interestingly, g calculated for an iridocyte cell parallels the photosynthetic efficiency spectrum for an algal cell very closely, with more efficiently used wavelengths having greater g, or forward-scattering. In marked contrast, a simple sphere of the same size has little wavelength dependence (figure 6c). Therefore, the DDA-scattering calculation shows that the greater the photosynthetic efficiency of a photon, the more likely it was predicted to be scattered by clam iridocytes into a 15°-wide cone in the forward direction.

2.5. Monte Carlo model of radiative transfer

Our DDA analysis showed that red and blue wavelengths of light are scattered from the iridocytes predominantly forward into a 15°-wide cone, whereas green and yellow wavelengths are scattered more isotropically. To understand the effects of this wavelength-dependent scattering from iridocytes in the spatial context of the arrangement of algal micropillars found within the clam, we incorporated this DDA calculation into a stochastic Monte Carlo model of radiative transfer through the tissue. Typically, Monte Carlo models of photon transport track photon rays through a material with statistical scattering and absorption of light based on the probable mean free path in the material [21]. However, because iridocytes and algae are not arranged randomly in the clam's mantle tissue, for this model we used explicit three-dimensional coordinates of algae and iridocytes as identified manually by serial sectioning and light microscopy. These three-dimensional coordinates were used in conjunction with ray tracing algorithms to track the intersection of photons with explicit cell positions. As in other Monte Carlo photon transport models, the absorption and scattering of the rays in our model are based on random sampling from a theorized probability distribution function (see the electronic supplementary material for details). Our system explicitly represents a 420 × 420 × 1290 µm deep volume of tissue containing 13 561 algae and 7917 iridocytes (figure 2). Our Monte Carlo model is therefore relatively computationally expensive, but in contrast to other methods, gives us the flexibility to explore the geometric order found in the algae/iridocyte system.

Using this model, we were then able to track the trajectories of 90 000 collimated rays entering the surface of the clam structure. In the model, each time a ray intersects a cell, the cell absorbs or scatters the ray according to probabilities for each event as defined for each cell type. We recorded the total light absorbed by each algal cell located on a three-dimensional Cartesian grid as a fraction of all incoming rays, thus allowing us to determine light levels resulting from stochastic scattering throughout the depth of our modelled clam tissue. The probability of a ray scattering in a particular direction from a cell comes from the normalized cell-specific phase function. We estimated the phase function for iridocyte cells using the DDA calculation as described above and for algal cells using Mie theory for homogeneous spheres [22]. We based the percentage of a ray that is absorbed by an algal cell on an empirical measurement of algal single-cell absorption [9,10], and we assumed that the iridocytes have no appreciable absorption in the visible. To simulate a broadband illuminant, we used the same number of rays (90 000) entering the tissue for each of 14 wavelengths evenly distributed between 400 and 700 nm. Error in the Monte Carlo model varied depending on the type of analysis and for each cell type; we verified that the number of rays we issued resulted in reasonable and statistically relevant convergence (see the electronic supplementary material for more information). We did not include in our model possible intracellular scattering from connective tissue or structures other than algae and iridocytes; in effect, we assume that any diffuse intracellular scattering is equal between clams with and without iridocytes. However, intracellular scattering in this system may in fact be very low; algae excrete glycerol as a major portion of photosynthate in symbiosis with clams [23], and glycerol is well known to reduce scattering in biological systems, acting as a ‘clearing agent’ promoting tissue transparency [24,25].

To understand the exact contributions of each parameter of tissue geometry and iridocyte scattering on light propagation within the system, we considered several nested cases of radiative transfer through the simulated tissue. The general outline of the nested cases of our model is as follows:

• — Cases with no iridocytes

  • (1) Simple, densely packed layer of algae; no iridocytes
  • (2) Algae organized as observed, in micropillars; no iridocytes
• — Cases with iridocytes

  • (3) Algae organized in micropillars; isotropically scattering iridocytes
  • (4) Algae organized in micropillars; simple, spherical iridocytes
  • (5) Algae organized in micropillars; iridocytes scatter according to DDA calculations

Because algal cells are spheres that are able to absorb light from any incident direction, light flux per cell and scalar irradiance (light intersecting an arbitrary point at a given position) are interchangeable quantities in our model and are expressed as a percentage of the flux present at the surface of the system.

We modelled two different situations without iridocytes present: first, we considered a system with a simple, dense layer of algae and no iridocytes (case 1), and then we rearranged the same number of algae into the micropillars actually observed in the clam, but with no iridocytes (case 2). Then, we modelled cases with the same algal micropillars as in case 2 but with iridocytes of different optical activity. We considered the possibility of iridocytes behaving as isotropic scatterers (using the Henyey–Greenstein equation to approximate their scattering phase function; case 3). We also considered iridocytes as 8-µm spheres but with no internal structure (using Mie theory to approximate the phase function, and with n = 1.4 as the calculated ‘effective medium’ refractive index of the iridocytes; case 4). Finally, we considered realistic iridocytes that scattered according to the DDA-predicted phase function (case 5). For reference, the model cases and sources of absorption and scattering parameters are outlined in table 1. The results of these modelled scenarios are illustrated and discussed sequentially (figures 4b and 5c; electronic supplementary material, figures S3 and S5).

Table 1.

Nested cases of Monte Carlo radiative transfer model and sources of optical behaviour for each.

case number	description	iridocyte optical behaviour	phase function used for iridocyte scattering	algal optical behaviour
1	algae in a simple layer 20 µm thick with same density as algal pillars	no iridocytes	none	scatter according to Mie theory for 8 µm sphere, absorb according to reported literature9,10
2	algae in pillars, no iridocytes	no iridocytes	none	"
3	isotropic iridocytes	all wavelengths scatter equally in all directions	Henyey–Greenstein approximation, g = 0	"
4	forward-scattering (lens-like) iridocytes	all wavelengths lensed forward	Mie theory for 8 µm sphere and n = 1.4	"
5	realistic, layered iridocytes	red and blue wavelengths scatter in +15° forward cone, green and yellow wavelengths equally scatter forward and back	DDA calculation	"

In case 1 (a simple, dense layer of algal cells), our analysis shows that cells experience scalar irradiances of near 100% of the input value at the surface of the tissue, and low scalar irradiance beneath that. This result is consistent with cells at the surface of the tissue receiving the level of flux input to the system and self-shading under the initial monolayer of cells at the surface (figures 3b and 4b). In case 2, when cells were arranged in the micropillars as observed in the clams but no iridocytes were present, the number of algal cells exposed to the surface level of flux was greatly reduced, and the majority of cells received flux of less than 10% of the surface value, consistent with fewer cells exposed at the surface of the tissue combined with intra-pillar self-shading under that (figures 3b and 4b; electronic supplementary material, figure S3).

By contrast, when iridocytes were introduced to our model in cases 4 and 5, flux per cell was nearly constant throughout the depth of the tissue (figures 3b, 4b and 5c). In both of these cases, scalar irradiance decreases from 100% of that at the surface to a near-constant value of approximately 10% of the surface value. Therefore, similar to our result from experimental radiometry, scalar irradiance as a function of tissue depth in our model behaved asymptotically when both algal micropillars and iridocytes were present. The value of the flux at the asymptote is significantly higher for productive red and blue wavelengths in case 5 (realistic iridocytes) than in any other model case (figure 4b). Therefore, for photosynthetically productive wavelengths, our model predicts that the structures actually present in the clams optimize the number of algae absorbing at moderate rates (figure 3b), optimize the absorption by algae deep in the tissue (figures 4b and 5) and optimize total absorption integrated over all algae in the tissue (figures 4b and 5) in comparison to any of the simpler, unrealized (i.e. non-natural) alternatives we considered.

If, in the clam system, iridocytes function to evenly redistribute incoming solar flux over the bulk surface area of the algal micropillars, we should expect the average flux reaching each cell, or the value of the flux at the asymptote with depth, to scale linearly with the ratio of pillar surface area to mantle surface area. Our three-dimensional cell coordinates show that the surface area of imaginary cylinders enclosing the algal micropillars is about 10 times greater than the area of the mantle surface under which the pillars are contained (figure 3a). Therefore, if iridocytes redistribute incoming flux evenly over the bulk surface area, the flux reaching the surfaces of the micropillars should be constant, and about one-tenth of the flux incident on the surface of the clam's mantle. In fact, in both our radiometry measurements and optical models of systems with iridocytes, there is a near-constant value of scalar irradiance with tissue depth. In our radiometry data, this near-constant value of flux is approximately 5% of the surface flux, and in the model it is approximately 10%, both on the order of the 10% that we would expect for a perfect, ideal redistribution over a 10-fold increase in bulk surface area. Furthermore, we should predict that even redistribution of photons per pillar surface area occurs in the presence of iridocytes, but not in their absence. Both our intra-tissue radiometry measurements and our radiative transfer model bear this prediction out (figures 3b, 4 and 5). Light levels in experiments and models without realistic iridocytes were always lower than the asymptote at 5% of the surface value observed with iridocytes, and therefore were farther from an ideal redistribution of flux over the surface area of the micropillars.

Because the radiative transfer model gives us direct access to the number of photons reaching each cell, we can also calculate a distribution of flux per algal cell among the cells in different model cases (figure 3b). An even redistribution of light should result in a narrower distribution of absorption per cell. The position of the peak of the distribution then indicates how the redistribution scales with surface area. As expected, in case 1 (algae in a simple sheet), most of the algae are exposed to the flux incident on the surface with some cells experiencing higher flux due to multiple scattering at the surface, and some lower due to self-shading. In case 2 (algae in micropillars but no iridocytes), algal cells are mostly in the dark, with only a few experiencing near-surface irradiance. However, in case 5, when both iridocytes and micropillars are present, a plurality of cells within the system absorb at approximately 10% of the rate of cells in the close-packed sheet case. This result is consistent with a near-even redistribution of light incident on the horizontal surface over the vertical surfaces of the pillars, and a near-complete conservation of energy input to the system.

Our model also predicts a further interesting difference in the wavelength dependence of scattering between the cases of realistic iridocytes and simple spheres with comparable dimensions and average effective refractive indices (case 4 versus case 5). Model algae in case 4 absorb more light at the inefficient wavelength of 580 nm than in case 5, but the total light absorbed by the system over all wavelengths is approximately equal in both cases. Therefore, iridocytes, as compared with simple spheres, seem to increase total productive absorption in the blue and red at the expense of absorption in the yellow and green. This is likely to be an energetically favourable compromise because yellow and green wavelengths are less photosynthetically efficient. It is also possible that the rejection of non-productive yellow and green light by iridocytes could help reduce overheating or non-photochemical quenching at high rates of solar flux to the system. Thus, as a result of several possible mechanisms, the observed system may result in greater photosynthetic energy capture and transduction for the symbiosis.

Our Monte Carlo model simulating the clam tissue corroborated our experimental measurements of scalar irradiance within the clam tissue with good accuracy in both wavelength distribution and relative increase of flux per cell and as a function of tissue depth (figures 3–5). The realistic iridocyte case resulted in the best replication of our experimental data compared with any of the other cases we considered (figures 4 and 5; electronic supplementary material, figure S5). This close corroboration of our experimental results with our optical model suggests that the increased irradiance in clams with iridocytes when compared with irradiance in clams without iridocytes can be explained by the presence of the iridocytes.

3. Discussion

Our results show that the even redistribution of photons over the surface area of algal micropillars is attributable to the particular scattering behaviour of the clam's iridocyte cells. The iridocyte structure appears to redirect photosynthetically efficient wavelengths of light away from the tissue surface to an even distribution along the algal pillars, both in our measurements in the real clam (figures 4 and 5) and in the model (figures 3–5). Previous studies postulated a photoprotective role for iridocytes [3,4]; our data suggest that any photoprotective function of the iridocytes results at least in part from the redirection of photosynthetically productive light evenly among a greater number of algae within the clam tissue, in addition to any protection by simple retroflection of incoming light. Our optical model of the clam tissue corroborates our experimental results and offers a complete mechanistic explanation for the enhanced light environment within the clam.

Given the high ambient light levels that typically occur on shallow coral reefs, the clam's flux redistribution system may simultaneously promote efficient use of available solar energy and prevent photodamage of Symbiodinium. It is very well established that typical mid-day irradiances found on coral reefs elicit an array of photoprotective physiological responses from Symbiodinium that limit the light-harvesting efficiency of individual cells [26–28]. In fact, in culture, Symbiodinium photosynthetic output shows an asymptote with increasing light: upon increase in surface radiance greater than approximately 300 µmol quanta m⁻² s⁻¹, there is little or no further increase in photosynthetic oxygen evolution [27]. Even increases in surface light greater than 100 µmol quanta m⁻² s⁻¹ result in detectable photostress and decreased photosynthetic efficiency in Symbiodinium [26]. These light levels are well below those reached at mid-day in the tropical Pacific (up to 2000 µmol quanta m⁻² s⁻¹) [29]. In corals, sufficient photostress of Symbiodinium ultimately leads to programmed cell death of both host and symbiont cells [30]. While our measurements and model best characterize scalar irradiance (all light intersecting a point) and most prior studies report planar radiances (all light normal to a plane), it is possible to deduce light levels per cell within the clam from a given initial planar radiance, as the initial condition in both our measurements and model restricted all light introduced to the clam as a planar radiance (i.e. all light was directed downward onto the simplified planar surface of the clam system).

Therefore, as our data are scalable, a typical shallow tropical Pacific light flux of 1700 µmol quanta m⁻² s⁻¹ will result in a near-constant illumination along the clam's micropillars of approximately 85 µmol quanta m⁻² s⁻¹, which is very close to the efficiency maximum of Symbiodinium (around 100 µmol quanta m⁻² s⁻¹) [27]. As photoinhibition in Symbiodinium is detectable at experimental light levels exceeding 100 µmol quanta m⁻² s⁻¹ [26], the system described here may exhibit efficiency gains relative to a simple layer of algae even at light levels lower than 2000 µmol quanta m⁻² s⁻¹.

There is an analogy between the clam system and solar energy, and a transformer in an electromagnetic system. A transformer changes the current density in a system while conserving energy in the system via induction through differing numbers of wire coils with different net cross-sectional area. As energy must be conserved, the energy flux per unit cross-sectional area of wire must also change. The giant clam system functions much the same way. Environmental solar flux on a coral reef is a high energy flux source. The clam's iridocytes, analogous to a transformer, distribute incoming solar flux over a greater area, reducing it to a rate safe for its energy consumers, the algae, while the total energy available to the system remains constant. It is not inevitable that incident energy should be conserved inside the clam tissue as photons could be lost via scattering out of the system, and the algae themselves have conversion efficiencies that depend on photon flux. However, our data show that most of the incident energy stays within the system to be absorbed by algae and that the specific ratio of incoming flux to flux per cell that occurs is likely to allow algae to operate at a flux most conducive to efficient photosynthesis. We also note that there is a thin layer of iridocytes on the shell-adjacent side of the mantle tissue on the edge of the mantle that often hangs over the edge of the shell (figure 2a). It is possible that these iridocytes could similarly function to forward-scatter light reflected from high albedo sand or from the highly reflective clam shell itself (M. Lim 2014, personal communication) back into the algae in the tissue, further increasing the efficiency of the system.

The specific arrangement of iridocytes and algae allows the forward- and laterally scattered light from the iridocyte layer to evenly illuminate the sides of the algal pillars while providing a high volumetric density of the photosynthetic algal cells, allowing more solar photons to be used efficiently for photosynthesis than would be the case if algae were arranged in a simple layer, or in micropillars without iridocytes. Given that the clam lives in shallow water at light levels that would otherwise be stressful to the microalgae, reducing their efficiency [29], this arrangement and subsequent redistribution of photon flux presumably increases the photon conversion efficiency of the microalgae, as well as the total number of cells that are able to perform photosynthesis. We speculate that the combined effects of the somewhat variable orientation of the Bragg lamellae, the curvature of the mantle tissue, and hourly and seasonal changes in the angle of maximum solar radiance may serve to further redistribute photons over the entire algal population; these factors will be investigated in future work on this system.

We also note for comparison the optical/symbiotic system observed in reef-building corals. These organisms contain symbiotic microalgae of the same genus, but completely lack iridocytes. In contrast to the optical system in the giant clam, the coral's optical arrangement consists of algae in just a thin layer close to the surface of the tissue (e.g. [31]) with scattering from the underlying, rugose coral skeleton possibly augmenting lateral light transport [32]. The colonial coral body plan allows the animal to become branching and rugose, perhaps providing a mechanism for building large quantities of relatively inexpensive surface area, and therefore able to harvest more light somewhat wastefully. Perhaps the constraint of photosymbiosis in the context of the low-surface area, near-spherical, solitary body plan of the clam was the evolutionary driving force behind the appearance of this apparently more spatially efficient system for solar energy.

The highly evolved ‘three-dimensional’ biophotonic system of giant clams, relying on wavelength-selective, bifunctional scattering elements, may suggest a blueprint for more efficient, damage-resistant photovoltaic materials and more spatially efficient solar production of algal biofuels, foods and chemicals. Technological applications of these insights are most obvious for photoconversion systems, like Symbiodinium, that suffer from decreases in conversion efficiency with increasing flux and/or photodamage at high flux. Therefore, photobioreactors for algal products and fuels, and polymer photovoltaics could benefit from attempts at direct mimicry of the clam system. The efficiencies of more traditional silicon wafer-based photovoltaic panels do not change with solar flux, so there is a less direct link from the giant clam to possible improvements in these solar energy conversion technologies. However, silicon photovoltaics do suffer decreases in efficiency and irreversible damage from overheating; we note that the clam's evolved design also resembles a heat sink, and the clam may suggest a strategy for even illumination while avoiding overheating in silicon-based materials. In particular, clam iridocytes show us a generic optical solution for evenly redistributing high levels of horizontal solar flux over organized, micrometre-scale vertical surfaces. Therefore, these iridocytes offer a promising target for biomimetic engineering efforts that could be coupled to any vertically pillared, photoconverting material, whether that material is photosynthetic or photovoltaic.

4. Material and methods

4.1. Optical microprobe construction

The termination of one end of a 100-μm silica core fibre optic assembly (Ocean Optics, Dunedin, FL, USA) was removed. The fibre's jacketing was stripped and the fibre's polyimide buffer was removed 5 cm from the fibre's end using a butane torch. A 10 g weight was attached to the end of the fibre and the fibre was then pulled, narrowing the diameter, upon heating with a butane torch. The narrowed region of the fibre was then cut using carborundum paper, to yield a flat fibre end with a diameter of 30–50 μm (adapted from [11]). The sides of the narrowed fibre were painted with a film opaquing pen to prevent stray light from entering, while leaving a small transparent opening at the fibre tip. For structural support, this bare, tapered fibre was then secured in the tip of a pulled glass Pasteur pipette using a drop of cyanoacrylate glue, leaving only 2–3 mm of bare optical fibre protruding. For spectral scalar irradiance measurements, we added a small light-scattering ball to the end of the tapered optical fibre (adapted from [12]). To do this, titanium dioxide was thoroughly mixed with a high-viscosity UV-curable resin, DELO-PHOTOBOND, GB368 (DELO Industrie Klebstoffe, Windach, Germany). The tip of a pulled fibre was quickly inserted and removed from a droplet of the resin and titanium dioxide mixture, resulting in a sphere with a diameter two to three times that of the tapered fibre. As all measurements from a given probe were normalized to the signal from the same probe in a gelatin blank, small variations in probe diameter have no effect on our results. The sphere was cured for 12 h using the Ocean Optics LED UV light source LS380 (Ocean Optics).

Probe acceptance angles were measured to characterize the probes’ sensitivity to collimated versus omnidirectional light; probe tips were placed in the focal point of a parabolic reflector (Pelican 1804 Super Pelilite Lamp Module) orthogonally oriented to the reflector's optical axis. The probe's optical fibre was attached to a white light source (LS-1 light source, Ocean Optics) and photographs of the reflector and probe tip inside were taken by a camera (Nikon D700) mounted in front of the reflector and centred in its optical axis. The distribution of light intensities in a circle centred on the probe tip and at the same height as the probe (the reflector's focal point) described the relative amount of light the probe accepts per scattering angle (electronic supplementary material, figure S2). Flat-tip tapered probes had very narrow angular acceptance in the forward direction, while probes with a scattering ball attached had nearly flat angular acceptance, with the exception of a small blind spot in the backward direction where the fibre entered the spherical tip.

4.2. Tissue radiometry apparatus

Tridacna derasa, T. maxima and T. crocea were purchased from clam aquaculture facilities in Palau and kept alive in running seawater at the Palau International Coral Reef Center, Koror, Palau. To prepare clam samples for optical measurements, the clam shell adductor muscle was severed from one valve, and then a 8 mm diameter biopsy of the complete thickness of the mantle margin (2–4 mm thick, depending on the animal) was performed using a standard biopsy punch. This circular piece of tissue was then placed in an 8-mm gelatin well in a 1 : 1 seawater : tapwater gelatin-filled Petri dish. The 8-mm gelatin well containing the clam biopsy was then infilled with molten 1% gelatin in 1 : 1 seawater : tapwater, cooled to room temperature, then refrigerated briefly to completely solidify the gelatin. Sample preparation after biopsy took less than 10 min, and radiometry experiments were completed in about 20 min; there was no visually obvious degradation of the iridocytes or clam tissue during this time. There was a 5 mm hole in the bottom of the Petri dish, covered with tape during sample preparation and removed for the experiment, to allow our optical probes to enter the tissue sample. The resulting rigidity of the gelatin provided a highly transparent matrix that was sufficiently rigid to immobilize the clam tissue in the dish during the experiment.

The Petri dish containing the clam sample was then mounted on a stage attached to a micromanipulator and positioned to centre the hole in the bottom of the dish around the fibre optic probe tip, which was mounted vertically and held stationary throughout the experiment. A 6 mm aperture in black plastic was placed over the biopsy to collimate the beam striking the sample and prevent side-welling light from entering our sample. The optical probe was connected to a USB2000 + fibre optic spectrometer operated with SpectraSuite software (Ocean Optics). The sample was illuminated from a 1.5 m distance with a halogen work lamp. We then lowered the dish in 125 µm increments onto the fixed optical probe, pushing the probe through the clam tissue, and a spectrum was recorded from the probe at each incremental advance (electronic supplementary material, figure S2). A given measurement was concluded when the probe tip was visible through a dissecting microscope at the top surface of the clam tissue, and in contact with a transparent, cuticular layer that was too tough for our probes to pierce without breaking.

4.3. Cell/particle detection for generation of three-dimensional coordinates

Three-dimensional coordinates for the algal and iridocyte positions were generated manually from panoramic light micrographs stained with toluidine blue using imagej software. Spatial statistics were then obtained using these manually generated coordinates to create a set of three-dimensional cell coordinates representing 13 561 algal cells and 7916 iridocyte cells in a 420 × 420 × 1290 μm volume of clam tissue (figure 2). These data were incorporated in the radiance transfer model. The comparative case of a simple dense layer of algae was generated using random cell coordinates within a smaller volume.

4.4. Discrete dipole approximation

The scattering intensity or probability density of scattering per angle (phase function) for tridacnid iridocytes was calculated using the DDA as developed by Draine and Flatau [15]. We used an optimized version of the DDA model that can handle large scatterers such as iridocytes. This technique was used by Vahidinia and co-workers for modelling large, porous aggregates and the code used in that study, and the current work, is available at http://code.google.com/p/ddscat/ [16]. Tridacnid clam iridocytes were simulated by populating a grid of dipoles to represent a 5 μm diameter sphere with internal layers of high (1.55)- and low (1.33)-refractive indices, representing alternating platelets of condensed protein and normal cytoplasm, respectively. Dispersion was not considered at this time. Each layer was specified to be 100 μm thick, as measured directly by TEM. This simulated layered sphere was illuminated with unpolarized light at normal incidence to the stacks and the scattered light was averaged over the azimuthal plane (plane parallel to plane of the iridocyte's internal platelets).

TEM images show that iridocytes and microalgae are closely packed in the clam tissue and that each cell is within the near-field scattering regime of other nearby cells. In this situation, the diffraction lobe in a phase function calculated for an isolated particle does not accurately represent the phase function for the same particles in a close-packed arrangement. This is because the diffraction lobe represents rays bending around the edges of an isolated particle and interfering at large distances and small angles close to the forward-scattering direction. Cells in the near field of a given scattering event do not ‘see’ these diffracted rays, while they do interact with rays resulting from multiple internal refraction at short distances and larger scattering angles, as shown in the electronic supplementary material, figure S4. Therefore, to approximate the algal and iridocyte phase functions in the closely packed situation we observed in the clam's tissues, we truncated the diffracted component of the scattered beam near 0^o scattering angle. This approach for modelling close-packed, large scatterers has been worked out in detail by Cuzzi et al. [33]. We adopted a similar approach by setting the scattered intensity at all scattering angles less than 2° equal to the calculated intensity at 2°, effectively truncating the narrow diffraction lobe within ±2° of the forward direction.

4.5. Three-dimensional Monte Carlo model

The measured three-dimensional spatial coordinates of the algae and iridocytes were used in a Monte Carlo optical model of photon transfer custom-written in matlab (Mathworks, Natick, MA, USA). The code recorded the interaction of each photon packet with a cell, either an alga or an iridocyte, and determined the resulting scattering direction and absorption based on cell-dependent probabilities derived from modelled phase functions and empirical absorption data. When intersected by a photon packet, algae absorbed a wavelength-dependent fraction of the photon packet. This absorption was normally distributed with a variance of 0.5. The mean absorption was set at the reported literature values for single-cell brown alga wavelength-specific absorption [9,10]. In order to spatially track individual packets of photons within the simulation for all interactions, iridocytes were assigned a negligible absorption, with a mean of 0.001% of the photon packet at all wavelengths, and with a variance of 0.5. The fraction of a photon packet not absorbed in a given interaction was scattered according to a phase function generated specifically for each cell type. Photon packets were scattered from algal cells using a wavelength-dependent phase function based on Mie-scattering calculations. Photon packets were scattered from iridocytes according to the following four distinct phase functions: either a Henyey–Greenstein phase function for back-scattering and isotropic-scattering scenarios (g = −0.98 and g = 0, respectively); Mie-scattering calculations from a 5 μm diameter sphere of n = 1.4 for the simple-sphere case, or the phase function generated by discrete dipole analysis for the realistic iridocyte case. Both algae and iridocytes were given a nominal diameter of 8 μm in the Monte Carlo model. Trajectories of 90 000 photon packets were modelled in a single run, with the error estimated by calculating the standard deviation in absorption per cell between 80 000 photon packets and 90 000 photon packets in the model. These runs converged on less than 1% error in total tissue algal absorption and on average approximately 1–5% error for single-cell absorption. Convergence occurred after 90 000 photon packets were run; this was verified by repeatedly running the model with 10 000 photon packets, and the photon packet number was increased in all model cases until the least-converged case had variation of less than 5% arb. units per cell.

Using this model, we explored several nested hypotheses about tissue geometry and iridocyte functions. First, we considered a set of coordinates with algal cells only, arranged in a simple, close-packed layer. Next, we arranged the same number of algal cells in the pillared geometry observed in the clam but excluded iridocytes from the model. We then used the same algal coordinates but added iridocyte positions to the model and varied the scattering phase function per run to test the four iridocyte scattering scenarios described above (using Henyey–Greenstein, Mie or DDA calculated phase functions depending on the model case). In this particular Monte Carlo model, we may consider each algal cell to be a location-specific 8 μm diameter detector, and we monitor the total absorption per cell, which is directly proportional to the amount of light (in photon packets) striking the cell. Thus, by tracking the absorption per cell, we can calculate the amount of light at depth in the tissue in arbitrary units by binning absorption per depth, scaled as a function of wavelength, across the total area of the tissue and dividing by the number of detectors in that volume. To a first-order approximation, the performance of the tissue is directly related to the amount of light available to the algae; given the flexibility of this model, future work will explore the effects of more biologically realistic physiological plasticity in the endosymbiotic microalgae.

Data accessibility

Data reported in this paper are available in the electronic supplementary material and DDA code is available at http://code.google.com/p/ddscat/.

Funding statement

This research was supported by grants from the Army Research Office (no. W911NF-10-1-0139) and the Office of Naval Research (through MURI award no. N00014-09-1-1053 to Duke University).