Complex contagion process in spreading of online innovation

Abstract

Diffusion of innovation can be interpreted as a social spreading phenomenon governed by the impact of media and social interactions. Although these mechanisms have been identified by quantitative theories, their role and relative importance are not entirely understood, as empirical verification has so far been hindered by the lack of appropriate data. Here we analyse a dataset recording the spreading dynamics of the world's largest Voice over Internet Protocol service to empirically support the assumptions behind models of social contagion. We show that the rate of spontaneous service adoption is constant, the probability of adoption via social influence is linearly proportional to the fraction of adopting neighbours, and the rate of service termination is time-invariant and independent of the behaviour of peers. By implementing the detected diffusion mechanisms into a dynamical agent-based model, we are able to emulate the adoption dynamics of the service in several countries worldwide. This approach enables us to make medium-term predictions of service adoption and disclose dependencies between the dynamics of innovation spreading and the socio-economic development of a country.

1. Introduction

Diffusion of news, ideas and innovations as well as the distribution of services and products are all examples of social spreading phenomena that have become an integral part of our everyday life, strongly accelerated by novel, Web-based interaction channels. These innovations serve as an engine of economic development [1], but only their diffusion throughout society brings them to success. The processes involved in innovation spreading have been the focus of research for decades [1–4], yet their dynamics and modelling have remained as challenges to our scientific understanding.

The propagation of innovations takes place in a social network [2–5] and is driven by the entanglement of individuals' decision-making processes [6] as well as by the influence of media and social interactions [7,8]. Although the effects of network structure on contagion processes have recently been shown to be important [9], knowledge about the social network itself is rather limited as its structure and dynamics usually remain hidden. In this respect, the digital age has opened up unprecedented opportunities, as online social networks and Voice over Internet Protocol services record detailed information of the connections and activities of their users. These services partially decode the underlying social structure by acting as proxies for the network of real social ties between individuals, and also provide accurate records of the users' adoption behaviour. In this way, the different sources of influence on the decisions of an individual immersed in a perpetually changing environment of social interactions become traceable. We are therefore encouraged to devise dynamic agent-based models to describe, simulate and even predict emergent behaviour of such social contagion phenomena [10–12].

These phenomena are identified as complex contagion processes when the exposure of an individual is conditional on the decision of a fraction of its peers [13]. This is particularly different from simple spreading processes, where a rate determines the transmission of infection between nodes and one infected neighbour is always sufficient to expose a susceptible node [9,14]. Complex contagion phenomena are commonly modelled by processes where the fractions of adopting neighbours necessary for exposure are set as individual thresholds. This idea was first introduced by Granovetter [15] who discussed the ideal network structure and threshold distribution to allow for the evolution of riots or other collective movements. Subsequently, Watts [16] proposed a simplistic model to explore sufficient structural and threshold conditions for the evolution of global adoption cascades. During the last 10 years, several studies contributed to the foundations of complex contagion [16–21], and in addition online experiments were carried out to provide empirical evidence about the effect of social influence [22,23]. Beyond the conventional threshold mechanism, the effect of homophily [5,20,24] and the role of external media influence [3] were also investigated recently.

Here, we study one of today's largest online communication services, the Skype network, with over 300 million monthly connected users [25]. Data cover the history of individuals that adopted Skype from September 2003 until March 2011 (i.e. 2738 days), including registration events and contact network evolution for every registered user around the world. For our investigation, we select user accounts with an identified country of registration and consider only their mutually confirmed connections, both within the country and abroad. To receive the best estimation of node degrees in the underlying social network, we integrate the evolving Skype network for the whole available period and count the number of confirmed relationships per node (including international ties). The adoption dynamics of a given country can be directly observed by assigning times of adoption (t_a) and termination (t_t) to all the accounts. These are, respectively, defined as the dates of registration and last activity (as regards to any of the services) in Skype. Explicitly, we identify any account as terminated if its last activity happened earlier than 1 year prior to the end of the observation period. In this way, we are able to build a complete adoption and termination history of Skype for 2373 days. As an illustration of the adoption process, in figure 1a,d we show a sample of the contact network of Switzerland for two intermediate times (for further details of the dataset, see the electronic supplementary material, §S1).

Figure 1.

Sample of the aggregated Skype network of Switzerland. (a,d) Snowball sample (maximum distance from seed d = 4) where user accounts and confirmed links between them are shown for two intermediate times in the adoption process. Nodes are coloured according to their adoption state: grey for future users, orange for current adopters and purple for terminated accounts (corresponding to states S, A and R in our compartmental model). A link has one of these colours if the states of the connected nodes are equal and is grey otherwise. (b,c,e,f) Decomposed networks for adoption (b,e) and termination (c,f). Nodes have the same colours as before but are shaded depending on their action (dark for spontaneous action and light for peer-pressure action). Only links connecting nodes with equal states are shown. The termination network has a larger fraction of dark nodes than its adoption counterpart, meaning that social interactions affect adoption more than termination.

Taking advantage of this large digital dataset, our goal is to fill the persisting gap between real observations and the assumptions made in models of product adoption spreading in techno-social networks. We empirically study the assumptions borrowed from conventional models of complex contagion and analyse the crucial effect of social influence. Finally, we introduce an agent-based model that combines the detected diffusion mechanisms and provides plausible medium-term predictions for the spreading of online innovations in several countries worldwide.

2. Results

2.1. The adoption dynamics

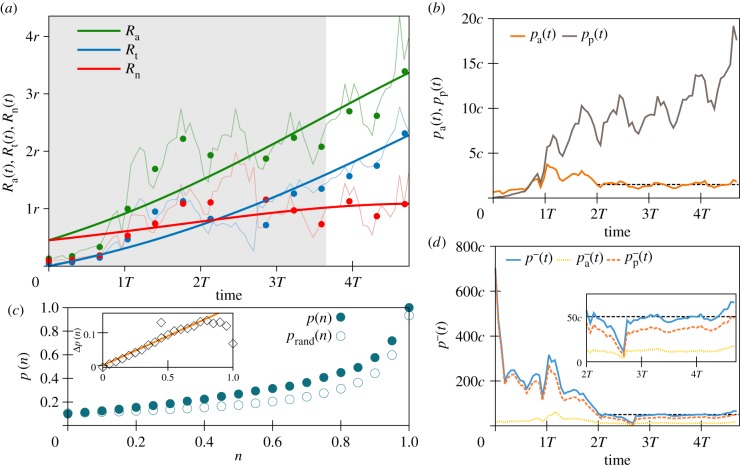
The spreading of the online service is determined by competing processes of adoption and termination as described by the evolution of the corresponding rates R_a(t) and R_t(t), which measure the fraction of all users that adopt or terminate the service in a given time window Δt (figure 2a). These simple rate functions already disclose interesting features of the adoption dynamics, as their overall growth signals continuously accelerating processes of adoption and termination. Yet the actual time evolution of spreading service is better characterized by the net adoption rate R_n(t) = R_a(t) − R_t(t) (for an overview of all empirical quantities, see table 1).

Figure 2.

Empirical rates and probabilities for Switzerland. (a) Thin curves denote empirical rates of adoption [R_a(t)], termination [R_t(t)] and net adoption [R_n(t)], while symbols are their corresponding binned values. A binned data point in [2T, 3T] has been removed due to systematic bias in R_t(t) caused by a major software update during this period. A shaded (white) area indicates the training (predicted) period for the theoretical fit of our model, drawn as thick lines with the same colours as the empirical rates. (b) Probabilities of spontaneous [p_a(t)] and peer-pressure [p_p(t)] adoption per unit time. (c) Average conditional probability of adoption as a function of the fraction of adopting neighbours n, measured in the original data [p(n), solid circles] and in the shuffled data corresponding to the null model [p_rand(n), open circles]. Inset shows the unbiased difference Δp(n) = p(n) − p_rand(n) (symbols) and a fitted linear function (continuous line). (d) Probabilities of overall termination 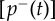, and of spontaneous 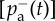and peer-pressure 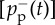termination per unit time. The inset depicts a zoom from time 2T onwards. T, r and c are arbitrary linear scaling constants, with time dimensions for T. Black lines in panels (b,d) are fitted constants.

Table 1.

Data and model quantities, including notation and a brief description of their meaning. Groups correspond to: quantities measured in both the data and model; empirical quantities; parameters used by the model; and parameters estimated from the data.

quantity	description
data/model quantities
Ra(t), Rt(t)	fraction of all users that adopt/terminate the service in a time window
Rn(t) = Ra(t) − Rt(t)	net rate of adoption
empirical quantities
ta, tt	time of adoption/termination of service for a user
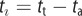
	lifetime of a user account in the service
Δt	time window used to define rates
I	number of Internet users in a country at the end of observation period
Na(t)	number of service users at time t
pa(t), pp(t)	rate of spontaneous/peer-pressure adoption at time t
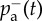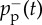
,	rate of spontaneous/peer-pressure termination at time t
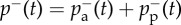
	rate of termination at time t
p(n)	probability that a user adopts, if a fraction n of its neighbours are adopters
prand(n)	value of p(n) after shuffling adoption times
Δp(n) = p(n) − prand(n)	unbiased measure of social influence in adoption
τ	inverse speed of innovation diffusion
model parameters
pa, pp	constant probability of spontaneous/peer-pressure adoption
ps, pr	constant probability of temporary/permanent termination
〈k〉	average degree of network
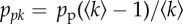
	peer-pressure adoption probability, weighted by degree
estimated parameters
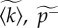
	estimates of average degree and asymptotic rate of termination
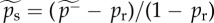
	estimate of temporary termination probability

Opening a user account constitutes a single event in the decision-making process of an individual that is triggered by spontaneous decisions, by the influence of media or by the social environment [5,16]. On the other hand, users may terminate their accounts for several reasons including vanishing demand or dissatisfaction, by switching to another product permanently or by simply abandoning the service with a chance of re-adoption (e.g. due to loss of password or intention for lower monitoring). Some of these processes are observable by investigating the data. An example is shown in figure 1, where the contact network of Switzerland is further decomposed into sub-networks of adopted and terminated users. In the former, some nodes appear disconnected, which indicates individuals that have adopted Skype prior to their friends. This so-called spontaneous adoption, where individual factors and external media play a role, is a typical adoption pattern in the beginning of the process (figure 1b). Alternatively, at the time of adoption many nodes have neighbours who are already existing users, a common pattern for later times (figure 1e). This second scenario of peer-pressure adoption indicates the possible influence of the social environment. By contrast, the termination network consists mostly of single nodes at all times (figure 1c,f), meaning that these users, although they are surrounded by adopters, decide individually to terminate. This observation suggests a negligible effect of social influence on termination.

2.2. Mechanisms of adoption

An analysis of the evolving network structure around a given user can help us to detect whether an ego adopted or terminated the product before any of its neighbours did; or else followed the decisions previously made by a fraction of them. In this way, we can label the performed action as either spontaneous or driven by peer pressure. To define the related measures, we consider the underlying social network as static, meaning that its evolution requires a much larger temporal scale than the adoption process itself. This static structure is defined as the aggregated social network of Skype at the end of the recorded period and provides a lower estimate for the total number of friends of each individual. Moreover, we assume that the maximum size of the static social network is the number I of Internet users in a given country at the end of the observation period [26], and thus define I − N_a(t) as the population that has not yet adopted Skype at time t.

Under these assumptions, the probabilities per unit time that a user adopts either spontaneously or due to peer pressure are defined as

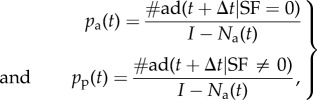2.1

where 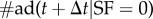[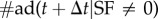] is the number of users who adopt the service in a time window Δt, under the condition that their number of adopting neighbours at time t is SF = 0 (SF ≠ 0). In a similar fashion, the probabilities per unit time that a user terminates the service either spontaneously or due to peer pressure are

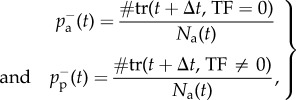2.2

where TF stands for the number of neighbours of a user that have terminated usage up to time t (for a discussion on the restrictions of these empirical quantities, see the electronic supplementary material, §§S2.1–S2.4).

The data show that after an initial, transient period, the rate of spontaneous adoption p_a(t) (figure 2b) and the rate of termination 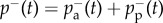(figure 2d) become constant apart from small fluctuations. The same holds separately for the rates of spontaneous 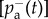and peer-pressure 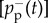termination. The time invariance of these rates is an obvious assumption for most biological epidemics, which, however, has never been empirically shown before in the case of social contagion phenomena, despite its wide use [27,28]. Our results provide the first validation of this quite fundamental assumption used in the conventional modelling of social spreading processes, where probabilities analogous to the ones described here are treated like constants at the outset.

When the ego is not the first adopter among neighbours, the rate p_p(t) of adoption via peer pressure is not constant but increases with time (figure 2b). This is mainly due to social influence arising from the user's social circle. An appropriate way to quantify such effects is to measure the conditional probability p(n) of adoption provided that a fraction n of the ego's neighbours have adopted the product before as

2.3

Here, the numerator counts the number of users with a fraction n of adopter friends at the time of adoption, while the denominator is the number of people with a larger or equal fraction m ≥ n, i.e. all individuals who had the chance to adopt Skype while having a fraction n of adopter neighbours (for further details, see the electronic supplementary material, §S2.3). We observe that the probability p(n) is monotonically increasing (figure 2c), an empirical finding in agreement with the assumptions of several threshold models for epidemic spreading and social dynamics [16,29–31]. However, as we cannot see the entire social network (only the part uncovered by the Skype graph), this probability is biased as n → 1. To estimate such bias, we build a reference null model by shuffling the adoption times of all accounts and measuring the corresponding conditional probability p_rand(n) for this system. The shuffling procedure removes the effect of social influence but conserves the adoption rates and keeps the social structure unchanged. In other words, the reference probability is biased in the same way as the original measurement, but is not driven by social influence as all such correlations have been removed by the shuffling. Consequently, the difference Δp(n) = p(n) − p_rand(n) quantifies the effect of social influence in the adoption process (inset of figure 2c): Δp(n) increases approximately in a linear fashion with the fraction of adopting neighbours. This observation is in agreement with previous studies where a similar scaling of social influence has been recognized through small scale experiments [22], data-driven observations [20] and modelling [29,32].

2.3. The model process

The analogy between epidemic spreading and social contagion has been widely used to model various societal diffusion processes [11,14,33,34]. Here, we take this approach to build a compartmental model based on the identified mechanisms in Skype usage, aimed at a generic description of the large-scale adoption dynamics of technological innovations. We depict individuals as agents in one of three non-overlapping states, susceptible (S), adopter (A) and removed (R), describing people who may adopt the product later, are users already, and will never use it again. In accordance with our observations, the behaviour of an agent can be characterized by four elementary processes. (a) Spontaneous adoption, influenced by individual factors or external media independently of the social network. This is certainly the dominant mechanism for agents with no user neighbours at the time of adoption. (b) Peer-pressure adoption, an intrinsic social effect implemented here by making use of the observed linear scaling of the probability p(n). (c) Temporary termination, describing the case in which agents stop usage with a chance of re-adoption. (d) Permanent termination, when users abandon the service altogether. The flow S → A is regulated by processes (a) and (b), A → S by (c), and A → R by (d). Finally, we assume that the underlying social network evolves with a much longer time scale than the ongoing adoption process, so that its structure may be considered static with fixed size.

For large systems, the modelled adoption process can be well characterized by a rate equation formalism using the heterogeneous mean-field approximation [9,35] (see appendix A). This approach takes agents with identical degree to be statistically equivalent and ignores fluctuations in their dynamical properties. Thus, assuming no degree–degree correlations in the network, the adoption dynamics is reduced to the following system of nonlinear ordinary differential equations:

2.4

2.5

2.6

where s(t), a(t) and r(t) are the average probabilities that an agent is in state S, A or R, respectively, and satisfy the normalization condition s(t) + a(t) + r(t) = 1. The elementary mechanisms (a–d) are parametrized through the constant probabilities of spontaneous (p_a) and peer-pressure (p_p) adoption, and of temporary (p_s) and permanent (p_r) termination (for an overview of all model parameters, see table 1). Under the above conditions, the model does not depend on the degree distribution of the social network, as p_p appears only in the weighted form 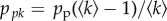, with 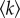the average degree of the network. Moreover, for large 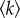, the model becomes independent of this quantity as p_pk ∼ p_p. The system (2.4)–(2.6) finally allows us to write the theoretical rates of adoption and termination as

2.7

and

2.8

that is, the gain and loss terms in equation (2.4) (detailed derivation in the electronic supplementary material, §S3).

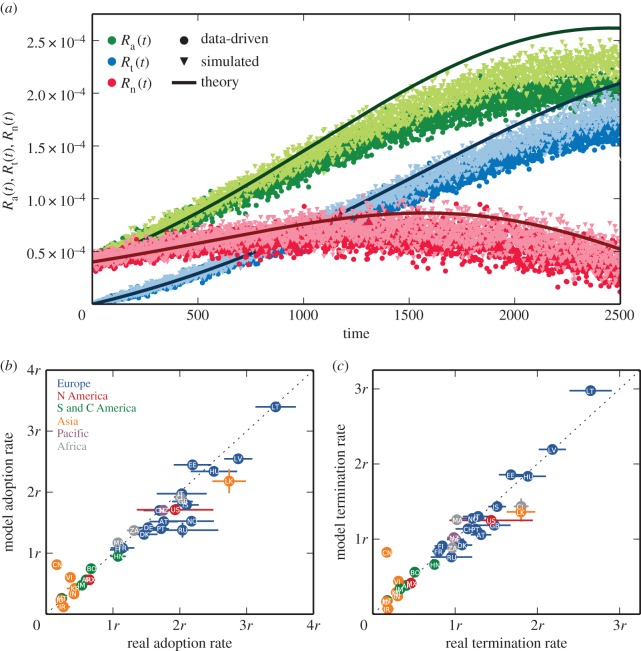
In order to measure the effect of degree–degree correlations on the spreading dynamics, we perform data-driven simulations by evaluating the model process over the integrated Skype network of a country (figure 3a). While this empirical network retains its full topological complexity (in terms of real community structure, assortativity, etc.), we consider a model scale-free network [36] of the same size and average degree as a control case. We then run the model process over the empirical and control networks and compare their corresponding rates of adoption and termination with the mean-field prediction of equations (2.7) and (2.8). As the average degree of the Skype network is not too small, deviations of the simulated rates from the theoretical values are not large, resulting in rates with the same qualitative behaviour. More interestingly, there is only a small discrepancy between the rates of the empirical and control networks. This suggests that topological correlations have a minor slowing-down effect on the spreading dynamics, and thus play a negligible role in the overall rates of the adoption process. Note that a similar independence of the population structure has been observed earlier in controlled experiments of networked public goods games [24] and a spatial Prisoner's Dilemma [37]. These observations validate retrospectively the theoretical considerations mentioned above, where we have assumed the background social network to be uncorrelated.

Figure 3.

Data-driven simulations and validation of model predictions. (a) Rates of the model process over the integrated Skype network of Switzerland (dark symbols) and over an uncorrelated scale-free network (light symbols) with similar size and average degree. Parameter values for the numerical simulations are arbitrarily set to p_a = 0.00004, p_p = 0.0024, p_s = 0.0004 and p_r = 0.0008. Solid lines indicate the theoretical rates calculated from equations (2.7) and (2.8). Similar scaling of the data-driven, simulated and theoretical curves suggests a minor effect of structural correlations. (b,c) Comparison between empirical and theoretical values of the rates of adoption and termination for 34 different countries. Symbols depict rates averaged over the last six months of the observation period, with their corresponding standard deviations as error bars. In-symbol letters are country abbreviations, colours denote continental territories, r is an arbitrary linear scaling constant and the dashed line is a linear function with unit slope.

2.4. Validation and socio-economic correlations

In order to validate our model process, we compare the theoretical rate functions of equations (2.7) and (2.8) with the empirical data by estimating some of the model parameters. An estimate 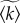for the average degree of the social network can be obtained from the fully aggregated Skype network of a country, if we consider the ego-network of each user with international links included. The estimated rate of termination, 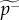, can be measured from the long-time behaviour of the spreading process (figure 2d) and then used to fix p_s to the value 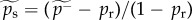, where p_r is a free parameter. While p_a could also be measured directly (by counting adoption events where no user neighbours are present at the time), the observation time of the dataset is not sufficiently long to estimate a constant value 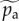in all countries. Therefore, we leave p_a, p_p and p_r as free quantities to be fitted (estimation of p_a for selected countries in the electronic supplementary material, §S4).

Overall, the model dynamics is characterized by 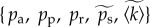, a set of three free parameters and two estimated quantities. The free parameters are used to simultaneously fit the model rates on the binned empirical rates R_a(t), R_t(t) and R_n(t), by means of a bounded nonlinear least-squares method. To ascertain the predictive power of our model, we fit over a 5-year training period and look for predictions in the last 1.5 years (figure 2a). Such prognosis can be quantified by comparing the average rates provided by the model with their corresponding empirical values during the final six months of observation. After repeating the calculations for 34 different countries (with diverse levels of technological development), the related values of the final empirical and modelled rates all collapse close to a line with unit slope (figure 3b,c), thus validating our model for the studied adoption process.

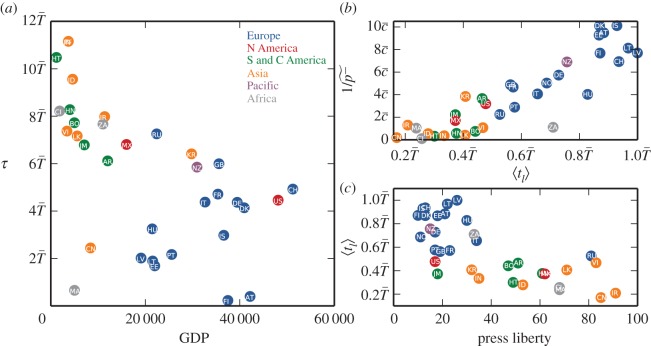
Our model may also be used to disclose relevant differences between the adoption dynamics of countries at various levels of societal and economical development. One characteristic indicator is the inverse speed of innovation diffusion, defined as the time τ when the theoretical R_n(t) is maximal (see the electronic supplementary material, §S3.4). If we relate τ with one of the standard measures of economical development, gross domestic product (GDP) per capita (the GDP dollar estimates used in our study are derived from purchasing power parity calculations using World Bank data, 2011; www.worldbank.org), large differences emerge between countries (figure 4a). Specifically, the larger the GDP of a country, the faster the adoption process is in its society. Another way to characterize the adoption dynamics is through the average account lifetime, 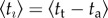, where t_a and t_t are the corresponding registration and termination times. We relate this empirical measure to its theoretical analogue, the inverse probability of termination 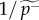obtained from the fitted model process (figure 4b). Their correlation indicates that our model captures this dynamical property correctly. Moreover, the typical duration of user engagement uncovers clusters of countries at different levels of socio-economic development. This can be better understood by linking 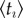with general civil liberty measures [38] (figure 4c). We observe that the weaker the press liberty is in a country, the shorter the time online accounts are used there (other liberty measures in the electronic supplementary material, §S4.3). Such observations indicate a quantifiable dependence between the dynamics of innovation spreading and the socio-economic status of a country.

Figure 4.

Measures of innovation spreading versus socio-economic development in a country. (a) Predicted inverse speed of adoption spreading τ as a function of GDP per capita (the GDP dollar estimates used in our study are derived from purchasing power parity calculations using World Bank data, 2011; www.worldbank.org) for various countries. (b) Theoretical inverse termination probability 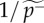as a function of the empirical average account lifetime 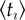. (c) 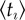as a function of a press liberty measure [38] (large scores imply weak liberties). 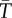and are arbitrary linear scaling constants with time dimensions for .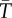

3. Discussion

Our analysis of one of the largest online communication services worldwide aimed at clarifying several long-standing questions about the spreading mechanisms of novel technologies. We have shown that innovation diffusion can be interpreted as a competition between service adoption and termination; a process characterized, after a transition time, by constant rates and by a linearly increasing influence of user neighbours on service adoption. In addition, we have integrated the identified mechanisms into a minimal modelling framework that provides accurate medium-term predictions for the spreading of an online service.

It should be pointed out that this study has some limitations. First, the complete structure of society cannot be mapped by using online interactions only, as observations taken from any online social network underestimate the real number of contact peers of an ego. This incompleteness allows us only to estimate effective degrees and adoption thresholds. Second, the observation of correlated adoption does not necessarily imply the presence of actual social influence, only its possibility; even more so since other mechanisms like homophily cannot be synthesized from this dataset. Despite these limitations, the presented results provide strong evidence of key mechanisms driving the complex contagion of online technologies, up to a level of detail and scale that has not been possible before.

These results may help fill an enduring gap between the theoretical understanding and the empirical observation of social contagion phenomena, validating several earlier studies based on similar assumptions, like constant adoption rates and the effect of social influence. In addition, we have shown how the adoption of novel technologies is related to the societal and economical development of a country. Beyond the clear advantage of these observations for the design of marketing and business plans, they also provide further insight into the differences in the development of modern online societies.

Appendix A. Model description

For a static social network G with degree distribution ρ_k, the probability that individual i becomes a user is 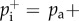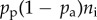with n_i = N_i/k_i. Here, N_i is the number of neighbours of i that have already adopted the product and k_i its degree. Furthermore, the probability that i stops being a user is 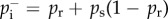. In the thermodynamic limit, we assume that all agents with the same degree are statistically equivalent, allowing us to group individuals and write rate equations for each degree class k. We denote by s_k, a_k and r_k the average probabilities that a randomly chosen agent with degree k is susceptible, adopter and removed, respectively. A first-order moment closure method leads to the rate equation 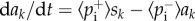. In other words, the average probability that an adopting agent becomes either removed or susceptible is 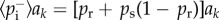, while the average probability that a susceptible individual adopts the product is 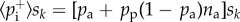with 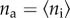. This approximation ignores higher moments of the dynamical quantities s_k, a_k and r_k, as well as any correlations between them. In the presence of degree–degree correlations in G, we have 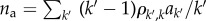, where 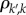is the conditional probability that an edge departing from an agent with degree k arrives at an agent with degree k′. Similar rate equations can be written for s_k and r_k, leading to a system of nonlinear ordinary differential equations that determines adoption at the degree class level (for further details, see the electronic supplementary material, §S3).

Funding statement

G.I. acknowledges the Academy of Finland for funding. J.K. thanks FiDiPro (TEKES) and the DATASIM EU FP7 project for support, and S. Fortunato for discussions. This research was partly funded by Microsoft/Skype Labs.