Cell morphology and focal adhesion location alters internal cell stress

Abstract

Extracellular mechanical cues have been shown to have a profound effect on osteogenic cell behaviour. However, it is not known precisely how these cues alter intracellular mechanics to initiate changes in cell behaviour. In this study, a combination of in vitro culture of MC3T3-E1 cells and finite-element modelling was used to investigate the effects of passive differences in substrate stiffness on intracellular mechanics. Cells on collagen-based substrates were classified based on the presence of cell processes and the dimensions of various cellular features were quantified. Focal adhesion (FA) density was quantified from immunohistochemical staining, while cell and substrate stiffnesses were measured using a live-cell atomic force microscope. Computational models of cell morphologies were developed using an applied contraction of the cell body to simulate active cell contraction. The results showed that FA density is directly related to cell morphology, while the effect of substrate stiffness on internal cell tension was modulated by both cell morphology and FA density, as investigated by varying the number of adhesion sites present in each morphological model. We propose that the cells desire to achieve a homeostatic stress state may play a role in osteogenic cell differentiation in response to extracellular mechanical cues.

1. Introduction

Extracellular mechanical cues, such as differences in passive substrate stiffness, externally applied mechanical strain and fluid-flow induced shear stress, have been shown to affect many aspects of cell behaviour, including migration, proliferation and differentiation [1–5]. The internal machinery of the cell, consisting of tensile (actin) and compressive (microtubule) elements, and FA attachment complexes play an important role in the translation of extracellular forces and alter fundamental cell behaviours, such as viability and migration, through the generation of intracellular stress [6].

Osteogenic cells have a highly developed cytoskeleton and it is known that their differentiation is regulated in part through mechanical forces imposed by their surrounding environment [4,7]. One of the most dramatic examples of osteogenic differentiation is the change in morphology from cuboidal osteoblasts to osteocytes, which display numerous, long, thin cell processes extending from a small, rounded cell body [8]. Various studies have demonstrated the effect of extracellular mechanics on osteogenic differentiation. In particular, it has been shown that osteoblast differentiation of both mesenchymal and embryonic stem cells (MSC and ESC) is controlled by passive differences in extracellular matrix (ECM) stiffness [9,10]. Meanwhile previous work by the authors has investigated the specific effect of substrate stiffness on the later stage of osteogenic differentiation, namely osteoblast to osteocyte development [11]. These results demonstrated that MC3T3-E1 cells will adopt the dendritic morphology of an osteocyte when cultured on soft collagen-based substrates. Changes in cell morphology have recently been shown to affect both intracellular stress [12] and osteoblast differentiation [13]. It is intriguing to speculate that the dramatic change in morphology previously observed under these culture conditions could be related to a change in intracellular stress.

Cell stiffness has been shown to be influenced by both cell morphology, specifically by cell height [14], and substrate stiffness [15]. The stiffness of various cell types has been measured using atomic force microscopy (AFM) [16–18], and it has recently been shown that cell stiffness can indicate osteoblast differentiation of MSCs [19]. It has also been shown that cells of various phenotypes alter their internal stiffness when subjected to external loading in order to achieve a homeostatic stress state [20,21]. Therefore, differences in the stiffness of the cells themselves, when cultured on different substrates, could also play a role in the control of the differentiation process, but this has yet to be examined.

FAs are multicomponent protein complexes that adhere cells to their ECM [22] and facilitate the transfer of external force through the stress fibres of the cell [23,24]. They are known to be specifically involved in the osteogenic differentiation of MSCs [25] and are thought to be of particular importance in osteoblast differentiation on collagen-based substrates [26]. FA formation is also known to be affected by changes in substrate stiffness [7]. However, as of yet, little is known about the interplay between FA formation, cell morphology and intracellular stress and the effect of each on osteogenic differentiation. The effects of these parameters on osteocyte differentiation must be uncovered if a greater understanding of osteocyte mechanobiology is to be achieved.

Finite-element modelling techniques have been widely used to investigate the effect of various stimuli, such as fluid flow [27,28], externally applied strain [29,30] or strain applied directly to individual cells [31,32], on the intracellular loading state. Typically, these models are built using a variety of passive material descriptions, which may be linearly elastic [33,34], hyperelastic [35] or viscoelastic [36,37] in nature. Recently, an active material model was implemented to examine the effects of extracellular mechanics on stress fibre formation [38,39] as well as the force generated by individual FAs in MSCs [40], thus highlighting the importance of the inclusion of realistic FA locations in such models. Other studies have demonstrated the effects of cell morphology [41] and osteocyte process formation [42] on the internal force generation of the cell. Together, these studies demonstrate that realistic cell morphologies are also vital in the creation of finite-element cell models.

In this study, we used a combination of experimental and finite-element techniques to test the hypothesis that a link exists between internal cell stiffness, intracellular stress, FA formation and the morphological alterations of the cells occurring as a result of changes in substrate stiffness. MC3T3-E1 pre-osteoblast cells were cultured at low initial seeding density (10³ cells cm⁻²) on soft collagen-based substrates, previously shown to induce early osteocyte differentiation [11]. Cell morphologies, cell stiffnesses and the location of FA complexes were quantified and used to create finite-element models of cell contraction against passively resistant substrates. FA location, cell morphology and stiffness were varied according to experimental results.

2. Material and methods

2.1. Experimental materials and methods

2.1.1. Collagen substrate preparation

Type 1 rat tail collagen (Life Technologies) was neutralized with NaOH (Sigma Aldrich) at 18.4 µM g⁻¹ collagen and diluted with 10% phosphate-buffered saline (PBS) (all Sigma Aldrich) and 68% distilled H₂O. The mixture was then pipetted in 150 µl volumes onto 13 mm diameter coverslips (Sarstedt) and incubated for 30 min at 37°C, before being rinsed with sterile PBS. This resulted in the formation of a soft, thick, gel-like coating on the coverslips. To produce substrates of different mechanical stiffness but identical ligand density, substrates were cross linked with 1-ethyl-3-[3-dimethylaminopropyl]carbodiimide hydrochloride (EDAC) (Sigma Aldrich) by incubating at 20 µM mg⁻¹ collagen or 100 µM mg⁻¹ collagen EDAC for 3.5 h at room temperature as described previously [11,43]. Substrates were then rinsed with PBS and incubated in fresh PBS for 3 h at room temperature to remove any remaining EDAC before being washed twice with sterile distilled H₂O. Uncoated tissue culture plastic was used as a control.

2.1.2. Cell culture

MC3T3-E1 cells are a murine-derived osteoblast cell line, which display the spread morphology associated with the osteoblast phenotype [44,45]. The cells are capable of differentiating into osteocytes and mineralizing their surrounding matrix [44] and are considered to be a good model of primary osteoblasts [45]. As such they are widely used in the study of osteoblast biology [46–48]. For these studies, MC3T3-E1 cells were maintained in alpha modified Eagle's medium supplemented with 10% fetal bovine serum, 100 U ml⁻¹ penicillin streptomycin and 100 µg ml⁻¹ l-glutamine (all Sigma Aldrich) prior to all experiments. Cells were cultured at an initial seeding density of 10³ cells cm⁻². These culture conditions have been previously shown to allow for a change in cell morphology from the spread cuboidal shape of osteoblasts to the osteocyte morphology, characterized by numerous long cell processes extending from a small rounded cell body [11].

2.1.3. Stiffness measurements

Cell and substrate stiffness measurements were taken after 4 days of culture, using a JPK Cellhesion 200 atomic force microscope (JPK Instruments, Berlin, Germany). Young's modulus of each substrate was measured in the vicinity (within 20 µm) of the cell. Following this, Young's moduli of five spread and five dendritic cells were measured on each substrate. All cells were measured at both the proximal and distal regions of the cell cytoplasm, while five measurements were conducted per location. A square-based silicon-nitride pyramidal tip with tip radius of 5 nm and edge angle of 35° was used for all measurements, with Young's modulus (E) of both the cells and substrates being related to the force generated by the AFM system through equations (2.1) and (2.2), where F is the force generated, z is the piezo movement, k is the spring constant of the cantilever, δ is the sample penetration and α is the edge angle of the AFM tip.

2.1

and

2.2

To ensure that the cell measurement is not significantly influenced by the stiffness of the underlying material, tip indentation should be less than 10% of the total cell depth [49,50]. To verify that this was the case for these experiments, the height of each cell was measured by approaching the surface both at the point of interest and the substrate directly adjacent to the cell and recording the absolute height values. Force–distance curves were then only analysed up to a maximum of 10% indentation.

2.1.4. Cell staining for focal adhesions and actin cytoskeleton

Cultures were fixed after 7 days of culture using 4% paraformaldehyde (Fluka) in piperazine-N,N′-bis[2-ethanesulfonic acid] (PIPES) buffer (Sigma Aldrich). Cells were permeabilized with Triton-X100 (Sigma Aldrich), diluted to 0.05% in PBS, before being treated with primary mouse anti-vinculin (V9131, Sigma Aldrich) and secondary goat anti-mouse (Alexa fluor 488, Life Technologies). Cells were then counterstained with tetramethylrhodamine (TRITC) labelled rhodamine-phalloidin (Life Technologies) to identify the actin cytoskeleton and mounted in 4′,6-diamidino-2-phenylindole (Vector Labs) containing hard set mounting media for imaging.

2.1.5. Morphological analysis of cell phenotype

Images were taken using a Zeiss LSM 510 Axiovert inverted confocal microscope at different locations on the coverslips at 10× magnification. Cell processes were defined as cellular features composed of actin, located at the cell membrane, which extended for a distance of at least 5 µm from the cell body. Cells with cell processes were classified as ‘dendritic’, while cells without any cell processes were classified as ‘spread’. Example morphologies are shown in figure 1. The number of processes on each dendritic cell, the longest and shortest axes of each spread cell as well as the cell body diameter and length of each process on each dendritic cell were measured. All parameters were measured for a minimum of 10 cells on each substrate and the average values were calculated for each parameter on each substrate.

Figure 1.

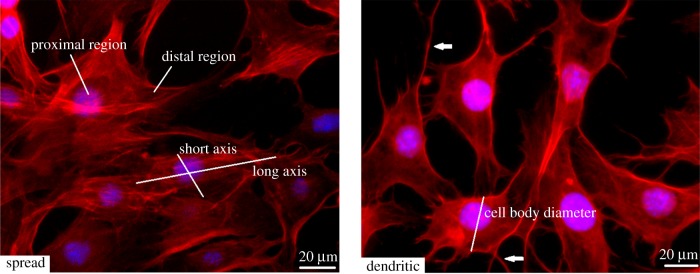
Cell morphological examples. Spread cell example is of cells cultured on the stiffest substrate (10 kPa). Dendritic cell example is of cells cultured on the softest substrate (0.6 kPa). Short and long axes in spread cell morphology and cell body diameter in dendritic cell morphology are labelled. White arrows indicate cell processes.

2.1.6. Focal adhesion location

FAs, as identified through vinculin staining, were imaged using a Zeiss LSM 510 Axiovert inverted confocal microscope (figure 2). Cells of each morphology were divided into regions and the number of FAs in each region was quantified for each cell morphology, with a FA defined as an area of vinculin staining of over 1 µm² in area. The cellular regions, as shown in figure 2, were as follows: (i) nucleus—the region of the cell directly under the cell nucleus, (ii) distal end—the cell border perpendicular to the direction of principle actin alignment (spread cells only) or the end of the cell process (dendritic cells only), (iii) edge—the cell border parallel to the direction of principle actin alignment (spread cells only) or the cell border excluding the cell process (dendritic cells only), (iv) process—the cell process excluding the most distal 1 µm (dendritic cells only) and (v) cell body—the remainder of the cell body. Measurement of FA density and location was conducted for at least 10 cells of each morphology on each of the three substrates.

Figure 2.

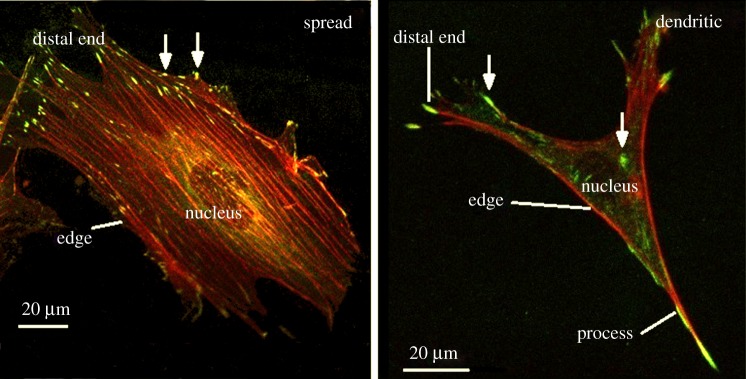
FA location on each cell morphology. Cellular regions labelled; nucleus, edge, distal end and process are labelled. White arrows indicate FA complexes as identified through vinculin staining.

2.1.7. Statistical analysis

A one-way ANOVA was performed on substrate stiffness measurements and on cell stiffness measurements to compare cells to one another. A paired t-test was conducted to compare the stiffness of the proximal and distal regions of the cell, whereas a one-way ANOVA was used to determine statistical difference between average cell measurements, as described in §2.1.5, on each substrate.

2.2. Methods: computational

2.2.1. Model development

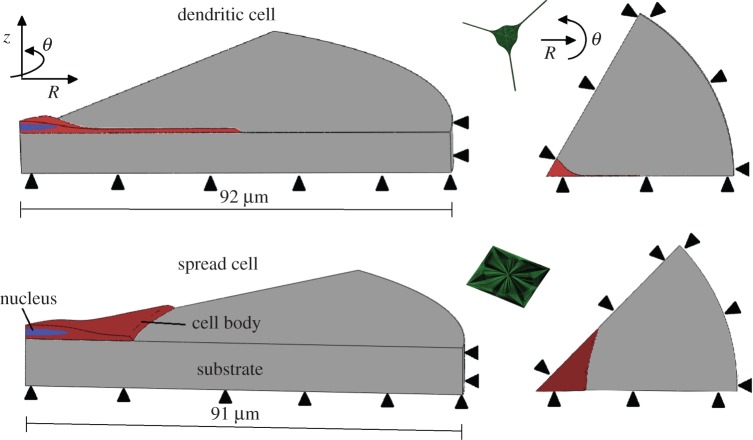
Representative models of spread and dendritic cell morphologies were created from the cell measurements shown in table 1. The substrates had an outer edge 50 µm from the most distal point of the cell, with a depth of 10 µm below the cell bottom (figure 3). Preliminary studies showed that edge effects were sufficiently small using these dimensions. Rounded edges were included wherever feasible to minimize the effect of stress concentrations due to geometry. Symmetrical domains were chosen so that a one-sixth (dendritic) or one-eighth (spread) section of the full domain needed to be simulated, thus improving computational efficiency.

Table 1.

Cell measurements for spread and dendritic cell morphologies. (Number in brackets indicates the number of cells measured.) All units of length are in μm.±indicates 1 s.d.

	spread [32]	dendritic [39]
nucleus diameter	18.3 ± 2	18.3 ± 1.1
long axis cell body	82 ± 15.8	n.a.
short axis cell body	45.2 ± 13.6	n.a.
cell diameter	n.a.	20.8 ± 2.1
no. processes	n.a.	3.2 ± 1.4
process length	n.a.	31.6 ± 15.1

Figure 3.

Isometric and plan views of spread and dendritic cell geometries, showing axial, radial and symmetrical boundary conditions (black arrows) present on substrate and cell body. Full cell models of each cell geometry are also included (green models).

Two cell models, representing spread or dendritic cell morphologies, were created using ABAQUS software (Dassault Systems) according to the average measured parameters from the experiments described above and summarized in table 1. Both models included a discrete nucleus exhibiting the same elastic material properties as the remainder of the cell body, with no contraction of the nucleus occurring. The highly developed cytoskeleton of osteogenic cells allowed for the cytoplasm and cytoskeleton to be modelled as an isotropic linearly elastic continuum, with elastic moduli of cells assigned based on cell stiffness measurements outlined in §2.1.3 and shown in table 2. The Poisson's ratio of all cells was set as 0.38, with previous measurements for the Poisson's ratio of eukaryotic cells being between 0.37 and 0.38 [37,51].

Table 2.

Young's moduli of substrates after 4 days of culture, as well as Young's moduli of spread and dendritic cells on each substrate at the same timepoint, as measured through AFM procedure described in §2.1.3. Asterisks (*, ** and ***) indicate statistical difference between values (p < 0.05) and±indicates 1 s.d.

	soft (kPa)	intermediate (kPa)	stiff (kPa)
substrate stiffness	0.6 ± 0.4*	1.8 ± 0.6*	10 ± 0.7*
spread cell stiffness	7 ± 8.5**	13 ± 12.1	18 ± 9.6**
dendritic cell stiffness	8 ± 8.2***	12 ± 8.2	24 ± 10.7***

The cells were attached to the substrate by three different methods. The first method involved the application of tie constraints along the entire cell substrate interface (entire FA). In the second method, a single individual FA site, measuring 1 µm² in area, was assigned per model (single FA). A high-density mesh was used at this site and at the corresponding substrate site to attach the cell to the substrate. Finally, FA complexes were assigned to the cell (realistic FA), according to the experimental results described below (table 3). Rigid no-slip boundary conditions were assigned along FA regions (u = 0, with u denoting nodal displacement), while nodes along the untied cell–substrate interface were assigned a rigid free-slip boundary condition (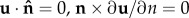). Approximately 150 000 (dendritic model) or 300 000 (spread model) quadratic tetrahedral C3D10R elements were used, with elements ranging in size from 16 000 nm³ at the FA sites to 10 µm³ at the outermost edge of the substrate were used for all models. Mesh convergence data were generated to verify the number of elements used.

Table 3.

FA location per cell region. Cell regions are described in §2.1.6 and shown in figure 2.±indicates 1 s.d.

cell type	nucleus	distal end	edge	body	process
spread [32]	4.1 ± 1.4	12.2 ± 6.8	7.3 ± 6.1	17.4 ± 15.1	n.a.
dendritic [19]	4.4 ± 2.7	3.5 ± 1.2	1.8 ± 1.3	2.5 ± 1.6	6.0 ± 3.4

2.2.2. Material behaviour

The cell body, nucleus and substrates in this study were modelled as linear isotropic Cauchy-elastic materials (material behaviour shown in equation). Young's moduli of the cell body and nuclei of spread and dendritic cells on the different substrates as well as those of the substrates themselves were assigned according to the stiffness measurements shown in table 2. Orthotropic expansion properties were assigned to the cell body, with a negative expansion load used to simulate the active contraction of the cell in the direction of principal actin fibre alignment. The expansion/contraction behaviour of the cell body is shown in equation (2.3), where ε contains contributions from both the displacement field and the applied material contraction as defined by equations (2.4) and (2.5).

2.3

where I is the identity tensor and Tr( ) denotes the trace. ɛ′ denotes the strain tensor, which is contains contributions from the displacement field u and the contraction term.

2.4

and

2.5

where T and λ_t indicate the applied contraction load and the material contraction coefficient, respectively.

2.2.3. Boundary conditions and loading

Symmetry conditions were assigned to each boundary surface lying in the z–R plane (i.e. the symmetric boundaries in each model), such that (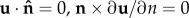) (where  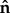is the unit vector normal to the boundary surface and ∂/∂n represents the derivative normal to the surface and [·] represents the change in a quantity across the interface. Meanwhile, similar conditions u = 0 were applied to prevent movement of the distal and bottom surfaces of the substrate, so as to simulate an infinitely stiff well plate/Petri dish (relative to the stiffness of the substrate), as shown in figure 3. The top surfaces of the substrate and cell body were described by a stress-free boundary (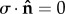). A continuous mesh between nucleus and cell body regions implied stress and displacement continuity between the two regions ([u] = 0, 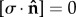). An orthotropic contraction was applied to the cell body in the direction of principal actin alignment (radial, as indicated with R in figure 3). A volumetric expansion coefficient of 0.05 K⁻¹ (listed in the Abaqus software as a thermal expansion coefficient) acting in the radial direction was used in conjunction with a negative expansion load of 1 K, similar to previous techniques used to simulate active cell contraction [29]. The radial stress generated in the cell body (σ_R) was measured and compared across the different cell models. Average radial stress for each model, termed 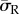was computed by averaging the stress in each element when normalized to element volume, as defined in equation (2.6).

2.6

where V is the total volume of the cell body, k is the element number, V_k is the volume of element k in the finite-element mesh, n is the total number of elements and σ_R is the radial stress in the element k ().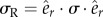

3. Results

3.1. Cell geometry

As shown in table 1, spread cells were found to have a larger area with an average long axis of 82 µm and an average short axis of 45 µm, compared with dendritic cells, which had an average diameter of 22 µm, excluding processes. Dendritic cells were also found to have an average of 3.7 processes per cell with an average process length of 31.6 µm (table 1). The nucleus diameter of the cells ranged from 17.8 to 19.1 µm but no statistical difference in nucleus size existed between the three morphologies. No statistical difference due to substrate stiffness existed in the parameters of the various cell morphologies. These results were used to generate the geometries for the finite-element models, as described in §2.2.

3.2. Focal adhesion location

It was observed that spread cells contained a statistically higher number of FA complexes than dendritic cells (p < 0.05, table 3), with an average of 41 compared to 18. The majority of FAs on spread cells were located in the centre of the cell, whereas on dendritic cells more adhesion sites were observed in the cell processes than anywhere else on the cell. It was also observed that a single FA was located on the distal end of all cell processes. FA density per cell was significantly higher on the stiffest (10 kPa) substrate (p < 0.05), as shown in table 4. However, comparison between cells of the same morphology revealed no significant difference in FA density in cells of the same morphology on substrates of different stiffness.

Table 4.

FAs per cell and percentage of cells containing processes on each substrate. * and ** indicate statistical difference in FA density between different substrates and±indicates 1 s.d.

substrate	soft	intermediate	stiff
FA per cell	29.9 ± 5.0*	35.1 ± 6.4**	48.2 ± 7.3*,**
percentage process-containing cells	67.0 ± 15.2*	75.1 ± 5.8**	37.2 ± 4.4*,**

3.3. Substrate and cell stiffness (experimental)

Young's moduli of the substrates were measured as 0.6, 1.8 and 10 kPa respectively, as shown in table 2, with all substrates being statistically different to one another. The stiffness of both spread and dendritic cells increased as the substrate stiffness was increased. On substrates of 0.6 kPa, spread and dendritic cells measured 7 and 6 kPa, respectively, while on substrates of 1.8 kPa, this increased to 13 and 12 kPa, respectively. As the substrate was further increased to 10 kPa, the stiffness of the cells increased to 18 (spread) and 24 kPa (dendritic), respectively. The stiffness of both cell morphologies measured on the 10 kPa substrate were found to be significantly (p < 0.05) higher than that measured on the 0.6 kPa substrate, but not that measured on the 1.8 kPa substrate. No statistical difference was observed between the proximal and distal stiffness measurements from either cell type, or between the stiffnesses of different cell morphologies on the same substrates.

3.4. Intracellular stress (computational model results)

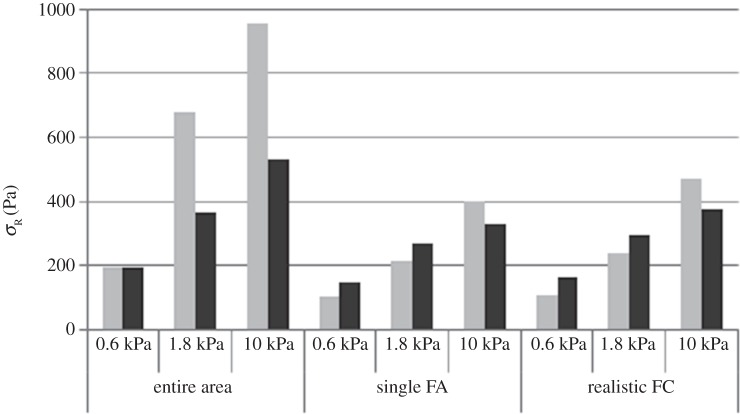
On all substrates, it was observed that high levels of average radial stress (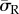) were generated in both morphologies when cells were attached to the substrate through the entire cell–substrate interface. The lowest average radial stress (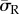) levels were generated when cells were attached through a single FA site per model. For example, as shown in figure 4, the average radial stress (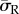) generated in a spread cell on a substrate of 0.6 kPa was 190 Pa when the cell was attached through the entire cell–substrate interface. This reduced to 110 Pa when the cell was attached through realistic FA locations and decreased further to 100 Pa when the cell was attached through a single adhesion site.

Figure 4.

Average radial stress in spread (light grey bars) and dendritic (dark grey bars) cell models. Results shown for cell attached through; entire cell–substrate interface, a single FA attachment site per model and realistic FA locations. Average stress was calculated by normalizing element stress to element volume.

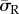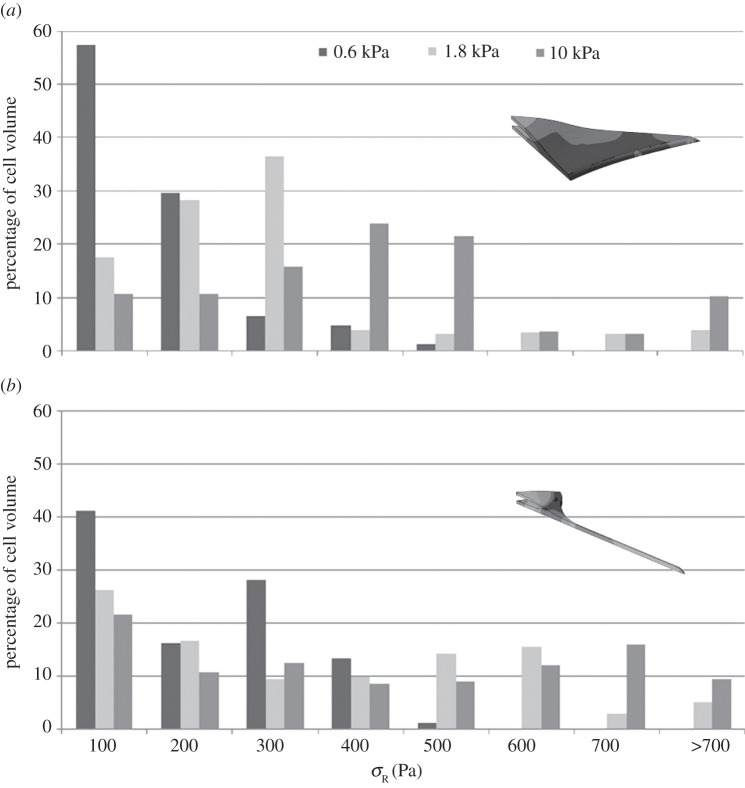
It was observed that substrate stiffness had less effect on intracellular stress for the dendritic cell morphologies compared to spread cells, when cells were attached through realistic FA locations. This can be seen in figure 4, where the average radial stress () in the dendritic cell increases from 160 Pa on the softest (0.6 kPa) substrate to 370 Pa on the stiffest (10 kPa) substrate, while the average radial stress (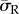) generated in the spread cell morphology increases from 110 to 470 Pa over the same two substrates. Figure 5 represents the percentage of cell volume experiencing each radial stress (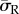) band and further demonstrates that substrate stiffness has less influence over the stress experienced by dendritic cells.

Figure 5.

Percentage of (a) spread cell morphology and (b) dendritic cell morphology finite-element models under various radial stress level when attached to substrate through realistic FA locations.

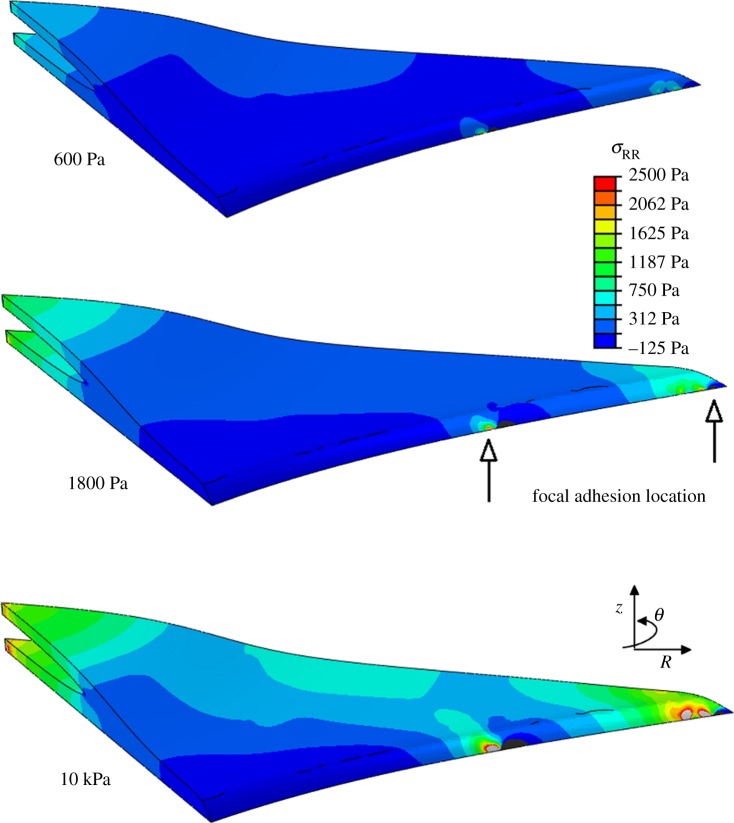
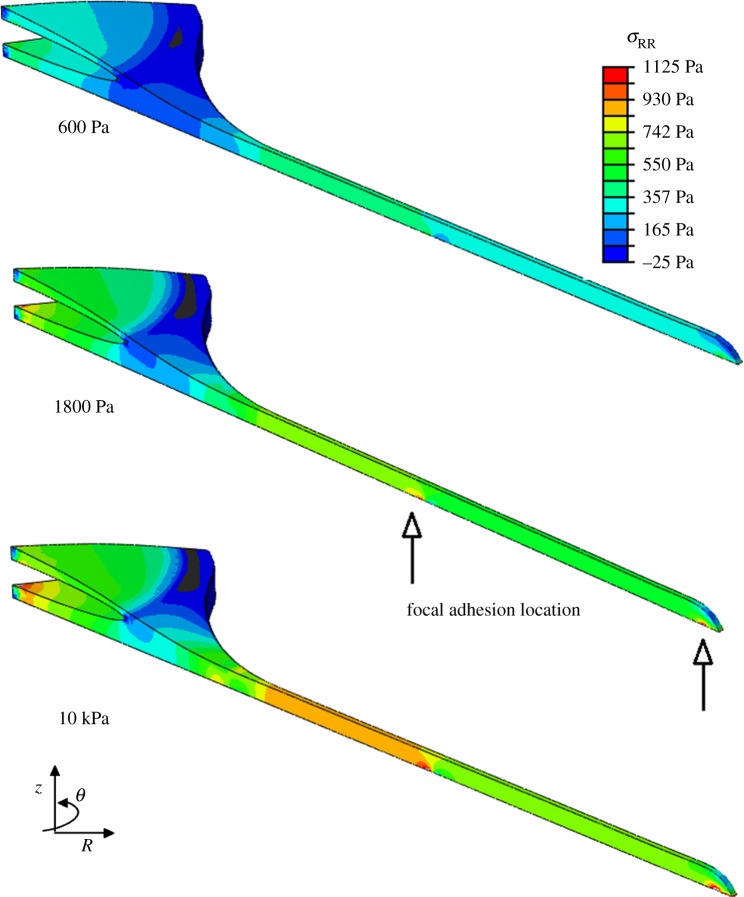
It was observed that the highest levels of intracellular stress are generated in the immediate vicinity of the FA attachment complexes. Moreover, a higher level of stress is generated in the process of the dendritic cell morphology compared with the remainder of the cell body, as shown in figures 6 and 7.

Figure 6.

Radial stress generated in the direction of principal fibre alignment in spread cell morphology, when the cell is attached to the substrate through realistic FA locations. The location of two FAs is indicated on the 1.8 kPa model to demonstrate the stress concentration in the region surrounding the adhesion site. (Online version in colour.)

Figure 7.

Radial stress generated in the direction of principal fibre alignment in spread cell morphology, when the cell is attached to the substrate through realistic FA locations. The location of two FAs is indicated on the 1.8 kPa model to demonstrate the stress concentration in the region surrounding the adhesion site. (Online version in colour.)

4. Discussion

These results show for the first time that cell stiffness, morphology, FA density and location, and substrate stiffness all have an important role to play in dictating intracellular stress. It is interesting to note that the method of cell attachment (FA complexes) strongly influenced the intracellular stress generated through cell contraction, with a larger adhesion area resulting in higher internal cell stress. This finding highlights the importance of the inclusion of realistic FA locations in computational models of cells. When realistic FA complexes were included, it is shown that substrate stiffness had a greater effect on the stress profile of the spread cell morphology than that of the dendritic cell morphology. Most interestingly, it was noted that the dendritic morphology experiences a higher average radial stress (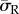) than the spread morphology on the two softest substrates. We propose that when cultured on softer substrates, MC3T3s might alter their morphology, to that of a dendritic cell, and internal stiffness in order to achieve a more desirable stress state.

A possible limitation in this work is the use of a linearly elastic continuum to model a complex viscoelastic structure, capable of active remodelling. Other studies have used more complex modelling techniques to include nonlinear elasticity [32,52] as well as discrete [27] or active cytoskeletal components [39]. However, the small strains generated by cell contraction in these models (less than 5%) minimize the need to incorporate active cell remodelling as strains of 15% have previously been shown to be required for widespread actin reorganization to occur [53]. Further to this, as the cytoskeleton becomes more developed (due to most of the cell body of osteogenic cells being composed of actin), the dissimilarity between a continuum model and the inclusion of a discrete cytoskeleton decreases. Meanwhile, the consequences of directionality in the transfer of force through the actin framework were accounted for by the inclusion of an orthotropic contraction within the models in the direction of principal actin fibre alignment. This allowed for the effects of cell morphology, substrate stiffness and FA location on intracellular stress to be investigated without excessive computational expense. A further limitation is in the use of the 10% indentation depth criterion, whereby indentation of a sample must not extend further than 10% of the sample depth so as not to be significantly influenced by the stiffness of the underlying material [49,50]. It should be noted that the experiments behind this criterion investigated samples which were significantly softer than their underlying substrate and that it cannot be said with certainty that the results reported were not influenced by the relatively low stiffness of the underlying substrate. However, the reported values of cellular stiffness are within the range of previously reported data [17,54–56], while previous work has confirmed that cells alter their stiffness as a result of changes in the stiffness of their underlying substrate [57,58].

Cell morphology is a widely used indicator of the differentiation stage of osteogenic cells [59,60], and MC3T3-E1 cells have previously been shown to alter their morphology in response to the same changes in the extracellular mechanical environment as induced here [11]. The dimensions of the dendritic cells measured in this study were similar to those reported for osteocytes in vivo [61], as was the average cell process length [62]. However, the number of processes present was fewer than either osteocytes in vivo [62] or isolated primary osteocytes cultured on two-dimensional substrates [63]. Nucleus shape and dimensions have also been shown to vary when cells are subjected to mechanical force [64], while control of nuclear shape has been shown to induce osteocalcin expression in isolated pre-osteoblasts [65]. Interestingly, no significant effect of substrate stiffness on the dimensions or FA formation of spread or dendritic cells was observed in this study, which is in contrast to previous studies which have established a correlation between substrate stiffness, cell area and FA formation [54,58,66,67]. However, this current study reveals that this difference is manifested as a significant change in the percentage of cells which adopt a spread or dendritic morphology; that is to say that spread cells exhibit a larger cell area as well as a greater number of FAs per cell than dendritic cells, so an increase in the percentage of spread cells (as observed on stiffer substrates) will cause an increase in the average cell area and number of FAs per cell.

FA complexes are known to play a key role in force transfer and cell mechanosensation [68–70], while the density of attachment complexes in MC3T3-E1 cells has been shown to be affected by changes in substrate stiffness [7]. Finite-element simulations have shown that cell-generated force depends strongly on both cell morphology [71] and FA area [40]. Despite this, a common assumption regarding force transfer between a cell and its underlying substrate used in finite-element simulations is the generation of tie constraints across the entire cell–substrate interface [34,72], while other studies have used single, arbitrarily assigned attachment sites [73,74] or attachment sites predicted through the internal tension profile of the cell [40]. The results presented here show that these approximations greatly alter both the magnitude and distribution of stress throughout the cell body, meaning that in order to accurately model cell–substrate interaction and interpret the findings of cell mechanics and mechanobiology experiments, realistic FA densities and locations must be included.

Intracellular stress has previously been shown to affect the osteogenic differentiation of MSCs [12]. Briefly, cell tension was reduced through Rho kinase (ROCK) inhibition of myosin activation by culture in Y-27632-containing media. It was found that this reduction in cell tension induced adipogenic rather than osteogenic differentiation, as measured by expression of liposome lipase (adipogenic) as well as ALP and CBFα1 (osteogenic). However, the interdependence between cell morphology and intracellular stress cannot be ignored as it has been shown that the disruption of the cytoskeleton through ROCK inhibition will prevent the formation of cell processes in MC3T3-E1 cells cultured on collagen substrates [75]. Cell morphology has also been shown to affect cell-generated stress, with bovine pulmonary smooth muscle cells and 3T3 mouse fibroblasts both shown to induce higher forces on micropost substrates when allowed to expand to a larger cell area [76]. The results presented here demonstrate the clear link between cell morphology and the stress generated during active cell contraction, whereby it was seen that the stress generated in process-containing (dendritic) cells was less influenced by the stiffness of the ECM.

It is intriguing to speculate that the osteoblastic cell adopts a dendritic morphology in order to achieve a more suitable stress state, and moreover that achieving this stress state is a crucial driver of osteocyte differentiation. Indeed, homeostasis of the intracellular stress has been widely cited as a cellular response to loading in various cell types [77–79]. Studies have shown that fibroblasts subjected to external loading alter their stress fibre formation in order to maintain a constant internal stiffness [20,21], while the concept of tissue-level homeostasis, or a set strain level, in bone has also been widely accepted [80–83]. Our study provides a new insight into the interplay between cell morphology and tension. We propose that, when cultured on a soft substrate (less than 2 kPa), the osteoblast cell experiences low stresses and in response actively changes its morphology in order to achieve a more suitable stress state. Moreover, we propose that this extracellular mechanical environment is similar in nature to osteoid, the tissue in which osteoblasts embed themselves before they differentiate into osteocytes, which thereby acts as a driver of osteocyte differentiation. It must be noted that changes in cell morphology are driven by cytoskeletal re-organization [84,85], with the cytoskeleton itself being another method of controlling intracellular stress [12,86]. With this in mind, the effects of cell morphology and cytoskeletal organization cannot be considered as independent drivers of cell differentiation, but work in concert to regulate differentiation through control of intracellular stress.

While it is clear that cell morphology and tension are key drivers of cell differentiation, the mechanisms behind the process are still poorly understood. Many enzymes and proteins are involved in the cellular differentiation process, and some have already been identified as also being affected by cell tension. In particular RhoA, a known regulator of cytoskeletal mechanics [87,88], has been shown to be affected by cell morphology in MSCs and in so doing affects the morphology and differentiation pathway of the cells [12]. As well as this, RhoA, along with another member of the GTPase family Rac1, have been shown to specifically affect process formation in neurites [89]. It is possible that a similar RhoA-based mechanism is used by osteogenic and neurogenic cells to regulate and maintain cellular processes, and that the continued activity of these molecules is regulated through intracellular stress [12,19]. This study provides an insight into the interplay between cell morphology and tension, specifically in relation to the development of cell processes, a vital feature of osteocyte differentiation.

5. Conclusion

The results presented here show that intracellular stress is affected by substrate stiffness and that this effect is mediated through FA complexes, the location and density of which influence the effect of substrate stiffness. We also show that both the levels and distribution profile of intracellular stress are directly affected by cell morphology and stiffness. Specifically, we observe that the stress profile of cells that adopt a dendritic morphology, similar to that of an osteocyte, are less sensitive to changes in substrate stiffness. It is therefore hypothesized that by changing their morphology, these cells can obtain a more desirable stress state on soft collagen-based substrates and that this extracellular mechanical environment is an essential cue in the differentiation process of osteoblasts to osteocytes.

Funding statement

The authors acknowledge funding from the European Research Council (ERC), grant no. 258992 (BONEMECHBIO, as well as from the European Commission—REBORNE (Regenerating BOne defects using New biomedical Engineering approaches) (HEALTH-2009–1.4.2–241879) and the NUI Galway College of Engineering and Informatics Research Fellowship.