Finite-element modelling reveals force modulation of jaw adductors in stag beetles

Abstract

Male stag beetles carry large and heavy mandibles that arose through sexual selection over mating rights. Although the mandibles of Cyclommatus metallifer males are used in pugnacious fights, they are surprisingly slender. Our bite force measurements show a muscle force reduction of 18% for tip biting when compared with bites with the teeth located halfway along the mandibles. This suggests a behavioural adaptation to prevent failure. We confirmed this by constructing finite-element (FE) models that mimic both natural bite situations as well as the hypothetical situation of tip biting without muscle force modulation. These models, based on micro-CT images, investigate the material stresses in the mandibles for different combinations of bite location and muscle force. Young's modulus of the cuticle was experimentally determined to be 5.1 GPa with the double indentation method, and the model was validated by digital image correlation on living beetles. FE analysis proves to be a valuable tool in the investigation of the trade-offs of (animal) weapon morphology and usage. Furthermore, the demonstrated bite force modulation in male stag beetles suggests the presence of mechanosensors inside the armature.

1. Introduction

Male individuals compete for mating opportunities in many species. Some convince females of their qualities with their (extremely) long tail (e.g. long-tailed widowbirds [1]) or brightly coloured plumage (e.g. blue tits and peacocks [2,3]). In other species, males try to impress their competitors in order to avoid a physical fight (e.g. calling in natterjack toads and ritualized fights in chameleons and stalk-eyed flies [4–6]). In those taxa where males engage in actual physical fights, they have often developed weapons by sexual selection. These weapons have emerged in a wide diversity of shapes for different fighting strategies (for a review, see [7]) and can attain impressive sizes. Male stag beetles, with their large mandibles that can become as long as their own body [8], are a paradigm for this. In spectacular fights, males grab their opponent with these mandibles, to lift and finally to hurl it backwards onto its back [9,10].

Most probably, the morphology of these weapons has to be a compromise, because different functions may impose different constraints. Male stag beetle mandibles should be lightweight, to enable efficient walking and flying [7,11]; their shape may have to be aerodynamically favourable [7,12]; and for the fights themselves, the mandibles should not only provide grip, transfer pinching forces and reach towards opponents, but they must also be strong enough to withstand the forces acting upon them. That these conditions pose conflicting demands on the weapon morphology has also been observed in other taxa. In several bovid and cervid species, the dimensions of the base of the horns and antlers are adjusted to body weight and fighting strategy: heavier animals and species with forceful wrestling have wider horns in order to maintain the same maximal stress at a minimal costs in terms of material and weight [13]. In a physiological context, heat loss in cold winters constrains the horn size of bovids in temperate climates [14].

Male Cyclommatus metallifer stag beetles have long and slender mandibles, which are therefore probably prone to mechanical failure. However, they do not exclusively use the more robust base of their mandibles in fights, instead they change their bite point position as a function of the fight situation.

To investigate the potential presence of trade-offs that shaped the weapon morphology, one should be able to link the morphological, behavioural and mechanical features of the weapons. Finite-element (FE) modelling provides a popular technique to relate (behaviourly imposed) forces on structures to deformations and material stresses thereof. A modelling approach is necessary, as experimental stress measurements are impossible, and strain measurements have limitations. Strain gauges can only measure strains on a limited number of locations, and the instrumentation may influence the results. Optical full-field methods (e.g. digital speckle pattern interferometry and digital image correlation (DIC)) overcome these drawbacks, but still the strains inside the material cannot be assessed [15]. FE modelling provides a method to approximate the strains and stresses in silico. In FE modelling, the results are obtained numerically, which makes it particularly suitable when analytical methods are either impossible or tedious (for a review, see [16]). FE analysis has proved to be an excellent technique to clarify shape–function relationships in animal models. For example, it was used by van der Meijden et al. [17] for scorpion chelae, who showed that slenderly shaped chelae are less effective weapons. FE analysis also proved relationships between morphology on the one hand and chewing system (in rodents, [18]) or food type (in Darwin finches, [19,20]) on the other hand. The range of mechanical properties of food items that are accessible with the jaws of Priacma beetles was also investigated by FE analysis [21], with the ultimate goal to understand the feeding behaviour and habitat of extinct ancestors.

In this paper, we develop and validate an FE model for C. metallifer stag beetle weaponry. The model development combines the three-dimensional structure of micro-CT scans with input forces from in vivo observations and material properties from experiments. The model outcomes are validated with bending experiments.

Once a validated model of the stag beetle weaponry is available, it can be used to mimic natural fighting situations. Moreover, it is also possible to simulate the effects of loadings that do not naturally occur in stag beetle fights. We will perform both types of simulations to explore how stag beetles adjust their muscle force when biting at different bite points along their mandibles. We hypothesize that they will reduce their muscle force when biting at the tip of their slender mandibles, so as to limit the mechanical stress in the cuticle.

2. Material and methods

2.1. Development of the finite-element model

2.1.1. Brief overview of the model construction

We developed the FE model of a stag beetle mandible using the FEBio software suite (FEBio 1.4.1, [22]). The three-dimensional model was obtained by micro-CT scanning, and converted into a mesh consisting of small tetrahedral elements. Boundary conditions were applied to specific parts of the model (groups of elements) to mimic the conditions during bites in fights: a muscle force was imposed on the muscle attachment region on the mandible, and the model was allowed to rotate about the joint axis. To simulate the resistance that the mandibles experience during bites, the movement of the bite point region was constrained. Using the material properties of the structure, FE algorithms calculated the deformations of all elements. Finally, material stress and strain were derived.

2.1.2. Micro-CT scanning

Adult C. metallifer stag beetles were obtained from a commercial dealer (Kingdom of Beetle, Taiwan). They were individually housed in plastic containers (length 39 × width 28 × height 14 cm), at a temperature of between 20°C and 25°C. They were fed beetle jelly and water ad libitum. After sacrification, the heads were fixed in Bouin's solution for two weeks (Sigma-Aldrich, St Louis, MO, USA). Then, they were preserved in 100% ethanol (via steps of 70, 80, 90 and 96% ethanol). Finally, because of the low X-ray absorption of the soft tissue inside the head, the contrast was enhanced with heavy chemical elements. For this purpose, the heads were submerged in a 1% iodine solution for 20 days (I₂ dissolved in 100% ethanol; Sigma-Aldrich; adapted from [23]), and washed and stored in 100% ethanol.

Micro-CT scanning was performed with a Skyscan 1172 high-resolution CT scanner (Bruker microCT, Kontich, Belgium). The specimen was scanned in air. The X-ray source was operated at 70 kV and 141 µA. Over a range of 180°, five shadow images were taken every 0.2°, with an exposure time of 440 ms. These five replications were averaged, to reduce noise. The scanning time was 6.42 h. The shadow images were back projected which resulted in 9455 reconstructed images of 4000 × 4000 pixels, with a voxel size of 4.1 µm (figure 1a). For further processing, this was downsized to 8.2 µm in order to facilitate manipulations.

Figure 1.

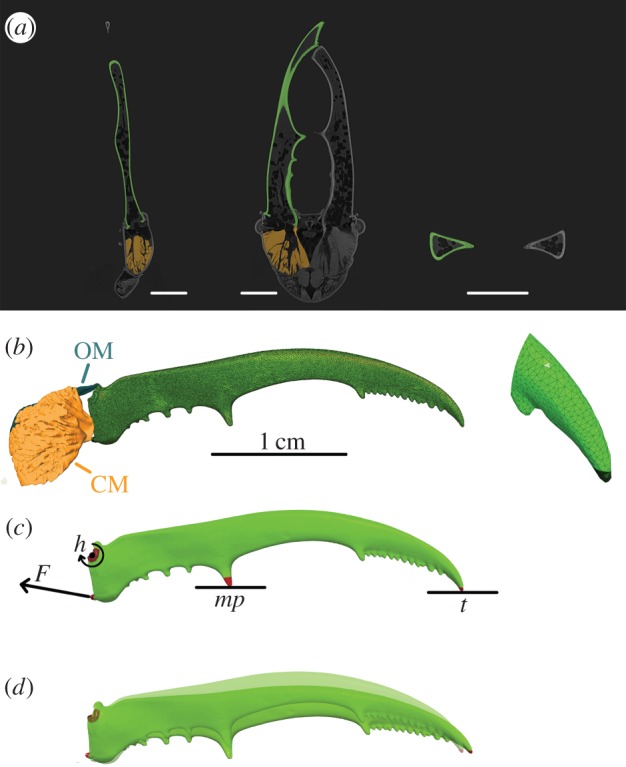
Illustration of the workflow from micro-CT scan to FE model. At the top (a), three orthogonal views of the micro-CT scan are shown. One mandible is segmented (shown in green), the associated closer muscle is depicted in orange. The scale bars indicate 0.5 cm. In the middle (b), the three-dimensional mesh of the entire mandible and a detail of the jaw tip are shown, with indication of the closer muscle CM and opener muscle OM. On the FE model (c), the muscle force F, mandible hinge h and constraints at two bite points (at the medial protrusion mp or tip t) are indicated and (d) shows the outcome of the FE analysis with muscle force 10 N at bite point t. The undeformed jaw is depicted transparently. For visualization purposes, the deformation is exaggerated by scaling by a factor 2.

2.1.3. Segmentation, tetrahedrization, three-dimensional model

We designated the voxels of the micro-CT reconstruction that belong to the mandible in Amira, a three-dimensional image processing software package (Amira 5.4.4; 64-bit version, VSG systems). This segmentation was performed by a combination of automatic thresholding, based on grey-scale values, and manual corrections in the three orthogonal views (figure 1a). Next, a triangulated surface mesh was created and smoothed. Finally, a tetrahedral volume mesh was produced using the Delaunay criterion with TetGen software [24] (figure 1b). We chose for Delaunay tetrahedralization, rather than an advancing front method, because it yields better results in thin objects [19,25].

2.1.4. Material properties: Young's modulus and Poisson ratio

Rectangular pieces of approximately 6 × 3 mm were cut out of the mandibular cuticle of three individuals immediately after sacrifice. This was done in three regions of the mandibles: at the tip, in the middle and at the base. The elasticity modulus (Young's modulus) was measured with a custom-built double indentation set-up, a technique especially designed for small, thin samples (for a detailed description, see [26,27]). To evaluate the potential difference in Young's modulus between the cuticle layers, the measurements were repeated after scraping away approximately 20% of the thickness of the samples of one individual.

Additional experiments were performed on dried jaws and jaws that were preserved in Bouin's fixative (see below). Therefore, we also assessed the influence of drying and preservation on the elasticity. For one individual, the measurements were repeated after 44 h and 5.5 month drying. For another individual, they were repeated after fixation in Bouin's fluid. Neither of the measurements differed significantly from those taken before the treatment (table 1).

Table 1.

Young's modulus of cuticle samples, measured by double indentation (average and standard deviation). There were three treatments: drying in air (4 h and 5.5 months), fixation in Bouin's fluid and scraping away the top part of the sample. The results before and after the treatment were compared with an n-way ANOVA, and the p-value is given.

	Young's modulus (GPa)	p-value
fresh samples	5.1 ± 1.3
drying 4 h drying 5.5 month	5.00 ± 0.56 5.22 ± 0.73	0.51
after fixation	5.05 ± 0.55	0.91
thinner sample	5.10 ± 0.55	0.65

To the best of our knowledge, the Poisson ratio for insect cuticle is not available in literature yet [28,29], but it must fall between 0 and 0.5. As a Poisson ratio of 0.3 was measured for lobster cuticle, we used this value [30,31]. Additionally, we determined the sensitivity of the model to the Poisson ratio by varying its value and comparing the effect on the maximal Von Mises stresses. The Von Mises yield criterion takes into account both the shear and normal stress and predicts the material yielding.

2.1.5. Bite force experiments

The maximal bite force was measured for nine male specimens that bit at the medial protrusions (figure 2) of their mandibles. These data were already presented in a biomechanical analysis [10]. For five of these individuals, also the maximal bite forces at the tips of the mandibles were collected. For a detailed description of the bite force set-up, see [10,32]. Briefly, animals bite two parallel plates, that are connected to a force transducer (range: −10 to 10 N for bites at the medial protrusions and −5 to 5 N for tip biting; isometric Kistler force transducer type 9203, Winterthur, Switzerland). From the force transducer, the analogue signal is first amplified (Kistler charge amplifier type 5058A, Winterthur, Switzerland) and subsequently A/D converted (National Instruments DAQ USB-6015, Austin, TX, USA) before it is read in a purpose-written labview routine (Labview 9.0.1f2, 32-bit version, National Instruments, TX, USA).

Figure 2.

Male stag beetle biting at the bite plates (a). This picture was taken by one of the DIC cameras. A speckle pattern for the DIC analysis is visible on the mandibles (b). The medial protrusion (mp) and tip (t) of one mandible are indicated, as well as the x- and y-directions.

Using the moment balance of the lever system, the maximal muscle force was derived from the bite forces (see the electronic supplementary material, S1 and for more details, see [10]). The lever ratio and the angles between the force vectors and their respective levers were obtained from micro-CT images and photographs [10].

2.2. Convergence analysis

The number of tetrahedral elements in the FE model should be a compromise between accuracy and computation costs. To find the optimal number of elements, we made a set of 10 models for which the number of tetrahedral elements ranged from 5 to 785 k elements. For an overview of the model constraints, see figure 1c. The bite point was constrained in the y-direction (aligned with the transverse axis of the body, see figure 2). We implemented this constraint at the tips (and not at the medial protrusions) to include the complete mandible in the analysis. The muscle force corresponded to that of the highest bite force in the validation analysis (5.7 N). Because we ultimately want to interpret Von Mises stresses, we exported this parameter to Matlab (Matlab R2013b, 64 bit version, Natick, MA, USA). We searched the location of the highest Von Mises stress in the largest model. We compared this stress amplitude with that at the same location in the smaller models. This comparison was quantified by the relative error: the difference in stress between the 785 k model and the simplified models, divided by the stress in the 785 k model.

2.3. Validation

A validation experiment must be carried out to check whether the FE model is a good mechanical representation of reality. We performed DIC experiments during the actual biting on the force transducer by a living beetle (figure 2) and compared the measured deformation with the FE model output that mimics the experimental conditions (figure 1c,d). We used DIC measurements, rather than other full-field techniques such as digital speckle pattern interferometry, because the latter requires a stability of the sample (subwavelength stability) that can not be attained in in vivo measurements [15]. Furthermore, the bending and displacement in our experiments is too large for the highly sensitive digital speckle pattern interferometry technique (typically up to only a couple of microns) [15].

2.3.1. Digital image correlation experiment

DIC is an optical full-field technique to calculated three-dimensional displacements and strains of deforming objects, which makes it a valuable set-up to validate biomechanical FE models [15]. The solution is obtained by applying speckles on the sample (figure 2), which are used to create a triangular mesh that is compared between photos of the non-deformed and the deformed sample [33]. We used this technique to determine the jaw deformation of living stag beetles. The individual in this experiment was the specimen that was also used for micro-CT scanning and FE analysis. This male bit the force transducer at the tips of his mandibles (cf. §2.1.5). The distance between the bite plates was 5 mm. Two high-speed cameras were placed above the beetle and recorded the deformation occurring during the bites at 250 frames s⁻¹ (Redlake HR1000 & Redlake Motion PRO cameras; spatial resolution: 1280 × 1024 pixels). The angle between the cameras was approximately 30°. The set-up was calibrated automatically with MatchID Calibration software [33]. After the experiment, two frames that were taken just before the onset of the bite were compared with the two frames at maximal bite force with MatchID 3D software.

2.3.2. Comparison of model and experiment

For three DIC measurements, the FE model was positioned in the same coordinate system as the DIC experiments. The muscle force in the DIC measurements was deduced from the bite force and implemented in the model (2.7, 4.8 and 5.7 N). Also in accordance with the DIC experiments, the movement of the tip of the mandible was constrained in the y-direction (figure 2). The displacements in the y-direction (u) were imported in Matlab (Matlab R2013b, 64 bit version, Natick, MA, USA). For each DIC pixel, we searched the corresponding element of the FE model by comparing the three-dimensional distance between that DIC pixel and all the FE elements. Since we have a lot more FE elements than DIC pixels, we could always locate one in very close proximity to the DIC pixel (maximal 0.1 mm apart). For both the DIC and the FE dataset, the derivative of u with respect to the shearing direction (x, parallel to the sagittal body axis) was calculated for each pixel/element, as the slope of a linear fit through 21 data points (10 points before and 10 points after the considered pixel/element). This derivative (du/dx) is a good parameter to describe bending [34]. The DIC bending measurements were very repeatable (see the electronic supplementary material, S2). We used bending for our validation, rather than strains, due to the noise in the strain results of the DIC experiment (see the electronic supplementary material, S3). Finally, the bending of the FE model was compared to that of the DIC experiment with the coefficient of determination (R²).

2.4. Finite-element model: bite force modulation

2.4.1. Finite-element models

To test the hypothesis that stag beetles modulate their bite force as a strategy to prevent mechanical failure (fracture of the mandible), we made three models:

• Model A with a constraint at the medial protrusion (mp, figure 1) and with the muscle force that we measured for bites at the medial protrusions.

• Model B with a constraint at the tip of the mandible (t, figure 1) and with the muscle force that we measured for tip bites.

• Model C with a constraint at the tip of the mandible and with the muscle force that we measured for bites at the medial protrusions.

Models A and B mimic natural situations, whereas model C simulates an unnatural combination of bite point and muscle force. If the hypothesis is right, the tip is more prone to failure. At a given muscle force, this would result in a higher maximal amplitude of the material stress for tip bites than for bites at the medial protrusions (model A versus C). Moreover, the hypothesis predicts that stag beetles will lower their muscle force for tip biting, which would result in the same maximal amplitude of the Von Mises stress in models A and B.

2.4.2. Failure strength experiments

To determine safety factors, we conducted failure experiments for both bite points. Mandibles (preserved in Bouin's solution) of three males were fixed at their base (approx. 3 mm) in epoxy resin. A stepper motor, connected to a translation stage, was used to deform the mandibles in steps of 20 µm (type 440–458, RS Components, Smithfield, Australia; controlled by a purpose-written MatLab routine). The orientation of the applied forces mimics the condition in the bite experiments. A force transducer (isometric Kistler force transducer type 9203, Winterthur, Switzerland) measured the force applied to the mandible at every step. The signal of the force transducer was amplified (Kistler charge amplifier type 5058A, Winterthur, Switzerland) and A/D converted (National Instruments DAQ USB-6015, Austin, TX, USA) before it was imported in Matlab. First, the mandibles were loaded at the tip until failure. In a second run, this procedure was repeated at the medial protrusion. For both bite points, the safety factor was calculated as the ratio of the force necessary for failure, to the maximal measured bite force (averaged over all individuals) at that bite point.

3. Results

3.1. Finite-element model: development and validation

3.1.1. Material properties

Young's modulus of the fresh cuticle samples is 5.1 ± 1.3 GPa. N-way ANOVAs were performed in Matlab, with factors ‘treatment’ and ‘region on mandible’ (table 1). This showed no significant change in elasticity after drying or Bouin fixation. The result was not altered by scraping away a layer of the cuticle either. Therefore, we will model the cuticle in the FE analysis as single uniform layer of material, with a value of 5.1 GPa for Young's modulus.

3.1.2. Convergence analysis

In the largest FE model (785 k elements), the maximal Von Mises stress was predicted to occur in the serrated region at the tip of the mandible. In figure 3, the Von Mises stress of the same region is shown for nine FE models with less elements. In the four ‘largest’ models, the Von Mises stress is almost identical and the relative error is lower than 3%. For ‘smaller’ models, the difference rapidly increases. As a compromise between calculation time and accuracy, we chose to continue with the 246 k model (i.e. the third ‘largest' model).

Figure 3.

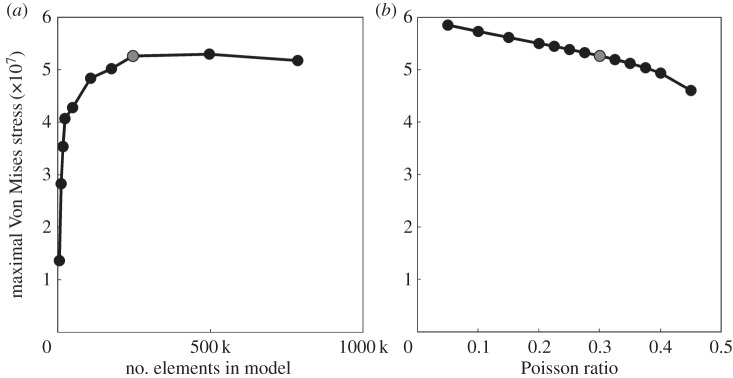
Influence of the size of the FE model (a) and the Poisson ratio (b) on the maximal Von Mises stress in the serrations at the tip of the mandible. The model that is further used in the bite force modulation analysis is highlighted in grey.

3.1.3. Sensitivity to Poisson ratio

Variation of the Poisson ratio does not have a large influence on the Von Mises stress in our FE model (figure 3). Therefore, we continue with the intermediate value of 0.3. The relative error compared to this model is always lower than 5%, except for the models with extreme values for the Poisson ratio (less than or equal to 0.15 or greater than or equal to 0.4).

3.1.4. Validation

To validate our FE model, we compared the simulated deformations with those that we observed in our DIC experiment. As in reality, the FE models of the mandible rotate about their hinge (figure 1d, scaled for visualization purposes). Also consistent with our in vivo observations of biting males, the structure straightens in the FE simulations: the outer lateral surface is compressed while the inner lateral surface is extended. To enable a qualitative visual comparison, figure 4 displays the bending in one of the DIC experiments (figure 4a) and the FE model (figure 4b). The DIC technique elicits more noise than the FE model and also causes some blind spots. However, it is very clear that the overall pattern is the same. This results in R² values of 0.87, 0.97 and 0.94 for the three DIC measurements with muscle forces of, respectively, 2.7, 4.8 and 5.7 N. When we repeat the same procedure on FE models of the contralateral mandible of the same individual, we obtain almost identical R² values (0.87, 0.97 and 0.93).

Figure 4.

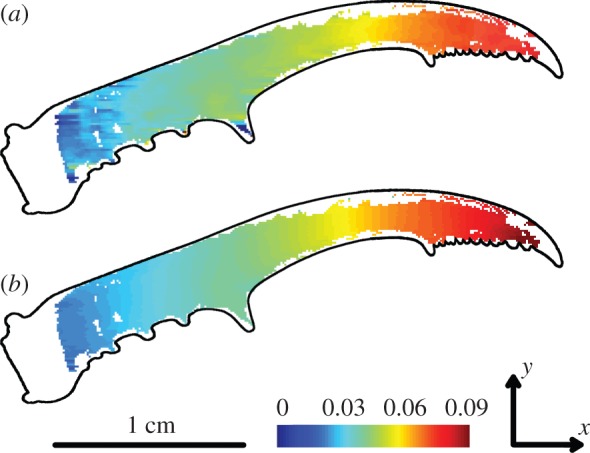
Bending (mm/mm) in the DIC experiment (a), and in the corresponding elements of the FE model with a muscle force of 5.7N (b). The blind spots in (b) arise from the comparison with (a), the FE model itself has no blind spots. The outline of the mandible is superimposed for clarity.

3.2. Finite-element model: bite force modulation

3.2.1. Bite force modulation

On average, the male maximal bite force at the medial protrusions is 6.76 ± 0.88 N at 5 mm bite plate distance (N = 9; three measurements per individual). The moment balance approach shows that this has been caused by muscle forces of 10 N at each lateral side. The maximal bite force at the tips of the mandibles is 2.36 ± 0.34 N (N = 5; between four and six measurements per individual). This corresponds to muscle forces of 8.4 N at each lateral side. The present observation—a 18% reduction for tip bites compared to bites at the medial protrusions—agrees with our hypothesis of bite force modulation.

3.2.2. Material stress modulation

Our hypothesis predicts that the mandible tips are more prone to failure than the robust base of the mandible. Our FE simulations of model A and C confirm this: for the same muscle input force (i.e. 10 N as obtained from the in vivo bite experiments at the medial protrusion mp), tip biting causes 16% more material stress (73 MPa) than biting at the medial protrusions (61 MPa, maximal amplitude Von Mises stress, figure 5). The hypothesis also predicts the same maximal material stress in both natural bite situations (models A and B, the latter using a muscle input force of 8.4 N as obtained from the in vivo bite experiments at the tip t). Again, this is confirmed by our simulations: the maximal amplitude of the Von Mises stress in these models is very similar (respectively, 61 and 59 MPa), despite the different stress distribution (figure 5). These findings suggest that individuals adjust their muscular input force according to the location of the bite point, in order to avoid overload of the mandibles. The maximal amplitude of the effective strain (total Green–Lagrange strain) gives exactly the same result (model A: 0.015; model B: 0.015; model C: 0.018).

Figure 5.

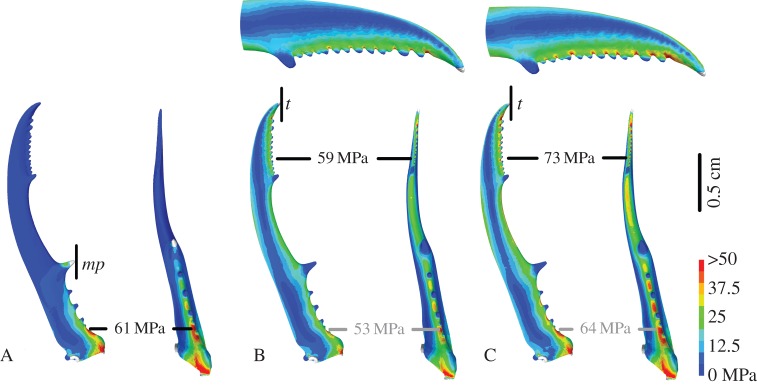
Deformed images of FE models A, B and C in dorsal (left) and sagittal (right) view. Colours indicate Von Mises stress. The location of the bite point constraint is designated by a vertical black line (at the medial protrusion mp in A, at the tip t in B and C). A and B represent simulations with the observed muscle force as input (respectively, 10 and 8.4 N). C represents tip biting with the unnatural muscle force of 10 N. The location of the maximal stress is indicated with the black labels. For models B and C, also an enlargement of the tips of the mandibles in dorsal view is given and the highest Von Mises stress at the base is indicated with the grey labels.

When experimentally breaking the mandibles, they usually fail at the location predicted by the FE model (i.e. the region of the highest Von Mises stress): for tip loading the mandibles broke between the serrations (except for one mandible that broke at the very tip of the mandible) and for loading at the medial protrusion they always broke at the base. The force necessary to break the mandible by pushing its tip is 6.13 ± 0.63 N. This corresponds to safety factors of 5.2 for natural tip biting, and 4.3 for the hypothetical tip bites with the higher muscle force of model C. Much more force is necessary for failure by pushing the medial protrusion: 24.35 ± 0.59 N. The according safety factor is 28% higher compared to biting at the tip (7.2).

4. Discussion

4.1. Finite-element model: development and validation

We built an FE model of a male stag beetle mandible to investigate the shape–function relationships of their armature. A good knowledge of the material characteristics is a fundamental requirement for a realistic FE model. More specifically, Young's modulus and the Poisson ratio have to be taken into account. For zoological FE modelling, these values are generally unknown and natural variation should be taken into consideration [16]. Therefore, we measured Young's modulus for stag beetle mandibles, determined the sensitivity of the model to the Poisson ratio and validated the model results with experimental data.

Young's modulus of sclerotized insect cuticle ranges from 1 to 20 GPa [35,36]. For adult insect mandibles, values between 5 and 11 GPa have been reported [36–39]. The value that we measured lies within this range (5.1 GPa). As in some other studies (e.g. on mandibles of termites and jewel beetles, [37,38]), Young's modulus was not altered by drying. However, other authors did report drying effects on the elasticity of various parts of insect cuticle (up to 10 times higher Young's modulus after drying, [35,36,39]). Perhaps the absence of a drying effect for stag beetle mandibles is caused by the sclerotization of the mandible cuticle. Mandibles, just as for example claws, have a reinforced cuticle to withstand their forceful interactions with the surroundings. In this process, the water content of the cuticle decreases heavily [35,36,38]. The fact that neither drying nor preservation changed the elasticity of stag beetle mandibles supports our failure experiments on preserved jaws. Furthermore, partly scraping away the cuticle had no impact on Young's modulus either. This reinforces the implementation of a single uniform material layer in the FE model.

Contrary to Young's modulus, literature on the Poisson ratio of (sclerotized) insect cuticle is scarce [40,41]. As to be expected for Poisson ratios that do not approach 0.5, our model outcomes hardly change for Poisson ratios in the range of 0.05–0.45 (figure 3). Also in other FE models of insect cuticle, the effect of the Poisson ratio on the model behaviour is negligible [29,42].

We validated our model and its material properties with the DIC technique. To the best of our knowledge, this is the first time that the DIC technique has been used in vivo. Because we made images of living beetles, we had to use a high-speed camera, which reduced the resolution and the depth of field of the pictures. Also, owing to the elongated shape of the mandibles, the size of the window that is used to calculate the strains is limited. Therefore, there is less averaging possible in the calculations of the strains. Both of these limitations increased the noise, and therefore the strains that we calculated from the DIC measurements were not useful for the FE model validation (see electronic supplementary material, S3). Instead, we calculated bending from the DIC experiments because the deformations resemble typical bending experiments. These bending data are a lot less noisy than the strains, as they are differentiated along the long axis of the mandible (the x-axis). Our validation (albeit based on bending instead of strains) shows that the results of our model closely mimic the natural behaviour of the mandibles. Therefore, we are confident that our model and the material properties used provide a good representation of stag beetle mandibles.

4.2. Finite-element model: bite force modulation

Weapon morphology is often adapted to limit material stress during fights. For example, bighorn sheep have a higher safety factor than blackbuck sheep, because they face more variable and unpredictable forces in their fights [43]. FE analysis showed that scorpion chela with low aspect ratios are more robust in terms of material stress. This corresponds to their ecomorphology: contrary to species with slender chela, they either burrow in hard soil or feed on hard-shelled prey [17]. In moose antlers, not only is the morphology adapted, but also the material properties thereof. Owing to their palmate shape, they are prone to bending and hence the stiffness of the antler bone is increased [44].

At first glance, the situation seems to be different in stag beetle mandibles. Their weapon morphology appears to be suboptimal, as they apparently have to restrain their muscular input force when biting at the tips. As a result, the local Von Mises stresses at the tips are not elevated excessively above those at the robust medial protrusions, as calculated by our FE models. This suggests that the animals behaviourally adjust their muscle force to avoid overload of the mandibles. Similarly, crabs of different instar numbers also regulate their bite force behaviourally, to compensate for the larger amount of fatigue and wear on their claws in the later stages [45]. Even though our estimation of the safety factors is based on a small sample of failure experiments, it indicates that male stag beetles increase their safety factor by 18% (from 4.0 to 5.2) by modulating their muscle force. This is still lower than that of bites at the medial protrusion (7.2). Nevertheless, both safety factors accord with those of other animals weapons (2–7 in crab claws [45,46], 3.4–10 in sheep horns [43]). If this behavioural muscle force modulation truly exists, then mechanosensors should be present in the mandibles. These have already been described in other insects (e.g. campaniform sensilla on dipteran halters and cockroach legs [47]). On the micro-CT scan, we see large numbers of narrow channels crossing the entire thickness of the mandibular cuticle. As the distribution of these channels corresponds to the stress pattern of our FE model, we assume that these structures accord to mechanosensors. Unfortunately, the resolution of the present micro-CT scan does not enable a reliable reconstruction of their morphology.

A remaining question is why the tips of the stag beetle mandibles are not more robust, so as to withstand higher bite forces. As a first possible explanation, forceful tip biting may not give a large selective advantage. A less forceful bite may suffice to daunt an opponent and to show the reach of one's armature. Trade-offs with functions other than fighting may pose an alternative (but not mutually exclusive) explanation: making the mandible distally more robust may be restricted due to weight limitations for locomotion. The heavy weaponry places the body centre of mass more anteriorly, which makes running male stag beetles statically unstable [11]. In addition, flight lift, drag and stability may suffer from eavier armature [7,12]. Finally, it may be deceptive to only look at male bite forces. Males bite approximately 18% less forcefully at the tips than at the medial protrusions. However, females (as a proxy for the hypothetical non-dimorphic male; cf. [10,11]) bite 66% less forcefully than males do at the medial protrusions (even after size-normalization, [10]). Therefore, male tip biting may still be considered ‘forceful’ biting, yet limited due to trade-offs between structural weight and locomotion. In that case, the behavioural limit of the bite force may be seen as an adaptation to enable larger jaw muscles and hence even higher bite forces at the more robust base of the mandible.

Funding statement

This study was funded by a BOF grand (ID BOF UA 2011-445-a) of the Research Council of University of Antwerp. The SkyScan 1172 high-resolution micro-CT scanner, located at the VUB facilities, was funded by the Hercules Foundation (grant UABR/11/004).