Social insect colony as a biological regulatory system: modelling information flow in dominance networks

Abstract

Social insects provide an excellent platform to investigate flow of information in regulatory systems since their successful social organization is essentially achieved by effective information transfer through complex connectivity patterns among the colony members. Network representation of such behavioural interactions offers a powerful tool for structural as well as dynamical analysis of the underlying regulatory systems. In this paper, we focus on the dominance interaction networks in the tropical social wasp Ropalidia marginata—a species where behavioural observations indicate that such interactions are principally responsible for the transfer of information between individuals about their colony needs, resulting in a regulation of their own activities. Our research reveals that the dominance networks of R. marginata are structurally similar to a class of naturally evolved information processing networks, a fact confirmed also by the predominance of a specific substructure—the ‘feed-forward loop’—a key functional component in many other information transfer networks. The dynamical analysis through Boolean modelling confirms that the networks are sufficiently stable under small fluctuations and yet capable of more efficient information transfer compared to their randomized counterparts. Our results suggest the involvement of a common structural design principle in different biological regulatory systems and a possible similarity with respect to the effect of selection on the organization levels of such systems. The findings are also consistent with the hypothesis that dominance behaviour has been shaped by natural selection to co-opt the information transfer process in such social insect species, in addition to its primal function of mediation of reproductive competition in the colony.

1. Introduction

1.1. Information flow in biological systems

Living organisms are characterized by various sequential processes operating at different biological levels, such as genetic, proteomic, cellular, neuronal, etc. Their survival depends heavily on the proper functioning of such coordinated processes and hence on an efficient dissemination of information through the communication systems of the respective levels [1]. Also for human-engineered systems such as electronic circuits or the Internet, the primary task is to pass information from one part of the system to another [2]. All these systems are known to maximize their performance under time or energy constraints. While structural stability and economics are responsible for the optimization of artificial systems, biological systems are generally optimized under natural selection. Therefore, it is of particular interest to know how such systems achieve their effective process of information transfer and what factors are responsible for their efficiency.

Flow of information is also an important criterion for the coordinated activities of group-living animals. Information transfer is crucial in processes such as collective motion of fish schools, flocks of birds, herds of quadrupeds, etc., where a single animal is inept to communicate at any moment with all the other members in a group [3]. In human society too, processes like reaching a consensus or the spreading of rumours and diseases are governed by an effective flow of information [4]. Social insect species such as ants, bees and wasps exhibit superlative forms of regulation in their colony life that rely largely on the exchange of information among the individuals [5,6]. In such species, only one or a small subset of individuals are fertile, known as the queens, who use ‘honest signals’ to maintain their reproductive monopoly over their workers [7]. Some of the social insect species are more advanced and are known as ‘highly eusocial’ species. They build large colonies and have evolved to use advanced methods of information transfer that can cater to thousands of workers. For example, trail-forming ants use chemical signals to communicate information about foraging sites, whereas honeybees use a dance language for the same purpose [5]. In the less advanced ‘primitively eusocial’ species, colony sizes are small, and direct physical interactions play a more significant role in the flow of information. Examples include tandem running in some species of ants, where specialist individuals lead nest-mates to the new location by maintaining physical contact [8]; cooperative nest-building by the temperate wasps, which is thought to rely on a qualitative stigmergic process, a mechanism that mediates worker–worker interactions [9]. In addition, in most of the primitively eusocial species, workers obtain information regarding the presence and/or fertility of the reproductive individuals by physical association with the reproductive individuals [10], often through aggression initiated by the latter [11]. Since in the course of evolution, these primitively eusocial species are considered to be intermediate between their solitary and highly eusocial counterparts [5], study of such species could shed light on the evolutionary processes by which their regulatory systems have been optimized.

1.2. The model system

Ropalidia marginata is a primitively eusocial wasp widely found in peninsular India and other southeast Asian countries [12]. They use several forms of pair-wise physical interactions such as dominance, antennation, allogrooming, etc., among which the dominance behaviour plays a major role in regulating the activities of the workers [13]. Some workers are found to be specialized to perform intranidal tasks such as building of cells or brood care, whereas the others opt for extranidal tasks like foraging for food and building materials [14]. Workers who spend most of the time on the nest to perform intranidal duties may obtain information about the colony needs directly by inspection and convey the same to the foragers. It has been experimentally demonstrated that the foragers receive more dominance than the non-foragers, and the frequency of the dominance received by the foragers is correlated with their foraging rates [15]. It was also found that the dominance received by the foragers increases when a colony is forced to starve [16], and decreases when a colony is fed in excess [17]. Similar correlations between dominance behaviour and worker activities are also observed in other species of the same subfamily Polistinae: Polistes dominulus [18,19], Polybia occidentalis [20] and Polybia aequatorialis [21]. These observations lead to the hypothesis that the social wasp workers use dominance behaviour to transfer information about the colony needs among themselves and hence achieve an effective regulation of their own activities. In this study, we investigate this hypothesis with respect to R. marginata by analysing the structure of the networks constructed from their interaction relationships.

1.3. Network substructures

Over the past two decades, network science has emerged as a very powerful tool with regard to the analysis of complex systems [2]. Study of different biological and other real-world networks has revealed that many of the networks share global statistical features such as the existence of short paths between any pair of components, highly clustered neighbourhoods and broad-tailed connectivity distributions [2,22–24]. These properties are far from random and therefore indicate possible involvement of certain design constraints in the overall structures. Beyond the global features, it is also possible to identify local structural elements, the fundamental building blocks, which reflect the underlying process of network generation. We focus our study on the structural analysis of the networks of paired interactions in R. marginata, specifically the dominance networks, and ask the following questions: how are the networks built? What is the underlying structural design? What is the function for which the networks are designed? What are the basic functional elements present in the networks? In particular, we search the networks for ‘motifs’ [25], basic units of interconnections that occur at frequencies significantly higher than those in their randomized counterparts. Earlier studies have demonstrated that information transfer networks such as gene transcriptional networks, neuronal connectivity networks and electronic circuit networks share common significant substructural patterns [25,26]. In a recent study on the seed harvester ant Pogonomyrmex californicus, a social insect species, Waters & Fewell [27] found the predominance of similar patterns in their antennation networks. Our hypothesis about the function of the dominance networks of R. marginata prompts us to expect similar patterns.

1.4. Boolean modelling

Similarity in structural patterns of networks, nevertheless, does not guarantee a similar functionality [28]. It would be necessary to investigate the dynamics of information flow in the networks and check whether the networks are robust and capable of efficient transfer of information. Boolean networks provide a useful framework to study generic dynamical systems with unknown or partially known structure or function [29–31]. The modelling scheme was first introduced by Kauffman [32,33] for studying gene transcriptional networks and subsequently applied successfully in different organization levels of biological regulatory networks within organisms [34–37], and also in various social networks [38,39]. We use Boolean modelling to analyse the dynamical behaviour of the networks and ask: how sensitive are the networks with respect to the smallest of perturbations? And how do the non-random architecture of the networks affect the efficiency of information transfer? These features are investigated by monitoring how the ‘Hamming distances’, differences in information between a pair of states, evolve in time as the network advances from a pair of predetermined initial states. Our investigation suggests that there is a design principle involved in the dominance networks of R. marginata that favours efficient transfer of information. We also believe that our analyses can help to develop an understanding about the evolutionary process by which the biological regulatory systems have been optimized.

2. The experimental data

We used the data from behavioural observations carried out on nine post-emergent colonies of R. marginata. The colonies were of different sizes ranging from 14 to 59 adults. The individuals on the nests were uniquely marked with spots of Testors quick-drying enamel paints prior to the observations. The major activity period of the day for R. marginata is the 10 h between 08.00 and 18.00, which was divided into four equal blocks of 2 h and 30 min each. Each colony was observed for 5 h in a day in two such alternate blocks, over 2 consecutive days, covering the entire activity period, thus yielding 10 h of data per colony. Blocks consisted of sessions lasting 5 min, followed by a break of 1 min between every session. Observation sessions were of two kinds, either ‘instantaneous scan’ sessions or ‘all occurrences’ sessions, and they were randomly intermingled in the ratio of 1 : 2. In the former case, a snapshot of the behavioural state of each individual was recorded, and in the latter, every occurrence of a set of chosen behaviours by any individual was noted down [12,40]. We would like to mention that, for eight of nine colonies, we have observational data for 30 h spread over 6 consecutive days, but we have used the data corresponding to 10 h of observation for our main analysis. It is worth mentioning here that the additional time did not have a significant effect on the results (explained in the following sections).

3. The dominance networks

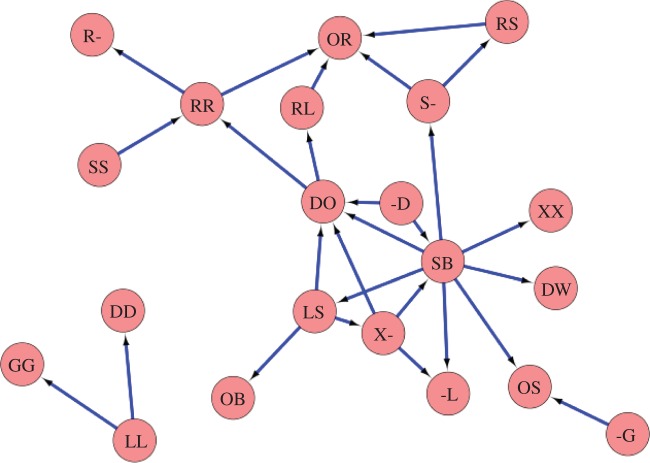
In the dominance networks of R. marginata, all individuals were considered as nodes. A single dominance interaction between a pair of nodes is considered as an exhibition of their dominance relationship, and such a relationship is represented by a directed link from the dominant to the recipient individual. Dominance is fundamentally a binary relationship, therefore, multiple interactions between a pair of nodes are also considered as single links. Nine distinct behaviours shown by the individuals are termed as dominance behaviour in R. marginata, they are attack, chase, nibble, peck, crash land on another individual, sit on another individual, being offered regurgitated liquid, aggressively bite and hold another individual in their mouth [12]. The behavioural interaction, where an individual (subordinate) is obliged to offer an incentive, by means of regurgitated liquid, to another individual (dominant), is termed as ‘being offered regurgitated liquid’ from the dominant individuals perspective; all the other terms are self-explanatory. Such dominance relationships, sampled by the 10 h of observation, were used to construct the unweighted, directed dominance networks for each of the nine colonies (electronic supplementary material, text S1). The network constructed for the colony V215 is shown in figure 1.

Figure 1.

The dominance network in the colony V215 of R. marginata. Nodes represent individuals with their unique identification codes, links represent dominance relationships directed from the dominant to the subordinate individual. The figure has been drawn by using Cytoscape [41]. (Online version in colour.)

While our aim was to uncover the structural pattern of the dominance networks in the colonies, we needed to take care of the fact that the structure of such networks would be sensitive to a minor extent to the time frame of observations. The dominance relationship between a pair of wasps may, albeit rarely, become inverted over time. Therefore, the choice of the duration of sampling was to be limited over a period in which such inversions do not occur. However, we also needed to sample the whole activity period of the wasps, ranging 10 h, between 08.00 and 18.00. As we made observations for 5 h in a day, we needed at least 2 consecutive days to sample the required period. We plotted the number of connected nodes and the number of observed links against the time span in hours over which the colonies were observed (electronic supplementary material, text S2). We found that, though most of the nodes were connected within the first 10 h of observations, the number of links did not saturate. As the observations continued to the third consecutive day, occasional reversal of dominance relationships was observed, indicating a change in the dynamics (details in §4.1). Therefore, we assumed that the networks remained unchanged over 2 consecutive days and used 10 h of observational data, spanning over the whole activity period of the wasps, for our main analysis.

3.1. The global structural patterns

The basic quantities measured pertaining to the global structure of the networks are shown in table 1. The quantities include (i) average path length: average number of links on the shortest path between any pair of nodes, (ii) clustering coefficient: average density of links in the neighbourhood of the nodes, (iii) assortativity coefficient: correlation between the connectivity of the connected nodes, and (iv) degree distributions: probability distribution of a random node having specific connectivity, independently for in-degree (the number of links that are directed towards a node) and out-degree (the number of links that are directed away from the node).

Table 1.

Basic global structural quantities measured on the dominance networks of R. marginata.

colony identity	number of nodes (N)	number of links (L)	average path length	clustering coefficient (C)	assortativity coefficient (r)	p for χ2 goodness of fit to Poisson distribution
						in-degree distribution	out-degree distribution
V213	43	64	3.66	0.07	−0.04	0.22	0.42
V215	21	27	1.88	0.12	−0.25	0.26	0.18
V217	29	32	2.25	0.00	−0.14	0.15	0.41
V219	14	22	2.10	0.20	−0.29	0.98	0.76
V220	15	19	1.21	0.10	−0.14	0.67	0.90
V221	14	18	1.37	0.14	−0.51	0.03	0.55
V222	20	41	1.85	0.21	−0.37	0.83	0.09
V223	17	26	1.85	0.16	−0.08	0.53	0.35
V224	14	23	1.68	0.20	−0.21	0.62	0.48

In order to uncover the global structural patterns, each network was compared with a corresponding random network that preserved the number of nodes N and links L of the original network. Such random networks, known as Erdős–Rényi random graphs [42], are characterized by Poisson-distributed in-degree and out-degree distributions with the ratio L/N as the parameter. Such expected Poisson distribution was tested against the distributions of the original networks by means of χ² goodness of fit test, and the corresponding probabilities are furnished in table 1. For both in-degree and out-degree, we found p > 0.1 in eight of nine colonies, which suggests lack of evidence in favour of the distributions to be different from Poisson. In a random network, the average path length is expected to grow logarithmically, and the clustering coefficient is expected to fall inversely with the network size N, but the sparseness of our data restricted the detection of such effects. The assortativity coefficient for random networks is expected to be zero, but the R. marginata dominance networks show an average of −0.23 ± 0.15 which is significantly less than zero (t =−4.532, p = 0.001). Therefore, the networks are said to be disassortative [43], which means that the more dominant individuals tend to dominate individuals who are less dominant; in other words, highly dominant individuals tend to avoid other highly dominant individuals. It has been found that many biological networks engaged in information transfer such as the protein interaction network in the yeast Saccharomyces cerevisiae, the metabolic network in the bacterium Escherichia coli, the neuronal connectivity network of the nematode worm Caenorhabditis elegans, and technological networks such as the Internet and the World Wide Web show disassortative mixing in their network structure [43]. It is possible that, in the course of information transfer, the components having information are more interested in passing it on to the functional components, rather than sharing it among themselves. Such a mechanism would certainly be economic and therefore favoured under selection mechanisms. The analyses in this section were performed by using the network analysis software Cytoscape [41].

4. Analysis of the substructures

The three-node substructures, or the triads, can be thought of as the basic building blocks of a network [44]. The 64 possible types of triads can be classified into 16 isomorphic classes [44], out of which we are interested in those 13 where all three nodes are connected (figure 2). Each network was searched for all these 13 triads, and the number of occurrences of each triad was recorded. The measured quantities were then compared with those of a properly randomized network. This time, the randomized networks were constructed by keeping the single-node characteristics preserved such that both the in-degree and out-degree of each node remained unaltered. The measurement over the ensemble provides dispersions in the measured quantities and therefore allows statistical comparisons with the original [45,46]. The statistical significance was tested by using two different methods. First, with the empirical sample estimate of probability P, which is defined as the probability that the particular triad appears in the randomized networks an equal or greater number of times than in the original network. The substructure is said to be significantly over-represented in the real network and subsequently called a ‘motif’, if P is lower than a small predetermined cut-off value [25]. The under-representation of a triad also can be inferred if P is found to be higher than some high cut-off. The other way to determine the statistical significance is to compute the Z-score; the normalized deviation of the occurrences from the expected mean value. If N_o is the number of times the ith triad occurs in the original network, and 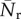and σ_r are the mean and standard deviation of its occurrence in the randomized networks, then the Z-score for the triad is defined as 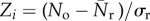. A higher value of the Z-score of a triad implies a higher significance of the occurrence of that triad in the network [26]. Both the methods of testing statistical significance have their own limitations; distributions may be undersampled or may be different from a Gaussian [47], so we decided to use both the methods for our purpose. The analyses were performed by using an application called FANMOD (fast network motif detection) [48]. The application made use of an algorithm named RAND-ESU which is an efficient algorithm especially in the case of substructures with low concentrations [49,50]. The results are summarized in table 2.

Figure 2.

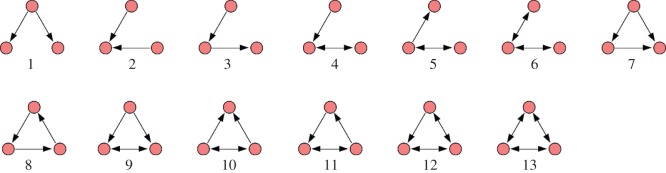
The 13 possible connected three-node substructures (triads). (Online version in colour.)

Table 2.

Frequencies of the triads and their significance in all the nine dominance networks of R. marginata put together.

triad identity	observed frequency (%)		observed in networks	significant in networks (count > 1, P < 0.1)	less significant in networks (count > 1, P > 0.9)
	mean	s.d.
1	36.66	9.35	9	0	4
2	21.72	10.47	9	1	4
3	31.18	11.03	9	1	0
4	0.00	0.00	0	0	0
5	0.00	0.00	0	0	0
6	0.00	0.00	0	0	0
7	10.22	5.80	8	6	0
8	0.22	0.49	2	0	0
9	0.00	0.00	0	0	0
10	0.00	0.00	0	0	0
11	0.00	0.00	0	0	0
12	0.00	0.00	0	0	0
13	0.00	0.00	0	0	0

4.1. The feed-forward loop

In the dominance networks of R. marginata, the prominently found substructures were triad 1, 2, 3 and 7. All these triads were previously shown as the most structurally stable triads among the 13 possibilities [51]. The only other triad found, though very rarely, was triad 8, which is one of the least stable triads [51]. It is worth noting that the number of occurrences of triad 7 was much less compared to the other three predominating triads, but when compared with randomized networks, triad 7 was found to be significantly over-represented in six networks (V213, V215, V219, V220, V223 and V224), whereas the significance of the others were negligible. Triads 1 and 2 were significantly underrepresented in four colonies each. Triad 7 showed an averaged normalized Z-score of 0.34 ± 0.39 which was significantly greater than zero (t = 2.566, p = 0.017), no other triads showed significant deviation from zero. By both the methods of significance testing, triad 7, commonly known as the feed-forward loop, emerged as the most consistently significant substructure present in the dominance networks. The analyses were repeated on the same set of nests (except in V222) with 20 and 30 h of behavioural data, and the results were found to be qualitatively similar (electronic supplementary material, text S3). The averaged normalized Z-score for the feed-forward loop with 20 h and 30 h of data were found to be 0.31 ± 0.40 and 0.40 ± 0.21, respectively, both were significantly greater than zero (t = 2.202, p = 0.032 and t = 5.374, p = 0.0005, respectively). Here, unlike the results pertaining to 10 h of observation, the presence of triads with mutual links could be recognized in small numbers. This observation indicates a possible reversal in dominance relationships among the individuals over time, thus reflecting a change in the dynamics of the colony. We would like to mention here that, considering weighted links would not have induced any significant change in the results. As during the randomization, the local properties of each node were to be preserved, this would only allow the links of similar weights to be swapped. Because the links with weight w > 1s are very few (electronic supplementary material, text S4), swapping them would produce very little effect on the overall results.

The feed-forward loop was previously found to be significant in transcriptional networks of bacteria namely Bacillus subtilis and E. coli, and the yeast S. cerevisiae [25,26,52–54]. The motif was also found in the neuronal connectivity network of the nematode C. elegans [25]. Since all these networks carry information from sensory components to the functional units, it has been argued that the structural elements common to them may play a functional role in information processing [25]. It has been shown, both by theory and experiment, that the feed-forward loop performs signal processing tasks such as persistence detection, pulse generation and acceleration of transcription responses [53,55,56]. The same signature found in the antennation networks of the seed harvester ant P. californicus while engaged in foraging activities also suggests a functional similarity and selection for efficiency of directional information flow [27]. Remarkably, we did not find any such pattern in the antennation networks of R. marginata (electronic supplementary material, text S5). Apart from dominance and antennation, the wasps exhibit other paired behaviours such as allogrooming, soliciting and food sharing; and we performed similar analyses with each of them, but no triad was found to be consistently significant over the colonies (electronic supplementary material, text S5). Only for the soliciting behaviour, triad 12 was significantly over-represented in four colonies, but the normalized Z-score for the triad was found to be 0.03 ± 0.33 which is not significantly different from zero (t = 0.309, p = 0.382). Also note that the dominance interactions comprising 14.19 ± 6.88% of the total paired interactions exhibited by the wasps. We would also like to mention that information transfer in social insect colonies through interactions other than dominance were recently addressed with the help of network analysis, though with approaches different from ours [57–59].

4.2. The triad significance profile

The comparison of Z-scores across the colonies is possible only after the data are subjected to normalization, since the size of the networks usually has substantial influence on their absolute values [25]. Therefore, for each colony, the vector of Z-scores was normalized to a length unity by computing 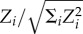for each of the triad. These normalized Z-scores for each triad were averaged over all the colonies to get the ‘triad significance profile’ of the species [26]; the profile is shown in figure 3. Except for triad 3, the profile shows fair resemblance to the superfamily of sensory transcriptional networks that controls gene expression in bacteria and yeast in response to external stimuli [26]. This similarity suggests that the networks may have evolved under similar constraints to perform tasks in a similar manner [26]. The sensory transcriptional networks are rate-limited networks, where the response time of each step in the networks is of the order of the response time required for the functioning of the networks [26]. If the dominance networks of R. marginata are used for the transfer of colony-level information and subsequently for the regulation of worker activity, the networks are indeed rate-limited, because the response time for the workers to a particular task is expected to be as short as the response time of each interaction. The over-representation of feed-forward loops and the rare occurrence of cycles (triad 8) are also consistent with the characteristics of rate-limited networks [26]. The rate limitation implies a rapid response by the functional components. Therefore, a structure that allows the output to be activated only if the input signal is persistent is expected to perform an important functional role in such networks, whereas a structure where a node indirectly influences itself is of little importance. It should be worth noting that the profile is largely different from the other superfamily of biological information processing networks that are not rate-limited and also from the superfamily of social networks [26]. Both these superfamilies display triads containing mutual links. In particular, non-rate-limited networks are characterized by two-node feedbacks that regulate or are regulated by a third node (triad 10 and 9) [26]. Such triads are absent in our networks. The rarity of cycles, along with the absence of triads with mutual links led to an almost acyclic structure for the networks, which might also be an important property of such rate-limited networks. Therefore, it is possible that the rate limitation plays an important role in shaping the local structure of the networks. We would like to infer that the specific non-random structure of the dominance networks of R. marginata has evolved under selection mechanisms similar to the other biological rate-limited regulatory networks.

Figure 3.

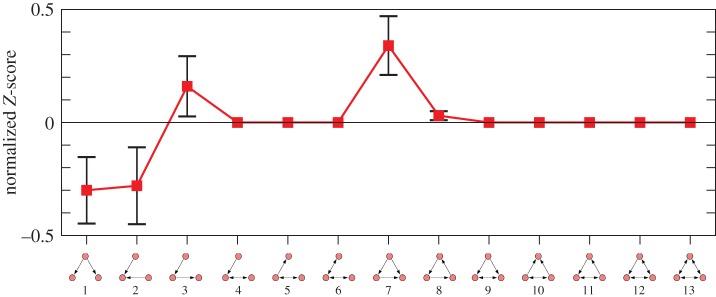
The ‘triad significance profile’ for the dominance networks of R. marginata. The normalized Z-scores corresponding to each kind of triad is averaged over nine colonies, whiskers show their standard errors of measurements, and the line connecting the Z-scores serves as a guide to the eye. (Online version in colour.)

4.3. Behavioural correlations

In the following, we try to better understand the interrelationships between the dominance behaviour, the structure of the feed-forward loop and the other behavioural aspects of the individuals that may be important from the point of view of information transfer. Behavioural experiments on R. marginata had already suggested the importance of dominance behaviour in the process of colony-level information transfer among the workers and subsequent control of worker activities [13,15–17]. We expect that the individuals who spend less time outside the nest would have a better chance to gather information about the colony needs, and therefore, would be better poised to pass on the information to the others. We calculated the fraction of time spent outside the nest for each individual and found a negatively correlated trend with their frequency of dominance behaviour, though non-significant (Pearson r = −0.082, F = 1.179, p = 0.132). Additionally, we investigated along this line by calculating the median value of the fractional time (0.25) and then split the dataset into two parts with respect to the median. We found that the individuals who spent less than 25% of their time outside the nest showed more frequent dominance behaviour (2.90 ± 7.30, n = 91) compared to the others who spent 25% or more time outside the nest (1.41 ± 1.61, n = 96, t = 1.909, p = 0.029), whereas the frequency of the dominance received by the two groups is indistinguishable (2.23 ± 2.68 and 2.04 ± 2.08, t = 0.537, p = 0.296). We further investigate the fractional time spent outside the nest for the individuals who constituted the feed-forward loops in the observed dominance networks. We performed Wilcoxon matched-paired test, and found that, the individuals holding the double-dominant positions in the observed feed-forward loops spent less time outside the nests compared to the individuals holding both the pass-along (V = 792, p = 0.0003) and the double-subordinate positions (V = 1120, p = 0.038).

5. Analysis of the dynamics

In a Boolean network model, each node can be in any of the two possible states, ‘active’ and ‘inactive’, represented by the binary values 1 and 0, respectively. In the dominance networks of R. marginata, the nodes with some information are considered as active, and the nodes with no information are considered as inactive. The information about the colony needs may not necessarily be a binary variable, but this simplification is justified, because a node can be considered to change its state from inactive to active (and vice versa) only when a certain threshold value of information is crossed [29]. Such threshold models for worker activity have already been tested in social insect species [60,61]. We assumed that the information can pass only from the dominant to the subordinate individual; therefore, the future state of a node is regulated by those nodes to which it is connected with incoming links. As the system evolves with time, the state of a node is updated according to a coupling between the node and the nodes dominating over it. These couplings are Boolean functions expressed generally through a combination of the logic operators AND, OR and NOT [29,31]. In a classical Boolean network model, the interconnections and the interaction rules are probabilistically chosen from predefined sets. However, having some understanding of the system, it is customary to use that knowledge to choose the rule that best describes the system [31,62]. We assumed that a single dominance interaction is sufficient to pass the information from the dominant to the subordinate individual, therefore we used the most generic form of OR logic as the interaction rule, hoping that the real systems share their most important properties with the most generic representation we are dealing with [29]. According to the OR rule, if any one of the input nodes is active, the output becomes active; otherwise, it is inactive; and a node with no incoming connection retains its initial state. Starting from a random configuration of active and inactive nodes, the system keeps on updating following the interaction rules until the system reaches a steady state. The synchronous-updating scheme used is the simplest and most convenient scheme, where at each time step, the states of all nodes are updated simultaneously depending on the states at the previous time step. The fact that the durations of the dominance interactions are mostly alike supports such an updating rule [34,62].

5.1. The Hamming distances

To study the stability of the system in terms of information transfer, we investigated the time development of small fluctuations in the system. We started with a pair of different possible initial states Σ₀ = {σ₁(0), σ₂(0), … , σ_N(0)} and 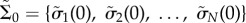sampled from the entire state space, where σs are the binary values of the states (0 or 1) for each of the N nodes at t = 0. The Hamming distance at time t, defined as 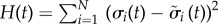, was then plotted against predefined initial distances H(0); the representation scheme is sometimes referred in the literature as a Derrida plot [34,63]. The slope of the curve near the low H region reflects the fate of small fluctuations in the system. If the curve is well above the H(t) = H(0) line, then the system transfers information to a number of nodes that grow exponentially with time and the system is said to be in a chaotic phase, which is an unstable state and easily prone to noise. On the other hand, if the curve is well below the line, the fluctuation decays exponentially and therefore propagates to only a few of other nodes and the system is said to be in a frozen or ordered phase. In the intermediate situation, very near the line, the information flows to a number of nodes that grow algebraically with time, and the system is said to be at the edge of chaos or in the critical phase. For efficient transfer of information, the system is expected to be in an ordered phase near the edge of chaos [30]. Figure 4 shows the plot for each of the nine colonies. For a given colony, the dynamics was started with integral values of H(0) ranging between zero and a maximum value equal to the size of the colony, and the value of the Hamming distances after a single time step was computed. In figure 4, we restrict the largest value of H(0) to 10 as we were interested in the low H region. The points are joined by solid lines as guides to the eye. Figure 4 shows that all the curves are below but near the H(1) = H(0) line, suggesting the stability against small perturbations and efficient flow of information.

Figure 4.

Evolution of the initial Hamming distances, H(0) with one time step to H(1), for networks obtained from nine different colonies of R. marginata. The dynamics corresponding to each of the H(0) is averaged over 10⁵ different initial random configurations. The dashed line signifies H(1) = H(0). Legends show colony identities. (Online version in colour.)

5.2. The effect of design

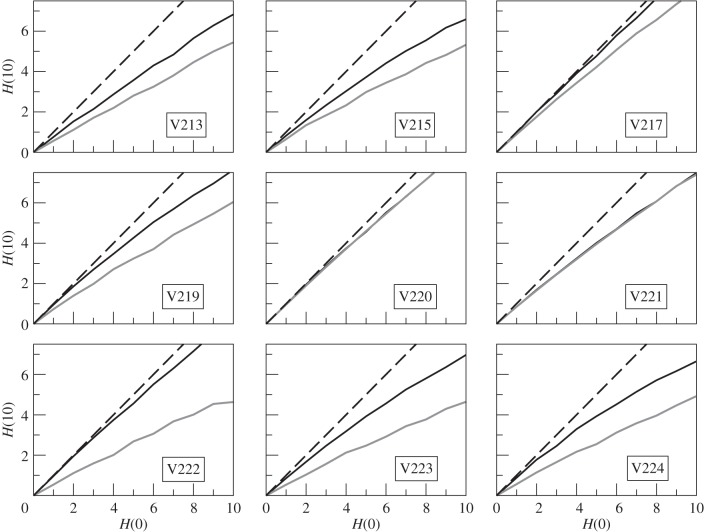
To examine the influence of network architecture over the information transfer dynamics, the time evolution of the Hamming distance as a function of initial distance was compared with that of the randomized version [45] of the network. If the architecture of the original networks influence information transfer, we expect to obtain patterns different from those of the randomized networks [34]. The differences, if any, would be prominent only after t = 1, because the changed outputs could be used as inputs only after the first time step [34]. We chose an arbitrary duration t = 10 and plotted H(10) against H(0) for both the original and randomized networks in figure 5. We found that the original networks (black curves) are near the critical phase, whereas the randomized counterparts (grey curves) are generally in more ordered phase. In particular, the randomized curves are significantly below the original curves in seven colonies (V213, V215, V217, V219, V222, V223 and V224, t-test, all p < 0.0005), whereas the other two are indistinguishable (t-test, both p > 0.4).

Figure 5.

Evolution of the initial Hamming distances, H(0) with 10 time steps to H(10), for networks obtained from nine different colonies of R. marginata. Black solid curves represent original networks, the dynamics corresponding to each of the H(0) is averaged over 10⁴ random initial conditions. Each original network is randomized 10² times and the dynamics being averaged over 10⁴ initial configurations (grey solid curves). The dashed lines signify H(10) = H(0). Legends show colony identities.

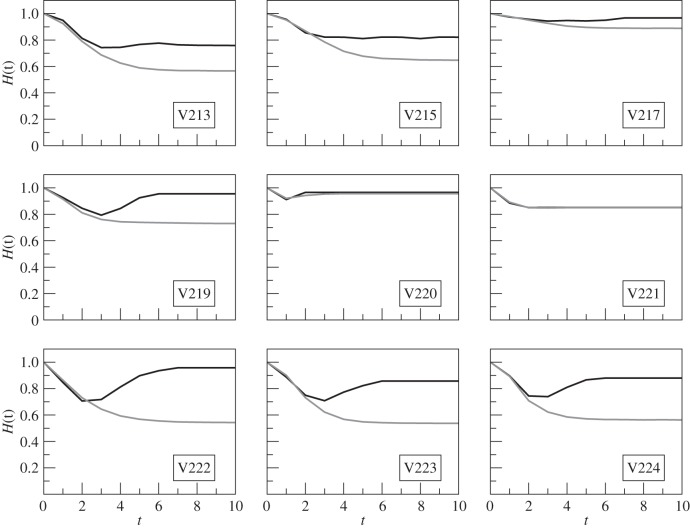
We also investigated changes in predetermined Hamming distances H(t) over time (figure 6). Starting from H(t) = 1 at t = 0, we plot the mean Hamming distances H(t) as a function of time t, for both the original networks (black curves) and the randomized networks (grey curves). We found that, in the same seven colonies, the randomized H(t) is significantly below the original H(t) (t-test, all p < 0.0005). In the results depicted in figures 5 and 6, standard errors of measurements were of the order of 0.01 or less; therefore, they would be rather invisible. Therefore, at least in seven colonies, the original network is less frozen than its randomized counterparts, which means that in the randomized networks information dies out more quickly and the original network is comparatively more capable of holding information. Since the structural pattern of the networks became destroyed in the randomization process, this less frozen property of the original networks could be attributed to their distinctive structure. This attribution is well supported by the observation that, of the seven less frozen colonies, five are in common with the six colonies where the feed-forward loop was observed significantly more than random. The mean normalized Z-score of the feed-forward loop for the seven less frozen colonies is 0.43 ± 0.26 which is larger than that for all the nine colonies taken together. Therefore, we would like to infer that the dominance networks of R. marginata are designed for the specific purpose of information transfer with the ‘feed-forward loop’ being a key functional element.

Figure 6.

The time evolution of the Hamming distances starting from H(0) = 1, for networks obtained from nine different colonies of R. marginata. Black solid curves represent original networks, the dynamics corresponding to each of the H(0) is averaged over 10⁴ random initial conditions. Each original network is randomized 10² times and the dynamics being averaged over 10⁴ initial configurations (grey solid curves). Legends show colony identities.

6. Conclusions and future directions

In recent years, network substructure analysis of complex systems has gained much attention among scientists. Several biological and technological networks have been grouped into superfamilies based on similarities in the statistics of possible substructures. It has been noted that the members of the same superfamily perform similar tasks. Our investigation into the local structure of the networks constructed from the dominance interactions in R. marginata allows parallels to be drawn with a distinctive superfamily of naturally evolved information processing networks. The structure of the latter networks is characterized by the statistical over-representation of a particular triad, the feed-forward loop. This triad is also over-represented in the dominance networks of R. marginata. The networks in the superfamily are known for their rate-limited dynamics. We have reasoned that the functioning of the dominance networks of R. marginata is also rate-limited. By contrast, the networks constructed from paired interactions in R. marginata, other than dominance, fail to show any such similarity or statistical significance. This result is supporting evidence favouring the role played by dominance interactions in information processing. However, the presence of substructures alone cannot ensure the overall functioning of a network. To understand whether the information transfer through dominance can indeed be called efficient, we model the dynamics of information transfer using simple Boolean functions and compare our results against a suitably randomized ensemble. Our result supports the idea that there exists common evolutionary design principles by which the biological regulatory networks are optimized. Further research along this direction would allow for more accurate prediction of the properties of a newly identified network on the basis of other networks in the same superfamily.

On the other hand, we have tried to reason the existence of the dominance behaviour, the purpose of which still remains an intriguing aspect among evolutionary biologists in the context of social insect colony organization [64,65]. The queen in the most studied primitively eusocial wasp P. dominulus is known to use dominance to gain reproductive monopoly over her colony members [11]. But in the colonies of tropical species R. marginata, the queen usually shows very little or no dominance at all [66], though a clear dominance hierarchy can be recognized in the colony [67]. Such dominance behaviour among the workers cannot be associated with the reproductive competition, because there is no correlation between the dominance rank of an individual and the probability that she will replace a lost or removed queen [68]. With some experimental correlates, it has been argued earlier that the workers use dominance to transfer information about the colony needs to their co-workers, which is essential for their self-organized regulation of work [15–17]. However, there has been no previous study of how efficient such a mechanism can be. This study suggests that the dominance networks of R. marginata are designed for efficient information transfer, and hence might be used for self-regulation, not only for meeting the colony demands for food, but also for other maintenance activities such as nest-building, thermoregulation, defence, etc. However, we should mention that a more direct approach would be a sequential analysis of dominance behaviour and the related worker activities, or a study of changes in the network substructures under experimental removal of key nodes. Therefore, a plausible hypothesis that could be favoured by our findings is that, in the course of evolution, the dominance behaviour in the social wasps has been adapted for information transfer in addition to its primal function of reproductive monopoly maintenance. This hypothesis also needs to be experimentally tested in this and other insect societies.

Dominance behaviour is known to have existed, not only in insect societies, but also in many other group-living animals; for example in birds [69], cattle [70], fish [71], primates [72] and in other quadrupeds [73,74]. It has also been long observed that, in most of the cases, the dominance relationships are surprisingly transitive [75]. Later studies with greater attention to the patterns in such relationships have revealed the relative abundance of acyclic triads (triad 7) and the relative lack of cycles (triad 8) when compared to their Erdős–Rényi random graph counterparts [76,77]. However, many of the real societies consist of individuals with diverse capacity of interaction that are non-random in nature [78], and an unconstrained choice of random graph ensemble, which assumes that the interactions are equally likely between any pair of nodes, may be erroneous [79]. Therefore, a biologically realistic null-model that preserves the characteristics of the individuals as well as the global structural properties (such as the degree-distribution), should be used to probe the local connectivity patterns of the networks [25,79,80]. This form of network randomization is rather rare in behavioural sciences [79], and ours is the first study that has used this stringent condition in the null-models of dominance networks. In the near future, we would like to investigate the procedure of randomization that preserves a predetermined hierarchy in a network.

Funding statement

This study was supported by the Department of Biotechnology, Department of Science and Technology, Ministry of Environment and Forests, Council for Scientific and Industrial Research, Government of India, and BITS Pilani Research Initiation Grant Fund.