The effects of relative food item size on optimal tooth cusp sharpness during brittle food item processing

Abstract

Teeth are often assumed to be optimal for their function, which allows researchers to derive dietary signatures from tooth shape. Most tooth shape analyses normalize for tooth size, potentially masking the relationship between relative food item size and tooth shape. Here, we model how relative food item size may affect optimal tooth cusp radius of curvature (RoC) during the fracture of brittle food items using a parametric finite-element (FE) model of a four-cusped molar. Morphospaces were created for four different food item sizes by altering cusp RoCs to determine whether optimal tooth shape changed as food item size changed. The morphospaces were also used to investigate whether variation in efficiency metrics (i.e. stresses, energy and optimality) changed as food item size changed. We found that optimal tooth shape changed as food item size changed, but that all optimal morphologies were similar, with one dull cusp that promoted high stresses in the food item and three cusps that acted to stabilize the food item. There were also positive relationships between food item size and the coefficients of variation for stresses in food item and optimality, and negative relationships between food item size and the coefficients of variation for stresses in the enamel and strain energy absorbed by the food item. These results suggest that relative food item size may play a role in selecting for optimal tooth shape, and the magnitude of these selective forces may change depending on food item size and which efficiency metric is being selected.

1. Introduction

One of the many ways in which mammals are unique is that they chew their food before they swallow. This has led to functional differentiation of mammal teeth, where anteriormost teeth (incisors) are used primarily to break food into smaller pieces and posteriormost teeth (molars) are used primarily to break down the food item prior to digestion [1]. Analyses of molars have led to a number of metrics that quantify tooth shape (e.g. orientation patch count [2,3], the relief index [4,5], angularity [6,7] and Dirichlet normal surface energy [8,9], see [10] for a review) in order to infer function. While distinct, these metrics share a common assumption: tooth shape reflects tooth function, which allows dietary signatures to be derived from tooth shape. Current metrics of tooth shape are used to infer broad dietary categories and/or foods with specific sets of mechanical properties. These dental metrics, however, disregard food item shape or size, and so they discount any potential relationship between the size of food items and tooth morphology.

One metric that has been used to quantify tooth shape is tooth cusp sharpness [11–13]. Tooth cusp sharpness is commonly measured by radius of curvature (RoC), where cusps with higher RoCs are duller and cusps with lower RoCs are sharper. During interactions between single cusps and food items, sharper cusps reduce the contact area between the tooth and the food item, leading to a reduction in energy and reaction force needed to induce a fracture in the food item [14–17]. This increases the efficiency of food breakdown, but at a potential cost to the tooth. The reduction in contact area also causes the stresses in the tooth to increase, increasing the probability of enamel fracture [18]. In complex, multi-cusped teeth, the relationships between cusp sharpness, efficiency and probability of enamel fracture are less obvious [19].

In single-cusped teeth, stresses, reaction forces and contact area between the tooth and food item are dependent on the relative and absolute size of the cusp and food item (see contact mechanics [20]). Consequently, a relatively small, spherical food item would cause different stresses, reaction forces and contact area when indented a given displacement into a tooth than would a relatively large, spherical food item. The same holds true when a sphere comes into contact with a flat plate (i.e. a tooth cusp indenting a flat food item). It is therefore reasonable to hypothesize that these efficiency metrics might also be affected by relative and absolute size during interactions between multi-cusped teeth and food items.

In multi-cusped teeth, RoC is measured in terms of either blade or cusp sharpness [11,19,21–23]. Blade and cusp sharpness differ in that they are affected by tooth wear in different ways. Cusps become duller as they wear (i.e. RoC increases) until dentin is exposed, whereas blades become duller or sharper depending on the levels of attrition (tooth–tooth wear) and abrasion (tooth–food item wear) [21,22,24–26]. Therefore, cusp wear prior to dentin exposure increases cusp RoC and probably decreases the tooth's efficiency, whereas blade wear can increase, decrease or maintain blade RoC and accordingly decrease, increase or maintain the tooth's efficiency [22,27].

The relationship between blade and cusp RoCs and size has been investigated in allometric studies, and has led to puzzling results [13,21,22]. There was no relationship between blade RoC and body size in mammals larger than 1 kg, but it does exist in more diminutive mammals [21]. However, the fact that large species of different body sizes but similar diets sometimes differ in tooth shape, with larger ones having duller teeth (e.g. Bison bison) and smaller ones having sharper teeth (e.g. Alcelaphus buselaphus), suggests that some type of allometric relationship may be present [22]. One possible explanation is that blade sharpness is correlated with another factor (e.g. bite force, enamel thickness, tooth size) that is correlated with body size [21,28]. The only study of allometric scaling in cusp sharpness revealed a weak, positive correlation between tooth cusp RoC and tooth cusp size in large animals [13]. However, data need to be gathered on smaller mammals before any definitive conclusions can be drawn.

Regardless of whether or not there is an allometric relationship between size and cusp sharpness, it is possible that tooth function changes based on the relative size of the food item. For example, patas monkeys (Erythrocebus patas), chimpanzees (Pan troglodytes) and gorillas (Gorilla gorilla, Gorilla beringei) are all known to eat ants [29] but they vary greatly in tooth size [30,31]. Ants are larger relative to tooth size for Erythrocebus than for either Pan or Gorilla. This leads to a different functional interaction between the food item and the tooth (figure 1). The function of the Erythrocebus tooth may be to cut and crush the ant, whereas the function of the Gorilla tooth may be to crush and grind the ant [26].

Figure 1.

An ant (length = 2.0 mm) being shown relative to a theoretical cross section of a tooth being isometrically scaled to the width of E. patas (left), P. troglodytes (centre) and G. gorilla (right) teeth. Note how the cusps of the tooth on the left look sharper relative to the ant than the cusps of the tooth on the right.

Here, we investigate the importance of taking relative food item size into account when analysing tooth cusp RoC by testing two hypotheses. The first hypothesis states that optimal tooth shape will be independent of relative food item size. As established under the complex cusp hypothesis in [19], an optimal morphology for brittle food item fracture maximizes the tensile stresses in the food item, causing food item fracture [19,32], while minimizing the tensile stresses in the enamel, preventing enamel fracture [18,33–35]. Optimality is judged using the following criterion:

1.1

More optimal teeth have higher optimality ratios. The first hypothesis would be supported if the optimal set of tooth cusp RoCs were constant across a range of food items that differ in size but not in shape (or material properties).

The second hypothesis is that the range of effective combinations of tooth cusp RoCs varies depending on the size of the food item. In other words, food items of certain sizes are best fractured with a limited range of tooth morphologies, causing a large level of variation in efficiency metrics across all tooth morphologies, whereas food items of other sizes can be fractured equally efficiently with a broad range of tooth morphologies, causing a low level of variation in efficiency metrics across all tooth morphologies. In addition to the optimality ratio, we gathered data on three measures of efficiency that have been hypothesized to be important in fracturing brittle food items: maximum tensile stresses in the food item [14,17,36,37], maximum tensile stresses in the enamel [33,34,36,38] and energy absorbed by the food item [26,39]. We quantified variation in efficiency metrics using the coefficient of variation, which provides a unitless measure of variation independent of size effects.

2. Material and methods

We used a parametric finite-element (FE) model of a four-cusped, maxillary molar in ANSYS APDL 13.0 (ANSYS, Inc., Canonsburg, PA) to test our null hypotheses (figure 2). Details concerning the construction of the model are discussed in [19]. All parameters other than tooth cusp RoCs were held constant at the following values: cusp height = 5 mm, valley height = 3 mm, enamel thickness = 1 mm, mesiodistal distance between cusps = 15.7 mm, buccolingual distance between cusps = 15.4 mm. Distances between cusps were based on the average width and length of a male gorilla tooth [31]. Cusp RoCs were assigned one of three values: sharp (3 mm), medium (5 mm) or dull (7 mm). Tooth cusp sharpness was allowed to vary independently in the buccolingual and mesiodistal directions, for a total of eight variables [13,23]. Food items were modelled as hollow hemispheres and isometrically scaled to be small, medium, large or x-large (outer radii = 5.9, 10.0, 14.1 and 18.2 mm, inner radii = 4.82, 8.16, 11.5 and 14.84 mm respectively; figure 3). Food item sizes were dictated by available materials (hemispheres) and not intended to represent a particular food item [36]. Each model (tooth and food item) consisted of approximately 110 000 linear tetrahedral elements and 150 000 nodes. A mesh convergence study previously conducted by the authors revealed this level of mesh refinement to be adequate [19,28].

Figure 2.

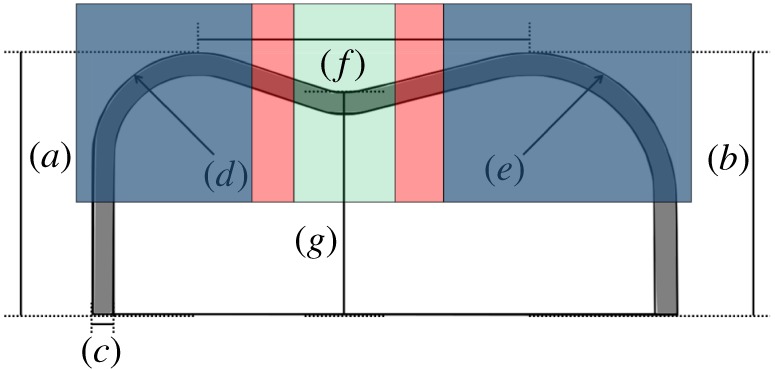
Cross section between two of the cusps (a,b) showing some of the parameters that can be varied in the model. a, height of cusp a; b, height of cusp b; c, enamel thickness; d, RoC of cusp a; e, RoC of cusp b; f, distance between cusps a and b; g, height of valley between cusps a and b. The blue panels on the outside depict two cusps, the green panel in the centre represents a valley, and the red panels represent two transitional zones, where the food item would interact equally with the cusps and valleys. (Online version in colour.)

Figure 3.

Four hollow, hemispherical, food items shown with the parametric molar. (Online version in colour.)

The proxy food item FE models were positioned slightly above and centred over the occlusal surfaces of the tooth FE models. Constraints were placed on the bottom of the hemisphere to prevent translation away from the tooth and to prevent rotation around an imaginary axis perpendicular to the tooth through the apex of the food item. This allowed the food item to settle into the position of minimum potential energy on the occlusal surface of the tooth during the simulations [36]. Constraints were also placed on the bottom of the tooth to prevent it from translating in the mesiodistal or buccolingual directions. The bottom of each tooth was displaced 3 mm, translating it into the food item in the inferior direction to simulate biting.

Contact elements (CONTA174) were placed on the outside surface of the food item models, and target elements (TARGE170) were placed on the outside surface of the tooth models, allowing ANSYS to detect when the tooth is interacting with the food item. Contact simulations were solved in a minimum of 10 substeps to increase accuracy. Results (maximum tensile stresses on the inner surface of the food item and along the enamel–dentine junction (EDJ), energy absorbed by the food item, displacement of the tooth and reaction force) were exported at each substep. Equations were constructed of reaction force versus displacement, and displacement versus stresses and energy, so the displacement, energy and stresses at a 2 kN reaction (aka bite) force could be interpolated [19,40].

To test the first hypothesis, optimal combinations of RoCs were determined for each of the four food item sizes. This was done by creating four morphospaces, one per food item size, using an L18 orthogonal array and the Taguchi sampling method. The Taguchi method is a statistical, partial factorial sampling method which allows users to run the minimum number of simulations necessary to construct a multi-variate morphospace [41–43]. Optimal subsections of the four morphospaces were sampled until the optimal RoCs were obtained for each food item size, resulting in an additional 25–40 simulations per morphospace. While RoCs are continuous variables in nature, they are treated as discrete variables here (RoC = 3, 5 or 7 mm). Any change in RoC would qualify as a change in tooth shape.

The Taguchi method allows for an unbiased sampling of design variables and provided 18 distinct tooth morphologies from 18 equally spaced points across the morphospace. These 18 morphologies thus provided an ideal set of teeth for testing the second hypothesis (see [19] for information concerning tooth morphologies created using the Taguchi method). While many measures of the efficiency of food item breakdown could be taken into account (e.g. stresses, reaction force, energy, displacement [16,17,19,33,36,37,44–48]), we chose to look at the four measures of efficiency hypothesized to be correlated with tooth cusp RoC: the optimality ratio, maximum tensile stresses in the food item and enamel, and energy absorbed by the food item. The first three criteria are of particular importance during brittle food item fracture, whereas the fourth is more important during ductile fracture of foods.

The coefficients of variation were calculated for each food item size using data from the 18 tooth morphologies samples from the morphospaces. Therefore, each food item size had four coefficients of variation, one per efficiency metric per food item size. As there were only four coefficients of variation per efficient metric, it was not possible to statistically test whether the coefficients of variation were changing with respect to food item size.

3. Results

Three distinct optimal tooth shapes were derived from the four morphospaces: one for the small food item, one for both the medium and large food items and one for the x-large food item (figure 4 and table 1). The optimal morphologies are similar in the location of cusp RoC magnitudes and directions, consisting of one mesiolingual cusp that is dull in both the buccolingual and mesiodistal directions, one mesiobuccal cusp that is sharp in the buccolingual direction and dull in the mesiodistal direction, and two distal cusps that are sharp in the mesiodistal direction. The differences in morphology lie in the buccolingual RoCs of the distal cusps, which are dull, sharp or a mixture of dull, medium and/or sharp.

Figure 4.

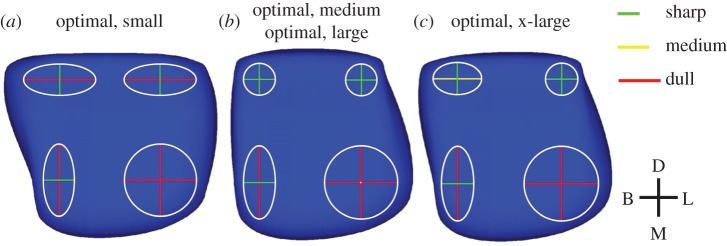
Three optimal morphologies for the small (a), medium (b), large (b) and x-large (c) food items. Sharp cusps are denoted by short, green lines, medium cusps are denoted by medium length, yellow lines and dull cusps are represented by long, red lines. (Online version in colour.)

Table 1.

Coefficients of variation for measures of efficiency drawn from morphospaces predicted for small, medium, large and x-large food items. A high coefficient indicates that a morphospace contains a narrow range of efficient morphologies, whereas low coefficients indicate that a morphospace contains a wider range of efficient morphologies.

	optimality ratio	maximum tensile stress, food item	maximum tensile stress, enamel	strain energy
small	10.1	13.0	10.1	10.8
medium	9.8	15.3	9.4	9.6
large	12.7	18.8	6.7	8.5
x-large	14.5	19.0	6.2	9.2

Numerical results from the Taguchi simulations, along with the simulations of the optimal morphologies, can be found in the electronic supplementary material, appendix A and table S1. Overall, there is an increase in the optimality ratio, maximum tensile stresses in the food item, maximum tensile stresses in the enamel and energy absorbed by the food item as the food item decreases in size. This is because, as the food item decreases in size, the thickness of the hemisphere decreases, reducing the effective stiffness of the system and allowing the smaller foods with thinner shells to deform more than the larger, thicker-shelled foods. This causes an increase in strains, which in turn causes an increase in stresses and an increase in the amount of energy absorbed by the smaller foods. The smaller foods also result in a decrease in contact area between the tooth and the food item, causing the 2 kN force to be transferred over a smaller area, leading to an increase in the tensile stresses in the enamel (figure 5). Because the maximum tensile stresses in the food decreased at a faster rate than in the enamel as the food item increased in size, the optimality ratio decreased as the food item increased in size.

Figure 5.

Tensile stress distributions along the EDJ (top) and inner surface of the hollow, hemispherical food item (bottom). (Online version in colour.)

The averages, 95% confidence intervals and coefficients of variation for the efficiency metrics are presented in figure 6 and table 2 (see electronic supplementary material, appendix A for numerical results). There are negative relationships between the coefficients of variation of maximum tensile stresses in the food item and the optimality ratio and food item size, and there are positive relationships between the coefficients of variation of maximum tensile stresses in the enamel and strain energy and food item size.

Figure 6.

Averages for the efficiency metrics with 95% confidence intervals.

Table 2.

Amount of force transferred from the dullest (mesiolingual) cusp of the optimal tooth models to the food item.

	force transferred (kN)	total bite force (%)
small	1.232	61.60
medium	1.215	60.75
large	1.147	57.37
x-large	1.135	56.75

4. Discussion

As food item size changed, so did the optimal tooth morphology, supporting the hypothesis that optimal tooth shape changes with the relative size of the food item. All optimal teeth were fairly similar, consisting of one very dull mesiolingual cusp, one blade-like mesiobuccal cusp, and two distal cusps that are sharp in the mesiodistal direction.

Each cusp serves a distinct purpose: either to promote high stresses in the food item or to stabilize the food item and cause it to interact in an efficient way with the mesiolingual cusp. In all optimal teeth, the dullest (mesiolingual) cusp transferred 57–62% of the 2 kN bite force to the food item (table 3), producing a high stress concentration along the inner surface of the food item while dissipating the stresses in the enamel (figure 5). The other three cusps acted primarily to stabilize the food item and force it to interact with the dull, mesiolingual cusp. All optimal teeth minimized the number of stress concentrations in the food item to two, whereas the least optimal teeth had up to four stress concentrations in the food item, causing a more uniform stress distribution in the food item. While a uniform stress distribution in the food item may be advantageous for crushing/grinding/pulverizing foods, it is not advantageous for creating the high stress concentrations necessary for breaking down brittle food items.

Table 3.

Results from the optimal tooth morphologies. Because the food item was hollow and isometrically scaled, the smaller food items are thinner than the large food items, making them more flexible and giving them the ability to deform more. This causes them to have higher stresses and for them to absorb more energy. This also affects the tensile stresses in the enamel.

tooth	optimality				strain energy (mJ)				maximum tensile stress, food item (MPa)				maximum tensile stress, enamel (MPa)
	food item size				food item size				food item size				food item size
	small	medium	large	x-large	small	medium	large	x-large	small	medium	large	x-large	small	medium	large	x-large
optimal, small	2.283	2.028	1.492	1.099	839	643	480	376	229	209	150	92	100	103	100	84
optimal, medium and large	2.212	2.039	1.640	1.204	820	652	495	393	207	209	150	99	93	102	91	82
optimal, x-large	2.127	2.016	1.594	1.272	828	652	489	370	209	210	149	94	98	104	94	74

While the three optimal tooth morphologies have different RoC values, they share similar characteristics, with only the buccolingual RoCs on the two distal cusps differing. This change occurred because, as the food item increased in size, the fundamental interactions between the tooth and the food item changed. The small food item interacted primarily with the valleys between the cusps, whereas the medium and large food items interacted nearly equally with the valleys between the cusps and the cusps themselves, and the x-large food item interacted primarily with the cusps themselves (figure 5).

The changes in the distal cusps of the optimal morphologies for the small and medium/large food items reflects changes necessary for food item stabilization. Small food items nestled in the valleys between the cusps and the distal cusps needed to be larger (i.e. duller) in order to maximize the stability of the food item, and force it to interact with the dull mesiolingual cusp. As the food item increased in size (i.e. medium and large food items), it still mostly fitted in the valleys between the cusps, but only when the distal cusps were sharper, increasing the size of the valleys. Therefore, food item stabilization was done by both the valleys and the cusps themselves. Finally, when the food item was x-large, it was too large to fit in the valleys and the food item could only be stabilized by the tips of the cusps themselves. This caused the distal cusps to be duller. Meanwhile, the mesiobuccal cusp remained sharp in the buccolingual direction to allow the food item to have enough space to interact primarily with the mesiolingual cusp, and dull in the mesiodistal direction to form a barrier that prevents the food item from drifting too far in the buccal direction.

The optimality ratio effectively summarizes how theoretical teeth fracture brittle food items, but it has limitations. First, fracture mechanics operate under the assumption that all materials have inherent flaws and microcracks, and these microcracks will propagate through the materials and cause failure after a given amount of energy has been absorbed through the application of stresses [49]. The optimality ratio does not take energy into account. However, dental enamel is riddled with microcracks and requires substantial overloading to fail [50,51]. The optimality ratio assumes these microcracks are evenly and randomly spread along the EDJ [19]. Therefore, high tensile stresses increase the likelihood that the material around one of these cracks will absorb enough energy to propagate and cause enamel failure. Second, there may be a threshold value for the optimality ratio above which there is no selective advantage, and so an animal with a higher optimality may not experience increased fitness.

There were clear associations between the coefficients of variation and food item size. The positive associations between the coefficients of variation for stresses in the food item and the optimality ratio and food item size suggest that there is a narrow range of tooth morphologies that are efficient at creating high stresses in the food item and optimal when the food item is large. Therefore, if efficiently creating stresses in the food item or having an optimally shaped tooth is important, there may be greater selective pressure on tooth cusp RoC when the food item is relatively large compared with when the food item is relatively small. The negative associations between the coefficients of variation for enamel stresses and strain energy and food item size suggest fewer tooth morphologies can efficiently reduce enamel stresses and strain energy when the food item is small compared with when it is large. Therefore, if efficiently reducing enamel stresses or strain energy is important, there may be greater selective pressure for tooth cusp RoC when the food item is relatively small compared with when the food item is relatively large.

On the basis of table 2, we predict that if selection acts to maximize the optimality ratio or to maximize tensile stresses in food items, there should be a narrower range of RoCs among species that consume large food items and a broader range in RoCs among species that consume small food items. Similarly, if selection acts to minimize strain energy absorbed by the food item or to maximize tensile stress in the enamel, there should be a narrower range of RoCs among species that consume large food items and a broader range of RoCs among species that consume small food items. Pongo pygmaeus is known to be a seed predator, and consumes relatively large Mezzettia seeds [40,52–54]. It also has a large coefficient of variation in tooth cusp RoC measurements, the largest of all the great apes (refer to table 2 [13]). Based on these analyses, this implies that selection may have acted towards reducing stresses in enamel or strain energy absorbed by the Mezzettia seeds in P. pygmaeus. This is consistent with the hypothesis that P. pygmaeus's thick molar enamel is an adaptation to reduce the stresses in the tooth and prevent enamel fracture [35,53,55]. It also supports the strong cusp hypothesis [36].

Although this study investigated the effects of food item size on low-crowned teeth, the results have implications that can apply to other tooth morphologies. As relative food item size changes, the fundamental interactions between the food item and any complex, multi-cusped teeth will change. Therefore, the relative sizes of food items that mammals consume could play a role in the evolution of optimal tooth shape. Similarly, the relative size of food items may also affect the evolution of simpler teeth if more than one tooth interacts with the food item during mastication. Finally, it is possible that these results can be extended to non-mammalian teeth, and even some structures that are used for crushing in invertebrates (e.g. claws, mandibles, beaks). While this study focused on one metric of tooth shape (RoC), it is possible that the results are applicable also to other metrics.

Many studies have demonstrated a close relationship between the mechanical properties of food items and tooth shape [11,15,56–58]. This study adds a new dimension to investigating the evolution of tooth shape by demonstrating that the relative size of food items may also be an important factor.

5. Conclusion

As brittle, spherical food items increase in size, their fundamental interactions with the occlusal surfaces of teeth change, going from interacting primarily with the valleys between the cusps to interacting primarily with the cusps themselves. This change leads to distinct optimal occlusal morphologies for food items of different size. We found evidence that food items of some sizes are best fractured with a limited range of tooth morphologies, whereas others can be fractured equally efficiently by a broad range of tooth morphologies. These results support the idea that tooth cusp RoC should not be normalized for by tooth size: instead, if it is necessary to normalize RoC, it should be done by relative food item size [13]. The fact that food item size may affect optimal tooth shape probably holds true for all complex, multi-cusped teeth, as well as simple, single-cusped teeth when multiple teeth interact with food items.

Further investigations into the impact of the relative size and shape of food items on other tooth shape metrics (e.g. relief index) may reveal correlations between these metrics and food item shape and size as well. Finally, extending these analyses to the microscale may offer some insights into the effects of internal tooth structure (e.g. enamel decussation [59] and the distribution of enamel thickness [60,61]) on food item breakdown, and be able to further expand our understanding of the biomechanics of microwear [62].