Comparison of nine methods to estimate ear-canal stimulus levels

Abstract

The reliability of nine measures of the stimulus level in the human ear canal was compared by measuring the sensitivity of behavioral hearing thresholds to changes in the depth of insertion of an otoacoustic emission probe. Four measures were the ear-canal pressure, the eardrum pressure estimated from it and the pressure measured in an ear simulator with and without compensation for insertion depth. The remaining five quantities were derived from the ear-canal pressure and the Thévenin-equivalent source characteristics of the probe: Forward pressure, initial forward pressure, the pressure transmitted into the middle ear, eardrum sound pressure estimated by summing the magnitudes of the forward and reverse pressure (integrated pressure) and absorbed power. Two sets of behavioral thresholds were measured in 26 subjects from 0.125 to 20 kHz, with the probe inserted at relatively deep and shallow positions in the ear canal. The greatest dependence on insertion depth was for transmitted pressure and absorbed power. The measures with the least dependence on insertion depth throughout the frequency range (best performance) included the depth-compensated simulator, eardrum, forward, and integrated pressures. Among these, forward pressure is advantageous because it quantifies stimulus phase.

I. INTRODUCTION

Widespread use of otoacoustic-emission probes (henceforth abbreviated to “probes”) containing both a low-noise microphone and sound sources has stimulated studies on the level calibration of acoustic stimuli in the human ear canal, where the substantial distance between the probe and the eardrum inevitably leads to spatially non-uniform pressure (Stinson et al., 1982; Siegel, 1994; Neely and Gorga, 1998; Farmer-Fedor and Rabbit, 2002; Scheperle et al., 2008; Scheperle et al., 2011; Keefe and Schairer, 2011). While these studies have yielded fundamentally important results, there has been no systematic evaluation of how well alternate calibration methods compare with the standard calibration of insert earphones in acoustic couplers or ear simulators. We report here a comparison of the sensitivity of behavioral thresholds of human subjects to intentional changes in the depth of probe insertion into the ear canal when referenced to nine measures of sound level. With an eye toward the eventual adoption as standards of those alternate methods that demonstrably improve on the state of the art, we included standardized calibration of the probe's sound sources in an ear simulator [American National Standards Institute (ANSI), 2009; International Electrotechnical Commission (IEC), 2010] as the baseline for comparison.

Standing waves pose a serious obstacle to accurate in-ear stimulus calibration. Otoacoustic-emission (OAE) probes and insert earphones are typically placed in the adult human ear canal some 15–20 mm from the eardrum. Emission probes are advantageous in that they directly measure the sound stimulus, but they also pose significant challenges. The initial forward going sound wave emitted by the probe is partially reflected by the eardrum. This first reflected wave is subsequently reflected at the probe back toward the eardrum in a series of multiple reflections that decay in amplitude as power is dissipated within the system (Keefe and Schairer, 2011). The steady-state pressure is determined by the relative magnitudes of the forward and reverse waves within the canal. For frequencies below 1 kHz, the wavelength is appreciably longer than the acoustic path between the probe inlet and the eardrum so that the phase shift between forward and reverse pressure waves measured by the emission probe's microphone is small and the pressure in the ear canal is essentially uniform. As the frequency is raised, the phase shift between forward and reverse waves increases, and the resulting interference creates standing waves in the canal (Stinson et al., 1982). Depending on the reflectances of the eardrum and probe (Keefe and Schairer, 2011), nulls in the pressure at the probe near odd multiples of $\frac{1}{4}$ wavelength can be as much as 20-dB deep (Siegel, 1994; Siegel and Hirohata, 1994; Dreisbach and Siegel, 2001). Equalizing the stimulus pressure according to the probe measurement results in large peaks in eardrum pressure within ∼$\frac{1}{3}$ octave of the quarter-wave frequencies (Siegel, 1994). Thus, stimulus calibration based on pressure at the probe, a common practice in OAE measurements, affords poor control of eardrum pressure.

The influence of standing waves is partly mitigated by calibrating the sound sources of OAE probes (or earphones) by means of acoustic couplers that approximate the ear to varying degrees of accuracy. The best are referred to as ear simulators, in that they approximate the acoustic impedance of average adult ears through the simulator's geometry and inclusion of acoustic networks. Two such devices, the Zwislocki Coupler (DB100) (ANSI, 2009) and its replacement, formerly specified in IEC-0711 (now described in IEC, 2010 and ANSI, 2009), mimic the adult human ear reasonably well, at least below 8 kHz. Ear-simulator calibration reduces the influence of standing waves because the microphone of the simulator serves as a surrogate eardrum and the pressure it measures approximates the pressure at the eardrum of the average adult ear. However, ear simulators do not take into account differences between individual ears. These variations are of particular concern for high-impedance sound sources inserted into the ear canal (Voss et al., 2000; Voss and Herrmann, 2005).

The most direct way to reduce the influence of standing waves in real ears is to measure the sound pressure at the tip of a flexible probe-tube microphone placed near the eardrum (Stelmachowicz et al., 1982; Dreisbach and Siegel, 2001, 2005). Probe-tube microphones provide a reasonably accurate measurement of eardrum pressure at frequencies <8 kHz, at which wavelengths are relatively long compared with the diameter of the ear canal and the canal and eardrum can be approximated by cylindrical geometry (Stinson, 1985; Gilman and Dirks, 1986). In this frequency range, pressures measured by a probe tube at a single site near the eardrum closely approximate pressures applied at any point on the eardrum. At higher frequencies, however, the cylindrical assumption fails: The tilted orientation of the eardrum (particularly severe for neonates), together with short wavelengths, produce eardrum pressures that vary with position, so that no single placement of a small probe tube accurately represents the eardrum pressure (Stinson et al., 1982; Rabbitt and Friedrich, 1991). Aside from these physical limitations of probe tubes, it is also difficult to assure proper placement near the eardrum, so this approach is not a good solution to calibration in humans over the full frequency range of hearing.

In the present study, we compare two general types of calibration method of the probe's sound sources: (a) using an ear simulator and either a standard protocol or a protocol that compensates for insertion depth (Lee et al., 2012), and (b) using pressure measurements in the ear canal. Most measurements in the latter category are based on the probe's Thévenin-equivalent source characteristics. Each are reviewed briefly and specific applications or modifications are discussed in the methods section.

A. Ear-simulator methods

Insert earphones are most often calibrated in hearing clinics using simple couplers (i.e., variants of the 2cc coupler specified in ANSI, 1995) that approximate the volume of the occluded ear canal but only crudely its geometry and acoustic impedance. Here we use two variants of ear simulators, more elaborate than the simple couplers, to assess whether alternate approaches to pressure calibration control the input to the ear better than the coupler methods defined in current acoustical standards.

1. Standard ear-simulator calibration

In the standard procedure for calibrating insert earphones the end of their ear tip is placed at a defined reference plane of the simulator so that they generate pressures working into the same acoustic impedance. The pressure measured by the simulator's microphone is then used to adjust the drive level to the earphone to produce a reference pressure at each of a set of standard frequencies [ANSI, 1995; International Organization for Standardization (ISO), 1997; ISO, 2006]. The standard calibration makes no adjustment for individual ears or for the depth of insertion of the earphone or emission probe into the ear canal. We will refer to the pressure measured using the standard simulator calibration as P_{sim_S}.

2. Depth-compensated ear-simulator calibration

In this method, insert earphones are calibrated at different insertion depths in an ear simulator to estimate the sound pressure at the eardrum (referred to here as P_{sim_D}). As summarized by Gilman and Dirks (1986), the simulator method produces “…a family of standing wave curves from which the precise values of eardrum sound pressure level (SPL) can be determined from measurements made in the ear canal at specified distances from the eardrum.” In the present study we implement a similar method (described in detail by Lee et al., 2012; see Sec. II C 1).

B. Acoustic quantities derived using Thévenin source calibration

It has been suggested that estimates of the input to the ear based on pressure remote from the eardrum in the relatively straight portion of the canal and combined with Thévenin-equivalent probe calibration, are inherently superior to estimates based on probe-tube measurements near the eardrum (e.g., Farmer-Fedor and Rabbitt, 2002; Keefe and Schairer, 2011). Following this notion, the second general type of calibration method in the present study yields several measures of the stimulus level, which in principle are not compromised by standing waves, derived from estimates of the Thévenin source pressure and impedance of the probe.

To perform the Thévenin-equivalent source calibration of the probe, a set of pressure responses to wideband excitation are obtained with the probe inserted into several test loads (such as hard-walled cylinders) for which the acoustic impedance can be calculated from theory (Allen, 1986; reviewed by Rosowski et al., 2013). The pressure responses are then used to solve a set of over-determined equations for the acoustic impedances of the cavities, with the unknowns being the probe's Thévenin source pressure (P_src) and impedance (Z_src) and the cavity length. The solution is optimized to obtain a minimum in its error function. The Thévenin calibration procedure, which takes less than five minutes, is performed before testing each subject.

After the source calibration, the probe is placed in the ear, and the ear canal pressure response (P_ec) at position x_probe is measured for the same wideband chirp stimulus. This, along with the Thévenin source calibration parameters, allows several acoustic quantities to be calculated. The ear canal impedance is calculated as

$$Z_{\mathit{e}\mathit{c}}=\frac{Z_{\mathit{s}\mathit{r}\mathit{c}}{P}_{\mathit{e}\mathit{c}}}{P_{\mathit{s}\mathit{r}\mathit{c}}-P_{\mathit{e}\mathit{c}}}.$$ (1)

The pressure reflectance can be calculated from Z_ec (Voss and Allen, 1994),

$$R=\frac{Z_{\mathit{e}\mathit{c}}-Z_0}{Z_{\mathit{e}\mathit{c}}+Z_0}.$$ (2)

Both Z_ec and R are complex. Z₀ is the surge impedance of the ear canal, defined as

$$Z_0=\frac{\rho c}{A},$$ (3)

where ρ is the density of air, c is the velocity of sound, and A is the cross-sectional area of the canal. The value of Z₀ is typically taken as that of a cylindrical tube with a diameter equal to the average adult ear canal (Scheperle et al., 2008; Keefe and Schairer, 2011). In this study, we used the procedure of Rasetshwane and Neely (2011) to estimate Z₀ from Z_ec.¹

Following the initial forward going wave emitted into the canal by the sound source, the sound undergoes multiple reflections between the probe and the eardrum. In the steady state, the forward pressure (P_for) is the sum of all forward going waves and the reverse pressure (P_rev) is the sum of all reverse-going waves. The interaction between P_for and P_rev results in standing waves. The forward component of the ear canal pressure is

$$P_{\mathit{f}\mathit{o}\mathit{r}}=\frac{1}{2}{P}_{\mathit{e}\mathit{c}}\left(1+\frac{Z_0}{Z_{\mathit{e}\mathit{c}}}\right)=\frac{P_{\mathit{e}\mathit{c}}}{(1+R)}.$$ (4)

The reverse pressure is

$$P_{\mathit{r}\mathit{e}\mathit{v}}=P_{\mathit{e}\mathit{c}}-P_{\mathit{f}\mathit{o}\mathit{r}}=R{P}_{\mathit{f}\mathit{o}\mathit{r}}.$$ (5)

A tube with the diameter of the ear canal and long enough so that reflections are negligible is an excellent coupler for high-frequency stimulus calibration (Goodman et al., 2009) because it is free of standing waves. Measuring the pressure with a probe inserted into such a “long lossy tube” (P_LLT) approximates the initial forward going sound wave (P_ifw) leaving the probe. Drawing on Keefe (1997) and Keefe and Schairer (2011), we note that the initial forward going wave in the ear canal at x_probe can be calculated as

$$P_{\mathit{i}\mathit{f}\mathit{w}}=P_{\mathit{f}\mathit{o}\mathit{r}}(1-R{R}_{\mathit{s}\mathit{r}\mathit{c}})=P_{\mathit{e}\mathit{c}}\frac{(1-R{R}_{\mathit{s}\mathit{r}\mathit{c}})}{(1+R)},$$ (6)

where R_src is an estimate of the in situ Thévenin source reflectance of the probe at x_probe,

$$R_{\mathit{s}\mathit{r}\mathit{c}}=\frac{Z_{\mathit{s}\mathit{r}\mathit{c}}-Z_0}{Z_{\mathit{s}\mathit{r}\mathit{c}}+Z_0}.$$ (7)

A useful acoustic quantity is the magnitude of the pressure at the eardrum (TM) at location x_TM using Eq. (4),

$$P_{\mathit{T}\mathit{M}}=P_{for(x_{\mathit{T}\mathit{M}})}+P_{rev(x_{\mathit{T}\mathit{M}})}=P_{for(x_{\mathit{T}\mathit{M}})}(1+R_{\mathit{T}\mathit{M}}),$$ (8)

where R_TM is the pressure reflectance at the TM. By assuming that $R_{\mathit{T}\mathit{M}}=\left|R_{\mathit{T}\mathit{M}}\right|$, $\left|P_{for(x_{\mathit{T}\mathit{M}})}\right|=\left|P_{for(x_{\mathit{p}\mathit{r}\mathit{o}\mathit{b}\mathit{e}})}\right|$, and $\left|P_{rev(x_{\mathit{T}\mathit{M}})}\right|=\left|P_{rev(x_{\mathit{p}\mathit{r}\mathit{o}\mathit{b}\mathit{e}})}\right|$, the magnitude of the pressure at the eardrum can be estimated as

$$\left|P_{\mathit{T}\mathit{M}}\right|\mathrm{\sim }\left|P_{for(x_{\mathrm{probe}})}\right|+\left|P_{rev(x_{\mathrm{probe}})}\right|.$$ (9)

This so-called “integrated pressure” (Lewis et al., 2009) is referred to here as the “summed” pressure (P_sum). The phase of the stimulus does not enter in the calculation of P_sum, explaining its insensitivity to standing waves and to the precise location where pressure is measured along the ear canal.

In addition to forward pressure, Withnell et al. (2009) calculated the pressure transmitted into the middle ear (P_trans) as

$$P_{\mathit{t}\mathit{r}\mathit{a}\mathit{n}\mathit{s}}=P_{for(x_{\mathit{T}\mathit{M}})}(1-R_{\mathit{T}\mathit{M}}).$$ (10)

By approximating the space in the ear-canal between the probe and TM as a pure delay, with $\tau =-(1/2)(d\theta /d\omega )$, where θ is the phase of R and ω is the angular frequency, one obtains the estimates

$$P_{for(x_{\mathit{T}\mathit{M}})}=P_{for(x_{\mathit{p}\mathit{r}\mathit{o}\mathit{b}\mathit{e}})}{e}^{\{-i\omega \tau \}}$$ (11)

and

$$R_{\mathit{T}\mathit{M}}=R\cdot e^{\{+i\omega \tau \}}$$ (12)

so that

$$[P_{\mathit{t}\mathit{r}\mathit{a}\mathit{n}\mathit{s}}]\mathrm{\sim }[P_{for(x_{\mathrm{probe}})}(1-R{e}^{\{2i\omega \tau \}})].$$ (13)

The preceding measures are all based on pressure, but the power absorbed by the ear has long been considered the critical quantity. The acoustic power transmitted to the middle ear (W_abs) can be estimated from measurements anywhere along the ear canal, as losses through its walls can be assumed negligible in normal adult ears. Its value at x_probe is given by

$$W_{\mathit{a}\mathit{b}\mathit{s}}=\frac{1}{2Z_0}{\left|P_{\mathit{e}\mathit{c}}\right|}^2{G}_{\mathit{e}\mathit{c}}=\frac{1}{2Z_0}{\left|P_{\mathit{f}\mathit{o}\mathit{r}}\right|}^2(1-{\left|R\right|}^2),$$ (14)

where $G_{\mathit{e}\mathit{c}}=\Re (1/Z_{\mathit{e}\mathit{c}})$ is the load conductance, the real part ($\Re$) of the load admittance (Neely and Gorga, 1998; Scheperle et al., 2008). The factor $(1-{\left|R\right|}^2)$ is the absorbance, the fraction of acoustic power transmitted into the middle ear. The area of the ear canal (A) is inversely related to Z₀ [see Eq. (3)]. The acoustic intensity (I_ec), the power flux through a unit area, is then (Keefe and Schairer, 2011)

$$I_{\mathit{e}\mathit{c}}=W_{\mathit{a}\mathit{b}\mathit{s}}/A.$$ (15)

The phase of the stimulus is retained in the complex quantities P_for, P_ifw, and P_trans but not for P_sum, W_abs, or I_ec, as the last three are calculated from scalar quantities. Stimulus phase is irrelevant to behavioral thresholds but is quite important for compensation of system delays and for computing optimized stimuli.

C. Eardrum pressure estimation from remote measurements

Another measure compared in this study recognized that the eardrum pressure can be predicted from pressure measurements in the ear canal, near its entrance (Stevens et al., 1987) or deeper inside (Hudde et al., 1999). This approach previously led to the development of an audiometer specialized to test high-frequency hearing (Stevens et al., 1987; Green et al., 1987; Stelmachowicz et al., 1989a) which, however, proved less reliable than standard methods when using circumaural earphones calibrated on a flat-plate coupler (Stelmachowicz et al., 1988; Stelmachowicz et al., 1989b). Furthermore, the audiometer's bulkiness discouraged widespread use, and it does not appear practical for applications such as measurement of reflectance or OAEs. We are not aware of published reliability tests of the procedure developed by Hudde et al. (1999). In the present study, we devised and evaluated a novel, much simpler method to predict eardrum pressure (described in detail in Sec. II C 3).

D. Previous tests of dependence of acoustic measures on probe insertion depth

This project used the sensitivity of behavioral thresholds as a metric to evaluate the candidate measures of sound pressure. Neely and Gorga (1998) demonstrated that thresholds are less dependent on probe insertion depth when referenced to intensity than when referenced to pressure. This is reasonable, inasmuch as acoustic intensity is a measure of the power input to the middle ear and neither forward pressure nor power absorbance should, in principle, be compromised by pressure standing waves [see Eq. (14)], and so neither should their product. The results of Neely and Gorga (1998) are entirely consistent with this prediction.

It is possible that stimulus-frequency OAEs (SFOAEs) evoked by near-threshold tones are large enough in some ears to affect behavioral thresholds and might compromise the intended use of thresholds in this study. The SFOAEs can be large enough to produce ripples in the spectrum of the ear canal pressure that appear to correspond to ripples in behavioral thresholds (Elliott, 1958; Kemp and Chum, 1980; Wilson, 1980). The amplitude of the pressure ripples decreases with increasing stimulus level. The presence of SFOAEs is thus expected to contribute to the variability of thresholds when insertion depth is changed, but this contribution should be essentially random between subjects and should therefore not impose systematic trends on the threshold changes. In the study of Neely and Gorga (1998), the effects of insertion depth were evaluated from measurements of (or calculations of acoustic quantities derived from) thresholds specified as attenuations from the system's maximum output. So any influence of SFOAEs that depends on insertion depth is already expressed completely in the attenuations at threshold and in the measured pressures or derived acoustic quantities. The latter are based on signals measured at levels high enough so that contamination by SFOAEs is negligible. In the current study, we adopt this aspect of the experimental design of Neely and Gorga (1998).

In another study which evaluated measures of stimulus level, Scheperle et al. (2008) reported reduced insertion-depth dependence of distortion-product OAEs (DPOAEs) for stimulus frequencies near the pressure nulls when stimulus levels were specified as forward pressure instead of emission-probe pressure. DPOAE measurements have the advantage of being objective but, to the extent that the canal pressures of the stimulus tones are not affected equally by standing waves, the effective intracochlear amplitude ratios are uncontrolled variables. Thus, because of their round-trip nature, interpreting level changes of DPOAEs is more difficult than interpreting level changes in thresholds, which depend primarily on forward propagation of stimuli into the cochlea.

It is fair to question the reliability of evaluating acoustic calibrations using behavioral measures. However, under controlled laboratory conditions, the standard deviation of test-retest measurements of thresholds in the 8–14 kHz range is only about 1.5 dB (Green et al., 1987). Therefore, variations due to calibration protocol should be readily identifiable (Neely and Gorga, 1998). The invariance of thresholds with respect to insertion depth in individual subjects does not indicate that stimulus levels are accurately measured. Rather, it merely indicates repeatability of stimulus delivery in a single subject. This is of great relevance to minimizing errors in repeated measurements of auditory function in longitudinal studies, for example, in monitoring the effects of environmental agents that damage the inner ear or in studies of aging. Other types of measurement are needed to judge accuracy. For example, if behavioral thresholds in a population of subjects are referenced to a constant W_abs, then thresholds should show reduced variability.

The studies of Neely and Gorga and Scheperle et al. were limited to 8 kHz. In the present study, a custom-designed system (described below) overcomes this limitation. Quantities compared in this study include (1) the pressure measured in the ear simulator with the probe placed near the reference plane (P_{sim_S}), (2) depth-compensated ear simulator pressure (P_{sim_D}), (3) forward pressure [P_for, see Eq. (4)], (4) integrated pressure [P_sum, see Eq. (9)], (5) transmitted pressure [P_trans, see Eq. (13)], (6) initial forward pressure [P_ifw, see Eq. (6)], (7) absorbed power [W_abs, see. Eq. (14)], (8) estimated eardrum pressure [P_TMest, defined below in Sec. II C 2, Eq. (18)], and (9) the pressure measured directly by the OAE probe (P_ec).

II. METHODS

A. Subjects

Thirty adult subjects (20 females), ages 21–35 years old, participated in the current study. None of the participants reported hearing loss or history of middle ear surgery. A history of having had ear-ventilation tubes or ear infections did not warrant exclusion from the study, as long as the ear could be considered normal. Otoscopy confirmed normal appearance of the tympanic membrane and the absence of cerumen, debris, or foreign bodies. Each subject was screened for normal middle-ear function and intact tympanic membranes on the day of testing via standard 226-Hz probe tone tympanometry using an Interacoustics AA220 Audio Traveler Middle Ear Analyzer. Normal middle ear function was also suggested by wideband reflectance, examined post hoc. The Northwestern University Institutional Review Board approved the experimental protocol. A consent form was reviewed and signed by each subject prior to the test session. Participants received monetary compensation for their time.

B. Instrumentation

Stimulus signals were generated using a 24-bit audio interface (Echo Audio Gina3G) on a PC running Microsoft Windows XP Professional. The sound source transducers, modified MB Quart 13.01 HX, were coupled to an Etymotic Research ER10-B+ OAE probe via flexible 16 gauge plastic tubing. The power amplifier used to drive the sound sources was custom built, using a Texas Instruments TPA6120A2 headphone driver integrated circuit with low output noise and a dynamic range of 120 dB. Tones were generated digitally by the audio interface with a sample rate of 44.1 kHz, using 8192-point buffers to store stimulus time waveforms and collect signal-averaged responses, yielding a frequency resolution of 5.31 Hz. Pressure responses to chirp excitation were measured using either SYSRES (version 2.24) (Neely and Stevenson, 2002) or EMAV (version 3.03) (Neely and Liu, 1994) at a level of nominally 80 dB SPL. Both programs have been used extensively in the Neely and Siegel labs, with results reported in several publications, including most of the ones cited in this paper. The programs and detailed documentation are freely available to researchers at the audres.org website. SYSRES was used to measure transfer functions for microphone and ear-canal calibration. EMAV was used to perform Thévenin calibration of the probe and to calculate the acoustic impedance and forward pressure from the pressure response measured in individual ear canals. Other acoustic quantities using the Thévenin approach were calculated post hoc using utilities developed in Visual Basic 6.0. Behavioral threshold tracking used custom-designed software which controlled stimuli delivered through the probe's sound sources.

C. Calibration procedures

Sound measures were expressed in decibels, using the appropriate pressure or power reference.

1. Ear-simulator calibration

For the standard calibration, the probe was inserted into the ear simulator so that the ends of the sound source tubes were positioned at the reference plane (defined in ANSI, 2009; IEC, 2010). The pressure response to chirp excitation at a nominal level of 80 dB SPL was measured using SYSRES. This single measurement allows the calculation of P_{sim_S} at the maximum output of the system.

The depth-compensated pressure calibration in the ear simulator, referred to here as P_{sim_D}, has three steps (described in detail by Lee et al., 2012). First, measurements are made with the probe inserted into the simulator using SYSRES. The pressures generated by the probe's sound source(s) are measured using both the probe microphone and the simulator's microphone (representing the eardrum). Pairs of such measurements are made with a series of insertion depths, spaced 0.5–1 mm apart. The flanged “canal” of the IEC 0318-4 simulator was replaced with a cylindrical extension to allow a range of insertion depths corresponding to the range of depths in human subjects (as determined in the Dhar and Siegel labs at Northwestern). Accurate measurement of the first half-wave resonance frequency was facilitated by normalizing each measured pressure response by the response of the probe measured in a 50-ft coil of copper tube (the “LLT”) with 3/8 in. od (7.9-mm id) that approximates the diameter of the average adult ear canal and exhibits negligible reflected pressure. This normalization removes most of the contributions from irregularities in the frequency response of the sound sources that could otherwise obscure the simulator (or ear canal) resonances. The distance between the simulator microphone and the probe microphone can be calculated from the frequency of the first half-wave resonance measured from the normalized probe response. The second step in the calibration procedure is to place the probe in a subject's ear and then measure the frequency of its first half-wave resonance. Finally, this frequency is matched as closely as possible to the corresponding stored ear-simulator calibration response of similar depth, and the pressure measured by the simulator's microphone is taken as the estimate of that subject's eardrum pressure. One reason for including the simulator method in this study is to check how well it performs in controlling the eardrum sound level for frequencies above 8 kHz. It was anticipated that the simulator would show deviations from real-ear behavior resulting in systematic errors in estimating eardrum sound levels at high frequencies due to its cylindrical geometry (Lee et al., 2012).

2. Thévenin source calibration and level measures derived from ear canal pressure

Thévenin source pressure and impedance calibration (to estimate parameters P_src and Z_src, see Sec. I B) of the Etymotic Research ER-10B+ probe was performed prior to each subject's test session using EMAV, as described by Scheperle et al. (2008) and elaborated subsequently by Rasetshwane and Neely (2011), using a five-tube assembly. An ER 10-14 foam ear-tip (the same type used in the subject's ear), was placed on the probe and secured within an adapter that fit over each cavity, making it easier to transfer the probe between cavities. (It was sometimes necessary to reduce the diameter of the ear-tip by trimming it to allow optimal fit in the ears of subjects with small ear canals. The probe was not re-calibrated in such cases.) The quality of each source calibration was judged with an error value generated by the optimization routine in EMAV. The source calibration was repeated if this arbitrarily scaled parameter exceeded 1.0.

Derived quantities were calculated using the equations specified in Sec. I. We calculated transmitted pressure (P_trans) using an approach similar to that of Withnell et al. (2009) [Eqs. (10)–(13)]. The propagation delay was estimated and subtracted from the reflectance using the slope of the reflectance phase to calculate the delay [Eq. (13)]. The reflectance phase rotates through one period from zero frequency to the first half-wave resonance in the canal pressure, and by another full period from the first to the second half-wave resonance. The delay for frequencies up to the first half-wave resonances was estimated from a straight-line approximation, with a phase of zero at dc and one period at the frequency of the first half-wave resonance. In real ears, the frequency of the second half-wave resonance is consistently less than twice the frequency of the first; a second estimate of delay was calculated from the slope of the phase between the first two resonances. This second estimate of delay was consistently longer than the first, a consequence of the smaller frequency difference for the same one-period phase shift. The notion of an acoustic-propagation delay that abruptly shifts at the frequency of first half-wave resonance is troubling, but this simple procedure provides an estimate of P_trans in all ears and leaves at least some part of the variation in reflectance phase due to the reactive component of the eardrum impedance. A better procedure to estimate and subtract the propagation delay might improve the estimate of P_trans. The slope of the reflectance phase vs frequency was previously reported to steepen abruptly at around 8–10 kHz (Hudde et al., 1999).

3. Eardrum pressure estimation

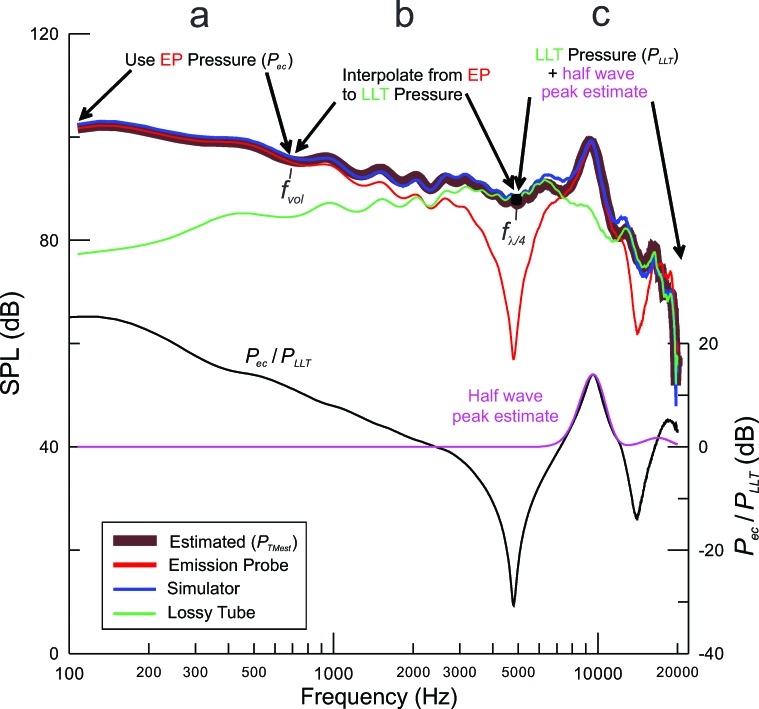
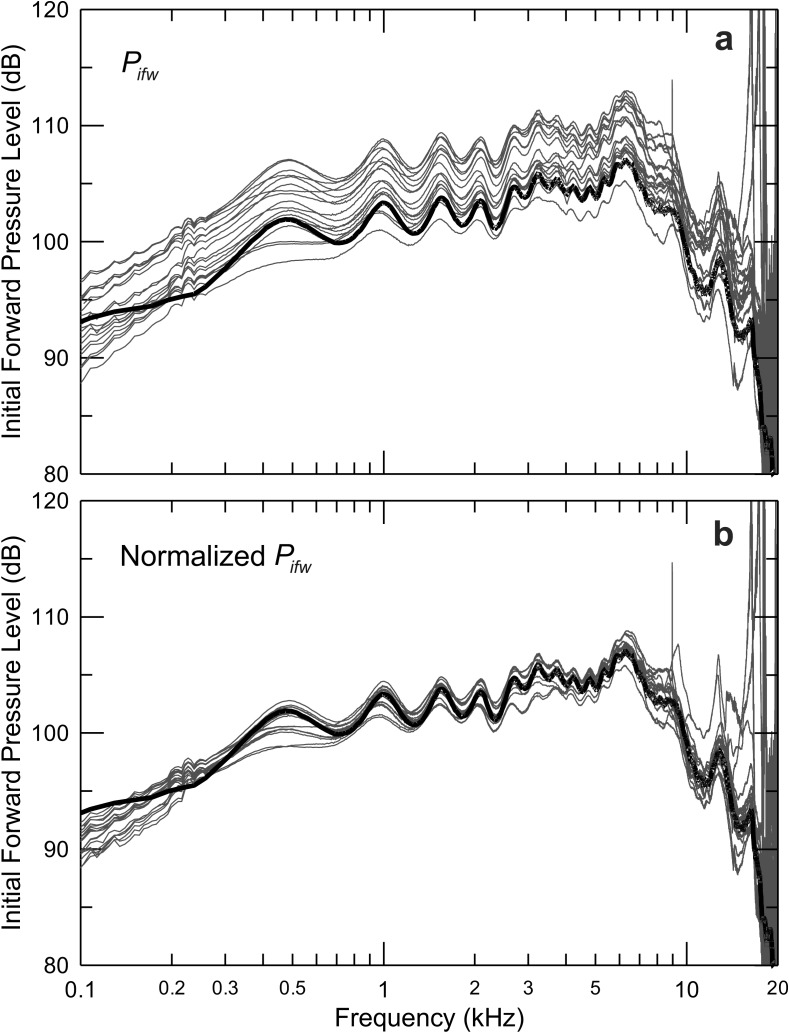
The eardrum pressure estimation method used in these experiments is a hybrid between the pressures measured in the ear canal (P_ec) and in the LLT (P_LLT) (Fig. 1). The ear canal is approximated as a cylinder terminated at a right angle by the eardrum. The estimate of eardrum pressure (P_TMest), expressed as an SPL (L_TMest), is constructed as follows:

• (a)At low frequencies (specified as f_vol ≤ 0.11 times the frequency of the first half-wave resonance), the pressure in the ear canal (P_ec at position x_probe) closely approximates the eardrum pressure. This is because the wavelength is long compared with the canal length and the canal approximates a simple volume. In this frequency range, there is a marked divergence between pressures at the ear canal and in the LLT.
• (b)
  The eardrum pressure at the frequency of the first quarter-wave pressure null (f_λ/4), measured by the probe in the ear canal, is closely approximated by P_LLT (Fig. 1). The eardrum SPL between f_vol and f_λ/4 is estimated by interpolation

  $$L_{T{M}_{\mathit{e}\mathit{s}\mathit{t}}}=L_{P_{\mathit{L}\mathit{L}\mathit{T}}}+\left(1-\left(20\hspace{0.17em}{\text{log}}_{10}\left(1+\left(\frac{9(f-f_{\mathit{v}\mathit{o}\mathit{l}})}{(f_{\lambda /4}-f_{\mathit{v}\mathit{o}\mathit{l}})}\right)\right)\right)\right)(L_{P_{ec\left(f_{\mathit{v}\mathit{o}\mathit{l}}\right)}}-L_{P_{LLT\left(f_{\mathit{v}\mathit{o}\mathit{l}}\right)}}).$$ (16)
• (c)At frequencies above f_λ/4, the pressure varies above and below the P_LLT, due to the interaction of forward and reverse pressure waves in ear canals, absent in the LLT. If the diameter of the LLT is close enough to that of the adult ear canal, then the response in the LLT is a good approximation to the eardrum pressure near the quarter-wave frequencies where nulls are measured at the probe. This is illustrated in Fig. 1 near 5 and 15 kHz, the frequencies of quarter-wave pressure nulls at the probe. In these two frequency ranges, P_LLT closely approximates the pressure at the eardrum.

FIG. 1.

Illustration of the method to estimate eardrum pressure (P_TMest). The thick brown line is the estimated eardrum SPL. (a) The estimate relies on the pressure measured directly by the probe (P_ec) (red curve) at low frequencies (≤ f_vol) where the pressure at the eardrum can be assumed equal to P_ec. (b) The pressure between f_vol and the frequency of the first quarter-wave null (f_λ/4) above is calculated using an interpolation described in the text. (c) The eardrum pressure at frequencies above f_λ/4 is calculated as the sum of the system's response in a long lossy tube (P_LLT) (green) and an estimate of half-wave resonances measured in the ear (magenta). The half-wave resonances are estimated by fitting a Gaussian curve to peaks detected in the pressure response measured in the ear normalized by the pressure response in the long tube (P_ec/P_LLT) (black curve in lower plot). The blue curve, representing the pressure measured by the microphone of the ear simulator, demonstrates the accuracy of the estimated pressure.

If the LLT response is used to normalize the in-ear response, estimates of eardrum sound pressure level are expected to be good near the half-wave resonance frequencies but poor near the quarter-wave nulls. For cylindrical cavities and real occluded ear canals, the half-wave resonances that are evident at both terminations of the cylinder arise from multiple reflections of forward and reverse waves reflected at the ends of the cylinder. The height of the resonance is determined by the parallel combination of the impedances terminating the two ends. Thus, normalizing by P_LLT, which measures only a forward propagating wave arising from the same source, reveals the pressure increase near the half-wave resonances. This is shown in the black curve in the lower plot of Fig. 1. The height of the half-wave resonances at the frequency of each peak (f_nλ/2) in the normalized pressure response [L_Peak(fnλ/2)] is measured (relative to 0 dB) and approximated by fitting with Gaussian peaks (i.e., the pink curve in the lower plot of Fig. 1)

$$L_{\mathit{P}\mathit{e}\mathit{a}\mathit{k}}(f)=L_{Peak(f_{n\lambda /2})}\hspace{0.17em}\text{exp}\hspace{0.17em}((-0.0007/B{W}_{\mathit{p}\mathit{k}}){(f_{n\lambda /2}-f)}^2),$$ (17)

where f is the frequency in Hz and BW_pk is the peak's −3 dB bandwidth (measured directly from the normalized response). The fitted peaks are then summed with the LLT response to create the eardrum pressure estimate for frequencies above f_λ/4,

$$L_{T{M}_{\mathit{e}\mathit{s}\mathit{t}}}=L_{\mathit{P}\mathit{e}\mathit{a}\mathit{k}}+L_{P_{\mathit{L}\mathit{L}\mathit{T}}}.$$ (18)

The pressures from each of the frequency ranges defined in (a)–(c) above are summed to yield P_TMest (thick brown curve in Fig. 1). Tests in an ear simulator revealed that the procedure accurately predicts the pressure measured by the microphone of the ear simulator within roughly +/−2 dB (compare the blue and brown curves of Fig. 1). The predicted eardrum pressure compensates for the frequency dependence of the sound sources and also compensates the half-wave resonances of the ear canal, which are typically not spaced as integer multiples of the first resonance (as they would be with cylindrical geometry).

D. Measurement procedures

Subjects were seated in a double-walled sound-treated room. An intercom permitted audio communication between tester and subject. Initial probe placement within a subject's ear was as deep as possible without causing discomfort (position x_probe1). It was observed that in most cases the probe could be inserted such that the distal surface of the foam ear-tip was slightly deeper than the concha bowl. The depth of the first insertion thus likely exceeded typical placements of insert earphones used in clinical audiometry.

An effort was made to orient the probe directly toward the eardrum under the (untested) assumption that this might minimize the amplitudes of early reflections at high frequencies. To do so, the probe was removed from the tip already placed in the ear, the tympanic membrane was visualized using an otoscope placed on the plastic tubing of the foam tip, the probe tip was adjusted as needed, and the probe itself was re-inserted into the foam tip and secured at the appropriate angle.

In-ear calibration was performed with the same wideband “chirp” signal used for Thévenin source pressure/impedance calibration. For the depth-compensated simulator method, the first half-wave resonance was identified using SYSRES, recorded and used to select the most appropriate ear-simulator calibration file to apply for threshold acquisition (adapted from Gilman and Dirks, 1986). This measurement also served as a basis for acoustic estimation of probe depth. In addition, the low-frequency pressure response was used to check for leakage of sound resulting from improper probe placement or tip size. Proper sealing of the probe into the canal was confirmed post hoc by verifying that the magnitude of the pressure reflectance approached 1.0 at 100 Hz. A 2-min recording of spontaneous OAEs (SOAEs) followed. SOAE measurements provided an additional cross-check of proper probe placement based on whether or not electrical noise was noted due to the probe tilting enough to touch the ear canal wall. Possible physical shifting of the probe could be caused by subject movement, expansion of the foam tip, or unusual canal geometry. If excessive noise was observed, the probe was repositioned and the SOAE measurement was repeated.

Thresholds at standard half-octave test frequencies of 0.125 to 8 kHz, and additional frequencies of 10, 11.2, 12.5, 14, 15, 16, 17, 18, 19, and 20 kHz, were obtained at two different insertion depths (one deep, one shallow) for each ear. All threshold measurements began with 1 kHz and ascended until the highest frequency to which the subject responded; lower frequencies were tested last. A modified Békésy tracking program was used to measure absolute hearing thresholds using procedures outlined previously (Dreisbach and Siegel, 2001, 2005; Badri et al., 2011; Lee et al., 2012). The software averaged a minimum of six upward threshold crossings or more if needed to reach a standard error of the mean less than 1.0 dB.

Following the first threshold measurement, the pressure response was measured using EMAV to calculate the canal impedance and derived stimulus measures using the Thévenin probe calibration. These quantities were re-analyzed subsequently using matlab routines that used improved calculations, including estimation of Z₀ from the canal measurements. Other acoustic stimulus-level measures and behavioral thresholds were calculated off-line. Measured pressure responses were compensated by normalizing by the transfer function of the probe's microphone (Siegel, 2007). The pressure frequency responses also used to assess whether the probe had shifted in the canal during the threshold measurements by comparing the half-wave resonance frequencies measured before and after the measurements. If a significant change in probe position was detected by a change in the frequency of half wave resonance greater than 0.3 kHz (in all such instances to a lower frequency indicating outward movement), the data were excluded from the study.

The probe was then pulled out as far as possible while still maintaining a good acoustic seal, confirmed via SYSRES (position x_probe2). Threshold tracking and measurement of acoustic stimulus quantities were repeated in the same fashion as for the deeper insertion. The left ear was always tested before the right ear. Each test session lasted 1.5 to 2.5 h, with most sessions averaging 2 h of subject contact time. Breaks were provided between testing of the left and right ear for all subjects and in between insertion depth changes for a given ear if requested.

E. Analysis

Following convergence of thresholds in the tracking procedure, the average threshold attenuation was calculated for each frequency and saved to allow post hoc calculation of thresholds referenced to the different acoustical measures. Data were processed with custom software developed in Visual Basic 6.0.

Thresholds were calculated using each of the nine measures of stimulus level for each probe depth (positions x_probe1 and x_probe2) and ear. Plots of thresholds referenced to each of these measures, displaying all subjects and separated by ear, were presented for initial method and population comparison. Statistical analyses were conducted using R version 3.02, 64 bit (R Core Team, 2013) running on an Apple Macintosh.

III. RESULTS

Of the 30 subjects tested, data from 26 subjects (24 left ears, 22 right ears) were analyzed. Five ears were not included due to errors in collection procedures resulting in missing or corrupted data files, five as a result of poor probe placement or inadequate sealing of the probe into the canal and four due to excessive motion of the probe.

A. Test of insertion-depth sensitivity of behavioral thresholds

The insertion depths (probe inlet to eardrum), estimated from the frequency of the first half-wave resonance, as well as the differences between deep and shallow insertions, were similar between left and right ears. The deep insertions averaged 18.9 (SD 1.8) mm for the left ear and 19.0 (SD 2.1) mm for the right ear, while the shallow insertions averaged 5.2 (SD 1.9) mm and 4.5 (SD 1.6) mm longer, respectively. Given the similarity between ears, their data were combined (N = 46). The surge impedance for deep and shallow insertions averaged 112.2 (SD 30.2) cgs ohms (N = 46) and 106.3 (SD 21.5) cgs ohms, respectively. The ratio of deep to shallow surge impedances, calculated for each ear separately, averaged 1.07 (SD 0.266). Neither the differences in surge impedance, nor the ratios for deep vs shallow insertion, were statistically significant (t-test, p > 0.9). Thus, it appears that the measurements, on average, were made in locations where the canal area was approximately constant. The differences in insertion depths were sufficient to shift the resonant frequencies in the measured canal pressure enough to form a solid basis for the test.

1. Example comparison of three measures in a single subject

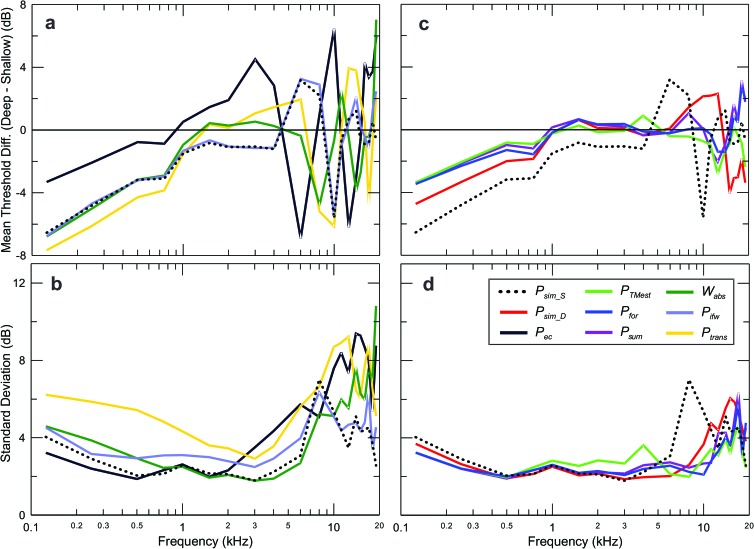
An example set of data from the left ear of one subject illustrates how the pairs of threshold measurements depend on insertion depth differently, depending on the acoustic quantity in which they are expressed. The three quantities chosen illustrate the range of insertion-depth dependence measured in the study. In the left-hand column of Figs. 2(a) and 2(b) thresholds are referenced to the SPL in the ear simulator with the sound source positioned near the reference plane of the simulator (P_{sim_S}), as specified by standards (ANSI, 2009; IEC, 2010). The same thresholds are expressed relative to the SPL measured directly by the probe in the middle column (P_ec) [Figs. 2(c) and 2(d)] and in the right-hand column referenced to the forward pressure (P_for) [Figs. 2(e) and 2(f)]. In other words, the voltage delivered to the sound source transducer at threshold is the same for the three columns of plots; only the acoustic quantity used to reference the thresholds is different. Pairs of plots in the upper part of the top row in Figs. 2(c) and 2(e) depict the maximum output of the system for each quantity, for the deep (solid line) and shallow (dotted line) insertions. In the case of the standard calibration in the ear simulator shown in Fig. 2(a), there is only one pressure response, measured with the probe inserted near the reference plane of the simulator, as no in-ear compensation is performed. In Figs. 2(c) and 2(d), the peaks in pressure at the frequencies of half-wave resonance (above 7 kHz) are apparent. The probe pressure responses also demonstrate the nulls near the quarter-wave frequencies as expected [Fig. 2(c)]. The differences in the pressure responses for the three acoustic quantities are shown in the bottom row of plots as the solid curves in Figs. 2(d) and 2(f). In the case of standard simulator calibration [Fig. 2(b)] there is only one pressure response, so the line at 0 dB represents the (absent) change in pressure used to reference thresholds using this method.

FIG. 2.

Example of measurements from one subject. The left-hand column depicts the pair of sets of behavioral thresholds referenced to the pressure measured in the B&K 4157 ear simulator using the standard calibration for insert earphones. (a) The pressure response measured by the simulator's microphone is the single solid curve. Behavioral thresholds referenced to simulator pressure (P_{sim_S}) for the deeper insertion [panel (a) solid line with filled circles] and shallower insertion [panel (a) dotted line with diamonds] are also shown. (b) Changes in P_{sim_S} at threshold between the two insertion depths are depicted with filled triangles. Thresholds at low frequencies were consistently higher for the shallower insertion depth and there was a biphasic deviation from 0 dB near 10 kHz. The middle column recasts the same sets of thresholds and their changes when referenced to the pressure measured by the emission probe (P_ec). (c) The measured P_ec is depicted for the deeper and shallower insertions (solid and dashed lines, respectively) along with the thresholds as in panel (a). (d) The change in thresholds referenced to P_ec is plotted as filled triangles as in panel (b) and the change in P_ec is plotted as the solid curve. Threshold changes are smaller below 2 kHz than when referenced to P_{sim_S} [panel (b)], while changes in thresholds are as large as +/−15 dB at higher frequencies and clearly associated with corresponding changes in P_ec near the frequencies of quarter-wave pressure nulls [arrows in (c) and (d)]. The right-hand column recasts the thresholds by referencing them to P_for. (e) P_for at the two insertion depths shows the change in the frequency of half-wave resonance from ∼10 kHz to ∼7.3 kHz that is also seen in P_ec [panel (c)], but the pressure nulls at the quarter-wave frequencies in P_ec are not present in P_for. (f) Thresholds referenced to P_for are resistant to changes in insertion depth (less than +/−3 dB change below 16 kHz), despite changes in pressure at the half-wave frequencies that exceed 10 dB [arrows in (e) and (f)]. Thus, the input level to the ear is controlled well by the change in P_for plotted in the solid curve.

A complete set of behavioral threshold measurements, referenced to the relevant stimulus measure, made at each probe position, are represented in the lower parts of Figs. 2(a), 2(c), and 2(e) as the curves with symbols and the corresponding differences in threshold are plotted in Figs. 2(b), 2(d), and 2(f) as symbols. The relative degree of stimulus control can be judged by the degree to which threshold shifts at different insertion depths deviate from 0 dB (ideal performance).² Distinct differences in the sensitivity of thresholds to insertion depth are clearly evident at 2 kHz and below between standard calibration [Fig. 2(b)] and the two in-ear measures [Figs. 2(d) and 2(f)]. The upward shift in P_ec [Fig. 2(d)] and P_for [Fig. 2(f)] results in thresholds that exhibit much less change in this frequency range than does standard calibration [Fig. 2(b)], as expected from the change in occluded canal volume. Thresholds uncompensated for canal volume demonstrate a deviation from ideal performance that grows with decreasing frequency, with a shift of 10 dB at 125 Hz. Threshold changes for standard calibration also show substantial deviations of 6.7 dB at 8 kHz, −11.7 dB at 10 kHz, and 6.2 dB at 11.2 kHz, the consequence of the change in the frequency of the first half-wave resonance in this ear from 10.05 to 7.5 kHz for the approximately 6.6 mm difference position for the deeper and shallower insertions, respectively [Fig. 2(b)]. Thresholds referenced to emission probe SPL show large deviations from ideal performance from 3 to 15 kHz, largely due to the shift in frequency of the first two quarter-wave pressure nulls measured by the probe and the change in pressure as large as +/−25 dB that resulted. The shift in P_for above 5 kHz exceeded +/−10 dB, caused by changes in the frequencies half-wave resonance [Fig. 2(f)]. However, thresholds referenced to P_for clearly come close to perfect compensation for insertion depth, with deviations less than +/−3 dB, except for 16 and 19 kHz.

2. Threshold changes with insertion depth for different measures of sound level

The pattern of changes in thresholds with insertion depth for standard coupler calibration (P_{sim_S}) was qualitatively similar for all subjects (Fig. 3), although there was considerable variability between subjects. These data illustrate the variation of behavioral thresholds that would result from variations in the depth of insertion into the same ear by different testers (or separate measurements sessions by the same tester) performing hearing tests with the insert earphones commonly used in hearing clinics and research labs. No in-ear adjustment is made because, with no measurement of the pressure in the occluded ear canal, none is possible. This is therefore a useful benchmark against which to evaluate alternate specifications of input level. Alternates that demonstrate less variation in threshold with changes in insertion depth than standard simulator calibration are good candidates to replace it, while alternate stimulus measures that show greater dependence on insertion depth than standard calibration are not.

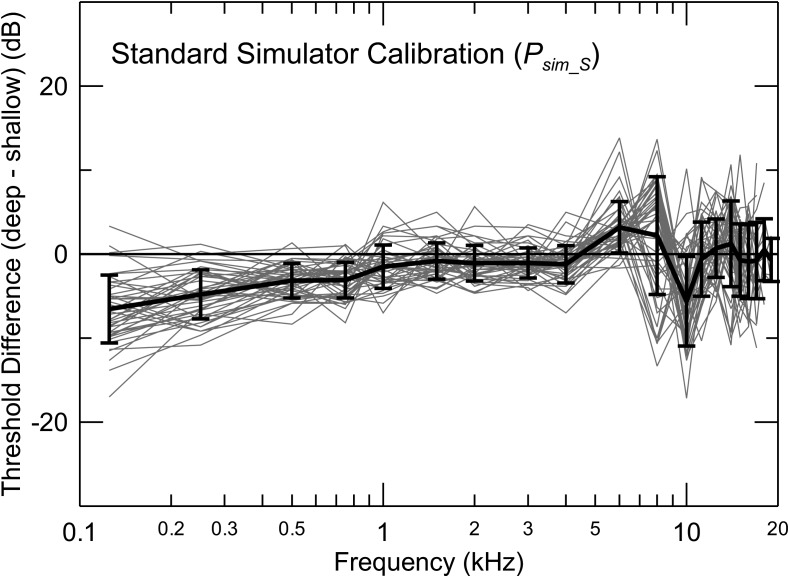
FIG. 3.

Changes in behavioral thresholds with insertion depth for standard calibration in an ear simulator. The thick line shows the mean (+/−1 SD). The systematic changes at low frequencies are partly due to uncompensated changes in the volume of the closed ear canal, while systematic biphasic changes between 6 and 10 kHz result from shifts in the frequency of the first half-wave resonance.

As depicted in the single example of Figs. 2(a) and 2(b), the data from the population of ears studied showed that P_{sim_S} fails to compensate for differences in canal volume, evident in the consistent change in the simulator pressure at threshold at frequencies below 1 kHz (the largest mean change of −6.5 dB is at 0.125 kHz). Similarly, the lack of in-ear compensation is also evident in the biphasic change in thresholds between 6 and 10 kHz near the frequency of the first half-wave resonance. The mean threshold changes were generally small (< +/−1 dB), with standard deviations of typically 4 dB, for frequencies above 10 kHz. It was expected that the changes in threshold and variability between subjects would instead be greatest at these high frequencies for which the wavelength is shortest.

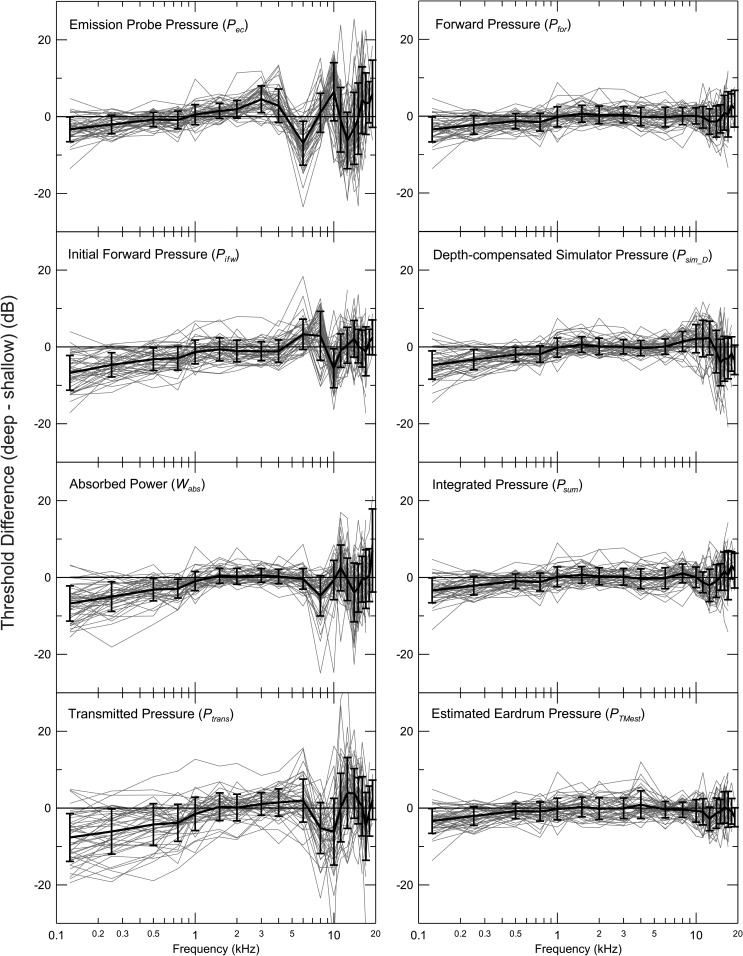
The threshold sensitivity to insertion depth for all subjects shows clear differences between stimulus-level measures (Fig. 4). The plots show the mean (+/−1 SD) for the sample, both of which contain important information. The left-hand column presents the measures that showed the greatest dependence on insertion depth, while those in the right-hand column showed the least. As expected, thresholds referenced to the pressure measured directly by the emission probe (P_ec) show strong insertion-depth dependence for frequencies above 2 kHz, where the effects of standing waves were expected to be large, but the initial forward pressure (P_ifw), absorbed power (W_abs) and transmitted pressure (P_trans) and also perform relatively poorly at high frequencies. Thresholds referenced to forward pressure (P_for), integrated pressure (P_sum) and estimated eardrum pressure (P_TMest) all showed relatively small insertion-depth dependence across the frequency range. Depth-compensated ear-simulator pressure (P_{sim_D}) also performs well, but a biphasic deviation from ideal performance is apparent for frequencies above 8 kHz.

FIG. 4.

Threshold changes with insertion depth in all subjects referenced to different acoustic quantities. The mean (+/−1 SD) is also shown.

Thresholds at frequencies below 1 kHz measured at the shallow insertion depth were consistently higher than for the deeper insertion, regardless of the level measure, so all plots show deviation below 0 dB in this frequency range. This is the case both for P_{sim_S} (Fig. 3) and P_{sim_D}, (Fig. 4) the only measures not based on direct measurement in the subject's ear canal, as well as for the rest of the measures based on in-ear measurements. This trend is clearly not due to the failure to control the eardrum pressure at these frequencies, as the pressure distribution between the probe and eardrum is uniform due to the long wavelength compared to the length of the occluded segment of the canal. The sensitivity of thresholds to insertion depth below 1 kHz was most variable between subjects for P_trans, with standard deviations about twice as large as the best-performing measures. Measuring sound pressure accurately at such low frequencies is not difficult. We will show that the variation in P_trans at low frequencies is caused by small changes in the magnitude of the pressure reflectance (near 1.0) that translate to large fractional changes in (1−|R|).

3. Statistical comparison of insertion-depth sensitivity of thresholds referenced to different acoustic measures

The averaged data from all subjects are summarized in Fig. 5. As in Fig. 4, the data are divided into two groups, with the measures showing greater dependence on insertion depth in the left column of Fig. 5 and those measures showing less dependence on insertion depth in the right column. The mean (upper row) and standard deviation of the mean (lower row) are plotted separately for clarity. The dashed lines in both sets of plots represent the results for the benchmark standard simulator calibration (P_{sim_S}). Aside from the trends noted earlier, patterns were similar for P_{sim_S} and P_ifw, both in the mean change in thresholds [Fig. 5(a)] and standard deviation [Fig. 5(b)]. It should be noted that P_{sim_S} is not compensated for insertion depth and P_ifw involves a calculation from several derived quantities [Eq. (6)]. We will discuss this result later. Also, it is noteworthy that, while the deviation from 0 dB of the mean change in thresholds at low frequencies is present for all measures, it is larger for P_{sim_S}, P_ifw, P_trans, and W_abs [Fig. 5(a)] than for the other measures [Fig. 5(b)]. The performance of P_{sim_S} was better than that for its depth-compensated cousin P_{sim_D} above 10 kHz [Figs. 5(c) and 5(d)]. In fact, no measure appeared to show better performance than P_{sim_S} in this frequency range.

FIG. 5.

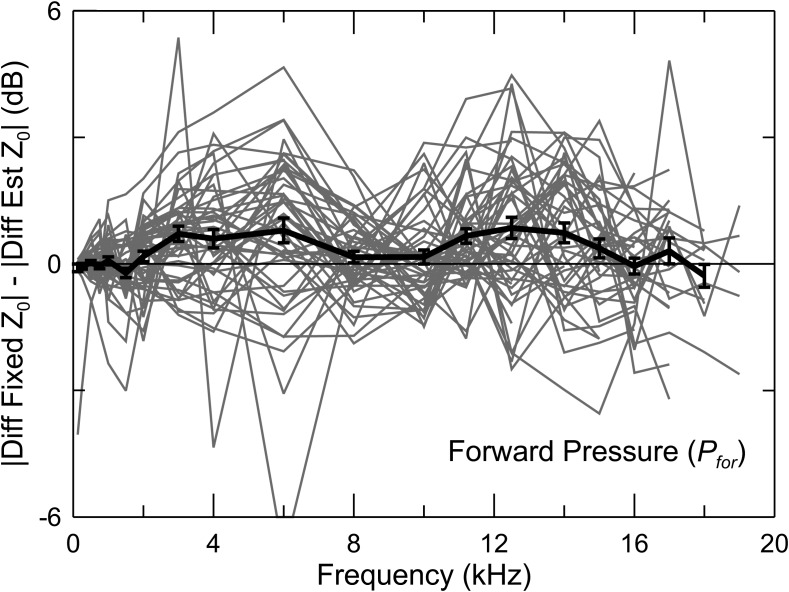
Summary of averaged threshold changes with insertion depth for all stimulus level measures, grouped into those measures with relatively poor performance (left column) and good performance (right column). The upper row depicts mean threshold changes, while the bottom row shows the standard deviations. Best performance overall was for forward pressure (P_for), integrated pressure (P_sum), estimated eardrum pressure (P_TMest), and depth-compensated ear simulator pressure (P_{sim_D}). Standard calibration in the ear simulator (P_{sim_S}) performs well above 10 kHz.

To better quantify variability of measures, insertion-depth threshold differences for averages of all ears were broken into frequency ranges of low (0.125 to 1 kHz), mid (1.5 to 6 kHz), and high (8 to 19 kHz). In general, all measures perform well in the mid-frequency range, but P_trans, P_ec, and W_abs show large insertion-depth dependence at frequencies above 5 kHz. A repeated measures two-way analysis of variance (frequency range × measure) indicated significant effects of both frequency range [F(2,7230) = 235.3, p < 0.0001] and measure [F(8,7230) = 10.04, p < 0.0001]. The interaction between frequency range and measure was also significant [F(16,7230) = 6.59, p < 0.0001].

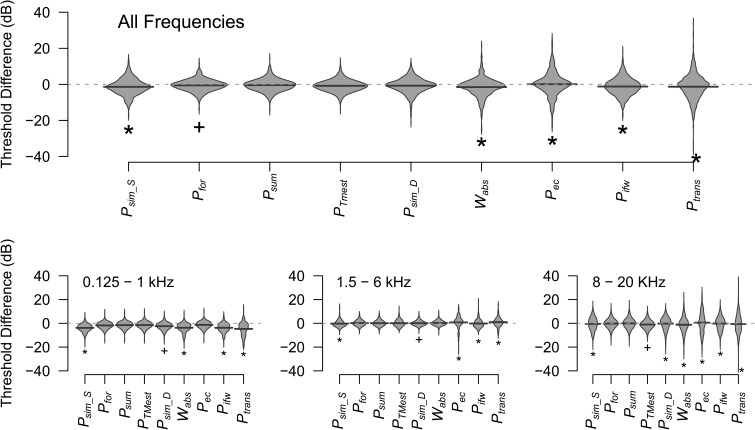
The Kolmogorov-Smirnov test was used to compare the distribution of threshold differences between the measures either across all frequencies or in the three frequency ranges using the Bonferroni correction for multiple comparisons in each set. This statistical analysis allows an objective appraisal of relative performance of the different acoustic measures that is much more powerful than, for example, comparing means and standard deviations. Two distributions with identical means and standard deviations could have significantly different distributions. In the case of our study, one of the two hypothetical distributions could have more large errors at extreme values, balanced by fewer errors of mid-range value. The impact of such large errors could influence clinical decisions, as they could result in errors in clinical categorization of an individual's hearing status. This approach provides a rigorous test of whether there is any basis to prefer one acoustic measure over another, the ultimate objective of this study. To provide a way to visualize the distributions analyzed using the Kolmogorov-Smirnov test, the results are presented in Fig. 6 in the form of beanplots. Each bean consists of a density trace (re: the vertical axis), which is mirrored horizontally to form a polygon shape. These plots allow intuitive comparison of multiple distributions of univariate data. Much like boxplots, beanplots show the data range but also display the distribution of data values that provides much more information than the range or mean value (Kampstra, 2008). P_for showed the smallest range when data across all frequencies were considered together (Fig. 6, top). This can be appreciated by the concentration of errors near 0 dB and the relatively small range of errors, compared to other measures. The thick horizontal lines across each bean serve two purposes. First, they show the mean value of each distribution. Second, they are the same length, which facilitates comparison of the sizes of the peaks in the distributions. The distributions of P_{sim_S}, P_trans, W_abs, P_ifw, and P_ec were all statistically significantly different from that of P_for (p < 0.01) in this set, demonstrating that P_for performed better. The distributions for P_for, P_sum, P_TMest, and P_{sim_D} were not significantly different over the full frequency range. Between 0.125 and 1 kHz the distributions of P_for, P_sum, P_TMest, P_{sim_D}, and P_ec were not significantly different, indicating comparably good performance. The distributions of P_{sim_S}, P_TMest, P_trans, W_abs, and P_ifw were statistically significantly different (p < 0.01) from P_for in the low frequency range. The distributions for P_{sim_S}, P_trans, P_ifw, and P_ec were significantly different (p < 0.01) from P_for in the mid frequency region (1.5–6 kHz), but those for P_sum, P_TMest, P_{sim_D}, and W_abs were not, indicating comparably good performance. Performance of P_for, P_sum, and P_TMest was comparably good in the highest frequency range (8–20 kHz) and the distributions of the rest of the measures were significantly different (p < 0.01) from P_for, indicating lower performance.

FIG. 6.

Comparison of distribution of threshold differences between measures for all frequencies (top) and for three smaller frequency ranges (bottom). The distribution of threshold differences for each measure is displayed using mirror images of the density trace forming a polygon shape (bean). The thick line inside each bean marks the mean difference for that measure. The measure yielding the smallest range in each set is marked with a (+). The measures with distributions statistically significantly different (p < 0.01, see text for details) from P_for are marked with asterisks.

B. Sensitivity of reflectance to changes in insertion depth

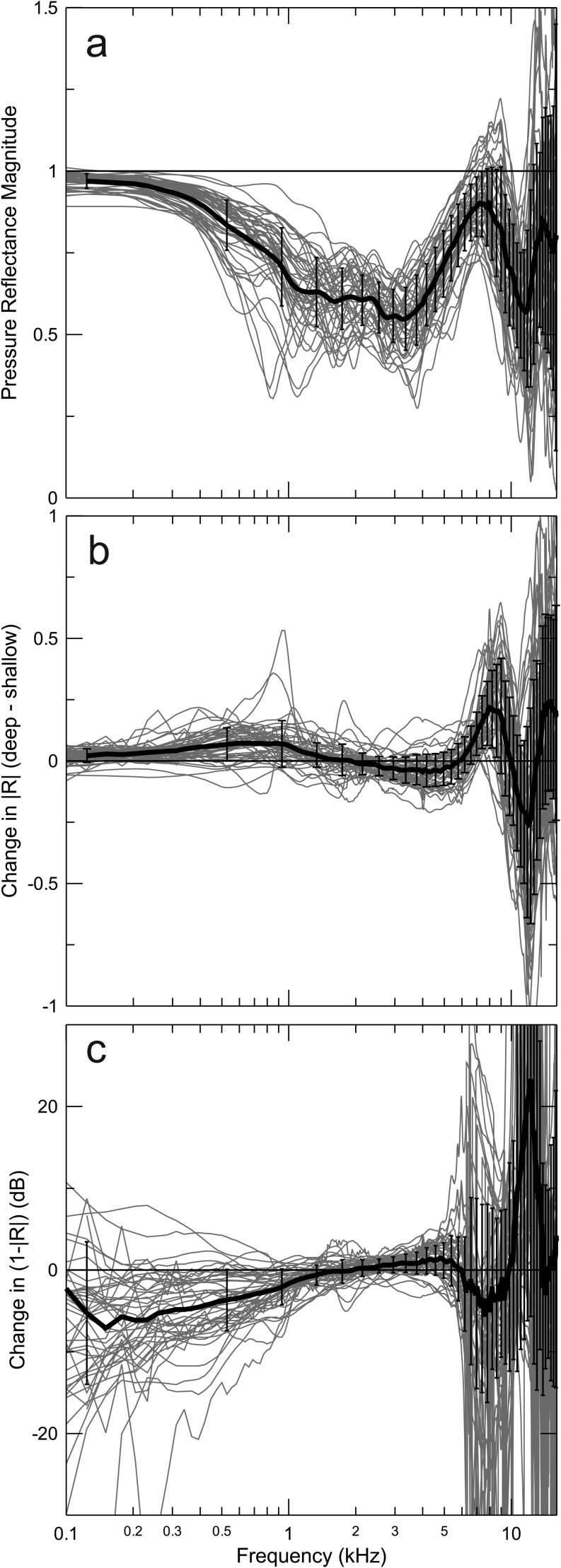
We traced the origin of the relatively poor performance of P_trans and W_abs at low and high frequencies to a strong dependence of the measured reflectance magnitude on insertion-depth. The trends are documented in Fig. 7. The magnitude of the pressure reflectance for the deepest insertions is shown in Fig. 7(a). The individual data, plotted for both ears of all subjects along with the mean (+/−1 SD), show the same pattern of reflectance decrease to a broad minimum from 1–4 kHz as reported previously (Stinson et al., 1982; Stinson, 1990; Keefe et al., 1992; Keefe et al., 1993; Voss and Allen, 1994; Farmer-Fedor and Rabbitt, 2002; Feeney et al., 2003). While reflectance in the average never exceeded 1.0, it did so in some ears at high frequencies. The reflectance measures reported here are presumed to be the product of a passive, linear system because contamination by OAEs is unlikely at the relatively high stimulus levels (∼80 dB SPL) used for these measurements. Reflectance magnitudes exceeding 1.0 must therefore be viewed as physically implausible. Even reflectances that approach but do not exceed unity, for example, in the frequency range of the peak near 8 kHz, likely overestimate the reflectance from the eardrum.

FIG. 7.

Pressure Reflectance and its changes with insertion depth. (a) Pressure reflectance magnitudes measured in all subjects with the deeper insertion depth are similar to those previously reported by others. (b) Reflectance magnitude is strongly influenced by insertion depth at frequencies above 5 kHz. (c) Corresponding changes in (1−|R|), expressed in dB also show large variability and systematic shifts below 1 kHz. The thick lines and error bars represent the mean (+/−1 SD).

Ideally, the magnitude of the reflectance of a cylindrical cavity with a fixed termination should not depend on the distance from the termination where reflectance is measured, ignoring losses during propagation. Relatively small changes in reflectance with varied insertion depth (deep minus shallow insertion) were measured below 6 kHz [Fig. 7(b)], but much larger changes were seen at higher frequencies. Although the between-subject variability was large at high frequencies, there was a consistent change in the positive direction reaching a peak near 8.5 kHz, with a minimum of reversed sign near 12 kHz and a secondary positive peak near 15 kHz.³ Transforming the reflectance changes of Fig. 7(b) into (1 −|R|), and plotting in decibels [Fig. 7 (c)], directly reveals the source of the large sensitivity to insertion depth of thresholds referenced to P_trans [see Eqs. (10)–(13)] and to changes in thresholds referenced to W_abs through the factor $(1-|R{|}^2)$ [see Eq. (14)] (Fig. 4). Large dependence of (1−|R|) on insertion-depth is evident above 5 kHz, but changes are also large at frequencies below 1 kHz. The large and highly individual variations at low frequencies are nevertheless consistently negative, approaching −10 dB with a large variance at 125 Hz. This trend is evident in the consistently positive change in reflectance over the same frequency range [Fig. 7(b)]. Relatively small changes in (1−|R|) with insertion depth were evident for frequencies between 1 and 5 kHz.

The variability of changes in (1−|R|) in Fig. 7(c) is somewhat artificially enlarged due to our need to truncate it to prevent it from becoming negative when reflectance exceeded 1.0. This manipulation also affects the variability of thresholds referenced to P_trans for the corresponding frequencies. Even though we would have preferred to avoid this complication, it is not possible to calculate decibels from a quantity with a negative sign. This complication contributes to our assessment that P_trans (at least for the methodology used in this study) is not a reliable measure of the input level to the ear.

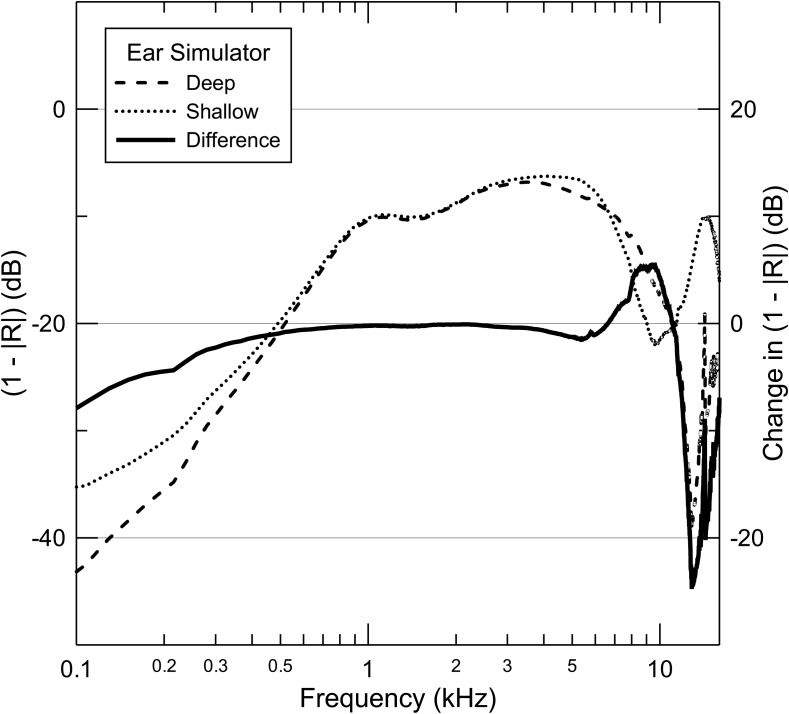
The pattern of change in reflectance [and (1−|R|)] with changes in insertion depth was largely replicated in the 60318-4 (IEC-711) ear simulator fitted with the standard tapered ear-canal segment (Fig. 8). The frequency of half-wave resonance for the deeper insertion of the probe into the simulator was 9.8 kHz (17.5 mm probe to termination distance), which was typical of the deeper insertions into the ears of human subjects. For the shallower insertion, the corresponding resonant frequency and distance were 6.8 kHz and 25.2 mm, respectively, typical of the shallower insertions in our subjects. For this shallower insertion, the end of the probe lay in the tapered segment of the ear simulator. The changes in (1−|R|) were similar to the average trend shown in our data measured in real ears [Fig. 7 (c)], except that the direction of changes in (1−|R|) above 6 kHz was reversed.

FIG. 8.

Changes in (1−|R|) measured in the ear simulator. The pattern of large changes at high frequencies and systematic shift below 1 kHz seen in real ears is demonstrated in analogous measurements in the simulator.

IV. DISCUSSION

We tested the sensitivity of thresholds to insertion depth using nine alternative measures of stimulus levels across the human hearing range. Large differences in insertion-depth sensitivity were noted, leading to the identification of the measures which best circumvent variations of probe insertion depth in a given ear. Overall, P_for, P_sum, and P_TMest showed similar and consistently smaller sensitivity to insertion depth than standard ear-simulator calibration (P_{sim_S}). The estimate of reflected pressure appears considerably less reliable than that of forward pressure.

The variability in the change in threshold with insertion depth partly depends on the test-retest variability of behavioral thresholds, which is only 1.5 dB (Green et al., 1987) to 2.1 dB (Stelmachowicz et al., 1989b). Accordingly, the contributions from acoustics to the standard deviations of measures reported here must be smaller than the ∼2.5 dB of the best-performing measures seen in Fig. 5(d).

The present experiments did not attempt to quantify the stimulus power and/or pressure that enter an individual inner ear, or to relate these quantities between ears.

A. Comparing insertion-depth sensitivity of thresholds referenced to different acoustic measures

1. Ear-simulator calibrations (P_{sim_S} and P_{sim_D})

Systematic deviations of ear-simulator calibrations from ideal performance were identified at frequencies below 1 kHz: Thresholds for shallow insertions required consistently higher simulator SPL than for deeper insertions (Figs. 3, 5, and 6). This trend is partly due to the absence of compensation for differences in the volume of the occluded ear canal segment. However, the same trend, though smaller, is also evident for all other measures including those in which pressure is directly measured and controlled (i.e., P_ec). One source of these deviations might be the diversion of volume velocity from the sound source by the increased compliance of the occluded canal volume for more shallow insertions. The sound-generating transducers of OAE probes have high source impedances, especially at low frequencies (data not shown), so they can be considered constant volume velocity sources. At 125 Hz, the wavelength is much larger than the distance between the source and the eardrum, so it is safe to assume that the pressure in the canal is uniform. A higher measured canal pressure at threshold for more shallow vs deep insertions then accurately measures the differences in eardrum pressures at threshold. The increased fraction of source volume velocity delivered to the canal volume for the shallower insertion results in reduced volume velocity into the middle ear. To maintain constant power delivery to the middle ear at threshold thus requires increasing the pressure from the source to compensate the decrease in volume velocity. An alternate explanation might be that eardrum stiffness could be slightly higher during deep insertions due to residual static pressure.

Performance of P_{sim_S} is relatively good between 1 and 4 kHz (Figs. 3, 5, and 6), but deviations exceeding +/−10 dB are seen in some subjects at 6, 8, and 10 kHz, with standard deviation approaching 10 dB at 8 kHz. The mean shows a biphasic change in this frequency range, caused by the change in the frequency of the first half-wave resonance that varies between ears. Performance is consistently better above 10 kHz. The worst performance is thus at the upper end of the conventional audiometric range (6 and 8 kHz) used in most hearing tests.

The performance of the depth-compensated ear-simulator method (P_{sim_D}) was generally as good or better than the standard ear-simulator calibration (P_{sim_S}) at 4 kHz and near the frequency of the first half-wave resonance (∼8 kHz) (Figs. 4–6). The negative trend in threshold changes for P_{sim_D} at frequencies below 1 kHz was consistently smaller than for P_{sim_S}, presumably because changes in canal volume with insertion depth are partly compensated in the P_{sim_D} method. While we rejected data from subjects where leaks were detected, it is possible that small leaks were not detected for the shallower insertions, thus exaggerating the downward trend in threshold changes at low frequencies. The performance of P_{sim_D} was not as good as for P_{sim_S} at frequencies above 12 kHz, likely due to the limited accuracy of the simulator in representing the geometry and impedance of real ears. Although our depth-compensated ear-simulator method matches the frequencies of first half-wave resonance between the simulator calibration and the ear under test, the second half-wave resonance in the simulator is close to twice the frequency of the first, while that of real ears is consistently lower (Lee et al., 2012) due to their non-cylindrical geometry (Stinson and Lawton, 1989; Hudde et al., 1999). The discrepancy between the frequencies of the second half-wave resonance in the simulator vs real ears causes the biphasic deviation of the mean threshold shift above 8 kHz (Fig. 4). On the other hand, this deviation is small, typically less than 4 dB in this frequency range, and the standard deviation of the mean does not appear significantly larger than for the best-performing measures (Figs. 5 and 6). The small insertion-depth dependence of thresholds referenced to P_{sim_D} at mid-frequencies, including the range of the first half-wave resonance, indicates that the depth-compensated simulator is a good approximation to the average ear in this range and sufficiently accurate for many applications. However, practical considerations, including monetary expense and the time-intensive calibration procedures, are likely to reduce the appeal of this approach.

It is important to note that the results of this study using simulator calibration do not depend on the type of acoustic coupler used for pressure calibration. While the absolute thresholds are presumably much more representative of those that would be measured at the eardrum with real ears if an ear simulator is used [i.e., as in Fig. 2(a)], the change in threshold resulting from a change in insertion depth for standard calibration (P_{sim_S}) is completely independent of the simulator/coupler pressure or the type of coupler itself. The threshold changes result entirely from the interaction between the characteristics of the sound source and the acoustics of the ear and are completely characterized by the changes in attenuation from the maximum output of the system at threshold. On the other hand, the success of the depth-compensated simulator method is critically dependent on accuracy with which P_{sim_D} approximates the eardrum pressure in real ears. The fact that thresholds vary more with changes in insertion depth using P_{sim_D} than for P_{sim_S} above 10 kHz is because the second half-wave resonance in the simulator deviates systematically from that of real ears. In this case, attempting to compensate introduces greater errors than not compensating for insertion depth as in standard calibration.

2. Acoustic quantities (P_for, P_sum, P_ifw, P_trans, W_abs) derived using Thévenin source calibration

Among measures derived from Thévenin methods, P_for and P_sum yielded the best performances (Figs. 4–6). It is curious that P_sum, which depends directly on reflectance and hence insertion depth (Fig. 7), performed as well as P_for. Because the performance of P_for is so good, we conclude that the separation of P_for and P_rev from P_ec, and hence the determination of pressure reflectance R, must also be reasonably accurate. The fact that R strongly depends on insertion-depth must then be accepted as real and in need of explanation. With cylindrical geometry and no losses through the walls, R should be independent of distance from the termination. The most obvious explanation for the relatively poor performance of measures that rely on estimation of the reverse wave(s) is that reflections do not occur at a single plane as would be the case with a cylindrical geometry. Especially at high frequencies, reflections are apparently not simply related to the signal transmitted into the cochlea. This view is supported by the observation that plausible estimates of ear canal geometry can be predicted from the reflectance measured using the same computations used in this paper (Rasetshwane and Neely, 2011).

One advantage of P_sum is that it estimates total eardrum SPL, a familiar quantity that is directly related to other pressure estimates in standard calibration procedures. P_sum was found useful to predict the pressure at the termination of a cylindrical cavity (Lewis et al., 2009; Scheperle et al., 2011). Because P_for and P_rev should be in-phase at the termination, the sum of their magnitudes should accurately predict the pressure at the termination. This predicted pressure would be in error in the presence of evanescent waves near the probe (which do not reach the termination). A drawback of P_sum is that phase is lost [see Eq. (9)] (Lewis et al., 2009). Whatever the size of inaccuracies and/or insertion-depth dependence contributed to P_sum by P_rev, the contribution from P_for appears to be a stronger factor in determining performance. The magnitude of the reflected pressure is consistently smaller than that of the forward pressure at most frequencies due to the fact that reflectance is generally less than 1.0. But it is puzzling that P_sum performed well even when the measured reflectance approached (or even exceeded) unity (Fig. 7). It may be relevant that reflectance calculated from longitudinal pressure gradients has been shown to be less dependent on deviations from cylindrical geometry than does reflectance calculated from the canal impedance at a single point (Farmer-Fedor and Rabbit, 2002).

The relative insensitivity to changes in insertion depth of behavioral thresholds referenced to P_for may be explained by the relative dominance of P_ifw over the contributions from higher-order forward going waves, which are affected by reflectance of the ear but are attenuated due to absorption at both the eardrum and the probe. The performance of P_for was improved by estimating the surge impedance from the measured canal pressure (see Sec. IV C below).

Thresholds referenced to the initial forward pressure (P_ifw) showed relatively large changes with insertion depth, especially near 8 kHz, almost identical to those for P_{sim_S} (Figs. 3–6). This observation argues against the possibility that the relatively good performance of P_for results from its dominance by P_ifw. Apparently, the contribution of secondary reflections from the plane of the probe, although attenuated, contributed significantly toward determining thresholds. Like the trend for P_{sim_S}, the biphasic shift in insertion depth errors in thresholds referenced to P_ifw (Fig. 4) corresponds approximately to the shift in the frequency of the first half-wave resonance in typical subjects. The close correspondence of P_ifw to the pressure response of our system measured in the LLT will be explored later (see Sec. IV C below).

Thresholds referenced to P_trans were nearly as strongly dependent on insertion depth as the pressure measured directly by the emission probe (P_ec). This measure appears strongly influenced by the dependence of reflectance on insertion-depth, both at frequencies below 1 kHz and above 4 kHz, most directly demonstrated in the critical factor (1−|R|) depicted in Fig. 7(c). This factor does not appear to reliably represent the pressure transmitted to the middle ear in these frequency ranges. Losses in the canal become more significant below 1 kHz (Voss et al., 2008) and the loss should be greater for the shallower insertions, assuming that loss is proportional to the length of the occluded canal segment. The small positive change in reflectance noted in Fig. 7(b) is consistent with this explanation. So P_trans may be compromised by variable, but systematic, errors in R caused by changes in P_rev at low frequencies where |R| approaches 1.0 and (1−|R|) approaches zero.

Thresholds referenced to W_abs were strongly sensitive to changes in insertion depth at both low and high frequencies, but performance was good between 1 and 6 kHz (Figs. 4–6). The degraded performance outside this range is due to the dependence of reflectance on insertion depth that also degrades the performance of P_trans and this sensitivity is magnified in the calculated absorbance [see Eq. (14)]. Thresholds referenced to I_ec (data not shown) showed virtually identical dependence on insertion depth as for W_abs. The two measures differ in that W_abs measures the total power flowing through the area of the canal at the measurement point, whereas sound intensity does not [Eq. (15)] (Keefe and Schairer, 2011). The similar performance of the two measures in our data is likely explained by relatively small and inconsistent changes in area between the deep and shallow insertions, indicated by the small and statistically insignificant changes in estimated surge impedance, implying that our measurements were made in a relatively uniform part of the ear canal. We chose to present only data for W_abs for this reason and because it is preferable on theoretical grounds. Following on the principle of optimal impedance matching by the middle ear, it is reasonable to assume that the power absorbed by the middle ear (and presumably that absorbed by the cochlea), should be the best measure of the input to the ear (e.g., Keefe and Schairer, 2011). However, temporal bone studies indicate that the pressure in the vestibule best predicts thresholds across the frequency range of hearing (Puria et al., 1997), suggesting that the ear is a receiver of pressure rather than power. Our data do not allow us to distinguish between these alternatives. The relatively poor performance of W_abs above 6 kHz is likely to be due to the difficulty interpreting reflectance measured using the impedance method, rather than indicating that thresholds at high frequencies are not determined by the power actually delivered to the inner ear (Farmer-Fedor and Rabbit, 2002).

3. Eardrum pressure estimation procedure (P_TMest)

The insensitivity to changes in insertion depth of thresholds referenced to eardrum pressure estimated using our novel procedure (P_TMest) is somewhat surprising because of its simplicity. Calibration of the sound sources only requires a long piece of 3/8 in. copper tubing (LLT), readily available at hardware stores. Most of the frequency dependence of the pressure delivered by the sound source is captured in P_LLT, which is modified to compensate for the half-wave resonances. Although the procedure does not compensate for differences in canal area between ears and does not yield an estimate of stimulus phase, its simplicity promotes easy implementation.

4. Pressure measured by the emission probe (P_ec)

Pressure measured directly by the emission probe (P_ec) is strongly influenced by standing waves (Siegel, 1994) [see Figs. 2(c) and 2(d)] and is reported here because it has been used for calibration in some commercial OAE applications. As shown in Figs. 4–6, P_ec deviated greatly from ideal performance for frequencies above 2 kHz and deviations above 4 kHz approached +/−20 dB in individual subjects (Fig. 4).

B. Evanescent waves

The acoustic stimuli are delivered by our probe through tubes that protrude slightly (∼1 mm) from the end of the ear tip, which constituted the calibrated plane of the emission probe's microphone transfer function (Siegel, 2007). The proximity of the microphone to the sound sources results in pressure measurements that contain evanescent waves that do not propagate more than a few mm down the ear canal. Only the approximately planar waves reach the eardrum (Rabbitt and Friedrich, 1991; Brass and Locke, 1997). An important difference between the present study and some previous impedance/immittance/admittance measurements (Rabinowitz, 1981; Huang et al., 2000; Keefe et al., 1992; Voss and Allen, 1994) is that in the referenced studies the probe microphone extended beyond the tip of the acoustic assembly where the stimulus was delivered to the ear canal, thus reducing the effects of evanescent waves.

The inevitability that evanescent waves made a significant contribution to the pressure measured by the emission-probe microphone makes it surprising that all measures of stimulus pressure, including P_for, appear to be good measures of the input to the ear. It is possible that the relatively large aperture of the probe's ear tip (∼4.5 mm) minimizes the influence of evanescent waves (Brass and Locke, 1997). But it seems more likely that the sensitivity of behavioral-thresholds to changes in insertion depth is not affected by evanescent waves.

It was straightforward to demonstrate the presence of evanescent waves in our system. With the emission probe inserted into the LLT, there is an elevation of P_ec above 10 kHz, measured using a separate probe tube microphone near the inlet or the OAE probe that appears to be caused by evanescent waves (data not shown). This elevation is not evident when the probe tube is advanced 3–5 mm from the sound source aperture.

Evanescent waves presumably contribute to both measured and derived quantities of sound at high frequencies and likely reduce the absolute accuracy of sound level control. However, the presence of evanescent waves does not appear to have compromised the insertion-depth measurements, probably because their contribution to the measured pressure is consistent enough to (at least partly) cancel when computing threshold changes. Indirect support for this interpretation comes from the fact that performance for P_{sim_S} was as good as for P_for, P_sum, and P_TMest at high frequencies. Evanescent waves are not a factor for P_{sim_S} because the simulator's microphone diaphragm was more than 5 mm from the sound source tubes of the emission probe.

Aside from the potential effects of evanescent waves, we have not found an obvious benefit to extending the sound source tubes to ∼5 mm beyond the microphone inlet, a distance that should be sufficient to minimize the influence of evanescent waves. The pressure reflectance of the B&K 4157 (IEC-60318-4) ear simulator measured with extended source tubing is virtually identical to that measured with no extension. However, a 5-mm source extension creates a large pressure null above 10 kHz at the eardrum that is not present in the emission probe's measured pressure (Siegel, 1994). As the sound propagates both toward the eardrum and toward the probe inlet, when delivered from a mid-canal position, nulls in measured pressure result from combining pressure waves traveling the shorter distance directly from the source and waves that follow the longer path after reflecting from the eardrum. In this situation, P_for and P_sum also demonstrate this null, so extending the sound source tubing has a serious consequence for controlling eardrum stimulus levels. In principle, this problem could be modeled and compensated, but it would likely be hard to implement without adding errors that can be avoided by not extending the source. A more direct set of measurements would be needed to assess the general impact of evanescent waves on the accuracy with which sound levels can be determined.

C. Estimating surge impedance (Z₀) improves performance

The Thévenin calculations were based on a procedure that estimates Z₀ from the ear canal impedance (Rasetshwane and Neely, 2011). This procedure proved superior to another (earlier) method that assumed a fixed value for Z₀ calculated from the diameter of the cavities used for source calibration. To quantify the differences in performance for the alternate choices of Z₀, we calculated the difference between the absolute values of the threshold changes at each frequency in each subject using the alternate calculations. Taking the absolute value of the changes recognizes the fact that divergence from perfect performance in either direction is equally undesirable. Positive differences between these absolute values indicate that the procedure that estimates Z₀ from the measured canal impedance came closer to perfect performance than assuming a fixed Z₀.

Consistently better and statistically significant performance, by ∼1 dB on average, was obtained for P_for computed using Z₀ estimated from the ear canal impedance at frequencies near the first two quarter-wave nulls in canal pressure 3 to 6 kHz and 11.2 to 14 kHz, respectively (p < 0.01, N = 46) (Fig. 9). In contrast, no statistically significant improvement in performance was observed at 2 kHz and below, 8 to 10 kHz, or 16 kHz and above. The latter two frequency ranges are near the frequencies of the first and second half-wave resonance in the canal pressure. This trend may be a consequence of the sensitivity to Z₀ of the calculated forward pressure in Eq. (4). This influence is strong for frequencies where Z_ec ≈ Z₀, specifically near the frequencies of quarter-wave pressure nulls, but vanishes for frequencies where Z_ec ≫ Z₀.

FIG. 9.

Dependence of thresholds referenced to P_for when the surge impedance (Z₀) is assumed fixed is reduced using a procedure that estimates Z₀ from the ear-canal impedance. The absolute values of threshold changes (errors) in each subject for the two calculations were subtracted, recognizing that the sign of the error was less important than its magnitude. Improved performance is greatest near the frequencies of quarter-wave resonance (∼5 and 13 kHz). The thick line and error bars represent the mean (+/−1 SEM).

The result depicted in Fig. 9 validates the procedure used to estimate the surge impedance from real-ear pressure measurements across the entire human hearing range. It also further indicates that forward pressure is estimated accurately. The interpretation of these data is consistent with the observation that the difference between the SPL at the termination of a cylindrical cavity and P_sum was most sensitive to changes in the diameter of the cavity near the frequencies of pressure nulls measured by a probe at the source end of the cavity (Scheperle et al., 2011)

Also related to the estimation of surge impedance is the observation that the estimated initial forward pressure (P_ifw) corresponds closely to the directly measured pressure with the probe inserted into the LLT (Fig. 10). The pressure P_ifw measured in the LLT can be calculated using the measured Thévenin source parameters P_src and Z_src as

$$P_{\mathit{i}\mathit{f}\mathit{w}}=P_{\mathit{s}\mathit{r}\mathit{c}}\frac{Z_0}{Z_0+Z_{\mathit{s}\mathit{r}\mathit{c}}}.$$ (19)

Since Z_src ≫ Z₀ for typical probes, at least at low frequencies, the relation is simplified,

$$P_{\mathit{i}\mathit{f}\mathit{w}}\approx P_{\mathit{s}\mathit{r}\mathit{c}}\frac{Z_0}{Z_{\mathit{s}\mathit{r}\mathit{c}}}=Z_0\left(\frac{P_{\mathit{s}\mathit{r}\mathit{c}}}{Z_{\mathit{s}\mathit{r}\mathit{c}}}\right).$$ (20)

Since the factor in brackets in Eq. (20) is independent of the load, P_ifw in long tubes with different diameters is simply proportional to Z₀ (or inversely proportional to cross-sectional area). If the ∼10 dB spread in level between different ears shown in Fig. 10(a) is caused primarily by differences in the cross-sectional area of the individual ear canals and represented in the estimated values of surge impedance, then normalizing the values of P_ifw measured in different ears by the ratio of surge impedances in the ear (Z₀) and the LLT (84.5 cgs ohms) should reduce the variability in Fig. 10(a) considerably and the normalized pressures should be close to the measured P_LLT,

$$P_{\mathit{L}\mathit{L}\mathit{T}}\approx P_{\mathit{i}\mathit{f}\mathit{w}}\frac{84.5}{Z_0}.$$ (21)

The normalized pressure responses satisfy the prediction [Fig. 10(b)], as they are clustered much more tightly around the measured P_LLT. This result indicates that the variation in Z₀ is, in fact, caused by variations in the cross-sectional area of each ear canal at the point of measurement and constitutes further validation of the procedure to estimate Z₀.

FIG. 10.

Initial forward pressure (P_ifw) at constant voltage is similar to the pressure response measured in the LLT, where reflected waves are negligible. The ∼10 dB spread in level between different ears shown in (a) is reduced considerably when the pressure is normalized by the ratio of the actual cross-sectional area of the LLT to the area of each ear canal, calculated from the estimated surge impedance (b). This result indicates that the variation in estimated surge impedance in each ear is, in fact, caused by variations in the cross-sectional area of each ear canal at the point of measurement.

V. CONCLUSIONS

Of the nine measures of stimulus level compared in the present study, P_for appears to be optimal because it minimizes errors caused by standing waves, has a solid theoretical basis, and includes stimulus phase, which is necessary for complete specification of acoustic stimuli. If stimulus phase is not required, as for measuring behavioral thresholds, then P_sum and P_TMest are also promising alternatives to standard calibration of insert earphones. Serious consideration should be given to incorporating one or more of these quantities into the roster of calibration standards. Virtually any measure of auditory system function would benefit from the use of P_for, particularly for frequencies in the upper range of human hearing. Such improved measures should lead to more reliable diagnostic tests (Kirby et al., 2011).

In cylinders, the contributions of evanescent waves to stimulus pressure do not vary with insertion depth. In real ear canals, which are not cylindrical, even the measures of sound that performed best in our insertion-depth tests can still be affected by evanescent waves.

Our study establishes the reliability of promising alternatives to standardized calibration. Nevertheless, the absolute accuracy with which each alternative predicts the pressure at the eardrum (Lewis et al., 2009; Scheperle et al., 2011) should be further investigated. To the extent that the alternative measures minimize the effects of standing waves, it seems likely that their absolute accuracy will also be good.

Glossary

Nomenclature

A

Cross-sectional area of the ear canal

BW_pk

Width of a half-wave resonance 3 dB below the peak

c

Speed of sound in air

f_λ/4

Frequency of the first quarter-wave pressure null at the probe

f_λ/2

Frequency of the first half-wave resonance in the ear canal

f_vol

Frequency below which the ear canal pressure can be assumed uniform

G_ec

Conductance of the ear canal

I_ec

Sound intensity in the ear canal

L_Peak

Sound pressure level at the peak of a half-wave resonance in the ear canal

P_ec

Pressure in the ear canal

P_for

Forward (toward eardrum) pressure

P_ifw

Initial forward (toward eardrum) pressure wave; sometimes referred to as incident pressure

P_LLT

Pressure measured in a long reflectionless tube

P_rev

Reverse (toward prove) pressure

P_{sim_D}

Insertion-depth-compensated pressure measured by the microphone of an ear simulator

P_{sim_S}

Standardized pressure measured by the microphone of an ear simulator

P_src

Thévenin equivalent source pressure

P_sum

Integrated pressure; the sum of magnitudes of the forward and reverse pressures

P_TM

Pressure at the tympanic membrane

P_TMest

Pressure at the tympanic membrane estimated from a remote measurement

P_trans

Pressure transmitted into the middle ear

R

Pressure reflectance

R_src

Source reflectance

R_TM

Reflectance at the tympanic membrane

ρ

Density of air

W_abs

Acoustic power absorbed by the middle ear

x_probe

Position of the calibrated plane of the probe in the ear canal

x_TM

Position of the eardrum at the end of the ear canal

Z₀

Acoustic surge impedance

Z_ec

Acoustic impedance of the ear canal

Z_src

Thévenin equivalent source impedance