Examining the spatially non-stationary associations between the second demographic transition and infant mortality: A Poisson GWR approach

Abstract

Based on ecological studies, second demographic transition (SDT) theorists concluded that some areas in the US were in vanguard of the SDT compared to others, implying spatial nonstationarity may be inherent in the SDT process. Linking the SDT to the infant mortality literature, we sought out to answer two related questions: Are the main components of the SDT, specifically marriage postponement, cohabitation, and divorce, associated with infant mortality? If yes, do these associations vary across the US? We applied global Poisson and geographically weighted Poisson regression (GWPR) models, a place-specific analytic approach, to county-level data in the contiguous US. After accounting for the racial/ethnic and socioeconomic compositions of counties and prenatal care utilization, we found (1) marriage postponement was negatively related to infant mortality in the southwestern states, but positively associated with infant mortality in parts of Indiana, Kentucky, and Tennessee, (2) cohabitation rates were positively related to infant mortality, and this relationship was stronger in California, coastal Virginia, and the Carolinas than other areas, and (3) a positive association between divorce rates and infant mortality in southwestern and northeastern areas of the US. These spatial patterns suggested that the associations between the SDT and infant mortality were stronger in the areas in vanguard of the SDT than in others. The comparison between global Poisson and GWPR results indicated that a place-specific spatial analysis not only fit the data better, but also provided insights into understanding the non-stationarity of the associations between the SDT and infant mortality.

Introduction

The second demographic transition (SDT), first proposed by Lesthaeghe and van de Kaa (1986), refers to a shift to living arrangements other than marriage, which are the result of changing socioeconomic conditions, education, and self-realization (Lesthaeghe and Neidert 2006). Increases in cohabitation, divorce, and non-marital childbearing, and delays in fertility and marriage are the major components of the SDT (Lesthaeghe 1995, 2010; Lesthaeghe and Neidert 2009; Lesthaeghe and Surkyn 1988). In the US, the onset of the SDT occurred in the 1950's when divorce rates were on the rise, and continued through the mid-1960s when fertility declined (Lesthaeghe 2010). During this time, marriage and parenthood decisions were postponed, educational opportunities expanded, and more stable and higher incomes were achieved (Lesthaeghe and Neidert 2006). Some of the consequences of these changes included a disconnect between marriage and procreation, a rise in premarital cohabitation (Lesthaeghe 2010), and a greater acceptability of procreation within cohabitation (Lesthaeghe and Neidert 2006).

Though SDT theory was sparked by the fertility transition, cyclical fertility theory, ideational and cultural changes, and Maslow's theory of changing needs (Lesthaeghe 2007), most research on the consequences or implications of the SDT has focused on political behaviors (e.g., voting) and fertility change in European countries (Kertzer et al. 2009; Lesthaeghe and Neidert 2009). Ecological or macro-level SDT research in the US (Lesthaeghe and Neidert 2006; 2009) has paid little attention to whether the SDT was associated with other outcomes such as health and mortality, and of specific interest in this paper, infant mortality. It should be noted that in our study, as with others we discuss, all refer to the infant mortality rate, which is defined as the number of deaths of infants under one year old in a given year per 1,000 live births in the same year. Overall population health in the US improved throughout the twentieth century; however, the life expectancy at birth is notably lower than other industrialized countries (World Health Organization 2010). The relatively high infant mortality rate in the US contributes to this phenomenon (Paneth 1995). In addition, the infant mortality rate remained at 6.9 deaths from 2000 to 2005, which is the first period of sustained lack of decline in the rate since the 1950s (MacDorman and Mathews 2008). While the goal of Healthy People 2010 was to reduce the infant mortality rate to 4.5 deaths per 1,000 live births (DHHS 2000), the current US rate is 6.14 deaths per 1,000 live births (about 40 percent higher than the Healthy People 2010 goal). The infant mortality rate should not be confused with the perinatal mortality rate (also high in the U.S. at a rate of 11.19 in the year 2000), which refers to the number of infant deaths of less than 28 days of age and fetal deaths of 20 weeks or more per 1,000 live births plus fetal deaths (MacDorman and Kirmeyer 2009). We believe that because the SDT regards parenthood as the product of self-realization, individual economic capacity, and cultural belief (education), an array of infant and child health outcomes should be closely related to the SDT. However, to our knowledge, no study has investigated such associations.

The goals of this study are to explore whether SDT has any implications for infant mortality in the US and to investigate if the implications, if any, differ across space. This study contributes to the infant mortality literature in three ways. First, due to the high infant mortality rate in the US, it is important to investigate potential new factors related to infant death. Recent decades have witnessed dramatic changes in family formation patterns (Smock and Manning 2004), with on average, approximately 5 percent of the population living in cohabiting unions, 44 percent of the population ages 25-29 years of age postponing marriage, and 9.7 percent of marriages ending in divorce. In addition, family formation experiences have been found to vary by geographic residence (Kreider and Simmons 2003). The SDT is a well established model and its main components may offer new insights into infant mortality in the US.

Second, few ecological studies of infant mortality have explicitly taken the three early signs of the SDT (marriage postponement, cohabitation, and divorce) into account, and the SDT theoretical framework has not been extended to the mortality literature. The prolonged formal education, aspirations for self-realization, and desire for consumption and leisure are the main explanations for why the SDT occurs (Lesthaeghe 2010). These explanations lead us to believe that the SDT is associated with infant mortality. We hypothesize the following three relationships between the early signs of the SDT and infant mortality (we review and discuss the literature in the next section): (1) marriage postponement is negatively associated with infant death rates. On average, couples in a delayed marriage and/or parenthood would be better educated, more willing to sacrifice self-realizations and personal desire for their children, and be better prepared for a future with their children than their counterparts entering marriage and/or parenthood early (Lesthaeghe and Neidert 2006; McLanahan 2004; Pittard, Laditka and Laditka 2008). Therefore, marriage postponement would provide an environment that facilitates infant health. (2) Cohabitation rates are positively associated with infant death rates. Unlike married couples, it is relatively rare for cohabiting (unmarried) partners to take advantage of the factors that reduce the opportunity cost of parenthood such as public welfare provisions (e.g., Family Medical Leave Act) and private organizational benefits (e.g., daycare) (Kimbro 2008); cohabiting couples cannot apply or are less likely to apply for some benefits available to married couples. Explicitly, the cohabiting partners may be burdened with higher costs and less resources than married couples, therefore, increasing the risk of infant death. (3) Divorce rates are positively associated with infant death rates. Divorce contributes to a loss in social, economic, and medical resources, which has been found to be adversely related to infant health and increase infant mortality (Amato 2000; King et al. 1998; Smock, Manning and Gupta 1999; South, Crowder and Trent 1998).

The third contribution of this paper is its explicit spatial modeling framework. It has been found that some states/counties in the US enter the SDT earlier than others, and several studies have revealed considerable spatial variation in the major components of the SDT across the 48 contiguous states (Lesthaeghe and Neidert 2006; Lesthaeghe and Neidert 2009). For instance, marriage postponement and cohabitation are common in states in the northeastern region including New York, Massachusetts, Rhode Island, New Jersey, and Connecticut, as well as in California and Nevada (Lesthaeghe and Neidert 2006). Despite the well-documented spatial variation of the SDT process, few SDT studies have analyzed ecological data with an explicit spatial perspective. As Logan et al (2010) suggested, spatial techniques not only could be used to explore spatial patterns, but also to examine and/or refine theories. To the best of our knowledge, no study has attempted to use a place-specific spatial analysis approach (i.e., Geographically Weighted Regression, GWR (Fotheringham, Brunsdon and Charlton 2002)) to examine the patterns revealed by the SDT advocates and to explore the implications of the SDT on infant mortality. Thus, in addition to the three substantive hypotheses stated above, this study will investigate whether the associations between infant mortality and the SDT echo the spatial patterns of the SDT found in the literature. Specifically, we hypothesize that the relationships between the SDT factors and infant mortality are stronger in the areas that are ‘in the vanguard of the SDT’ (Lesthaeghe and Neider, 2006; p.681). Following Lesthaeghe and Neider, we used “vanguard” to represent those regions/states/counties with high SDT indicators. GWR is a powerful tool that can be used to investigate spatial non-stationarity and has been proven to also handle spatial dependence inherent to ecological data (Fotheringham et al. 2002). GWR has been increasingly used in health studies to unveil the place-specific associations (Chen et al. 2010; Edwards et al. 2010; Shoff, Yang and Matthews 2011) and we will use this approach to test this final hypothesis.

Literature Review

What is the relationship between marriage postponement and infant mortality?

Marriage postponement (and delay in childbearing) has been linked to resources for children (McLanahan 2004) and child health (Pittard et al. 2008). Delayed marriage has been found to increase marital stability, which contributes to parenting quality and consequently, infant health (Martin 2004; McLanahan 2004). Three possible explanations for this empirical linkage are suggested (Martin 2004). First, delayed marriage indicates an increase in psychological maturity because couples may experience more years of adult and social life before marrying, resulting in high levels of patience and willingness to cooperate. Second, delayed marriage is correlated with higher education, which is associated with lower rates of marital dissolution. Third, delayed marriage implies an extended search time for a compatible partner, making the marriage stable and the partners more involved in child care. Thus, high psychological maturity, education, and partners’ involvement in parenting are found to improve parenting quality and parental resources, which may, in turn, improve infant health (Barrington 2010; McLanahan 2004).

In addition to the social explanations discussed above, maternal age itself has been related to infant mortality. Specifically, for singleton births in the US, the infant mortality rate of teenage mothers is the highest (10.28 deaths per 1,000 live births); whereas, mothers in their early thirties have the lowest rate (5.47). It is noteworthy that the infant mortality rate increases slightly for mothers aged 35 years and over due to biological constraints (Mathews and MacDorman 2008). For multiple births, there is a descending trend with increased maternal age. Mothers aged 40 years and older have the lowest infant mortality rate (17.45), which is only about one quarter of the rate among teenage mothers (66.69) (Mathews and MacDorman 2008). The differences in infant mortality by age could be attributed not only to socioeconomic factors (Phipps, Blume and DeMonner 2002), but also to biological immaturity (Kirchengast and Hartmann 2003; Misra and Ananth 2002), and an increased risk of prematurity and low birth weight with younger maternal age, especially for mothers having their first births (Nabukera et al. 2006).

A study used the infant-mother linked data in North Carolina to thoroughly examine whether early childbearing is associated with poor infant health outcomes (Pittard et al. 2008). Accounting for both maternal and infant characteristics, Pittard and colleagues (2008) concluded that infants of adolescent mothers were more likely than infants of older mothers to have poor health outcomes, despite the significant mediating effects of maternal socioeconomic status. That is, early childbearing undermines infant health. The literature discussed above suggests that marriage postponement or delayed childbearing should be, in general, negatively associated with infant mortality on account of the accompanying mental, biological, and social maturity.

What is the association between cohabitation and infant mortality?

In Sweden and other Nordic countries, cohabitation has moved from a deviant status to a prelude to marriage during the SDT. According to this pathway, cohabitation becomes an equivalent to marriage, where the relationships among the cohabiting partners are as stable as those in marriages (Kiernan 2000). Raley (2001), using data from the National Survey of Families and Households and the National Survey of Family Growth, shows how this pathway has not been the case in the US where cohabitation is not a marriage alternative. While most Americans still marry at some point in their lives, cohabitation has significantly altered the marriage process (Smock and Manning 2004). Cohabitation is the precursor to the majority of marriages and remarriages (Smock and Manning 2004). While the rate of cohabitation has increased among couples of all age groups, the majority of young men and women will cohabit (Smock and Manning 2004). Research has shown that 45 percent of women and 38 percent of men under the age of 30 cohabiting (Cherlin 2010). While cohabitation is common among people of all educational levels, people with less education are more likely to cohabit (Cherlin 2010). In addition, couples living in cohabiting unions are also more likely to have fewer economic resources (Smock and Manning 2004).

In the US, cohabiting unions are becoming less stable over time. For example, relationships that begin as cohabiting unions are now less likely to result in marriage, and are now more likely to dissolve within five years than they were 20 years ago (Bumpass and Lu 2000). It has been suggested that one of the key distinctions between cohabitation and marriage in the US is the duration of the relationship (Smock and Manning 2004), and that the underlying “contract” of cohabitation is more fragile than that of marriage (Brines and Joyner 1999). Approximately half of all children born to cohabiting parents experience their parents separating by the time they are nine years of age compared to only 20 percent of children born to married parents (Kennedy and Bumpass 2008).

Cohabitation has become increasingly common over time; as a result, births to women living in cohabiting unions have increased and have become widely accepted (Luo, Wilkins and Kramer 2004; Raley 2001). Approximately 40 percent of all cohabiting couples have at least one biological child of either partner living with them (Cherlin 2010). Despite the increase in cohabiting unions, unmarried women continue to have a greater risk of adverse pregnancy outcomes compared to married women (Luo et al. 2004). There has been research that has shown that marriage is a protective factor for many adverse birth outcomes, including low birth weight, preterm delivery, and infant mortality. Marriage is believed to promote the health of mothers through several mechanisms that are correlated with favorable birth outcomes, such as increased socioeconomic status, social support, adequate prenatal care, and few risky behaviors (Barrington 2010; Kiernan and Pickett 2006).

In recent reviews, Alio et al. suggested that paternal involvement is beneficial for reducing infant mortality (Alio et al. 2010; Alio et al. 2009). The amount of paternal involvement before birth is partially associated with the relationship status of the mother and father (Alio et al. 2009). Young and Declercq (2010) identified that there is a risk gradient for experiencing a poor birth outcome according to the marital status of the mother. Using weighted logistic regression models, they found that unmarried mothers without partners followed by unmarried mothers with partners had the greatest risk of experiencing a poor birth outcome, and that married mothers have the smallest risk of giving birth to a premature or low birth weight infant. Orr (2004) identified maternal social support as a factor that has been shown to improve pregnancy outcomes either by offsetting the effects of stress or by directly improving women's health. Using data from the Fragile Families and Child Wellbeing Study, Kimbro (2008) found that mothers who were cohabiting, dating, or recently separated all had a higher odds of inadequate prenatal care, smoking, drinking, and drug use during pregnancy compared to those mothers who were married. The previous literature has shown how the availability of financial, emotional, and social support is associated with improved birth outcomes, and that these resources are associated with the relationship status of the parents (Kimbro 2008).

What is the relationship between divorce and infant mortality?

There are several mechanisms by which divorce may have an impact on infant mortality. First, divorce has been shown to inhibit legal access to the previous partner's tangible resources such as health insurance benefits, income, and assets. In many cases, women who experience divorce typically encounter striking declines in family income and economic well-being (Smock et al. 1999). With the decrease in family income, it is not uncommon for women to move to poorer neighborhoods following their divorce (South et al. 1998). Divorce also has been shown to reduce, and in some cases, eliminate the social bonds among friends and family members of both parties in the marriage, resulting in the likelihood that they may not provide as much, if any, financial support as they did during the marriage (Duncan, Wilkerson and England 2006).

Second, not only can the loss of friends, family members, and spouse cause a loss in economic support, but divorce can also cause a loss in social support. Social support from partners and family relationships may provide social control over health behaviors and the loss of this support can be harmful to health (King et al. 1998). The loss of socioeconomic, social, and health resources following a divorce may negatively influence the quality and timing of prenatal care (Abrevaya and Dahl 2008), maternal and infant nutrition status (De Silva and Harpham 2007), and maternal behaviors during pregnancy such as smoking and depression (Elsenbruch et al. 2006). Therefore, infants of divorced parents, specifically mothers, would experience higher infant mortality rates than infants of married parents.

A third explanation is that during the time that the marriage is ending and immediately following the divorce, new events emerge that have the potential to affect people's emotions, behavior, and health (Amato 2000). Divorce can result in less effective parenting (Amato 2000) and often causes conflict among partners, increasing the likelihood of abuse, which adds to the vulnerability of mothers and imposes greater threats to infant health (Burke, Lee and O'Campo 2008).

We argue that while relatively little research has explicitly focused on the association between divorce and infant health, especially in the US context, the literature suggested that divorce is closely associated with women's economic well-being, which in turn, has been adversely related to infant health. Extending this thought, to examine if divorce is linked to infant mortality at the ecological level, it is imperative to consider socioeconomic status and divorce simultaneously.

What is the geographic variation of SDT in the US?

SDT theorists conclude that the strong spatial correlation between the different SDT components distinguishes the US from the European countries (Lesthaeghe and Neidert 2006). A state level analysis showed that the New England and Mid-Atlantic states (e.g., New Jersey, Massachusetts, Rhode Island, and Vermont) were in the early stages or vanguard of the SDT (Lesthaeghe and Neidert 2009). Although some Pacific and Mountain states (e.g., California, Nevada, and Arizona) were in the vanguard of the SDT as those in the northeast, the woman and children were found to be more vulnerable on the west coast (Lesthaeghe and Neidert 2006). This is an important finding as it indicates that the associations between the SDT components and the vulnerability of women and children were not distributed equally across space.

At the county-level, Lesthaeghe and Neidert (2006) investigated the spatial distributions of cohabitation and marriage postponement in the US (the detailed maps can be found at www.sdt.psc.isr.umich.edu). The counties located in the Great Plains, Black Belt, the middle and southern Appalachian Region and Utah had low cohabitation scores. By contrast, the counties around the Four Corners and in North Carolina, South Carolina, and Virginia had relatively high cohabitation scores (Lesthaeghe and Neidert 2006). The counties with high marriage postponement scores were concentrated in California, Oregon, Washington, New Mexico, Colorado, and the Boston-Washington corridor. The marriage postponement scores were low in the counties of Kentucky, Tennessee, Missouri, Arkansas and Oklahoma.

What do we learn from these earlier studies? First, while the state level analysis demonstrated a general pattern whereby the coastal states enter the SDT earlier than the inland states, the county-level findings reveal spatial variation within and across state boundaries. Second, it is possible that a composite SDT score may disguise the dissimilarity in spatial distribution between marriage postponement and cohabitation. To more fully explore the association between the SDT and infant mortality, marriage postponement and cohabitation will be analyzed separately in this study. Third, SDT research to date has not provided a clear picture of how the divorce component is distributed spatially. Although divorce is not as strongly predictive of the SDT in the US as it is in Europe (Lesthaeghe and Neidert 2006); it remains a sign of the SDT (McLanahan 2004). Further investigation on the spatial pattern of divorce is warranted and we incorporate this dimension into our analysis of infant mortality.

Data and Methods

Measures and data sources

The Areas Resource File, a county-level database maintained by the Bureau of Health Professions, provided the infant health data used in this study (Area Resource File 2008). Three variables centered on 2003 were extracted for the counties in the contiguous US: (1) number of infant deaths before the first birthday; (2) number of live births; and (3) number of low birth weight infants (weighing less than 2,500 grams at birth). All three variables are calculated by averaging three-year (2002-2004) data to reduce the annual fluctuation in rates. Based on these variables, we calculated low birth weight rates, and the expected number of infant deaths. Low birth weight rates were defined as the number of low birth weight infants per 1,000 live births. To obtain the expected number of infant deaths, we first calculated the national infant mortality rate (number of infant deaths per 1,000 live births) and then multiplied the national rate by the total live births in each county, according to the mother's county of residence. The actual (observed) number of infant deaths was used as the dependent variable with the expected number of infant deaths as the offset variable. As low birth weight has been found to be a factor closely related to infant death (Barton, Hodgman and Pavlova 1999), it was included in the analysis as a control to fully explore the associations between the SDT and infant mortality. To reiterate the temporal order of our dependent and independent variables, the infant mortality data are centered on the year 2003 whereas most of the independent variables described below were collected around year 2000. The temporal lag can help better frame the associations we are interested in but note that this study is not designed to address causal relationships between SDT and infant mortality. The model specifications are discussed in greater detail below.

We measured the concept of the SDT with three covariates: marriage postponement, cohabitation, and divorce. We extracted data from the 2000 US Census and measured marriage postponement as the percent of population aged 25 to 29 years of age and never married. Cohabitation was measured with the percent of all households headed by unrelated adults and the divorce measure was the percent of the population aged 15 years and over reporting their marital status as divorced. These same measures have been used in previous research on the SDT (Lesthaeghe and Neidert 2006). Counties with higher percentages on these variables indicate that they are in later stages of the SDT (Lesthaeghe and Neidert 2006).

Our study relies on the 2000 US Census (US Census Bureau 2000) for ecological measures of both demographic and socioeconomic structure. Since the 1980s, the importance of social factors (e.g., race/ethnicity) in infant mortality research has been emphasized (Cramer 1987; Sparks, McLaughlin and Stokes 2009). Infant mortality rates are found to be higher among minorities (DHHS 2000) than among whites so our analysis included three county-level racial/ethnic composition measures: percentage non-Hispanic black, percentage Hispanic, and percentage of other races, excluding the percentage white to avoid problems with multicollinearity. In addition, socioeconomic conditions in a county need to be considered as they have been found to be the fundamental causes of diseases/deaths and have been used in earlier studies (Link and Phelan 1995; Phelan, Link and Tehranifar 2010; Yang, Teng and Haran 2009). We used 2000 Census variables to create factors that describe county-level socioeconomic conditions. Specifically, following Sampson and colleagues (1997), we used principal component analysis with the Varimax rotation method. Eight covariates were reduced to form two measures: affluence (eigenvalue = 4.42) and disadvantage (eigenvalue = 1.73). The former was based on the log of per capita income (0.78), the percentage of the population aged 25 years and over with a bachelor degree or higher (0.94), the percentage of the population working in professional, administrative, and managerial occupations (0.79), and the percentage of families with annual incomes over $75,000 (0.89). The latter was based on the individual poverty rate (factor loading = 0.84), the percentage of persons receiving public assistance (0.81), the unemployment rate (0.84), and the percentage of female-headed households with children (0.80). These two factors explained 77 percent of the variances among the eight variables and the factor scores calculated with the regression method were used in the analysis. Another measure of social conditions was residential stability. In this study, residential stability is an average standardized score of the percentage of the population living at the same house for at least 5 years and the percentage of owner-occupied housing units.

The final independent variable was the three-year (1999-2001) average percentage of mothers receiving late or no prenatal care (where late = after the first trimester of pregnancy). We extracted the data from the Office on Women's Health Quick Health Data Online whose data came from the National Vital Statistics System Detail Natality Files maintained by the National Center for Health Statistics (NCHS 1999-2001). It is suggested that prenatal care improves infant health by identifying the risk factors related to infant mortality and low birth weight (Laditka et al. 2005; Lauderdale et al. 2010). We included the percentage of late or no prenatal care to minimize the impacts of confounders (e.g., SES and prenatal care) on the associations between infant mortality and the SDT, enhancing the validity and reliability of our analytic results.

Analytic methods: Geographically weighted Poisson regression (GWPR)

As infant deaths have been relatively rare in the US, a Poisson regression model is more appropriate than a Gaussian model (Yang et al. 2009). However, a conventional Poisson model would not suffice for testing all research hypotheses, particularly because of the explicit spatial focus and posited spatial variation in effects. We employed both a conventional Poisson regression model and a GWPR model. A conventional (global) Poisson regression model is written as:

$$\begin{array}{cc}\hfill & O_i\sim Poisson\left[E_i\exp \left(\sum _j{\beta }_j{x}_{j,i}\right)\right]\hfill \\ \hfill & \log \left(O_i\right)=\log \left(E_i\right)+{\beta }_0+\sum _j{\beta }_j{x}_{j,i}\hfill \end{array}$$ (1)

where O_i and E_i represent the observed (actual) and the expected number of infant deaths, respectively. E_i is treated as an offset variable and forced to have a regression coefficient of 1. β₀ is the intercept and β_j are the coefficients for the independent variables j of county i, x_j,i . Following Nakaya et al (2005), our dependent and offset variables can be understood as the standardized mortality ratio (SMR) and the model (1) could be rewritten as:

$$\log (O_i∕E_i)=\log \left(SM{R}_i\right)={\beta }_0+\sum _j{\beta }_j{x}_{j,i}$$ (2)

The conventional Poisson regression model does not consider geographical locations and is unable to show the potential spatial varying associations between the SDT and infant mortality.

The GWPR was developed to examine the spatial varying coefficients over space and a GWPR model is expressed as:

$$\log (O_i∕E_i)=\log \left(SM{R}_i\right)={\beta }_{0,i}+\sum _j{\beta }_{j,i}{x}_{j,i}$$ (3)

The most notable difference with model (2) is that the regression coefficients β's are specific to each county i (i.e. spatial varying coefficients). The GWPR allows geographically varying parameters and generates local spatial statistics. The best approach to summarizing the information generated by GWPR is to map and show the distributions of the local estimates (Fotheringham et al. 2002).

The GWPR uses a kernel-based geographical weighting function to create spatial weights for each county. The principle of weighting is to place a kernel around a county, and to compute the local coefficients (β's) using all the observations within the kernel window, which is determined by the bandwidth, h. Conventionally, the value h that yields the smallest Akaike Information Criterion corrected (AICc) is selected as the most appropriate bandwidth in the kernel function. The estimation technique is based on iteratively reweighted least squares, with weights based on the bisquare kernel function:

$$w_{ik}={\left[1-{\left(\frac{d_{ik}}{h}\right)}^2\right]}^2\text{if}{d}_{ik}\le h;\text{otherwise}0$$

where d_ik is the distance between the county i and a nearby county k. According to the kernel function, counties closer to the county i would carry more weight and have greater influences on parameter estimation than those farther away (if the distance between two counties is larger than h, the weight equals zero). Our analyses use GWR 3.0 to estimate the GWPR models (Fotheringham et al. 2002).

Several GWPR modeling issues should be noted. First, both Monte Carlo and Leung tests for spatial non-stationarity are only applicable to the Gaussian models. For the geographically weighted generalized models, comparing the global with local variations is the appropriate approach to the non-stationarity test (Fotheringham, Brunsdon and Charlton 2003). Second, while various kernel functions are available, it has been suggested that the choice of kernel functions does not dramatically alter the geographically weighted regression results (Fotheringham, Brunsdon and Charlton 2001). Third, this study uses adaptive bandwidth selection, which has been found to better fit unevenly distributed spatial data, such as when using the centroids of the US counties (which vary in geographical size) (Fotheringham et al. 2001).

The coefficients in both global and local regression models can be interpreted exponentially as the sensitivity of the number of infant deaths to a change of one unit difference in the corresponding independent variable. The only difference in the coefficient interpretation between model (2) and (3) is that the GWPR coefficients can only be generalized to the number of infant deaths (or SMR) within the zone covered by the kernel function and not to the whole research area. For instance, in a global Poisson model, holding others equal, the exponentiated β₁ (e^β₁) indicated an infant mortality rate ratio (relative rate) corresponding to a one unit change in x_j,1 or the (e^β₁ — 1) percent (multiply by 100) increase or decrease in the number of infant deaths over the whole data set. However, in GWPR, the same one unit change in x_j,1 may provoke different levels of change in infant mortality because the coefficient of x_j,1 is specific to each location that can be summarized in map forms.

Results

The descriptive statistics of the variables in this study are displayed in Table 1. On average, there were almost 9 infant deaths and about 1,300 live births in a county between 2002 and 2004. The SMR ranged from 0 to 16, the mean value was almost 1, but the standard deviation (0.76) was relatively large in contrast to the mean, indicating great variation.¹ Regarding the SDT measures, in the average county almost 32 percent of the population aged 25 to 29 is not married (implying some degree of marriage postponement). The mean cohabitation percentage in the US counties was slightly higher than 4. On average, approximately 10 percent of people aged 15 years and over reported being divorced.

Table 1.

Descriptive statistics of all variables used in this study (N=3,071)

Variables	Minimum	Maximum	Mean	Std. Deviation
Number of infant deaths	0.00	776.00	8.93	30.12
Number of infant births	1.00	152,960.00	1,300.85	4,684.32
Standardized mortality ratio	0.00	16.18	0.99	0.76
Low birth weight rate	0.00	333.33	80.14	24.47
Marriage postponement	0.00	84.85	31.92	10.74
Cohabitation	0.00	15.33	4.21	1.42
Divorce	2.26	19.13	9.49	1.94
% Non-Hispanic Black	0.00	86.08	8.54	14.36
% Hispanic	0.00	98.10	6.17	12.14
% Other races	0.00	93.58	3.49	6.79
Affluence	−2.43	5.75	0.00	0.99
Disadvantage	−2.54	9.06	0.00	1.00
Stability	−5.67	2.76	0.03	0.97
Late or no prenatal care	0.00	54.05	17.38	7.04

The variations in counties’ racial compositions were conspicuous. The average percentages of non-Hispanic black and Hispanic populations were approximately 9 and 6 percent, respectively, but the maximums for both were very high (86 and 98 percent, respectively). In addition, although the socioeconomic conditions, affluence and disadvantage, were standardized, the ranges of these two variables were wide. Finally, a mean of 17 percent of mothers received late or no prenatal care.

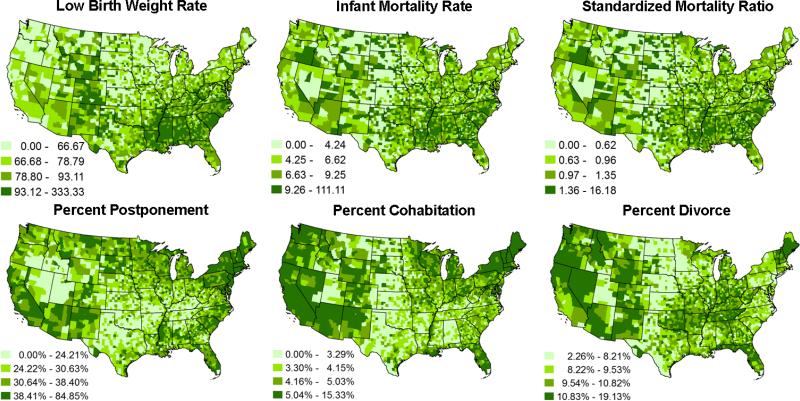
Figure 1 visualizes the spatial distributions of key variables (by quartiles). In the top row we showed the low birth weight rate, the infant mortality rate, and the standardized mortality ratio. A common spatial pattern in these infant health variables was the concentration of high rates in the Appalachia region, the Black Belt, the Mississippi Valley, and some Mountain states (e.g., Arizona and Colorado), and low rates in the Great Plains. The bottom row showed the key SDT measures (marriage postponement, divorce, and cohabitation). A noticeable pattern for marriage postponement and cohabitation was that the counties in Pacific states, some Mountain States, and the northeastern regions had higher values for all SDT measures than their counterparts in the Great Plains. A concentration of high divorce rates straddles the Mississippi in an area focused on Tennessee, Kentucky, Arkansas, Oklahoma and parts of the Ohio Valley and its spatial distribution was unique to divorce. These patterns not only reproduced the geographical distributions of the main components of SDT (Lesthaeghe and Neidert 2006), but also revealed the potential spatial non-stationarity between individual components of SDT and infant health.

Figure 1.

Descriptive maps of the key infant health and second demographic transition variables

The global Poisson regression results were shown in Table 2. For these models, we tested for multicollinearity utilizing the variance inflation factor (VIF) (results available upon request). The highest VIF is 4.76 (disadvantage), which is well below the common cut-point of 10 (Menard 2002) and indicates that multicollinearity is not a problem in our analyses. Model I served as the base model where only the SDT measures and low birth weight rate were considered. Racial/ethnic composition variables were added in Model II and all of the independent variables were included in Model III. We summarized important findings drawn on these global results. First, all of the SDT measures were significantly associated with infant mortality. Specifically, marriage postponement was negatively related to infant mortality. Model III suggested that a one percent increase in marriage postponement, ceteris paribus, was associated with 0.3 percent decrease in the number of infant deaths. Cohabitation and divorce were adversely related to infant health. Without considering socioeconomic conditions (Model II), the number of infant deaths in a county would, on average, increase by 4 percent in response to one percent increase in cohabitation. This association was, in part, explained by the socioeconomic variables (see Model III), but remained significant. The relationship of divorce with infant mortality was relatively stable across models. In general, the number of infant deaths increased by 2 percent with a one percent increase in divorce. It is also worth noting that all the associations between the SDT measures and infant mortality held, even after taking all of the racial/ethnic composition and socioeconomic covariates into account.

Table 2.

Global Poisson regression results and AICs (N=3,071)

	Model I				Model II				Model III
Variables	Estimate	S.E.	Exp(est)	Sig.	Estimate	S.E.	Exp(est)	Sig.	Estimate	S.E.	Exp(est)	Sig.
Intercept	−1.284	0.050	0.277	***	−0.823	0.062	0.439	***	−0.825	0.068	0.438	***
Low birth weight rate	0.014	0.000	1.014	***	0.009	0.001	1.009	***	0.008	0.001	1.008	***
Marriage postponement	−0.004	0.001	0.996	***	−0.007	0.001	0.993	***	−0.003	0.001	0.997	*
Cohabitation	0.023	0.008	1.024	**	0.043	0.008	1.044	***	0.022	0.008	1.022	**
Divorce	0.020	0.004	1.020	***	0.015	0.004	1.015	**	0.016	0.005	1.017	***
% Non-Hispanic Black					0.007	0.001	1.007	***	0.006	0.001	1.006	***
% Hispanic					−0.002	0.000	0.998	***	−0.003	0.001	0.997	***
% Other races					−0.002	0.001	0.998		−0.002	0.001	0.998
Affluence									−0.049	0.011	0.953	***
Disadvantage									−0.002	0.013	0.998
Stability									−0.010	0.008	0.990
Late or no prenatal care									0.003	0.001	1.003	**
Global Model AIC	2090.211				1932.242				1878.252
GWPR Model AIC	1399.831 (bandwidth=792)‡				1341.720 (bandwidth=1,503)				1281.668 (bandwidth=2,023)

^*p<.05

^**p<.01

^***p<.001

^‡bandwidth indicates the number of counties included in the local estimation.

Second, the association between low birth weight rate and infant mortality decreased with the inclusion of the racial/ethnic composition and socioeconomic variables. In Model I, it is suggested that a one low birth weight infant increase (per 1,000 live births) was associated with 1.4 percent increase in the number of infant deaths. However, in Model II and III, this relationship was attenuated to 0.8 percent, but remained significant. Third, among the socioeconomic variables, only affluence was significant (Model III). That is, counties characterized with more educated and professional residents and wealthier families had infant mortality rates lower than their counterparts featured by residents or families with less education or lower income. More specifically, a one unit increase in the affluence score was related to an almost 5 percent decrease in the number of infant deaths. Finally, we used AIC (Akaike 1974) to compare the global Poisson model with the GWPR model. The AIC takes the number of parameters of a model into account, and a comparison of AIC values can be used to determine whether the spatial (i.e., local) perspective significantly improves the model fit. The AIC comparisons between the global Poisson and local GWPR models suggested that GWPR models were preferred. It is suggested that when the difference in AIC is greater than 10, the model with lower AIC fits the data better (Burnham and Anderson 2002). In Table 2, the differences in the AIC between the global and local GWPR models are all greater than 10. We had strong evidence that the local GWPR models were more appropriate for our data compared to the global models.

As noted above, GWPR modeling generates a large amount of output; therefore, visualization and the 5-number summary of the local statistics are proposed as the best ways to present results (Fotheringham et al. 2002). We use a newly developed technique to effectively map the local statistics (Matthews and Yang 2012). For the purpose of brevity, on these maps we only show the significant associations between the SDT measures and infant mortality (exponentiated values) and we also show a map of the residuals (note, the current GWPR cannot calculate the pseudo-R²), in Figures 2~4 (Model I~III). The maps of the other independent variables are available upon request.

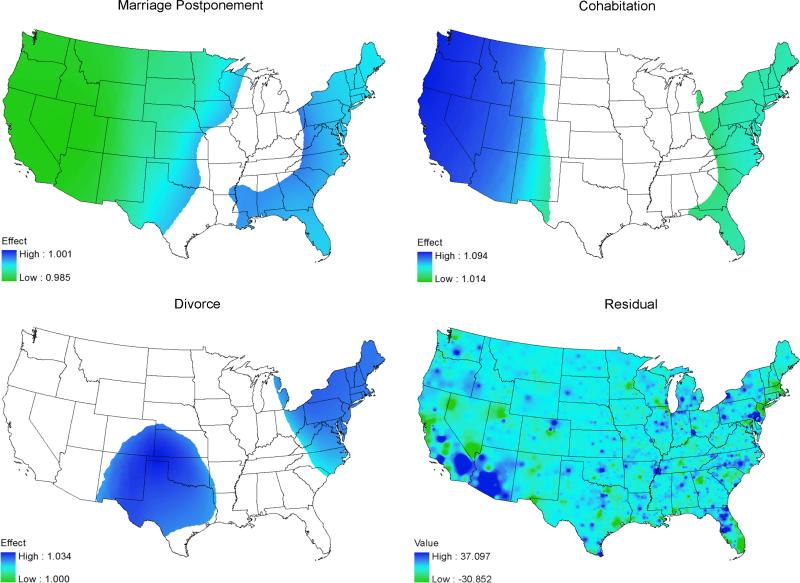
Figure 2.

Spatially non-stationary associations between infant mortality and second demographic transition variables and residual for Model I

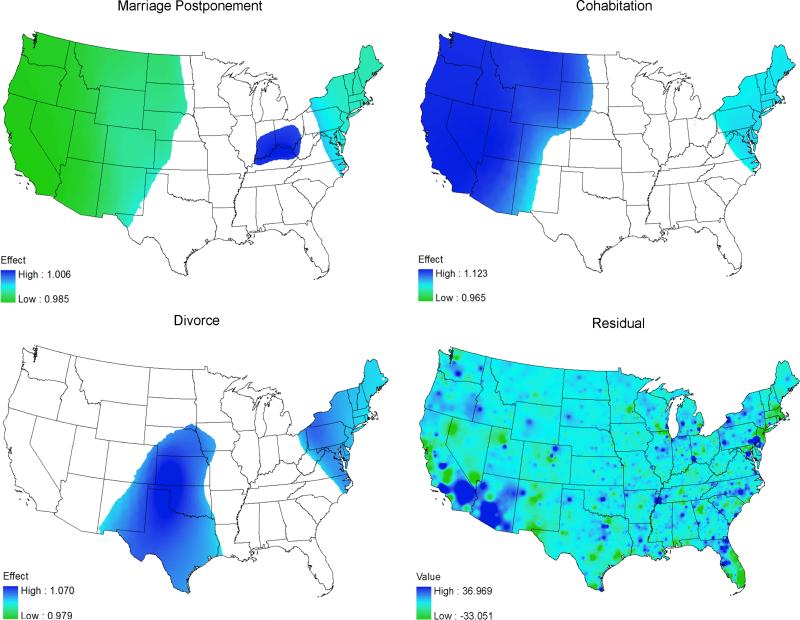
Figure 4.

Spatially non-stationary associations between infant mortality and second demographic transition variables and residuals for Model III

The spatial relationship between marriage postponement and infant mortality in Model I was significant in most of the contiguous US counties (see Figure 2), except for a wide strip running from Mid-West to the Gulf of Mexico. Again, note that the maps only show the significant parameter estimates (+/− 1.96). It should be mentioned that the counties in the West demonstrated stronger relationships than those in the East. Our GWPR also indicated that the associations between marriage postponement and infant mortality varied from 0.985 to 1.001 across the US counties. Explicitly, a one percentage point increase in marriage postponement would invoke as much as a 1.5 percent decrease in the number of infant deaths in some counties (in the West); however, in some areas, the same stimulus would be associated with 0.1 percent increase in the number of infant deaths (mostly in the East). These results indicate the existence of spatial non-stationarity in the relationship between marriage postponement and infant mortality.

The spatial associations between cohabitation and infant mortality were slightly more concentrated on the coasts than marriage postponement, and the range of the associations fell between 1.09 and 1.01. Similarly, the counties in the West were found to have stronger changes in infant mortality in response to a one percent increase in cohabitation compared to their counterparts in the East. Divorce had a somewhat different spatial patterning. The significant relationships between divorce and infant mortality were only found in Texas and the neighboring states to the north, as well as in the northeastern region. The strongest association was approximately a 3.4 percent increase in the number of infant deaths corresponding to a one percent increase in divorce.

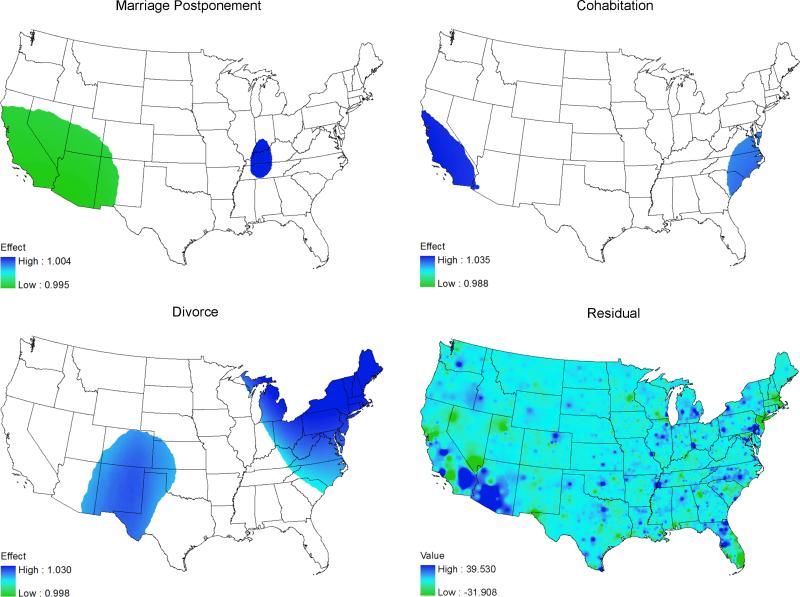
Controlling for the racial composition of a county did not greatly alter the spatial patterns. Compared with Figure 2, the significant areas of marriage postponement in Figure 3 shrank toward the coasts and in the Ohio River Valley (Ohio, Indiana, and Kentucky) there was a positive association between marriage postponement and infant mortality. Cohabitation demonstrated a similar pattern from Figure 2 to 3, but the significant areas were concentrated on the northeastern states and as far south as North Carolina. While the spatial associations of divorce with infant mortality changed very little, the areas of significant association in the central US expanded and those in the northeastern corner became smaller in Figure 3 than in Figure 2.

Figure 3.

Spatially non-stationary associations between infant mortality and second demographic transition variables and residuals for Model II

The spatial patterns of the SDT measures shifted dramatically when both racial/ethnic and socioeconomic variables were considered (see Figure 4). Marriage postponement demonstrated two divergent patterns: negative relationships were found in states in the South West, and positive associations were focused in a small area covering parts of Indiana, Kentucky, and Tennessee. The significant areas covered a smaller geographical area than those in the previous models (Figure 4). With respect to cohabitation, while its association with infant mortality remained positive, the significant areas were only found in California, coastal Virginia, and in the Carolinas. In contrast to other SDT components, divorce had a stable spatial pattern. The significant areas were in the southwest (centered on Colorado and New Mexico) and northeast, and the associations between divorce and infant mortality were positive. The residual map in Figure 4 suggested that the GWPR model fit the data well in most of the US. However, the GWPR Model III underestimated the number of infant deaths, indicated by the positive residuals, concentrated in southern Arizona, the border between California and Arizona, and several major metropolitan areas such as Orlando, Cincinnati, and Philadelphia. The negative residuals (overestimation) were more conspicuous in Las Vegas, Salt Lake City, San Francisco, and Miami. This residual pattern was persistently observed across the GWPR models/figures.

While the spatially non-stationary associations between the SDT and infant mortality were shown in the figures, a formal test for spatial non-stationarity is still necessary. Following Fotheringham et al. (2002), we summarized the local statistics of Model III in Table 3 and compared the interquartile range (IQR) with the standard errors of the global estimates (see footnote in Table 3). For a given independent variable, when the IQR of the local statistics is at least two times the global standard error, we have evidence to conclude that the spatial association of this independent variable with the dependent variable is non-stationary across space.

Table 3.

GWPR Model III and non-stationarity test results (N=3,071)

Variables	Min	Q1	Median	Q3	Max	Global S.E.	Status†
Intercept	−1.302	−0.974	−0.781	−0.708	−0.583	0.068	Non-Stationary
Low birth weight rate	0.006	0.007	0.007	0.008	0.011	0.001	Stationary
Marriage postponement	−0.005	−0.001	0.000	0.002	0.004	0.001	Non-Stationary
Cohabitation	−0.012	−0.004	0.007	0.020	0.035	0.008	Non-Stationary
Divorce	−0.002	0.008	0.015	0.019	0.030	0.005	Non-Stationary
% Non-Hispanic Black	0.002	0.003	0.005	0.006	0.011	0.001	Non-Stationary
% Hispanic	−0.008	−0.005	−0.004	−0.003	−0.001	0.001	Stationary
% Other races	−0.009	−0.003	0.002	0.004	0.008	0.001	Non-Stationary
Affluence	−0.085	−0.067	−0.056	−0.044	−0.030	0.011	Non-Stationary
Disadvantage	−0.042	−0.025	−0.015	−0.004	0.051	0.013	Stationary
Stability	−0.050	−0.031	−0.022	−0.013	0.007	0.008	Non-Stationary
Late or no prenatal care	0.000	0.002	0.005	0.007	0.010	0.001	Non-Stationary

^†For an independent variable, when the interquartile range (Q3-Q1) of the local estimates is at least twice greater than the standard error of the global estimate (Global S.E.), the non-staionarity is found.

Table 3 confirmed that all of the SDT covariates were not stationarily associated with infant mortality across space, even though low birth weight rate, percent Hispanic, and disadvantage were found to be stationary. Coupled with the AIC comparison results in Table 2, the non-stationarity found in this study challenges the global model approach by demonstrating that the global relationships between the SDT measures and infant mortality cannot be generalized to every county in the contiguous US. Without the place-specific perspective of GWPR, the local associations between the SDT and infant mortality would not be revealed.

Discussion and Conclusion

Let us re-examine our four hypotheses. We first hypothesized that infant deaths are negatively associated with marriage postponement. Getting married late could be regarded as a proxy of high psychological maturity, education, and parenting, which would benefit infant health (McLanahan 2004; Pittard et al. 2008). The global models provided evidence to support this hypothesis, despite the weak relationship. The GWPR results confirm but also reject the hypothesis. That is, the GWPR model suggests that the relationship between marriage postponement and infant mortality varies across space: marriage postponement was negatively associated with infant mortality in the southwestern states, but positively related to infant mortality in parts of Indiana, Kentucky, and Tennessee.

The literature suggested that cohabitation was a determinant of adverse birth outcomes such as low birth weight and infant mortality (Luo et al. 2004), and the infants born to parents in cohabiting unions received less social support and paternal involvement than infants born to married parents (Alio et al. 2010; Alio et al. 2009). Therefore, we hypothesized that cohabitation was positively associated with infant deaths. This hypothesis was confirmed by both the global and local models. It is worth mentioning that the association of cohabitation with infant mortality was, in part, explained by socioeconomic conditions. While accounting for these social factors changed the spatial distributions of the associations, the results still suggested that a one percent increase in cohabitation was related to more than a three percent increase in the number of infant deaths.

We expected that divorce would be positively associated with infant mortality because divorce results in dissolution of economic, social, and health benefits for women and their infants, which can result in a higher risk of poor health (Amato 2000; Smock et al. 1999). Across the global models, one percent increase in divorce was related to roughly two percent increase in the number of infant deaths. This relationship seemed to be independent of racial/ethnic compositions and socioeconomic conditions. Unlike marriage postponement, we only found statistically significant positive relationships between divorce and infant mortality, which is consistent with the theoretical pathways between divorce and infant health and confirms our hypothesis.

The final hypothesis was that the relationships between the SDT components and infant mortality were stronger in the areas that enter the SDT early than others. Visualizing the GWPR results helped identify the spatial non-stationarity and the formal test using IQRs and global standard errors (Table 3) provided evidence to support our hypothesis. Importantly our local models mirrored the geographical variations of the SDT and confirmed our final hypothesis. For instance, the North Atlantic and New England states appear to have entered the SDT earlier than other states (Lesthaeghe and Neidert 2009). Our GWPR results suggested that the associations between divorce and infant mortality were significantly stronger in these areas than in other areas. In addition, several Pacific and Mountain states, such as California, Nevada, and Arizona, have followed a similar SDT path to the northeastern states and the children and women in these areas were found to be vulnerable (Lesthaeghe and Neidert 2006). Our cohabitation and marriage postponement findings suggested that infant health would be undermined by the increase in cohabitation, especially in California, and that infant mortality would be reduced with the increase in the percent of marriage postponement in Nevada and Arizona. Lesthaeghe and Neidert (2006) also found that the counties in Virginia, North and South Carolina were featured by high cohabitation scores. Our GWPR map indicated that the relationship between infant mortality and cohabitation was significantly stronger in these counties than in counties in their neighboring states.

This study corresponds to the two trajectories of the family formation trends related to the SDT proposed by McLanahan (2004). The first trajectory, which is associated with delays in childbearing, results in gains in resources; while the second trajectory, which is associated with divorce and non-marital childbearing, reflects a loss of resources (McLanahan 2004). It is suggested that women who follow the first trajectory have the most opportunities and resources, and their children are more likely to be born into stable unions and spend more time with their fathers (McLanahan 2004). Our finding of marriage postponement and infant mortality generally supported this perspective, but the spatial non-stationarity further suggested that a place- or population-specific study is necessary. On the other hand, the second trajectory suggested that women who follow this path have the fewest opportunities and resources, and their children make smaller gains in resources, their parents’ relationships are unstable, and in many instances, support from their biological fathers is minimal (McLanahan 2004). The persistently positive associations of cohabitation and divorce with infant mortality found in this study bolstered this statement, though the magnitude of these associations varied across space.

Several policy implications could be drawn from the findings. As our analysis is based on an investigation of area-level data and an exploration of non-stationarity it is important to note that the policies we briefly describe need to be tailored for specific places, and specifically to those areas with different SDT paths. First and foremost, depending on the SDT trajectory, policies focusing on reducing infant mortality should pay extra attention to the infants born into cohabiting unions. Second, places with high divorce rates should offer more marriage counseling and support programs to help reduce the divorce rate, and in turn reduce the infant mortality rate. Third, as marriage postponement was negatively related to infant mortality, this finding reconfirms the need for parenting education, skills consulting, and other support programs be offered to young parents. Finally, while the positive relationship between marriage postponement and infant mortality was only found in a small area in the US, future efforts are required to understand why infant mortality increases with the percentage of people aged 25-29 and never married. It may be possible that certain cultural factors that are not included in this study could explain this positive association, but it requires detailed data collected from the specific areas to test this argument.

The main goals of this study were to utilize GWR techniques to explore whether there were stationary or non-stationary associations between the components of the SDT and infant mortality. Our findings are instructive and contribute to our knowledge of the SDT in the US. However, we also acknowledge there may also be additional opportunities worth pursuing in future research. For example, the SDT theory does not imply that the process varies by racial groups; however, infant mortality differs greatly by race in the US (MacDorman and Mathews 2008). Future efforts should focus on such issues, though we note that this line of inquiry would face many data and methodological challenges related to the construction of the required race-specific measures and the handling of sparse, skewed, and unstable data values based on the small numbers of infant deaths by racial groups (even aggregating across years may not easily solve this problem). Another possible line of research relates to rurality. Specifically, it is not clear whether the relationship between SDT and infant mortality varies by rurality. It has been suggested that rurality plays an important role in explaining the residential infant mortality differentials in the US counties (Sparks et al. 2009). In the future work, scholars will need to develop an appropriate rurality measure and then incorporate this into the SDT and infant mortality research framework. We also note that other measures capturing dimensions of religiosity, voting, and the abortion landscape in the US (use/access and legal landscape) may need to be incorporated into future work, though again not all of these measures are easily available at the county-level.

This study has several limitations. First, this is an ecological study. The empirical findings of this study should not be used to make inferences at the individual-level. It is possible that a change in spatial scale or units of analysis (e.g., county to census tract) may alter our findings; a methodological issue known as the modifiable areal unit problem (Openshaw 1983). Second, due to data limitations, we were not able to analyze the associations between the SDT variables and infant mortality below the county-level. Third, following on from the first and second limitation, it is important to note that we are not able to address several important methodological issues that are frequently discussed in family, marriage and health research based on individual-level data (e.g., selection effects in the marriage market and maternal health). As proposed by Eberstein (1989), more efforts should be warranted to develop a hierarchical model where both individual and contextual/ecological determinants of infant mortality are considered. Third, it is inappropriate to make causal inferences based on the analytic results. While we used data sources from different time points, a longitudinal research design is needed to better understand and test any causal relationship between the components of SDT and infant mortality. Fourth, although our data were collected and maintained by Federal agencies, measurement errors could exist. Last, while the current geographically weighted regression has a Monte Carlo stationarity test (Fotheringham et al. 2002), it could not be applied to the GWPR. The formal tests we used are some of the most common used in the literature.

Some caveats of the geographically weighted generalized regression need to be noted. First, this technique serves best to explore, rather than confirm, spatial non-stationarity (Wheeler and Tiefelsdorf 2005). Second, multicollinearity may exist across the local estimates and it should be cautious to make inferences based on the local results (Paez, Farber and Wheeler 2011; Wheeler 2007). Third, the local statistics could not be linearly combined into the global statistics. The connection between the global and local analytic approaches needs to be further developed (Boots and Okabe 2007). Finally, we note that there are other spatially varying coefficients regression methods (Gelfand et al. 2003). While the applicability of geographically weighted generalized regression has been verified, the difference between GWPR and these other methods has not been fully explored (Waller et al. 2007; Wheeler and Calder 2007).

In sum, the most significant contribution of this study is to incorporate a place-specific perspective into population research and to reveal the spatial non-stationarity of the relationships between the SDT variables and infant mortality. Though a spatial analytic approach has been promoted in demographic studies in the past decade (Voss 2007; Weeks 2004), most analytic tools attempt to account for spatial dependency but overlook spatial heterogeneity (nonstationarity). The SDT literature clearly indicated that the US counties/states entered the SDT in different times, which implies spatial non-stationarity. We have also attempted to link the SDT theory to mortality, specifically infant mortality. Using both global and local analytic tools, we provided evidence to support the spatially non-stationary relationships between the SDT measures and infant mortality, and demonstrated how we can improve our understanding of the SDT beyond the one-model-fits-all global modeling approach.