Using Mendelian Inheritance To Improve High-Throughput SNP Discovery

Abstract

Restriction site-associated DNA sequencing or genotyping-by-sequencing (GBS) approaches allow for rapid and cost-effective discovery and genotyping of thousands of single-nucleotide polymorphisms (SNPs) in multiple individuals. However, rigorous quality control practices are needed to avoid high levels of error and bias with these reduced representation methods. We developed a formal statistical framework for filtering spurious loci, using Mendelian inheritance patterns in nuclear families, that accommodates variable-quality genotype calls and missing data—both rampant issues with GBS data—and for identifying sex-linked SNPs. Simulations predict excellent performance of both the Mendelian filter and the sex-linkage assignment under a variety of conditions. We further evaluate our method by applying it to real GBS data and validating a subset of high-quality SNPs. These results demonstrate that our metric of Mendelian inheritance is a powerful quality filter for GBS loci that is complementary to standard coverage and Hardy–Weinberg filters. The described method, implemented in the software MendelChecker, will improve quality control during SNP discovery in nonmodel as well as model organisms.

THE advent of next-generation sequencing technologies has revolutionized biological research by allowing the pursuit of fundamental ecological and evolutionary genomics questions in nonmodel organisms (Hudson 2008). It is now feasible to discover genome-wide markers in any species, even if few or no prior genetic resources are available (Ellegren and Sheldon 2008). However, many modern studies now require high-quality genotypes for tens or hundreds of individuals. While recent technological advances have significantly lowered the cost of DNA sequencing, it is still expensive to assay genetic variation in large numbers of individuals (Narum et al. 2013).

Several methods have been developed to reduce the cost of high-throughput genotyping by restricting the complexity of the genome. These methods selectively sequence regions of the genome near restriction sites, allowing simultaneous discovery and genotyping of thousands of single-nucleotide polymorphisms (SNPs) distributed across the genome. Several variations exist, but these methods are generally known as restriction site-associated DNA sequencing (RAD-seq) or genotyping by sequencing (GBS) (reviewed in Davey et al. 2011). GBS methods have been used successfully in a variety of applications, including phylogenetics (Rubin et al. 2012), population genomics (White et al. 2013), genome-wide association studies (Parchman et al. 2012), speciation genomics (Taylor et al. 2014), and genetic mapping (Andolfatto et al. 2011).

A central challenge in analyzing GBS data is the high variation in coverage across individuals and across loci, creating uncertainty in SNP calls and genotype assignments (Davey et al. 2011). In addition to the polymerase chain reaction (PCR) and sequencing error associated with next-generation sequencing platforms, this cost-effective method of high-throughput genotyping comes with its own set of caveats: restriction fragment length bias and PCR GC content bias contribute to high variation in read depth among loci, and restriction-site polymorphism can skew allelic representation and therefore estimates of population genetic parameters (Arnold et al. 2013; Davey et al. 2013; Gautier et al. 2013). In the absence of a reference genome, spurious SNP calls may also result from collapsed paralogs or repeats during de novo assembly of reads into putative unique loci. Most GBS studies have used a set of heuristic criteria to filter out spurious sites, including read depth, proportion of missing data, and observed heterozygosity (Davey et al. 2011). While these simple filters are expected to discard most problematic loci during variant discovery, and applications such as trait mapping and phylogenetic inference may be robust to spurious calls at some loci, the use of GBS in population genomics studies may require careful consideration (Rubin et al. 2012; Arnold et al. 2013; Gautier et al. 2013). Depending on the experimental design and biological question, more sophisticated bioinformatic filtering tools are needed, especially since validation of large sets of SNPs remains prohibitively expensive (Davey et al. 2013; Narum et al. 2013). Here we present a fast and powerful method for filtering spurious GBS loci based on a quantitative assessment of Mendelian errors in nuclear families.

Checking for Mendelian inheritance of genotypes has long been standard practice for removing genotyping errors in human linkage studies (Sobel et al. 2002), and there are multiple software packages that identify genotyping and pedigree errors [MENDEL (Stringham and Boehnke 1996), PedCheck (O’Connell and Weeks 1998), MERLIN (Abecasis et al. 2002), and PLINK (Purcell et al. 2007)]. These algorithms assume that genotypes are known with certainty (O’Connell and Weeks 1998; Purcell et al. 2007) or leverage linkage information to identify pedigree or genotyping errors (Abecasis et al. 2002; Sobel et al. 2002). A recent study showed that imposing Mendelian inheritance constraints when assigning genotypes in parent–offspring trios results in higher genotyping accuracy and haplotype inference (Chen et al. 2013). To date, only a handful of GBS studies have used Mendelian inheritance as an additional filter. Most of these studies simply discarded any loci with extreme segregation distortion (Miller et al. 2012) or non-Mendelian inheritance patterns (Gagnaire et al. 2013; Ogden et al. 2013). Senn et al. (2013) used an estimate of Mendelian error rate to set a threshold for genotype confidence scores, but they considered only two cases of Mendelian error and did not incorporate genotype probabilities or sex linkage into their estimates. Ignoring sex linkage is problematic because the different inheritance patterns of sex-linked sites may cause true sex-linked sites to be erroneously discarded as Mendelian errors under an autosomal model of inheritance.

Here we describe a statistical framework that combines genotype probabilities with pedigree information to perform a quantitative analysis of Mendelian violation across sites and pedigrees and calculates the probability that a given SNP is sex-linked. Instead of identifying individual genotyping errors, our goal is to evaluate the quality of putative variant sites during the SNP discovery process. Although we primarily discuss GBS data in this article, our method, implemented in the C++ program MendelChecker, can be applied to any data set containing probabilistic genotype calls for at least one parent–offspring trio. The performance of MendelChecker on simulated and real data sets demonstrates that adding a Mendelian inheritance filter substantially improves the removal of spurious sites during SNP discovery.

Methods

Checking for Mendelian inheritance

In diploid organisms, true nuclear genetic variants should follow patterns of Mendelian segregation in families, assuming no pedigree errors and no novel mutations in the offspring. In this article, we define Mendelian errors as genotypes that are inconsistent with their respective pedigree. Sites that exhibit true segregation distortion are not considered Mendelian errors because individual offspring have genotypes that are consistent with Mendelian inheritance of the genotypes of their parents. Only with very large offspring arrays and extreme segregation distortion might pedigree likelihoods be low enough to affect inference using our method. Because genotyping errors may create Mendelian errors in otherwise legitimate segregating sites, it is important to consider genotype probabilities when evaluating Mendelian inheritance. We developed an efficient and scalable algorithm that iterates over all possible genotypes in all individuals at a given site and calculates the likelihood of the pedigree given the genotype probabilities. Also, we use these pedigree likelihoods to evaluate the quality of each site and assign a probability of sex linkage for each SNP. Note that if there are insertion/deletion calls with associated confidence estimates, the method outlined below can easily be extended to include this kind of segregating variation as well.

For diploid individuals, there are 10 possible genotypes at each biallelic SNP. For a given site, we assign each individual a vector of genotype probabilities: (p_AA, p_AC, p_AG, p_AT, p_CC, p_CG, p_CT, p_GG, p_GT, p_TT). By considering all 10 genotype probabilities, our method is flexible enough to accommodate multiallelic sites. We calculate the frequencies of all four alleles (p_A, p_C, p_G, p_T) from the observed genotype probabilities of all the parents (who are assumed to be unrelated) and impute a vector of expected genotype frequencies in the population:

$$\begin{array}{l}{G}_{\text{exp}}=(p_A{p}_A,p_A{p}_C,p_A{p}_G,p_A{p}_T,p_C{p}_C,p_C{p}_G,p_C{p}_T,\\ p_G{p}_G,p_G{p}_T,p_T{p}_T).\end{array}$$ (1)

The statistical framework for our method was adapted from Jurg Ott’s pedigree likelihood (Ott 1974). For a nuclear family with s offspring, the likelihood of the pedigree for an autosomal locus is proportional to the sum of the product of the genotype probabilities for each individual and the transmission probability,

$$L_{\text{A}}=L\left(\text{pedigree}|\text{data}\right)={\displaystyle \sum _{g_i}{\displaystyle \prod _{i=1}^{s+2}P\left(g_i\right)}{\displaystyle \prod _{o=1}^s\text{Trans}\left(g_o|g_f,g_m\right)}},$$ (2)

where P(g_i) is the probability that individual i has genotype g_i and Trans(g_o|g_f, g_m) is the probability that two parents with genotypes g_f and g_m produce an offspring o with genotype g_o. Due to the high sampling variance of GBS data, not all individuals will be genotyped at all putative sites. If the genotype is missing for a particular individual, we substitute the expected genotype frequency (from G_exp) for P(g_i). In situations where the number of founders is too low to reasonably infer expected genotype frequencies in the population, we allow the option of using a uniform prior instead of G_exp.

To account for varying numbers of offspring in each nuclear family and variable minor allele frequency (MAF), we normalize the pedigree likelihoods for the number of informative trios in each family. We do so by dividing the pedigree likelihood by the likelihood of a completely uninformative pedigree, i.e., the likelihood of the pedigree if the genotype probability vectors for all individuals were G_exp (Equation 1). We sum the log-likelihood ratios for all n pedigrees to obtain a score for each site, M:

$$M={\displaystyle \sum _{i=1}^n\text{log}\frac{L_i\left(\text{pedigree}|\text{data}\right)}{L_i\left(\text{pedigree}|G_{\text{exp}}\right)}}.$$ (3)

Note that our metric for quantifying the degree of Mendelian inheritance, M, is dependent on several factors. The highest-scoring sites will have high-quality genotype calls in multiple individuals, a low rate of missing data, and a large proportion of genotype configurations consistent with Mendelian transmission.

Assessing the probability of sex linkage

Sex-linked sites have different transmission probabilities compared to autosomal sites (Elston and Stewart 1971). Some true sex-linked sites would erroneously appear as Mendelian errors under an autosomal model of inheritance. Thus, for each SNP, we calculate pedigree likelihoods and M under both an autosomal and a sex-linked model of inheritance. Transmission probabilities for sex-linked sites depend on the sex of the offspring. Therefore, the likelihood of the pedigree under a sex-linked model incorporates the sex of each offspring o:

$$\begin{array}{c}{L}_{\text{S}}=L\left(\text{pedigree}|\text{data},\text{sex-linked}\right)\\ ={\displaystyle \sum _{g_i}{\displaystyle \prod _{i=1}^{s+2}\text{P}\left(g_i\right)}{\displaystyle \prod _{o=1}^s\text{Trans}\left(g_o|g_{\text{f}},g_{\text{m}},{\text{sex}}_o\right)}}.\end{array}$$ (4)

If the sex of the offspring is unknown, we take the average of the male and female transmission probabilities. We use the pedigree likelihoods to compute the posterior probability that a given site is sex-linked, S, using Bayes’ theorem,

$$S=\frac{\mathrm{\alpha }{\displaystyle {\prod }_{i=1}^n{L}_{\mathrm{Si}}}}{\mathrm{\alpha }{\displaystyle {\prod }_{i=1}^n{L}_{\mathrm{Si}}+\left(1-\mathrm{\alpha }\right)}{\displaystyle {\prod }_{i=1}^n{L}_{\mathrm{Ai}}}},$$ (5)

where α is the prior probability of sex linkage and is estimated as the proportion of the genome on the X or Z chromosome, and n is the number of pedigrees. To evaluate each SNP, we first classify the site as autosomal or sex-linked based on S and then evaluate the SNP with the appropriate M.

Simulations to assess performance

We performed a series of simulations to assess the performance of our method under different scenarios. We used a custom Perl script to generate genotype probability vectors for nuclear families of varying offspring number, Mendelian error rate, proportion of missing data, MAF, and genotype quality for both sex-linked and autosomal sites. Normalized, Phred-scaled genotype likelihood (PL) scores for each possible genotype (similar to the PL field in Variant Call Format or VCF files) were simulated based on an exponential distribution with means estimated from real data (see below). In our GBS data, genotypes had conditional genotype quality (GQ) scores (the GQ field in the VCF file format) ranging from 0 to 99. Sites with GQ < 20, 20 < GQ < 80, and GQ > 80 were considered low, medium, and high quality, respectively. For each biallelic site, we examined the distribution of the PL scores, which are normalized, phred-scaled likelihoods for all three possible genotypes given the called alleles. In our simulations, we sampled genotypes from exponential distributions with means of 100, 500, and 3000 for low-, medium-, and high-quality genotypes, respectively (Supporting Information, Figure S1). Specifically, for high-quality sites, the most likely genotype was assigned a Phred-scaled likelihood of 0, the second most likely genotype was sampled from an exponential distribution with mean 300, and the third most likely genotype was sampled from an exponential distribution with mean 3000. Mendelian errors were introduced by forcing an offspring to have a genotype that would be inconsistent with Mendelian transmission, given the parental genotypes. We assumed a 50:50 sex ratio when assigning sex to each offspring. Unless otherwise specified, we simulated 5000 autosomal and 5000 sex-linked SNPs with MAF of 0.05 or 0.25 in Hardy–Weinberg genotype proportions for each scenario and ran our simulated data through MendelChecker.

To verify the functionality of our Mendelian SNP score, we simulated 10 parent–offspring trios and varied the proportion of families containing a Mendelian error from 0 to 1. All SNPs had high genotype quality and no missing data, allowing us to assess the sensitivity of MendelChecker under ideal conditions. We first evaluated the extent to which we could assign sex linkage from pedigree likelihoods by comparing individual autosomal and sex-linked pedigree likelihoods. To determine the sensitivity of our sex-linkage posterior probability to the prior, we ran MendelChecker on the same data set, using different prior probabilities of sex linkage (0.1, 0.5, and 0.9).

We assessed the performance of MendelChecker given a known number of Mendelian errors, assuming that all sampled trios were informative. However, in real data, not all genotype errors will lead to inconsistent pedigrees. To more realistically assess our power to detect spurious SNPs, we simulated genotyping errors that are consistent with Mendelian transmission. In these simulations, we introduce spurious sites by simulating offspring genotypes independent of the parental genotypes, i.e., as if they were unrelated. The next set of simulations focused on testing the power to detect Mendelian errors under different genotype qualities, proportion of missing data, and MAF in 10 parent–offspring trios. The full range was tested for each parameter: we varied genotype quality from low (mean phred score of 100) to high (mean phred score of 3000), the fraction of missing data from 0 to 1, and the MAF from 0.01 to 0.5.

We examined the influence of sampling scheme by simulating nuclear families of different sizes. First, we assessed the performance of variable numbers of parent–offspring trios. Then, we held the number of meioses constant and changed the family configuration: we compared results for 10 trios, five families with 2 offspring each, two families with 5 offspring each, and one family with 10 offspring. We assessed the power of MendelChecker when samples include both parents, only the homogametic parent, or only the heterogametic parent. For these simulations, we generated SNPs with medium- to high-quality genotypes and 0–20% missing data.

We estimated the ability of MendelChecker to assign sex linkage or to detect Mendelian errors in each scenario by generating receiver operating characteristic (ROC) curves and calculating the area under the curve (AUC), using the package ROCR (Sing et al. 2005) in the R statistical package (http://www.r-project.org). The AUC is a commonly used statistic for model comparison that reflects the probability the classifier will rank a random positive case above a random negative case. An AUC value of 1 indicates a perfect classifier, while an AUC value of 0.5 indicates the classifier is no better than a random guess.

Data collection

We validated our method using data obtained from a long-studied population of Florida Scrub-Jays (Aphelocoma coerulescens) from Archbold Biological Station. Florida Scrub-Jays are genetically monogamous (Townsend et al. 2011); therefore we can confidently assume that the pedigrees constructed from field observations are accurate. We sampled 103 individuals in 27 nuclear families from 1989 and 2008. Genomic DNA was extracted from blood samples stored in lysis buffer, using the QIAGEN (Valencia, CA) DNeasy kit. We slightly modified the GBS protocol of Elshire et al. (2011) to generate multiplexed reduced representation libraries for Illumina sequencing. Briefly, 500 ng of DNA from each individual was digested with the enzyme PasI (New England Biolabs, Beverly, MA) before ligation of barcoded adapters. Individual samples were then pooled and cleaned using a QIAGEN Minelute PCR purification kit. Libraries were amplified with PCR with short extension times to favor amplification of shorter fragments (98° for 30 sec; 18 cycles of 98° for 30 sec, 65° for 7 sec, and 72° for 7 sec; and 72° for 5 min). Final library cleanup was performed with AMPure XP beads (Agencourt). We generated multiplexed libraries consisting of 6–12 individuals per lane and sequenced five lanes on the Illumina GA II (84- and 86-bp reads) and eight lanes on the Illumina HiSequation 2000 (56- and 101-bp reads). Three libraries were sequenced twice. Sequencing was done at the Cornell University Biotechnology Resource Center Genomics Facility and the Weill Cornell Genomics Resources Core Facility. All sequence data have been submitted to the NCBI Sequence Read Archive (http://www.ncbi.nlm.nih.gov/sra) under accession no. SRP041511.

Pipeline for obtaining probabilistic genotype calls

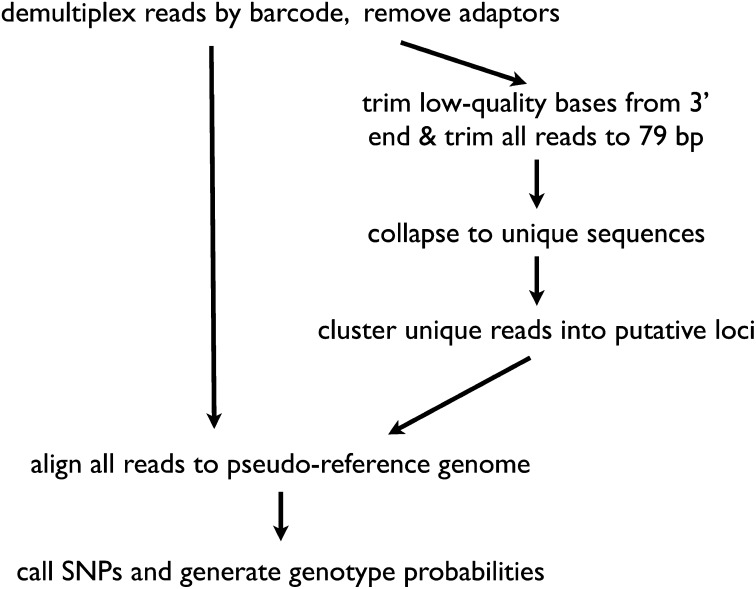
Because it is crucial for our downstream analysis to obtain probabilistic genotype calls and propagate error throughout the analysis, we created a flexible analysis pipeline for calling genotypes from GBS data (Figure 1). Although we developed our own custom pipeline, MendelChecker can be used with any pipeline that provides genotype probabilities. We used custom Perl scripts to sort the raw reads by barcode into individual files and trim off adapters and low-quality bases. These demultiplexed and processed reads were all trimmed to 79 bp.

Figure 1.

Overview of our custom pipeline for obtaining probabilistic genotype calls from GBS or RAD-seq data.

To take advantage of well-established software for variant detection and genotyping in the absence of a reference genome, we generated a “pseudoreference genome” that contains all sites in the genome sampled in this reduced representation sequencing approach. We took the entire set of sequences from all individuals and collapsed the reads into a set of unique sequences, removing singletons in the process. We used the program SlideSort (Shimizu and Tsuda 2011) to perform a rapid all-by-all pairwise comparison of all unique reads and generate a list of all pairs that differ by ≤10 bp. Reads were grouped into clusters with the Markov cluster algorithm (MCL) (Van Dongen 2000), which allows the formation of clusters with multiple SNPs. A single sequence from each cluster was included in the pseudoreference genome.

We retained and used base quality scores from the original reads. We aligned the processed reads from each individual to the pseudoreference, using the Burrows-Wheeler Aligner, BWA (Li and Durbin 2009). Binary Alignment/Map (BAM) files were sorted and merged with Picard tools (http://picard.sourceforge.net) before indel realignment and variant calling with the UnifiedGenotyper in the Genome Analysis Toolkit (GATK) (Depristo et al. 2011). Although our method can be used to filter indel calls as well, here we focus only on SNPs. GATK performs SNP discovery and probabilistic genotype calling across all samples simultaneously, which is advantageous because multiple-sample variant calling is more accurate than calling SNPs in each individual separately (Nielsen et al. 2011).

Validation on real data

We ran MendelChecker on the resulting VCF file to assess Mendelian inheritance. In the 1.2-Gb Zebra Finch genome, the Z chromosome is ∼73 Mb in length (Warren et al. 2010). Assuming the Florida Scrub-Jay has similar chromosome sizes to those of the Zebra Finch, we used a prior probability of sex linkage of 0.06. Using VCFtools (Danecek et al. 2011), we removed individual low-quality genotype calls (GQ < 20) before calculating statistics about each site. We applied a series of stringent filters, removing all sites with low mapping quality (Root Mean Square Mapping Quality, MQ) or read depth (Qual by Depth, QD) (MQ < 35, QD < 5) or high levels of missing data (>20%). From this set of higher-quality SNPs, we (1) removed sites that deviated from Hardy–Weinberg proportions in the 50 founders (p < 0.001) or had a high proportion of heterozygote calls (>75%), (2) removed sites with M < −10, or (3) applied both filters. We selected 1160 high-quality SNPs for genotyping in 96 individuals, using custom Illumina iSelect Beadchips. The genotyping accuracy of iSelect BeadChips exceeds 99% (Steemers and Gunderson 2007), and here we use these BeadChip genotypes as our validation set. We calculated genotype concordance as the proportion of maximum-likelihood genotypes from the GBS data that match the BeadChip genotype calls. All genotype data have been submitted to dbSNP (http://www.ncbi.nlm.nih.gov/SNP/) under accession nos. NCBI ss995818232–995820422.

To test the ability of our method to predict sex linkage, we used a two-step approach to determine the putative chromosomal location of high-quality SNPs. First, we aligned the pseudoreference genome (the collection of all sampled loci) to the Florida Scrub-Jay draft genome (N. Chen, J. W. Fitzpatrick, and A. G. Clark, unpublished data), using BWA. The Florida Scrub-Jay genomic scaffolds were aligned to the Zebra Finch genome, using standalone BLAST (Camacho et al. 2009), and assigned to putative chromosomes based on the best BLAST hit. The robustness of this annotation method relies on the high degree of synteny among extant bird lineages (Ellegren 2010). We calculated the AUC value, using these chromosomal assignments. All analyses were done in the R statistical package.

Implementation

Our method for checking for Mendelian inheritance, MendelChecker, has been implemented in C++ and is available for download at http://sourceforge.net/projects/mendelchecker. MendelChecker is computationally efficient: run time for 1.8 million SNPs on one 64-bit 3.0-GHz core is 841 sec. Computation of the likelihoods given by Equations 2 and 4 is a performance bottleneck as it takes exponential time, O(33 × 4^s + 51 × 2^s + 16) ∼ O(4^s). However, a substantial speedup is achieved by a simple algebraic factorization (Equation 6), which has a linear-time complexity of O(10² × s) ∼ O(s):

$$\begin{array}{c}{L}_{\text{A}}=L\left(\text{pedigree}|\text{data}\right)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}={\displaystyle \sum _{g_{\text{f}}}{\displaystyle \sum _{g_{\text{m}}}P\left(g_{\text{f}}\right)P\left(g_{\text{m}}\right){\displaystyle \prod _{o=1}^s{\displaystyle \sum _{g_o}P\left(g_o\right)\text{Trans}\left(g_o|g_{\text{f}},g_{\text{m}}\right)}}}}.\end{array}$$ (6)

The simulation script is available on the MendelChecker website. Scripts and instructions for our custom pipeline for obtaining probabilistic genotype calls from GBS data are available in File S1.

Results

Simulations

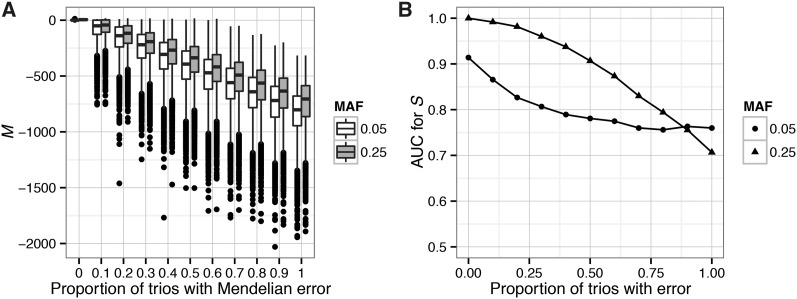
We used simulations to verify the accuracy of our quantitative framework for assessing Mendelian violations and evaluate the performance of our metrics (S, the posterior probability of sex linkage, and M, the log-likelihood ratio estimating the degree of Mendelian consistency) under different scenarios. In the initial verification step, we simulated SNPs with no missing data and high-quality genotype calls in 10 trios with varying amounts of Mendelian error. As the proportion of families containing a Mendelian error increases, M decreases. M is lower for SNPs with lower MAF (Figure 2A). For autosomal SNPs, the pedigree likelihood calculated under an autosomal model of inheritance is greater than the likelihood calculated under a sex-linked model of inheritance and vice versa for sex-linked SNPs (Figure S2). Therefore, we can use pedigree likelihoods to calculate the posterior probability that a given SNP is sex-linked. The posterior probability of sex linkage is an accurate classifier. For SNPs with MAF = 0.25, AUC values range from 0.99 to 0.91 for SNPs with no Mendelian errors and five Mendelian errors, respectively. As the number of Mendelian errors increases, our ability to distinguish sex-linked SNPs from autosomal SNPs decreases (Figure 2B). We calculated S for the same data set, using different prior probabilities of sex linkage (α = 0.1, 0.5, 0.9), and found that the AUC values changed by <0.002 in all cases. Thus, S is not sensitive to the prior for these simulation parameters.

Figure 2.

Verifying the assumptions underlying MendelChecker. We simulated 5000 autosomal and 5000 sex-linked SNPs for 10 offspring trios and varied the proportion of families containing a Mendelian error, i.e., an error that is inconsistent with the pedigree. Here we show results for sites with MAF of 0.05 and 0.25. (A) Boxplots for M, our metric of Mendelian inheritance. Results for SNPs with MAF of 0.05 are shown as open boxes, and SNPs with MAF of 0.25 are shown as shaded boxes. M decreases as the proportion of families containing a Mendelian error increases. (B) Performance of the sex-linkage classifier. Here, points indicate the MAF of the SNPs. The AUC value for S decreases as the proportion of trios with a Mendelian error increases.

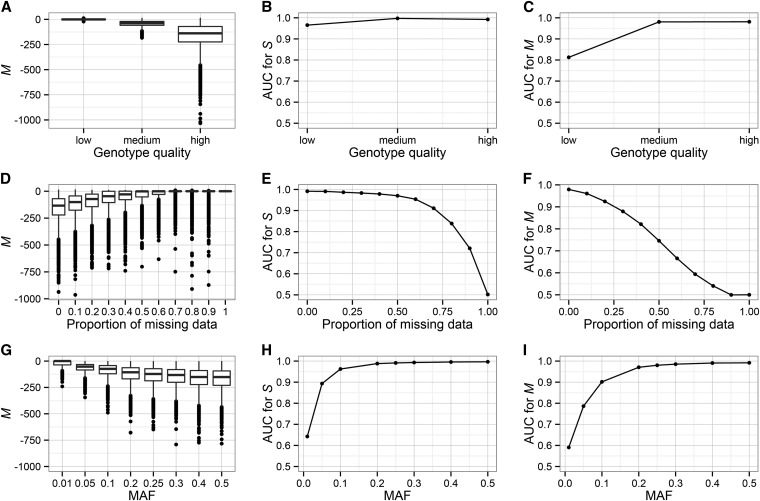
This first set of simulations used ideal conditions—high genotype quality and no missing data. However, these conditions are rarely met in real data. Because the pedigree likelihoods are influenced by genotype quality and proportion of missing data as well as by MAF, our next set of simulations explored the relative contribution of these three factors to S and M. We generated spurious SNPs by simulating offspring genotypes independently of the parental genotypes, allowing both Mendelian consistent and inconsistent errors. We simulated true and spurious SNPs in 10 trios and systematically varied genotype quality, the proportion of missing data, and MAF. MendelChecker can correctly assign sex linkage under almost all conditions. AUC values for S decrease below 0.9 only when the proportion of missing data exceeds 0.7 or the MAF = 0.01 (Figure 3). As expected, as genotype quality decreases and the proportion of missing data increases, M increases for spurious SNPs, indicating lower probability of detecting Mendelian errors (Figure 3, A–F). AUC values for M stay >0.98 for medium genotype qualities but drop to 0.81 for low-quality genotypes (Figure 3C). Missing data have a larger impact on the performance of MendelChecker; our ability to detect a Mendelian error decreases with the proportion of missing data, with AUC dropping below 0.9 when >20% of the individuals have missing genotypes (Figure 3F). The ability to detect errors is low for SNPs with MAF < 0.05 because most individuals are homozygous for the major allele, resulting in few Mendelian inconsistent errors (Figure 3, G–I).

Figure 3.

The influence of confounding factors on the ability to identify errors. Here we used a sample of 10 parent–offspring trios and simulated 10,000 SNPs with no errors and 10,000 SNPs with error. A, D, and G show M values for spurious SNPs; B, E, and H plot AUC values for S; and C, F, and I show AUC values for M. Note that higher M values for spurious sites indicate a decreased power to detect error. (A–C) Genotype quality has a minimal effect on the performance of MendelChecker. (D–F) As the proportion of missing data increases, the ability to assign sex linkage and detect spurious sites decreases. (G–I) MendelChecker has decreased performance for SNPs with very low MAF (<0.1). In our simulations, the AUC for M drops below 0.9 only for low-quality genotypes, >20% missing data, or MAF < 0.1.

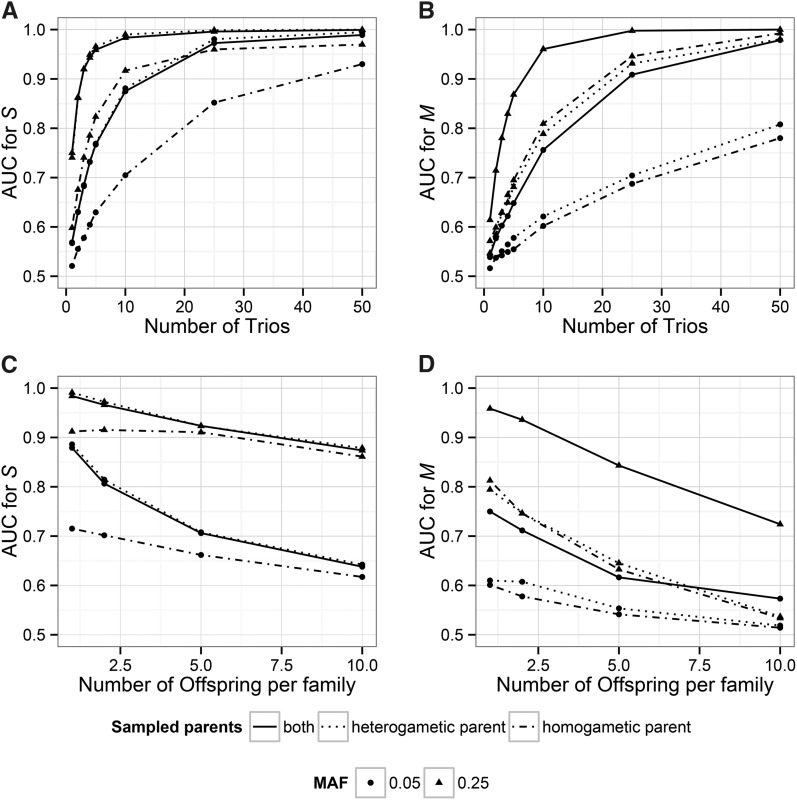
After characterizing the influence of Mendelian errors as well as data quality and proportion of missing data on both S and M, we assessed the performance of MendelChecker for different sampling schemes. The power to assign sex linkage and detect error increases as we sample more trios (Figure 4, A and B). Sex-linkage assignment is accurate (AUC > 0.9) with a sample size of 4 trios when MAF = 0.25 (Figure 4A). The AUC for M exceeds 0.90 with just 10 trios for SNPs with MAF = 0.25 (Figure 4B). More trios (25) are needed to achieve an AUC > 0.90 for rare SNPs (MAF = 0.05; Figure 4, A and B). Given a fixed number of meioses, we tested whether it is better to sample more families with fewer offspring each or fewer families with more offspring each. We simulated several possible family configurations when sampling 10 meioses and found that it is more advantageous to sample multiple smaller families (Figure 4, C and D). In all cases, missing one parent decreases the AUC for M, although, as expected, performance of the sex-linkage assignment is lower only if the heterogametic parent is missing.

Figure 4.

The influence of sampling scheme on the ability to identify spurious variant sites based on Mendelian errors. Here, lines indicate whether both parents are sampled or only one parent is sampled, and the points indicate the MAF of the SNPs. (A and B) The power to assign sex linkage and identify spurious SNPs increases as the number of sampled parent–offspring trios increases. (C and D) The configuration of the families also affects power. For a fixed number of meioses, AUC values are higher for a sample of 10 families with 1 offspring each compared to a sample of a single family with 10 offspring. Sampling more founders increases the probability of sampling informative trios. As expected, performance of MendelChecker is lower when only one parent is sampled.

Real data analyses

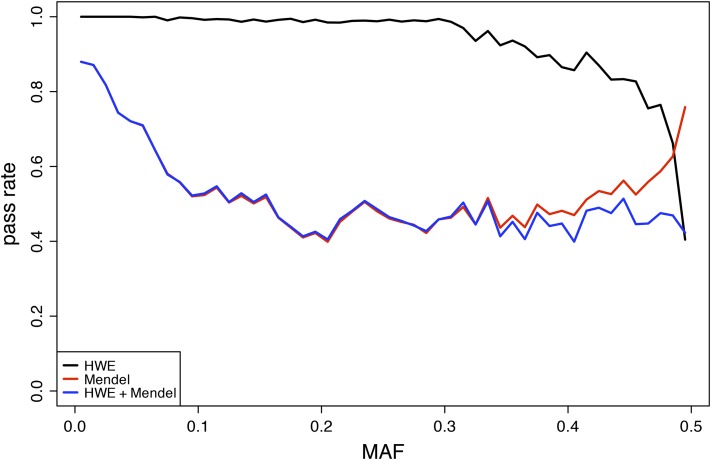
We tested the performance of our method on GBS data collected from 103 Florida Scrub-Jays in 27 nuclear families. Illumina sequencing produced a total of 935,765,768 reads, of which 814,341,664 contained a unique barcode and minimal adapter sequence contamination. Our custom pipeline identified 266,806 biallelic SNPs. Distributions of various quality metrics for the full SNP set can be found in Figure S3. However, after filtering on individual genotype quality and overall per-site quality, only 20,347 SNPs were genotyped in >80% of our individuals. Of these SNPs, 11,758 passed our Mendelian inheritance filter (M > −10), 19,241 passed a Hardy–Weinberg equilibrium (HWE) test (p > 0.001), and 10,855 passed both filters. In this case, M is a more conservative filter: 43.6% of the SNPs that pass the HWE test fail MendelChecker at this threshold for M. Applying a HWE filter after filtering based on M eliminates 7.7% of the Mendelian SNPs, all of which have MAF > 0.07 (Figure S4). MendelChecker is a more powerful filter than HWE for rare variants, but HWE performs better for sites with high MAF (Figure 5). At high MAF, the probability of two heterozygous parents increases, which in turn decreases the probability an error can be detected as a Mendelian inconsistency. For a biallelic site, two heterozygous parents can produce offspring with all four genotype configurations; therefore only errors that introduce a novel allele would be inconsistent with Mendelian inheritance patterns. It is important to consider different models of inheritance: 62.2% of putative sex-linked SNPs would have failed the Mendelian inheritance test under an autosomal model of transmission.

Figure 5.

The proportion of SNPs with different MAFs that pass different QC filters. The HWE test (black) has low power to filter SNPs with MAF < 0.3. Mendelian inheritance (red) can filter out low-frequency variants but loses power for variants with high MAF. At high MAF, the probability that both parents are heterozygous increases, and fewer errors can be detected as Mendelian inconsistencies. A combination of HWE and Mendelian inheritance tests (blue) can filter erroneous SNPs of all MAFs. Comparison of pass rates as a function of MAF shows the complementary nature of the two filters.

We validated the genotype calls for 96 individuals at 1160 SNPs, using custom Illumina iSelect Beadchips. Mean genotype concordance is high (98.2%), and only 5.9% of these SNPs have genotype concordances <95%. These SNPs are all high quality (QD > 5, MQ > 35, <20% missing data), consistent with HWE, and have relatively high M scores (M > −10). If we consider only the 686 SNPs with M > 0, mean concordance increases to 98.7%, and the percentage of SNPs with concordance values <95% drops to 3.2%. We acknowledge that an ideal validation experiment would have included low-quality SNPs. However, the high concordance of our validation set indicates that the coverage, HWE, and Mendelian inheritance filters we applied were successful in eliminating spurious sites.

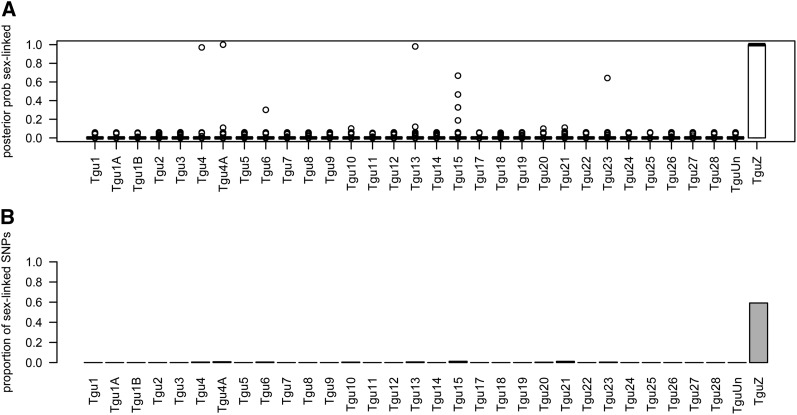
Using alignment to the Zebra Finch genome, we were able to reliably assign putative chromosome locations to 7744 of the 10,855 SNPs that passed all filters, with a minimum of 33 SNPs on every chromosome except chromosome 16. The posterior probability of sex linkage proved to be a reliable classifier: <0.2% of autosomal SNPs and 59% of Z-linked SNPs were classified as sex-linked (Figure 6) with an AUC of 0.85. The remaining 41% of Z-linked SNPs had low posterior probabilities of sex linkage (S) and were therefore classified as autosomal SNPs. Note that not all genotype configurations have different sex-linked and autosomal patterns of transmission, so it is not possible to identify all sex-linked SNPs based on a finite number of pedigrees. We suspect that the few autosomal SNPs with high probabilities of sex linkage could have been aligned to the wrong chromosome.

Figure 6.

Assessment of our ability to assign sex linkage. (A) Boxplots of the posterior probability of sex linkage for SNPs on each chromosome. (B) The proportion of SNPs on each chromosome classified as sex-linked. Because not all genotype configurations have different autosomal and sex-linked transmission probabilities in our sample set, we do not expect to be able to classify all SNPs on the Z chromosome as sex-linked.

Discussion

GBS has become a popular approach for a myriad of ecological and evolutionary studies, but more advanced bioinformatic methods are required for quality control of SNP discovery using GBS, especially since GBS genotype calls are rarely validated. Here we present a framework for filtering spurious GBS loci based on a quantitative assessment of Mendelian errors in nuclear families and evaluate the performance of our method using simulated and real data. This is one of the few GBS studies to date to validate genotype calls using a different genotyping platform. MendelChecker assigns each site a probability of being sex-linked, S, and a quantitative score of Mendelian consistency, M. Users can use S to classify each site as putatively autosomal or sex-linked before ranking SNPs with the appropriate M score and specifying a threshold to identify spurious sites.

To obtain the highest-quality set of SNP calls, we recommend using a filter on Mendelian consistency, such as M, in addition to other standard quality control measures, such as coverage and Hardy–Weinberg filters. Our simulations show that the power to detect a single Mendelian error decreases as the information content of the genotype data decreases. The ability to detect spurious sites is relatively poor (AUC < 0.9) when all genotypes have low quality or when the proportion of missing genotypes is >0.2. Many previous GBS studies routinely filter out sites with low quality or >20% missing data. Applying these standard genotype quality and coverage filters will remove sites with low information content. In analyzing GBS data collected from 103 Florida Scrub-Jays, we show that MendelChecker and HWE are complementary tests (Figure 5). A significant advantage of our method is that it can detect errors in rare variants, whereas tests of HWE have low power to filter SNPs with low MAF. The performance of MendelChecker is lower at high MAF, in part because the probability of detecting a genotyping error as a Mendelian inconsistency is greater when the MAF is <0.5 (Douglas et al. 2002). The fact that Mendelian inheritance patterns can provide no information about the validity of the SNP if both parents are heterozygous can be problematic when trying to identify spurious SNPs generated by collapsed paralogs: if every individual is heterozygous at a site, MendelChecker will assign it a high M score. Therefore, we recommend filtering based on both Mendelian inheritance and Hardy–Weinberg proportions to remove spurious sites at all MAFs.

The genomic locations of GBS loci are unknown in organisms without a closely related reference genome, and sex-linked loci are often of special interest. For instance, rates of evolution differ between sex chromosomes and autosomes, and sex-linked genes are thought to play an important role in speciation (Charlesworth et al. 1987; Presgraves 2008; Qvarnström and Bailey 2009). Thus the ability to classify SNPs as putatively autosomal or sex-linked expands the scope of questions that can be answered with GBS data. In addition to assessing Mendelian violations, MendelChecker calculates the posterior probability that a site is sex-linked. Our software can accommodate XY, ZW, and XO sex determination systems and can accurately assign sex linkage to simulated and real SNPs. The transmission probabilities of some sex-linked SNPs differ from those of autosomal SNPs; therefore, assuming an autosomal pattern of inheritance for all loci may lead one to discard perfectly valid sex-linked SNPs. However, not all genotype configurations have different sex-linked and autosomal patterns of transmission, so MendelChecker does not have the ability to identify all sex-linked SNPs given finite numbers of pedigrees. For example, in organisms with pseudoautosomal regions, SNPs in those regions cannot be distinguished from autosomal SNPs. Note that sex-linked sites could also be identified by testing for an association with sex. Future versions of MendelChecker could incorporate tests for other markers with unusual inheritance patterns, such as mitochondrial DNA or chloroplast DNA.

Despite additional difficulty in obtaining pedigree data, sampling pedigrees has many advantages beyond improving SNP discovery: pedigrees are key to answering several fundamental questions in evolutionary biology (Kruuk and Hill 2008; Pemberton 2008). Pedigree information can be obtained by performing crosses, by observing mating or parental care in captive or wild populations, or by collecting gravid females (Pemberton 2008). Several software programs to assign parentage based on highly variable genetic markers have been developed (reviewed in Blouin 2003; Jones and Ardren 2003). Of course, not all GBS experiments will consist solely of family groups. For experiments that require sampling multiple unrelated individuals, the inclusion of just four parent–offspring trios is sufficient to allow some filtering based on Mendelian inheritance for SNPs with MAF > 0.05 (AUC > 0.80; Figure 4B). In this case, the multiple unrelated individuals can be used to estimate population allele frequencies, and SNPs can be filtered based on inheritance patterns in the included nuclear families. For a given sample size, there is a trade-off between sampling families and sampling additional unrelated individuals, but the advantage of obtaining a more accurate set of variant calls may be worth the slightly decreased sample size.

Currently, MendelChecker considers only nuclear families. Extended pedigrees can be broken into several separate nuclear families. While linkage map construction benefits greatly from multigenerational families, nuclear families are sufficient for identifying spurious SNPs based on Mendelian violations. Power to identify spurious SNPs based on Mendelian inheritance increases as more meioses are sampled. This is consistent with previous work showing that genotyping additional siblings in a family increases the genotyping error detection rate by 10–13%, depending on the allele frequencies of the variant (Gordon et al. 2000). For a fixed number of meioses, our simulations showed improved performance when multiple smaller families were sampled instead of fewer large families. This is due, in part, because including more pairs of parents increases the probability of sampling informative parental genotype combinations.

Although MendelChecker assumes accurate pedigrees, one can sum the pedigree likelihoods over all or a subset of high-confidence SNPs to identify pedigrees with disproportionally high rates of Mendelian error or to test alternative pedigrees. This alternative use of MendelChecker can prove especially useful in organisms for which parental assignments are uncertain, e.g., birds with extra-pair paternity. However, the primary goal of MendelChecker is to identify high-quality sites. Given a set of high-quality genotypes, other software packages exist for identifying potential pedigree errors [e.g., PedCheck (O’Connell and Weeks 1998), RELPAIR (Epstein et al. 2000), and PLINK (Purcell et al. 2007)].

Loci that display segregation distortion should not be classified as Mendelian errors under our model. In this scenario, each individual offspring still has genotypes that are consistent with the genotypes of its parents, and therefore that combination will have a nonzero transmission probability. Because the pedigree likelihood is a function of the genotype probabilities and the transmission probabilities in parent–offspring trios, deviations from expected Mendelian genotype frequencies across multiple offspring should have a minor effect on M. However, it is possible that for some MAF and parental genotype configurations, extreme segregation distortion in families with a large number of offspring could be detected as sites with lower M scores. The parameters for which this would be possible could be explored using simulation studies.

There are a number of well-developed applications for de novo analysis of GBS data, such as Stacks (Catchen et al. 2011), Peterson’s ddRAD pipeline (Peterson et al. 2012), UNEAK (Lu et al. 2013), RApiD (Willing et al. 2011), pyRAD (Eaton 2014), RADtools (Baxter et al. 2011), and Rainbow (Chong et al. 2012). We developed a custom pipeline for additional flexibility and full control over the parameters at each step of the process. Compared to UNEAK, the most widely used reference-free pipeline designed specifically for the Elshire et al. (2011) GBS method, our pipeline is less conservative when creating clusters and therefore more appropriate for systems with greater nucleotide diversity. MendelChecker is compatible with any pipeline that provides posterior genotype probabilities.

In conclusion, we have designed a flexible quantitative test for Mendelian inheritance that propagates genotype uncertainty, accommodates missing data, and distinguishes between autosomal and sex-linked SNPs. Our method is powerful for rare variants and complementary to existing quality control filters, such as tests of Hardy–Weinberg proportions. We recognize that including families in population-scale data sets may require additional effort; however, we argue that future studies would benefit from including a subsample of nuclear pedigrees when possible because filtering based on Mendelian inheritance will result in a more accurate set of variant sites. Performance of MendelChecker increases as more meioses and more families are sampled, but the inclusion of 10 trios is sufficient for high performance (AUC > 0.90). MendelChecker provides a statistical test for Mendelian errors and identifies sex-linked loci, making it a valuable tool for researchers using GBS data to explore ecological and evolutionary questions.