Soft Polymer Magnetic Nanocomposites: Microstructure Patterning by Magnetophoretic Transport and Self-Assembly

Abstract

A method to produce and pattern magnetic microstructure in a soft-polymer matrix is demonstrated. An externally applied magnetic field is used to influence the dynamics of magnetophoretic transport and dipolar self-assembly of magnetic nanoparticle clusters in the liquid precursor of poly-dimethylsiloxane (PDMS). Magnetic nanoparticles agglomerate by an interplay of van der Waals forces and dipolar interactions to form anisotropic clusters. These clusters are concentrated on a substrate by magnetophoresis, wherein they self-organize by dipolar interactions to form microscopic filaments. The polymer is cured in the presence of the magnetic field to preserve the microstructure shape. The externally applied magnetic field and its gradient are the two main control variables of interest when considering magnetic control during nanoparticle self-assembly. Their influence on microstructure geometry is investigated through correlations with the height of a characteristic self-assembled filament, fraction of the substrate area covered by the microstructure and its shape anisotropy. These relations enable a priori design.

Introduction

We present a bottom up method for generating magnetic microstructure in a soft polymer matrix by using magnetophoretic transport and self-assembly. The method provides simple and effective control over microstructure geometry produced on a substrate. Magnetic nanoparticles (MNPs) are self-assembled within a poly-dimethylsiloxane (PDMS) prepolymer in the presence of an externally applied magnetic field B^ext. First, MNPs are dispersed in diluted PDMS prepolymer. Combined van der Waals and dipolar interactions lead to agglomeration of MNPs forming anisotropic clusters. Next, the dispersion is exposed to B^ext wherein its gradient dB^ext / dx induces magnetophoretic transport of the clusters towards a substrate in the dispersion, more specifically a wall of the cuvette containing it. As the clusters approach the substrate, dipolar interactions self assemble them into filaments. The polymer is cured in the presence of the field to preserve the structures. The geometry of the microstructure filaments depends on B^ext and dB^ext / dx, as illustrated in Figure 1. Such a method of organizing nanoparticles into patterned arrays can be used to engineer and impart desirable mechanical,^{1, 2} magnetic,³ electrical, thermal and optical⁴ properties to composites forming a novel tool for material design.^{5, 6}

Fig. 1.

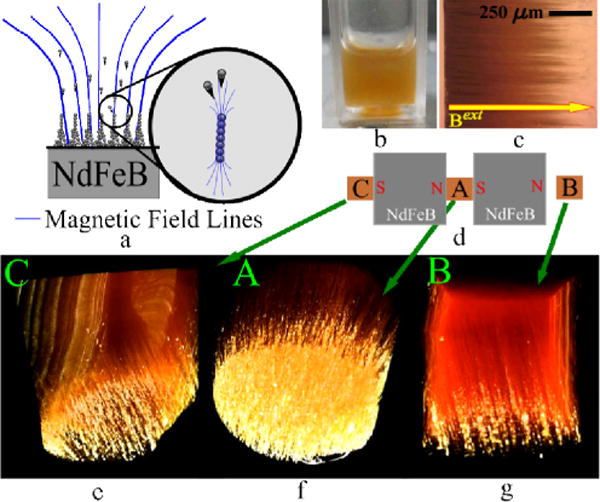
(a) Magnetic nanoparticles dispersed in a liquid move towards locations that experience a stronger magnetic field. The particles initially agglomerate into clusters. Strong dipole-dipole interactions amongst clusters enable self-assembly into filaments on the substrate. (b) The nanoparticles are initially uniformly dispersed in liquid PDMS prepolymer. (c) The polymer is cured while the system experiences an externally imposed magnetic field. The polymer matrix preserves the shapes of the self-assembled structures when the field is removed. (d) The structure morphology can be controlled by varying |B^ext| and |dB^ext / dx|, as shown for three experimental conditions obtained by three curing positions relative to a system of two NdFeB permanent magnets. The values obtained, labeled A, B and C, are listed in Table 1. (e–g) Three-dimensional images obtained by X-Ray MicroCT reconstructions demonstrate variations in the microstructure geometry.

MNPs find applications in spin based devices,⁷ data storage,⁸ particle sorting,^{9, 10} drug targeting,^{11, 12} composite materials,¹³ and magnetic actuation in microdevices.^14–16 These applications either require control over the relative positions of spatially distributed nanoparticles in packed structures, or could significantly benefit from it. Due to the inherent physical properties of MNPs, magnetostatic interactions between them permit the formation of reversible self-assembled structures in a liquid dispersion.^17–23 This eliminates the need for sophisticated chemical processing, potentially enhancing throughput and facilitating cost benefits. However, the structures that are formed by MNPs in a liquid dispersion when a magnetic field is applied are lost due to thermal agitation once the field is removed. This has motivated investigations of alternate self-assembly methods for MNPs²⁴ involving, for instance, solvent evaporation,²⁵ templates,²⁶ and molecular linkers.^{27, 28}

Polymer melt based colloidal dispersions of MNPs have recently enabled the development of composites that contain self-assembled magnetic microstructure.^1–3 However, the focus of the few reported investigations thus far has been on the influence of the microstructure on bulk mechanical^{1, 2} and magnetic³ properties. These studies have generally limited themselves to applications of homogeneous magnetic fields that produce linear self-assembled chains dispersed throughout the polymer matrix. The presence of a gradient in the field enforces magnetophoretic transport, thereby facilitating controlled localization and structural patterning, as observed in ferrofluids.²² A more complete understanding of how the microstructure geometry can be designed and controlled in a soft material is required to exploit the influence of heterogeneities on its material properties.

Here we investigate how the microstructure geometry can be controlled in a soft polymer by using an external magnetic field, thus demonstrating the influence of both B^ext and dB^ext / dx, which together impose magnetic control during self-assembly. This form of magnetophoretic transport is capable of producing high particle concentrations near a substrate. We provide the first direct nanoscale visualization of such dipolar self-assembly outside of thin films. The TEM images provide confidence in our analysis that MNPs agglomerate in polymeric dispersions through a combination of isotropic van der Waals forces and anisotropic dipolar interactions.

Results and Discussions

The morphology of the self-assembled structures can be controlled by varying B^ext and dB^ext / dx using a set of permanent magnets. Here, we use a pair of NdFeB magnets for the purpose, illustrated in Figure 1 (d). MNP dispersions in diluted PDMS prepolymer are cured at three spatial positions relative to the magnet pair, leading to the three different values of B^ext and dB^ext / dx listed in Table 1. The method for obtaining these values is discussed in greater detail in Supplement 1. Quantitative aspects of the microstructure geometry are correlated with these magnetic control variables.

Table 1.

Magnetic field |B^ext| and its gradient |dB^ext / dx| for the three different configurations shown in Figure 1 (d). The values are obtained using the Finite Element Method Magnetics software and verified by a Hall Probe magnetometer. Supplement 1 details these methods.

	Field |Bext| (T)	Field Gradient, |dBext / dx| (T cm−1)
A	0.6974	0.1217
B	0.4090	0.2435
C	0.5093	0.2742

A very dilute dispersion aids a controlled magnetophoretic self-assembly process, since it significantly diminishes the irreversible and uncontrolled agglomeration of a large number of particles.^{18, 29} However, at such low concentrations, magnetostatic interactions are also insignificant due to the large separation between adjacent particles. The observed self-assembly is thus minimal.^{3, 30} Hence, beginning from a sparse dispersion, we use gradual and controlled magnetophoretic transport of MNPs towards a wall of the cuvette containing the dispersion. This transport is enabled by the force induced on each dipole due to the gradient in the magnetic field, which produces the filament-like microstructure shown in Figure 1 (e–g).

Control over the microstructure geometry is investigated by measuring (1) the heights h of the self assembled filaments, and, (2) the fraction of the substrate area covered by the microstructure, which is denoted by ξ. Optical micrographs of the microstructure are analyzed for these measurements for which results are presented in Figure 2. Figures 2 (a–c) visually demonstrate the variation of h with the magnetic control variables, while Figures 2 (d–f) show similar variations of ξ for an MNP mass fraction in PDMS, ψ = 0.5%. Figures 2 (g–h) present quantitative results for h and ξ corresponding to this and other values of ψ in the starting dispersion.

Fig. 2.

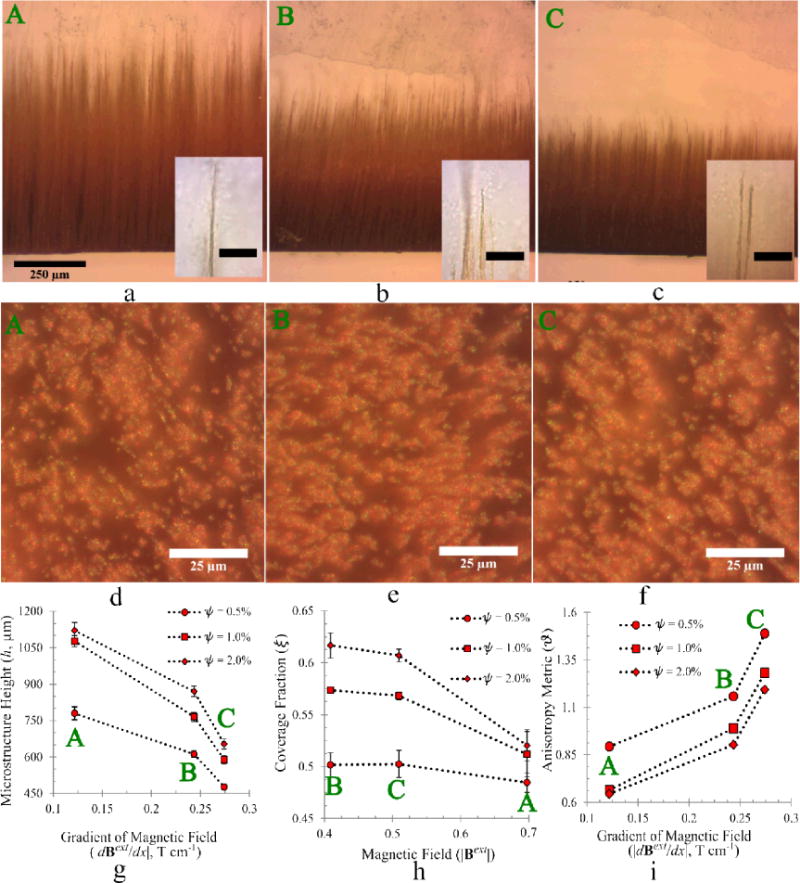
(a–c) Optical micrographs of self-assembled structure profiles for three different conditions labeled A, B and C in Table 1 for an MNP mass concentration ψ = 0.5%. Insets are high magnification images of the corresponding tips. The scale bar in the insets are 25μm. (d–f) Optical micrographs of the substrate in the dispersion, showing the base of the filamentous microstructure. (g) The height of the microstructure decreases monotonically with |dB^ext / dx| whereas (h) the fraction of the substrate covered by nanoparticles decreases monotonically with |B^ext|. (i) The anisotropy metric ϑ determined from this data increase monotonically with |dB^ext / dx|, which we predict through a scaling law applicable for the experimental conditions (Supplement 3).

The self-assembled microstructure geometry depends on both B^ext and dB^ext / dx. Establishing a strategy for magnetic control over the self-assembled structures that are produced requires that the dynamics of interacting dipoles in a magnetic field be examined. The influence of a magnetic field on the dispersed MNPs is explained by the Zeeman energy of a point dipole in a field, U = −m·B. Each dipole experiences a force F = (m·∇)B that pulls the particle towards regions where the magnetic field is stronger, and a torque τ = m × B, which aligns the dipole with the field direction. The magnetic field B experienced by a dipole m is the sum of B^ext and the field produced by neighboring dipoles B^dip. Hence, magnetostatic self-assembly occurs through interplay between (1) interparticle dipole-dipole interactions (DDI), and (2) the dipole-field interactions (DFI).

The collective influence of B^ext on participating dipoles is summarized thus. (1) A dipole attaches to another so that their individual moments point along the line joining their centers. (2) The dipole-dipole ‘bonds’ are oriented along the local direction of B, the most simplified manifestation of which is the formation of linear chains in the direction of B^ext. (3) Each dipole experiences a force in the direction of strengthening magnetic field, resulting in magnetophoretic transport in that direction. Here, a dipole is not an individual MNP but is rather formed as an MNP cluster,¹⁹ which is discussed later.

Considering these dynamics, a control strategy for h follows intuitively. Consider an MNP cluster approaching a self-assembled structure, as shown in Figure 1 (a). The net force on it is directed along the gradient of the local magnetic field. Since B = B^ext + B^dip, this net force is the result of two competing components, i.e., the force due to B^dip (F_DDI) and that due to B^ext (F_DFI). When F_{D F}>_I>_DF_{D I}, an MNP cluster moves towards the substrate instead of joining the terminus of a preexisting self-assembled structure. As F_DFI ~ |dB^ext / dx|, h decreases monotonically with |dB^ext / dx| as shown in Figure 2 (g). Similar observations can be made by examining the experimental configurations for previous experiments on ferrofluids,²² although for a homogeneous field the length of a self-assembled chain increases with |B^ext|.¹ Further, in Figure 2 (g), h increases monotonically with ψ because of the increase in the number of dipolar clusters available for microstructure generation.

The observed variations in the coverage fraction ξ are not as intuitive. A larger |dB^ext / dx| should lead to larger ξ as more particles are drawn to the substrate by the larger F_DFI. This is however not observed when samples from configurations B and C, which experience very similar values of the field gradient, are compared. Figure 2 (h) instead shows variations that correlate monotonically with |B^ext| but not with |dB^ext / dx|. The dynamics of microstructure formation can explain this. By Stokes’ formulation, the magnetophoretic velocity of each particle towards the substrate U ~ a² is very sensitive to cluster size (see Supplement 2). Consequently, the largest clusters reach the substrate much sooner than smaller ones. These clusters are restrained on the substrate, or cuvette wall, by the magnetic field and behave as a two-dimensional gas of repulsive dipoles.²¹ Due to the large structure sizes, the associated inter-cluster dipolar interactions, i.e., the repulsive force are strong. These seed clusters form the nucleation sites for the smaller clusters that arrive later. The repulsion, hence the separation distance, increases with increasing |B^ext| due to a greater alignment of the magnetic moment of each MNP within the seed clusters with B^ext. Consequently, the seeding clusters are more sparsely distributed at larger |B^ext| values, leading to lower ξ, which is evident from Figures 2 (d–f).

The structure anisotropy is not governed solely by the ability of the magnetic field to orient dipoles and thereby enhance intercluster repulsion as would be expected for homogeneous magnetic fields,¹ but also by the magnetophoretic force experienced by each MNP due to the field gradient. A smaller gradient of the magnetic field promotes filament formation, while a very large gradient will cause all clusters to form a uniform coating on the substrate. To establish this, we consider a metric for anisotropy based on a length associated with the coverage fraction, $\mathrm{\Lambda }=\sqrt{\xi }$. The anisotropy metric

$$\vartheta =h/\mathrm{\Lambda },$$ (1)

is a measure of the tip angle of the filaments where smaller ϑ corresponds to higher anisotropy. A simple analysis of the dynamics of two dipoles provides an estimate of the dependence of ϑ on the control variables B^ext and dB^ext / dx (see Supplement 3). Comparing the relative magnitudes of these variables, the dimensionless parameter

$$\mathrm{\Pi }=\frac{a|d{B}^{\mathit{ext}}/\mathit{dx}|}{{\mu }_0{M}_s}$$ (2)

describes the anisotropy in these structures. With all other factors constant, ϑ should increase monotonically with the field gradient, thus increasing Π, as observed in Figure 2 (i).

The agglomeration of interacting dipolar particles has been the subject of numerous idealized theoretical and numerical studies.^{31, 32} Recently, direct observations of MNP agglomerates in vitrified liquid films have demonstrated that increasing the particle size, thus the magnetic moment m, causes the dominant forces for agglomeration to transition from van der Waals interactions to dipolar interactions so that the formed clusters transition from being isotropic to anisotropic.^{17, 29} Tuning the particle size in a system is difficult to achieve, specially for industrial processes that will make use of commercially available MNPs. The value of |m| for most commonly used magnetite NPs is too small to produce significant dipolar interactions.²⁹ The dipolar parameter λ,¹⁹ defined as the ratio of dipolar interaction potential energy to the energy of thermal fluctuations, is very small for the magnetite nanoparticles of radius a ~ 5 nm (EMG 1400, Ferrotec, Inc.) that we have used at a temperature T ~ 3600 K. Consequently, the dipolar interactions between particle-pairs are insignificant so that initially van der Waals dominated inter-particle interactions lead to isotropic clustering. Such clusters are known to have a zero magnetization in the absence of an external field but become magnetized in the presence of a nonzero B^ext so as to possess a much larger m compared to an isolated nanoparticle.³³

Figure 3 shows that each structure is comprised of several smaller clusters of different shapes, sizes and orientations. Figure 3 (b) shows that these clusters are anisotropic, differing significantly from the isotropic clusters driven by van der Waals forces observed otherwise.^{19, 29} This indicates the role of both dipolar and van der Waals interactions during cluster formation, which is a plausible explanation noting that the dispersion was exposed to B^ext immediately after preparation. Individual clusters magnetized to possess a large m result in stronger dipolar interactions with neighboring nanoparticles. Any subsequent growth in the cluster progressed in a preferred direction due to these strong interactions, ultimately leading to the observed anisotropy. Intercluster ‘bonding’ on the other hand is clearly dipolar, as evidenced in Figure 3 (a) by observing the long-range global order that is enforced in the overall direction of the applied magnetic field. This is also apparent from the formation of the filamentous microstructure, which is highly anisotropic as seen in Figure 1 (e–g) and Figure 2 (a–c). The complexity of the structures is a possible consequence of the subsequent evaporation of the diluent (tetrahydrofuran) from the prepolymer and the onset of cross-linking reactions. The wide variations in the shapes of the structures are attributed to strong thermal fluctuations, which are exaggerated by the relatively high temperature (~45°C) used to cure the polymer.

Fig. 3.

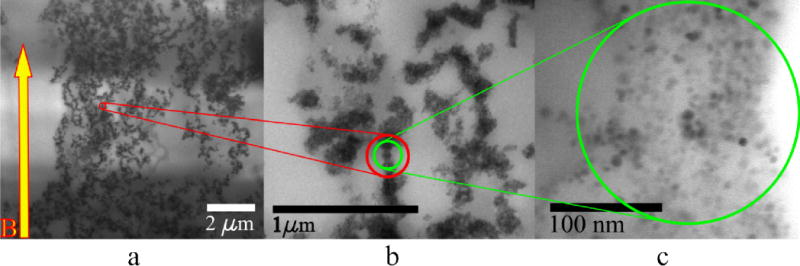
TEM images show that the structures consist of nanoparticle clusters organized along the magnetic field. (a) Individual clusters behave as dipoles enabling long-range organization. However, the polymerization process interferes with such interactions to form irregular chains. (b) The clusters are not isotropic as expected from van der Waals interactions alone, indicating that there is an interplay between dipolar and van der Waals interactions in their formation. (c) The clusters are roughly 100 nm thick, but their lengths are much larger. The uneven brightness in the background is a consequence of the microtoming process.

Experimental

Generation of Composite Microstructure

This involved the magnetophoretic transport and self-assembly of MNPs in diluted PDMS prepolymer. The magnetite nanoparticles (EMG 1400, Ferrotec Inc.) were dispersed in tetrahydrofuran (THF) by sonication in a water bath (Branson 2510) for 15 minutes. Subsequently, PDMS (Sylgard™ 184, Dow Corning) was added to the dispersion (1:1 w/w PDMS to THF), stirred vigorously and sonicated for another 15 minutes. The PDMS cross-linker was then added to the dispersion (10 % w/w cross-linker to PDMS). The resulting dispersion was exposed to the externally applied magnetic field B^ext for 30 minutes at room temperature within which the bulk of MNPs settled on the cuvette wall closest to the nearest magnet. The dispersion was then heated at 45 °C for 12 hours while still exposed to B^ext. Within this time, the THF was lost by evaporation as observed by a reduction in the volume of the dispersion, and solid PDMS was obtained. Experiments were conducted for three different particle concentrations ψ (w/w MNP to PDMS).

Sample preparation for X-Ray computed tomography

The cured PDMS was cut into cubes with ~1 mm sides. One of the sides was the substrate S at which the self-assembled structures were formed, i.e., the polymer surface cured adjacent to the wall of the cuvette facing the nearest magnet. These specimens were individually mounted on a sample holder with S facing upwards and scanned using XRADIA MicroXCT-400 with a 20× objective. 360 projection images were obtained spanning a total axial rotation of 179°. The volume data was reconstructed from these images using the XRADIA reconstruction software.

Sample Preparation for TEM

The PDMS blocks that enclosed the self-assembled structures were trimmed to create a pointed edge near the surface S. Each sample was then sliced using a microtome at a temperature of −170 °C (RMC Products CR-X Cryosectioning system). Individual slices were ~100 nm thick and perpendicular to S so that the root of the self-assembled microstructure could be imaged. The slices were subsequently transferred on to TEM grids for visualization using Philips EM420.

Conclusion

We demonstrate a method to produce a filamentous magnetic microstructure on a substrate in a soft-polymer matrix through the self-assembly of magnetic nanoparticles. The microstructure in such a composite material can be patterned externally using B^ext. Magnetic control is enabled through two variables, i.e., B^ext and dB^ext / dx. The dependence of structural metrics of the microstructure, such as height h, coverage area ξ and structure anisotropy ϑ, on these magnetic control variables are explained by examining the mechanics of magnetophoretic transport and the self-assembly of magnetic dipoles dispersed in a liquid. We demonstrate that these dipoles consist of clusters that are formed through the interplay between the van der Waals and dipolar interactions at the length scale of individual particles. For a large cluster size, interactions between adjacent clusters are primarily dipolar, enabling magnetic control over their self-assembly.