Dynamic Functional Imaging of Brain Glucose Utilization using fPET-FDG

Abstract

Glucose is the principal source of energy for the brain and yet the dynamic response of glucose utilization to changes in brain activity is still not fully understood. Positron emission tomography (PET) allows quantitative measurement of glucose metabolism using 2-[¹⁸F]-fluorodeoxyglucose (FDG). However, FDG PET in its current form provides an integral (or average) of glucose consumption over tens of minutes and lacks the temporal information to capture physiological alterations associated with changes in brain activity induced by tasks or drug challenges. Traditionally, changes in glucose utilization are inferred by comparing two separate scans, which significantly limits the utility of the method. We report a novel method to track changes in FDG metabolism dynamically, with higher temporal resolution than exists to date and within a single session. Using a constant infusion of FDG, we demonstrate that our technique (termed fPET-FDG) can be used in an analysis pipeline similar to fMRI to define within-session differential metabolic responses. We use visual stimulation to demonstrate the feasibility of this method. This new method has a great potential to be used in research protocols and clinical settings since fPET-FDG imaging can be performed with most PET scanners and data acquisition and analysis is straightforward. fPET-FDG is a highly complementary technique to MRI and provides a rich new way to observe functional changes in brain metabolism.

INTRODUCTION

Although the brain represents only 2% of the body weight, it receives 15% of the cardiac output, 20% of total body oxygen consumption, and 25% of total body glucose utilization. Glucose utilization in the human brain, both at rest and during cognitive tasks, has been studied over the past 40 years using 2-[¹⁸F]-fluoro-deoxyglucose (FDG) with positron emission tomography (PET) (Phelps et al., 1979; Reivich et al., 1979). However, the measurement of glucose utilization represents an integral of neuronal processes during 20-40 minutes following an intravenous bolus injection of FDG. This “snapshot” of glucose utilization is like a picture with a very long exposure, with poor temporal resolution and without intra-scan information about dynamic changes occurring during this extended image acquisition. Inferences of changes in glucose metabolism in response to stimuli or tasks are obtained with state-contrast experiments. The bolus FDG method, widely used clinically, can provide a quantitative measurement of the basal cerebral metabolic rate of glucose (CMR_glu) and is a very powerful way to characterize functional metabolic responses to stimuli that are presumed to sustain a constant state, including visual, auditory or cognitive tasks, and even drug administration (Gould et al., 2012; Kushner et al., 1988; Molina et al., 2009; Pietrini et al., 2000; Vlassenko et al., 2006; Yehuda et al., 2009). However, one of the main limitations of the bolus method is the lack of temporal information, which is critical for interpreting brain-state changes. Current methods for determining changes in FDG uptake due to a stimulus are confounded by numerous factors: 1) glucose metabolism may not be at equilibrium over the full time course of the experiment (90 minutes or longer) even though a single metabolic rate is derived; 2) sequential measurements often made days or weeks apart introduce uncontrolled variables (e.g. caffeine, sleep status, blood chemistry changes); and 3) mis-registration can occur across scan sessions.

Contrary to traditional FDG-PET imaging, functional magnetic resonance imaging (fMRI) has a good temporal resolution and can be used to dynamically measure multiple responses within a single imaging session (Kwong et al., 1992; Ogawa et al., 1992). Although widely employed for human brain mapping, blood oxygen level dependent (BOLD) fMRI measurements are not quantitative in an absolute sense. The magnitude of the BOLD response reflects a complex interplay between hemodynamic and metabolic responses (Pike, 2012). Measurements of CMR_glu, relative to cerebral blood flow (CBF) and cerebral metabolic rate of oxygen (CMRO₂), are important for understanding brain function. Yet, dynamic measurements have been largely ignored in the literature due to the static nature of the FDG technique (Fox et al., 1988, 1986; Raichle and Mintun, 2006).

In this study, we demonstrate that FDG PET can be used in a more dynamic manner and is capable of repeatedly detecting changes in glucose utilization within a single FDG imaging session, a method we termed “fPET-FDG”. The fundamental principle behind the fPET-FDG method is to control the delivery of FDG to the blood through continuous infusion. By maintaining a constant plasma supply of FDG, dynamic changes in glucose utilization in response to a stimulus or task can be measured with greater sensitivity than with a bolus method. The infusion concept has been pioneered by Carson and others (Carson et al., 1993) as a method to demonstrate changes in receptor occupancy in a single PET scan. Other experiments following the line of this work have applied infusion paradigms that continuously supply radiotracer to take advantage of the increased sensitivity to brain-state changes and the simplifications associated with data acquisition in a single session. In fact, recently, constant infusion of FDG has been applied to dynamically measure the effect of a photodynamic therapy in tumor treatment in mice (Bérard et al., 2006; Cauchon et al., 2012).

The aim of our study is to develop a new method using infusion of FDG to provide better sensitivity to dynamic changes in FDG signal to be used as a human neuroimaging tool. We hypothesized that relative changes in FDG metabolism could be quantified without being confounded by hemodynamic responses, and that the improved temporal resolution would enable multi-task challenges within a single session, thus fundamentally improving PET FDG capabilities. We also hypothesized that the FDG signal using our fPET-FDG protocol could be processed with a modified fMRI pipeline to get statistical maps of the brain activations. In addition to the human neuroimaging studies we report, we also applied a hypercapnic stimulation while acquiring fPET-FDG data concurrently in baboons in order to verify that FDG signal changes are not sensitive to CBF changes.

METHODS

Data acquisition

PET/MRI Acquisition

All studies involving human subjects were reviewed and approved by the Institutional Review Board (IRB) at Massachusetts General Hospital. All subjects provided written, informed consent in accordance with the Human Research Committee at Massachusetts General Hospital. The imaging studies were performed on a 3-T Tim MAGNETOM Trio MR scanner (Siemens Healthcare, Inc) with an MR-compatible BrainPET insert (Siemens). Three-dimensional (3D) coincidence event data were collected and stored in a list-mode format. Magnetic resonance imaging was performed using two concentric head coils: an outer circularly polarized transmit coil and an inner 8-channel receive-only coil specially designed for the BrainPET with considerations for 511 keV photon attenuation properties.

PET imaging protocol

FDG in saline solution was administered intravenously at a constant infusion rate of 0.01 ml/s for 90 min to healthy subjects (1 female/2 males, mean age 32 ±2 years) using a Medrad® Spectra Solaris syringe pump (initial activity = 5±0.6 mCi). Venous blood samples were collected every 10 min from the other arm of all subjects during scanning, then centrifuged to obtain plasma, and aliquoted in a gamma counter that had been calibrated to the PET scanner to measure the venous activity during the experiment.

For reconstruction, the list mode files were sorted into line-of-response space and further compressed into sinogram space. The PET data were reconstructed with a standard 3D ordinary Poisson ordered-subset expectation maximization algorithm using both prompt and variance-reduced random coincidence events as well as normalization, scatter, and attenuation sinograms. The attenuation correction maps were derived from an individual’s structural MRI using an MR-based attenuation correction method. The fPET-FDG data were binned into 90 one-minute frames. The data were reconstructed with an isotropic voxel size of 1.25-mm into a volume consisting of 153 transverse slices of 256 × 256 pixels. All volumes were smoothed using a 3D filter with a 3-mm isotropic Gaussian kernel down-sampled to 76 slices with 128×128 voxels (2.5×2.5×2.5 mm³).

MRI imaging protocol

Anatomical studies consisted of a high-resolution T1-weighting acquisition using multi-echo MPRAGE (TR = 2530ms, TE₁/TE₂/TE₃/TE₄ = 1.64/3.5/5.36/7.22 ms, TI = 1200 ms, flip angle =7°, and 1 mm isotropic) that was used to derive the PET attenuation map. Slice geometries were parallel to the anterior commissure–posterior commissure (AC–PC) plane.

Visual stimulation

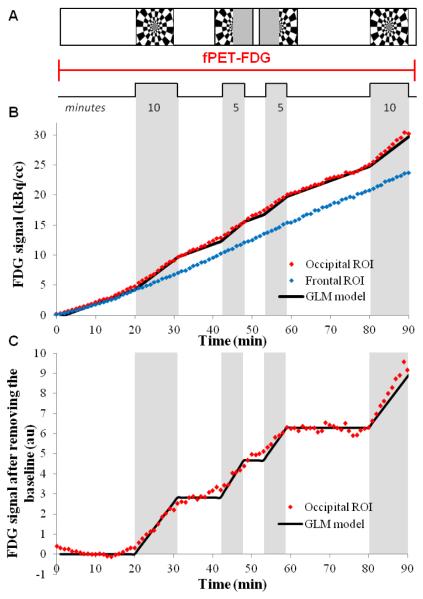
The human visual system, a standard and robust test bed for new neuroimaging techniques, was used to demonstrate that PET FDG studies can operate in a temporally dynamic mode. To induce hemodynamic and metabolic responses, we periodically presented a conventional visual stimulus consisting of an 8-Hz counterphase flickering “checkerboard” pattern (Polimeni et al., 2010) as shown in figure 1.A. The stimulus was projected onto a screen mounted at the end of the magnet bore, and subjects viewed the stimulus through a mirror. Three different types of visual stimuli were used: full-field checkerboard, presented twice for a duration of 10 minutes each, and hemi-field checkerboard stimuli (right and left) each presented for a duration of 5 minutes (figure 1.A).

Figure 1. fPET-FDG experimental design.

A) fPET-FDG experimental design for a 90 minutes experiment during visual paradigm alternating between a full checkerboard and left and right half checkerboard, B) fPET-FDG signal in the occipital ROI (red), defined as the voxels activated during the full checkerboard paradigm, and in the frontal ROI (black) in kBq/cc, the GLM used in the analysis in shown in black C) FDG signal in the occipital ROI after removing the baseline term, the black line represents the model we used to discriminates the slope changes for each stimulus.

Principles of the fPET-FDG method

Relationship of fPET-FDG to CMR_glu

The aim of our experimental design was to dynamically measure changes in FDG metabolism in response to multiple visual stimuli during one FDG infusion. In this section we will outline our mathematical approximation for the resulting FDG signal. Our treatment of data relates the slope of the tissue time-activity curve from FDG infusion to a rate of metabolism and by extension to CMR_glu. To give the discussion context, we first point out the strengths and caveats associated with traditional FDG kinetic models.

One classic analysis of FDG kinetics employs an irreversible two-tissue compartment model, which forms the basis of the relationship between the slope of our fPET-FDG method and CMR_glu. FDG is trapped in the tissue after initial phosphorylation, such that the reverse rate constant k₄ is small and approximated as null for the duration of experiment (Sokoloff et al., 1977). Using this compartmental model, the following differential equations describe the system (Phelps et al., 1979):

$${\stackrel{.}{C}}_t={\stackrel{.}{C}}_m+{\stackrel{.}{C}}_f$$ [1]

$${\stackrel{.}{C}}_m=k_3{C}_f$$ [2]

$${\stackrel{.}{C}}_f=K_1{C}_p-(k_2+k_3)C_f$$ [3]

where C_t (total tissue concentration) is the sum of C_m and C_f. C_m represents the metabolized (phosphorylated) FDG concentration and C_f represents the free/unmetabolized FDG concentration.

In the classic treatment, it is assumed that glucose metabolism measured by FDG is at steady state. The assumption simplifies the kinetic model solution, but comes with the caveat that the assumption is rarely verified or even verifiable using the bolus method. The deviation from steady-state cannot often be extracted from the data to begin to assess what error is introduced through the mathematical simplification. In fact, the bolus method and steady state assumption have been applied in many cases where it is clear that the steady-state assumption is not valid; for instance, acute drug injections produce an evolving physiological response but have been assessed assuming a steady-state (London ED et al., 1990).

In our approach to infusion FDG, we have elected a similar steady-state approximation with the full recognition that the assumption is violated. In fact, any functional imaging technique will violate the steady-state assumption by virtue that changes in metabolism are induced. Given that FDG was infused at a constant rate during the fPET studies herein, we assumed that after an initial equilibration period (discussed later), the freely available FDG for metabolism at rest is nearly constant, hence ${\stackrel{.}{C}}_f=0$, and ${\stackrel{.}{C}}_t=k_3{C}_f={\stackrel{.}{C}}_m$. Over the course of the entire imaging session, the plasma concentration does change, but over the shorter times of visual stimulation the plasma concentration is reasonably constant.

When making the steady-state approximation, the equation above can be ‘corrected’ to obtain CMR_glu using the lumped constant (Graham et al., 2002; Hasselbalch et al., 2001; Reivich et al., 1985), which converts FDG metabolic rate to glucose and $C_a^0$, which is a measurement of plasma glucose:

$${\mathit{CMR}}_{\mathit{glu}}=\frac{C_a^0}{\left(\mathit{LC}\right)\left(C_p\right)}{\stackrel{.}{C}}_m$$ [4]

Hence, the tissue derivative is proportional to CRM_glu at equilibrium, corrected for the lumped constant and the blood concentration according to the steady-state assumption above (Morris et al., 2004). It is worth noting that lumped constant values vary across studies (0.52 to 0.89) and that absolute measurements have additional ambiguities and assumptions (Graham et al., 2002). Since the potential ‘error’ introduced in the choice of lumped constant is so large, many simply use the ‘rate of FDG metabolism’ as a surrogate for CMR_glu.

Changes in the slope of the time activity curve of the tissue FDG concentrations are thus proportional to changes in the rate of FDG metabolism and by extension changes in CMR_glu using a steady state approximation. During initiation of a task, the compartmental equilibrium concentrations, such as C_f, may be disrupted transiently. If we assume that during the task, a new steady state (different from rest) will be reached, then again $\frac{{\mathit{dC}}_f}{\mathit{dt}}=0$ with the transition between states occurring asymptotically. Therefore, we can again approximate CMR_glu during the task using the slope of the time activity curve. The % change between slopes measured during two states (rest and task) is thus equal to % change in CMR_glu, when $C_a^0$ and C_p are constant.

Since $\frac{{\mathit{dC}}_f}{\mathit{dt}}$ cannot be measured, we assessed the steady state assumption through comparisons of our measured data to simulations. Thus, for the infusion method we have the added benefit that we can determine the extent to which the steady state assumption is an approximation. For any functional study based upon FDG uptake, the steady state will be violated, and so results need to be interpreted through compartment models, as in other PET experiments such as displacement studies of receptor-targeted ligand by endogenous neurotransmitter.

CMR_glu maps derived from the FDG slope: subject and group level

Aiming to validate our model, we derived CMRglu maps for each subjects to compare the values we get with values from the literature. The brain voxel-wise time activity curves for FDG uptake were divided by the interpolated venous blood plasma radioactivity concentrations. Maps of the time activity curve slopes were generated voxel-by-voxel using a linear regression from this blood-normalized FDG signal. CMR_glu maps were derived from equation 4 using this slope map with the measured blood glucose concentration (in mmol/L) for each subject and a lumped constant of 0.89 (Graham et al., 2002). An average group FDG slope map was then computed based upon data from the three subjects.

Simulation of the fPET-FDG signal in response to a change in k₃

In order to compare experimental data with theoretical models, simulations were performed using equations [1]-[3]. The blood was simulated as a constant input with a bi-exponential washout function. A gamma function was used to model a rapid neural response in terms of CMR_glu, and then kinetic equations described transient fluctuations of compartmental concentrations, the approach to the new equilibrium state, and the total (free plus bound) tissue concentration. Kinetic rate constants K₁=0.1 mL/min, k₂=0.15 min⁻¹, k₃=0.08 min⁻¹, and k₄=0 min⁻¹ were used in the model (Reivich et al., 1985). FDG signal increases from 10% to 50% were simulated with 10% incremental steps, over a 10-minute period in order to span the range observed in our experimental paradigm.

Individual results and group analysis

fPET-FDG processing: subject level

We processed each subject’s fPET-FDG data using a GLM analysis to verify that our method is sensitive enough to map the visual cortex during a visual activation at the individual subject level.

The PET data were smoothed with a 12 mm Gaussian kernel and analyzed using a general linear model (GLM) consisting of 3 different explanatory variables (EV): (i) 2 blocks of the 10 minutes full-field checkerboard paradigm (EV1), (ii) a 5 minute block of left hemi-field checkerboard (EV2) and (iii) a 5 minute block of right hemi-field checkerboard (EV3). .

Two separate types of GLM analyses were performed. In one analysis, tissue TACs first were differentiated to form a rate parameter that is closely related to CMR_glu (figure 4), and then analysis proceeded using a binary (“on-off”) stimulus paradigm similar to fMRI. However, this method exhibits the low signal to noise ratio of individual frames, so an alternative analysis used the original TAC of FDG uptake (figure 1B). In this analysis, the hypothesized form of changes in CMR_glu produced a set of initial GLM regressor, identically to the first analysis method, and then the regressors were integrated to form the basis set for data analysis using original TACs. Hence, a binary stimulus paradigm for the rate of uptake becomes a series of ramp functions in the analysis of the raw FDG TAC (figure 1.C).

Figure 4. Comparison of simulated and experimental responses with exponential fitting of the data.

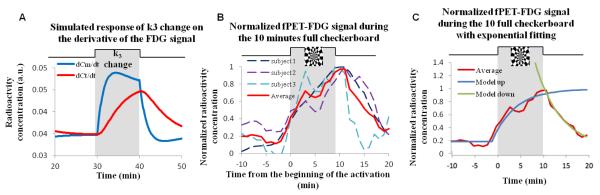
A) Simulation of the effect of a brief change in k3 on the derivative of the FDG signal in the course of the infusion protocol. The red line represents the derivative of the FDG signal and the blue line represents the metabolized FDG. (B) Normalized FDG signal change during the 10 minute full checkerboard for the 3 individual subjects (dashed lines) and the average response (red line). (C) Average normalized FDG signal change during the 10 minute full checkerboard for the 3 individual subjects (red line) with an exponential fit for the increase in FDG signal after the beginning of the activation period ( blue, R² = 0.96, τ = 4.9 min) and for the decrease in FDG signal after the end of the activation period (green, R² = 0.98, τ = 5.6min). Exponential fitting was accomplished using GraphPad Prism® software (Prism6, GraphPad Software Inc., La Jolla, CA, USA).

Statistical analyses for figures 5 and 6 used the integral formulation illustrated in figure 1, whereas the FDG uptake rate (figure 4.B) was derived by differentiating the FDG TAC with respect to time.

Figure 5. fPET-FDG activations maps for a single subject.

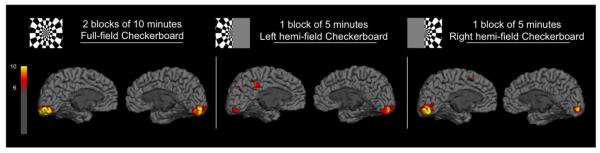
Statistical maps (T-score > 6) of the activations observed for a single subject during the two blocks of 10 minutes full-field checkerboard presentation, the single 5 minute block of left hemi-field checkerboard and the single 5 minute block of right hemi-field checkerboard.

Figure 6. Fixed-effects group analysis.

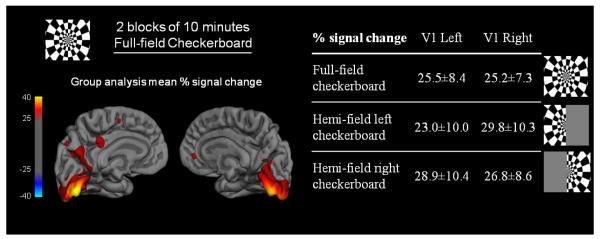
(top and bottom left) Percent signal change maps obtained for the fixed-effects group analysis (n = 3) during the single 5 minute block of left hemi-field checkerboard, the single 5 minute block of right hemi-field checkerboard and the two blocks of 10 minutes full-field checkerboard; (bottom right) Percent signal change values obtained in the a priori anatomical V1 ROI from the Jülich histological atlas for the fixed-effect group analysis (n = 3) during the two blocks of 10 minutes full-field checkerboard, the single 5 minute block of left hemi-field checkerboard and the single 5 minute block of right hemi-field checkerboard.

fPET-FDG processing: group analysis

A second level group analysis was used to validate the statistical significance of our results and also to measure the average changes in FDG metabolism during the visual tasks. The individual subjects’ high-resolution anatomical MRI data (acquired concurrently with PET) were coregistered to the MNI152 atlas brain using an affine linear transformation (12 degrees of freedom). The derived transformations were then applied to the dynamic PET data. Statistical significance and effect sizes were determined using a fixed-effects, single-group model. The statistical maps were then projected on surface of the using the FreeSurfer software (Fischl, 2012). Mean percent change ± standard deviation for the left and right V1 a priori ROIs (defined anatomically using the Jülich histological atlas) were extracted from FSL for each of the 3 contrasts.

Non-human primate (NHP) experiment with hypercapnia

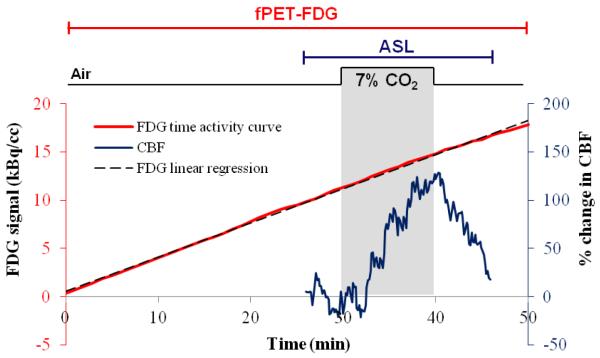
To assess the influence of cerebral blood flow changes on FDG signal we administered inhaled carbon dioxide, a strong vasodilatory stimulus, to two baboons (2 females, ~10-12 kg) simultaneously with fPET-FDG and arterial spin labeling (ASL) MRI for CBF measurements. The protocol was approved by the Institutional Animal Care and Use Committee. Animals were anesthetized with isoflurane (1%) and mechanically ventilated. Physiological parameters were continuously monitored and maintained within the normal range. All images were acquired on the same 3T Siemens TIM-Trio with a BrainPET insert as the human data, using a custom PET-compatible 8-channel array coil. Similar to the human protocol, ~5 mCi of FDG was continuously infused intravenously at a rate of 0.01 mL/sec for each study. PET data were stored in list mode and binned into 1-min frames. Dual echo pseudo-continuous arterial spin labeling (pCASL) data were acquired simultaneously (TR/TE1/TE2 = 4000/12/30ms, 2.2 × 2.2 × 4 mm) (Wey et al., 2010). During a 50 min dynamic fPET/fMRI scan, a hypercapnic challenge (7% CO₂) was given for 10 minutes between 30 and 40 minutes. All data were motion and slice-time corrected, skull stripped, spatially smoothed and registered to a standard NHP atlas. Percent changes in gray matter CBF were calculated.

RESULTS

Principles of the fPET-FDG method

The use of sequential but varied visual stimuli allowed us to confirm that the observed metabolic signal changes were specific to each visual stimulus, and that multiple stimuli (four in this case) can be measured dynamically during a single scan. PET TACs from a single subject are shown in figure 1.B. Using the activated voxels to define a post-hoc volume-of-interest, the subject’s TAC for visual stimulation was created and compared to the frontal cortex, a volume-of-interest that did not significantly respond to the visual stimulus. Changes in FDG signal are easily observed as changes in the TAC slope (FDG utilization rate) during visual stimulus presentation in the activated voxels (occipital region) but not in the frontal cortex (figure 1.B). These same data are presented after removing the baseline in figure 1.C together with the GLM model used in the analysis. The baseline term was removed by mathematically modeling a baseline term in the GLM analysis. This baseline term accounts for basal metabolism throughout the experiment, and also for small changes in plasma FDG concentration over the long time course of the overall scan. It is important to note for clarity that we are not using a reference region in this analysis (see Discussion) and that each voxel was processed independently. The TAC for the whole brain (figure 2.B) demonstrates that the uptake slope of FDG in the brain is quite constant during the entire exam. The derivative of the time activity curve in figure 2.C also shows that after a delay of about 30 minutes the slope of the FDG signal is stable.

Figure 2. Radioactivity concentration in the venous blood plasma and average time activity curve and derivative of the FDG signal in the whole brain.

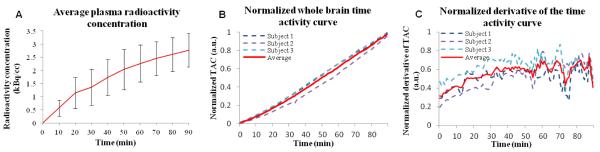
(A) Venous blood was collected every 10 minutes in the arm of our 3 subjects during the 90 minute experiments. The interpolated average radioactivity concentration in the venous blood plasma of our 3 subjects (mean ± std) is shown. (B) The normalized time activity curve in the whole brain for the 3 subjects shows a linear increase during the entire 90 minutes experiment. (C) The smoothed derivative of the normalized time activity curve in the whole brain for the 3 subjects shows that after around 30 minutes the derivative of the signal is stable.

The average concentration of radioactivity in the venous blood from our subjects is shown in figure 2. Radioactivity concentration in blood exhibits an initial equilibration followed by a slight increase. Measured blood glucose concentration was 5.6 ± 0.4 mmol/L (mean±sd). Using the FDG signal slope, we calculated average CMR_glu values for whole brain from 3 subjects as 0.37±0.02 μmol/100g/min. Our CMR_glu quantification is consistent with published data (Huisman et al., 2012). The average CMR_glu map is shown in figure 3 at five axial cuts.

Figure 3. Average CMR_glu map.

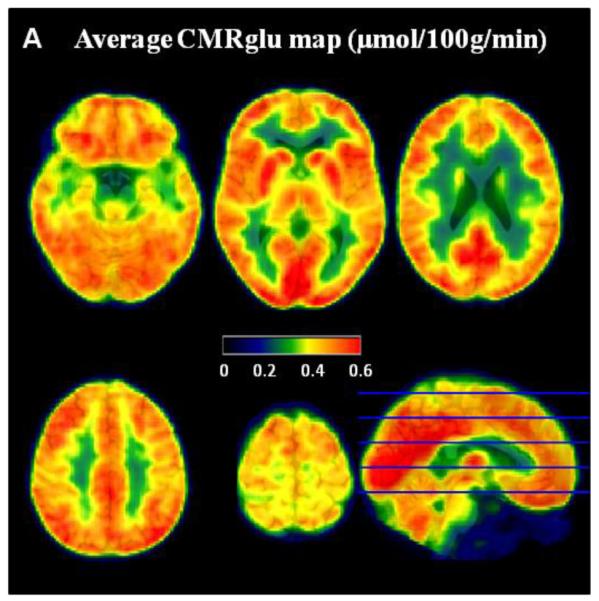
Average CMR_glu map in μmol/100g/min (scale from 0 to 0.6) across the 3 subjects. The CMR_glu maps were derived from the slope of the TAC, normalized to venous blood plasma radioactivity concentration (in min⁻¹), multiplied by the glucose measurement (mmol/L) and divided by the lumped constant (0.89).

Using multi-compartmental simulations (Eqs. 1-3), we modeled the relative dynamic responses of free, bound, and total FDG concentrations. As shown in figure 4.A, the total tissue concentration, which is the measured experimental quantity, increases more slowly than the bound concentration following a stimulus, due to a corresponding drop in the free concentration. However, the two curves converge toward the end of the stimulus as a new equilibrium is approached. As a way to quantify changes in the metabolized compartment based upon measured changes in total tissue concentration, we compared the area under the curve (AUC) of the tissue and the metabolized TACs following a simulated stimulus. Although the magnitude of the tissue and metabolized compartments do not quite converge in the simulation, the integral of the two curves are much more similar. Across a range of changes in FDG signal from 10% - 50%, the AUC ratio was about unity and did not vary significantly (with an averaged AUC ratio of 1.02 ± 0.02 from 5 levels of signal changes), demonstrating that the integral of tissue and metabolized compartmental concentrations are comparable following stimulation.

Figure 4.B shows experimental data for the derivative of the FDG TAC averaged across three subjects. In accordance with the simulation of figure 4.A, the rate of total tissue uptake increases slowly after stimulation onset and resolves slowly after stimulation offset. Hence, the fPET-FDG signal exhibits the expected dynamics due to visual stimulation, based upon simulated tissue radioactivity concentrations after a brief change in k₃. This figure also shows that equilibrium is almost completely reached during a brief 10 minute stimulus period (figure 4.C) and that as predicted from the model, the new equilibrium is approached asymptotically. We are able to estimate the asymptotic value by fitting the data to an exponential response shape, which projects that the magnitude at the end of stimulation is about 98% of the maximum steady-state magnitude. The exponential fit also shows us that the tau of the exponential increase after the beginning of the activation is 4.9 minutes (figure 4.C) and the tau of the exponential decrease after the activation is 5.6 minutes (figure 4.C). Hence, approximately 15 min spacing between the end of a task and the beginning of another may be necessary to ensure ‘return’ to a baseline equilibrium state before a new activation. The extent to which the exponential increase and decrease during and after activation are governed by physiological changes (versus experimental design) is an area we are actively exploring.

Individual results and group analysis

We used the GLM analysis to create fPET-FDG activations for the three contrasts of interest (full field checkerboard and right and left hemi-field checkerboard), a representative subject is shown in figure 5. Maps show T values, derived from the general linear model, as a measure of the contrast to noise ratio (CNR). Note that CNR values greater than 10 were obtained for each contrast from a single subject in a single session. Confirmation of functional specificity is inherent in our analyses as both hemispheres of the visual system respond equally to the full-field checkerboard (figure 5.A) whereas the contralateral hemisphere has a higher response to a hemi-field checkerboard (figure 5.B,C).

Group analysis of the fPET-FDG dataset from three subjects was accomplished using a fixed-effect analysis to determine the average percent change in glucose utilization during each visual stimulus (i.e. left-, right- and full-checkboard) compared to baseline. The percent change map for the full-field checkerboard stimulus at the group level is shown in figure 6. The mean percent increase in glucose utilization derived from fPET-FDG for our three subjects was 25% for the full-field checkerboard, 26% for the left hemi-field checkerboard and 28% for the right hemi-field checkerboard (figure 3). The absolute changes in FDG utilization as measured by fPET-FDG are consistent with previous studies measuring single response in a two-scan paradigm (Newberg et al., 2005).

Non-human primate experiment with hypercapnia

In order to assess the impact of CBF changes on fPET-FDG signal, and thus CMR_glu estimation, we experimentally modulated CBF in NHP brains using mild hypercapnia. MRI measurements of CBF were obtained simultaneously with fPET-FDG signal. Figure 7 shows the PET TAC and the ASL CBF data from the gray matter for one baboon. CBF data demonstrated robust signal changes in responses to hypercapnia with a 70% increase on average during the 10 minutes of hypercapnia. Conversely, hypercapnia did not alter FDG uptake rate, indicating that flow effects do not compromise the FDG infusion protocol. This result provides strong empirical evidence that changes in fPET-FDG signals we observe during visual stimuli are not due to changes in blood flow. It is important that we note for both the NHP data and the human data that the tissue response, $\frac{{\mathit{dC}}_t}{\mathit{dt}}$, (i.e. whole-brain TACs and stimulus-non-responding regions like the FC) are much more constant than the plasma radioactivity (which is changing) would predict.

Figure 7. Non-human primate experiment.

The red line shows a linear increase of FDG signal in the grey matter of one anesthetized baboon during the 50 minute constant infusion. A hypercapnic challenge (7% CO₂) was administered between 30 and 40 minutes (shaded area) and ASL was acquired around the challenge to measures changes in CBF. The blue line shows an increase in average percent signal change in CBF measured in the grey matter using ASL during the hypercapnic challenge, followed by a decrease in CBF after the end of the hypercapnic challenge.

DISCUSSION

fPET-FDG provides a simple method to observe brain glucose utilization changes dynamically in a single imaging session. We demonstrated that our method enables measurements of changes in FDG signal during multiple tasks within a single imaging session in individual human subjects, a fundamental improvement over the standard bolus technique. Moreover, the hypercapnia data demonstrate that this method exhibits negligible contamination from flow, as expected based upon the low FDG extraction fraction. The processing stream is comparable to other fMRI and PET time-series analyses, thus allowing neuroscientists to adopt this technique easily. This proof-of-concept demonstration is not devoid of questions that need to be fully addressed through subsequent work.

As with any new method, kinetic models and mathematical treatments will need to be refined. While the steady-state approximation we have applied here is reasonable and supported by our data, we fully acknowledge it is an approximation with certainly limitations. Relaxing the steady-state assumption is a necessary concession to biology in order to accomplish functional brain imaging, and thus analysis models not based upon steady-state approximations are required in order to interpret the data. Further experimental explorations and better models will be needed to interpret the temporal response of FDG using fPET, in the same way models have been created for receptor displacement studies. Even with our current approximations, there are clear strengths in improved temporal resolution and the ability to perform within-session differential comparisons of FDG metabolism that are imparted by the fPET FDG method.

A key limitation of the present study is the small sample size. As a feasibility and proof-of-concept study for fPET-FDG, our results indicate that this method is reliable even at the subject level (figure 5). Undoubtedly, additional refinements can be obtained in data acquisition and analysis. Note that we chose a relatively sparse stimulus paradigm that is not statistically efficient (figure 1) in order to monitor baseline variations in signal during the infusion protocol. One goal of future studies will be to optimize paradigm designs after characterizing signal and noise frequency components. In order to increase the temporal resolution, the signal to noise ratio (SNR) of the fPET-FDG method will need to be increased. This optimization might be achieved by modifying the infusion protocol, for example by increasing the infusion rate (radioactivity per time). Additionally, bolus plus continuous infusion paradigms can reach a nearly constant plasma concentration more quickly than infusion without a prior bolus, so that paradigm might offer some additional stability in plasma levels particularly at earlier time points.

In data analysis, improvements in motion correction and reductions in noise of the PET data may improve statistical power. The derivative signal is particularly noisy due to the subtraction method (figure 2.C) and because of this noise, we elected not to use the derivative signal for the GLM analysis but rather the more ‘raw’ time-activity curve with the slope (baseline metabolism) as a regressor in the GLM. Additionally, the signal to noise ratio changes throughout the study; initial analyses using weighted least squares based upon a standard PET noise model (Logan et al., 2001) did not substantially alter results, but further investigations into optimal analysis strategies are warranted.

We demonstrated that the basal CMR_glu values derived from the slope of FDG signal normalized to blood radioactivity concentration are in very good agreement with values from the literature (average CMR_glu values for the all brain of 0.37±0.02 μmol/100g/min). Hence, we used the slope of the tissue concentration as a function of time as a surrogate for relative CMR_glu changes. We are aware that this is an approximation because the transition between steady states and activation period is a function of tracer kinetics. Our simulation results (figure 4) show that the metabolized compartment changes more abruptly than the total signal we are acquiring, and our data are in good agreement with this kinetic model.

We have considered many sources of influence and error. One potential source of error could be CBF-induced changes of FDG signals. To address this concern, we demonstrated experimentally that fPET is not influenced measurably by CBF changes. A relatively large increase in CBF (120% change at maximum) due to a hypercapnia stimulus did not induce any measurable change in the FDG signal slope. As such, fPET with FDG appears to be a flow-independent process under normal physiological conditions; however, caution should be exercised under extreme conditions such as hypoglycemia (Schuier et al., 1990), where it is known that the bolus FDG method becomes flow sensitive. From a mathematical point of view, it should be noted that the rate constant for deoxyglucose transport from blood to brain (K₁~0.1mL/min) is smaller than the rate constant for its transport back from brain to blood (k₂~0.15min⁻¹), and both K₁ and k₂ are greater than k₃ (k₃~0.08min⁻¹), the rate constant for its phosphorylation in the brain tissue. These relationships indicate that the blood-brain exchange of deoxyglucose is fast compared to the metabolic rate and so utilization is not limited by supply to the brain through the circulation. Similarly, small changes in CBV also occur during visual activation (Belliveau et al., 1991) and will contribute to the fPET-FDG signal minimally given that each image voxel consists of a small blood component (on average < 5%). By measuring blood radioactivity during the infusion protocol (maximum 4 kBq/cc of venous plasma blood), we determined that a 20% change in CBV, would increase the fPET-FDG signal only by 1 %. Such a change would make a negligible contribution to our current fPET signal, and could be corrected based upon measured changes in CBF or CBV in situations where greater effects might be considered.

The fPET-FDG method is an operationally straightforward “repurposing” of a fundamental PET index of metabolism using concepts and tools from fMRI. This method can easily be performed on any commercial PET scanner using a widely available and inexpensive radiotracer. Looking forward, the complementary nature of fPET-FDG to fMRI capitalizes on the emerging technology of hybrid MR-PET scanners. In particular, fPET-FDG and emerging quantitative fMRI methods (Buxton, 2012; Hoge, 2012; Pike, 2012) will allow us to simultaneously measure dynamic changes in glucose utilization, hemodynamics and oxygen consumption, addressing vital questions about neuronal and neurovascular relationships across tasks and disease states.

More broadly, our data point towards the capacity of fPET to dynamically image molecular events with the exquisite sensitivity of PET during multi-task challenges. The molecular specificity of a wide range of metabolic and neuroreceptor targeted PET tracers undoubtedly expand fPET beyond measurements of glucose utilization dynamics, for example by improving the temporal resolution of analogous MR-PET dynamic neuroreceptor studies (Mandeville et al., 2013; Sander et al., 2013). We anticipate that fPET will become a modular imaging technique that is extensible to both existing radiotracers and those to be designed specifically for fPET, and one which will provide new temporal information on multifaceted neuronal molecular events, which heretofore have been measured as static ‘state’ functions or an accumulated value. While the temporal resolution of such methods will depend on a number of factors, both technical and biological, dynamic imaging of metabolic or neuroreceptor status will provide an important new dimension to quantify brain functional relationships.

Highlights NEMG-14-964.

• fPET-FDG is a method to dynamically measure FDG metabolism.

• The new PET method uses constant infusion FDG.

• Feasibility of the technique, termed fPET-FDG, was demonstrated with visual stimuli.

• fPET-FDG can be used in an analysis pipeline similar to fMRI.

• fPET-FDG can be performed with most PET scanners and is ideal for MR-PET.