Additive Interactions Between Susceptibility Single-Nucleotide Polymorphisms Identified in Genome-Wide Association Studies and Breast Cancer Risk Factors in the Breast and Prostate Cancer Cohort Consortium

Abstract

Additive interactions can have public health and etiological implications but are infrequently reported. We assessed departures from additivity on the absolute risk scale between 9 established breast cancer risk factors and 23 susceptibility single-nucleotide polymorphisms (SNPs) identified from genome-wide association studies among 10,146 non-Hispanic white breast cancer cases and 12,760 controls within the National Cancer Institute's Breast and Prostate Cancer Cohort Consortium. We estimated the relative excess risk due to interaction and its 95% confidence interval for each pairwise combination of SNPs and nongenetic risk factors using age- and cohort-adjusted logistic regression models. After correction for multiple comparisons, we identified a statistically significant relative excess risk due to interaction (uncorrected P = 4.51 × 10⁻⁵) between a SNP in the DNA repair protein RAD51 homolog 2 gene (RAD51L1; rs10483813) and body mass index (weight (kg)/height (m)²). We also compared additive and multiplicative polygenic risk prediction models using per-allele odds ratio estimates from previous studies for breast-cancer susceptibility SNPs and observed that the multiplicative model had a substantially better goodness of fit than the additive model.

Genome-wide association studies (GWAS) have identified at least 74 independent susceptibility loci for breast cancer (1–12) or for specific subtypes, such as estrogen receptor (ER)-negative breast cancer (13–16). Characterization of the joint effects of multiple susceptibility loci and established risk factors such as number of livebirths and body mass index (BMI; weight (kg)/height (m)²) may shed light on biological mechanisms of breast cancer etiology and help improve risk prediction, potentially influencing public health guidelines. To date, 4 large-scale studies have explored gene-environment interactions between GWAS-identified single-nucleotide polymorphisms (SNPs) and breast cancer risk (17–20). While 3 of these studies found no evidence for departure from multiplicativity after correction for multiple comparisons, the fourth found evidence of effect-measure modification between the lymphocyte-specific protein 1 gene (LSP1) variant rs3817198 and breast cancer risk by parity (20).

Epidemiologists most frequently report departure from multiplicativity while characterizing interactions (21), and they assume multiplicative joint effects on the absolute risk scale while predicting risk (22–24). It is important to consider other measures of interaction between risk factors as well, such as additive joint effects on the absolute risk scale, in order to benefit from the additional information obtained from them (25, 26). To our knowledge, tests for additive interaction between confirmed susceptibility SNPs and established breast cancer risk factors have not been reported.

Additive interactions—departures from additivity on the absolute risk scale—have public health as well as etiological implications (25, 27, 28). Additive interactions between an environmental risk factor (exposure) and a genetic risk factor (SNP) test whether the excess in absolute risk of the disease due to presence of the exposure is the same in persons who carry the SNP and those who do not. They help identify subgroups of individuals for whom a targeted intervention designed to reduce a modifiable exposure could have the highest impact. Assessment of changes in risk differences between exposed and unexposed subjects is straightforward when genotype and exposure data are available on a full cohort of subjects with prospective disease follow-up. However, departures from additivity on the absolute risk scale can also be estimated from case-control data. Several measures of additive interaction that can be calculated from case-control data have been introduced (29–31). The relative excess risk due to interaction (RERI) may be the most useful in terms of assessing synergism between 2 binary risk factors (32, 33).

GWAS SNPs have also been used to improve existing breast cancer risk prediction models (22, 24, 34–37). In these studies, polygenic models have generally assumed multiplicative joint effects of SNPs on the relative risk scale. Under this multiplicative model, the absolute risk in the tails of the distribution can be strikingly elevated relative to the average risk. As more markers are identified and added to the risk model, the increase in risk in the tails may be clinically useful—for example, by identifying women who would benefit from earlier screening or chemoprevention. However, for most women (those in the middle of the risk distribution), their estimated risks under additive and multiplicative risk models are quite similar, while the estimated absolute risks in the tails under an additive risk model are much less extreme (women in the top 1% of the distribution have a 1.3-fold higher risk of breast cancer than average) (38). Thus, how well the multiplicative model fits the observed risk in the tails is an important practical question that has not yet been extensively studied.

Our objective in this study was to test for departures from additivity on the absolute risk scale between 9 established risk factors for breast cancer and 23 GWAS-identified breast cancer susceptibility SNPs within the National Cancer Institute's Breast and Prostate Cancer Cohort Consortium (BPC3). We also assessed whether an additive joint-effects model or a multiplicative joint-effects model based on external individual-marker odds ratio estimates was a better fit for the combined effects of 19 independent GWAS-identified breast cancer susceptibility SNPs (excluding 4 ER-negative SNPs).

METHODS

Study population

Cases and matched controls were drawn from 8 prospective cohort studies (39–46) conducted in the United States, Europe, and Australia, as described in the Web Appendix (available at http://aje.oxfordjournals.org/). We restricted analysis to 10,146 cases of invasive breast cancer and 12,760 controls of European ancestry, matched on age and additional criteria specific to the cohorts.

SNP selection and genotyping

We selected for analysis 23 independent SNPs from 23 distinct risk loci that had been identified in GWAS published before November 2012. Details on the selection process and genotyping are given in the Web Appendix.

Assessment of established nongenetic breast cancer risk factors

Risk factor data were obtained prior to disease diagnosis (at the time of inclusion in the cohort or at blood draw) using structured questionnaires. These data were sent to the German Cancer Research Center (Deutsches Krebsforschungszentrum, Heidelberg, Germany) for systematic, centralized data checks, removal of inconsistencies, and harmonization. We had information on established breast cancer risk factors, including age, height, weight, BMI, age at menarche, number of full-term pregnancies, age at first full-term pregnancy, age at menopause, history of oral contraceptive use, smoking status (never, former, or current smoker), alcohol intake (g/day), and family history of breast cancer in first-degree relatives (Web Table 1).

Statistical analysis

For analyses of gene-gene and gene-environment interaction, we converted all genetic and exposure variables into binary forms to allow for easy interpretability and to draw possible mechanistic conclusions within the sufficient-cause framework (47). Furthermore, since these SNPs and exposures were established risk factors for breast cancer, it was possible (at least for very strong risk factors such as family history) to code our variables so that their expected marginal odds ratios, based on previous literature, would be greater than 1.0. This is consistent with the monotonicity assumption for synergism, but we note that this assumption cannot be verified empirically, as it is based on individuals’ disease outcomes under counterfactual exposure patterns (48). Therefore, all SNPs were assumed to have a dominant effect of the risk allele and were represented in models by a coding of 0 or 1, based on whether the study participant had at least 1 risk allele for the SNP. The 9 exposure variables were transformed to their binary forms based on previously used cutpoints (19)—height (≤1.63 m vs. >1.63 m), BMI (<30 vs. ≥30), age at menarche (>11 years vs. ≤11 years), ever having a full-term pregnancy (yes vs. no), age at first full-term pregnancy (<30 years vs. ≥30 years), age at menopause (<50 years vs. ≥50 years), smoking (never vs. ever), alcohol intake (<14 g/day vs. ≥14 g/day), and family history of breast cancer in a first-degree relative (no vs. yes).

In addition to the 9 exposure variables, we created a risk score based on the Gail model (49), henceforth called the “modified Gail score,” because we did not have information on number of biopsies for all study participants. The modified Gail score was set to missing for 7,085 study participants who had missing values on any of the remaining variables used to calculate the Gail score (age, age at menarche, age at first livebirth, and number of first-degree relatives with breast cancer). The modified Gail score was converted to its binary form by using the 90th percentile among controls as the cutoff. We created a similar polygenic risk score (PRS) for SNPs, which was the count of the number of risk alleles in 19 SNPs (excluding 4 SNPs identified in ER-negative breast cancer GWAS scans), weighted by their log odds ratios as reported in external GWAS (Web Table 2). Missing values for the 19 SNPs were imputed on the basis of allele frequencies in cases and controls. The observed count of risk alleles ranged from 9 to 30, with a mean of 18.3 among controls and 19.1 among cases. The PRS (weighted count of risk alleles) was used to dichotomize participants into 2 groups using the 75th percentile among controls, thus creating a binary variable named the “polygenic score.”

Unconditional logistic regression models were used to test for associations between each of the 23 SNPs (Table 1) and breast cancer, as well as ER-negative breast cancer. All models adjusted for age at baseline (5-year interval groups) and for cohort using indicator variables.

Table 1.

Associations of Selected Single-Nucleotide Polymorphisms With the Risks of Breast Cancer and Estrogen Receptor-Negative Breast Cancer in the Breast and Prostate Cancer Cohort Consortium

SNPa	Locus and/or Gene	Chr	Position	First Author, Year (Reference No.)	All Breast Cancer			ER-Negative Breast Cancer
					ORb	95% CI	P Value	ORb	95% CI	P Value
rs11249433	NOTCH2/1p11.2	1	120,982,136	Thomas, 2009 (4)	1.13	1.06, 1.20	0.0002	1.04	0.92, 1.17	0.534
rs1045485	CASP8	2	201,857,834	Cox, 2007 (8)	1.29	1.02, 1.64	0.035	1.69	0.98, 2.92	0.059
rs13387042	2q35	2	217,614,077	Stacey, 2007 (2)	1.18	1.10, 1.26	7.31 × 10−6	1.10	0.96, 1.26	0.178
rs4973768	3p24.1/SLC4A7	3	27,391,017	Ahmed, 2009 (11)	1.13	1.05, 1.20	0.0006	1.01	0.89, 1.15	0.870
rs10069690c	TERT	5	1,332,790	Haiman, 2011 (14)	1.05	0.99, 1.12	0.089	1.13	1.01, 1.27	0.032
rs10941679	5p12	5	44,742,255	Stacey, 2008 (3)	1.16	1.09, 1.23	7.20 × 10−7	1.02	0.90, 1.14	0.798
rs889312	MAP3K1	5	56,067,641	Easton, 2007 (1)	1.13	1.07, 1.20	4.78 × 10−5	1.04	0.93, 1.16	0.531
rs17530068c	6q14.1	6	82,249,828	Siddiq, 2012 (15)	1.09	1.02, 1.15	0.006	1.09	0.96, 1.24	0.165
rs2046210	6q25.1/ESR2	6	151,990,059	Zheng, 2009 (10)	1.11	1.05, 1.18	0.0005	1.14	1.01, 1.28	0.030
rs1562430	8q24.21	8	128,457,034	Turnbull, 2010 (5)	1.16	1.07, 1.25	0.0004	1.03	0.87, 1.23	0.699
rs1011970	CDKN2BAS	9	22,052,134	Turnbull, 2010 (5)	1.08	1.02, 1.15	0.012	1.14	1.00, 1.30	0.055
rs865686	9q31.2	9	109,928,299	Fletcher, 2011 (6)	1.19	1.09, 1.30	5.87 × 10−5	1.32	1.09, 1.61	0.005
rs2380205	10p15.1	10	5,926,740	Turnbull, 2010 (5)	1.05	0.97, 1.13	0.209	1.04	0.89, 1.22	0.592
rs10995190	10q21.2/ZNF365	10	63,948,688	Turnbull, 2010 (5)	1.30	1.04, 1.62	0.021	1.28	0.79, 2.09	0.312
rs1250003d	ZMIZ1	10	80,516,820	Turnbull, 2010 (5)	1.08	1.02, 1.15	0.014	0.98	0.86, 1.11	0.744
rs2981582	FGFR2	10	123,342,307	Easton, 2007 (1); Hunter, 2007 (7)	1.25	1.18, 1.33	1.87 × 10−12	1.04	0.92, 1.17	0.533
rs909116	LSP1	11	1,898,522	Turnbull, 2010 (5)	1.06	0.98, 1.14	0.133	1.04	0.89, 1.21	0.625
rs614367	11q13	11	69,037,945	Turnbull, 2010 (5)	1.16	1.09, 1.24	7.91 × 10−6	1.07	0.93, 1.23	0.339
rs10483813d	RAD51L1	14	68,101,037	Thomas, 2009 (4)	1.28	1.11, 1.47	0.0005	0.99	0.77, 1.28	0.947
rs3803662	TNRC9/TOX3	16	51,143,842	Easton, 2007 (1); Stacey, 2007 (2)	1.23	1.16, 1.31	6.12 × 10−12	1.11	0.99, 1.24	0.079
rs6504950	COX11	17	50,411,470	Ahmed, 2009 (11)	1.10	0.98, 1.24	0.091	1.11	0.89, 1.40	0.344
rs8170c	C19ORF62	19	17,250,704	Antoniou, 2010 (13)	1.01	0.95, 1.07	0.780	1.25	1.11, 1.41	0.0002
rs2284378c,d	20q11.22/RALY	20	32,051,756	Siddiq, 2012 (15)	1.00	0.94, 1.05	0.878	1.11	0.98, 1.25	0.087

Abbreviations: CASP8, caspase 8, apoptosis-related cysteine peptidase gene; CDKN2BAS, CDKN2B antisense RNA (non-protein coding) gene; Chr, chromosome; CI, confidence interval; C19ORF62, chromosome 19 open reading frame 62 gene; COX11, cytochrome C oxidase assembly homolog 11 gene; ER, estrogen receptor; ESR2, estrogen receptor 2 gene; FGFR2, fibroblast growth factor receptor 2 gene; LSP1, lymphocyte-specific protein 1 gene; MAP3K1, mitogen-activated protein kinase kinase kinase 1, E3 ubiquitin protein gene; NOTCH2, Notch (Drosophila) homolog 2 gene; OR, odds ratio; RAD51L1, DNA repair protein RAD51 homolog 2 gene; RALY, RALY heterogeneous nuclear ribonucleoprotein gene; SLC4A7, solute carrier family 4, sodium bicarbonate cotransporter, member 7 gene; SNP, single-nucleotide polymorphism; TERT, telomerase reverse transcriptase gene; TNRC9, trinucleotide repeat-containing 9 gene; TOX3, TOX high mobility group box family member 3 gene; ZMIZ1, zinc finger, MIZ-type containing 1 gene; ZNF365, zinc finger protein 365 gene.

^a Associations in the Breast and Prostate Cancer Cohort Consortium were determined for each SNP, assuming a dominant effect of risk alleles reported in previous studies.

^b ORs and 95% CIs were calculated using unconditional logistic regression models adjusting for age at baseline (5-year intervals) and cohort.

^c SNP identified from an ER-negative genome-wide association study scan.

^d Some cohort studies genotyped proxy SNPs for the reported SNP. For example, rs704010 was a proxy for rs1250003 (r² = 1 in the HapMap CEU population (Utah residents with Northern and Western European ancestry) (65)); rs999737 was a proxy for rs10483813 (r² = 1 in the HapMap CEU population); and rs6059651 was a proxy for rs2284378 (r² = 1 in the HapMap CEU population).

We tested for departure from additivity on the absolute risk scale for the joint association of each SNP-exposure combination, by estimating the RERI and computing 95% confidence intervals around the estimated RERI, using the delta method described by Hosmer and Lemeshow (29). RERIs and 95% confidence intervals were calculated for all pairwise combinations of 24 genetic variables (23 SNPs and polygenic score) with 10 exposure variables (including modified Gail score), using unconditional logistic regression models adjusting for age at baseline (5-year interval groups) and for cohort. We accounted for multiple comparisons through family-wise error rate correction of P values (Bonferroni correction); that is, adjusted P values were calculated by multiplying unadjusted P values by 240 (the number of tests).

When the adjusted P value for the RERI was less than 0.05, we also calculated point estimates and confidence intervals for other measures of additive interaction—the attributable proportion and the synergy index. For these SNP-exposure combinations, we also further characterized interactions after stratifying participants by menopausal status and by restricting analysis to ER-positive or ER-negative cases.

We next tested whether an additive or multiplicative model was a better fit for the simultaneous combination of 19 SNPs known to be associated with overall breast cancer. To this end, we calculated expected cell counts in the cross-tabulation of case-control status by risk allele count, conditional on the marginal distribution of genotypes and disease indicators and under the assumption of multiplicative combined effects of SNPs (PRS_M) and of additive combined effects (PRS_A). For calculation of PRS_M and PRS_A, we weighted each risk allele by the strength of the association (relative risk estimate from log additive models) obtained from external, independent GWAS or GWAS validation studies (Web Table 2). The expected number of cases from multiplicative and additive models was compared with the observed number of cases within each observed count of risk alleles. Participants with fewer than 10 risk alleles (n = 9) were assigned a value of 10, and participants with more than 28 risk alleles (n = 4) were assigned a value of 28, to ensure adequate numbers in each cell. We assessed the goodness of fit of the multiplicative model by comparing a model containing counts of risk alleles as indicator variables with a model in which the β estimate for log(PRS_M) was constrained to 1 using the likelihood ratio test. The goodness of fit for the additive model was calculated similarly.

We estimated allele-count-specific 1-year risks via Bayes’ theorem (50, 51) and 95% confidence intervals for 50-year-old non-Hispanic white females, using relative risks estimated from the BPC3 case-control data and assuming the average annual breast cancer incidence rate to be 200 per 100,000 women (approximated from Surveillance, Epidemiology, and End Results data (52)). These values were then compared with predicted absolute risks for each study participant, calculated under the assumptions of multiplicative joint effects (using PRS_M) and additive joint effects (using PRS_A).

All statistical inferences were made using 2-sided tests. Statistical analyses were conducted using R, version 2.13.1 (R Foundation for Statistical Computing, Vienna, Austria), and STATA/SE, version 11.2 (StataCorp LP, College Station, Texas).

RESULTS

Web Table 1 shows average age, stage at diagnosis, and tumor characteristics (ER status and progesterone receptor status) for the 10,146 case participants, by cohort. The average age at diagnosis was lower in the Nurses’ Health Study II cohort (47.6 years, as compared with 61.3 years for all cohorts combined), because it is predominantly a cohort of premenopausal females (67% premenopausal, compared with 23% in all other cohorts combined). Our study population included a total of 2,540 cases of advanced breast cancer and 1,563 cases of ER-negative breast cancer.

Table 1 shows the associations between the 23 selected SNPs and breast cancer and ER-negative breast cancer. Seventeen SNPs (including 1 of the 4 ER-negative SNPs) were statistically significantly associated with breast cancer. All statistically significant associations were comparable in magnitude and direction with those reported in previous literature. We did not see a statistically significant association for 3 of the 19 breast cancer SNPs (rs2380205/10p15.1 (intergenic); rs909116/LSP1; rs6504950/cytochrome C oxidase assembly homolog 11 (COX11)). Five SNPs, including 2 of the 4 ER-negative SNPs, showed an association with ER-negative breast cancer (Table 1). The associations of the selected nongenetic risk factors with breast cancer and with ER-negative breast cancer are reported in Web Table 3.

RERI point estimates and 95% confidence intervals for the 240 pairwise SNP-exposure combinations are shown in Web Table 4, and Q-Q plots are shown in Web Figure 1. Five SNP-exposure additive interactions with unadjusted P values less than 0.005 were observed, of which 3 involved a SNP in the DNA repair protein RAD51 homolog 2 gene (RAD51L1), rs10483813. After family-wise error rate correction, departure from additivity on the absolute risk scale was observed for this RAD51L1 SNP and BMI (BMI <30 vs. BMI ≥30; RERI = 0.49 (95% confidence interval: 0.26, 0.73); unadjusted P = 4.51 × 10⁻⁵, family-wise error rate-corrected P = 0.011). To preserve consistency of interpretation across several measures of additive interaction (53), we recoded the reference category based on the lowest risk stratum in the joint-effects model (Web Table 5). We observed main-effects odds ratios greater than 1 for the TA/TT genotype as well as BMI <30; however, the estimated increase in absolute risk of breast cancer among persons with BMI <30 and the TA/TT genotype was less than expected by addition of the excess risk due to BMI reduction alone or by TA/TT genotype alone: RERI = −0.95 (95% confidence interval: −1.77, −0.12). We observed an inverse association between BMI and breast cancer risk among women with the rs10483813 AA genotype but not among women with the TA or TT genotype (Tables 2 and 3). This interaction pattern did not change substantially within strata of menopausal status or family history (Web Table 6). We note that the risk allele for rs10483813 is quite common (minor allele frequency = 0.23), so the reference category (women homozygous for the reference allele and with BMI ≥30) was rather small (n = 148; 0.9% of total). This suggests that this interaction may have been a false-positive finding due to low power or to statistical properties of the RERI in small samples.

Table 2.

Relative Excess Risk of Breast Cancer Due to Interaction^a Between the RAD51L1 Single-Nucleotide Polymorphism rs10483813 and Body Mass Index in the Breast and Prostate Cancer Cohort Consortium

rs10483813b Genotype	Genotype Frequency	Body Mass Indexc
		<25				25–<30				≥30
		No. of Cases	No. of Controls	OR	95% CI	No. of Cases	No. of Controls	OR	95% CI	No. of Cases	No. of Controls	OR	95% CI
AA	0.056	180	287	1.00	Referent	110	186	0.92	0.68, 1.24	34	114	0.50	0.33, 0.78
TA	0.347	1,153	1,725	1.05	0.86, 1.29	774	1,086	1.12d	0.90, 1.38	378	560	1.07e	0.85, 1.35
TT	0.598	2,122	2,933	1.15	0.95, 1.40	1,286	1,755	1.15f	0.94,1.40	724	971	1.18g	0.95, 1.46

Abbreviations: CI, confidence interval; OR, odds ratio; RAD51L1, DNA repair protein RAD51 homolog 2 gene; RERI, relative excess risk due to interaction.

^a The RERI is a measure of departure from additivity on the absolute risk scale. RERIs and 95% CIs were calculated using unconditional logistic regression models adjusting for age at baseline (5-year intervals) and cohort.

^b Some cohort studies genotyped the proxy single-nucleotide polymorphism rs999737 for rs10483813 (r² = 1 in the HapMap CEU population (65)). The T allele is the risk allele for rs10483813, and the A allele is the protective allele (4). The P value for multiplicative interaction between rs10483813 and body mass index was 0.002. Synergy indices for interaction between rs10483813 and body mass index were undefined using this reference category.

^c Weight (kg)/height (m)²; categorized into 3 levels based on the World Health Organization classification (66).

^d RERI = 0.15 (95% CI: −0.15, 0.45); P-RERI = 0.335.

^e RERI = 0.52 (95% CI: 0.25, 0.79); P-RERI = 0.000168.

^f RERI = 0.08 (95% CI: −0.21, 0.38); P-RERI = 0.603.

^g RERI = 0.52 (95% CI: 0.22, 0.82); P-RERI = 0.000621.

Table 3.

Relative Excess Risk of Breast Cancer Due to Interaction^a Between the RAD51L1 Single-Nucleotide Polymorphism rs10483813 and Body Mass Index After Designation of the Lowest Risk Category (Body Mass Index ≥30 and AA Genotype) as the Reference Category in the Breast and Prostate Cancer Cohort Consortium

rs10483813b Genotype	Body Mass Indexc
	≥30		≥25–<30		<25
	OR	95% CI	OR	95% CI	OR	95% CI
AA	1.00	Referent	1.81	1.15, 2.85	1.98	1.29, 3.04
TA	2.13	1.42, 3.20	2.21d	1.48, 3.29	2.08e	1.41, 3.09
TT	2.33	1.57, 3.47	2.27f	1.54, 3.37	2.29g	1.55, 3.38

Abbreviations: CI, confidence interval; OR, odds ratio; RAD51L1, DNA repair protein RAD51 homolog 2 gene; RERI, relative excess risk due to interaction.

^a The RERI is a measure of departure from additivity on the absolute risk scale. RERIs and 95% CIs were calculated using unconditional logistic regression models adjusting for age at baseline (5-year intervals) and cohort.

^b Some cohort studies genotyped the proxy single-nucleotide polymorphism rs999737 for rs10483813 (r² = 1 in the HapMap CEU population (65)). The T allele is the risk allele for rs10483813, and the A allele is the protective allele (4). The P value for multiplicative interaction between rs10483813 and body mass index was 0.002.

^c Weight (kg)/height (m)²; categorized into 3 levels based on the World Health Organization classification (66).

^d RERI = −0.73 (95% CI:−1.6, 0.14); P-RERI = 0.097; synergy index = 0.62 (95% CI: 0.45, 0.86).

^e RERI = −1.02 (95% CI: −1.95, −0.101); P-RERI = 0.030; synergy index = 0.51 (95% CI: 0.40, 0.67).

^f RERI = −0.87 (95% CI: −1.76, 0.015); P-RERI = 0.054; synergy index = 0.59 (95% CI: 0.45, 0.78).

^g RERI = −1.03 (95% CI: −1.91, −0.14); P-RERI = 0.023; synergy index = 0.56 (95% CI: 0.43, 0.73).

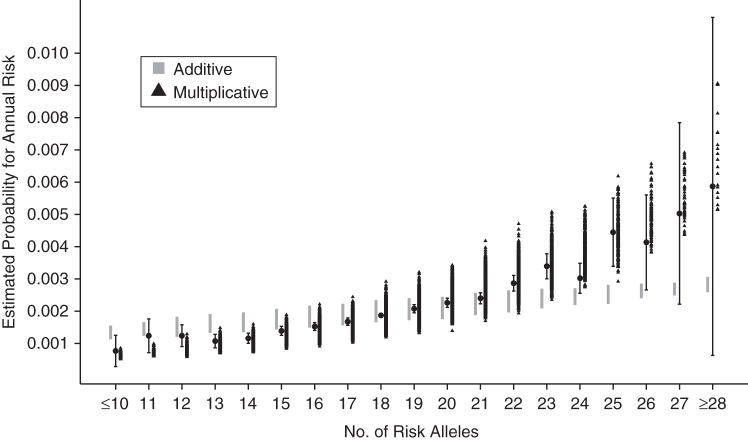
When comparing risks predicted on the basis of a PRS using external weights with the observed data in the BPC3, there was evidence of departure of the observed data from additivity (P < 10⁻¹⁵) as well as from multiplicativity (P = 0.0027) (Table 4). This departure was in the direction of submultiplicative but supra-additive effects (Figure 1), and it did not change substantially within the 3 strata of modified Gail score (Web Figures 2–4). Therefore, based on the comparison of the assessed goodness of fit with respect to a full model containing counts of risk alleles as indicator variables, the multiplicative model was a substantially better fit for the empirical data than the additive model.

Table 4.

Expected and Observed Numbers of Breast Cancer Cases Under Additive and Multiplicative Joint-Effects Model Assumptions in the Breast and Prostate Cancer Cohort Consortium

No. of Risk Alleles	No. of Cases Expected (Additive Model)	No. of Cases Observed	No. of Cases Expected (Multiplicative Model)
≤10	15.5	11	9.3
11	30.4	28	19.8
12	73.5	67	50.9
13	152.4	124	111.5
14	329.7	268	255.9
15	559.0	495	460.1
16	873.3	796	757.9
17	1,158.8	1,085	1,061.0
18	1,382.9	1,354	1,328.8
19	1,398.8	1,414	1,412.0
20	1,298.5	1,340	1,369.5
21	1,087.7	1,132	1,196.1
22	808.5	896	924.0
23	480.3	561	569.2
24	275.9	299	337.1
25	126.5	161	159.9
26	58.8	69	75.4
27	24.7	32	33.0
≥28	10.8	14	14.7

Figure 1.

Estimated absolute risk of breast cancer according to number of risk alleles among 50-year-old non-Hispanic white females, derived using case-control data from the Breast and Prostate Cancer Cohort Consortium (19, 39) and population incidence rates from the Surveillance, Epidemiology, and End Results Program (52), and comparison with expected risk assuming multiplicative and additive joint-effects models. Bars, 95% confidence intervals.

DISCUSSION

In this large breast cancer consortium study with prospectively obtained risk factor data, we investigated departure from additive combined effects on an absolute risk scale of 23 susceptibility SNPs and 9 established risk factors in the risk of breast cancer. We observed evidence of additive interaction between BMI and a SNP in RAD51L1, rs10483813. BMI was inversely associated with breast cancer risk among women with the AA genotype but not among women who carried the T allele at rs10483813.

The biological mechanisms behind such an interaction, particularly the inverse association between BMI and breast cancer among persons with the AA genotype, are unclear. There is limited information about the functional significance of rs10483813 alleles. This SNP has been not been shown to have significantly different associations with different breast cancer subtypes (54) or to interact with ionizing radiation exposure (55). Vachon et al. (56) recently reported an inverse association between the rs10483813 A allele and mammographic density, after adjusting for age and BMI. Mammographic density—a measure of the proportion of nonfat breast tissue—is one of the strongest known risk factors for breast cancer and is also known to be inversely associated with BMI. Because this is the first report of an additive interaction between rs10483813 and BMI, to our knowledge, and because of the small numbers of cases and controls in some strata, these intriguing results could possibly be false-positive and should be replicated.

Our results regarding the RAD51L1 locus cannot be directly compared with other studies that have previously examined risk ratio heterogeneity between confirmed GWAS-identified SNPs and breast cancer risk, including 1 from the BPC3 (17–20). Campa et al. (19) and Nickels et al. (20) reported no departure from multiplicativity between BMI and the RAD51L1 locus. The other studies did not examine SNPs at this locus.

Although most large studies testing for interaction between GWAS-identified breast cancer risk alleles have not found any statistically significant multiplicative interactions, Nickels et al. (20) recently showed multiplicative interactions between SNPs at the LSP1 locus and number of births. Specifically, they found that the per-risk-allele odds ratio for rs3817198 increased with increasing number of births, from 1.03 among women with 1 birth to 1.26 among women with 4 or more births (P_trend = 2.4 × 10⁻⁶). We did not genotype rs3817198, but we did genotype another SNP at LSP1, rs909116 (r² = 0.33). In our sample, the trend was reversed and nonsignificant: The per-risk-allele odds ratios for women with 4 or more births and women with 1 birth were 1.03 and 1.14, respectively (P_trend = 0.43). The multiplicative trend interaction odds ratios (1.06 for Nickels et al. (20) and 0.98 for this study) were statistically significantly different (P < 0.001). These differences may be due to the relatively modest linkage disequilibrium between these 2 SNPs, or the interaction observed by Nickels et al. may not generalize to our sample.

Overall, the paucity of heterogeneity in odds ratios or risk differences for the combined effects of genes and exposures in breast cancer risk is consistent with supra-additive and submultiplicative effects of SNP-exposure combinations, which would reduce the power to detect differences from either side. Moreover, we tested only for 2-level interactions—pairwise for each genetic variant and each exposure—and specific higher-order interactions may have been missed because they were not investigated (although power to detect such interactions will typically be lower than for pairwise interactions). Due to the lack of strongly statistically significant interactions and the violation of monotonicity assumptions, strong public health recommendations as well as sufficient component-cause inferences could not be made from this study.

We also investigated whether an additive joint-effects model or a multiplicative joint-effects model is a better fit for empirical data on the combined effects of 19 confirmed breast cancer susceptibility loci. We found a statistically significant deviation from both the additive model and the multiplicative models, in the direction of submultiplicativity and supra-additivity. The heterogeneity of the observed data from the additive joint-effects model was very strong in magnitude and highly statistically significant.

Polygenic models used in disease risk prediction have generally assumed multiplicative joint effects of SNPs on the absolute risk scale. We find that a multiplicative model for the joint effects of multiple risk SNPs is substantially better than an additive model. This provides some support for the use of a multiplicative model based on individual-SNP marginal odds ratios, as has been suggested in the context of risk screening and implemented by several consumer genetics companies (24, 57–60).

However, the statistically significant submultiplicative deviation of empirical data from multiplicative effects leaves some scope for improvement. This deviation may reflect the fact that the external odds ratios used to define the multiplicative risk score were overestimated due to the “winner's curse” (61, 62). In sensitivity analyses where we adjusted all per-allele β coefficients by a constant deflation factor (adjusted β = 0.9 × unadjusted β) or by a factor proportional to the per-allele odds ratio (ranging from 0.92 to 0.997 (63)), the multiplicative model was a much better fit (goodness of fit: P = 0.99 for constant adjustment and P = 0.45 for proportional adjustment). This suggests that multiplicative risk models constructed using odds ratios from initial discovery publications are likely to be overestimates (or underestimates) in the upper (respectively lower) tails. However, when accurate odds ratio estimates from large studies independent of the original discovery samples are used, a multiplicative polygenic risk model may be a good fit, and this model could be utilized to identify a small number of women at markedly increased risk who would benefit from risk-reducing interventions or more intensive screening. We stress that risk estimates for women in the tails of the risk distribution are projections beyond the support of the bulk of the training data and that we had limited statistical power to detect departures from multiplicativity in the tails; note the wide confidence interval for the count ≥28 group in Figure 1.

Tests for pairwise interactions between the 23 SNPs failed to show statistically significant departures from additivity between these low-penetrance variants. This may reflect the low power to detect small departures from a pairwise additive risk model, even with our large sample size. The departure from an additive joint-effects model from the observed fitted risks for the combination of 19 SNPs suggests the presence of additive interactions between the SNPs and breast cancer risk.

This study had several other weaknesses. First, although data on exposure variables were prospectively collected in all of the cohorts, the instruments used to collect the information were not uniform across cohorts, potentially inducing exposure misclassification during harmonization. It has been demonstrated that nondifferential misclassification of 2 independent exposures preserves the validity of tests for additive interaction (64). Furthermore, for ease of interpretation of additive effects, these exposure variables were represented using dichotomized categories, which may not be the optimal modeling strategy for reflecting their biological associations with breast cancer. However, in most cases the cutoffs for exposure variables were not arbitrary, and a priori information was used to choose them. Similarly, genetic variants were also dichotomized assuming a dominant effect for the risk allele, without a priori evidence for the same. Our results for marginal effects of most of the SNPs were not substantially different from results of previous studies that assumed log-additive SNP effects. Moreover, adjustment for age and cohort may not have sufficiently controlled for the variability among the included studies. The calculation of exposure risk score (Gail score) could not be done in a manner that would allow for comparison with previous studies, because we did not have information on the number of biopsies for all study participants.

The results from our study are generalizable only to females of European descent, since participants who self-reported ethnicities other than non-Hispanic white were excluded from the analyses due to the limited sample size.

To our knowledge, this is one of the largest studies (10,146 cases and 12,760 controls) to have investigated interactions between known breast cancer risk factors and GWAS-identified susceptibility loci, and the first study to find additive interactions. In this study we also replicated previous associations of 23 known SNPs with breast cancer risk using the risk-dominant model. We did not observe strong evidence of 2-level additive interactions between SNPs and the established breast cancer risk factors, except for a statistically significantly protective association with rs10483813 in RAD51L1 among obese females. This study also showed that the multiplicative joint-effects model is a substantially better fit than the additive joint-effects model in the prediction of absolute risk of breast cancer.