Continuous removal of glycerol from frozen-thawed red blood cells in a microfluidic membrane device

Abstract

Cryopreservation of human red blood cells (RBCs) in the presence of 40% glycerol allows a shelf-life of 10 years, as opposed to only 6 weeks for refrigerated RBCs. Nonetheless, cryopreserved blood is rarely used in clinical therapy, in part because of the requirement for a time-consuming (∼1 h) post-thaw wash process to remove glycerol before the product can be used for transfusion. The current deglycerolization process involves a series of saline washes in an automated centrifuge, which gradually removes glycerol from the cells in order to prevent osmotic damage. We recently demonstrated that glycerol can be extracted in as little as 3 min without excessive osmotic damage if the composition of the extracellular solution is precisely controlled. Here, we explore the potential for carrying out rapid glycerol extraction using a membrane-based microfluidic device, with the ultimate goal of enabling inline washing of cryopreserved blood. To assist in experimental design and device optimization, we developed a mass transfer model that allows prediction of glycerol removal, as well as the resulting cell volume changes. Experimental measurements of solution composition and hemolysis at the device outlet are in reasonable agreement with model predictions, and our results demonstrate that it is possible to reduce the glycerol concentration by more than 50% in a single device without excessive hemolysis. Based on these promising results, we present a design for a multistage process that is predicted to safely remove glycerol from cryopreserved blood in less than 3 min.

I. INTRODUCTION

Each year over 100 million blood donations are collected worldwide, enabling millions of blood transfusions. The availability of this life-saving medical treatment requires careful management of the blood supply. Red blood cells (RBCs) are most commonly preserved through refrigeration, which permits a shelf-life of up to 6 weeks.¹ The short shelf-life of refrigerated blood creates logistical challenges, leading to problems with outdating and periodic inventory shortages.² Moreover, recent studies suggest that the acceptable refrigeration period may be even shorter, as transfusion of “older” blood has been linked to severe complications.^3,4

Cryopreservation has the potential to mitigate these logistical challenges by extending the product shelf-life from weeks to years. In North America, RBCs are routinely cryopreserved in the presence of 40% glycerol,¹ enabling an FDA approved shelf-life of 10 years. This procedure yields good cell recovery, and recent evidence indicates that cryopreserved RBCs have superior biochemical profile and tissue oxygenation capabilities compared with refrigerated RBCs.^5,6 Nonetheless, cryopreservation is currently only used for rare or autologous units, mainly because of the prohibitively time consuming post-thaw wash process required to remove the glycerol before the cells can be transfused.

The current deglycerolization process takes about 1 h per unit of blood and involves a series of washes with progressively decreasing saline concentrations in an automated centrifuge.^1,7,8 This method was empirically developed decades ago using the rationale that slow changes in solution composition would minimize damage from osmotically induced cell volume changes.⁹ However, RBCs are well-known to be highly permeable to glycerol,^10–12 and theoretical predictions suggest that the deglycerolization process can be safely completed in less than 20 s, as long as the extracellular solution composition is appropriately controlled.¹³ We recently tested this idea by diluting a blood sample with saline solution in multiple steps while carefully controlling the timing of each step to avoid osmotic damage. Our results demonstrate that the deglycerolization process can be completed in 3 min with less than 20% hemolysis, meeting AABB standards for in vitro cell recovery.¹³

This dramatic reduction in deglycerolization time requires control over the solution composition at a time scale of seconds, and such precise control is not possible using centrifugal cell washers. Microfluidic devices allow control over fluid flow and mass transfer at the microscale,^14,15 offering the potential for precisely controlling the solution composition during glycerol removal. Microfluidic devices have previously been investigated for post-thaw washing of cryopreserved cells^16–19 but not for removal of glycerol from blood. In addition, dialysis or filtration cartridges containing microscale hollow fibers have been investigated for RBC deglycerolization.^20–22 However, these studies did not attempt inline glycerol removal and they did not optimize the methods for time efficiency.

In this study, we examine the potential for RBC deglycerolization using a microfluidic device consisting of two microchannels separated by a dialysis membrane. We present a mathematical model describing mass transfer within the device and show that the predictions are consistent with experimental measurements of solution composition and hemolysis at the device outlet. We then use the mathematical model to design a multistage deglycerolization process that theoretically allows inline removal of glycerol in less than 3 min. Our results pave the way for development of a clinical device for ultra-rapid glycerol extraction, which would greatly improve the logistics of blood banking.

II. MATERIALS AND METHODS

A. Device fabrication

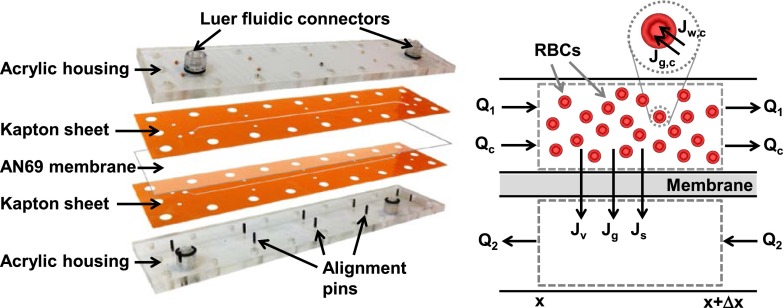
The microfluidic device is illustrated in Fig. 1 (left). It consists of a two laser-patterned Kapton® sheets, an AN69 hemodialysis membrane, and a clear acrylic housing. The channel design was first sketched in Solidworks® and then laser patterned into the Kapton® sheets using an ESI Model 5330 UV Laser μVIA Drill (Portland, OR, USA). The target channel width and length were 400 μm and 15 cm, respectively. The channels were cut into 50 μm and 130 μm thick Kapton® sheets to enable the creation of two devices with the different channel depths. The housing was fabricated by machining ¼ in. thick acrylic plates to create screw holes aligning with the Kapton® sheets. Pins fashioned in the housing as well as the Kapton® sheets were used to ensure proper alignment of the channels when the device was assembled. Ports to introduce fluid into the device were made using Luer fittings.

FIG. 1.

Membrane-based microfluidic device. Left: exploded view of the device. Right: differential volume element used for development of mathematical model.

B. Mathematical model

To assist in selecting appropriate operating conditions for the microfluidic device, a mathematical model was developed to predict the transport of water, glycerol, sodium chloride, and the resulting cell volume changes. The system was divided into three different domains—the cell stream, the extracellular solution stream, and the wash stream—as illustrated in Fig. 1 (right). Mass transfer in the three domains was modeled using differential equations derived from solute and volume balances. Detailed derivation of the model equations can be found in the electronic supplementary material.²³ Nomenclature and parameter values are given in Table I.

TABLE I.

Nomenclature.

Symbol	Definition	Units	Value
$J_{w,c}$	Water flux across cell membrane	m/s	Variable
$J_{g,c}$	Glycerol flux across cell membrane	mol m−2 s−1	Variable
$J_v$	Solution flux across AN69 membrane	m/s	Variable
$J_g$	Glycerol flux across AN69 membrane	mol m−2 s−1	Variable
$J_s$	Sodium chloride flux across AN69 membrane	mol m−2 s−1	Variable
C	Concentration	mol/m3	Variable
Q	Flow rate	m3/s	Variable
P	Pressure	Pa	Variable
g	Glycerol, subscript	…	…
s	Sodium chloride, subscript	…	…
c	Cell stream, subscript	…	…
1	Extracellular stream, subscript	…	…
2	Wash stream, subscript	…	…
$M_{s,c}$	Osmolarity of intracellular salts	osmol/m3	Variable
${\dot{n}}_c$	Cell flow rate	cells/s	Variable
ns,c	Osmoles salts per cell	osmol/cell	2.0 × 10−14
Vb	Osmotically inactive cell volume	m3	2.7 × 10−17
Ac	Cell surface area	m2	1.3 × 10−10
Lp,c	Hydraulic permeability of cell membrane	m Pa−1 s−1	1.5 × 10−12
Pg,c	Glycerol permeability of cell membrane	m/s	3.0 × 10−8
Lp	Hydraulic permeability of AN69 membrane	m Pa−1 s−1	Variable
Pg	Glycerol permeability of AN69 membrane	m/s	Variable
Ps	Sodium chloride permeability of AN69 membrane	m/s	6.5 × 10−6
σg	Glycerol reflection coefficient	…	0.009
μ	Viscosity	Pa·s	Variable
W	Channel width	m	350 × 10−6
H	Channel height	m	(50 or 130) × 10−6
R	Gas constant	J mol−1 K−1	8.314
T	Temperature	K	295
vg	Molar volume of glycerol	m3/mol	7.1 × 10−5

1. Cell membrane transport

Water and glycerol are predominantly transported through the membrane of human RBCs using separate pathways.^24,25 Therefore, we used a two parameter model to describe water and glycerol flux across the RBC membrane²⁶

$$\begin{array}{c}{J}_{w,c}=L_{p,c}RT(C_{g,c}+M_{s,c}-C_{g,1}-2C_{s,1}),\\ J_{g,c}=P_{g,c}(C_{g,1}-C_{g,c}).\end{array}$$ (1)

The relative permeability of the components of salts to the RBC membrane is six orders of magnitude less than that of glycerol.²⁷ Thus, in this study, the RBC membrane was assumed to be impermeable to salts.

2. Transport across the AN69 membrane

In the AN69 membrane, water and solutes are transported through the same pores. Therefore, the most appropriate mass transfer model is the Kedem-Katchalsky formalism, which incorporates a solute-solvent interaction term or reflection coefficient, σ.²⁸ This model was used to predict the volume flux of solution and molar fluxes of glycerol and sodium chloride across the AN69 membrane

$$\begin{array}{c}{J}_v=L_p[(P_1-P_2)-{\sigma }_{g}RT(C_{g,1}-C_{g,2})],\\ J_g=C_{m,g}{J}_v(1-{\sigma }_g)+P_g(C_{g,1}-C_{g,2}),\\ J_s=C_{m,s}{J}_v+P_s(C_{s,1}-C_{s,2}),\end{array}$$ (2)

where C_m is the effective intramembrane solute concentration, which was obtained by integration of the local solute flux between the membrane edges, as described previously.^29,30

3. Volume balances

The flux equations (systems 1 and 2) were used to predict the rate of volume transfer between streams, resulting in the following differential equations describing the volumetric flow rates of each stream:

$$\begin{array}{c}\frac{d{Q}_c}{\mathit{d}\mathit{x}}=(J_{g,c}{\upsilon }_g+J_{w,c})\frac{A_c{\dot{n}}_{c}WH}{Q_1+Q_c},\\ \frac{d{Q}_1}{\mathit{d}\mathit{x}}=-(J_{g,c}{\upsilon }_g+J_{w,c})\frac{A_c{\dot{n}}_{c}WH}{Q_1+Q_c}-J_{v}W,\\ \frac{d{Q}_2}{\mathit{d}\mathit{x}}=-J_{v}W.\end{array}$$ (3)

The volume of individual cells flowing through the channel can be determined by dividing the volumetric flow rate of the cell stream ($Q_c$) by the cell flow rate (${\dot{n}}_c$).

4. Solute balances

The flux equations were used to derive differential equations describing the concentration of glycerol in each stream, resulting in

$$\begin{array}{c}\frac{d{C}_{g,c}}{\mathit{d}\mathit{x}}=\frac{1}{Q_c-{\dot{n}}_c{V}_b}\left(J_{g,c}\frac{A_c{\dot{n}}_{c}WH}{Q_c+Q_1}-C_{g,c}\frac{d{Q}_c}{\mathit{d}\mathit{x}}\right),\\ \frac{d{C}_{g,1}}{\mathit{d}\mathit{x}}=-\frac{1}{Q_1}\left(J_{g,c}\frac{A_c{\dot{n}}_{c}WH}{Q_c+Q_1}+J_{g}W+C_{g,1}\frac{d{Q}_1}{\mathit{d}\mathit{x}}\right),\\ \frac{d{C}_{g,2}}{\mathit{d}\mathit{x}}=-\frac{1}{Q_2}\left(J_{g}W+C_{g,2}\frac{d{Q}_2}{\mathit{d}\mathit{x}}\right).\end{array}$$ (4)

Because salts were considered to be impermeable to the RBC membrane, the osmoles of salts per cell (n_s,c) are constant and the intracellular salt concentration can be calculated by dividing n_s,c by the osmotically active cell volume

$$M_{s,c}=\frac{n_{s,c}}{(Q_c/{\dot{n}}_c-V_b)}.$$ (5)

The osmolarity of intracellular salts ($M_{s,c}$) refers to the combined osmotic contribution of all intracellular salts, including sodium, potassium, calcium, magnesium, chloride, etc.

The salts in the extracellular solution and wash streams are almost entirely made up of sodium chloride (with a small amount of phosphate buffer). Sodium chloride balances on the extracellular solution and wash streams result in

$$\begin{array}{c}\frac{d{C}_{s,1}}{\mathit{d}\mathit{x}}=-\frac{1}{Q_1}\left(J_{s}W+C_{s,1}\frac{d{Q}_1}{\mathit{d}\mathit{x}}\right),\\ \frac{d{C}_{s,2}}{\mathit{d}\mathit{x}}=-\frac{1}{Q_2}\left(J_{s}W+C_{s,2}\frac{d{Q}_2}{\mathit{d}\mathit{x}}\right).\end{array}$$ (6)

5. Pressure drop

The pressure in each stream was estimated using a published pressure drop equation for a rectangular channel.³¹ The cell and the extracellular solution were modeled as a combined stream and the viscosity of this stream was approximated using the composition of the extracellular solution, neglecting the effects of cells. The resulting differential equations for the combined stream and the wash stream are

$$\begin{array}{c}\frac{d{P}_1}{\mathit{d}\mathit{x}}=\frac{4{\mu }_1(Q_1+Q_c)}{W{H}^3}{\left(\frac{1}{3}-\frac{64H}{{\pi }^{5}W}\text{tanh}\frac{\pi W}{2H}\right)}^{-1},\\ \frac{d{P}_2}{\mathit{d}\mathit{x}}=\frac{4{\mu }_2{Q}_2}{W{H}^3}{\left(\frac{1}{3}-\frac{64H}{{\pi }^{5}W}\text{tanh}\frac{\pi W}{2H}\right)}^{-1}.\end{array}$$ (7)

C. Numerical simulation method

The differential equations were solved numerically in MATLAB® using the built-in function ode45. The boundary conditions were determined as follows. The cell and extracellular solution streams were assumed to be in equilibrium at the device inlet (x = 0), allowing C_g,c = C_g,1 and M_s,c = 2C_s,1 to be determined from the inlet solution composition. The total volumetric flow rate at the inlet was set by the syringe pump; the fraction of this volumetric flow rate owing to cells (Q_c) was determined by multiplying by the measured hematocrit. The cell flow rate (${\dot{n}}_c$) was determined by dividing this value of Q_c by the cell volume at the inlet (i.e., ${\dot{n}}_c=Q_c/V_c$, where V_c = V_b + n_s,c/M_s,c). At the wash stream inlet (x = L), the concentrations C_g,2 and C_s,2 were determined from the solution composition and the flow rate Q₂ was set by the syringe pump. The pressure was assumed atmospheric at the device outlets (x = L for the cell and extracellular streams; x = 0 for the wash stream). Because the device is operated using a countercurrent configuration, some boundary conditions are known at x = L, but not at x = 0. To solve the model, initial guesses for the unknown boundary conditions at x = 0 were set, and the MATLAB® function fminsearch was used to iteratively revise the initial guesses until the model prediction at x = L matched the known target values. This solution strategy is similar to the shooting method which has been used previously to predict heat transfer parameters in countercurrent heat exchangers.³²

D. Collection, glycerolization, freezing, and thawing of RBCs

Whole blood from participating volunteers was collected into citrate phosphate dextrose vacutainers using an IRB approved protocol. Packed RBCs were isolated from whole blood and used for preparation of the experimental samples. To prepare fresh RBCs, the packed cells were simply resuspended in isotonic saline to achieve the desired hematocrit. To prepare RBCs in 10% w/v glycerol, 1.25 ml of a relatively concentrated glycerol solution (16% w/v glycerol and 0.9% w/v saline solution) was added dropwise to 5 g of packed cells over 3 min, the sample was allowed to equilibrate for 5 min, and an additional 6.25 ml of the concentrated glycerol solution was added dropwise over 3 min. The hematocrit of the resulting solution was adjusted to the desired value by addition of 10% w/v glycerol solution. Frozen-thawed RBCs in 40% w/v glycerol were prepared according to the procedure detailed in our previous work.¹³ All solutions were buffered using 12.5 mM disodium phosphate and adjusted to a pH of 7.

E. Operation of the microfluidic device

To assemble the device, the membrane was laid between the two Kapton® sheets and placed in between the acrylic housing plates. The device was sealed by tightening screws around the perimeter of the housing to 80 cN-m using a torque wrench to ensure even pressure distribution around the plates. Syringes filled with the desired solutions were connected to the device using 0.02 in. ID Tygon® tubing and 20-gauge blunt dispensing needles. The syringes were then loaded onto syringe pumps (New Era Pump Systems, Farmingdale, NY, USA) to introduce fluids into the device. Before each experiment, the microfluidic device was flushed using a 2 g/l pluronic F108 solution (BASF, Florham Park, NJ, USA) to eliminate particle debris and air bubbles inside of the channels. The experimental solutions were then introduced. After establishment of steady-state, the effluents from the cell and the wash streams were collected and analyzed as described below. The device was reassembled with a fresh piece of AN69 membrane for each experiment.

F. Hemolysis measurement

A small volume of the cell stream effluent was used for measurement of hematocrit using a SpinCrit hematocrit centrifuge (Indianapolis, IN, USA). A portion of the sample was also diluted by 500 fold with ultrapure water to prepare the total hemoglobin standard. The remaining sample was centrifuged to separate the supernatant from the surviving cells. The concentration of free hemoglobin and the percent hemolysis were then estimated using the spectrophotometric method described by Han and colleagues.³³

G. Thermogravimetric analysis (TGA)

The mass fractions of water, glycerol, and sodium chloride in the supernatant were measured using a TGA instrument (TA Instruments, New Castle, DE, USA). The sample was first heated at 5 °C/min to 100 °C and held at that temperature for 15 min to allow evaporation of water. The sample was then heated at 10 °C/min to 290 °C and held for 10 min to allow evaporation of glycerol. The remaining solid mass left at the end of the procedure is sodium chloride and soluble intracellular contents released into the supernatant from damaged cells. The concentration of sodium chloride was obtained by subtracting the hemoglobin concentration (as determined using the hemolysis assay) from the total solids concentration. Experimental results confirming the accuracy of the TGA method are presented in the electronic supplementary material.²³

H. Comparison of model predictions and experimental results

The model allows predictions of the conditions in each stream at the device outlet. However, as equilibrium has yet to be reached, mass transfer will continue to occur between the cells and the extracellular solution after they exit the device. The TGA results reflect the concentrations of solutes after the cells have reached equilibrium with the extracellular solution. Thus, all experimentally measured solute concentrations were compared with the predicted equilibrium concentrations, as calculated using the predicted outlet composition.

I. Statistical analysis

All experimental data are reported as averages of three replicates. Each replicate was carried out with cells originating from different donors. Error bars show the standard error of the mean. Statistical analyses of the mechanical fragility control experiments were done using t-tests. All other analyses were done using analysis of variance (ANOVA), followed by Fisher's least significant difference tests for pairwise comparisons. Differences were considered to be significant at a 95% confidence level. All statistical analyses were performed using StatGraphics software.

III. RESULTS AND DISCUSSION

A. Mechanical fragility control experiments

The microfluidic deglycerolization process subjects the cells to potentially damaging osmotic stresses, as well as mechanical stresses caused by shear and interactions with solid surfaces within the microfluidic channel. To isolate the effects of mechanical damage from osmotic damage, we perfused RBCs countercurrent to an isosmotic wash solution. These control experiments were performed at the highest flow rates used in subsequent deglycerolization experiments in order to establish an upper limit for mechanical damage.

We first investigated mechanical damage to fresh RBCs by perfusing the cells through the 130 μm thick channel at a fluid velocity of 6.1 cm/s, using isotonic saline as the wash solution. These flow conditions—which correspond to a maximum apparent shear stress³⁴ of approximately 25 dynes/cm²—resulted in a slight but statistically insignificant increase in hemolysis from 0.17% ± 0.02% at the device inlet to 0.69% ± 0.36% at the outlet (p = 0.22). The low hemolysis observed under these conditions is consistent with the previous studies of shear-induced damage to RBCs, which report a threshold of approximately 1500 dynes/cm² above which significant hemolysis occurs.^35,36

Because cryopreservation of RBCs can heighten sensitivity to mechanical stresses,³⁷ we also performed control experiments for frozen-thawed RBCs in 40% glycerol using a wash solution with the same composition. We first subjected the frozen-thawed RBCs to the same flow conditions as described above, corresponding in this case to a slightly higher maximum apparent shear stress of 100 dynes/cm² due to the increased solution viscosity. These flow conditions resulted in a statistically insignificant increase in hemolysis from 2.8% ± 1.3% to 3.2% ± 1.4% (p = 0.84). We also perfused frozen-thawed RBCs through the 50 μm thick channel at a velocity of 4.0 cm/s, which corresponds to a maximum apparent shear stress of 170 dynes/cm². The cells used in these experiments had a starting hemolysis of 5.3% ± 1.9% and an ending hemolysis of 7.7% ± 1.4%. Once again, the increase in hemolysis was not statistically significant (p = 0.34). The results of these experiments confirm that RBCs can be flowed through the device without incurring excessive membrane damage from mechanical stresses.

B. Glycerol removal

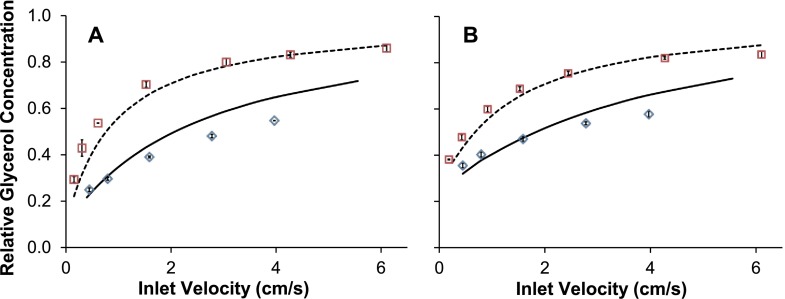
To facilitate the design of a microfluidic deglycerolization process, we developed a mathematical model for predicting mass transfer and the resulting cell volume changes within the device. Experiments were conducted over a range of operating conditions to validate the model. Fig. 2 shows the relative glycerol concentration at the device outlet as a function of inlet fluid velocity for two different channel heights (130 μm and 50 μm) and for two different inlet concentrations: RBCs in 10% glycerol (panel (a)) and frozen-thawed RBCs in 40% glycerol (panel (b)). In general, the relative glycerol concentrations at the outlet decreased with flow velocity, consistent with the expected increase in glycerol removal as fluid residence time in the device increases. The extent of glycerol removal was also higher for the shallower channel, which is consistent with the expected intensification of mass transfer as surface-area-to-volume ratio increases. The predicted relative glycerol concentrations are in reasonable agreement with the experimental data for the 130 μm channel but show slight discrepancies for the 50 μm channel, especially for faster fluid velocities. This deviation could be caused by several factors. The channel depth used in model simulations was 50 μm, but manufacturer's specifications for the Kapton® sheet indicate tolerances of ±8 μm. Simulations using a reduced channel height would increase mass transfer, decreasing the discrepancy between model predictions and experimental results at high fluid velocities. Additionally, fluid flow through the 50 μm channel would result in a relatively high pressure drop, particularly for higher fluid velocities. High pressures within the device may have caused the fluid to bleed from the confinement of the channel, resulting in an increase in the area available for mass transfer and a concomitant increase in glycerol removal. Despite the slight discrepancies, the model predictions match the general trends in the data with reasonable accuracy.

FIG. 2.

Glycerol removal in the microfluidic device. (a) RBCs in 10% glycerol, isotonic saline wash. (b) Frozen-thawed RBCs in 40% glycerol, 3.4% saline wash. The relative glycerol concentration was calculated by normalizing the outlet glycerol concentration to the inlet glycerol concentration. Squares and diamonds are data points obtained from experiments conducted in the 130 and 50 μm device, respectively. The corresponding model predictions are represented by the dashed and solid lines, respectively.

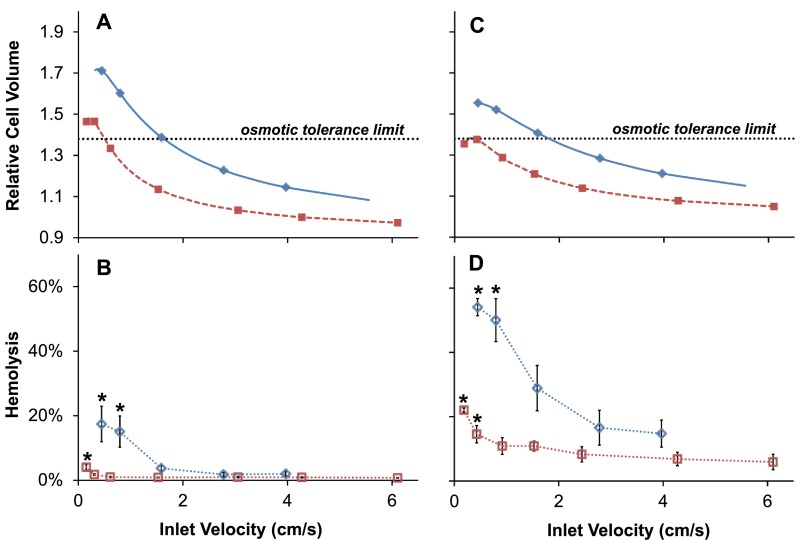
C. Measured hemolysis and predicted cell volumes

The removal of glycerol from the extracellular medium creates an osmotic imbalance that drives water influx and concomitant cell swelling, resulting in a maximum cell volume at the device outlet. Fig. 3(a) shows the predicted cell volume at the device outlet for RBCs glycerolized to 10% w/v. In general, the extent of cell swelling is predicted to increase under conditions that result in increased glycerol removal; the maximum cell volume is higher for low fluid velocities and low channel heights. RBCs are known to undergo hemolysis if their volume exceeds a maximum threshold, known as the osmotic tolerance limit.^38,39 As shown in Fig. 3(a), the cell volume is predicted to exceed the osmotic tolerance limit for the two slowest fluid velocities tested in the 130 μm channel and the three slowest fluid velocities in the 50 μm channel.

FIG. 3.

Cell volume predictions and corresponding hemolysis measurements. (a) and (b) show results for RBCs in 10% glycerol. (c) and (d) show results for frozen-thawed RBCs in 40% glycerol. Squares and diamonds are data points obtained from experiments conducted in the 130 and 50 μm device, respectively. Asterisks indicate a statistically significant difference compared with the fastest fluid velocity.

In Fig. 3(b), we compare these cell volume predictions with the measured hemolysis at the device outlet. Hemolysis was higher for the 50 μm channel than for the 130 μm channel, and hemolysis was observed to increase with decreasing fluid velocity, consistent with the cell volume predictions shown in Fig. 3(a). For both the 130 μm and 50 μm channels, fluid velocity had a significant effect on hemolysis (p = 0.0008 and p = 0.015, respectively). Pairwise comparisons revealed that hemolysis was significantly higher for the slowest fluid velocity in the 130 μm channel and the two slowest fluid velocities in the 50 μm channel.

Predicted cell volume changes and the corresponding hemolysis values for experiments with the frozen-thawed RBCs in 40% glycerol are presented in Figs. 3(c) and 3(d), respectively. The cell volume is predicted to exceed the osmotic tolerance limit for the three slowest fluid velocities in the 50 μm channel and approximately reaches the osmotic tolerance limit for the two slowest velocities in the 130 μm channel. Hemolysis measurements were consistent with these predictions. Fluid velocity was found to have a significant effect on hemolysis (p = 0.0018 and p = 0.0041 for the 130 μm and 50 μm channels, respectively), and pairwise comparisons showed that hemolysis was significantly higher for the two slowest velocities in both the 130 μm and 50 μm channels.

The overall amount of hemolysis was higher in experiments with frozen-thawed RBCs in 40% glycerol than unfrozen RBCs in 10% glycerol despite lower predicted cell volumes. The increased hemolysis may be due to increased sensitivity to osmotic and mechanical stresses caused by freezing and thawing. Another possible explanation is underestimation of the predicted cell volume due to inaccuracy in the assumed value of the cell membrane glycerol permeability. Published values of P_g,c vary by more than an order of magnitude,^10–12 and in some studies P_g,c has been found to decrease with increasing glycerol concentration.¹¹ The use of a lower P_g,c would increase the predicted cell volume at the device outlet, particularly for slower fluid velocities, which may explain the higher hemolysis values observed for frozen-thawed RBCs in 40% glycerol.

D. Transport of sodium chloride

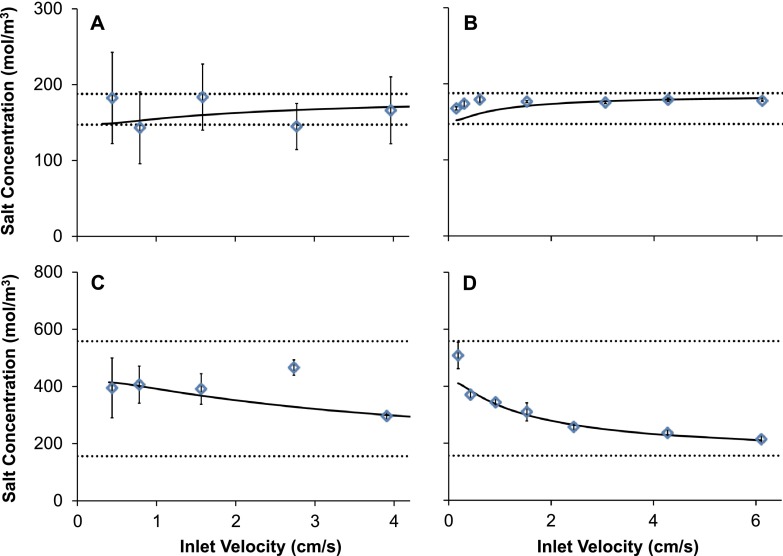
The amount of swelling the cells endure, particularly for slow velocities, can be easily controlled by increasing the saline concentration in the wash stream. This is because transport of sodium chloride across the AN69 membrane increases the osmotic strength of the extracellular solution, which opposes influx of water into the cells. Therefore, the ability to predict sodium chloride transport in the device is particularly important for designing a washing procedure that avoids damaging osmotically induced changes in cell volume.

The experimentally measured concentration of sodium chloride at the outlet is compared to model predictions in Fig. 4. In general, the model predictions are in reasonable agreement with the experimental data. For experiments with RBCs in 10% glycerol (panels (a) and (b)), the sodium chloride concentration remained approximately constant for all velocities tested. This was expected because the sodium chloride concentrations in the RBC stream and the wash stream were approximately equal in this case. However, in the case of frozen-thawed RBCs in 40% glycerol (panels (c) and (d)), substantial transport of sodium chloride from the wash stream to the RBC stream was observed. The sodium chloride concentration was higher at the RBC stream outlet, and the results show an increase in the outlet concentration with decreasing fluid velocity. This is consistent with the increased time available for mass transfer at slow velocities.

FIG. 4.

Sodium chloride concentration in the RBC stream effluent. (a) and (b) show results for RBCs in 10% glycerol using the 50 and 130 μm device, respectively. (c) and (d) show results for frozen-thawed RBCs in 40% glycerol using the 50 and 130 μm device, respectively. Solid lines show predicted sodium chloride concentrations in the RBC stream effluent and dotted lines show the inlet concentrations in the RBC and wash streams.

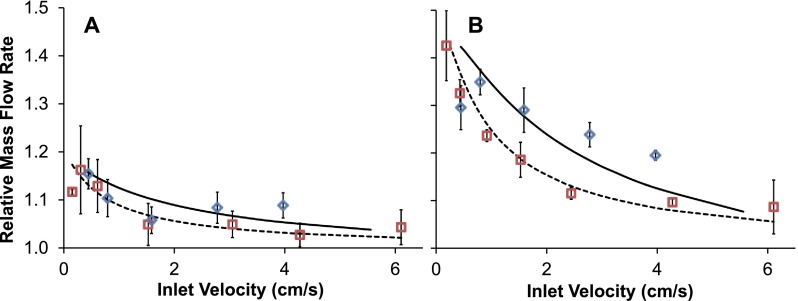
E. Effect of reflection coefficient

As shown in Fig. 5, the mass flow rate of the cell stream was higher at the outlet than the inlet, and the relative increase in flow rate became more pronounced with decreasing fluid velocity. This effect is consistent with model predictions and can be explained in terms of the glycerol reflection coefficient. Partial exclusion of glycerol from the AN69 membrane pores leads to a relatively low pressure inside the pore on the side of the membrane with the higher glycerol concentration. This drives flow of solution through the membrane pores towards the glycerol-rich stream. Reflection coefficients for small cryoprotectants like glycerol and dimethyl sulfoxide have previously been neglected from the solution flux equation when modeling mass transfer through hemodialysis membranes, as it is assumed that these molecules are small enough to pass through the membrane pores unhindered.²⁰ Although the glycerol reflection coefficient for the AN69 membrane is nearly zero, its effect on mass transfer is considerable when highly concentrated glycerol solutions are used and therefore cannot be neglected.

FIG. 5.

Mass flow rate of the cell stream at the device outlet. (a) RBCs in 10% glycerol, isotonic saline wash. (b) Frozen-thawed RBCs in 40% glycerol, 3.4% saline wash. The relative mass flow rate was calculated by taking the ratio of the cell stream mass flow rates at the outlet and inlet. Squares and diamonds are data points obtained from experiments conducted in the 130 μm and 50 μm device, respectively. The corresponding model predictions are represented by the dotted and solid lines, respectively.

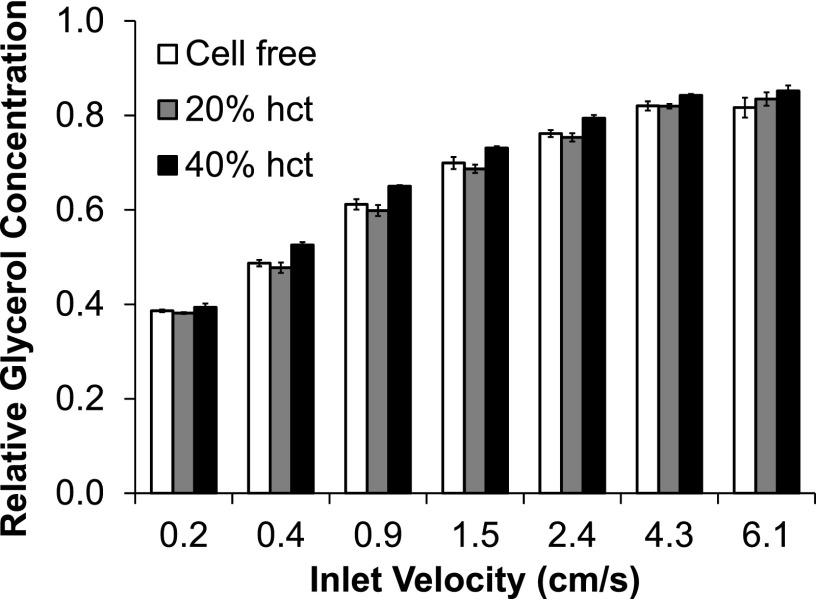
F. Effect of cell density on mass transfer

To examine the effects of cell density on the glycerol removal capabilities of the device, experiments were performed using frozen-thawed RBCs with hematocrits ranging from 0% to 40%. The results of these experiments are shown in Fig. 6. As expected, fluid velocity had a clear and statistically significant effect on the relative glycerol concentration at the device outlet (p < 0.0001). However, the effect of hematocrit was more subtle. Although statistical analysis revealed a significant effect of hematocrit (p < 0.0001), the relative glycerol concentrations were nearly identical for all of the hematocrits tested. Therefore, cell density would most likely not have an apparent effect on the performance of the device from a practical standpoint.

FIG. 6.

Effect of hematocrit (hct) on removal of glycerol from frozen-thawed RBCs in 40% glycerol using a 3.4% saline wash and a device with 130 μm thick channels.

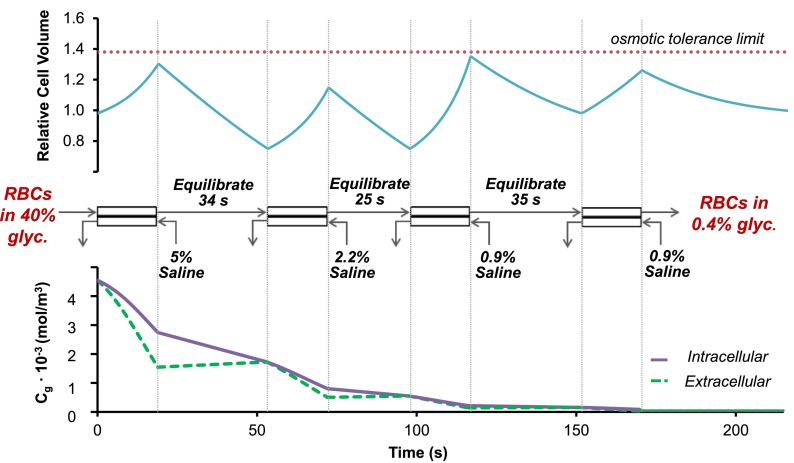
G. Design of a continuous deglycerolization process

The design of an effective deglycerolization protocol must take into consideration two important criteria: limiting cell volume excursions to the osmotic tolerance limits and minimizing the total process time. The results presented thus far have demonstrated successful partial deglycerolization of frozen-thawed RBCs in a single channel microfluidic membrane device. By linking multiple devices in series and appropriately selecting the operating conditions in each device, it is possible to design a complete continuous deglycerolization procedure that would achieve the desired ending glycerol concentration while maintaining the cell volume excursions within the osmotic tolerance limits. Simulations indicate that it is possible to reduce the glycerol concentration to a clinically acceptable level⁴⁰ in a total of 170 s using four devices in series, as illustrated in Fig. 7. To achieve this, the cells may be washed with 5% saline in the first stage and allowed to equilibrate for 34 s, washed with 2.2% saline in the second stage and allowed to equilibrate for 25 s, washed with isotonic saline in the third stage and allowed to equilibrate for 35 s, and finally washed with isotonic saline in the fourth stage. These results demonstrate the potential for using continuous microfluidic processing to significantly reduce the deglycerolization time compared with the centrifugal methods that are currently in use. Moreover, we expect that more rigorous optimization of the procedure will reveal operating conditions that would allow even faster processing.

FIG. 7.

Four-stage microfluidic deglycerolization process designed using the mass transfer model. Each microfluidic device has a channel height of 50 μm and is operated at a fluid velocity of 0.8 cm/s. The predicted glycerol concentration (bottom) and corresponding cell volume (top) are shown throughout the deglycerolization process.

Several challenges will need to be overcome to achieve continuous microfluidic deglycerolization at clinical scale. To deliver the flow rate commonly used for transfusions in non-hemorrhagic patients (∼4 ml/min)⁸ using this size channel and fluid velocity, the device must be scaled up to approximately 480 parallel channels. Although the number of channels may seem large, the internal volume of each device would only amount to approximately 1.3 ml of fluid due to the microscale dimensions of the channels. Such arrayed microchannel devices have unique design considerations that must be addressed, including selection of an appropriate manifold geometry to evenly distribute the blood into the parallel microchannels⁴¹ and management of bubble clogging issues.⁴² Moreover, it has recently been demonstrated that nonuniform fluid velocity across the height of microchannels can lead to a distribution of cell residence times, which can negatively impact the performance of microfluidic cell washing devices.⁴³ Although our model predictions were reasonably accurate for a single deglycerolization device, the multistage process shown in Fig. 7 may result in a relatively broad distribution of cell residence times. Thus, it may be necessary to refine the mathematical model to account for this phenomenon. The design of a clinical deglycerolization process will also require an analysis of manufacturability,⁴⁴ as well as the tradeoffs between single use and reusable devices. Although device reuse would reduce cost, it would increase the risk of pathogen contamination. A sterile disposable device would most likely be preferred to ensure patient safety.

IV. CONCLUSIONS

The results presented in this study demonstrate three main points relevant to continuous microfluidic processing of cryopreserved RBCs: (1) frozen-thawed RBCs can be flowed through a microfluidic membrane device without causing excessive mechanical damage; (2) predictions of solution composition and cell volume are in reasonable agreement with experimental data, opening opportunities for model-guided design of microfluidic deglycerolization processes; and (3) using a four-stage microfluidic process, it is theoretically possible to remove glycerol in less than 3 min, more than an order of magnitude faster than existing deglycerolization methods.