Frequency Dependence of Electron Spin-lattice Relaxation for Semiquinones in Alcohol Solutions

Abstract

The spin-lattice relaxation rates at 293 K for three anionic semiquinones (2,5-di-t-butyl-1,4-benzosemiquinone, 2,6-di-t-butyl-1,4-benzosemiquinone, and 2,3,5,6-tetramethoxy-1,4-benzosemiquinone) were studied at up to 8 frequencies between 250 MHz and 34 GHz in ethanol or methanol solution containing high concentrations of OH^-. The relaxation rates are about a factor of 2 faster at lower frequencies than at 9 or 34 GHz. However, in perdeuterated alcohols the relaxation rates exhibit little frequency dependence, which demonstrates that the dominant frequency-dependent contribution to relaxation is modulation of dipolar interactions with solvent nuclei. The relaxation rates were modeled as the sum of two frequency-independent contributions (spin rotation and a local mode) and two frequency-dependent contributions (modulation of dipolar interaction with solvent nuclei and a much smaller contribution from modulation of g anisotropy). The correlation time for modulation of the interaction with solvent nuclei is longer than the tumbling correlation time of the semiquinone and is consistent with hydrogen bonding of the alcohol to the oxygen atoms of the semiquinones.

Introduction

Semiquinones are ubiquitous in biology, from photosynthesis to environmental toxicology [1, 2]. They are involved in many electron transfer reactions [3, 4]. Semiquinones have been studied extensively by EPR [5], and their spin relaxation properties are important to understanding their EPR spectra. Semiquinones were selected for studies of mechanisms of electron spin relaxation because their g values are higher than for carbon-centered radicals, but their nuclear hyperfine couplings are smaller than for nitroxides.

Semiquinones were among the first species for which spin-lattice relaxation rates were measured directly by saturation recovery in fluid solution [6, 7]. Semiquinone relaxation rates have been studied extensively at X-band as a function of temperature and viscosity [7-12]. In alcohol solutions relaxation rates could be fit with the relationship shown in Eq. (1) [7-11].

$$\frac{1}{T_1}=\frac{AT}{\mathrm{\eta }}+B{\mathrm{e}}^{-\mathrm{\Delta }\mathrm{E}/\text{RT}}$$ (1)

where η is the viscosity of the solution, ΔE was found to be about 1 kcal/mole (ΔE/R = 500 K), A and B were determined experimentally and depend both on semiquinone and on solvent [7-11].

There is general agreement that the term in Eq. (1) in T/η is due to spin rotation, which is usually written as in Eq. (2) [13, 14].

$$\frac{1}{T_1^{\mathit{\text{SR}}}}=\frac{\sum _{i=1}^3{(g_i-g_e)}^2}{9{\mathrm{\tau }}_R}$$ (2)

where i = x,y,z and g_e is 2.0023.

The origin of the second term in Eq. (1) was not well understood and has been attributed to hindered rotation [7, 11] and/or spin rotation [10]. A study at X- and Q-band of five semiquinones in glass-forming solvents between 25 and 295 K found that the dominant contributions to relaxation at 295 K were spin rotation and a local mode [15]. The energy for the local mode was 600 K, which is similar to the activation energy reported previously for the second contribution to semiquinone relaxation (Eq. 1). The full expression for a local mode is given by Eq. (3) [16].

$$\frac{1}{T_1^{\text{local}}}=C_{\mathit{\text{local}}}\frac{{\mathrm{e}}^{{\mathrm{\Delta }}_{\mathit{\text{loc}}}/\mathrm{T}}}{{({\mathit{e}}^{{\mathrm{\Delta }}_{\mathit{\text{loc}}}/\mathrm{T}}-1)}^2}$$ (3)

where Δ_loc is the energy of the local mode in Kelvin and C_local is determined experimentally. The local mode relaxation mechanism was initially proposed for defects in ionic lattices [16]. The temperature dependence of relaxation described by Eq. 3 has been observed for molecular species in glassy matrices, including organic radicals and transition metal complexes [17-19]. The magnitude of the contribution from the local mode is larger in soft matrices such as sucrose octaacetate than in harder ones such as sorbitol [18]. For a molecular species in a glass the local mode is interpreted as an intramolecular vibration that is impacted by interaction with the matrix. For nitroxides in highly viscous media [18, 19] and for trityl radicals in water:glycerol [20] the local mode dominates relaxation in the glassy state below the glass transition temperature. There is no change in slope for a plot of log(1/T₁) vs. log(T) in the vinicity of the glass transition temperature, so it is proposed that the local mode relaxation mechanism persists in solution.

If Δ_loc ≫ T, Eq. (3) can be approximated as in Eq. (4), which has the same temperature dependence as the second term in Eq. (1).

$$\frac{1}{T_1^{\text{local}}}\sim C_{\mathit{\text{local}}}{\mathrm{e}}^{-{\mathrm{\Delta }}_{\mathit{\text{loc}}}/\mathrm{T}}$$ (4)

These results indicate that the two dominant contributions to spin-lattice relaxation at X-band for semiquinones tumbling rapidly in solution are spin rotation and a local mode with an energy of 500 to 600 K. The contributions from these two relaxation mechanisms are independent of resonance frequency.

Studies of the frequency dependence of spin-lattice relaxation for carbon-centered trityl radicals [21] and nitrogen-centered nitroxide radicals [22-24] in fluid solution have demonstrated the significance of additional relaxation mechanisms. These frequency-dependent processes modulate anisotropic interactions – g anisotropy (Eq. 5) [25, 26], hyperfine (A_i) anisotropy (Eq. (7) [25-27], dipolar coupling to solvent nuclei (Eq. 8) [21], or involve a thermally-activated process (Eq. 9) [23].

$$\frac{1}{T_1^g}=\frac{2}{5}{(\frac{{\mathrm{\mu }}_B\mathrm{\omega }}{g\mathrm{\beta }})}^2\{\frac{{(\mathrm{\Delta }g)}^2}{3}+{(\mathrm{\delta }g)}^2\}J(\mathrm{\omega })$$ (5)

where Δg = g_zz − 0.5(g_xx+g_yy), δg = 0.5(g_xx − g_yy), μ_B is the electron Bohr magneton and J(ω) is the Bloembergen, Purcell, Pound (BPP) spectral density function (Eq. 6).

$$J(\mathrm{\omega })=\frac{{\mathrm{\tau }}_R}{1+{(\mathrm{\omega }{\mathrm{\tau }}_R)}^2}$$ (6)

where τ_R is the tumbling correlation time of the semiquinone and ω is the resonance frequency.

$$\frac{1}{T_1^A}=\frac{2}{9}I(I+1)\sum _i{(A_i-\overline{A})}^{2}J(\mathrm{\omega })$$ (7)

where A_i is a component of the nitroxide nitrogen hyperfine coupling in angular frequency units, Ā is the average nitrogen hyperfine, and I is the nitrogen nuclear spin.

$$\frac{1}{T_1^{\text{solvent}}}=C_{\mathit{\text{solvent}}}\frac{{\mathrm{\tau }}_{\mathit{\text{solvent}}}}{1+{(\mathrm{\omega }{\mathrm{\tau }}_{\mathit{\text{solvent}}})}^2}$$ (8)

where τ_Solvent is the correlation time for motion of the solvent relative to the radical, and C_solvent is a function of the dipolar interaction with solvent nuclei.

$$\frac{1}{T_1^{\text{therm}}}=C_{\mathit{\text{therm}}}\left(\frac{\mathrm{\omega }}{{\mathrm{\omega }}_{\mathit{\text{ref}}}}\right)\frac{{\mathrm{\tau }}_{\mathit{\text{therm}}}}{1+{(\mathrm{\omega }{\mathrm{\tau }}_{\mathit{\text{therm}}})}^2}$$ (9)

where τ_therm = τ_c⁰ exp(E_a/RT), E_a is the activation energy, τ_c⁰ is the pre-exponential factor, C_therm is the coefficient for the contribution of the thermally-activated process, and ω_ref = 9.5 GHz. Variable temperature studies of semiquinone spin lattice relaxation did not find evidence of a thermally-activated process as described by Eq. (9) [7, 15] so this contribution was not included in the models used in this paper.

To determine the extent to which frequency-dependent processes (Eq. 5,7,8) contribute to the relaxation of semiquinones in alcohol solvents at 293 K, the three radicals shown in Figure 1 were studied at frequencies between 250 MHz and 34 GHz.

Figure 1.

Structures of the semiquinones studied.

2. Experimental

2.1 Semiquinone preparation

2,5-Di-t-butyl-1,4-benzosemiquinone (25DTBSQ) was prepared by mixing equal volumes of air-saturated ethanol solutions of 2,5-di-t-butyl hydroquinone (5 mM, Alfa Aesar, 98% purity) and KOH (5 mM) [28]. 2,6-Di-t-butyl-1,4-benzosemiquinone (26DTBSQ) was prepared from 2,6-di-t-butyl-1,4-benzoquinone (Aldrich, 98% purity) using the same procedure. 2,3,5,6-Tetramethoxy-1,4-benzosemiquinone (TMBSQ) was prepared by mixing a 2:1 volume ratio of 25 mM KOH and 5mM tetraflouro-1,4-benzoquinone (Sigma-Aldrich, 97% purity) in methanol. Formation of the radicals was confirmed by X-band CW EPR [28]. Concentrations of the semiquinones were determined by comparison of the double integrals of the EPR spectra with double integrals of signals for 0.20 mM ¹⁵N-CTPO (3-carbamoyl-2,2,5,5-tetramethyl-3-pyrroline-1-oxyl) in the same solvent. Concentrations were in the range of 0.2 to 0.5 mM. 1,4-benzosemiquinones form adducts with, and react with, O₂ [29]. The EPR signals of the semiquinones in air-saturated solution are very broad and difficult to observe. Air-saturated solutions stored at 4°C for up to 30 days produced well-resolved semiquinone EPR signals after deoxygenation. In deoxygenated sealed tubes the EPR signal decays within hours to days.

2.2 Oxygen Removal

Samples were purged with N₂ to remove O₂. Relaxation time measurements were repeated, with continued N₂ purging, until no further increase in relaxation time constant was observed. At Q-band the samples were in Teflon tubes with 0.30 mm ID and 0.66 mm OD that were placed inside a 1.6 mm OD quartz capillary tube that was open at both ends. The Bruker cryostat was purged with N₂ throughout the measurements. At frequencies between 1 and 9 GHz samples were in 4 mm OD quartz tubes. The vapor space in the tube was initially purged vigorously with N₂, after which N₂ was gently bubbled into the solution through thin Teflon tubing. At X-band the resonator also was purged with N₂. At L-, S-, and X-band samples were purged continuously with N₂. At 600 MHz and 250 MHz 16 mm and 25 mm OD quartz tubes were used, respectively. The height of the solution in the tube was about 3 cm. To purge the large vapor space in these tubes the following protocol was developed: 15 min purging at the top of the tube, 15 min near the top, 15 min in the middle of the tube and 30 min gentle bubbling into the solution followed by constant gentle purging with N₂ at the top of the tube during the relaxation time measurements.

2.3 Relaxation times measurements

Spin-lattice relaxation times, T₁, were measured by inversion recovery at 250 MHz [30], 600 MHz [23], L-band (1.0, 1.5 GHz) [31], S-band (2.57, 3.0 GHz) [31], and X-band (9.5 GHz) [32] on locally designed spectrometers and at Q-band (34 GHz) on a Bruker E580 spectrometer. The experiments were performed at a resonator temperature of ∼293 K. Multifit, a locally written program based on the algorithms of Provencher, was used to determine T₁ from the decay curves [33]. Single exponential fits were in good agreement with the data. Replicate measurements demonstrated that uncertainties were in the range of 5 to 15%, as shown Fig. 2 - 4. At lower frequencies the signal-to-noise was poorer than at higher frequencies, which resulted in greater uncertainty in T₁.

Figure 2.

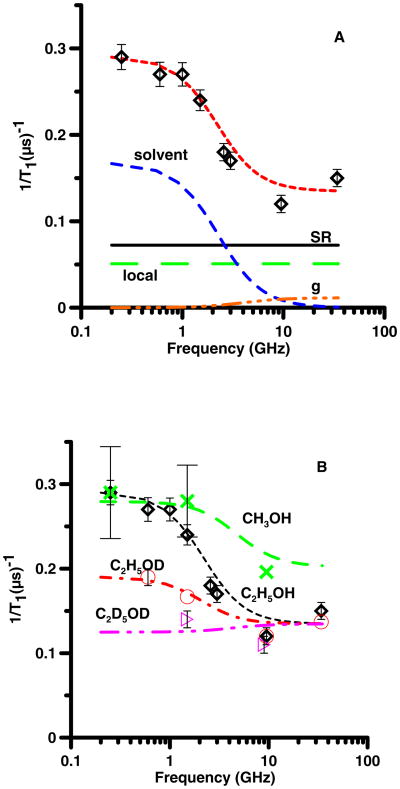
(A) Frequency dependence of 1/T₁ ( ) for 25DTBSQ in ethanol at 293 K. The relaxation is modeled as the sum (- -, short dash) of contributions from spin rotation (SR) (—, solid) Eq. (2), a local mode (local) (— —, long dash) Eq. (3), modulation of g-anisotropy (g) (— - - -, dash dot) Eq. (5) and modulation of dipolar interactions with solvent nuclei (solvent) (– –, medium dash) Eq. (8). (B) Frequency dependence of 1/T₁ in C₂H₅OH ( ), in CH₃OH (x), in C₂H₅OD (○) and in C₂D₅OD (▷). The dashed lines through the data are the sums of contributions to the spin lattice relaxation as described in the text, calculated with Eq. 2, 3, 5, and 8.

Figure 4.

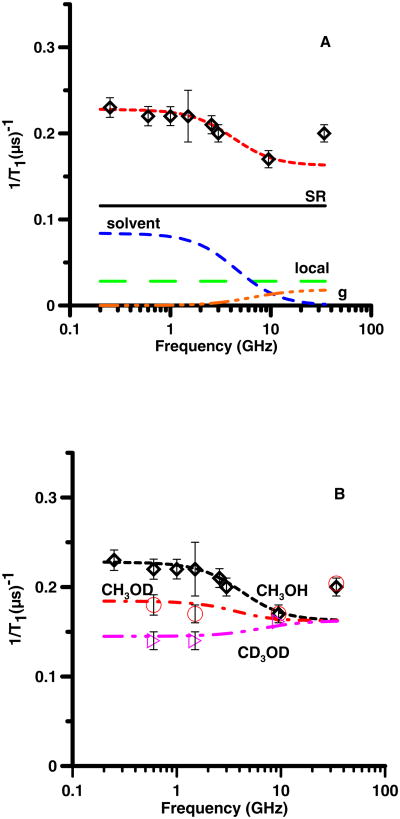
(A) Frequency dependence of 1/T₁ ( ) for TMBSQ in methanol at 293 K. The relaxation is modeled as the sum (- -, short dash) of contributions from spin rotation (SR) (—, solid) Eq. (2), a local mode (local) (— —, long dash) Eq. (3), modulation of g-anisotropy (— - - -, dash dot) Eq. (5) and modulation of dipolar interactions with solvent nuclei (solvent) (– –, medium dash) Eq. (8). (B) Frequency dependence of 1/T₁ in CH₃OH ( ), in CH₃OD (○), and in CD₃OD (▷). The dashed lines through the data are the sums of contributions to the spin lattice relaxation as described in the text, calculated with Eq. 2, 3, 5, and 8.

3. Modeling the frequency dependence of 1/T₁

3.1 Frequency-independent contributions to 1/T₁

The two frequency-independent contributions to 1/T₁ for molecules tumbling rapidly in fluid solution are spin rotation (Eq. 2) and the local mode (Eq. 3,4). The contribution 1/T₁^local was calculated using Eq. (3) with Δ_loc = 500 K to be consistent with ΔE = 1 kcal/mole from the extensive early work on semiquinones [7]. In Ref. [7] the value of B (Eq. 1) for 25DTBSQ in ethanol or methanol was 0.29×10⁶ s^-1. A value of Δ_loc = 500 K in Eq. (3) is not large enough to be fully in the limit of Δ_loc ≫ T at 293 K. To make the value of 1/T₁^local at 293 K calculated using Eq. (3) with Δ_loc = 500 K equal to that calculated with Eq. (1) and ΔE = 1 kcal/mole requires multiplication of B by about a factor of 0.7, which gives C_local ∼ 0.19×10⁶ s^-1. In ref. [15] the contribution from the local mode for 25DTBSQ in 1:4 glycerol:ethanol or 1:2 glycerol:ethanol was calculated with Δ_loc = 600 K and C_local = 0.18×10⁶ s^-1 or 0.13×10⁶ s^-1, respectively. To obtain the same magnitude of contribution at 293 K with Δ_loc = 500 K would require C_local = 0.11×10⁶ s^-1 or 0.08×10⁶ s^-1 for the two solvent mixtures, respectively. Since there is a weak dependence of C_local on solvent and semiquinone, and there are uncertainties in parameters obtained in prior experiments, the values of C_local in the modeling of the frequency dependence of 1/T₁ were constrained to be between 0.08×10⁶ and 0.19×10⁶ s^-1.

Calculation of 1/T₁^SR requires g values and τ_R. The g values for 25DTBSQ, 26DTBSQ, and TMBSQ in hydrogen-bonding solvents are g_x = 2.0065, g_y = 2.0052, and g_z = 2.0023 [15]. The viscosities at 298 K are 0.545 cP for CH₃OH and 1.08 cP for C₂H₅OH [34]. Based on these viscosities, tumbling correlation times calculated using the Stokes-Einstein equation are 109 ps for 25DTBSQ or 26DTBSQ in C₂H₅OH and 57 ps for TMBSQ in CH₃OH at 293 K. In the early studies of semiquinone relaxation the spin rotation term was expressed as AT/η (Eq. 1), which can be related to the expression in Eq. (2) by using τ_R = c_slip V η/kT where V is the molecular volume and k is Boltzmann's constant [35, 36]. The adjustable parameter c_slip ranges from 0 to 1.0 depending on the extent of solute-solvent interaction [35, 36]. When molecular volumes were calculated assuming a density of 0.90, the values of A (Eq. 1) in ref. [7] correspond to c_slip ranging from 0.10 to 0.40 with an average of 0.24, including c_slip = 0.40 and 0.25 for 25DTBSQ in CH₃OH and C₂H₅OH, respectively, and c_slip = 0.36 for TMBSQ in CH₃OH. These values of c_slip are larger than those for nitroxides [23] which are 0.11 for tempone (which has a keto group) in water, 0.15 for mHCTPO (which has a carboxamide group) in water, and 0.21 for proxyl (which has a carboxy group) in water. The larger values of c_slip for the anionic semiquinones than for neutral nitroxides are consistent with the expectation of stronger interaction of the semiquinones with the H-bonding polar solvents. Values of c_slip in water:glycerol mixtures for trityl radicals with three carboxy groups are about 0.65 [21]. Since the molar masses of the trityls are in the range of 975 to 1695 [21] and the Stokes-Einstein model results in c_slip closer to 1 for larger molecules, the values of c_slip for semiquinones with molar masses about 220 are expected to be smaller than for the trityls. In modeling the frequency dependence of 1/T₁ the values of c_slip were constrained to be between 0.24 and 0.50. It was assumed that c_slip was similar in ethanol and methanol, unaffected by solvent deuteration, and similar for 25DTBSQ and 26DTBSQ. The resulting values of c_slip were 0.37 for 25DTBSQ and 26DTBSQ and 0.44 for TMBSQ (Table 1). The higher value for TMBSQ may reflect additional solvent interaction with the methoxy oxygens.

Table 1. Contributions to Spin-Lattice Relaxation of Semiquinones at 293 K in Fluid Solution.

Semiquinone	Solvent	τR (ps)a, (cslip)	Δloc (K)b	Cloc (s-1)	τsolvent (ps)	Csolvent (s-1)
25DTBSQ	C2H5OH	40 (0.37)	500	0.18×106	70	2.4×1015
	C2H5OD	40 (0.37)	500	0.18×106	70	1.0×1015
	C2D5OD	40 (0.37)	500	0.18×106	70	<5×1013
	CH3OH	20 (0.36)	500	0.18×106	35	2.4×1015
26DTBSQ	C2H5OH	40 (0.37)	500	0.18×106	70	2.6×1015
	C2H5OD	40 (0.37)	500	0.18×106	70	1.2×1015
TMBSQ	CH3OH	25 (0.44)	500	0.10×106	35	2.4×1015
	CH3OD	25 (0.44)	500	0.10×106	35	1.2×1015
	CD3OD	25 (0.44)	500	0.10×106	35	<5×1013

^ag = 2.0065, 2.0052, 2.0023 [15]

^bFixed at the value obtained by variable temperature studies [7].

3.2 Frequency-dependent contributions to 1/T₁

The contribution from modulation of g anisotropy (Eq. 5) is calculated from the known g values and the value of τ_R that was determined by analysis of the contributions from frequency-independent terms at X-band.

Eq. (7), the contribution from modulation of anisotropic nuclear hyperfine interaction, was derived for a single nuclear spin. That contribution is proportional to the square of the hyperfine anisotropy. Analogous equations to treat the contributions to relaxation from couplings to the two semiquinone ring protons in 25DTBSQ or 26DTBSQ have not been derived. The anisotropic hyperfine couplings to the two ring protons are (1.92, 2.14, 2.35 G) and (0.92, 1.28, 1.44 G), respectively [15]. If it is assumed that the contributions from multiple protons are additive, the estimated contributions from modulation of hyperfine anisotropy for the two ring protons are about two orders of magnitude smaller than the observed frequency dependence of 1/T₁ (Fig. 2-4). Although the assumption of additivity is over-simplified, more sophisticated analyses are unlikely to dramatically change the magnitude of the contribution, so modulation of the anisotropic ring proton hyperfine coupling was omitted from the analysis.

The parameters C_solvent and τ_solvent were adjusted to match the experimental data. The inflection point in the plot of 1/T₁^solvent vs. frequency is strongly dependent on τ_solvent so those values are tightly constrained. The value of C_solvent was adjusted to model the magnitude of the frequency-dependent contribution at low frequency.

4. Results and Discussion

The spin lattice relaxation rates for the three semiquinones were studied at 293 K at up to 8 frequencies between 250 MHz and 34 GHz. As reported previously [7] there was negligible concentration dependence of T₁ for semiquinone concentrations of the order of 1 mM. This lack of concentration dependence has been attributed to the solvent cage around the radicals [7]. The negative charge on the anionic semiquinones also may decrease collision probabilities. In a comparable concentration range significant concentration dependence has been observed for nitroxide radicals [37].

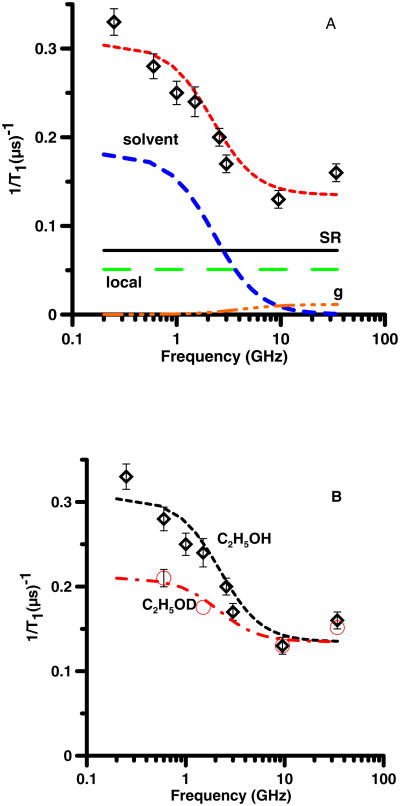
For 25DTBSQ in C₂H₅OH or CH₃OH (Fig. 2), 26DTBSQ in C₂H₅OH (Fig. 3), and TMBSQ in CH₃OH (Fig. 4) the spin lattice relaxation rates were about a factor of two faster at lower frequencies than at 9 GHz. The relaxation was modeled as the sum of contributions from two frequency-independent processes, (spin rotation (Eq. 2) and a local mode (Eq. 3)), and two frequency-dependent processes (modulation of dipolar interaction with solvent nuclei (Eq. 8) and a smaller contribution from modulation of g-anisotropy (Eq. 5)) (Table 1). Spin-lattice relaxation at X-band is dominated by the frequency-independent processes and is unchanged by solvent deuteration. Decreasing τ_R increases the contribution from spin rotation which can be compensated by increasing the coefficient C_local. The range of acceptable values of τ_R is limited by the range of C_local found in prior variable temperature experiments [7, 15]. At 295 K the viscosity of CH₃OH (0.545 cP) is about half that of C₂H₅OH (1.08 cP) so τ_R decreases by about a factor of 2 when the solvent is changed from C₂H₅OH (Fig. 2A) to CH₃OH (Fig. 2B). Comparison of relaxation rates for 25DTBSQ in C₂H₅OH and CH₃OH permitted separation of the tumbling-dependent spin-rotation contribution from the tumbling-independent local mode contribution. These constraints permitted definition of the values of τ_R. Calculation of T₁ at X-band for four semiquinones in ethanol at 293 K by substitution of reported values of A and B into Eq. (1) [7] shows that in this rapid tumbling regime the contribution from the first term (spin rotation) is 1.3 to 2.1 times larger than the contribution from the second term (the local mode). For 25DTBSQ in ethanol at X-band the ratio of the contributions from spin rotation and the local mode is 1.5, which is consistent with the earlier reports. Although the molar masses differ by only about 20%, τ_R for semiquinones (Table 1) in ethanol (η=1.05 cP) are longer than for neutral tempone (Table 2) in water (η= 1.0 cP), which is attributed to hydrogen bonding between the anionic semiquinones and the solvent [38-40].

Figure 3.

(A) Frequency dependence of 1/T₁ ( ) for 26DTBSQ in ethanol at 293 K. The relaxation is modeled as the sum (- -, short dash) of contributions from spin rotation (SR) (—, solid) Eq. (2), a local mode (local) (— —, long dash) Eq. (3), modulation of g-anisotropy (— - - -, dash dot) Eq. (5), and modulation of dipolar interactions with solvent nuclei (solvent) (– –, medium dash) Eq. (8). (B) Frequency dependence of 1/T₁ in C₂H₅OH ( ) and in C₂H₅OD (○). The dashed lines through the data are the sums of contributions to the spin lattice relaxation as described in the text and calculated with Eq. 2, 3, 5, and 8.

Table 2. Properties of Representative Trityl, Semiquinone, and Nitroxide Radicals.

Radicalb	Solvent	g-values	Molar mass	τR (ps)a	Ref.
Trityl-OX31	H2O	2.0030	1695	500	[20, 21]
		2.0027
		2.0021
Trityl-CH3	H2O	2.0030	975	300	[20, 21]
		2.0027
		2.0021
25DTBSQ	C2H5OH	2.0065	220	40	This work
		2.0052
		2.0023
25DTBSQ	CH3OH	2.0065	220	20	This work
		2.0052
		2.0023
Tempone-d16	69% glycerol	2.0092	186	50	[23]
		2.0061
		2.0022
Tempone-d16	H2O	2.0092	186	9	[23, 42]
		2.0061
		2.0022

^aAt 293 K

^bAbbreviations for radicals are defined in the papers cited.

The modulation of g anisotropy by molecular tumbling (Eq. 5) makes a relatively small contribution to 1/T₁ and is significant for the semiquinones only at Q-band. For each of the semiquinones the relaxation rates at Q-band were faster than predicted by modeling with Eq. (2, 3, 5, and 8). It is therefore proposed that an additional process contributes at higher frequencies, which will require further study. Studies of spin lattice relaxation for nitroxides at Q-band and W-band also have found rates that are faster than at X-band, and the mechanism is not known [24, 41].

The dominant frequency-dependent contribution to 1/T₁ was decreased by deuteration of the solvent (Fig. 2 – 4). For all three semiquinones replacement of solvent OH by OD decreased the contribution from the frequency-dependent contribution by about a factor of two (Table 1). Complete solvent deuteration eliminated this contribution, which demonstrated domination of the frequency dependent contribution to relaxation by interaction with solvent nuclei. The contributions calculated from Eq. (8) are strongly dependent on the value of τ_solvent. The simulations required τ_solvent about twice as long as τ_R The uncertainties for τ_solvent are about ±10% and the uncertainties for τ_R are about 25%, so the difference of about a factor of 2 is larger than the uncertainties in the correlation times. The observation of τ_solvent > τ_R indicates that the dynamic process that modulates the interaction between the unpaired electron and the solvent nuclei is not molecular tumbling. The OH proton is only one of 4 protons in CH₃OH and one of 6 protons in C₂H₅OH, so the factor of two reduction in the frequency-dependent contribution to relaxation (Eq. 8) when only the OH proton is replaced by a deuteron is substantially larger than predicted if all of the protons contributed equally. Water and alcohols are strongly hydrogen bonded to semiquinones [38-40]. The observations that (i) the contribution from Eq. (8) decreased by about a factor of 2 when only the OH was replaced by OD (Fig. 2 – 4), (ii) the frequency dependent contribution to relaxation was eliminated by solvent perdeuteration, and (iii) values of τ_solvent differ from τ_R, are consistent with assignment of fluctuations in hydrogen bonding as the process that drives τ_solvent. Hydrogen bonding to the semiquinone oxygens is the most probable source of the frequency-dependent contribution to relaxation.

4.1 Comparison with relaxation rates and mechanisms for trityls and nitroxides

Differences in relaxation rates between trityls, semiquinones, and nitroxides illustrate factors that impact relaxation for organic radicals in liquid solution (Table 3). Carbon-centered trityl-CH₃ and trityl-OX31 have relatively high molar masses, and therefore long τ_R, as well as g values close to 2, so spin rotation is not an effective spin lattice relaxation mechanism [21]. At X-band 1/T₁ for trityls is dominated by a local mode [21]. At lower frequencies modulation of dipolar interactions with the many protons in the radicals by molecular tumbling causes 1/T₁ to be larger than at X-band [21]. Relaxation rates for semiquinones at X-band are faster than for the trityls because tumbling correlation times are shorter and g values are further from g = 2 (Table 2), so spin rotation makes a substantial contribution, along with a local mode. The relative importance of spin rotation and the local mode depends on τ_R. At lower frequencies it is proposed that the relaxation rates for semiquinones are faster than at X-band because dipolar interactions with solvent protons are modulated by fluctuations in the hydrogen bonding between the solvent and the semiquinone oxygens. For nitroxides the contribution to relaxation from modulation of the large anisotropic nitrogen hyperfine coupling is strongly dependent on frequency and τ_R [23]. The contribution from this process is larger at lower frequency and for longer τ_R (Eq. 7). This process is not significant for trityls or semiquinones because these molecules do not have large anisotropic hyperfine couplings. The relaxation rates for all three classes of radicals are faster at lower frequencies than at X-band (Table 3). Although the mechanisms are different, in each case an additional contribution becomes significant as the frequency is decreased and as the rate of a dynamic processes become comparable to the resonance frequency, ie ω ∼ 1/τ. For the slowly tumbling trityls this occurs below about 1 GHz, and for the more rapidly tumbling semiquinones it occurs below about 5 GHz.

Table 3. Frequency Dependence of Relaxation Times and Mechanisms for Representative Trityl, Semiquinone, and Nitroxide Radicals.

Radicala	Solvent	9 GHz			250 MHz			Ref.
		T1 (μs)	1/T1 (μs)-1	mechanism	T1 (μs)	1/T1 (μs)-1	mechanism
Trityl-OX31	H2Ob	14	0.071	local mode	5.9	0.17	modulation of proton dipole interactions by trityl tumbling	[21]
Trityl-CH3	H2Ob	16	0.062	local mode	7.9	0.13		[21]
25DTBSQ	C2H5OH	7.8	0.13	spin rotation + local mode	3.4	0.29	modulation of solvent proton interactions by solvent motion	This work
25DTBSQ	CH3OH	5.0	0.20	spin rotation + local mode	3.4	0.29		This work
Tempone-d16	69% glycerolb	2.2	0.45	modulation of Ad	0.25e	4.0e	modulation of Ad	[23]
Tempone-d16	H2Oc	0.58	1.7	spin rotation + modulation of Ad	0.60	1.7	spin rotation + modulation of Ad	[22, 23]

^aAbbreviations for radicals are defined in the papers cited

^b0.2 mM concentration

^c0.5 mM concentration

^dA refers to the nitrogen hyperfine coupling

^eMeasured at 630 MHz

Research Highlights.

• Spin lattice relaxation was measured for benzosemiquinones in alcohol + OH^-.

• Relaxation at 293 K is faster at 250 MHz than at 34 GHz.

• In perdeutered solvent, frequency dependence of relaxation is dramatically reduced.

• Enhanced relaxation at low frequency is attributed to modulation of hydrogen bonding.