Mediation analysis when a continuous mediator is measured with error and the outcome follows a generalized linear model

Abstract

Mediation analysis is a popular approach to examine the extent to which the effect of an exposure on an outcome is through an intermediate variable (mediator) and the extent to which the effect is direct. When the mediator is mis-measured the validity of mediation analysis can be severely undermined. In this paper we first study the bias of classical, non-differential measurement error on a continuous mediator in the estimation of direct and indirect causal effects in generalized linear models when the outcome is either continuous or discrete and exposure-mediator interaction may be present. Our theoretical results as well as a numerical study demonstrate that in the presence of non-linearities the bias of naive estimators for direct and indirect effects that ignore measurement error can take unintuitive directions. We then develop methods to correct for measurement error. Three correction approaches using method of moments, regression calibration and SIMEX are compared. We apply the proposed method to the Massachusetts General Hospital lung cancer study to evaluate the effect of genetic variants mediated through smoking on lung cancer risk.

1. Introduction

Mediation analysis investigates the role of intermediate variables (mediators) in governing an observed relationship between an exposure variable and an outcome variable. Rather than hypothesizing only a direct causal relationship between the independent variable and the dependent variable, a mediational model hypothesizes that the exposure variable causes the mediator variable, which in turn causes the outcome variable [1]. The use of mediation analysis in biomedical and social sciences is widespread and has been strongly influenced by the seminal paper of Baron and Kenny [2]. More recently, new advances in mediation analysis have been made by applying the counterfactual framework in this field [3-7].

A recent epidemiological study on the etiology of lung cancer motivates the present work. VanderWeele et al. [8] investigated the extent to which the effect of genetic variants rs8034191 and rs1051730 on chromosome 15q25.1 on the risk of lung cancer is direct and to what extent that association is mediated by pathways related to smoking behavior. The question was addressed using a case-control study at Massachusetts General Hospital. A potential concern about the validity of their findings arises from the fact that the mediator, measured as self-reported average cigarettes smoked per day, was likely subject to measurement error. It is of interest to understand how sensitive the results of their study are with respect to measurement error in the intermediate variable (smoking), while allowing for gene-environment interaction.

The literature on measurement error in generalized linear models is rich and rapidly evolving. In this study, we extensively use results that have been derived about the consequences of measurement error on parameter estimators in parametric regression models when a covariate is mis-measured [9-13].

The problem of measurement error on a continuous intermediate in mediation analysis has been explored for the simple and linear mediation model [14]. le Cessie et al. [15] provide simple correction formulas for direct effects estimates in a variety of mediator measurement error scenarios when the mean of the outcome is modeled using either linear or logistic regression. However, their work is restricted to the study of direct effect in the absence of interactions. In this paper, we extend results on measurement error correction in mediation analysis further by developing correction approaches that allow for exposure-mediator interaction, by considering more general classes of statistical models, and by comparing different correction methods. A commentary to le Cessie et al. paper [16] cites some of the results that we derive here.

The present work makes two main contributions. First, we study the implications of classical non-differential measurement error in the mediator variable on the validity of mediation analysis. We derive the asymptotic bias of direct and indirect causal effects estimators in closed form when interaction between exposure and mediator may be present in the outcome model, which follows a generalized linear model (GLM). We demonstrate that even if the error is assumed to be non-differential, regression coefficient estimators obtained in mediation analysis ignoring measurement error can sometimes be severely biased and therefore induce bias in estimation of causal direct and indirect effects.

The second contribution is to propose strategies for measurement error correction that yield consistent or approximately consistent estimators of the direct and indirect causal effects under classical non-differential measurement error model. We propose three different functional correction approaches, that do not require assumptions on the distribution of the latent intermediate, coupled with sensitivity analyses when no gold standard or validation samples for the mis-measured mediator are available. In particular, we compare the performance of measurement-error-corrected estimators for direct and indirect causal effects using method of moments [13,17], regression calibration [18-21] and SIMEX [22-23] estimators.

The paper is organized as follows. Section 2 discusses some results from mediation analysis and reviews the direct and indirect causal effects. Section 3 introduces mediation measurement error models, and studies the asymptotic bias in direct and indirect causal effects when the mediator is measured with error. In Section 4 we propose three approaches for measurement error correction and compare their performance in estimating direct and indirect causal effects via a simulation study. In Section 5 we apply the proposed method to the Massachusetts General Hospital (MGH) lung cancer genetic epidemiological study, followed by discussion in Section 6.

2. Mediation analysis within the counterfactual framework in the absence of measurement error

Let A be an exposure or treatment, Y an outcome, M a mediator and C, a k-dimensional vector of covariates. As represented in the causal diagram in Figure 1, the exposure can have an effect on the outcome by either exerting a causal effect on the mediator which in turn is causally related to the outcome, or by affecting the level of the outcome independently of its impact on the intermediate variable.

Figure 1.

Mediation Directed Acyclic Graph (DAG). Y denotes the outcome, A the exposure, M the mediator. C₁ denotes a set of confounders of the exposure-outcome and exposure-mediator relationship and C₂ denotes confounders of the mediator-outcome relationship.

The use of the causal inference approach to mediation analysis gives rise to the counterfactual definition of direct and indirect effects of the exposure [3-4]. Let Y_a and M_a denote respectively the values of the outcome and mediator that would have been observed had the exposure A been set to level a. Let Y_am denote the value of the outcome that would have been observed had the exposure, A, and mediator, M, been set to levels a and m, respectively. The controlled direct effect (CDE(m)), defined by E[Y_am − Y_ãm|C], measures how much the mean of the outcome would change if the mediator were controlled at level m uniformly in the population but the treatment were changed from level ã to level a. The natural direct effect (NDE), defined by E[Y_aMã − Y_ãMã|C], measures how much the mean of the outcome would change if the exposure were set at level a versus level ã but the mediator were kept at the level it would have taken under ã. The natural indirect effect (NIE), defined by E[Y_aMa − Y_aMã|C],measures how much the mean of the outcome would change if the exposure were controlled at level a, but the mediator were changed from the level it would take under ã to the level it would take under a. These causal contrasts can be recovered from the observed data under the assumption of no unmeasured confounding of (i) the exposure-outcome relationship, (ii) the mediator-outcome relationship, (iii) the exposure-mediator relationship, and (iv) that there are no mediator-outcome confounders affected by the exposure [5-6]. In the counterfactual notation this is: (i) Y_am Ц A|C, (ii) Y_am Ц M|A,C, (iii) M_a Ц A|C, (iv) Y_am Ц M_ã|C (See [4, 27] for further discussion of these assumptions).

For the case of a continuous mediator and outcome, the following regression models can be defined [2]:

$$E(Y|A=a,M=m,\mathit{C}=\mathit{c})={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\mathit{\theta }}_{\mathbf{4}}^{\mathbf{\prime }}\mathit{c}$$ (1)

$$E(M|A=a,\mathit{C}=\mathit{c})={\beta }_0+{\beta }_{1}a+{\mathit{\beta }}_{\mathbf{2}}^{\mathbf{\prime }}\mathit{c}.$$ (2)

Baron and Kenny proposed that the causal direct effect of the exposure can be assessed by estimating θ₁ and that the indirect causal effect of the exposure can be assessed by estimating β₁θ₂.

Using counterfactual definitions of direct and indirect causal effects of the exposure, the approach of Baron and Kenny can be extended to non-linear models and to allow for the presence of exposure-mediator interaction. Let A and C be continuous or categorical and assume M continuous. Assume that the conditional mean, μ, of the outcome Y given the exposure A, the mediator M, and the covariates C follows a generalized linear model (GLM) [24]

$$g(\mu )={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_3\mathit{\text{am}}+{\mathit{\theta }}_{\mathbf{4}}^{\mathbf{\prime }}\mathit{c},$$

where g(·) is a monotone link function.

When we have a continuous outcome and mediator, and both are modeled using the linear link, the mediator regression remains as in model (2), but the outcome regression, allowing for exposure-mediator interaction, is as follows:

$$E(Y|A=a,M=m,\mathit{C}=\mathit{c})={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_3\mathit{\text{am}}+{\mathit{\theta }}_{\mathbf{4}}^{\mathbf{\prime }}\mathit{c}.$$ (3)

If the identifiability assumptions hold and the models are correctly specified, then from models (2) and (3) what can be defined as the controlled direct effect (CDE(m)), natural direct effect (NDE) and natural indirect effect (NIE) for a change in exposure from level ã to level a are given by [5]:

$$\begin{array}{c}\mathit{\text{CDE}}(m)=({\theta }_1+{\theta }_{3}m)(a-\stackrel{\sim }{a})\\ \mathit{\text{NDE}}=({\theta }_1+{\theta }_3{\beta }_0+{\theta }_3{\beta }_1\stackrel{\sim }{a}+{\theta }_3{\mathit{\beta }}_{\mathbf{2}}^{\mathbf{\prime }}\mathit{c})(a-\stackrel{\sim }{a})\\ \mathit{\text{NIE}}=({\theta }_2{\beta }_1+{\theta }_3{\beta }_{1}a)(a-\stackrel{\sim }{a}).\end{array}$$

These expressions generalize those of [2] to allow for interaction between the exposure and the mediator (See Web Appendix B1). While controlled direct effects are often of greater interest in policy evaluation [4,25] natural direct and indirect effects may be of greater interest in evaluating the action of various mechanisms [25-26].

Under the same assumptions, the total effect of the exposure on the outcome (TE = E[Y_a − Y_ã]) is given by the sum of natural direct and natural indirect effects (TE = NDE + NIE)[3-4] and the proportion of the total effect explained by the hypothesized mechanism, also known as proportion mediated (PM), is given by:

$$\mathit{\text{PM}}=\mathit{\text{NIE}}/\mathit{\text{TE}}$$

When the outcome is binary and the mean is modeled with a logit link, equation (3) can be replaced by (See Web Appendix C1)

$$\mathit{\text{logit}}\{P(Y=1|A=a,M=m,\mathit{C}=\mathit{c})\}={\theta }_0+{\theta }_{1}a+{\theta }_{2}m+{\theta }_3\mathit{\text{am}}+{\mathit{\theta }}_{\mathbf{4}}^{\mathbf{\prime }}\mathit{c}.$$ (4)

If the outcome is binary and rare, then from models (2) and (4) the average controlled direct effect (CDE(m)), natural direct effect (NDE) and natural indirect effect (NIE) for a change in exposure from level ã to level a are given in terms of odds ratios by [6]:

$$\begin{array}{c}{\mathit{\text{OR}}}^{\mathit{\text{CDE}}\left(m\right)}=\mathit{\text{exp}}\{({\theta }_1+{\theta }_{3}m)(a-\stackrel{\sim }{a})\}\\ {\mathit{\text{OR}}}^{\mathit{\text{NDE}}}\approx \mathit{\text{exp}}[\{{\theta }_1+{\theta }_3({\beta }_0+{\beta }_1\stackrel{\sim }{a}+{\mathit{\beta }}_{\mathbf{2}}^{\mathbf{\prime }}\mathit{c}+{\theta }_2{\sigma }^2)\}(a-\stackrel{\sim }{a})+0.5{\theta }_3^2{\sigma }^2(a^2-{\stackrel{\sim }{a}}^2)]\\ {\mathit{\text{OR}}}^{\mathit{\text{NIE}}}\approx \mathit{\text{exp}}\{({\theta }_2{\beta }_1+{\theta }_3{\beta }_{1}a)(a-\stackrel{\sim }{a})\}.\end{array}$$

The approximations hold to the extent that the outcome is rare.

If the outcome is rare, the identifiability assumptions hold, and the models are correctly specified, then the total effect of the exposure on the outcome (OR^TE = [P(Y_a = 1)/{1 − P(Y_a = 1)}]/[P(Y_ã = 1)/{1 − P(Y_ã = 1)}]) is given by the product of the odds ratio natural direct and natural indirect effects (OR^TE = OR^NDE × OR^NIE) and the proportion mediated (PM), can be computed on the risk difference scale as proposed by VanderWeele and Vansteelandt [6]:

$$\mathit{\text{PM}}={\mathit{\text{OR}}}^{\mathit{\text{NDE}}}\times \{{\mathit{\text{OR}}}^{\mathit{\text{NIE}}}-1\}/\{{\mathit{\text{OR}}}^{\mathit{\text{NDE}}}\times {\mathit{\text{OR}}}^{\mathit{\text{NIE}}}-1\}$$

The same formulas apply exactly if the logit link in (4) is replaced by a logarithmic link for continuous, binary or count outcome. In this case the average controlled direct effect (CDE(m)), natural direct effect (NDE) and natural indirect effect (NIE) have a risk ratio or rate ratio interpretation [28]. In the context of our motivating example, where the outcome is the binary variable lung cancer status, the exposure variable is the genetic variant and the mediator is number of cigarettes smoked per day, the controlled direct effect can be interpreted as the odds ratio comparing the risk of lung cancer with the genetic variant present versus absent if smoking behavior were set to an arbitrary level m. Say, interest could lie in the effect of the genetic variant if none of the individuals smoked so that m = 0. Natural direct effect can be interpreted as the odds ratio comparing the risk of lung cancer with the genetic variant present versus absent if smoking behavior were what it would have been without the genetic variant. Finally, the indirect effect can be interpreted as the odds ratio for lung cancer for those with the genetic variant present comparing the risk if smoking behavior were what it would have been with versus without the genetic variant.

If we replace $({\beta }_0,{\beta }_1,{\mathit{\beta }}_{\mathbf{2}}^{\mathbf{\prime }})$ and $({\theta }_0,{\theta }_1,{\theta }_2,{\theta }_3,{\mathit{\theta }}_{\mathbf{4}}^{\mathbf{\prime }})$ with their maximum likelihood estimators, we will, by the continuous mapping theorem, have consistent estimates for the direct and indirect effects.

3. Asymptotic bias of direct and indirect effects when the mediator is measured with error

3.1. GLM with mis-measured mediator

Using the notation in section 2, assume that both A and C, as well as the outcome Y, are correctly measured. Let M be the continuous mediator at its true level and M* the version of M measured with error. Let the error, u, be additive with mean zero and constant variance ${\sigma }_u^2$,

$$M^{\ast }=M+u.$$

When the mediator is mis-measured, the generalized linear model for the outcome where the true intermediate M is replaced by the observed intermediate M* is given by

$$g^{\ast }(\mu )={\theta }_0^{\ast }+{\theta }_1^{\ast }a+{\theta }_2^{\ast }m\ast +{\theta }_3^{\ast }\mathit{\text{am}}\ast +{\mathit{\theta }}_{\mathbf{4}}^{{\ast }^{\prime }}\mathit{c},$$ (5)

where θ* is the asymptotic limit of the estimators of the outcome regression parameters, θ̂*, when M is replaced by M*.

In the following we assume that the measurement error is characterized by the property of Cov(M, u) = 0 and Cov(M*, u) ≠ 0, usually referred as classical measurement error. Moreover, we assume that the measurement error, u, is independent of the outcome, the exposure, and the covariates (i.e. non-differential).

When the mediator is continuous and measurement error follows the classical measurement error model, it has been shown [10] that ordinary least squares (OLS) estimators of the coefficients of the mediator regression (2) are asymptotically unbiased. However, the assumption that Cov(M*,u) ≠ 0 typically causes parameter estimates of the outcome regression to be asymptotically biased. We proceed by deriving the asymptotic limit for the coefficients' estimators of the outcome equation assuming that mediator-exposure interaction may be present. We will present the results for the outcome regression parameters that are involved in the estimation of direct and indirect effects, that is, θ₁, θ₂, θ₃.

3.2. Asymptotic Limit of parameters of the outcome regression in the presence of exposure-mediator interaction

Suppose that M is subject to classical measurement error and measured as M* and that we fit the outcome regression model with either a linear (3), a logit (4), or any other link under the GLM framework using M* rather than M. Let $({\widehat{\theta }}_1^{\ast },{\widehat{\theta }}_2^{\ast },{\widehat{\theta }}_3^{\ast })$ be the naive maximum likelihood estimators of the outcome regressors if M is replaced by M*. Let (θ₁, θ₂, θ₃) be the true parameters of the regressors. We study the asymptotic limit of the naive estimators of the exposure, mediator and the exposure-mediator interaction coefficients and we denote them by ${\theta }_1^{\ast },{\theta }_2^{\ast }$ and ${\theta }_3^{\ast }$ respectively (See Web Appendix B2 and C2).

Let ${\sigma }_m^2$ and ${\sigma }_u^2$ denote the variance of the true mediator given the exposure and the additional covariates C in the outcome model, and of the measurement error respectively. Set $\lambda ={\sigma }_m^2/({\sigma }_m^2+{\sigma }_u^2)$, which takes values from 0 to 1 and encodes the reliability of the measure for the observed mediator. Recall that β₀, β₁, and ${\beta }_2^{\prime }$ are the coefficients of the mediator regression from equation (2). Let X = (1, A,M, AM,C) and X* = (1, A,M*, AM*,C) denote the matrix of the true and observed covariates respectively. Let Cov (X*, AC) denote the matrix of covariances between the variables in X* with the variables in AC and Cov(X*,A²) denote the vector of covariances between the variables in X* with A². Note that by the assumption of independence between the error, u, and the covariates A and C, the covariances just defined do not depend on the moments of u and therefore Cov(X*, AC) = Cov(X, AC) and Cov(X*,A²) = Cov(X, A²). Define δ_A, δ_M*, δ_AM* to be the row vectors of the matrix E(X*^TX*)⁻¹.

For outcome modeled with any link under the GLM framework we can obtain the following approximation of the asymptotic limit (See Web Appendix B2 and C2)

$$\begin{array}{c}{\theta }_1^{\ast }\approx ({\theta }_1+(1-\lambda )[{\theta }_2{\beta }_1+{\theta }_3\{{\beta }_0+{\delta }_A\mathit{\text{Cov}}(X\ast ,A\mathit{C}){\mathit{\beta }}_{\mathbf{2}}+{\delta }_A\mathit{\text{Cov}}(X\ast ,A^2){\beta }_1\}])H_A(0)\\ {\theta }_2^{\ast }\approx [{\theta }_2\lambda +(1-\lambda ){\theta }_3\{{\delta }_{M\ast }\mathit{\text{Cov}}(X\ast ,A\mathit{C}){\mathit{\beta }}_{\mathbf{2}}+{\delta }_{M\ast }\mathit{\text{Cov}}(X\ast ,A^2){\beta }_1\}]H_{M\ast }(0)\\ {\theta }_3^{\ast }\approx ({\theta }_3[\lambda +(1-\lambda )\{{\delta }_{\mathit{\text{AM}}\ast }\mathit{\text{Cov}}(X\ast ,A\mathit{C}){\mathit{\beta }}_{\mathbf{2}}+{\delta }_{\mathit{\text{AM}}\ast }\mathit{\text{Cov}}(X\ast ,A^2){\beta }_1\}])H_{\mathit{\text{AM}}\ast }(0),\end{array}$$

where H_Z(0) is a function of the joint conditional distribution of AC − E(AC), A² − E(A²)|Z with Z equal to either A, M*, or AM*. When Y is either continuous modeled using a linear link, or is continuous, binary or count and modeled using the log link, the function H_Z(0) takes value 1 and the bias formula is exact (i.e. we can replace the ≈ term with the equality). In general this functional is not recoverable in closed form [29]. However, a numerical bias analysis can still be carried out [23].

Finally, if we assume a binary exposure for which A = A², then the two terms can be incorporated and if additionally the true model included the exposure-covariates interaction terms then the asymptotic limit of the estimators of the regression coefficients could be easily derived in closed form as

$$\begin{array}{c}{\theta }_1^{\ast }=\{{\theta }_1+{\theta }_2(1-\lambda ){\beta }_1+{\theta }_3(1-\lambda )({\beta }_0+{\beta }_1)\}/\tau \\ {\theta }_2^{\ast }={\theta }_2\lambda /\tau \\ {\theta }_3^{\ast }={\theta }_3\lambda /\tau ,\end{array}$$

where for a binary outcome $\tau ={(1+{\theta }_2^2\lambda {\sigma }_u^2/S^2)}^{\frac{1}{2}}$ with $S=\frac{15\pi }{16\sqrt{3}}\sim 1.7$ when logit link is used and S=1 for probit link (note that allowing for exposure-covariates interaction would change the form of the direct and indirect causal effects estimators).

We note that when an exposure-mediator interaction is present, the asymptotic bias has a complex structure. The bias induced by measurement error is coupled with an omitted-variable type of bias induced by the interaction between a variable measured with error, the mediator, and another covariate in the model, the exposure. The above calculations show that when the true model has interaction terms and the outcome is binary, in general no closed form solutions of the asymptotic bias are available. The magnitude of the distortion is related to the magnitude of the measurement error expressed by the reliability factor, λ and to the magnitude of the parameters θ₂ and β₁. We also observe that the magnitude of the distortion is related to the magnitude of the interaction term, θ₃, and the covariance between the variables in the outcome model has impact on how bad the bias could be.

Finally, note that under the non-differential and classical measurement error model and in the absence of exposure-mediator interaction, measurement error typically induces a dilution of the effect of the mediator on the outcome and an over-estimation or an under-estimation of the effect of the exposure on the outcome depending on the sign of the effect of the mediator on the outcome and the sign of the effect of the exposure on the mediator [12]. The above results rely on the assumption of mean zero measurement error. The interested reader can refer to Web Appendix section F for a characterization of the biases relaxing this assumption.

3.3. Asymptotic bias of direct and indirect causal effects

Given the asymptotic convergence of the outcome regression parameters, the asymptotic bias of the estimators of direct and indirect effects when the mediator is measured with error can be obtained. Let γ₁ = δ_ACov(X*, AC), γ₂ = δ_M*Cov(X*, AC), γ₃ = δ_AM*Cov(X*, AC), γ₄ = δ_ACov(X*,A²), γ₅ = δ_M*Cov(X*, A²), and γ₆ = δ_AM*Cov(X*,A²). The asymptotic bias for controlled direct effects, natural direct effects and natural indirect effects when the mean of a continuous outcome is modeled using a linear link and exposure-mediator interaction is present is derived as (See Appendix B3 and C3):

$$\begin{array}{c}\mathit{\text{ABIAS}}(\widehat{\mathit{\text{CDE}}}(m))=(1-\lambda )[{\theta }_2{\beta }_1+{\theta }_3\{{\beta }_0+{\gamma }_1+{\beta }_1{\gamma }_4+m({\gamma }_3+{\beta }_1{\gamma }_6-1)\}](a-\stackrel{\sim }{a})\\ \mathit{\text{ABIAS}}(\widehat{\mathit{\text{NDE}}})=(1-\lambda )[{\theta }_2{\beta }_1+{\theta }_3\{{\beta }_0+{\gamma }_1+{\beta }_1{\gamma }_4+({\beta }_0+{\beta }_1\stackrel{\sim }{a}+{\mathit{\beta }}_{\mathbf{2}}^{\mathbf{\prime }}\mathit{c})({\gamma }_3+{\beta }_1{\gamma }_6-1)\}](a-\stackrel{\sim }{a})\\ \mathit{\text{ABIAS}}(\widehat{\mathit{\text{NIE}}})=(1-\lambda )[{\theta }_3\{{\gamma }_2+{\beta }_1{\gamma }_5+a({\gamma }_3+{\beta }_1{\gamma }_6-1)\}-{\theta }_2]{\beta }_1(a-\stackrel{\sim }{a}).\end{array}$$

We find that in the presence of exposure-mediator interaction the direction of the bias is hard to predict since it depends not only on the relationship among exposure, mediator, outcome and confounders but additionally on the exposure and confounders distributions as we show in the numerical analyses below.

When exposure-mediator interaction is absent the formulas can be simplified and we note that measurement error typically induces an under-estimation of the indirect effect and an over-estimation of the direct effect

$$\begin{array}{c}\mathit{\text{ABIAS}}(\widehat{\mathit{\text{NDE}}})=\mathit{\text{ABIAS}}(\widehat{\mathit{\text{CDE}}}(m))=\{{\theta }_2(1-\lambda ){\beta }_1\}(a-\stackrel{\sim }{a})\\ \mathit{\text{ABIAS}}(\widehat{\mathit{\text{NIE}}})=\{{\theta }_2(\lambda -1)\}{\beta }_1(a-\stackrel{\sim }{a}).\end{array}$$

In the absence of exposure-mediator interaction, if a continuous, count, or binary outcome is modeled using the log link, the asymptotic bias of the estimators of direct and indirect effects on the log-risk ratio scale takes the same form as that given above. If the binary outcome is modeled using logit or probit link, the asymptotic bias for the indirect effect on the log-odds ratio scale is similar to the one derived above (with λ replaced by λ/τ) while the asymptotic bias of the natural direct effect on the log-odds ratio scale is given by

$$\mathit{\text{ABIAS}}(\mathit{log}(\widehat{{\mathit{\text{OR}}}^{\mathit{\text{NDE}}}}))=\mathit{\text{ABIAS}}(\mathit{log}({\mathit{\text{OR}}}^{\widehat{\mathit{\text{CDE}}}(m)}))=\{{\theta }_1(\frac{1}{\tau }-1)+\frac{{\theta }_2(1-\lambda ){\beta }_1}{\tau }\}(a-\stackrel{\sim }{a}),$$

which depends additionally on the magnitude of the effect of the exposure on the outcome, θ₁, and the term τ. Therefore, the choice of link function shapes the impact that measurement error can have on the estimation of direct and indirect causal effect. Results on asymptotic bias of direct and indirect effects for outcome modeled using other links under the GLM framework are more complex and less intuitive in presence of exposure-mediator interaction as explained in Web Appendix C3.

For continuous and binary outcomes, we carried out a simulation study for large sample size to investigate the change of relative bias for the naive direct and indirect causal effect estimators as a function of the magnitude of ${\sigma }_u^2$. We consider four scenarios. We generate samples of dimension n= 10,000 with r = 1000 runs. In the first scenario we define a binary exposure A_i ∼ Ber(p_a) with p_a = 0.4 and a continuous covariate C ∼ N(0,1). The true mediator conditional on A and C is defined as $M|A,C\sim N({\mu }_M,{\sigma }_M^2)$, where μ_M = β₀ + β₁A + β₂C and ${\sigma }_M^2=1$, with β₀ = 0, β₁ = 1, β₂ = 1. The outcome is either normal or binary and in particular we generate $Y|A,M,C\sim N({\mu }_Y,{\sigma }_Y^2)$, where μ_Y = θ₀ + θ₁A + θ₂M + θ₃AM + θ₄C and ${\sigma }_Y^2=1$, with θ₀ = 0, θ₁ = 1, θ₂ = 1, θ₃ = 0, θ₄ = 1 or Y|A, M, C ∼ Ber(p_Y) with p_Y = F(μ_y) where F(u) = exp(u)/(1 + exp(u)) and μ_y = θ₀ + θ₁A + θ₂M + θ₃AM + θ₄C with θ₀ = −2, θ₁ = 0.25, θ₂ = 1, θ₃ = 0, θ₄ = 0.25. In the second scenario we consider a positive interaction and we set θ₃ = 1, in the third scenario we consider a negative interaction and we set θ₃ = −2. The fourth scenario differs from the third in that we specify a normally distributed exposure A ∼ N(0,5). For all simulation settings the observed mediator is defined as M* = M + u and $u\sim N(0,{\sigma }_u^2)$, with ${\sigma }_u^2$ taking values in the range (0,1) which correspond to λ = (0.5,1). The naive outcome and mediator regression models are run simply substituting M with the observed mediator M*.

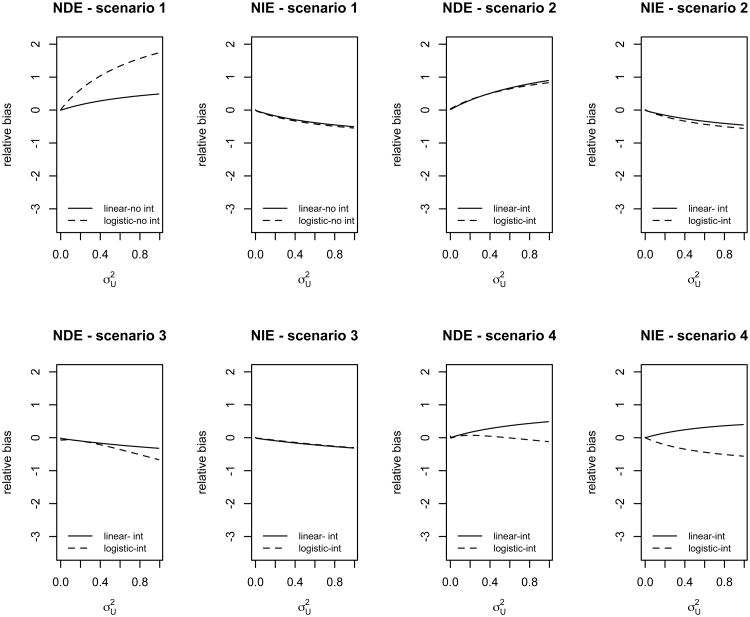
Figure 2 summarizes the findings for naive direct and indirect effect estimators under the settings just described assuming either no interaction and binary exposure, a positive interaction and binary exposure, a negative interaction and binary exposure, or a negative interaction and continuous exposure. Web Figure 1 describes the numerical relative bias study for naive estimators ${\widehat{\theta }}_1^{\ast },{\widehat{\theta }}_2^{\ast },{\widehat{\theta }}_3^{\ast }$ in these scenarios. The numerical study of relative bias for naive direct and indirect effects estimators (Figure 2) helps illustrating that bias due to measurement error could take unexpected directions in the presence of non-linearities. Moreover, in certain cases, measurement error might exert a stronger impact when the outcome is binary rather than continuous in the estimation of direct effects. In the absence of exposure-mediator interaction (first scenario) the estimated direct effect is biased upward and the indirect effect is biased downward; the bias is found to be larger when the outcome is binary. When a positive interaction is present (second scenario) results are similar but for binary outcome the bias of the direct effect is notably smaller compared to that when there is no interaction. For the case of negative interaction and binary exposure (third scenario), natural direct and indirect effects are found to be under-estimated both when the outcome is continuous and binary. In the fourth scenario, for normally distributed outcome and exposure, both direct and indirect effects are found to be over-estimated, while for binary outcome and normally distributed exposure, direct and indirect effects are both found to be under-estimated. Web Figures 2 and 3 describe the bias analysis using the asymptotic bias formulae given in the previous section. The results of the asymptotic bias analyses matched exactly the numerical analyses in most cases. Since no closed form bias formulae are available when the outcome is binary in the presence of interaction, we used the asymptotic results obtained for normally distributed outcome to approximate the true bias in this case. The approximation is found to perform well for binary outcome as generated in scenarios 2 and 3 but departures are observed in scenario 4. We note that measurement error could induce either downward or upward biases of both direct and indirect effect estimators in the presence of interaction, depending on the sign and the magnitude of the vector of parameters θ and β and the distribution of the exposure variable. This contrasts with the result obtained in the context of simple mediation models with no interaction for which it is known that measurement error will bias the direct effect upward and the indirect effect downward [14]. The counterintuitive result occurs because covariate measurement error in non-linear models induces additionally an omitted variable problem. We showed that the relative bias of the outcome regression parameters estimators in the presence of exposure mediator interaction contains covariances involving the terms A² and AC, which are not included the naive outcome regression (5), which consequently is mis-specified. It can be shown that although measurement error in the mediator induces biased direct and indirect effects, the combination of these biased effects, when non-parametric estimators are used, is in fact unbiased for the total effect [16]. However, this statement is true only if the mediator and outcome models with M* replacing M are correctly specified.

Figure 2.

Numerical analysis of relative bias of direct (NDE) and indirect (NIE) effect naive estimators. Simulations run for continuous outcome modeled using linear regression and binary outcome modeled using logistic regression; exposure-mediator interaction both present or absent. Sample size n = 10, 000. Measurement error variance, ${\sigma }_U^2\in (0,1)$, corresponding to a reliability ratio, λ ∈ (0.5, 1). In the absence of interaction, (a) SCENARIO 1 (θ₃=0, A ∼ Ber(0.4)) for Y continuous NDE = 1 and NIE = 1, and for Y binary NDE =1.28 and NIE = 2.71. In the presence of interaction (b) SCENARIO 2 (θ₃=1, A ∼ Ber(0.4)) for Y continuous NDE = 1 and NIE = 2, for Y binary NDE = 1.70 and NIE = 3.49. (c) SCENARIO 3 (θ₃ =-2, A ∼ Ber(0.4)) for Y continuous NDE = 1 and NIE = − 1, for Y binary NDE = 1.28 and NIE = 0.36. (d) SCENARIO 4 (θ₃ =-2, A ∼ N(0,5)) for Y continuous NDE = 1 and NIE = − 1, for Y binary NDE = 1.28 and NIE = 0.36.

4. Correction strategy for direct and indirect effects estimators

In what follows we consider three different approaches to measurement error correction of the outcome regression models, namely method of moments, regression calibration, and SIMEX [12-13,18-23]. These methods are among the most popular and widely used in statistics and epidemiology but they have not been applied to mediation problems and their behavior in this context has not been evaluated. All three methods are appealing for several reasons. First, they require assumptions on the moments of the error, rather than assumptions on its complete distribution, which is typically assumed in structural measurement error models. Second, they can be implemented even when auxiliary data on the mediator are not available but the investigator is willing to implement sensitivity analyses on the measurement error magnitude. Finally, their rationale is very intuitive. We will first describe the proposed methods and we will then illustrate their salient properties via a simulation study. We will compare their performance considering continuous and binary outcomes, and allowing for exposure-mediator interaction.

4.1. Method of moments estimators

The most intuitive way to recover consistent estimators for the outcome regression parameters is by solving the system of equations that arises from the study of the limit of the naive estimators with respect to the true parameters. The limit of the naive estimators depends not only on the true parameters but also on population moments and the measurement error variance. Method of moments estimators arise when the system is solved with respect to the true parameters and the population moments are replaced by sample moments.

If the assumptions on the measurement error mechanism and the modeling assumptions hold, and if we assume that the variance of the measurement error, ${\sigma }_u^2$ is known or can be specified in a sensitivity analysis, and we assume that there is no exposure-mediator interaction, then estimators that consistently estimate θ₁ and θ₂ are easily derived from the results given in the previous sections (See Web Appendix section B4 and C4). When the outcome is continuous, binary or count with mean modeled using linear or logarithmic link the method of moments estimators are given by:

$$\begin{array}{c}{\widehat{\theta }}_2^{\mathit{\text{MoM}}}={\widehat{\theta }}_2^{\ast }/\lambda ,\\ {\widehat{\theta }}_1^{\mathit{\text{MoM}}}={\widehat{\theta }}_1^{\ast }-{\widehat{\theta }}_2^{\mathit{\text{MoM}}}(1-\lambda ){\widehat{\beta }}_1\end{array}$$

where ${\widehat{\theta }}_1^{\ast }$ and ${\widehat{\theta }}_2^{\ast }$ are the naive estimators of θ₁ and θ₂. Note that either setting ${\sigma }_u^2\mathrm{\text{or}}\lambda ={\sigma }_m^2/({\sigma }_m^2+{\sigma }_u^2)$ could be used as sensitivity analysis parameters.

For a binary outcome with mean modeled using either logit or probit link, the system that arises from the approximate limit of the naive estimators can again be solved and the method of moments estimators are given by:

$$\begin{array}{c}{\widehat{\theta }}_2^{\mathit{\text{MoM}}}={\widehat{\theta }}_2^{\ast }/{({\lambda }^2-{\widehat{\theta }}_2^{\ast }\lambda {\sigma }_u^2/S^2)}^{\frac{1}{2}},\\ {\widehat{\theta }}_1^{\mathit{\text{MoM}}}={\widehat{\theta }}_1^{\ast }\{1+{({\widehat{\theta }}_2^{\mathit{\text{MoM}}})}^2{\sigma }_u^2\lambda \}-{\widehat{\theta }}_2^{\mathit{\text{MoM}}}(1-\lambda ){\widehat{\beta }}_1\end{array}$$

where $S=\frac{15\pi }{16\sqrt{3}}\sim 1.7$ when logit link is used and S = 1 when probit link is used.

When exposure-mediator interaction is present in the true model, if again the assumptions on the measurement error mechanism and the modeling assumptions hold, if we assume that the variance of the measurement error, ${\sigma }_u^2$, is known, then estimators for θ₁, θ₂, and θ₃ are derived from the results given in the previous sections. For continuous, binary and count outcomes modeled using linear and log-linear links the method of moment estimators for θ₁, θ₂ and θ₃ are given by:

$$\begin{array}{c}{\widehat{\theta }}_3^{\mathit{\text{MoM}}}={\widehat{\theta }}_3^{\ast }/\{(1-\lambda )({\gamma }_3+{\widehat{\beta }}_1{\gamma }_6)+\lambda \}\\ {\widehat{\theta }}_2^{\mathit{\text{MoM}}}=[{\widehat{\theta }}_2^{\ast }-(1-\lambda ){\widehat{\theta }}_3^{\mathit{\text{MoM}}}\{{\gamma }_2+{\widehat{\beta }}_1{\gamma }_5\}]/\lambda \\ {\widehat{\theta }}_1^{\mathit{\text{MoM}}}={\widehat{\theta }}_1^{\ast }-(1-\lambda )\{{\widehat{\theta }}_2^{\mathit{\text{MoM}}}{\widehat{\beta }}_1-{\widehat{\theta }}_3^{\mathit{\text{MoM}}}({\widehat{\beta }}_0+{\gamma }_1+{\widehat{\beta }}_1{\gamma }_4)\}\end{array}$$

where γ₁, …, γ₆ are as given in section 3.3. When the mean of the outcome is modeled using other links the estimators described above are an approximation of the method of moments estimators. See Web Appendix for further details.

Finally, estimators for direct and indirect causal effects are easily obtained by substituting the naive estimators ${\widehat{\theta }}_1^{\ast },{\widehat{\theta }}_2^{\ast }$, and in the presence of exposure-mediator interaction, ${\widehat{\theta }}_3^{\ast }$ with the method of moments estimators. For example, we can define method of moments estimators of direct and indirect effects when Y is continuous with mean modeled using linear link as follows:

$$\begin{array}{c}\widehat{\mathit{\text{CDE}}}{(m)}_{\mathit{\text{MoM}}}=({\widehat{\theta }}_1^{\mathit{\text{MoM}}}+{\widehat{\theta }}_3^{\mathit{\text{MoM}}}m)(a-\stackrel{\sim }{a})\\ {\widehat{\mathit{\text{NDE}}}}_{\mathit{\text{MoM}}}=({\widehat{\theta }}_1^{\mathit{\text{MoM}}}+{\widehat{\theta }}_3^{\mathit{\text{MoM}}}{\widehat{\beta }}_0+{\widehat{\theta }}_3^{\mathit{\text{MoM}}}{\widehat{\beta }}_1\stackrel{\sim }{a}+{\widehat{\theta }}_3^{\mathit{\text{MoM}}}\mathit{c})(a-\stackrel{\sim }{a})\\ {\widehat{\mathit{\text{NIE}}}}_{\mathit{\text{MoM}}}=({\widehat{\theta }}_2^{\mathit{\text{MoM}}}{\widehat{\beta }}_1+{\widehat{\theta }}_3^{\mathit{\text{MoM}}}{\widehat{\beta }}_{1}a)(a-\stackrel{\sim }{a}).\end{array}$$

Standard errors for the method of moments estimators of direct and indirect effects are derived using the delta method in Web Appendix section B6 and C6.

The implementation of method of moments estimators is straightforward in the absence of exposure-mediator interaction in the true outcome regression model. In Web Appendix C4 we discuss the method of moments estimator for continuous, count and binary outcome with mean modeled using non-linear links in the presence of exposure-mediator interaction. In general, for these cases the method of moments estimator is not of practical use since it involves the previously described functions H_Z(0) with Z equal to either A, M*, AM*, or C which depends on the conditional distribution of $(A\mathit{C}-E(A\mathit{C}),A_i^2-E(A^2))$ given the covariates in the outcome regression model, an object that is usually hard to derive. When the function H_Z(0) cannot be recovered, the method of moments estimators for the outcome parameters that we just gave for the linear link case or other estimators such as regression calibration and SIMEX estimators, which will be approximately consistent in these settings, should be considered.

4.2. Regression calibration estimators

The use of regression calibration to obtain consistent estimators for linear regression coefficients and approximately consistent estimators in the case of logistic regression is based on the assumption of non-differential measurement error of a continuous variable [12,18-21,30]. This approach has been successfully applied in the context of classical measurement error but can be adapted to multiplicative measurement error as described in [12] as well as to non-zero mean measurement error as we illustrate in Web appendix section F.

Regression calibration estimators ${\widehat{\theta }}_1^{\mathit{\text{rc}}},{\widehat{\theta }}_2^{\mathit{\text{rc}}},{\widehat{\theta }}_3^{\mathit{\text{rc}}}$ can be recovered in a rather simple way (Web Appendix section B5 and C5). First, a calibration model for the regression of the unknown continuous covariate M on the observed mediator M*, exposure A and the covariates C is developed and fitted (in the present study we considered a linear calibration model as suggested by [12]). This can be accomplished using replication, validation, or instrumental data. When auxiliary data are not available and the variance of the measurement error is unknown, the value of the measurement error variance ${\sigma }_u^2$ is set as a sensitivity analysis parameter. As before, either ${\sigma }_u^2\mathrm{\text{or}}\lambda ={\sigma }_m^2/({\sigma }_m^2+{\sigma }_u^2)$ could be used as sensitivity analysis parameters. Note that regression calibration does not require M to be normally distributed. The unobserved M is then replaced by its predicted values M̂ from the calibration model in a standard analysis. Finally, the standard errors are adjusted to account for the estimation of the unknown covariates.

Regression calibration estimators ${\widehat{\theta }}_1^{\mathit{\text{rc}}},{\widehat{\theta }}_2^{\mathit{\text{rc}}},{\widehat{\theta }}_3^{\mathit{\text{rc}}}$ can be recovered in a similar way in the case of logistic regression. For binary outcome regression calibration estimators will yield approximately consistent estimators, provided measurement error is small and the effect of the mediator on the outcome is not too large in absolute value [30]. Note that regression calibration estimators and method of moments estimators for parameters of linear regression, under the assumption that ${\sigma }_u^2$ is known, coincide if there is no exposure-mediator interaction and are consistent [12]. However, they won't coincide when the outcome model is modeled using non-linear links or in the presence of exposure-mediator interaction. For continuous outcome and normally distributed mediator, in the presence of exposure-mediator interaction, the approaches are consistent [17]. For binary outcome the approaches will be only approximately consistent [12,30]. In particular, in the absence of exposure-mediator interaction, the method of moments estimator might be preferred to the regression calibration estimator since it provides a better approximation to the consistent estimators and is expected to perform better when measurement error is large. In the presence of exposure-mediator interaction regression calibration might be preferred since the method of moments estimator is hard to recover. Standard errors for the regression calibration estimators of direct and indirect effects can be obtained using bootstrapping procedures [12].

4.3. SIMEX

SIMEX is a simulation-based approach for measurement error correction, a full description is given by [12,22]. The SIMEX-method exploits the functional relationship between the measurement error variance, ${\sigma }_u^2$, and the limit of the naive estimators, θ*.

Let $\mathcal{G}({\sigma }_u^2)$ be a function of the measurement error variance, called extrapolation function. A consistent estimator of θ when there is no measurement error is such that (0) = θ. SIMEX, by employing a parametric approach, defines the extrapolation function as $\mathcal{G}({\sigma }_u^2,\mathrm{\Gamma })$ where Γ denotes an unknown vector of parameters governing the relationship between the measurement error variance, ${\sigma }_u^2$, and the limit of the naive estimators, θ*. A typical default for the extrapolation function is quadratic, ${\mathcal{G}}_{\mathit{\text{quadratic}}}({\sigma }_u^2,\mathrm{\Gamma })={\gamma }_0+{\gamma }_1{\sigma }_u^2+{\gamma }_2{({\sigma }_u^2)}^2$.

Given ${\sigma }_u^2$ either known or specified in a sensitivity analysis, the SIMEX approach consists of two steps. To estimate Γ a simulation step is carried out that adds measurement error with variance $\xi {\sigma }_u^2$ to the contaminated variable. The resulting measurement error variance is then $(1+\xi ){\sigma }_u^2$. The naive estimator for this increased measurement error is calculated and repeated B times. The average over B converges to $\mathcal{G}((1+\xi ){\sigma }_u^2)$. Repeating this simulations for a fixed grid of positive values ξ, for which the larger ξ the larger is the magnitude of measurement error, leads to an estimator Γ̂ of the parameters ${\mathcal{G}}_{\mathit{\text{quadratic}}}({\sigma }_u^2,\mathrm{\Gamma })$, for example by least squares. In a second step, the extrapolation step, the approximated function ${\mathcal{G}}_{\mathit{\text{quadratic}}}({\sigma }_u^2,\widehat{\mathrm{\Gamma }})$ is extrapolated back to the case of no measurement error and so the SIMEX estimator is defined by ${\theta }_{\mathit{\text{SIMEX}}}({\sigma }_u^2)={\mathcal{G}}_{\mathit{\text{quadratic}}}(0,\widehat{\mathrm{\Gamma }})$, which corresponds to ρ = −1.

Some drawbacks of this method should be mentioned. The SIMEX method is almost always only approximately consistent due to the fact that we generally don't know the true extrapolation function. When the magnitude of the measurement error is substantial the method might not perform well if the extrapolation function is far from the truth. Moreover, SIMEX is computationally less efficient than the regression calibration and method of moments estimators.

Even if this method is only approximately consistent and computationally less efficient than the regression calibration estimator, we consider implementing it for several reasons. First of all, we have seen in the previous sections that, in general, intuitive analytical formulae for asymptotic bias for binary outcome regression parameters in the presence of exposure-mediator interaction, cannot be recovered. Therefore, the first step of the SIMEX approach can be useful in visualizing the effect of measurement error on the parameter estimates for a given or estimated value of ${\sigma }_u^2$. Second, this method is particularly robust against modeling the structure of the unobservable mediator since it does not require any assumptions on the latent mediator nor on the moments of the measurement error. Finally, this approach has been widely used in the context of generalized linear models.

When the outcome is linear and there is no exposure-mediator interaction, SIMEX approach and regression calibration will yield very similar estimators but otherwise they can in general differ. Standard errors for the SIMEX estimators of direct and indirect effects can be obtained using bootstrapping procedures [12,22].

4.4. Simulations

We now evaluate the performance in estimating the outcome regression parameters and the direct and indirect effects of interest of the three methods proposed for measurement error correction, namely method of moments, regression calibration and SIMEX (with quadratic extrapolation function). To compare the methodologies for each estimator we estimate their relative bias, variance and mean squared error. In particular we are interested in comparing their behavior in the presence of non-linearities, which in our study arise when an exposure-mediator interaction is present and if the link is non-linear.

The simulation settings are the same as the first and second scenarios considered in the numerical bias analysis in section 3.3 in which the indirect effect of A on Y through M as well as the positive exposure-mediator interaction, if present, are particularly strong. The simulations are now run using a sample size of n = 1, 500, which mimics a more realistic study sample size, and r = 1000 runs. In the Web Appendix section E we display results of additional simulation studies considering the setting of non-normally distributed mediator. Tables 1 and 2 present the simulations results for ${\sigma }_u^2=(0.1,0.5)$ which correspond to a reliability ratio λ = (0.90,0.67), considering cases of small and moderate measurement error.

Table 1. Simulations for naive, method of moments (MoM), regression calibration (RC) and SIMEX estimators of direct, indirect and total effects with continuous (linear link) outcome. Measurement error variance is set to ${\sigma }_u^2=(0.1,0.5)$ which correspond to a reliability ratio λ = (0.90,0.67).

( ${\sigma }_u^2=0.1$, n = 1,500) Effect (θ3 = 0)	Relative Bias				Variance				MSE
	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX
NDE=1	0.093	-0.006	0.006	0.006	0.003	0.003	0.003	0.003	0.01	0.003	0.003	0.003
NIE= 1	-0.087	0.004	0.004	0.000	0.003	0.004	0.004	0.004	0.01	0.004	0.004	0.004
TE=2	0.0015	0.0015	0.0015	0.0015	0.005	0.005	0.005	0.005	0.005	0.005	0.005	0.005
( ${\sigma }_u^2=0.5$, n = 1,500) Effect (θ3 = 0)	Relative Bias				Variance				MSE
	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX
NDE=1	0.332	-0.004	-0.004	0.099	0.004	0.005	0.005	0.005	0.11	0.005	0.005	0.014
NIE=1	-0.333	0.008	0.008	0.096	0.002	0.007	0.007	0.005	0.1	0.007	0.007	0.014
TE=2	0.0015	0.0015	0.0015	0.0015	0.005	0.005	0.005	0.005	0.005	0.005	0.005	0.005
( ${\sigma }_u^2=0.1$, n = 1,500) Effect (θ3 ≠ 0)	Relative Bias				Variance				MSE
	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX
CDE(m=0)=1	0.158	-0.016	-0.001	0.117	0.005	0.005	0.005	0.005	0.030	0.005	0.005	0.018
NDE=1	0.187	0.041	0.026	0.144	0.007	0.008	0.008	0.007	0.040	0.009	0.009	0.027
NIE=2	-0.077	0.006	0.001	-0.057	0.013	0.015	0.015	0.014	0.037	0.015	0.015	0.027
TE=3	0.009	0.009	0.009	0.009	0.011	0.011	0.011	0.011	0.012	0.012	0.012	0.012
( ${\sigma }_u^2=0.5$, n = 1,500) Effect (θ3 ≠ 0)	Relative Bias				Variance				MSE
	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX
CDE(m=0)=1	0.587	0.190	-0.004	0.506	0.007	0.009	0.011	0.008	0.352	0.045	0.011	0.254
NDE=1	0.626	0.219	0.020	0.543	0.009	0.013	0.016	0.010	0.383	0.058	0.016	0.265
NIE=2	-0.292	-0.093	0.004	-0.251	0.011	0.018	0.023	0.0112	0.352	0.053	0.023	0.265
TE=3	-0.01	-0.01	-0.01	-0.01	0.01	0.01	0.01	0.01	0.00	0.00	0.00	0.00

Table 2.

Simulations for naive, method of moments (MoM), regression calibration (RC) and SIMEX estimators of direct, indirect and total effects with binary (logistic link) outcome. Measurement error variance is set to ${\sigma }_u^2=(0.1,0.5)$, which correspond to a reliability ratio λ = (0.90,0.67).

( ${\sigma }_u^2=0.1$, n = 1,500) Effect (θ3 = 0)	Relative Bias				Variance				MSE
	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX
NDE=1.28	0.258	-0.059	-0.107	-0.06	0.022	0.019	0.019	0.019	0.022	0.019	0.019	0.019
NIE=2.71	-0.09	0.009	0.001	0.010	0.008	0.011	0.010	0.011	0.016	0.011	0.010	0.011
TE=3.46	-0.02	-0.004	-0.02	-0.004	0.018	0.019	0.018	0.019	0.019	0.019	0.019	0.019
( ${\sigma }_u^2=0.5$, n = 1,500) Effect (θ3 = 0)	Relative Bias				Variance				MSE
	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX
NDE=1.28	1.141	-0.090	-0.145	0.35	0.016	0.019	0.02	0.018	0.097	0.021	0.021	0.026
NIE=2.71	-0.36	0.01	-0.038	-0.118	0.004	0.011	0.013	0.010	0.135	0.014	0.013	0.02
TE=3.46	-0.06	-0.006	-0.06	-0.024	0.017	0.019	0.017	0.018	0.022	0.019	0.022	0.019
( ${\sigma }_u^2=0.1$, n = 1,500) Effect (θ3 ≠ 0)	Relative Bias				Variance				MSE
	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX
CDE=1.28	0.133	0.030	0.017	0.242	0.094	0.081	0.080	0.128	0.123	0.082	0.081	0.225
NDE=1.70	0.092	0.030	0.028	0.006	0.071	0.066	0.066	0.068	0.095	0.069	0.067	0.068
NIE=3.49	-0.108	-0.016	-0.005	-0.098	0.181	0.254	0.265	0.183	0.323	0.257	0.265	0.299
TE=5.93	-0.027	0.010	0.015	-0.093	1.247	1.558	1.591	1.140	1.272	1.561	1.598	1.444
( ${\sigma }_u^2=0.5$, n = 1,500) Effect (θ3 ≠ 0)	Relative Bias				Variance				MSE
	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX	Naive	MoM	RC	SIMEX
CDE=1.28	0.525	0.194	0.044	0.856	0.138	0.096	0.083	0.286	0.594	0.158	0.086	1.494
NDE=1.70	0.351	0.159	0.075	0.065	0.102	0.097	0.103	0.099	0.454	0.169	0.119	0.111
NIE=3.49	-0.370	-0.191	-0.077	-0.356	0.055	0.147	0.239	0.056	1.724	0.591	0.311	1.599
TE=5.93	-0.150	-0.061	-0.006	-0.315	0.743	1.497	1.659	0.668	1.497	1.628	1.68	4.115

Comparing the three proposed methods of correction we note that regression calibration has consistently good performance over all the scenarios considered. We notice that SIMEX does substantially worse than regression calibration in the presence of exposure-mediator interaction and moderate to severe measurement error. These results are mainly driven by the fact that SIMEX estimator for the interaction term has relatively poor performance. Notably, when the outcome is binary and in the absence of exposure-mediator interaction, as expected, regression calibration, being an approximately consistent estimator, does slightly worse than method of moments in terms of relative bias. Method of moments in this case gives a better approximation to the consistent estimator. In the presence of exposure-mediator interaction and severe measurement error, instead, regression calibration performs slightly better than method of moments. We implemented a small sample version of methods of moments proposed by Murad and Freedman [17] and the performance did not substantially improve relatively to regression calibration (See Web Appendix section D). The simulation results on mean squared error for SIMEX are similar to regression calibration and method of moments when measurement error is small. However, when measurement error is moderate, the other two approaches are found to outperform SIMEX for the cases considered.

5. Example

We applied the proposed methods to a recent study on the etiology of lung cancer.

VanderWeele et al. [8] investigated the extent to which the effect of genetic variants rs8034191 and rs1051730 on chromosome 15q25.1 on lung cancer is direct and to what extent that association is mediated by cigarette smoking. Mediation analysis allowing for gene-environment interaction, as described in the second section, was applied to a case-control study of Massachusetts General Hospital (MGH) where 1836 cases and 1452 controls were sampled. Eligible cases included any person over the age of 18 years, with a diagnosis of primary lung cancer that was further confirmed by an MGH lung pathologist. The controls (with no previous history of cancer) were recruited from among the friends or spouses of cancer patients or the friends or spouses of other surgery patients in the same hospital.

The study [8] reported statistically significant additive interaction (P=2 × 10⁻¹⁰ and P=1 × 10⁻⁹) and multiplicative interaction (P=0.01 and P=0.01) between the genetic variants and smoking behavior, measured in terms of square-root average cigarettes per-day. The authors implemented the methodology for mediation analysis in the presence of exposure-mediator interaction adjusting for race, sex, and college education (results in Table 3).

Table 3.

Sensitivity analysis results for direct (OR^NDE), indirect (OR^NIE) effects and proportion mediated (PM = OR^NDE × (OR^NIE − 1)/(OR^NDE × OR^NIE − 1)) for variants rs1051730 and rs8034191 allowing for exposure-mediator interaction and attenuation factor λ up to 0.25.

rs1051730	λ =1 (naive)	λ =.75	λ =.50	λ =.25
ORNDE	1.26 (1.19,1.33)	1.278 (1.13,1.46)	1.271 (1.12,1.45)	1.307 (1.16,1.49)
ORNIE	1.00 (1.00,1.01)	1.014 (0.99,1.03)	1.021 (0.99,1.04)	1.045 (0.99,1.10)
PM*	0.03 (-0.02, 0.10)	0.063 (-0.03,0.18)	0.095 (-0.03,0.26)	0.159 (-0.06,0.37)
rs8034191	λ =1 (naive)	λ =.75	λ =.50	λ =.25
ORNDE	1.26 (1.19,1.33)	1.299 (1.14,1.47)	1.292 (1.14,1.47)	1.330 (1.17,1.49)
ORNIE	1.01 (1.00,1.01)	1.014 (0.99,1.03)	1.021 (0.99,1.05)	1.044 (0.99,1.11)
PM*	0.03 (-0.01,0.10)	0.059 (-0.01,0.17)	0.088 (-0.02,0.26)	0.152 (0.03,0.40)

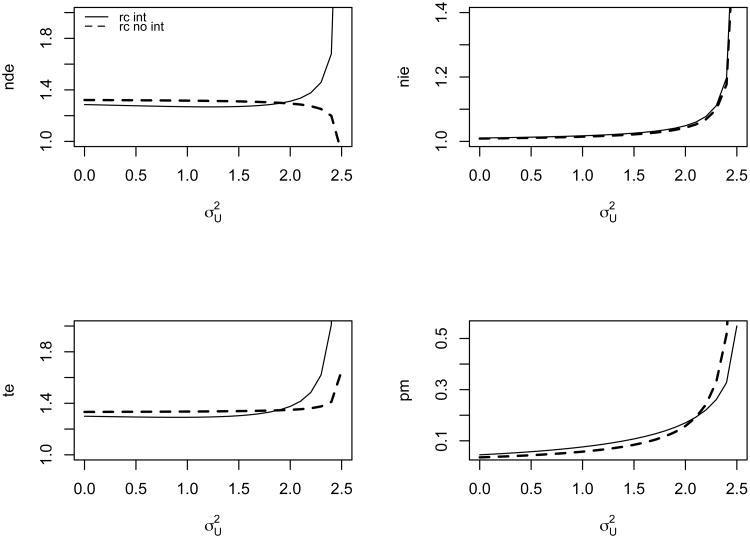
We now present the results of the adjustment for measurement error allowing for the presence of exposure-mediator interaction by means of a sensitivity analysis using regression calibration which was the method that performed best in the simulation study. Setting the attenuation factor λ equal to 0.75, 0.5, and 0.25 (which correspond, given our data, to a variance of the measurement error variable u, ${\sigma }_u^2$, equal to 0.65,1.3, and 2 respectively), we obtain the corrected direct and indirect effects and percentile confidence intervals from 1,000 bootstrap replications and proportion mediated presented in Table 3. Additional sensitivity analyses employing the method of moments and SIMEX approaches yielded very similar results (see Web Figure 2 and Web tables 2 and 3).

The analysis reveals that measurement error induces an underestimate of the indirect effect of the genetic variants on lung cancer mediated by smoking behavior. The direct effect is also found to be slightly underestimated. Figure 3 depicts the sensitivity of the estimates of total effect of the variants on lung cancer (TE), natural direct (NDE), natural indirect effects (NIE) and proportion mediated (PM) to the increase of measurement error had we assumed exposure-mediator interaction either present or absent.

Figure 3.

Sensitivity analyses for direct (OR^NDE), indirect (OR^NIE), total (OR^TE = OR^NDE × OR^NIE) effects and proportion mediated (PM = OR^NDE × (OR^NIE − 1)/(OR^NDE × OR^NIE − 1)) for variant rs1051730. Absent to severe measurement error $({\sigma }_U^2\in (0,2.5))$ which corresponds to a reliability ratio, λ ∈ (0, 1).

We note that ignoring the presence of gene-environment interaction, for large measurement error (λ < 0.25), the sensitivity analysis would show an upward bias for the direct effect, which is the opposite from what the analysis taking into account the interaction reveals. Moreover, the sensitivity analysis shows a downward bias for the indirect effect both ignoring the interaction and when taking it into account. Although correcting for measurement error we obtain slightly different results from the naive analysis, we can still conclude that for all the values considered in the sensitivity analysis (λ = 0.75, 0.5, 0.25) the association of the variants with lung cancer is primarily through pathways other than cigarettes per day (with proportion of the effect of the genetic variants on lung cancer mediated through smoking (PM) taking up to the values of 16% in case of lager measurement error). Further analyses were conducted to relax the mean zero error assumption allowing for a systematic under-reporting of the number of cigarettes smoked per day and the results remained qualitatively consistent (see Web appendix section F and Web Figure 3). The violation of the assumption of non-differential measurement error is a potential limitation of the analyses. In particular, in some instances cases might be more likely to over-report their smoking habits while control individuals might actually be more likely to under-report their smoking habits [31]. Recall bias would induce an over-estimate of the effect of the effect of the mediator on the outcome and therefore an over-estimate of the indirect effect. In this scenario, our conclusion that most of the effect is not through average number of cigarettes smoked per day would still be valid, since even under large measurement error our already small indirect effect estimate might be an overestimate.

6. Discussion

We have studied the problem of measurement error in the context of causal mediation analysis in GLMs, where exposure-mediator interaction can be present. We have demonstrated that classical and non-differential measurement error on a continuous mediator can undermine the validity of the estimators of direct and indirect causal effects that have been employed. The theoretical results and a numerical study illustrate that when exposure-mediator interaction is present or the outcome is not continuous, the impact of measurement error might be severe. We showed that the bias of the causal effects estimators that ignore measurement error can take unintuitive directions in the presence of non-linearities.

VanderWeele et al. [16] show that although measurement error in the mediator induces biased direct and indirect effects, the combination of these biased effects is in fact unbiased for the total effect. However, this statement is true only if the mediator and outcome models with M* replacing M are correctly specified. In both the simulations and the example above, when exposure-mediator interaction is present or the link function of the outcome model is non-linear, the total effect of the exposure on the outcome (computed as either the sum or the product of direct and indirect effects) was also biased. This phenomenon occurs because covariate measurement error in non-linear models additionally induces model mis-specification, which is what gives rise to the bias in the estimates of total effects as well. We note that for the mediation setting described in section 2, assuming a linear relationship between the exposure and the mediator, under the null hypothesis of no mediated effect, the naive estimator of the natural indirect effect will be unbiased even in non-linear models (See Web Appendix section G).

We proposed a solution to the problem of measurement error that does not require distributional assumptions on the latent mediator observed with error. We considered regression calibration, a SIMEX procedure, and a moment method as possible strategies of correction for measurement error. We compared the performance of corrected estimators for direct and indirect effects in a simulation study. Regression calibration has been found to perform well over the scenarios considered. Method of moments estimators outperformed the other two approaches in the case of binary outcome in the absence of interaction. Regression calibration was found to improve over method of moments in the presence of exposure-mediator interaction and severe measurement error. The SIMEX approach performed poorly when the magnitude of measurement error was moderate to severe. Note that the regression calibration approach does not require the mediator to be normally distributed. In additional simulation studies, the approaches performed fairly well for mediators with symmetric, heavy-tailed distribution. However, the approaches may not eliminate bias for mediators displaying highly skewed distributions, in which case the investigator should consider transforming the mediator variable (see Web Appendix section E for further discussion).

In many instances auxiliary information on the mis-measured intermediate is not available in mediation studies. We illustrated in a real data example the correction strategy coupled with sensitivity analysis for the unknown variance of the measurement error, ${\sigma }_u^2$, for which no validation data or replicates for the mis-measured mediator is needed. Although the correction strategy using sensitivity analysis does not require validation data or replicates for the mis-measured mediator, the corrected estimators could be recovered by making use of this information, if available.

Throughout the paper we took a functional approach rather than a structural approach to measurement error. The former makes no assumptions about the distribution of the unobservables, the latter typically makes distributional assumptions. The appeal of functional modeling is model robustness. Alternatively, we could have taken a structural approach as in [1]. In this paper, we assumed classical measurement error for which Cov(M,u) = 0 and Cov(M*,u) ≠ 0. We could have assumed Cov(M,u) ≠ 0 and Cov(M*,u) = 0, also called Berkson measurement error model. Note that under the Berkson model, for the case of continuous mediator and outcome, it follows from [12] that the estimators of direct and indirect effect result in asymptotically unbiased estimates, even if measurement error was ignored.

Some possible extensions of our study should be mentioned. While leaving the distribution of the latent mediator unspecified, we make the strong assumptions of independence between the measurement error, u, and all the other variables measured without error. In particular, the assumption about the independence between the measurement error variable, u, and the outcome, Y, is critical for the validity of our asymptotic bias calculations as well as the proposed methods of correction. Care should be given in evaluating the plausibility of the assumption of non-differential measurement error. The effect of a misclassified binary mediator on the validity of mediation analysis would be of interest in future work.