One-year test-retest reliability of intrinsic connectivity network fMRI in older adults

Abstract

“Resting-state” or task-free fMRI can assess intrinsic connectivity network (ICN) integrity in health and disease, suggesting a potential for use of these methods as disease-monitoring biomarkers. Numerous analytical options are available, including model-driven ROI-based correlation analysis and model-free, independent component analysis (ICA). High test-retest reliability will be a necessary feature of a successful ICN biomarker, yet available reliability data remains limited. Here, we examined ICN fMRI test-retest reliability in 24 healthy older subjects scanned roughly one year apart. We focused on the salience network, a disease-relevant ICN not previously subjected to reliability analysis. Most ICN analytical methods proved reliable (intraclass coefficients > 0.4) and could be further improved by wavelet analysis. Seed-based ROI correlation analysis showed high map-wise reliability, whereas graph theoretical measures and temporal concatenation group ICA produced the most reliable individual unit-wise outcomes. Including global signal regression in ROI-based correlation analyses reduced reliability. Our study provides a direct comparison between the most commonly used ICN fMRI methods and potential guidelines for measuring intrinsic connectivity in aging control and patient populations over time.

1. Introduction

Large-scale distributed neural networks organize healthy brain function and represent the selective targets of neurodegenerative illness (Seeley et al., 2009). “Resting-state” or intrinsic connectivity network (ICN) fMRI provides a new tool for examining network integrity and, potentially, for following networks over time (Fox et al., 2005; Fox and Raichle, 2007; Damoiseaux et al., 2006). Across neuropsychiatric diseases, more sensitive longitudinal imaging biomarkers would increase the efficiency of drug discovery pipelines, most of which continue to rely on long-term clinical outcome measures. Emerging data suggest that ICN fMRI represents a promising method for tracking longitudinal change, but rigorous evaluation is needed about the test-retest reliability of ICN measures (Achard and Bullmore, 2007; Harrison et al., 2008).

A few recent studies have examined ICN fMRI reliability in healthy young subjects (Shehzad et al., 2009; Zuo et al., 2010; Schwarz and McGonigle, 2011; Wang et al., 2011). Collectively, these studies covered diverse analytical strategies, including the seed-based region-of-interest (ROI) approach, ROI correlation matrices, graph theoretical analyses, and independent component analysis (ICA). Across these strategies, ICN fMRI showed moderate to good reliability (intraclass correlation coefficients (ICCs) > 0.4) in healthy young adults re-scanned after one year. These initial studies were conducted on the same publicly available dataset but examined different ICNs, making it difficult to compare results across methods and studies. To support neurodegenerative disease research, ICN fMRI reliability needs to be established in healthy older individuals, and lingering questions regarding optimal methods need to be resolved.

Here, we examined test-retest reliability of ICN fMRI in 24 healthy older adults scanned approximately one year apart. To provide a direct comparison between several related analytical strategies, we focused on a single ICN, the salience network (Seeley et al., 2009; 2007). This ICN has been widely replicated in the ICN literature and pertains to several neurological and psychiatric illnesses (Seeley et al., 2009; Zhou et al., 2010; Habas et al., 2009; White et al., 2010; Greicius et al., 2008), but has not been the subject of previous reliability analyses. The findings provide a valuable guide for ICN analysis in aging populations.

2. Materials and methods

2.1. Subjects

Twenty-four right-handed healthy older subjects (13 female) were recruited through the University of California, San Francisco (UCSF) Memory and Aging Center. All underwent a comprehensive neuropsychological assessment and a neurological exam within 180 days of MRI scanning (Table 1) and had a Clinical Dementia Rating (CDR) Scale total score of 0, a Mini Mental State Examination (MMSE) of 28 or higher, no significant history of neurological disease or structural lesion on MRI, and a consensus diagnosis of cognitively normal. Subjects were scanned twice, 13 months (s.d. 3) apart. The mean age at the first scan was 66.7 years (s.d. 6.4).

Table 1.

Subject demographics and reliability results summarized for the present older control analyses and for the young controls assessed in previous studies. Reliability results listed here are those assessed on all subjects in both the present and previous studies.

Dataset	Older control	Young control
Age at 1st scan, yrs (s.d.)	66.7 (6.4)	20.5 (8.4)
Gender, M/F	11/13	11/15
Scan interval, mos (s.d.)	13 (3)	11 (5)
Education, yrs (s.d.)	17.5 (1.8)	N.A.

Network evaluated	Salience	Multiple
Seed-based ROI approach
Map-wise ICC	0.54-0.68	N.A.
Voxel-wise ICC	0.27-0.33	0.13-0.45#a
ROI matrix analysis
Map-wise ICC	0.49	0.50b
ROI pair-wise ICC	0.26	0.22-0.23a
ROI matrix analysis (wavelet)
Map-wise ICC	0.59	N.A.
ROI pair-wise ICC	0.32	N.A.
Weighted clustering coefficient
Map-wise ICC	0.54	~0.5b; ~0.2d
Node-wise ICC	0.41	~0.2d
Weighted clustering coefficient (wavelet)
Map-wise ICC	0.52	N.A.
Node-wise ICC	0.53	N.A.
TC-GICA
Map-wise ICC	0.58	N.A.
Voxel-wise ICC	0.31	N.A.
	0.62+	0.45-0.65+c

Note: ICC values for older controls were computed with white matter, CSF and non-brain signals as the nuisance regressors and averaged across all units (voxels, ROI pairs and nodes), unless noted otherwise.

^#Seeded separately at posterior cingulate cortex (PCC), supplementary motor area (SMA), and the inferior parietal sulcus (IPS) and ICC averaged across significant voxels (positive and negative)

⁺Modal ICCs of voxels in the identified components

^aMutiple networks; White matter, CSF, global signals and movement parameters removed (Shehzad et al., 2009)

^bWhole brain network based on ROIs defined by automated anatomical labeling (AAL) altas. White matter, CSF signals and movement parameters removed (Schwarz and McGonigle, 2011)

^cComponents associated with sensory, motor, higher order cognitive function and the default mode network (Zuo et al., 2010).

^dWhole brain network based on ROIs defined by AAL, Harvard-Oxford atlas and meta-analysis. Global signal and movement parameters removed (Wang et al, 2011). Indicate that values listed are means (except where specified)

2.2. Image Acquisition

All structural and functional images were acquired at the UCSF Neuroscience Imaging Center, on a 3 Tesla Siemens Tim Trio scanner equipped with a 12-channel receiver head coil. A volumetric magnetization prepared rapid gradient echo (MP-RAGE) sequence was used to obtain T1-weighted images of the entire brain (TR/TE/TI = 2300/3/900 ms, flip angle of 9 degrees, a bandwidth of 240 Hz/pixel, sagittal orientation with a FOV = 256 × 240 mm and 160 slices). “Resting state” or task-free fMRI scans were obtained using 36 axial slices (3 mm thick) parallel to the plane connecting the anterior and posterior commissures and covering the whole brain using a T2*-weighted gradient echo–echo planar sequence (TR/TE = 2000/27 ms, flip angle 80°; FOV = 230 × 230 mm; matrix size: 92 × 92; 3 mm slices with 2.5 × 2.5 × 3 mm resolution). All subjects underwent 8 minutes of scanning after being instructed only to remain awake with their eyes closed.

2.3. Image processing and analysis

After discarding the first eight frames to allow for magnetic field stabilization, functional images were realigned and unwarped, slice-time corrected, normalized and smoothed with a 4mm full-width at half-maximum Gaussian kernel using SPM8 (http://www.fil.ion.ucl.ac.uk/spm/). Normalization was carried out by calculating the warping parameters between the mean T2* images and the Montreal Neurological Institute (MNI) echo planar imaging template and applying them to all images in the sequence. Subsequently, the images were resampled at a voxel size of 2 mm³.

Motion parameters calculated during realignment were used to separate the 24 subjects into two subgroups. Group ‘mvmt<3’ (N = 20) included subjects with less than 3 mm of movement fluctuation in either translation or rotation during both scans, and group ‘mvmt<2’ (N = 15) included subjects with less than 2 mm movement fluctuation during both scans. Reliability analyses were performed separately on ‘All subjects’, ‘mvmt<3’ and ‘mvmt<2’ groups to assess the effects of motion on the reliability of ICN fMRI measures.

2.4. Test-retest reliability

The reliability of each ICN fMRI measure was quantified by calculating the intra-class coefficient (ICC) across the two scans (Shrout and Fleiss, 1979; McGraw, 1996). A oneway ANOVA was applied to the measures of the two scan sessions across subjects, to calculate between-subject mean square error (MS_p) and within-subject mean square error (MS_e). ICC values were then calculated as:

$$ICC=\frac{MSp-MSe}{MSp+(d-1)MSe}$$

where d = the number of observations per subject

This form of the ICC measures the absolute agreement between the measures of the two different scan sessions and has been used in previous reliability analyses of fMRI data (Shehzad et al., 2009; Zuo et al., 2010; Telesford et al., 2010; Schwarz and McGonigle, 2011; Wang et al., 2011). For the present study, test-retest reliability was characterized as excellent (ICC > 0.8), good (ICC 0.6 – 0.79), moderate (ICC 0.4 – 0.59), fair (ICC 0.2 – 0.39) or poor (ICC < 0.2).

2.5. ICN fMRI measures

We compared the test-retest reliability of commonly used ICN analytical strategies, including three model-driven approaches, the seed-based ROI approach, ROI correlation matrix, and graph theoretical analyses, and two model-free approaches, ICA with template-matching and temporal concatenation group ICA with back reconstruction (Supplementary Table 1). To make meaningful comparisons between methods, we assessed the reliability of these approaches in measuring functional connectivity within the same network – the salience network.

2.6. Seed-based ROI approaches

Previous studies identified the right frontoinsula as an effective ROI seed for deriving the salience network (Seeley et al., 2007; Sridharan et al., 2008). Since our purpose was to assess reliability of seed-based ROI approaches more generally, we used four clusters within the anterior insula as salience network ROI seeds to ensure that our reliability findings would not be biased by any one ROI seed. These four anterior insula clusters were drawn from a activation likelihood estimate meta-analysis of task-based fMRI studies that activated the insula and represent foci related to cognitive and social-emotional paradigms. The cognitive clusters are located in the dorsal anterior insula (one per hemisphere), whereas the social-emotional clusters are positioned in the ventral anterior insula (also one per hemisphere - for further details, see Kurth et al. 2010).

The four anterior insula clusters were used as seeds in separate seed-based ROI functional connectivity analyses, following previous methods (Seeley et al., 2007). Briefly, temporal filtering was performed on each brain voxel using a band-pass filter (0.0083/s < f < 0.15/s) to reduce the effect of low-frequency drift and high-frequency noise (Lowe et al., 1998). Then, the average voxel-wise time series from each ROI was detrended and used as a covariate of interest in a whole-brain, linear regression, statistical parametric analysis. This procedure generated a statistical parametric map from each scan session, where each voxel was scored based on its spontaneous BOLD signal correlation with the seed ROI used in the analysis (henceforth referred to as “connectivity”). Additionally, we manipulated several frequently used noise reduction strategies, including regression of white matter, CSF, non-brain (voxels that are not gray matter, white matter or CSF) and global signal time courses and motion parameters, to determine the impact of these nuisance regressors on reliability.

For every ICN derivation approach, we assessed reliability at the map-wise and individual unit-wise levels. Specifically for the seed-based ROI approach, the map-wise level was defined as the average connectivity across all gray matter voxels within the whole-brain map, whereas the unit-wise level was defined as the individual voxel. Therefore, reliability was calculated from the baseline and follow-up scans using (1) the mean connectivity score across all gray matter voxels, generating a single ICC and (2) the connectivity score of each gray matter voxel, generating ICCs for all voxels, which were then averaged to produce a single mean ICC representing the unit-wise level reliability (Supplementary Table 1).

Previous studies suggest that voxels strongly connected to the ROI seed show higher reliability (Shehzad et al., 2009). To reassess this issue, we ranked all gray matter voxels based on their connectivity strength as determined through group-level analyses. For each of the four ROI seeds, statistical parametric maps from all scans (24 subjects × 2 scans = 48 scans) were entered into a second-level, random-effects analysis (Poline et al., 1997) to generate a group-level connectivity map. Age and gender were included as nuisance regressors. The voxel values in the resulting group images were used to determine voxels in the top 25^th percentile for connectivity to the ROI seed.

2.7. ROI correlation matrix

A second major ROI-based approach employed in ICN fMRI analyses involves the construction of region-, cluster-, or voxel-level pair-wise matrices, which represent the connectivity of each “unit” to every other unit in the matrix. As part of a separate ongoing study, we used the connectivity maps derived from the four anterior insula ROIs described in the previous section to generate a group of “connectivity clusters” representing brain areas with connectivity only to the dorsal anterior insula clusters (averaging maps from left and right hemisphere seeds), only to the ventral anterior insula clusters (averaging maps from left and right hemisphere seeds), or to both cluster pairs. The resulting 68 connectivity clusters, because they represent data-driven, connectivity-based contours, may offer advantages over standard spherical ROIs or landmark-based parcellation units often used in matrix-based analyses (Shirer et al., 2011). Connectivity was calculated between each ROI and the other 67 ROIs, generating 2278 unique ROI pair-wise connectivity measures.

As in the seed-based ROI approach, band-pass filtering (0.0083/s < f < 0.15/s) was applied to the BOLD signal time courses for each voxel during preprocessing. Then, the mean time series from each ROI was extracted and detrended. Pearson (partial) correlation between the time series of each ROI pair was computed in Matlab (http://www.mathworks.com), controlling for one or several of the confounding signals, including white matter, CSF, non-brain and global signal time courses and motion parameters. The Pearson correlation coefficients were then converted to z scores with Fishery's transformation for reliability analysis.

Again, we assessed test-retest reliability of the ROI connectivity matrix at the map-wise and individual unit-wise levels. Here, the map-wise level was defined as the average connectivity across all 2278 ROI pairs within the matrix, whereas the unit-wise level was defined as the connectivity of each individual ROI pair. Therefore, reliability was calculated from the baseline and follow-up scans using (1) the mean connectivity score across the matrix of ROI pairs, generating a single ICC and (2) the connectivity score of each ROI pair, generating 2278 ICCs, which were then averaged to produce a single mean ICC representing the unit-wise level reliability (Supplementary Table 1).

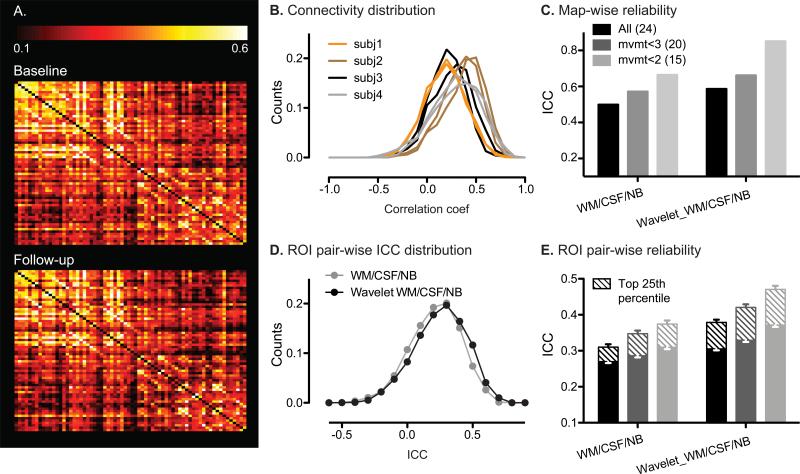
To test whether ROI pairs with stronger connections were more reliable, we ranked the matrix ROI pairs based on their connectivity strength. A group-level connectivity matrix was determined by averaging ROI connectivity matrices from all scans (24 subjects × 2 scans = 48 scans). The values in the resulting group-level matrix were used to determine the ROI pairs in the top 25^th percentile for connectivity strength. To visualize the reproducibility of ROI matrix at the group level, two connectivity matrices were derived for baseline and follow-up by averaging ROI connectivity matrices across the baseline and follow-up scans of all subjects (Fig. 3A).

Figure 3. Reliability of ROI matrix analysis.

A. Group-level ROI connectivity matrix averaged from all subjects’ baseline (top) and follow-up (bottom) scans. B. Distribution of correlation coefficients between all ROI pairs in the salience network matrix. For visual clarity, data are shown for four representative subjects. C. Mapwise ICCs from ROI matrix analysis on all subjects, mvmt<3 and mvmt<2 groups, without and with wavelet transformation at scale 3. D. Distribution of ROI matrix pair-wise ICCs without (gray) and with (black) wavelet transformation at scale 3. E. Mean ROI pair-wise ICCs of ROI matrix analysis on all subjects (black), mvmt<3 (gray) and mvmt<2 (light gray) groups, without and with wavelet transformation at scale 3. Error bars signify s.e.m. across the ROI pairs examined. Mean pair-wise ICCs of voxels in the top 25^th percentile for connectivity are shown as striped bars. WM, white matter; NB, non-brain; Wavelet, wavelet transformation at scale 3.

2.8. Wavelet transformation of ROI time series

Wavelet transformation produces a time-scale decomposition that partitions the total energy of a signal into different scale components, corresponding to certain frequency ranges (see (Bullmore et al., 2004) for a review). Wavelet analysis is particularly well suited to analysis of signals that have fractal scaling or 1/f properties, as is typical of fMRI BOLD timeseries at rest (Maxim et al., 2005). Here, we performed wavelet analysis on the salience network ROI clusters used to construct the ICN matrix described in the previous section, using the WMTSA Wavelet Toolkit for MATLAB (http://www.atmos.washington.edu/~wmtsa/). We applied a maximum overlap discrete wavelet transform (MODWT) to each ROI timeseries during each scan session to obtain the contributing signal in the following four frequency components: scale 1 (0.15 to 0.25 Hz), scale 2 (0.08 to 0.15 Hz), scale 3 (0.03 to 0.08 Hz) and scale 4 (0.01 to 0.03 Hz). In other words, each ROI timeseries was transformed to four series of wavelet coefficients at the four scales. Then, Pearson (partial) correlation was computed between the wavelet coefficients of each ROI pair at each scale. Thus, each ROI pair's connectivity was scored by the (partial) correlation coefficient between their four wavelet correlation coefficients. Using these transformed timeseries, we constructed wavelet correlation matrices. This procedure generated four wavelet correlation matrices corresponding to the four scales. Additionally, wavelet coefficients of one or several of the confounding signals, including white matter, CSF, non-brain and global signal time courses and motion parameters, were removed in the partial correlation analyses. The Pearson correlation coefficients were then converted to z scores with Fisher's transformation for reliability analysis.

Test-retest reliability analysis and group-level analysis were performed on the wavelet correlation matrices in the same manner as the original ROI matrices, separately at the four scales. Since wavelet-transformed ROI matrix analysis was most reliable at scale 3, as expected based on the frequency spectrum associated with ICNs, only the reliability results from scale 3 are presented in the main text.

2.9. Graph theoretical analysis

Graph theoretical analyses were performed using the adjacency matrices generated from the ROI matrix approach, by applying a series of thresholds (from 0 to 1 in increments of 0.05) to determine the presence of connections between ROI pairs. In these adjacency matrices, each of the 68 ROIs represented one network node, and the connectivity between each pair of ROIs represented an edge in the network. Both binary and weighted adjacency matrices were analyzed for reliability. To generate binary matrices, edges with supratheshold correlation coefficients were considered connected and assigned values of 1, whereas edges with subthreshold coefficients were considered not connected and assigned values of 0. To generate weighted matrices, each suprathreshold edge retained its correlation coefficient as its edge weight, whereas subthreshold edges below threshold were assigned values of 0.

The following graph metrics were calculated for each node in the salience network matrix: degree (K), clustering coefficient (C), and betweenness centrality (B), using the Brain Connectivity Toolbox (http://www.brain-connectivity-toolbox.net) (Rubinov and Sporns, 2010) and matlab_bgl within the Matlab environment. Degree measures the connectivity of each node, calculated as the sum of number/weight of links connected to each node. Clustering coefficient measures local neighborhood connectivity, calculated as the fraction of a node's neighbors that are neighbors of each other. Betweenness centrality measures node centrality, calculated as the fraction of all shortest paths in the network that contain a given node.

These graph metrics were selected because 1) they assign value to each individual node, allowing us to determine reliability at both the map-wise and unit (node)-wise levels and 2) they can be applied to both weighted and binary matrices, allowing us to compare reliability between these matrix types across different thresholds.

We assessed test-retest reliability for each graph metric at the map-wise and individual unit-wise levels. Here, the map-wise level was defined as the average graph metric across all 68 nodes within the graph, whereas the unit-wise level was defined as the graph metric for the individual node. Therefore, reliability was calculated from the baseline and follow-up scans using (1) the mean graph metrics across the graph, generating a single ICC and (2) the graph metric of each node, generating 68 ICCs, which were then averaged to produce a single mean ICC representing the unit-wise level reliability (Supplementary Table 1).

2.10. Independent component analysis (ICA) with template matching

Spatial probabilistic ICA was used to isolate ICN maps following previous methods (Beckmann and Smith, 2004, Zhou et al., 2010). Briefly, preprocessed images from each scan were concatenated into one 4D file and entered into FSL 4.0 Melodic ICA software (http://www.fmrib.ox.ac.uk/fsl/index.html). We allowed the program to determine the dimensionality of each data set automatically, including the number of components. Next, we used an automated template matching procedure to obtain subject-specific best-fit ICN maps for the salience network (Seeley et al., 2007; 2009). Goodness-of-fit was calculated by comparing each component from each subject to binarized group ICA maps of the salience network built from 15 healthy young subjects (ages 19–40; mean age, 26.5 years; nine females, all right-handed) from a separate dataset (Habas et al., 2009). Within the selected ICA component for the salience network, each voxel was given a z-score, which reflects the degree to which its timeseries correlates with the overall ICA component timeseries.

For the ICA with template matching approach, we assessed test-retest reliability at the map-wise and individual unit-wise levels. Here, the map-wise level was defined as the average z-score across all gray matter voxels within the whole-brain map, whereas the unit-wise level was defined as the individual voxel's z-score. Therefore, reliability was calculated from the baseline and follow-up scans using (1) the mean z-score across all gray matter voxels, generating a single ICC and (2) the z-score of each gray matter voxel, generating ICCs for all voxels, which were then averaged to produce a single mean ICC representing the unit-level reliability (Supplementary Table 1).

To assess whether voxels more significantly belonging to the ICA-derived salience network component had higher reliability, we ranked all gray matter voxels based on their connectivity (z-score), as determined from a group-level analysis in which the selected ICA components for each scan were entered into second-level, random-effects analyses (Poline et al., 1997) to generate the salience network at the group level (24 subjects × 2 scans = 48 scans). Age and gender were included as nuisance regressors. The resulting group images were used to determine the voxels in the top 25^th percentile for connectivity within the ICA-derived salience network component.

2.11. Temporal concatenation group ICA

Temporal concatenation group ICA with back reconstruction (TC-GICA) was performed using the Group ICA of fMRI Toolbox (GIFT, http://icatb.sourceforge.net/groupica.htm), implemented in Matlab. Briefly, TC-GICA involves three stages: data reduction, ICA, and back reconstruction (Calhoun et al., 2004). First, Principal Components Analysis (PCA) was used to reduce the data dimensionality for each subject. After each subject's functional data were reduced, the data were concatenated and entered into a second data reduction step using PCA. Second, the reduced, group-concatenated data were entered into the ICA algorithm to calculate spatially independent components. Following the previous reliability study to examine ICA methods, the number of components was set to 20 (Zuo et al., 2010). Third, back reconstruction was performed using GICA3, which previous studies have suggested may improve accuracy of estimating subject subject-specific spatial maps and time courses over the original GICA and spatio-temporal regression (dual-regression) (Erhardt et al., 2010).

We again assessed test-retest reliability at the map-wise and unit-wise levels using each voxel's TC-GICA z-scores, in similar manner as described for ICA with template matching (Supplementary Table 1). Then, to assess whether voxels that more significantly belonged to the ICA network showed higher reliability, we ranked all gray matter voxels based on the group-level significance scores produced by TC-GICA to identify the voxels in the top 25^th percentile of z-scores.

2.12. Statistical tests

Statistical tests were carried out in Graphpad Prism 5. To test the significance of nuisance regressors’ impact on map-wise reliability for the seed-based ROI approach, paired t-tests were used to compare ICC values with and without the given nuisance regressor across the ROI analyses for each of the four seed ROIs. To test the significance of nuisance regressors’ impact on voxel-wise reliability for the seed-based ROI approach, paired t-tests were used to compare the mean gray matter voxel-wise ICC values with and without the given nuisance regressor across the four ROI analyses.

3. Results

Twenty-four older controls underwent task-free fMRI at two time points, 300-400 days apart. Demographic characteristics and scan details are shown in Table 1. Salience network intrinsic connectivity was determined using three model-driven approaches, seed-based ROI, ROI correlation matrix, and graph theoretical analyses, and two model-free approaches, ICA with template-matching and temporal concatenation group ICA with back reconstruction (TC-GICA). Test-retest reliability was assessed at the map-wise level, using summary measures of network connectivity from each scan session, or at the individual unit level, using connectivity measures of each individual unit (voxel, node-pair, or node), which were then averaged to reflect reliability across the individual units of analysis (Supplementary Table 1).

3.1. Seed-based ROI analysis provides good map-wise reliability

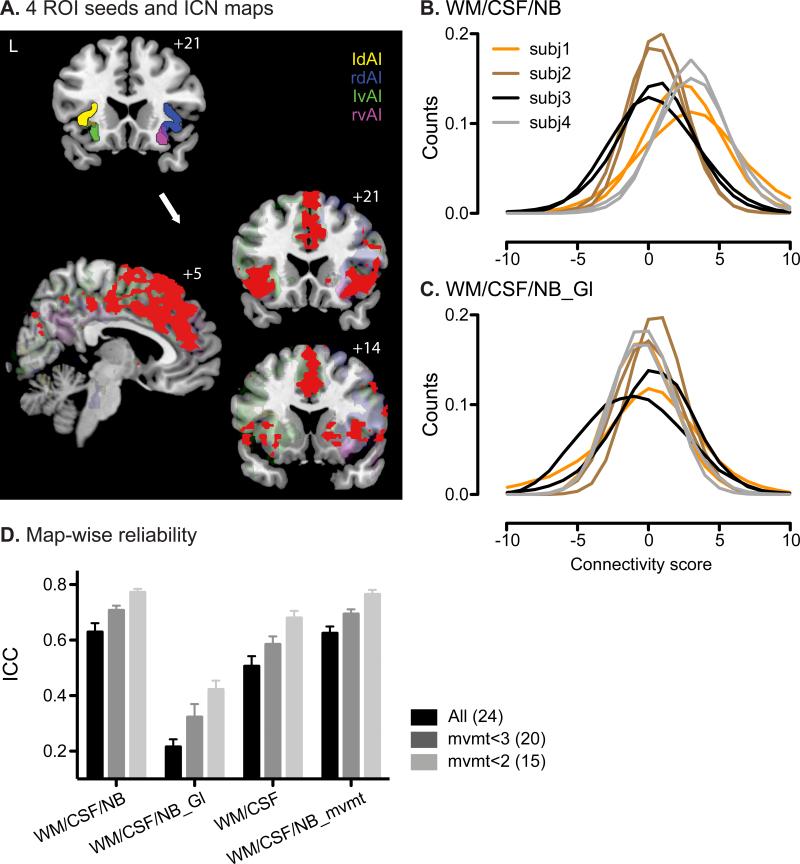
We used four anterior insula ROIs (Kurth et al., 2010) to generate four overlapping but distinct ICNs closely related to the salience network (Fig. 1A) and covering key network regions as reported previously, including bilateral anterior insula, anterior cingulate cortex, striatum and additional frontal and temporal areas (Fig. 1A, red colormap representing the overlap of the four connectivity maps at the group level).

Figure 1. ICNs generated by seed-based ROI analysis and their map-wise reliability.

A. The four anterior insular (AI) clusters used as ROI seeds (upper left image; left dorsal AI, ldAI – yellow; right dorsal AI, rdAI – blue; left ventral AI, lvAI– green; right ventral AI, rvAI – magenta) and their corresponding group-level functional connectivity maps, threshold at t > 7, cluster size > 300 voxels (lower images; individual maps are in transparent colors corresponding to their ROI seeds; overlap of all four maps is in red). B. Distributions of gray matter voxels’ connectivity scores from the ROI analysis using right ventral AI as the seed. White matter, CSF and non-brain signals were included as nuisance regressors. For visual clarity, data from four representative subjects are shown. Lines of the same color represent data from the two scans of the same subjects. C. Same as B, except the global signal was included as a nuisance regressor, in addition to white matter, CSF and non-brain. Data are from the same four subjects as in B. D. Average map-wise ICC across the four ROI analyses for all subjects (black), mvmt<3 (gray) and mvmt<2 (light gray) groups. Number of subjects in each group is indicated in parentheses. Error bars signify s.e.m across the four ROI analyses. Nuisance regressors included in the analyses are indicated along the x-axis. WM, white matter; NB, non-brain; Gl, Global signal; mvmt, movement parameters.

To assess the map-wise reliability of salience network connectivity, we calculated the mean connectivity score across all gray matter voxels within the four seed-based ROI connectivity maps for each scan and used these mean connectivity measures to compute the map-wise ICC across the two scans. Using the ROI analysis with the right ventral anterior insula ROI seed as an example, the distribution of voxel connectivity scores was right-shifted toward positive values (Fig. 1B). More importantly, these connectivity distributions varied more between subjects than they did within subjects and between scans. All four seed-based ROI analyses showed good reliability (Fig. 1D), with a mean ICC = 0.63 (s.e.m = 0.06), suggesting that seed-based ROI approaches were reliable at the overall network level.

Subject motion during scanning had a significant impact on reliability when using the seed-based ROI approach. Reliability was higher for scans with less motion – ICC reached almost 0.8 for group ‘mvmt<2’, but fell just above 0.6 in the total group, including subjects with significant motion (Fig. 1D). The effect of scan motion was consistent across ROI analyses using the four ROI seeds.

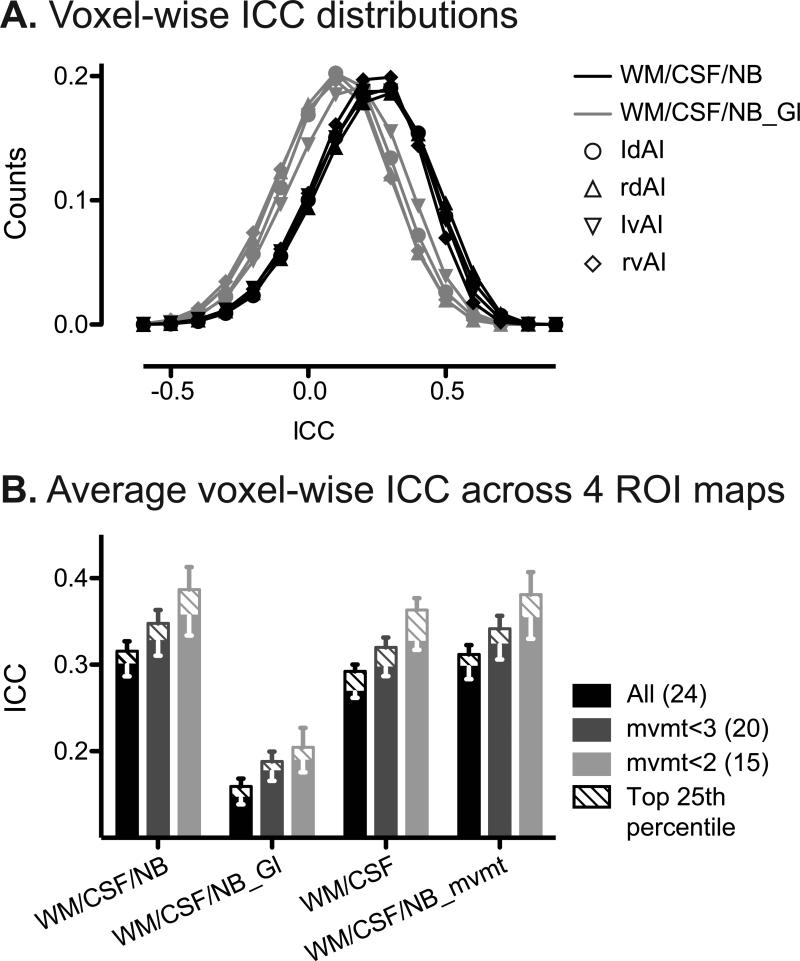
3.2. Voxel-wise reliability of seed-based ROI analysis: improved reliability among voxels with higher connectivity

Test-retest reliability of seed-based ROI analyses varied widely at the voxel level, with a distribution that spanned from poor to good (Fig. 2A, black). ICC was calculated for each voxel based on its connectivity to the seed ROI at baseline and follow-up. The voxel-wise ICC distributions showed modal values in the fair range for all four anterior insula seeds, with mean ICCs of 0.3-0.4 (Fig. 2A, black) across the four seeds, when WM, CSF and non-brain signals were removed as nuisance regressors. Across the four ROI analyses, roughly 35% of the voxels showed moderate reliability or better (ICC > 0.4).

Figure 2. Voxel-wise reliability of seed-based ROI analysis.

A. Distribution of ICC values of all gray matter voxels from each of the four ROI analyses, with white matter, CSF and non-brain nuisance regressors (black) and with global signal regressor added (gray). B. Average voxel-wise ICC across the four ROI analyses for all subjects (black), mvmt<3 (gray) and mvmt<2 (light gray) groups. Number of subjects in each group is indicated in parentheses. Error bars signify s.e.m. of the mean ICC values across the four ROI analyses. Nuisance regressors included in the analyses are indicated along the x-axis. Mean voxel-wise ICCs of voxels in the top 25^th percentile for connectivity are shown as striped bars. WM, white matter; NB, non-brain; Gl, Global signal; mvmt, movement parameters.

Voxels with stronger connectivity to the ROI seeds showed greater reliability. For each of the four ROI seeds, gray matter voxels were ranked based on connectivity strength. Voxels in the top 25^th percentile for connectivity showed ICCs roughly 10% higher than the overall voxel-wise ICC average (Fig. 2B).

Similar to seed-based ROI map-wise reliability, subject motion greatly reduced voxel-wise reliability (Fig. 2B).

3.3. Effects of global signal and other nuisance regressors on reliability

Including the global signal as a regressor altered the distribution of functional connectivity computed with the seed-based ROI approach and had a striking impact on map-wise and voxel-wise reliability. Consistent with previous studies (Murphy et al., 2009; Schwarz and McGonigle, 2011), we found that removing the global signal introduced negative correlations and reduced positive correlations (compare Fig. 1B,C). Comparing the distributions of connectivity strength with and without global signal as a nuisance regressor, including global signal regressor created a more symmetric distribution centered at 0 (Fig. 1C). More importantly, including the global signal significantly reduced both map-wise and voxel-wise ICCs, by more than 50% (Fig. 1D and Fig. 2B; P < 0.0001, paired t test).

Other regressors in the model also significantly influenced reliability, yet to a much lesser extent (Fig. 1D and Fig. 2B; P < 0.05, paired t test). Seed-based ROI analysis was most reliable when including WM, CSF and non-brain signal but not the global signal regressors (Fig. 1D and Fig. 2B). On the other hand, although subjects with greater head movement showed lower reliability, including movement parameters as nuisance regressors did not significantly improve reliability nor did it mitigate reliability differences seen among groups with more or less head movement (Fig. 1D, P = 0.67; Fig. 2B, P = 0.26; paired t test).

3.4. ROI correlation matrix analysis showed moderate matrix-wise reliability

While the seed-based ROI approach examines connectivity of each voxel to a single ROI, ROI correlation matrix analysis allows researchers to explore connectivity between all regions within a network. We evaluated the reliability of an ROI correlation matrix composed of 68 salience network ROIs, derived from the same four ROI seeds used in the seed-based ROI analyses. As was seen for the single seed-based analyses, in ROI matrix analyses, the highest reliability was achieved by including WM, CSF and non-brain signal regressors and omitting the global signal and movement parameters. Therefore, for simplicity, all subsequent results are described and illustrated with those settings applied.

Overall, ROI matrix-wise analysis showed moderate-to-good test-retest reliability. For each ROI pair, we computed the partial correlation coefficient (Pearson's r) between their BOLD signal time courses (controlling for nuisance covariates). The qualitative stability of these correlation matrices was evident at the group level, with baseline and follow-up scans showing convergent group-averaged matrices (Fig. 3A). The Pearson's r distributions were right-shifted towards positive values (Fig. 3B). Figure 3B shows these correlation distributions for four representative subjects baseline and follow-up scans, which again exhibit greater between-subjects than within-subjects variance. ROI matrix analysis showed moderate to good matrix-wise reliability (ICC = 0.49, Fig. 3C), which is lower than the good to nearly excellent map-wise reliability seen with the seed-based ROI approach (Fig. 1D).

We assessed unit-wise reliability by calculating ICCs for each ROI pair. This approach revealed a wide ICC distribution across region pairs in the matrix (Fig. 3D, gray). The distributions of pair-wise ICC were skewed towards positive values, with mean ICC of 0.2-0.3 (Fig. 3E, left columns). Around 25% ROI pairs had moderate reliability (ICC > 0.4. ROI pairs with stronger connectivity showed greater reliability. Pair-wise ICCs of the top 25^th percentile for connectivity showed 15% higher ICCs than the overall average (Fig. 3E, left columns).

3.5. Wavelet analysis increased ROI matrix reliability

ROI matrix reliability improved substantially when ROI timeseries correlations were computed after wavelet transformation. We applied maximal overlap discrete wavelet transform (MODWT) to the BOLD time courses of the 68 matrix ROIs to extract frequency-dependent correlation matrices. First, ROI time courses were transformed to wavelet coefficients at four scales, capturing signals within the corresponding four frequency domains. Then, partial correlation coefficients were computed between matrix ROIs’ wavelet coefficients to produce four wavelet matrices corresponding to the four frequency domains (see Methods for details). We found that the salience network matrix was most reliable at scale 3 (0.03 to 0.08 Hz), consistent with previous reports that neural intrinsic connectivity is represented by low frequency BOLD signal fluctuations (<0.1 Hz). Thus, results from wavelet transformation at scale 3 are presented as follows.

Matrix-wise ICC scores were consistently higher after wavelet transformation across the three levels of subject motion (Fig. 3C). In particular, matrix-wise reliability for subjects with less than 2 mm of motion amplitude was excellent (ICC = 0.84). Furthermore, wavelet transformation improved ROI pair-wise reliability, improving the ICCs by around 20% across groups (Fig. 3E).

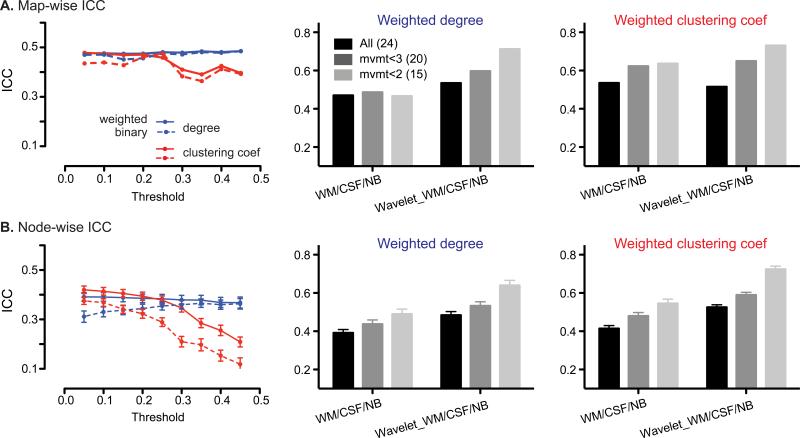
3.6. Graph theoretical measures showed good reliability at the map-wise and individual unit-wise levels

We further examined the reliability of graph theoretical measures calculated from the salience network matrix. To derive graphs and graph metrics, we hard-thresholded the salience network ROI correlation matrix (from 0 to 1 in increments of 0.05) to generate binary and weighted adjacency matrices (see Methods for details). Each ROI represented a node in the network, and the connectivity between each ROI pair represented an edge. Here, we present reliability analysis for weighted and unweighted degree and clustering coefficient, two of the most common graph metrics examined in fMRI analyses. Degree and clustering coefficient were the most reliable and representative in our reliability analysis (Fig. 4). Betweenness centrality, in contrast, had poor reliability (Supplementary Fig. 1).

Figure 4. Reliability of graph theoretical analysis.

A.left panel, map-wise ICCs across different thresholds, for degree (blue) and clustering coefficient (red) from weighted (solid line) and binary (dashed line) adjacency matrices. Map-wise ICCs of degree (middle panel) and clustering coefficient (right panel) from the weighted matrix thresholded at r > 0.05, for all subjects (black), mvmt<3 (gray) and mvmt<2 (light gray) groups, without and with wavelet transformation at scale 3. B. left panel, mean node-wise ICCs across different thresholds, for degree (blue) and clustering coefficient (red) from weighted (solid line) and binary (dashed line) adjacency matrices. Mean node-wise ICCs for degree (middle panel) and clustering coefficient (right panel) from weighted matrix threshold at r > 0.05, for all subjects (black), mvmt<3 (gray), and mvmt<2 (light gray) groups, without and with wavelet transformation at scale 3. Error bars signify s.e.m. across nodes. WM, white matter; NB, non-brain; Wavelet, wavelet transformation at scale 3.

We assessed map-wise reliability by calculating graph-wise ICCs for each graph metric. We found moderate ICCs for unweighted and weighted graphs (Fig. 4A), which were stable (~0.5) across a range of connectivity thresholds from 0.05 – 0.45 (Fig. 4A), although clustering coefficients showed slightly lower reliability with more stringent matrix thresholding (Fig. 4A). Alternative thresholding methods, such as soft-thresholding and proportional-thresholding, did not substantially impact reliability. Thus, in the following section, we present reliability results from weighted matrices thresholded at r > 0.05.

Node-wise graph metric reliability proved superior to unit-wise (voxel or ROI pair-wise) reliability derived from the seed-based ROI or ROI matrix approaches, with graph metrics showing roughly 30% higher ICCs (Fig. 4B; compare with Fig. 2B, 3D). Clustering coefficients derived from weighted matrices provided the most reliable graph metric at the node level, particularly at less stringent hard thresholds (Fig 4B, solid red line). As seen for the ROI matrix correlation analyses, reliability of graph metrics was improved by wavelet transformation of the nodal timeseries. In the low subject motion group, wavelet transformed matrices (scale 3) produced degree and clustering coefficient ICCs reflecting good node-wise reliability (ICC > 0.6, Fig. 4B, right panel).

3.7. Temporal concatenation group ICA improved reliability over ICA with template matching

We further examined reliability of a widely used model-free ICN fMRI approach, spatial ICA, implemented using the template-matching approach and the more recently developed temporal concatenation group ICA with back reconstruction. With both methods, each subject's final salience network map consists of voxel-wise z-scores, which represent the degree to which that voxel belongs to the overall ICA component.

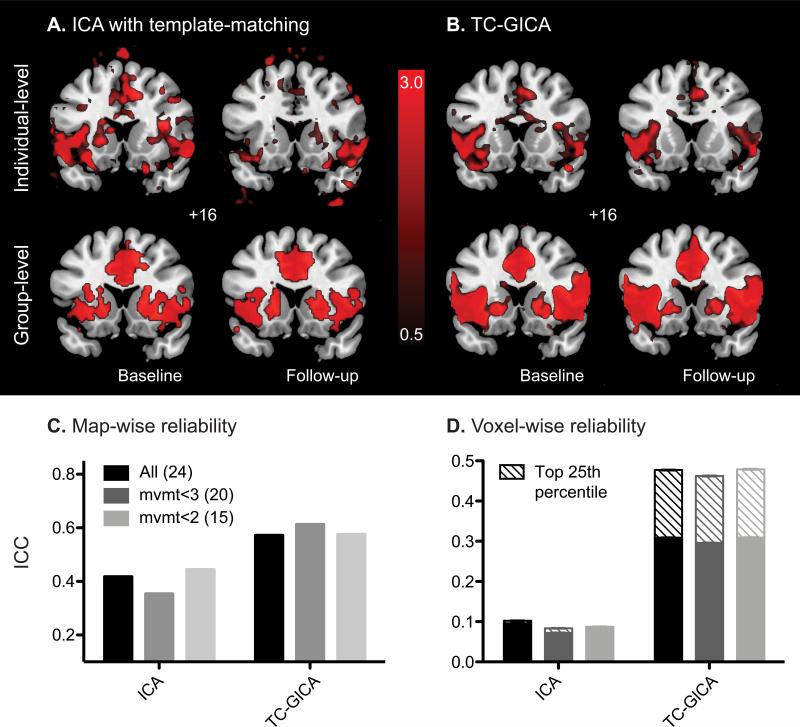
The template-matching ICA approach showed moderate map-wise reliability (ICC ~ 0.4), but poor voxel-wise reliability (ICC ~ 0.1, Fig. 5C,D). Although, the group-level salience network maps at baseline and follow-up showed remarkably similar spatial patterns (Fig. 5A, lower panel), examination of the individual subject-level data revealed that the best-fit components selected were often dissimilar, as illustrated by one randomly selected subject (Fig. 5A, upper panel). As a result, voxel-wise ICC was low (~0.1, Fig. 5D). Previous studies suggest that target components can be reproducibly chosen by trained investigators using visual inspection (Damoiseaux et al., 2006). We therefore repeated the reliability analysis on components selected visually, but no improvement in reliability was realized, suggesting that the poor reliability of ICA was not due to template-matching algorithm alone.

Figure 5. Reliability of ICA.

A. Salience network components identified using ICA with template-matching of a randomly selected subject's baseline (left) and follow up (right) scans (upper panel), and the group-level maps averaged from all subject's baseline and follow-up scans (lower panel). Individual maps are shown at z > 1.5. Group level maps are shown at p<0.01 uncorrected height and p<0.01 corrected extended thresholds B. Individual-level (of the same subject as in A; upper panel) and group-level (lower panel) salience network components identified using TCGICA, for baseline (left) and follow-up (right) scans. Maps are shown at z > 1.5. C. Map-wise ICCs using ICA with template-matching or TC-GICA for all subjects (black), mvmt<3 (gray) and mvmt<2 (light gray) groups. Number of subjects in each group is indicated in parentheses. ICA methods used are indicated along the x-axis. D. Average voxel-wise ICCs using ICA with template-matching or TC-GICA for all subjects (black), mvmt<3 (gray), and mvmt<2 (light gray) groups. Error bars signify s.e.m. across all voxels. Mean voxel-wise ICCs of voxels in the top 25th percentile for connectivity are shown as striped bars.

Temporal concatenation group ICA with back reconstruction (TC-GICA) greatly improved both map-wise and voxel-wise reliability (Fig. 5C,D), consistent with a previous study in young controls (Zuo et al., 2010). Map-wise reliability approached the good range (ICC ~0.6) and voxel-wise ICC was in the fair range (ICC ~0.3). Furthermore, voxel-wise reliability improved by ~60%, into the moderate range, for voxels within the top 25^th percentile for component z-scores (Fig. 5D). Moreover, ICCs were similar across the range of subject motion, suggesting that ICA reliability was less sensitive to movement artifacts compared to other analytical approaches, perhaps because movement-related noise is separated from neural signal by the ICA algorithm (Fig. 5C,D).

4. Discussion

This study provides a comprehensive investigation of the test-retest reliability of task-free intrinsic connectivity fMRI in healthy older adults. We performed a systematic analysis and direct comparison of commonly employed ICN analytical strategies and preprocessing manipulations. To constrain scope and complement previous studies, we focused on the salience network, an ICN of broad clinical and neuroscientific relevance for which reliability has not been examined. In general, we found that model-driven methods based on ROI BOLD signal correlations provided the highest map-wise reliability, whereas graph theoretical measures provided the highest unit-wise reliability. Within the model-free methods, temporal concatenation group ICA improved reliability over subject-level ICA approaches. Single summary measures for each subject, derived at the map-wise level, showed greater reliability than the averaged reliability calculated across individual units, such as voxels or ROIs. Inclusion of global signal regressors and subjects with greater head motion worsened reliability, whereas inclusion of averaged non-brain signal regressors and wavelet transformation of functional timeseries improved reliability. These findings provide a foundation for developing ICN fMRI as a longitudinal biomarker for diseases of aging.

4.1. Reliability of ICN-fMRI on older controls is comparable to younger controls

In general, our results on the long-term test-retest reliability in older controls are comparable to previous findings in young controls, despite substantial differences in subjects’ age and the ICNs examined (Table 1, but see below for discussion on (Wang et al., 2011)). Our findings extend previous work, however, by providing reliability estimates for the same network on the same subjects using a diverse array of methods. Accordingly, these data may serve as a guide for researchers seeking to compare methods for their specific research purpose.

4.2. Effects of global signal and other regressors on reliability

Preprocessing of task-free fMRI data is designed to remove potential sources of noise, usually by entering nuisance covariates thought to capture such noise in the general linear model. However, there remains a lack of consensus regarding the optimal choice of covariates. At one extreme, some studies removed no potentially confounding signals (van den Heuvel et al., 2008; Nakamura et al., 2009; Wang et al., 2010), whereas others removed WM, CSF, and global signals along with time courses of movement parameters (Shehzad et al., 2009; Hayasaka and Laurienti, 2010). Most studies, including our own, have removed some subset of these confounding signals (Achard and Bullmore, 2007; Liu et al., 2008; Wang et al., 2009; Mumford et al., 2010). Here, we compared three combinations of nuisance covariates and found that the highest reliability was achieved by removing WM, CSF and non-brain signals but not the global signal. Including movement parameters had little impact. These findings do not indicate an optimal choice of noise-related covariates for all task-free fMRI analyses; most likely, the decision will depend on the research question and networks under study. For longitudinal ICN studies in which test-retest reliability is most critical, however, the findings raise caution against incorporating the global signal as a nuisance covariate.

Global signal regression in task-free fMRI has been debated on other grounds (Vincent et al., 2006; Birn et al., 2006; Murphy et al., 2009; Fox et al., 2009; Chang and Glover, 2010; Schölvinck et al., 2010). Arguments in favor of global signal correction emphasize the value of removing non-neural noise, such as respiration-induced fluctuations. The procedure, however, markedly shifts the distribution of correlation among brain voxels, reducing positive correlations and inducing anti-correlations (Fig. 1C; (Murphy et al., 2009; Schwarz and McGonigle, 2011). More importantly, global signal correction had a profound effect on both map-wise and unit-wise reliability of correlation-based analyses in this study (Fig. 1D,2B), and in one previous analysis, (Schwarz and McGonigle, 2011). A comparison between (Wang et al., 2011) and (Schwarz and McGonigle, 2011) suggests that since both studies analyzed the reliability of graph theoretical analysis on the same whole brain network (based on parcellation units derived from the AAL atlas), but (Wang et al., 2011) reported much lower ICCs than (Schwarz and McGonigle, 2011) and our study. This discrepancy could be explained by the removal of global signal in (Wang et al., 2011) but not in (Schwarz and McGonigle, 2011). The impact of global signal regression on reliability may reflect the recentering of each subject's connectivity distribution about a mean of zero, which diminishes between-subject variance (Fig. 1B,C), thus lowering ICC.

Motion-related artifact remains a major concern for ICN fMRI data, especially in aging or diseased subjects who may struggle to achieve complete stillness during the scan. We found that head motion had a major negative impact on reliability, in particular for analytical strategies based on correlations between ROIs. The impact of motion was not rescued by including motion parameters as nuisance regressors. In one reliability study of the whole brain connectivity in a young control dataset, the authors found that removing motion signals improved reliability (Schwarz and McGonigle, 2011). These disparate findings could reflect differing magnitudes of head motion, the different networks investigated, or differences in the methods used to remove motion signals – in (Schwarz and McGonigle, 2011), motion parameters were deconvolved from each gray matter voxel during image preprocessing.

4.3. Summary ICN measures showed the greatest reliability

For both seed-based ROI and ROI correlation matrix approaches, map-wise reliability was considerably higher than unit-wise reliability. Moreover, graph theoretical measures produced the best unit-wise reliability, based on metrics calculated from individual nodes. Overall, our results suggest that summary measures that reflect network connectivity as a whole provide the highest reliability, falling within the good to excellent range. This observation is consistent with reliability studies on young controls and with studies of test-retest reliability over shorter (days) intervals. For ROI correlation matrices, map-wise reliability (Schwarz and McGonigle, 2011) was more than twice as high as the average ROI pair-wise reliability (Table 1). As for short-term reliability, graph theoretical analysis was reported to have high reliability in older subjects (ICC > 0.75, (Telesford et al., 2010). On the other hand, even in the young controls, ROI matrix pairs showed only moderate to good short-term reliability (Schwarz and McGonigle, 2011). These studies differed somewhat, however, in the data preproocessing steps and ICNs analyzed, limiting the inferences that can be reached through direct comparisons.

The greater robustness of map-wise measures might not be surprising, considering that these measures incorporate a greater body of the acquired data, but it is encouraging, since single-value (map-wise) measures that capture the biological phenomenon of interest are more attractive as longitudinal biomarkers than multiple measures (voxel-wise or ROI pair-wise) derived for each subject. On the other hand, a small number of particular voxels and ROI-pairs within the salience network provided higher reliability than the map-wise measures, suggesting that future studies aiming to capture longitudinal change may benefit from exploring both map-wise and unit-wise measures.

4.4. Reliability of ROI correlation-based methods was improved by wavelet transformation

ROI correlation matrices and graph metrics have most commonly been studied using Pearson's correlation between ROIs’ BOLD signal timeseries. Several recent studies, however, have applied wavelet analysis to generate matrices and graph metrics from the correlations between ROI-based wavelet coefficients (Achard et al., 2006; Achard and Bullmore, 2007; Meunier et al., 2009; Supekar et al., 2008)}}. These studies did not, however, compare the effectiveness of wavelet analysis to alternative methods directly. The present study provided a quantitative comparison between ICN fMRI reliability with and without wavelet transformation of the ROI timeseries and found that test-retest reliability was significantly improved after applying MODWT wavelet transformation. This observation suggests that wavelet transformation may constructively augment standard image analysis strategies, especially for longitudinal studies.

4.5. Reliability of subject-level ICA with template matching vs. temporal concatenation group ICA

In older controls, we replicated a previous study in young controls, which suggested that temporal concatenation group ICA was more reliable than standard ICA with template-matching based on individual subject scans (Zuo et al., 2010). Several studies on age-related diseases have employed the ICA template-matching approach, combining components across subjects for group analysis (Greicius et al., 2004; Seeley et al., 2009; Zhou et al., 2010; Mohammadi et al., 2009). Although standard ICA approaches may suffice for between-group comparisons, producing biologically plausible effects, the present data argue against the use of this method for longitudinal within-subjects ICN analysis.

The higher reliability provided by TC-GICA is encouraging, yet the application of this method to diseases of aging requires further validation. The first step in the method is to concatenate the task-free fMRI data from all subjects in a study into a single timeseries. While this approach may be straightforward for examining ICNs in healthy subjects, it could create problems for disease studies by incorporating diseased networks into the dataset used to define the components for the overall group. When the goal is to detect deviations of a patient group from normal, using patients to define components may reduce the sensitivity of this method. This issue merits further study.

4.6. Future directions

Application of task-free fMRI as a longitudinal biomarker will require both reliability and sensitivity. In other words, the ideal measures should be not only proven stable over time in the absence of disease but also highly attuned to longitudinal decline or improvement. The best measures will allow detection of clinical meaningful benefits over short intervals in few subjects; this goal may require trade-offs between reliability and sensitivity. Future studies on aging and neurodegenerative populations are needed to explore the sensitivity of available and new analytical methods to longitudinal changes.