Do We Really Become Smarter When Our Fluid-Intelligence Test Scores Improve?

Abstract

Recent reports of training-induced gains on fluid intelligence tests have fueled an explosion of interest in cognitive training—now a billion-dollar industry. The interpretation of these results is questionable because score gains can be dominated by factors that play marginal roles in the scores themselves, and because intelligence gain is not the only possible explanation for the observed control-adjusted far transfer across tasks. Here we present novel evidence that the test score gains used to measure the efficacy of cognitive training may reflect strategy refinement instead of intelligence gains. A novel scanpath analysis of eye movement data from 35 participants solving Raven’s Advanced Progressive Matrices on two separate sessions indicated that one-third of the variance of score gains could be attributed to test-taking strategy alone, as revealed by characteristic changes in eye-fixation patterns. When the strategic contaminant was partialled out, the residual score gains were no longer significant. These results are compatible with established theories of skill acquisition suggesting that procedural knowledge tacitly acquired during training can later be utilized at posttest. Our novel method and result both underline a reason to be wary of purported intelligence gains, but also provide a way forward for testing for them in the future.

Can intelligence be improved with training? For the most part, the numerous training methods attempted through the years have yielded disappointing results for healthy adults (e.g., Detterman & Sternberg, 1982). Nonetheless, if an effective training method could be designed, it would have immense practical implications. Therefore, when Jaeggi, Buschkuehl, Jonides, and Perrig (2008) recently published some encouraging experimental results, they were greeted with remarkable enthusiasm. Cognitive enhancement is now a billion-dollar industry (“Brain sells,” 2013). Millions of customers buy “brain building” games and subscribe to “mental gyms” on-line where they perform various “cognitive workouts” in the hope of raising their IQ (Hurley, 2012). Hundreds of millions of dollars are being invested in educational (e.g., Cogmed, http://www.cogmed.com), military, and commercial programs (e.g., Lumosity, http://www.lumosity.com) on the assumption that intelligence can be improved through training. But can it really? Given the massive societal resources that are at stake and the checkered track record of similar initiatives in the past (e.g., Detterman & Sternberg, 1982; Melby-Lervåg & Hulme, 2013; Owen et al., 2010), this claim must be evaluated very carefully. Here we present novel evidence that suggests reasons for skepticism. The evidence is not definitive and the question remains open. It leads directly to three other questions: (i) What is intelligence? (ii) How can we measure intelligence? (iii) How can we measure gains of intelligence? The first two of those have been debated and researched for over a century (see, e.g., Neisser et al., 1996, for an authoritative review). The last question, however, has not received the attention it deserves. One goal of this article is to point out how methodologically challenging it is to measure the change of a latent variable.

With respect to the first two questions, we adopt the popular (though not universally accepted) psychometric approach that both defines and measures fluid intelligence as the latent variable explaining the intercorrelations in performance on tasks such as analogy making, reasoning, and problem solving. This approach is grounded in the fact that individual differences in performance across a wide variety of cognitive tasks are positively correlated (Spearman, 1927). Through factor analysis, the matrix of intercorrelations can be explained in terms of a hierarchical arrangement with a general intelligence factor G at the apex and various more specialized abilities arrayed below it (Carroll, 1993; Jensen, 1998). The second tier in the hierarchy includes the distinction between crystalized (Gc) and fluid (Gf) intelligence (Cattell, 1963; Carroll, 1993). Gc refers to overlearned skills and static knowledge such as vocabulary, which undoubtedly accumulate with experience. In contrast, Gf refers to the ability to detect patterns and relations, solve problems, and “figure things out” in novel environments. Empirically, fluid intelligence predicts many forms of achievement, especially school achievement (Gottfredson, 1997). There is strong evidence that Gf is highly heritable—between 50% and 75% of the variance of intelligence test scores in healthy adults is linked to genetic variation (Neisser et al., 1996). Although heritability does not entail immutability (Dickens & Flynn, 2001), most psychometricians conceptualize Gf as a stable trait that is relatively immune to interventions in adulthood (Carroll, 1993; Jensen, 1998).

This is why a recent study by Jaeggi et al. (2008) triggered such excitement and controversy. The study used a pretest-train-posttest design with an untrained control group. A titrated, adaptive dual n-back task was practiced for up to 18 sessions in the experimental group (N = 34) but not in the control group (N = 35). All participants were pre- and post-tested on two parallel short-form versions of a matrix-based Gf test—either Raven’s Advanced Progressive Matrices (Raven, Raven, & Court, 1998) or BOMAT (Hossiep, Turck, & Hasella, 1999). Whereas the results showed statistically significant score gains in both groups, the average gain in the trained group was significantly higher than that in the control (p < 0.05, ${\eta }_p^2=0.07$, Jaeggi et al., 2008). The latter finding—a significant control-adjusted gain—was interpreted as an improvement in Gf and fueled the current boom in the cognitive enhancement industry, as well as a big controversy in the scientific literature. Of particular relevance to the controversy is that the original study (Jaeggi et al., 2008) had various methodological shortcomings (Moody, 2009) and subsequent attempts to replicate the putative improvement in Gf have produced mixed results (e.g., Chooi & Thompson, 2012; Harrison et al., 2013; Jaeggi, Buschkuehl, Jonides, & Shah, 2011; Jaeggi et al., 2010; Redick et al., 2012; Thompson et al., 2013). This rapidly growing field is characterized by large variations in reported effect sizes (see Melby-Lervåg & Hulme, 2013, for a meta-analysis of 23 studies), polarization of opinion, and contradictory reviews (e.g., Buschkuehl & Jaeggi, 2010; Morrison & Chein, 2011, on the optimistic side; Melby-Lervåg & Hulme, 2013; Shipstead, Redick, & Engle, 2012, on the skeptical side).

The neurobiological interpretation of Gf (M. Anderson, 2005; Duncan et al., 2000) emphasizes its linkage to factors such as processing speed (Jensen, 2006; Sheppard & Vernon, 2008) and working memory capacity (Fry & Hale, 2000; Gray & Thompson, 2004; Halford, Cowan, & Andrews, 2007; Kane & Engle, 2002). The interest in the latter linkage surged after Jaeggi et al.’s (2008) publication because their participants trained on a WM task. The hypothesis that fuels the current enthusiasm is that WM training increases WM capacity (near transfer), which in turn improves Gf (far transfer). There is a strong analogy with athletics, where swimming workouts, for example, increase cardiovascular capacity, which in turn improves the general athletic ability. Thus, Jaeggi et al. (2011) characterize WM as “taking the place of the cardiovascular system.”

This hypothesis is simple and elegant but the methodology for testing it empirically is fraught with difficulties because an objective method for measuring Gf gains is required. The commonly used test-retest method is seriously flawed. The overwhelming majority of studies use test-retest score gains to measure Gf gains. This practice is based on the misleading intuition that if a test such as Raven’s APM is a valid measure of Gf, then a gain in the score on this test is a valid measure of Gf gain. This is not necessarily true because, in addition to Gf, the scores reflect non-Gf factors such as visuospatial ability, motivation, and test-taking strategy. The latter factors—and hence the test scores—can improve while Gf itself remains stable. Indeed, Raven’s APM scores increase significantly on repeated testing without any targeted training (e.g., Bors & Vigneau, 2003; Bors & Forrin, 1995; Denney & Heidrich, 1990). Worse, a large meta-analysis of 64 test-retest studies (te Nijenhuis, van Vianen, & van der Flier, 2007) indicates a strong negative correlation between score gains and the G loadings of test items. To control for such “mere retest” effects, the common practice in the field is to compare the score gains in the treatment group to those in an untreated control group. Cognitive enhancement advocates (e.g., Jaeggi et al., 2008) acknowledge the interpretive problems of unadjusted score gains but assume that control-adjusted gains necessarily measure real gains in Gf. As we argue below, however, this assumption is incorrect because the adjustment does not guarantee validity either.

These methodological difficulties can be illustrated by analogy with athletics. In a classic study of motor skill learning (Hatze, 1976), an athlete practiced kicking a target as rapidly as possible. His performance improved at first and then plateaued. However, after seeing a film about kicking technique, the athlete immediately improved his time considerably and with additional practice was able to reach a much higher asymptote. For our purposes, this illustrates the relationships between the following three variables. The first is kicking time, which was the only objective measurement. The second variable is general athletic ability, which includes factors such as cardiovascular capacity, agility, muscle strength, and so forth. The third is kicking technique—the optimal way to execute a kick so as to minimize kicking time, all else being equal. Importantly, because the kicking time reflects a mixture of athletic ability and technique, gains in kicking time can occur without any change in athletic ability. Indeed, watching a movie could not have changed the strength or agility of the participant in Hatze’s (1976) experiment. Analogously, gains in test scores can occur without any change in “brainpower” factors such as WM capacity or processing speed.

This brings us to the central topic of transfer across tasks. The most widely used inference pattern in the cognitive enhancement literature is to infer gains in Gf on the basis of control-adjusted gains in test scores. This inference pattern logically requires the auxiliary assumption that only Gf can transfer across tasks. Few cognitive-enhancement advocates would endorse such a strong claim, and the more cautious authors explicitly disavow it, often near the end of their Discussion sections (e.g., Morrison & Chein, 2011, p. 58). But without this assumption, there is no logically necessary link from the observed control-adjusted score gains to the theoretical conclusion of Gf gains. Why not? Because non-Gf-related factors can transfer across tasks too.

The athletic analogy can easily be extended to illustrate this. Suppose that instead of watching a movie, the athlete in Hatze’s (1976) experiment practiced a seemingly unrelated task such as high jump. The problem is that tasks that seem unrelated on the surface can still share critical technical components. For example, the approach of the high jump may actually be as important as the take off. It requires the right amount of speed and the correct number of strides—factors that affect kicking too. So, if an athlete practices high jump for many hours and then can kick a ball faster than before, is this because the jumping practice improved the explosive power of their leg muscles? Or is it because it provided an opportunity to learn to control the approach better? In other words, was there transfer of athletic ability, of technical components, or both? These possibilities cannot be differentiated on the basis of measured gains in kicking speed alone. Analogously, a control-adjusted gain on an intelligence test may stem from genuine Gf transfer from the training task, from transfer of some non-Gf -related component(s), or from a combination thereof.

Despite these interpretive problems, the research community continues to explore various combinations of treatment tasks, control tasks, and tests (see Morrison & Chein, 2011; Melby-Lervåg & Hulme, 2013, for recent reviews), and in many studies the only dependent variable is the (adjusted) gain in test scores from pretest to posttest. This approach treats the test as a black box and yields very few data points per participant, which exacerbates the practical difficulties inherent in multi-session between-subject designs. Progress has been slow and the results have been inconsistent and open to conflicting interpretations as referenced above. In the final analysis, the problems persist because no conclusive inferences can be drawn on the basis of test-retest comparisons alone. A richer data source is needed.

There are two complementary ways to marshal more data to test whether WM training improves Gf. The first is to assess Gf not with a single test but with a broad battery of multiple tests. The second approach is to use tools from cognitive psychology to open the black box and investigate the actual processes that determine the test scores and the gains thereof. In this article we follow the second approach. The topic of multiple tests is introduced only briefly here and will be discussed in more detail later. This literature is in active development and the results are still tentative. Two emerging patterns are particularly relevant to the present analysis. First, when a battery of multiple Gf tests was administered before and after WM training, strong inter-test correlations were found as expected, and yet only some tests showed a significant control-adjusted transfer effect (Colom et al., 2013; Harrison et al., 2013; Jaeggi, Buschkuehl, Shah, & Jonides, 2014; Stephenson & Halpern, 2013). This selectivity of transfer highlights that test scores and gains can index distinct aspects of the variability across individuals. The high inter-test correlation presumably reflects the shared Gf loading of scores, whereas the dissociable gains suggest plasticity in one or more non-Gf -related factors. This dissociation reinforces the methodological caveats discussed above. The second pattern that emerges from the recent literature is that the tests that did show significant control-adjusted transfer were tests with a prominent visuospatial component¹ (Colom et al., 2013; Jaeggi et al., 2014). This raises the possibility that the experimental intervention in these and earlier studies (e.g., Jaeggi et al., 2008) may have improved the visuospatial ability rather than the fluid intelligence of the participants, via the visuospatial demands of the dual n-back task intended for WM training (Moody, 2009; Stephenson & Halpern, 2013).

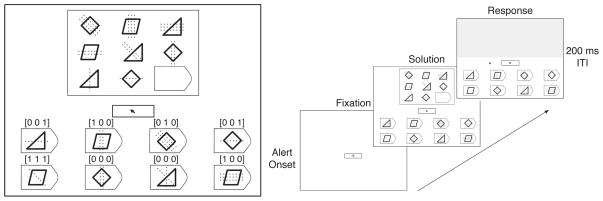
In this article, we focus on Raven’s Advanced Progressive Matrices (APM, Raven et al., 1998) as the paradigmatic example of the class of matrix-based visual analogy tests that are commonly used in cognitive enhancement research (Buschkuehl & Jaeggi, 2010). A Raven problem consists of a matrix and 8 response alternatives. There are multiple distinct relations among the entries in a given row or column (Figure 1, left). To answer the problem correctly, the participant must identify the relations and select the response that matches the pattern. This requires relational reasoning, pattern matching, working memory, executive control, and other abilities central to fluid intelligence. However, Raven scores also depend on test-specific factors, including a prominent visuospatial component. These factors are unrelated to Gf and are potential confounds in cognitive enhancement research. Thus, it is important to understand them, find ways to measure them, evaluate their potential to contaminate the assessment of Gf gains, and correct this contamination.

Figure 1. Example of the Raven’s problem format, relational coding, and trial sequence.

Left: The problem matrix and the 8 response alternatives are shown with solid lines. The height of the rectangular box around the matrix subtended 9 degrees of visual angle. Eye fixations were assigned to 10 areas of interest (AOIs): nine for the matrix cells (top row = 1–3, middle = 4–6, bottom = 7–9) and one for the entire response area. This example item (generated by the authors) requires the extraction of three relations: distribution of three shapes (diamond, triangle, parallelogram), distribution of three line orientations (0°, 45°, 90°), and quantitative pairwise progression of line numbers (3→2→1). The vectors above each response were not shown to participants but illustrate the respective relations captured in each possible response. Right: Each trial had three phases: fixation, solution, and response. Eye movements and verbal protocols were collected during the solution phase. Moving the mouse cursor out of the fixation box triggered the response phase, during which the problem matrix was masked and the participant clicked on their chosen answer. The inter-trial interval (ITI) was 200 ms.

In this article we open the black box of Raven’s APM with the help of detailed eye-tracking data and a novel method for scanpath analysis (Hayes, Petrov, & Sederberg, 2011). This rich data source allows us to investigate the information-processing mechanisms associated with the observed gain in test scores. Arguably, this variable—the score gain on a matrix reasoning test—is the most frequently used and potentially misunderstood dependent measure in cognitive enhancement research.

Recently we (Hayes et al., 2011) demonstrated that approximately 40% of the variance of Raven’s APM scores across participants can be predicted on the basis of individual differences in eye-fixation patterns. Critical for this success was a novel data-processing algorithm called Successor Representation Scanpath Analysis (SRSA, Hayes et al., 2011) that captures the statistical regularities of scanpath sequences of arbitrary lengths. SRSA uses temporal difference learning (Sutton, 1988) to represent these regularities by a fixed-size matrix called a successor representation (SR, Dayan, 1993) that can be aggregated across trials and analyzed with standard multivariate methods such as principal component analysis (PCA, Everitt & Dunn, 2001). Importantly, the SRs are interpretable: Different test-taking strategies give rise to characteristic SR patterns that can be traced in the human data (Figure 2). SRSA thus provides unprecedented insight into the role of strategic processing in matrix reasoning tests.

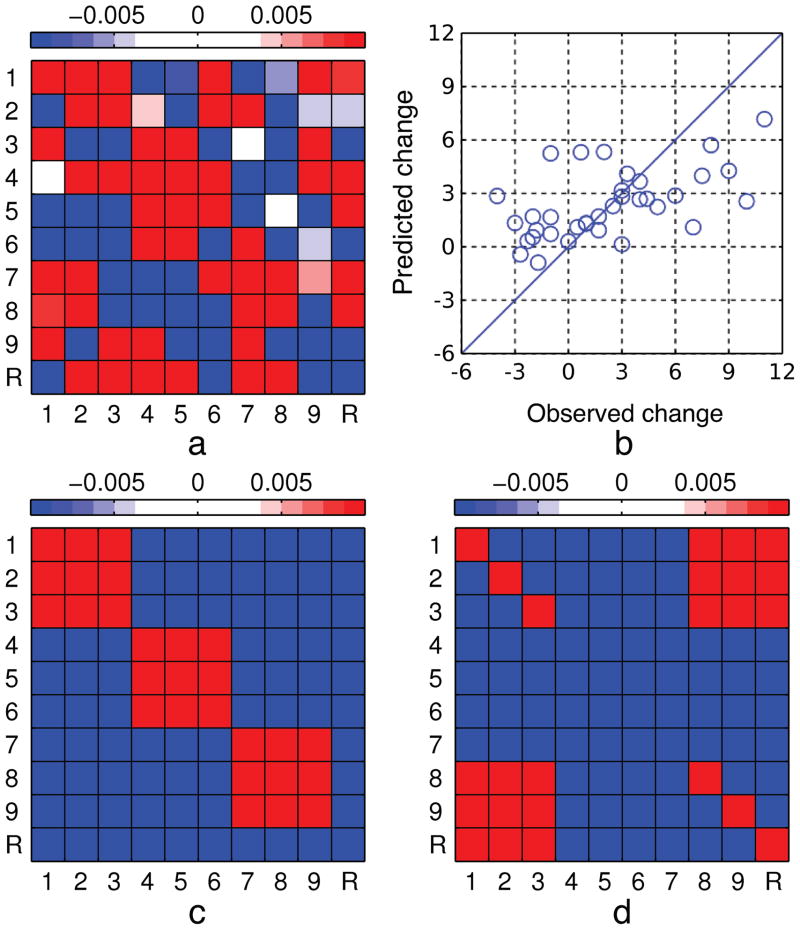
Figure 2. Weight matrices, relational score gain predictions for the full cross-validated model, and Simulated SR differences.

The cross-validated model prediction weight matrix across 35 leave-one-out fits (a) revealed a strong relationship between systematic scanning and relational score gains across sessions. The relational score gain was predicted by a separate model that had no access to the data for the respective individual. Panel b plots the predicted versus observed relational score gain for all 35 participants ( $R_{cv}^2=.32$). Panel c and d were generated using simulated scanpath sequences to highlight important structure. Panel c shows an idealized difference SR resulting from simulated sequences with a 90% increase in row-systematicity on session 2. Panel d shows an idealized difference SR resulting from simulated sequences with a 20% boost in answer checking on session 2. The x- and y-axes represent the sender and receiver areas of interest, respectively. R = response area of interest. SR = successor representation of the regularities in scanpath sequences.

Our goal in this article is to apply this powerful new tool to investigate whether strategy refinement can account for the test-retest improvement of Raven scores. The answer is a clear yes. We observed a highly significant practice effect, replicating published results (Bors & Vigneau, 2003; Denney & Heidrich, 1990). Approximately 30% of the variance of score gains across participants could be predicted on the basis of individual differences in the changes in eye-fixation patterns as captured by SRSA. Moreover, the latter changes had a clear interpretation in terms of strategy refinement: Individuals that moved toward a more systematic scanning pattern at posttest also tended to improve their scores. Furthermore, when the strategy-dependent variance was partialled out, the residual score gains were no longer statistically distinguishable from zero. These results indicate that strategy is a critical latent variable and a strong potential confound that must be considered whenever matrix reasoning tests such as Raven’s APM are used to measure fluid intelligence gains.

Method

Thirty-five university students with normal or corrected-to-normal vision completed two short-form tests from Raven’s Advanced Progressive Matrices, Set II (Raven et al., 1998) on two separate days approximately a week apart. The participants were paid $6 per hour plus $1 bonus for each correct answer. Half of them completed items 2, 4, 6, 9 10, 11, 16, 17, 19, 21, 23, 24, 26, and 29 on the first session and 1, 3, 5, 7, 12, 13, 14, 15, 18, 20, 22, 25, 27, and 28 on the second. The other half completed the same subsets in the opposite order. The instructions followed the Raven APM Manual guidelines for individual test administration (Raven et al., 1998). Between the two test sessions, 23 participants completed two additional sessions of paper-and-pencil training on Raven-like problems (Matzen et al., 2010). The remaining 12 participants were no-contact controls.

Each trial began with a brief alert sound. A fixation cross appeared on a 21” CRT monitor in a darkened room (Figure 1, right). After the participant fixated for 1 s, the Raven problem appeared and remained onscreen until the participant selected a response using the mouse. Eye-tracking data were collected on both test sessions² using a desktop Eyelink 1000 tracker (SR Research, 2006). Saccades and fixations were segmented with Eyelink’s standard algorithm using velocity and acceleration thresholds (SR Research, 2006). Each fixation was assigned to one of 10 distinct areas of interest (AOIs, see Figure 1 for details). A single AOI (labeled R) covered the entire response area so that the spatial layout of the answers could not be used to decode the participants’ choices. The few (<1%) fixations outside the 10 designated AOIs were ignored.

Relational Item Scoring

Most APM items contain multiple distinct relations that must be extracted to arrive at the correct answer (Carpenter, Just, & Shell, 1990). However, it is often the case that even when items are answered incorrectly the participant still extracts some of the correct relations. On items in which incorrect answers captured some of the correct relations, we used that information to infer which relations were successfully extracted by the participant and were able to increase statistical power by capturing this information. Seven relational rules were identified within the APM items: the five rules introduced by Carpenter et al. (1990) plus two new rules, opacity and unique:

• Constant in a row (CIR): Relation in which an element is the same across rows, but changes down columns.

• Quantitative pairwise progression (PP): Relation in which an element increases or decreases down rows or across columns.

• Figure addition or subtraction (ADD/SUBTRACT): Relation in which an element from one column is added or subtracted from another column to produce a third column element.

• Distribution of three values (D3): Relation in which three values from a categorical attribute are distributed across a row or column.

• Distribution of two values (D2): Relation in which two values from a categorical attribute are distributed through a row, and the third value is null.

• Opacity (OPACITY): Relation indicating which figural elements occlude other figural elements when elements overlap.

• Unique (UNIQUE): Used to demarcate special relations that are specific to an individual APM item.

For every item, each of the eight responses were scored as a vector indicating whether they contained a given relation (1) or did not³ (0). See Figure 1 for an example item coding and Appendix A for the complete relational coding scheme. With this form of relational coding, the participant’s performance for each session was measured as the total number of relations extracted (i.e., the sum of their response vectors) during pre- and posttest, respectively.

Successor Representation Scanpath Analysis

We used SRSA (Hayes et al., 2011) to assess changes in participant strategy by quantifying individual differences in pre- and posttest eye-fixation patterns. SRSA quantifies regularities in sequences of eye-fixations using temporal-difference learning (Sutton, 1988) to construct a matrix called a successor representation (SR, Dayan, 1993). The key idea behind SRSA is that upon observing a transition from one AOI to another, instead of simply updating the transition probability from the first to the second AOI, we associate the first AOI with the second AOI and all expected subsequent AOIs based on prior visits to the second AOI. In this way the SRSA algorithm learns to predict future scanpaths based on past scanpaths. After traversing the entire fixation sequence for a trial, the resulting SR can be conceptualized as having extracted the statistical regularities in temporally extended scanpaths. Specifically, an SR matrix contains, for each AOI, the temporally discounted number of expected future fixations to all AOIs (Dayan, 1993). Given their uniform size and that they are based on the same set of AOIs, the SR matrices from different observers and/or trials can be analyzed using standard statistical methods to identify significant pattern regularities for various comparisons of interest. Since we were interested in examining the change in strategy between pre- and posttest, our present approach was to use the differences between the pre- and posttest SRs to predict the difference between pre- and postest Raven performance.

The first step in SRSA is to convert each trial scanpath into a trial SR. Each trial scanpath was defined as the sequence of fixations across the 10 distinct AOIs (9 cells of the problem matrix and the response area) on a given trial.⁴ A successor representation (Dayan, 1993) was calculated for each trial scanpath, resulting in one 10 ×10 SR matrix M per trial for each participant. Each trial SR matrix is initialized with zeros and then updated for each transition in the scanpath sequence. Consider a transition from state i to state j. The ith column of the matrix—the column corresponding to the “sender” AOI—is updated according to:

$$\mathrm{\Delta }{\mathit{M}}_i=\alpha ({\mathit{I}}_j+\gamma {\mathit{M}}_j-{\mathit{M}}_i),$$ (1)

where I is the identity matrix, each subscript picks a column in a matrix, α is a learning-rate parameter (0 < α < 1), and γ is a temporal discount factor (0 < γ < 1). The learning rate parameter α controls the incremental updating and γ controls the amount of temporal discounting. The latter term is the key to extending the event horizon to encompass both immediate and long-range transitions—it includes the discounted future states in the prediction from the current state. For example, suppose a participant scans the top row of a Raven problem systematically from left to right: 1 → 2 → 3 → 1 → 2 … Then the successors of location 1 will include both location 2 and, weighted by γ, location 3. After traversing the whole scanpath, the estimated SR matrix approximates the ideal SR matrix, which contains the temporally discounted number of expected future fixations on all AOIs (rows), given the participant just fixated on any individual AOI (column). Note that the entries in the SR matrix are not probabilities, they are (discounted, expected) numbers of visits. When γ is set to zero the SR is equivalent to a first-order transition matrix and as γ increases the event horizon is extended farther and farther into the future. Note also that the learning parameter α does not reflect a cognitive learning rate, but only the learning rate that optimizes the temporal-difference learning algorithm.

The second step in SRSA depends on the question of interest—in our case the contribution of strategy to Raven APM improvement. Since we were interested in examining strategy differences between sessions, the trial SRs were not averaged across both sessions as they were in Hayes et al. (2011). Instead, for each participant a difference SR matrix was computed by averaging across the session 1 trial SRs and session 2 trial SRs separately, and then taking their difference (mean session-2 SR minus mean session-1 SR), resulting in 35 participant difference SRs. Conceptually, each 10 × 10 difference SR captured the difference in eye-fixation patterns between pre- and posttest for the corresponding participant. To reduce the dimensionality of this 100 feature space and prevent over-fitting, we performed a principal-component analysis (PCA, Everitt & Dunn, 2001) of the difference SRs.⁵ PCA is a standard machine learning technique for reducing dimensionality by finding the most informative viewpoints (i.e. variance-maximizing orthogonal rotations) of a high-dimensional space. The result is a set of linear orthogonal variables called principal components. Conceptually, the principal components of the SR differences represent dimensions of individual differences in fixation patterns between pre- and posttest. These are expressed mathematically as orthogonal basis vectors in the 100-dimensional difference SR space. Each participant was characterized by 20 projections onto this rotated basis. The difference SR projections were then used as predictor variables in a multiple linear regression analysis to predict relational score gain (i.e. the difference in the number of relations extracted, posttest minus pretest).

The final step in SRSA is to optimize and cross-validate the model fit between the difference SR projections and relational score gain. We implemented a two-tier algorithm to maximize the fit. In the inner loop, it calculated the difference SRs for given parameters α and γ (Equation 1), then calculated the first 20 principal components and the corresponding projections for each participant, picked the three projections that correlated most strongly with the relational score gain, and constructed a linear regression model with these three predictors.⁶ In the outer loop, a Nelder-Mead optimization routine searched for α and γ that maximized the multiple regression coefficient of the inner-loop model. To guard against over-fitting, we performed leave-one-out cross-validation to test the generalization performance of the two-tier fitting algorithm. We partitioned the data into a training set of 34 participants and a test set of 1 participant. We ran our two-tier algorithm on the training set. The parameters α and α optimized on the training set were then used to calculate the SRs for the fixation sequences in the test set. Finally, we calculated the model’s prediction of relational score gain by multiplying the test set difference SR matrix by the weight matrix estimated from the training set. We repeated this process 35 times, testing on the data from each participant in turn. This produced 35 predicted relational score gains, each one based on a model that had no access to the data that was subsequently used to test it. For all SRSA analyses a cross-validated ( $R_{cv}^2$) fit is reported.

Results and Discussion

The relational scores varied between 13 and 32 (M=26.8, SD=4.6) at pretest and between 16 and 33 at posttest across the 35 participants (M=29.0, SD=3.7). The relational score gain (posttest minus pretest) was 2.2 relations on average and varied across individuals (SD=3.9, min=−4, max=11).⁷ The practice effect was highly statistically significant (t(34) = 3.30, p = .001 (one-tailed), d = .56) and consistent with earlier reports of practice-induced effects (Denney & Heidrich, 1990; Bors & Vigneau, 2003). Our effect size (d = .56) was in the upper half of the range of effect sizes typically reported in the Gf enhancement literature (Melby-Lervåg & Hulme, 2013). The larger effect size may reflect the increased statistical power of our relational scoring scheme compared to Raven’s standard scoring. Despite this abundant statistical power, the paper-and-pencil training manipulation had no significant effect relative to the no-contact control (F(2, 32) = .98; paper-and-pencil M=2.6, SD=4.2; no-contact control M=1.4, SD=3.4). Thus even without training, Raven performance increased significantly. This illustrates that the mere test-retest procedure is sufficient to induce score gains even when short test forms are used.

A multiple linear regression was performed using the difference SR projections from the PCA to predict the relational score gain for each participant. Utilizing the two-tier fitting algorithm detailed earlier, the best fit R² = .56 was achieved with three principal components, learning rate α^* = .35, and discount parameter γ^* = .29. As was shown in Hayes et al. (2011), eye-movement data are susceptible to overfitting and so it is essential to perform leave-one-out cross validation to test the generalization performance. Using cross-validation we were still able to account for approximately a third of the variance in relational score gains from pre- to posttest: $R_{cv}^2=.32$. Panel a in Figure 2 shows the average prediction weight matrix across the 35 leave-one-out fits and panel b plots the cross-validated predictions against the observed gains. The average prediction weight matrix reflects the sum of the principal components (scaled by their respective regression coefficients) averaged across the 35 leave-one-out fits.

Just as important as the amount of variance explained by the difference SRs is the clear interpretation offered by the prediction weights themselves. The dominant patterns that were observed in the difference SR principal components are reflected in the prediction weights. In particular, the diagonal box structure indicates systematic row-wise scanning (cf. Figures 2a and 2c). This finding suggests that a significant portion of the practice effect was associated with refinements in information processing strategy whereby participants scanned rows of the problem more systematically and were less prone to haphazard scanning at posttest. In addition to the diagonal box structure indicative of a constructive matching strategy, the weight matrix in Figure 2a also has “hot spots” in the bottom-left and top-right corners. This pattern indicates an increase in the systematic scanning of cells 1 2 3 (top row) followed by cells 8 and 9 (which need completion), followed by inspection of the response area (cf. Figures 2a and 2d).

To get a clearer picture of the differences between participants that improved and those that got worse, we ran separate cross-validated models for the 11 participants that improved the most and the 11 participants that performed worse or showed no improvement at posttest. For both subgroups, the difference SRSA was able to predict a significant portion of the variance in relational score (low group $R_{cv}^2=.30$; high group $R_{cv}^2=.44$). The average prediction weights across the 11 leave-one-out fits are shown in Figure 3. The low group prediction weights shows more diffuse weights with no clear diagonal structure as well as some off-diagonal values, indicative of more haphazard scanning. This means that participants whose scores stayed the same or worsened at posttest used the same or less optimal scanning strategies on session 2 relative to session 1. The high group prediction weights shows the opposite pattern with an even stronger diagonal box structure than the full model, which clearly shows a strategically driven improvement in relational extraction. The bottom-left and top-right weight pattern is also brought into better focus in this high-improvement group. As discussed above, this pattern can be generated from a sequential systematic scanning of the first row, cells 8 and 9, and then the response area (Figure 2d). We interpret this sequential pattern as an indication that participants are checking their answer more carefully at posttest prior to selecting it. These results are a further demonstration that strategy refinement between pre- and posttest can account for changes (gains and losses) in Raven’s APM performance.

Figure 3. Comparison of cross-validated prediction weights for high- and low-improvement groups.

Relational score gains were predicted separately for the eleven highest and eleven lowest improvement participants across 11 leave-one-out fits ( $\text{low}{R}_{cv}^2=.30;\text{high}{R}_{cv}^2=.44$). Each value was predicted by a separate model that had no access to the data for the corresponding individual. Panel (a) shows the average prediction weight matrix for the low-improvement group and panel (b) for the high-improvement group. A comparison of the prediction weight matrices shows markedly more diffuse scanning in the low-improvement group (panel a) and a gain in systematicity in the high-improvement group (panel b).

To determine whether our practice effect remained after removing strategic gains in our participants, we performed a residual analysis to determine whether the significant practice effect we observed would survive in the absence of the strategic improvements that are clearly evident from the SRSA analysis. In both the entire group (t(34) = .30) and even the high-improvement subgroup (t(10) = .25), the practice effect was no longer statistically significant after the SR covariate was partialled out.

General Discussion

In this article we used eye-tracking data and a novel method for scanpath analysis to investigate the information-processing mechanisms associated with practice effects on matrix-based visual analogy tests. The results showed significant test-retest gains in the Raven scores (Bors & Vigneau, 2003; Denney & Heidrich, 1990). Importantly, over 30% of the variance of score gains across participants could be attributed to refinements in problem-solving strategies as revealed by characteristic changes in eye-fixation patterns. Moreover, when the strategy-related variance was partialled out, the residual score gains were no longer significant, even in the high-improvement subgroup. This indicates that strategy refinement is a powerful determinant of score gains—it controls a major portion of the variance and can change the substantive conclusion of an experiment. Consequently, it must be considered carefully when interpreting score gains on Raven’s APM and similar matrix-based tests.

The central topic in the cognitive enhancement literature is the topic of transfer across tasks. We acknowledge that, given the lack of a transfer group in our experiment, our data do not bear directly on this topic. Nevertheless, the present article contributes to this literature in two ways: empirical and conceptual. The empirical contribution is to examine in detail the information-processing mechanisms underlying the most frequently used dependent measure in the Gf enhancement⁸ field—the score gain on a Raven-like matrix test. Until recently (e.g., Buschkuehl & Jaeggi, 2010; Morrison & Chein, 2011), the overwhelming majority of positive reports of far transfer of WM training to fluid intelligence relied exclusively on control-adjusted score gains on such tests. In effect, our results provide unprecedentedly detailed information on the likely mechanism for the score gains observed in the control groups of these experiments. Further research is needed to investigate whether the same mechanism can account for the gains in the WM training groups as well. The parsimonious hypothesis is that it does, barring evidence to the contrary.

This hypothesis is also consistent with the longstanding distinction between the acquisition of skills and the improvement of abilities (e.g., J. R. Anderson, 2000). The former supports transfer only between tasks that have procedural and/or declarative knowledge in common, whereas the latter implies gains in general mechanisms and capacities that carry the potential for widespread transfer across diverse tasks. The difficulty of achieving such broad transfer has long frustrated educators. Decades of instructional research have demonstrated that it is hard enough to acquire specific skills but much, much harder to improve general abilities (J. R. Anderson, 2000). Given this general pattern, it seems much more likely that the transfer of WM training to Raven-like tests (Jaeggi et al., 2008) is due to skill acquisition—including strategy refinement—rather than improvement of Gf.

The conceptual contribution of this article is to articulate an assumption that is logically required for inferring Gf gains on the basis of test score gains—namely, that only Gf can transfer across ostensibly different tasks such as n-back and Raven’s APM. As we argued in the introduction, this assumption cannot be taken for granted because non-Gf -related factors can transfer across tasks too.

Consider motivation as a case in point: Participants who have invested time and effort to practice a challenging WM task are likely to be more motivated on the posttest compared to control participants. Higher motivation is expected to raise the test scores in the experimental group even when the treatment has no effect on fluid intelligence. When a suitably chosen “placebo” practice made the control participants equally motivated, their test scores improved by approximately the same amount in some studies (Redick et al., 2012; Melby-Lervåg & Hulme, 2013). Thus, motivation is an example of a factor that can sometimes transfer across different tasks and yet is clearly distinct from Gf. It should be mentioned that some studies (e.g., Jaeggi et al., 2011, 2014) suggest that motivation by itself cannot account for the totality of the improvement on reasoning tests. This fact, however, does not invalidate our general methodological point: It cannot be assumed that nothing except Gf can transfer from a WM task to a reasoning task. This is a substantive hypothesis that must be articulated explicitly and supported experimentally (Harrison et al., 2013; Shipstead et al., 2012).

Our results identify another factor that must be considered carefully: cognitive strategy. This is consistent with the evidence that strategy plays an important role in many tasks (e.g., Pressley et al., 1990; McCormick, Miller, & Pressley, 1989; Sternberg & Weil, 1980), tests (Bond & Harman, 1994), and specifically in Raven’s APM (Bethell-Fox, Lohman, & Snow, 1984; Carpenter et al., 1990; Hayes et al., 2011; Vigneau, Caissie, & Bors, 2006). Hence the correlation between strategy refinement and Raven score gains is not too surprising. Nevertheless, it is notable how strong the correlation is and that it accounts for a significant portion of the improvement in test scores.

Raven’s APM includes a significant visuospatial component in addition to its well established Gf component. Jensen (1998) estimates that 64% of the variance in Raven’s scores are attributable to Gf. Other studies (e.g., Kane et al., 2004; Schweizer, Goldhammer, Rauch, & Moosbrugger, 2007) yield similar estimates. Thus, 30–40% of Raven’s variance is not related to Gf. While some of this residual variance is just random noise, some of it is systematic. In the study of Schweizer et al. (2007), for instance, there was 11% and 7% variance overlap between Raven’s APM and Horn’s (1983) visualization and mental-rotation scales, respectively. This is not surprising given the visual nature of the test (Figure 1). Theoretical (e.g., Carpenter et al., 1990), and computational (e.g., A. Lovett, Tomai, Forbus, & Usher, 2009) models of Raven’s APM also include a prominent visuospatial component. Analogous considerations apply to BOMAT (Hossiep et al., 1999) and all other matrix reasoning tests used in Gf enhancement research.

It is important to dispel a tempting interpretive mistake that arises at this point. For concreteness, let us assume that 60% of the variance in Raven’s scores are attributable to Gf, whereas less than 10% are attributable to visuospatial ability. One might argue on the basis of these figures that the the main Gf component dwarfs the visuospatial “contamination.” This is the rationale for the widespread acceptance of Raven’s APM as a unidimensional measure of Gf (Raven et al., 1998). However, these figures apply to Raven’s scores across individuals, whereas the dependent measure in WM training studies is the difference between two scores for the same individual. If Gf is a stable latent variable, it will contribute equally to the pre- and posttest scores and this contribution, no matter how large, will cancel out in the subtraction. Therefore, the variance of the score gains can have a radically different composition than the variance of the scores themselves. Indeed, a meta-analysis of 64 test-retest studies (te Nijenhuis et al., 2007) found a strong negative correlation between score gains and the G loadings of test items.

This illustrates a general limitation of score gains—they can lead to fallacious conclusions and hence must be interpreted with great caution. Some prominent methodologists have even advised against their use altogether: “Gain scores are rarely useful, no matter how they may be adjusted or refined. … Investigators who ask questions regarding gain scores would ordinarily be better advised to frame their questions in other ways” (Cronbach & Furby, 1970, p. 80).

Given that fluid intelligence is defined as the latent variable explaining the intercorrelations in performance on a wide spectrum of tasks (Cattell, 1963; Carroll, 1993; Jensen, 1998; Martínez et al., 2011; Spearman, 1927), one must employ a comprehensive battery of tests to evaluate whether Gf improves with practice at the latent level—that is, “at a level that represents the components of the variance common to the set of tasks indexing a given ability” (Schmiedek, Lövden, & Lindenberger, 2010, p. 2). This methodological imperative is gradually being acknowledged in the field and there is a growing number of studies that administer multiple tests (Colom et al., 2013; Harrison et al., 2013; Jaeggi et al., 2014, 2011; Schmiedek et al., 2010; Stephenson & Halpern, 2013; von Bastian & Oberauer, 2013). As these studies are too complex to review in detail here, we will restrict our discussion to findings related to the topic of visual strategies.

These recent multi-test data suggest the possibility that the putative gain in fluid intelligence may actually be gain in visuospatial ability. The study of Stephenson and Halpern (2013) was designed to test this possibility. It included multiple training groups practicing purely visual, purely auditory, or dual versions of the n-back task. The results showed significant control-adjusted gains on only two out of four Gf tests and only for participants who had a visuospatial component in training. A limitation of Stephenson and Halpern’s (2013) design was that it tested transfer exclusively in the visual modality. By contrast, Jaeggi et al. (2014) included non-visual tests in the battery of outcome measures. The results showed significant transfer on the visuospatial reasoning tests in the visual training and the auditory training group, but no significant transfer on the verbal reasoning tests in either training group relative to the control group. Again, this is consistent with the hypothesis that transfer might be restricted to the visuospatial domain. Jaeggi et al. (2014) temper this conclusion with the caveat that the verbal reasoning measures have lower reliability and hence afford less statistical power than the visuospatial measures. A third study (Colom et al., 2013) also administered both visuospatial and verbal reasoning tests, and used item response theory (IRT) to derive indices of Gf and other constructs. No statistically significant transfer was obtained for any construct, although there was a trend for Gf (p < .06). This trend was undermined by the lack of significant near transfer to the WM construct (cf. Melby-Lervåg & Hulme, 2013; Shipstead et al., 2012). Moreover, once again the Gf transfer was limited to the visuospatial tests, whereas the verbal reasoning test improved equally in both training and control groups. A study with older adults (Stepankova et al., 2014) also found improvement in visuospatial skills following verbal n-back training. Finally, two studies (Schmiedek et al., 2010; von Bastian & Oberauer, 2013) report statistically significant Gf transfer at the latent level. Upon closer examination, however, these data too are compatible with the visuospatial hypothesis because the gain in the latent reasoning factor seems driven by visuospatial tests in both studies. This is hard to evaluate from von Bastian and Oberauer’s (2013) report because it tabulates the results only in terms of an aggregate reasoning score that lumps the verbal and visuospatial modalities together. There is a purely verbal reasoning test—syllogisms—included in the report and the error bars in von Bastian and Oberauer’s (2013) Figure 5 suggest that it did not transfer significantly. We should also note that all data are reported and analyzed in terms of standardized gain scores, which must be interpreted with caution as discussed above. The statistical analysis of Schmiedek et al. (2010) is more sophisticated. It employs a latent difference score model (McArdle & Nesselroade, 1994) that uses factor-analytic techniques to evaluate gains at the latent level. This study compared younger and older adults. The results showed a small (effect size d = .19) but statistically significant transfer effect for the Gf latent factor in the younger experimental group (relative to younger control) and nonsignificant transfer in the older experimental group (relative to older control). At the level of individual tasks in the younger group, the greatest transfer in the reasoning category occurred in the visuospatial modality (d = .38), whereas the verbal modality showed a trend (d = .13) but did not reach statistical significance (p = .26). Interestingly, reasoning was also tested in the numerical modality and it did show significant transfer (d = .33) in the younger group (Schmiedek et al., 2010, Table 3). The interpretation of these results is complicated by the fact that both experimental groups practiced a diverse array of 12 tasks spanning all three modalities. Thus, it is possible that the transfer to numerical reasoning is driven by training on a numerical task, the transfer to visuospatial reasoning is driven by training on a visuospatial task, etc. Consequently, even this rich data set does not allow definitive conclusions with respect to the aforementioned distinction between the acquisition of skills and the improvement of abilities. In summary, the issues are complex and the results are not easy to interpret. Still, the available multi-test data seem consistent with the hypothesis that the observed Gf gains may be visuospatial gains in disguise.

Turning to the question of mechanism, the strategies for scanning a Raven’s problem matrix (Figure 1) can be modeled within a skill acquisition framework. They are a type of procedural knowledge and, after decades of research, a lot is known about how such knowledge is represented and acquired from experience (e.g., J. R. Anderson, 2000). Our discussion focuses on the ACT-R cognitive architecture (Adaptive Control of Thought–Rational, J. R. Anderson, 2007; J. R. Anderson et al., 2004) as the flagship example of this multifaceted research tradition. Procedural knowledge in ACT-R is represented as a large set of production rules (or productions), each of which can be summarized in English as an if-then statement. For example, “if the current goal is to determine whether object X appears on the top row of the display then scan the top row from left to right and search for object X.” Productions are designed to work in a coordinated manner while remaining relatively independent. Because of this independence, procedural knowledge can be acquired and practiced incrementally (J. R. Anderson, 1987; Taatgen, 2003). ACT-R has learning mechanisms that can construct new rules by proceduralization of declarative knowledge or by recombination of existing rules. Once these productions are created, a reinforcement-learning mechanism incrementally updates the system’s estimates of their utility. These estimates provide a principled basis for selecting among competing productions and thereby choosing among alternative behaviors (e.g., M. C. Lovett, 1998, 2005). These mechanisms are consistent with neural-network models of action selection and reinforcement learning in the basal ganglia (Frank, Loughry, & O’Reilly, 2001; Jilk, Lebiere, O’Reilly, & Anderson, 2008; Stocco, Lebiere, & Anderson, 2010). A detailed theory of skill acquisition has been developed in the ACT-R framework. It accounts for a large body of behavioral (e.g., J. R. Anderson, 1987, 2007; Taatgen, Huss, Dickison, & Anderson, 2008) and neuroimaging data (e.g., J. R. Anderson, Betts, Ferris, & Fincham, 2010). Specifically, it accounts in quantitative detail for key aspects of skill acquisition in multi-tasking (e.g., Salvucci & Taatgen, 2008; Taatgen, 2005) and for patterns of eye movements in complex displays (e.g., Lee & Anderson, 2001). ACT-R is also a proven platform for the development of instructional software (e.g., Ritter, Anderson, Koedinger, & Corbett, 2007).

These ideas can be applied to the type of visual scanning strategies relevant to our study. Consider the visual n-back task (e.g., Jaeggi et al., 2008) as a concrete example. On each trial, a small square appears in one of several positions in a rectangular grid. The participants must encode the location of the square and compare it to stored locations from previous trials. Three ACT-R models of the n-back task have been developed (Juvina & Taatgen, 2007; Kottlors, Brand, & Ragni, 2012; M. C. Lovett, Daily, & Reder, 2000), one of which (Juvina & Taatgen, 2007) explicitly focuses on control strategies and another (M. C. Lovett et al., 2000) on individual differences in WM capacity. Unfortunately, these models work with verbal stimuli such as letters and, to our knowledge, no model of the visual n-back task has been developed yet. Nevertheless, it is possible to extrapolate from the existing models. An ACT-R model of this task would include various production rules that, when chained together, implement various strategies for scanning the grid—e.g., by rows, by columns, outward from the center, etc. It would also include productions that encode the target location—e.g., as a visual icon, by associating it to a digit on an imaginary keypad, by associating it to the letter formed by the empty cells on the grid, etc. A third set of rules would be needed to retrieve traces of past trials and compare them to the current one. Importantly, each of these unit-tasks can be performed in alternative ways implemented by competing productions. In ACT-R, productions with higher utility have a greater chance to fire on a given trial. The reinforcement learning mechanism increases the utilities of the productions that fired on correct trials and decreases those on incorrect trials. Gradually, productions that lead to success are strengthened and hence selected more often, whereas productions that lead to errors tend to drop out. This process is automatic and is a form of implicit learning. The improvements in accuracy and speed on practiced tasks are explained in terms of increased reliance on productions that achieve the goal with higher probability of success and in fewer steps (J. R. Anderson, 1987; Taatgen et al., 2008).

The learning effects in our data set also have a natural explanation in the ACT-R framework. On this interpretation, different visual strategies are implemented by sets of productions that can be chained together in various combinations. With practice, the reinforcement learning mechanism updates the utilities of these productions. This alters both the pattern of eye movements and the probability of solving the problem correctly. This common learning mechanism explains the correlation between the refinement in scanpath patterns and the gains in Raven’s scores (Figure 2).

Furthermore, the skill acquisition framework provides a straightforward explanation of the transfer from the visual n-back task to Raven’s APM. Both tasks share a lot of unit-tasks such as scanning a rectangular grid in search of an object that matches some description, encoding the location of such objects on the grid, comparing it to stored locations of other objects, and so on. Because production rules encode small and relatively independent bits of procedural knowledge, they can be used in multiple tasks. Productions constructed (e.g., from instruction) while learning one task can later be used in other tasks. Importantly, the utility of a given production rule reflects the history of successes and failures of applying this rule across all tasks it has been tried on. Thus, the utilities learned from practice on one task will affect the probabilities with which competing productions are selected while the system performs another task. This leads to positive transfer when many productions are beneficial in both contexts, and to negative transfer when most productions that were beneficial in the first turn out to be detrimental in the second. In a nutshell, these are some of the key ideas of the ACT-R theory of skill acquisition (J. R. Anderson, 1987, 2007; Taatgen et al., 2008). Given its obvious relevance to WM training and transfer, it deserves to be widely known and discussed in the cognitive enhancement literature. It is, therefore, unfortunate that the latter currently makes virtually no references to ACT-R and only oblique references to skill acquisition research more generally. This is an instance of the unfortunate but still widespread estrangement of the comparative and information-processing traditions in psychology (Cronbach, 1957).

ACT-R provides a solid framework for a mechanistic characterization of the distinction between skill acquisition and ability improvement. The model of Lovett and colleagues (2000) is particularly relevant in this context because it accounts for individual differences in WM capacity in terms of the so-called source-activation parameter W. This is a global architectural parameter that remains fixed throughout a given run but is assumed to vary across individuals. Lovett and colleagues (2000) estimate it from one task (modified digit span) for a given individual and then produce zero-parameter fits to the same individual’s performance on another task (n-back). In this framework, ability improvement can be modeled as an increase of W after practice, whereas skill acquisition can be modeled as outlined in the previous paragraph. A very promising direction for future research is to develop two ACT-R models—one with modifiable W and fixed production utilities, and another with fixed W and modifiable utilities. These two models can then be compared in terms of their fit to behavioral data.

In conclusion, let us recapitulate the diverse strands of evidence considered in this article. Fluid intelligence (Gf) is defined as a latent variable that cannot be measured directly but must be inferred from the intercorrelations in a diverse battery of tests. There is strong evidence that Gf is highly heritable. The prevailing opinion among psychometricians, based on decades of research and disappointments with past efforts at improvement, is that Gf is a relatively stable trait. The recent wave of enthusiasm in Gf enhancement was triggered by reports of score gains on matrix reasoning tests. The interpretation of these results is questionable because no single test score is identical with Gf and because score gains can be dominated by factors that play marginal roles in the scores themselves. The data reported here show score gains on Raven’s APM that are commensurate with the effect sizes typical of cognitive enhancement studies. Importantly, these gains can be accounted for in terms of refinements in problem-solving strategies as revealed by characteristic changes in eye-fixation patterns. Our data do not address whether the same mechanism can account for the entire transfer of WM training to Raven-like tests. However, the newest studies that assessed Gf via a diverse battery of tests raised the possibility that the transfer may be restricted to the visual modality. This indirectly supports the hypothesis that at least some of this transfer may be driven by refinements in visual scanning strategies. This hypothesis is also consistent with established theories of skill acquisition that explain transfer in mechanistic terms. By contrast, the alternative hypothesis is usually formulated by means of vague analogies with athletics. We are not aware of a mechanistic proposal of how n-back training improves WM capacity. The Gf improvement hypothesis is advanced on the basis of data showing higher score gains on Raven-like tests following WM training compared to control. This inference logically depends on the assumption that Gf gain is the only possible explanation for such control-adjusted transfer. This assumption cannot be taken for granted because non-Gf -related factors can transfer across tasks too. Notably, procedural knowledge can transfer in subtle ways even between tasks that seem unrelated on the surface, and especially between overlapping tasks such as visual n-back and Raven’s APM.

On the basis of this converging evidence, we conclude that it is entirely possible, indeed likely, that the reported transfer of WM training to Raven-like tests is due at least in part to refinements in visual scanning strategies. More broadly, the control-adjusted score gains probably include a contribution from procedural knowledge tacitly acquired and fine-tuned during the WM training and later utilized at posttest.

If strategic procedural knowledge transfers across tasks, does WM training induce Gf gains that cannot be explained in terms of strategic transfer? The remainder of this article outlines some methodological recommendations on how to investigate this question experimentally in the future.

The most informative experimental designs are characterized by two features: focused training interventions in several distinct groups, and pre- and post testing with a comprehensive suite of outcome measures. The study of Jaeggi et al. (2014) illustrates a well designed set of training interventions: one group practiced exclusively the auditory n-back task, a second group practiced the dual (audio and visual) n-back task, and there was also an active control group. As for the outcome measures, it is necessary to assess three types of outcomes for each participant before and after training. First, Gf must be assessed with a battery of tests as discussed above. It is important to include both visual and non-visual reasoning tests in this battery. The tacit assumption that Raven’s APM (or any other test, for that matter) equals Gf is too simplistic. Second, a battery of visual and non-visual WM measures is needed to assess near transfer (Shipstead et al., 2012). Third, the visual scanning strategies must also be assessed, and the tools developed here provide the means to do so. Our data demonstrated that strategy refinement can control a substantial portion of the variance and that, therefore, strategies must be monitored and taken into account in the analysis. We recommend to administer all visual tests with an eye tracker and to process the scanpath data with the SRSA algorithm (Hayes et al., 2011). The resulting successor representations (or, more parsimoniously, the first few principal components thereof) should be included to the suite of outcome measures and used as covariates in the main statistical analysis.

The statistical analysis must estimate latent variables and test whether Gf improves at the latent level (McArdle & Nesselroade, 1994; Schmiedek et al., 2010). We share Cronbach and Furby’s (1970) reservations about score gains as measures of change, particularly with respect to a variable that is defined at the latent level. Fortunately, quantitative psychologists have developed sophisticated methods for analyzing learning and change at the latent level.⁹ A test of the training effect on Gf can be realized by using a bifactor model (Yung, Thissen, & McLeod, 1999) with Gf as the general dimension. The model must guarantee that the nature of the latent variable does not change from pretest to posttest and that the training effect is an effect on this general dimension. One method that guarantees this is the Multiple-indicator multiple-cause (MIMIC) model (Goldberger, 1972) with pretest-versus-posttest as an external covariate of the general dimension that is shared by pretest and posttest. The same modeling framework also makes it possible to estimate effects on more specific latent variables and to isolate a strategy-specific effect from a genuine effect on Gf. The Latent difference score model (McArdle & Nesselroade, 1994) is based on similar principles and has similar virtues. It has already been applied successfully to cognitive enhancement data (Schmiedek et al., 2010). A second approach to guarantee comparability between pretest and posttest is to analyze the data at the level of individual test items instead of aggregate scores. Item response theory (De Boeck & Wilson, 2004) can then be used to impose constraints on the item parameters at pretest and posttest. This approach is developed in Embretson’s (1991) model of learning and change.

Empirical research along these lines has the potential to identify which aspects of intelligent performance improve after what kind of practice via what mechanisms. We are aware of the logistical difficulties in collecting so much data per participant, including eye tracking, and latent-level modeling. However, no simpler methodology can overcome the interpretative difficulties inherent in demonstrating change in a latent variable in the presence of intercorrelated confounds, and pinpointing the causes for this change. Given the massive societal resources at stake and the enormous potential benefit, this research burden is clearly warranted.

Finally, we come full circle to our opening question: Can intelligence be improved with training? The issues are complex and much of the current disagreement stems from incompatible interpretations of the vague and ambiguous term “fluid intelligence.” One important piece of this large puzzle is the ability to flexibly deploy a judicious variety of cognitive strategies and to adaptively learn their utilities for various tasks. If this ability is taken to be part and parcel of Gf then the answer to the opening question may well be yes. If, however, Gf is interpreted in narrow neurobiological terms (e.g., Duncan et al., 2000; Gray & Thompson, 2004) then the answer remains elusive. So far we have seen no conclusive evidence that the brain can be trained like a muscle.

Hayes-Petrov-Sederberg-INTEL-14 Highlights.

• We use eye data to examine the role of strategy in improvements in matrix reasoning

• We explain why control groups do not necessarily rule out strategic confounds

• We show how eye movements can be used to quantify and remove strategic contaminants

• One-third of the variance of score gains could be attributed to strategy refinement

• Test score gains are logically questionable as measures of intelligence enhancement

Appendix A. Relational scoring details

Raven’s Advanced Progressive Matrices (APM) is traditionally scored as the total number of items correct. Preliminary SRSA analysis that used SR differences to predict total number of APM items correct showed an overall trend for an increase in systematicity on session 2 (Hayes et al., 2011). To explore this finding in more detail, we needed to increase our overall power to resolve individual differences. The APM at its core tests the ability to extract relational information from complex, novel visual environments. Therefore, given that most APM items contain multiple distinct relations and an assortment of these relations are found within the 8 possible responses, we were able to increase our power to resolve individual differences by inferring the number of relations extracted for both correct and incorrect responses based on how many correct relations the chosen response contained.

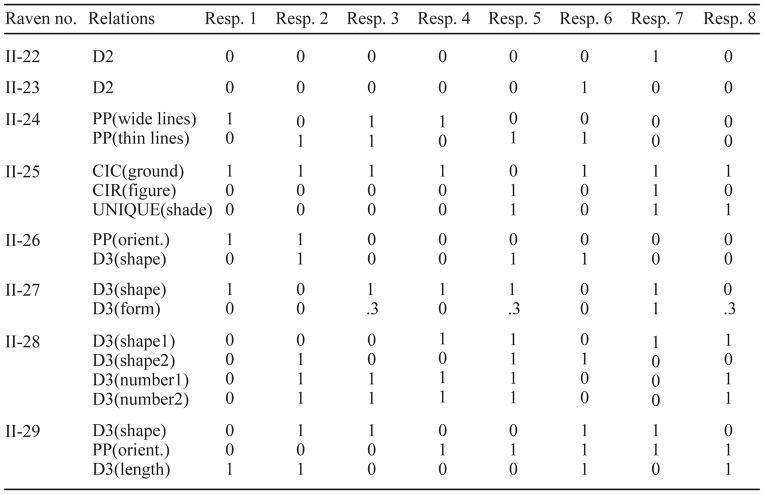
When it was possible to tie the relation to a single feature, the feature to which the relational rule is applied is shown in parentheses (e.g., shape, shading, orientation, position, figure/ground, length). Finally, each of the eight possible responses were scored as either capturing (indicated by a 1) or failing to capture (indicated by a 0) each relation within an item. Four items (11, 14, 18, 27) had relations where partial credit was awarded for relational capture. For instance on item 11, response 1 was credited with .8 instead of 0 because it captured the addition relation but lacked a thin outside border around the figural item. For the other 24 remaining items, each response either clearly contained or lacked the relation(s). Table A1 lists the relational score of each response for each item.

Figure A1. Raven Relational Scoring By Item.

Items are identified by their standard numbers in Raven’s Advanced Progressive Matrices. The Relations column lists which rules are present in the problem matrix and the feature to which that relational rule is applied in parentheses. The last eight columns represent the eight possible responses (moving left to right, top row is 1 2 3 4 and bottom row is 5 6 7 8) and whether or not they contain the corresponding relation.

Appendix B. SRSA technical details

The successor representation was introduced to the reinforcement-learning literature by Dayan (1993) and was developed by White (1995). The SR is essentially identical to the fundamental matrix in the theory of Markov chains (Kemeny & Snell, 1976). More recently, Gershman, Moore, Todd, Norman, and Sederberg (2012) identified a formal connection between the SR and an influential model of episodic and semantic memory, the Temporal Context Model (e.g. Howard & Kahana, 2002; Sederberg, Howard, & Kahana, 2008).

We use a version of the successor representation that differs slightly from the standard definition (Dayan, 1993; White, 1995). The difference is that, when visiting a state i, our version does not include this same visit in the total (temporally discounted) number of visits to i. Assuming a first-order Markov chain with transition probability matrix T, our SR matrix M is based on the power series:

$$\mathit{M}=\mathit{T}+\gamma {\mathit{T}}^2+{\gamma }^2{\mathit{T}}^3+\dots =\mathit{T}{(\mathit{I}-\gamma \mathit{T})}^{-1}.$$ (2)

The standard definition (Dayan, 1993; White, 1995) is based on the power series I + γT + γ²T² + … = (I − γT)⁻¹. To revert to the standard formulation of the SR learning algorithm, the term I_j in our Equation 1 must be replaced by I_i. In the special case when γ = 0, our algorithm tracks the transition matrix T instead of the identity matrix I.

The proof that the temporal-difference learning algorithm in Equation 1 converges to the true successor representation M (White, 1995) is a direct application of more general convergence proofs about TD(λ) learning in the reinforcement-learning literature (Dayan, 1992; Jaakkola, Jordan, & Singh, 1994; Sutton, 1988). To ensure convergence, it is necessary to decrease the learning rate α as the data accumulate. The technical conditions include:

$$\sum _{n=0}^{\infty }{\alpha }_n=\infty \text{and}\sum _{n=0}^{\infty }{\alpha }_n^2<\infty ,$$ (3)

where n is the number of observations (Dayan & Sejnowski, 1993, cited in White, 1995).