Role of Anisotropic Interactions for Proteins and Patchy Nanoparticles

Abstract

Protein–protein interactions are inherently anisotropic to some degree, with orientation-dependent interactions between repulsive and attractive or complementary regions or “patches” on adjacent proteins. In some cases it has been suggested that such patch–patch interactions dominate the thermodynamics of dilute protein solutions, as captured by the osmotic second virial coefficient (B₂₂), but delineating when this will or will not be the case remains an open question. A series of simplified but exactly solvable models are first used to illustrate that a delicate balance exists between the strength of attractive patch–patch interactions and the patch size, and that repulsive patch–patch interactions contribute significantly to B₂₂ for only those conditions where the repulsions are long-ranged. Finally, B₂₂ is reformulated, without approximations, in terms of the density of states for a given interaction energy and particle–particle distance. Doing so illustrates the inherent balance of entropic and energetic contributions to B₂₂. It highlights that simply having strong patch–patch interactions will only cause anisotropic interactions to dominate B₂₂ solution properties if the unavoidable entropic penalties are overcome, which cannot occur if patches are too small. The results also indicate that the temperature dependence of B₂₂ may be a simple experimental means to assess whether a small number of strongly attractive configurations dominate the dilute solution behavior.

1. Introduction

Protein–protein interactions in aqueous solution are of long-standing interest for those seeking to understand and control liquid–liquid and liquid–solid phase separation of proteins,¹⁻⁶ protein and peptide aggregation,⁷⁻¹⁰ and assembly of transient or long-lived amorphous clusters of proteins in solution.¹¹⁻¹⁵ In some cases, this involves interactions between partially or fully unfolded proteins, and the resulting self-assembled or aggregated states are often effectively irreversible under the solution conditions that they form.^16,17 For interactions between native or folded proteins, assembly processes are more easily reversible, and one of two limiting behaviors is typically observed.

In one case, protein–protein interactions are highly specific, and there is a “lock-and-key” binding step such as what occurs with protein–ligand docking.¹⁸⁻²¹ The vast majority of other possible configurations of the two proteins then result in energetically and statistically negligible interactions compared to the highly attractive interactions for protein configurations in the “docked” or “bound” states. As a result, there is a well-defined and experimentally measurable equilibrium constant for association (or dissociation, K_d).^22,23 In this case, one can experimentally quantify the strength or magnitude of the interactions in terms of the equilibrium free energy of dissociation, and the corresponding enthalpy and entropy of dissociation or binding.²⁴ Proteins in this category are natively monomeric when the bulk protein concentration is below approximately 1 order of magnitude below K_d, and they form structurally well-defined dimers or oligomers of finite size at concentrations near and above K_d.²⁵

In other systems, strong attractions between proteins instead lead to bulk phase separation at sufficiently high protein concentration, with the dense or concentrated phase being a protein-rich liquid,^1,26 amorphous solid,²⁷ or crystal.¹⁻³ If the less dense phase is not highly concentrated then the dominant protein species in solution is often monomeric, in that it does not form long-lived complexes or “bound” states with neighboring proteins. A similar situation holds if one is at sufficiently dilute protein concentrations that deviations from ideal solution behavior are small, independent of the proximity to a phase transition. Interestingly, under some solution conditions with relatively high protein concentrations, one can form short- or long-lived clusters that may or may not be under equilibrium control.¹¹⁻¹⁴ It is not yet fully understood how, if at all, these high-concentration intermediate states are related to bulk phase separation and physical properties of concentrated protein solutions such as viscosity and opalescence;²⁸⁻³¹ however, recent models suggest that such clusters can frustrate phase separation.³² A future report will focus on concentrated protein solutions; the remainder of this report focuses on dilute conditions, as these are historically where most experimental measurements to quantify protein–protein interactions have been conducted.

Experimentally, when one is dealing with dilute, natively monomeric solution conditions, there are a number of techniques available to quantify the interactions in a statistical mechanically well-defined way. These include small-angle light, X-ray, or neutron scattering,³³ equilibrium ultracentrifugation,³⁴ and osmometry.³⁵ Provided the solution is sufficiently dilute in terms of protein concentration, and/or the interactions are sufficiently weak such that the product of B₂₂ and the protein concentration is small,³⁶ one obtains B₂₂ as the measure of protein–protein interactions. B₂₂ is an ensemble-averaged quantity, and is a Boltzmann-weighted average of the direct and solvent-mediated interactions between all configurations involving pairs of proteins in solution. It is defined from statistical mechanics as³⁷

1

where T denotes absolute temperature, and k is Boltzmann’s constant. The integrals are over all possible values of the distance (R) between centers-of-mass (COM) for two proteins, and all possible sets of relative orientations (Ω ≡ Ω₁, Ω₂) of each protein. Ψ denotes the solvent-averaged potential of mean force, and is a function of both R and the protein orientations unless one is dealing with structurally isotropic nano particles that are analogues to proteins.³⁸ A single configuration of two proteins is defined uniquely by R and Ω, with the latter dictating where each amino acid, in each protein, lies relative to its COM.

Ψ is a sum over the interactions between all amino acids on both proteins, and includes the interactions due to steric repulsions, van der Waals attractions, hydrophobic attractions, preferential exclusion or attraction of cosolutes, hydrogen bonding, and screened electrostatics. If one is working at sufficiently high ionic strengths, then all of these interactions are expected to be highly short-ranged compared to the effective hard-sphere diameter (σ) of most proteins of practical interest—a notable exception is if the cosolute is large compared to σ, such as when dealing with high molecular weight, hydrophilic, polymer additives.^39,40 The range of interactions between uncharged amino acids is typically short enough that interactions between two neighboring proteins is dominated by interactions between those amino acids that are presented at the solvent-accessible surface of the protein. In addition, charged amino acids are typically present only at the solvent-exposed surface of the protein, unless they exist as paired charges of opposite sign (i.e., a salt bridge) within the interior of a folded protein.

The arrangement of hydrophilic and hydrophobic amino acids on the protein surface can vary widely among different proteins, but what generally results is a heterogeneous mix of apolar, uncharged polar, and net positively or negatively charged “patches” on the protein surface. There is no unique definition of how to delineate the boundaries between adjacent “patches”, but there is clear evidence that clustering hydrophobic amino acids or charged amino acids can have a large impact on protein solubility and binding.^21,41 In addition, the surface of a protein is not smooth at atomic or amino-acid level resolution. This surface roughness can result in particular configurations for a pair of proteins, in which there is a high or low degree of shape complementarity, e.g., a convex region on one protein complementing a concave region of similar radius of curvature on the other protein.^42,43 Such complementary patches can potentially achieve very close contact between one another, thereby accessing very low energy states.^42,44,45

In each of the examples above, one anticipates that Ψ must necessarily be sensitive to the choice of Ω to some extent, although that dependence is difficult to succinctly codify in mathematical terms without resorting to simpler models than an all-atom force fields and exhaustive enumeration of all distinguishable configurations in the (R, Ω) space. One way to potentially overcome these computational limitations, yet preserve the essential physics of the effects of anisotropic interactions in Ψ and B₂₂, is to adopt simple “patch” and “patch/anti-patch” models to provide strongly anisotropic or orientation-dependent, short-ranged interactions that are relevant when one can neglect long-ranged electrostatic interactions.^43,44,46

Interaction models of “patchy” particles, where the range of the patch–patch interactions is much shorter than the protein or particle diameter, have been used in computer simulations and theories of phase separation,^{43,44,47−52} and the effects of patch size and interaction range on phase behavior and self-assembly have been systematically tested for selected patch placements such as the two-patch, “Janus” particle limiting case,^{48−51,53,54} and the relation of patch number and type to a generalized priniciple of correspononding states for highly anistropic, short-ranged interactions.^55,56 Kern and Frenkel considered an arrangement of four identical patches placed in a tetrahedral geometry relative to the center of a spherical particle, and determined the liquid–liquid phase behavior^32,46 as well as the relative stabilities of crystalline states.⁴⁴ This tetrahedral four-patch model is one of the simplest that captures the “patchy” nature of protein surfaces while not biasing the system toward ordering in one and two-dimensions, such as one finds with the Janus particle systems. It is also of interest as a network-forming fluid for its interesting phase behavior and analogies to water and other molecular fluids that form tetrahedral networks.^{50,51,57−59} This is the geometry considered throughout the first part of the work presented here.

In contrast to the examples given above, simple isotropic models for Ψ have been shown to capture liquid–liquid phase separation and the existence of a metastable liquid–liquid critical point for proteins,^38,60,55 the small-angle scattering profiles and thermodynamics of protein solutions,⁶⁰⁻⁶³ as well the qualitative and semiquantitative clustering behavior of proteins.^14,60 As such, there is an outstanding question of whether experimental quantities such as B₂₂ are best interpreted in terms of a highly anisotropic Ψ with a small number of highly favorable interactions that dominate the Boltzmann-weighted integral in eq 1. That is, if the size of highly attractive patches becomes small, but the attraction is sufficiently strong, will only those select patch–patch interactions dominate the net value of B₂₂ that is measured? Or will the thermal averaging over many different configurations within eq 1 cause the measured B₂₂ to be dominated by many weaker interactions, such that the orientationally averaged potential of mean force can be well approximated by a weaker, but effectively isotropic interaction when predicting and interpreting B₂₂ and the thermodynamics of protein solutions?

This question is first examined here using simple patchy models that can be solved exactly. The results motivate a simple but exact reformulation of the statistical mechanical representation of eq 1 to allow this question to be answered more quantitatively and unambiguously for real proteins where one cannot easily know or define the exact location and “type” of patches to use in defining the patch–patch interactions, or more generally in quantifying the orientation-dependent potential of mean force between proteins. The results also suggest a simple experimental means to assess whether B₂₂ and Ψ are dominated by a small number of strong attractions.

2. Methods

This section is organized as follows. The first subsection describes a lattice model for proteins interacting through patches that are placed in a tetrahedral arrangement on the protein surface, while assuming that all attractions or repulsions between patches are highly short ranged, e.g., such as might be expected when otherwise long-ranged electrostatic interactions are screened by added salt. The lattice model is solved for different scenarios that depend on which patch–patch pairs between proteins are attractive or repulsive, a well as the size of the patches. The next subsection describes an off-lattice version of the tetrahedral patch model with all attractive patches, akin to that of Kern and Frenkel,⁴⁶ again with all patch–patch interactions being highly short ranged. The results of those first two subsections illustrate a pattern that motivates the final subsection, in which the statistical mechanical expression for B₂₂ is reformulated into an exact expression in terms of the distance- and orientation-dependent density of states that is useful in later analysis to assess when a small number of very low energy configurations can reasonably dominate the observed values of B₂₂.

2.1. Lattice Model for “Tetrahedral Patchy” Proteins with Highly Short-Ranged Attractions

Figure 1 shows a schematic depiction of the anisotropic arrangement of different “faces” or “patches” on a sphere. These are simplified depictions of what is otherwise a rugged surface for a protein, separated into a set of nonabutting faces or patches that have a simple geometry to allow for analytical evaluation of the model in what follows below. While the faces in Figure 1 appear identical in how they are drawn, each one should be treated as distinguishable when solving the model, as no two faces or patches are chemically and structurally identical for a typical protein.

Figure 1.

(A) Schematic representation of the available orientations for two NN particles that have an aligned pair of patches or faces. For Cases 1–3 in Section 2, patches are much larger than how they are shown here; the smaller patch areas correspond to Case 4 in Section 2, to illustrate the situations where many of the possible orientations are ones in which patches or faces do not point toward the corners of the bcc cell surrounding a central molecule. Arrows are unit normals, shown only for easier visualization of the possible orientations. (B) Enumerated bcc sites around a central (gray) site, to illustrate that tetrahedrally placed pactches on a central molecule can point simultaneously to only one sublattice (sites 1,2,3,4) or the other (sites 5,6,7,8).

The interactions between proteins are defined as follows. The translational degrees of freedom of the center of mass of each protein are accounted for by discretizing the overall volume of the system (V) into a body-centered cubic (bcc) lattice composed of N_s identical sites, with the volume per site denoted as v₀. Therefore, the total volume of the system is V = N_sv₀. To account for disallowed steric overlaps among neighboring proteins, each site of the lattice can be occupied by only protein at a time, or it can be vacant. The protein volume fraction ϕ is therefore equal to N/N_s, and is equivalent to the number density in treatments of one-component lattice systems.^58,59,64

The solvent is implicit, and therefore all attractions or repulsions between neighboring proteins are on an energy scale that is relative to the average protein–solvent interaction. Proteins only interact with one another if they occupy nearest neighbor (NN) sites: for a bcc lattice, each site has 8 NN sites surrounding it. Any pair of NN proteins interacts via a nonspecific attraction (-ε, with units of kT) to account for favorable, nonspecific interactions between NN proteins. In addition, contacts between certain kinds of faces or patches are treated as attractive or repulsive, with interaction energy −γ_a or γ_r, respectively (units of kT). Each face may point toward at most one NN site at a time (i.e., one corner of the bcc unit cell in Figure 1).

Physically, the scenarios enumerated below are intended to correspond in a simple way to (i) a set of hydrophobic patches on an otherwise hydrophilic surface, or, by analogy, a set of similarly charged patches on an otherwise uncharged surface (Case 1); (ii) a set of patches in which some have charge of one sign, some are oppositely charged, and some are uncharged (Cases 2 and 3). In addition, the effect of changing the surface area of the patches for Case 1 is tested in Case 4.

One can begin^37,65 with the definition of B₂₂ for a protein solution with implicit solvent, independent of whether one is dealing with a lattice or continuous-space system,

2

where Q_i is the canonical partition function for i proteins, and V is the total volume of the system. For a lattice system composed of proteins with distinguishable orientations and either unoccupied or singly occupied lattice sites, the partition function for i = 1 is simply

3

with q denoting the total number of distinguishable orientations for a given protein on a lattice site, and W(N,E,V) denoting the density of states, i.e., the number of distinguishable ways of having N proteins with an overall energy E for a system with volume V. In eq 3 and what follows, factors of v₀ that accompany each term with a factor of N_s are understood, as they cancel when all terms are combined in eq 3. Similarly, kinetic energy contributions to E are neglected since they necessarily cancel in the final expression for B₂₂.³⁷ In all examples below, the total energy E is zero for N = 1 because the solvent is implicit; independent of what one chooses for the spatial arrangement of hydrophobic, hydrophilic, and/or charged patches or faces on the protein surface.

For Cases 1 to 3, we consider situations where the patches are as large as they possibly can be while still maintaining tetrahedral symmetry and not having neighboring patches overlap. If one considers a case where two patches are aligned with each other between the central site and a NN site, then in order to maintain that patch–patch alignment or “bond’”, the central molecule and the NN molecule may each rotate only around the axis connecting the COM of central and NN molecules. For concreteness, consider a central molecule that aligns one of its patches with the NN site labeled 1 in Figure 1B. In order to maintain the patch–patch contact between the central molecule and a molecule on site 1, the remaining tetrahedral patches on the central site can only point to sites 2, 3, and 4; and with all patches being distinguishable, there are 3 distinguishable ways to do this. Case 4 will consider the more general case where the patches are much smaller, and the number of distinguishable orientations is then much greater.

Case 1: All Attractive or All Repulsive Large Patches

Consider first the case where all patches have attractive short-ranged interactions with one another, and the magnitude of the attraction is denoted γ_a. As noted above, each NN pair of molecules has a nonspecific attractive energy with magnitude ε (independent of the relative orientation of NN faces or patches). The partition function for i = 2 in this case consists of three terms, as there are three energy levels: E = -ε - γ_a for the states where two proteins are NN and also align their attractive patches; E = −ε for the states where two proteins are NN but do not align their attractive patches; and E = 0 for states where the proteins are not nearest neighbors.

For E = −ε – γ_a, there are N_s choices of where to place the first protein. For this geometry of patches, with all patches considered distinguishable and pointing toward corners of the bcc cell, q = 24. In addition, for this tetrahedral arrangement of attractive patches on the surface, it is only possible to point attractive patches to four of the NN sites at the same time. As such, there are q/2 distinguishable orientations in which attractive patches are pointing at sites 1, 2, 3, and 4 in Figure 1B. The second protein can sit on any of these 4 sites. However, it must also align one of its attractive patches toward the central site in Figure 1B. There are q/2 distinguishable ways to accomplish this. There is an identical term for the case in which the attractive patches of the central molecule instead face sites 5, 6, 7, and 8. Finally, one must divide the entire expression by 2 because the two proteins are interchangeable. Together, this gives the degeneracy or density of states for this energy level as,

4

By similar reasoning, the degeneracy for E = −ε is given by

5

In this case, the factor of N_s/2 is the same as before, and the factors of q/2 before each square bracket account for the ways of orienting the central molecules patches toward sites 1–4 or 5–8, respectively. The terms inside the brackets account for the two ways in which there can be NN sites without also aligning the attractive patches favorably. If one sits on one of the four NN sites that face the attractive patches of the central molecule, then one must take on one of the q/2 orientations that do not align with the central molecule. Alternatively, if one sits on one of the other four NN sites (that do not point toward the attractive faces of the central molecule), then one can adopt any of the possible q orientations for that corner molecule.

Finally, the degeneracy for the E = 0 state is simply

6

This follows because there are N_s sites for the first molecule, and the second molecule cannot sit on the same site as the first molecule, nor can it sit on any of the eight NN sites or it would experience an attractive interaction. As there are no NN pairs in this case, the two molecules may adopt any of their respective q orientations and still have E = 0.

As a check on the derivation and reasoning above, note that the sum of the three degeneracies listed above must add to (N_s/2)(N_s – 1)q², as that is the total number of distinguishable ways of placing two interchangeable molecules on the lattice, irrespective of the value of E. Summing the degeneracies from eqs 4, 5, and 6 gives this required result (not shown). For Q₂ one sums the products of each degeneracy with its Boltzmann factor. Using that sum for Q₂, and eq 3 for Q₁, eq 2 gives

7

with β = kT, and using the substitution B_22,S = v₀/2, with subscript S denoting the purely steric (hard sphere) or athermal value of B₂₂ for a lattice fluid of molecules.^64,65

In the case of all patches instead being repulsive, all four of the attractive patches from the preceding example are simply switched to being repulsive, with a repulsive energy γ_r. To a first approximation, this may arise by each of the patches having the same charge, and with sufficient charge screening that only one pair of patches on opposing molecules can interact significantly at the same time. In this case, the derivation above is exactly the same, except that one switches −γ_a with γ_r. The result is

8

In this case, it is possible to have B₂₂/B_22,S > 1, if γ_r ≫ ε. The maximum B₂₂/B_22,S value in this case is 3.

If one instead considered the more extreme case where all NN interactions are repulsive–akin to a colloidal particle with a uniform charge on the surface, and a high net charge (still with screened NN interactions), the largest value of B₂₂/B_22,S is 9, corresponding to a completely vacant NN shell around a central molecule. That is, this is the case where it is statistically impossible for a NN pair to form. As such, it places a useful semiquantitative upper bound on what might be considered as a physically realistic value for B₂₂/B_22,S under net repulsive conditions when charge–charge interactions are screened to length scales on the order of the protein diameter.

Case 2: One Negative and Three Positive Large Patches

Based on a similar line of reasoning as used for Case 1, it is clear that the degeneracies for E = 0 and for E = −ε are identical to those in eq 5 and 6, respectively. However, the configurations that provided patch–patch interactions in Case 1 must now be segregated into those that yield E = −ε – γ_a and those that yield E = −ε + γ_r. The former (latter) occurs when patches with opposite (the same) charge state align with each other. The particular example here is for three positive patches and one negative patch (same magnitude of charge on each patch), corresponding semiquantitatively to a case where the pH is significantly below the pI of the protein, but not so low of a pH value that all acidic groups become protonated. By symmetry, one would obtain identical results for the case of three negative patches and one positive patch. Based on reasoning analogous to that for deriving eq 4, the degeneracy for E = −ε – γ_a is

9

and that for E = −ε + γ_r is

10

These results can also be obtained by the following argument. Label each of the charged faces of a given molecule A, B, C, and D. Let A be negatively charged, and the others be positively charged. For a given pair of NN sites (one at the center and one on a corner in Figure 1B), there are 16 possible pairings (AA, AB, AC, AD, BA, BB, BC, BD, etc.). Simply enumerating those pairings shows that 10 out 16 result in a positive-positive or negative-negative pairing (thus repulsive interactions), with a positive–negative pairing for the other 6 out 16 possibilities. Using the same basic steps for deriving B₂₂ as used in the preceding subsection, the result for the present case is

11

Case 3: Two Positive and Two Negative Patches

Extension of the reasoning in the preceding subsection shows that there are an equal number of attractive pairings and repulsive pairings for faces on two NN sites. Therefore, the degeneracies for E = −ε – γ_a and for E = −ε + γ_r are the same, and equal (1/2)N_sq². The resulting expression for B₂₂ is

12

Case 4: Shrinking the Surface Area of the Patches

In all of the preceding examples, the interacting patches constituted a relatively large fraction (approximately one-half) of the total surface area. As a result, each patch was always aligned with a corner of the cell in Figure 1B. If we instead shrink the patch size, then orientations are possible such that the patches do not point to a neighboring corner, and thus cannot interact with a patch on an NN site even if that site is occupied by a protein with a properly oriented patch. One way to formulate this problem is analogous to what was done previously for a lattice model of network-forming molecular fluids in which the molecules had “bond arms” that pointed in a tetrahedral geometry.⁵⁷

In order to use this approach, one must first specify how many distinguishable orientations there are when one patch is facing a corner of the cell in Figure 1B. This will be denoted as n. For all of the cases above, n = 3. For example, when one fixes one patch of the central molecule to face site 1 in Figure 1, then this creates an axis between those two sites, along the unit normal vector for that patch. The minimum number of distinguishable ways of rotating about this axis is 3, as this corresponds to rotating in 120 degree increments -- after each rotation a different set of patches point toward sites 2, 3, and 4, respectively. The next largest value of n is 6, as this corresponds to shrinking the area of the patches by a factor of 2, and then rotating in 60 degree increments in the example above. By analogy, the subsequent values of n occur in increments of 3. As shown in Figure 1A, when a patch on the central molecule is aligned with a patch on an NN molecule, there are then n distinct ways to rotate by the angle (Δθ) about the axis created by the two unit normals that are aligned. In Figure 1A, the arrows are included simply to show the unit normal for each patch so as to make the geometry and possible orientations easier to visualize. The relationship between n and Δθ is simply Δθ = 2π/n.

The Appendix extends an earlier result^57,66 and shows the relationship between n and q in the case of four distinguishable tetrahedrally placed patches is

13

This result is independent whether the patches are attractive or repulsive, as it simply counts the number of distinguishable ways of orienting a single molecule with tetrahedrally arranged patches.

The degeneracies for N = 1 and for E = 0 with N = 2 are identical to those derived in preceding subsections, with q now taking on larger values. However, the degeneracies for E ≠ 0 with N = 2 must be rederived for n > 3. This is explained in detail in the Appendix. The results are

14

15

Finally, combining the Boltzmann factors with their corresponding degeneracies in the expression for B₂₂, as done in the preceding subsections, gives

16

with f = (4n/q)². Physically, f is the fraction of the orientational configuration space for two proteins that allows two faces or patches to align. If the face–face interactions are repulsive, γ_a is replaced with −γ_r. Inserting n = 3 in the above expression, and rearranging, one recovers eq 7 or eq 8 for the case of attractive or repulsive faces, respectively.

2.2. Off-Lattice “Tetrahedral Patchy” Proteins with Highly Short-Ranged Attractions

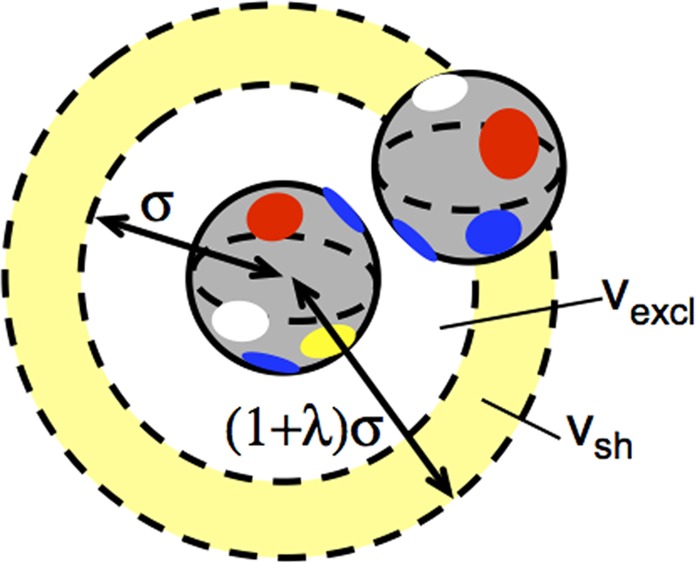
The derivation of eq 16 and those for earlier Cases can be generalized to an off-lattice system in the following way. Consider the interactions between two spherical particles that have their surfaces divided into N_p nonoverlapping patches with s types; e.g., a natural choice for s is 4 (1 = hydrophilic, 2 = hydrophobic, 3 = positively charged, 4 = negatively charged). The shape and placement of the patches is somewhat arbitrary, provided the interactions are short ranged compared to the particle or protein diameter (σ), and patches are not so large that one patch can interact appreciably with more than one patch on a neighboring particle at the same time. (e.g., as depicted in Figure 2 with different colored patches indicating different patch “types”). In addition, the magnitude and sign of a given patch–patch interaction energy can be different for different patches. For simplicity and just to illustrate the major conceptual results, only three interaction energy levels are considered here: −ε (polar interactions), −γ_a (hydrophobic or van der Waals interactions with high shape complementarity⁴²), and −μ (attraction between oppositely charged patches). As shown in Section 3, repulsive patch–patch interactions do not contribute significantly to B₂₂ if there are strong attractions unless one considers longer-ranged repulsions such as at low ionic strength.

Figure 2.

Schematic of an off-lattice model for patchy particles or proteins interacting via short-ranged “patchy” attractions with a variety of different patch “types” (different colors); the center of the second particle cannot lie within v_excl (white annulus and particle at its center), and the particles have no interactions if the second particle lies further away than within v_sh (yellow annulus).

Therefore, each of the possible patch–patch pairs have either zero, −ε, −μ, or −γ for its characteristic energy value (all in units of kT). One could of course generalize to a large, eventually continuous, set of energy values, or treat ε, μ, and γ being a function of the patch surface area. Only these three attractive patch–patch interaction energy levels are used below, for simplicity in illustrating the concepts and similarities to section 2.1. Section 2.3 considers the more general case of an arbitrary chemically heterogeneous protein surface.

In the present case, the value of W(N = 1, E = 0, V) is qV, with q and V defined as in previous sections. For N = 2, there are V possible positions to place the first particle, and the second particle cannot overlap the exclusion volume (v_excl) of the first particle (see also Figure 2). In addition, the center of the second particle must lie sufficiently close to the first particle in order for the short-ranged attraction to be non-negligible. For simplicity, the attraction is treated as being appreciable only if the center-to-center distance lies within a narrow annulus or shell with volume v_sh around the first particle, such as depicted in Figure 2. If the interaction is sufficiently short ranged then the value of γ_a or μ can be treated as independent of protein–protein COM distance for the second protein that lies within v_sh.

The possible energy states for N = 2 are now: E = 0, −ε, −γ, −μ. The total configuration space for two particles in V is V(V – v_excl)q²/2, with q² representing the total orientational configuration space for two particles once their COM positions have been specified. The degeneracy for E = 0 is simply W(N = 2, E = 0, V) = V(V – v_sh – v_excl)q²/2 + V·v_sh(1 – f_ε – f_γ – f_μ). That for E = −ε is W(N = 2, E= −ε, V) = V·v_sh·q²·f_ε/2; that for E = −γ is W(N = 2, E = −γ, V) = V·v_sh·q²·f_γ/2, that for E = −μ is W(N = 2, E= −μ, V) = V·v_sh·q²·f_μ/2. Here, f_ε, f_γ, and f_μ are defined as the fraction of the q² distinguishable ways of orientating two particles that results in a patch–patch interaction with energy −ε, −γ, or −μ, respectively. This is an extension of the definition of f in eq 16, except now it can take on any value between 0 and 1, provided that all fractions sum to 1. As noted earlier, the present case is not restricted to the earlier simpler geometries or placement of patches.

Following an analogous procedure to what was done for Cases 1 to 4 to obtain B₂₂ from eq 2, one obtains after some rearrangement,

17a

or

17b

where B_22,S = v_excl/2. Equation 17a is functionally similar to eq 16 except for the factors of 8 and v_sh/v_excl, because lattice models underestimate the correct value of B_22,S for an off-lattice system. Equation 17b illustrates that there is a balance between the favorable energetics of having patch–patch attractions (with ε, γ, μ > 0) and unfavorable entropic penalty for constraining the patches to contact each other; i.e., the terms ln f_ε, ln f_γ, and ln f_μ are all negative since f_ε, f_γ, and f_μ are each necessarily less than 1.

Finally, if one uses v_excl = (4/3)πσ³ and v_sh = (4/3) πσ³ (1 – λ)³ – (4/3)πσ³ as in Figure 2, their ratio in eq 17 can be replaced with simply (1+λ)^3–1, similar to a result derived by Kern and Frenkel for a patch–patch model that is analogous to the model above if ε = μ = 0 and one considers very small λ. f_γ is then equivalent to χ² in the nomenclature of ref (45), with χ denoting the fraction of a single-sphere surface area that is occupied by all patches combined, and χ ≪ 1.

2.3. Generalized B₂₂ Expression for Short- and Long-Ranged Anisotropic Interactions

To generalize the preceding examples further, consider the following derivation of an alternative but equivalent form to eq 2. This derivation is general, and does make assumptions about the range of the interactions, the type or even the existence of definable “patches”, or the magnitude of different interactions. It can also be generalized to the case of an explicit solvent, but that is unnecessary if Ψ properly accounts for the solvent contributions to protein–protein interactions for a given configuration (R, Ω₁, Ω₂).

The total set of distinguishable orientations (q) for one particle or protein is defined as q∫_Ω dΩ with Ω denoting the orientation space, i.e., 8π² radian³ for a single particle or protein with no axis of symmetry. The partition function for one particle is then Q₁ = Vq, and eq 2 can be expressed as

18

where the subscripts denote particles 1 and 2, and r₁₂ is the center-to-center distance between the two particles. The triple integral in eq 18 is equivalent to an integration over the space represented by Vq². Equation 18 can therefore be expressed as

19

Using the definition of q, and defining f_Ω(E | r₁₂) dE as the fraction of the two-particle orientation space (q²) for which the interaction energy lies between E and E + dE when two particles are at a separation distance r₁₂, gives

20

with v_excl defined as the excluded volume of one particle, and with the integral including only configurations where the particles or proteins do not overlap. In the above expression, f_Ω(E | r₁₂) is normalized for a given r₁₂ such that it does not include contributions from orientations that have particle–particle overlaps.

Calculating f_Ω(E | r₁₂) is equivalent to the following exercise. Take the two-particle density of states W(N = 2, V, E) and first divide out the factor of V for the number of ways of placing the first particle, then partition it into “slices” W(N = 2,E, r₁₂ → r₁₂ + dr) for a given volume annulus (bounded by r₁₂ and r₁₂ + dr) where the second particle can be placed, and finally keep only configurations without particle overlap. Normalizing this function gives f_Ω(E | r₁₂), such that

21

for any annulus r₁₂ → r₁₂ + dr.

Using eq 21 in eq 20, and defining B_22,S= v_excl/2 gives

22a

22b

This expression is general, and applies for nonspherical particles that may or may not be “patchy”. It highlights again that the contribution to B₂₂ from configurations with a given energy E is a balance of both the Boltzmann factor for that energy state, and the entropic contribution due to the fraction of configuration space that it constitutes. Very energetically favorable states will contribute significantly to B₂₂ only in situations where their density of states is sufficiently large. In addition, once longer-ranged interactions exist, the fact that the contributions to B₂₂ are weighted by a factor of r₁₂² will make it difficult for a small number of highly attractive configurations to dominate B₂₂.

3. Results and Discussion

Figure 3 shows the dependence of B₂₂/B_22,S on the magnitude of the attractive or repulsive interaction parameter (ε, γ_a, or γ_r) for the simplest cases for the lattice model: panel A is for an isotropic interaction (no patches); panel B and panel C are for four attractive or repulsive large patches (both Case 1), without including a nonspecific attraction (i.e., ε = 0) with eq 7 and 8, respectively. The curves in panels A and B show a gradual decrease in B₂₂/B_22,S as the strength of the interaction increases. Typical experimental values of B₂₂/B_22,S fall between 1 and −10 if one does not have long-ranged electrostatic repulsions. At significantly lower B₂₂/B_22,S values, proteins typically undergo phase separation.^1,8,67,68

Figure 3.

B₂₂/B_22,S for the lattice model for: (A) isotropic case, no patches; (B) large patches (Δθ =120°) with four attractive patches arranged tetrahedrally; (C) same as panel B but with repulsive patches.

Qualitatively similar results occur (not shown) for the cases with a mix of attractive and repulsive patches, as expected by inspection of eq 7, 11, and 12, except that B₂₂ does not have strong contributions from the nonsteric repulsions once significant attractions are present (see also discussion below regarding interactions with smaller patches). If one considers purely repulsive patches (panel C), then there is an analogous increase in B₂₂/B_22,S as one increases γ_r. In all cases, the values of ε, γ_a, or γ_r that provide experimentally reasonable values of B₂₂/B_22,S are of the order of 1 kT. If one also includes a nonspecific nearest neighbor attraction (ε ≠ 0 in eqs 7, 11, and 12), it simply shifts the B₂₂ curves down slightly (see panels B and C), but does not impact the qualitative behavior or any of the conclusions below. As such, ε = 0 is used throughout the remainder of the results and discussion below.

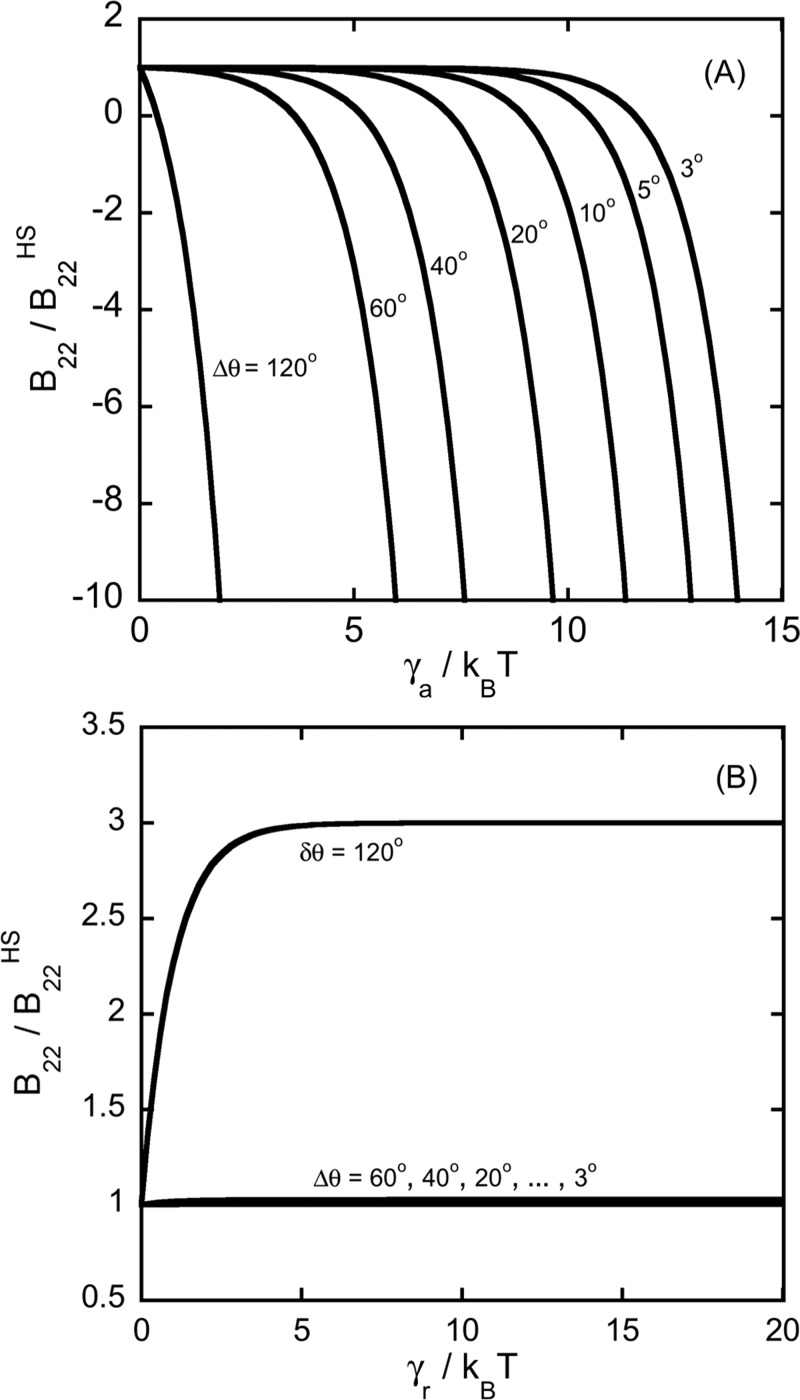
Figure 4 shows the change in B₂₂/B_22,S as a function of γ_a (panel A) or γ_r for Case 4 (eq 16) where the size of the patches is reduced (with four tetrahedral patches of equal size or value of n or Δθ). Panel A shows that, at first, B₂₂/B_22,S has little dependence on the strength of the attraction up until a certain point, after which there is a dramatic decrease of B₂₂/B_22,S with a small increase in γ_a, and this ultimately drops B₂₂/B_22,S to unphysically large negative values. Conversely, if one considers purely repulsive short-ranged interactions between patches, then panel B shows that those repulsive interactions have negligible contributions to B₂₂/B_22,S once the patches become even slightly smaller than the largest patch size that could be accommodated in the model. This highlights that when interactions are all very short ranged, repulsions other steric clashes are likely to contribute negligibly to B₂₂, due the nature of the Boltzmann factor biasing toward attractive energies, as noted previously.⁴² In what follows, only attractive interactions are included until the end of the report, when the question of how longer-ranged interactions influence B₂₂/B_22,S is revisited.

Figure 4.

B₂₂/B_22,S for case 4 as a function of patch size: (A) four attractive patches or (B) four repulsive patches arranged tetrahedrally as in Figure 1. Curves are labeled with the value of Δθ, with smaller Δθ corresponding to smaller patch sizes. All curves are for ε/kT = 0.

Figure 5 illustrates the results from the off-lattice model of very short-ranged attractions for the case of ε = μ = 0, as a function of γ, for the case where γ is a function of the size of the patch. This is akin to the known dependence of hydrophobic attractions as being linearly proportional to the solvent-accessible surface area. While there is debate on the exact number one should use for that dependence, a value of the order of magnitude of 2.5 kcal nm^–2 mol^–1 is typical and is used here. The results below do not change significantly if one uses alternative values proposed in the literature.

Figure 5.

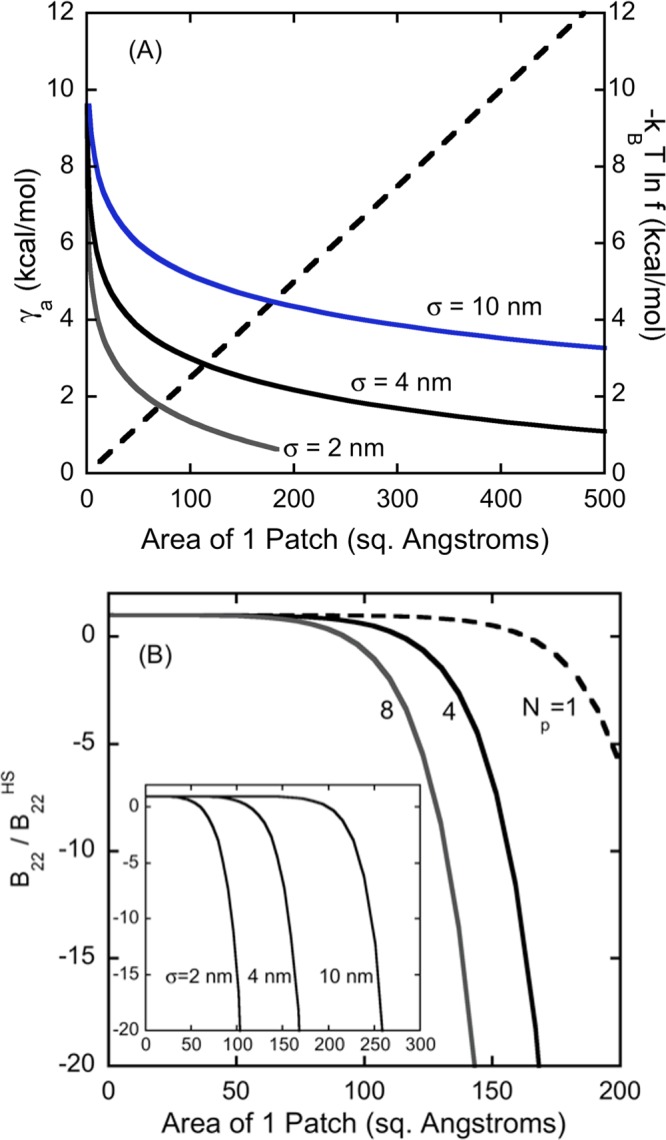
Illustrative results for an off-lattice case, assuming attractive hydrophobic patches with the strength of patch–patch attractions scaling with the surface area of a patch (∼0.25 cal mol^–1 nm^–2). (A) comparison of the contributions to B₂₂ from the magnitude of the attraction γ_a (dashed line) and the entropic penalty for aligning patches, −kT ln f (solid curves) for a tetrahedral patch geometry akin to that in ref (46). (B) Effects of changing the number of patches N_p (main panel) and protein diameter σ (inset) for the dependence of B₂₂/B_22,S on the area of a patch for the off-lattice model, assuming λ is based on an annulus width of 0.5 nm in Figure 2. The inset is for N_p = 4, with axis labels identical to the main panel.

The results show that while the strength of patch–patch interactions scales linearly with patch size (area), the entropic penalty one pays for aligning patches, i.e., based on the fraction of the two protein orientation space (q²) that allows such patch–patch contacts, scales logarithmically with the patch size. In addition, eqs 16, 17, and the definitions of f show that f^1/2 scales as the total patch surface area divided by the total protein surface area. As a result, larger proteins (larger σ) will pay a higher entropic penalty (−kT ln f) than will smaller proteins, for having equivalently sized patches interacting with one another.

In panel A, if the solid curve lies far above the dashed curve, then B₂₂/B_22,S will not be appreciably negative. If the solid curve lies far below the dashed curve, then B₂₂/B_22,S will be so large as to be unphysical, and one would expect low solubility for the protein in those solution conditions. This suggests that for proteins that remain soluble but have net attractive B₂₂/B_22,S values, the protein surface must be engineered or evolved to have a delicate balance between the size and number of attractive patches, with a larger number needed for larger proteins unless B₂₂/B_22,S is not largely negative. This conclusion is in keeping with the observation that large proteins such as monoclonal antibodies tend to not display the same quantitative patterns in terms of typical B₂₂/B_22,S values, when compared to their much smaller, globular protein counterparts.^4,8,68

Panel B illustrates this further by showing how B₂₂/B_22,S is essentially unaffected by the average patch size until a threshold range where the values of E and −kT ln f switch from entropically to energetically dominating contributions to B₂₂/B_22,S. Note that these results use ε = 0, so if one included the weaker, nonspecific interactions (ε ≠ 0) such as in Figure 3A, then those would dominate the value of B₂₂/B_22,S under conditions where the patch–patch entropic penalties preclude significant patch–patch contributions to B₂₂/B_22,S. The precipitous drop for each curve in Figure 3B shows that there is only a small range of magnitudes for the patch–patch attraction energy to effectively dominate B₂₂/B_22,S before the effect becomes so pronounced that the protein would either dimerize/oligomerize via specific patch–patch binding, or the protein would become insoluble if the arrangement of patches allowed for a space-filling (crystalline or amorphous) network of patch–patch contacts to form. If one considers the results in Figure 4A within the same context, a similar conclusion is reached, and this is in keeping with recent results elsewhere.³²

In practice, there are currently no unambiguous ways to take a known three-dimensional structure for a protein and transform it to a simple “patchy” model such as those used for conceptual illustrations above. Rather, one must consider the more realistic case where one does not have well-defined and discrete patches, and take a more structurally detailed and realistic depiction of the protein surface and its chemical heterogeneity. In this case, the patchy models are difficult to generalize in any quantitative or rigorous detail, but one can instead rely on the reformulation of B₂₂ in terms of the 2-body, distance-dependent fractional density of states f_Ω(E|r₁₂) and eq 22. This allows one to consider not just interactions that are extremely short ranged compared to σ, but also different protein–protein COM distances, r₁₂. Inspection of eq 22 and comparison to eqs 7, 11, 12, 16, and 17 shows that they all share a similar pattern, with a balance occurring between the low-energy, low entropy (small f) portions of Q₂, and vice versa. Therefore, the same qualitative conclusions and behavior of B₂₂ as a function of the size and strength of attractive “patches” will hold for this more general case. However, it is untenable to generally map out B₂₂ as a function of all or even a reasonably large number of the possible protein surface topologies one can imagine. It is also not clear what the minimum number of energetic parameters to describe the protein surface would be, akin to how ε, γ, and μ were used in Section 2.2. Therefore, it is not realistic to construct quantitative plots that are analogous to Figures 3, 4, and 5.

However, eq 22 can be used directly if one can estimate or calculate f_Ω(E|r₁₂) from molecular models. This is particularly useful if one employs biased sampling methods that effectively supply the density of states for a given system,⁶⁹ as f_Ω(E|r₁₂)dE is readily obtainable simply by adding a bookkeeping step to partition Ω for different “bins” of r₁₂. Using the methods described elsewhere,¹⁵ such calculations were performed with replica-exchange molecular dynamics (REMD) simulations⁶⁹ of γ-D Crystallin; an eye lens protein that is of interest for its role in cataract formation⁷⁰⁻⁷² and as a model for non-native aggregation of proteins.⁷³⁻⁷⁵ The model treats each amino acid explicitly, while coarse graining the interactions and treating the solvent implicitly so as to make the detailed enumeration of f_Ω(E|r₁₂) computationally tractable.

The results are shown in Figure 6 for the case when all electrostatic interactions are highly screened and therefore are effectively negligible, akin to what was approximated previously in both molecularly detailed and approximate model calculations.^42,46f_Ω(E|r₁₂) is plotted as a function of E for a given r₁₂. Each solid curve is for a different bin of protein–protein COM distances. The dashed curve is E/kT vs E with T = 300 K; the corresponding value of B₂₂/B_22,S is approximately −1.5, as that is the largest negative value γD-Crys shows at high salt concentrations and room temperature for this pH.¹⁵

Figure 6.

Density of states (ln f vs E, given as solid lines) as a function of r₁₂ for two human γ-D Crystallin molecules, based on replica-exchange molecular dynamics, using the methods in ref (15). The dashed line is E/kT vs E for T = 300 K.

Colder (warmer) temperatures give a different solid line with the same intercept at (0,0), but with a steeper (shallower) slope. For a given choice of temperature, eq 22 shows that any values of E for which the dashed curve lies significantly above a given portion of a solid curve corresponds to configurations that contribute negligibly to B₂₂. The basic shape of f_Ω(E|r₁₂) is expected to hold for other proteins, and is akin to what one must recover for macroscopic systems at thermodynamic equilibrium.³⁷ Therefore, Figure 6 shows that for any protein, one expects there to be low E states that are too entropically penalized (i.e., poorly populated) to contribute to B₂₂, and high E states that are also too poorly populated or are too close to E = 0 to contribute significantly. States with extremely large negative E/kT values will necessarily have extremely low ln f_Ω values if one is to recover physically realistic values for B₂₂. Rather, the configurations that will dominate B₂₂ are those that provide a balance in terms the magnitude of E and the number of configurations with that E (or more accurately, E dE unless E is discretized or quantized). One must also realize in considering Figure 6 that the contributions to B₂₂ for a given r₁₂ must then be multiplied by the square of r₁₂ within eq 22. Therefore, configurations from larger distances are weighted more heavily than shorter distances. Eventually, all contributions are negligible for sufficiently large r₁₂ values.

For the particular example in Figure 6, ultimately many of the configurations with E values falling between zero and approximately 12 kT (0 and −7 kcal/mol), with most between 3 and 10 kT, contribute significantly to B₂₂. Based on the broad peak in ln f_Ω that lies well above the dashed lines for the smallest r₁₂ values, it is clear that E values in the middle of that range are most important for determining B₂₂, rather than the configurations that correspond to the lowest energy states one can sample.⁴² The values on the y axis in Figure 6 (and the cumulative distribution, not shown) highlight that the overall fraction of the possible orientations that contribute to B₂₂ at short protein–protein distances is of the order of 0.1 or higher. It remains to be tested whether significantly different results will hold for proteins that exhibit much larger negative B₂₂ values, using free energy sampling techniques such REMD to ensure that the density of states are being accurately sampled at large negative E values.

Taken together, all of the results considered here are consistent with an interpretation of negative B₂₂ values as being dominated by one of the following: (i) a relatively large fraction (∼0.01 to 0.1 or larger) of all the possible orientations that give rise to “intermediate” strength attractions (∼ a few kT); (ii) a significantly smaller fraction (≪ 10³) of all possible orientations, which have very large attractive energies. If (ii) occurs, the results and analysis here indicate that one should expect one of two experimental observations. Either the proteins have such strong specific interactions that they form stable dimers or other molecular complexes that are easily detectable with scattering methods, or the proteins remain effectively monomeric but a small change in temperature will cause B₂₂ to change dramatically (e.g., as observed via dramatic downturns in Figures 4A and 5B). If (i) occurs, then one would not expect a small change in temperature to have a dramatic change in B₂₂ because it would just cause a small shift in the otherwise broad distribution of energies and configurations that were being sampled to provide the experimental B₂₂ value(s), e.g., a small change in slope of the dashed line in Figure 6.

It is currently common practice to measure B₂₂ at only a single temperature except when one is in the vicinity of the critical temperature for a phase transition, but in that case it is questionable whether one can actually measure B₂₂ accurately since its magnitude becomes so large as to require unrealistically low protein concentrations to accurately determine B₂₂.³⁶ It would be interesting in future work to assess whether the temperature dependence of B₂₂ is a pragmatic means to assess when a small number of configurations with very strong attractions is dominating the behavior. One hypothesis is that such conditions will also be those that are most prone to forming transient clusters that are implicated in causing problems with high viscosities of more concentrated protein solutions,²⁸⁻³⁰ and possibly serve as precursors to phase transitions or metastable clustered states of protein solutions.^11,12,14,32

Appendix

The particular form of eq 13 arises in the following way. There are 24 distinguishable ways of orientating a molecule such that all patches face sites in the bcc geometry. There are 32 (n – 3) distinguishable ways to point only one patch to a corner, i.e., eight corners to choose from, four different patches to select from to face that corner, and based on the definition of n, there are n – 3 ways of orientating the other patches such that they do not face a corner. Finally one takes each configuration with one patch facing a corner and creates an imaginary axis along the unit normal for one of the patches not facing the corner. Rotating about this axis gives n – 3 additional orientations that do not point to any corners. Doing this for each of the 32 (n – 3) configurations that start with one patch facing a corner gives 32 (n – 3)² distinguishable configurations that have no patches facing corners. Additional rotations about other axes normal to different faces do not produce new configurations that are distinguishable from others that have already been enumerated; this was also confirmed via by-hand enumeration of all distinguishable orientations of an analogous model in earlier work.^57,66 Equation 13 differs from the previous result by a factor of 2, simply because in the present case all four patches are distinguishable. By inspection, choosing n = 3 in eq 13 gives the required result of q = 24 for the case where all orientations only point all faces or patches toward corners of the bcc cell.

To proceed, we separate the degeneracy for E = −ε, N = 2 into three terms that account for three different possibilities for the orientation state of the molecule occupying the central site in Figure 1: (a) all faces of the central molecule point toward corners; (b) only one face points toward a corner; (c) no faces point toward corners. For (a), there are 12 possible configurations for the central molecule where it points to the first sublattice (e.g., sites 1–4 in Figure 1). There are eight corners where the second molecule could possibly sit. If it sits on a site that has a face of the central molecule pointed toward it, then it can only adopt one of q – 4n of its possible q orientations, as the other 4n would point a face at the central site, and therefore gain an additional interaction. If the second molecule instead lies on the other sublattice then it is impossible for it to face an attractive/repulsive face of the central molecule, and so it may adopt any of its q orientations. Finally, the same reasoning applies if the central molecule adopts one of the 12 orientations where it points all of its interactive faces toward sites 5 to 8 in Figure 1. Taking these terms together gives 12 [4(q – 4) + 4q] × 2 distinguishable configurations for case (a).

For (b), one first enumerates for the case of one face pointing toward the first sublattice. There are four possible corners toward which the central molecule may point a face, and for each corner that face may be any of the four distinguishable interacting faces on the central molecule. With any one face fixed toward a corner, there are n – 3 ways of orientating the central molecule such that none of the other faces are pointing at a corner. For each of the configurations just enumerated, the second molecule can sit either on the site that is aligned with a face of the central molecule, or on one of the seven other NN sites. If the former, then it can adopt only q – 4n orientations to avoid having two faces aligned with each other. Otherwise, it may take on all q distinguishable orientations. Finally, one simply doubles this term to account for the case of pointing toward the second sublattice. Combining these terms together gives 4 × 4(n – 3) [(q – 4n) + 7q] × 2 distinguishable configurations for case (b).

For (c), there are 32(n – 3)(n – 3) ways of having the central molecule point none of its interactive faces toward a corner (see also the derivation of eq 13, above). The second molecule can occupy any of the eight corners, and may take on any of its q orientations since it cannot possibly align with an interactive face of the central molecule in this case. Taking these terms together gives 32(n – 3)² × 8q configurations for case (c). The overall degeneracy for E = −ε is obtained by summing (a), (b), and (c), multiplying by N_s since the choice of the location for the central site is arbitrary, and dividing by 2 since the two molecules are not distinguishable. Doing so gives eq 14 after some algebra. Using a similar path of reasoning, one obtains eq 15 for the degeneracy when the interactive faces of two NN molecules are aligned.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States