ADAPTIVE RETROSPECTIVE CORRECTION OF MOTION ARTIFACTS IN CRANIAL MRI WITH MULTI-COIL 3D RADIAL ACQUISITIONS

Abstract

Despite reduction in imaging times through improved hardware and rapid acquisition schemes, motion artifacts can compromise image quality in magnetic resonance imaging, especially in 3D imaging with its prolonged scan durations. Direct extension of most state-of-the-art 2D rigid body motion compensation techniques to the 3D case is often challenging or impractical due to a significant increase in sampling requirements. This paper introduces a novel motion correction technique that is capable of restoring image quality in motion corrupted 2D and 3D radial acquisitions without a priori assumptions about when motion occurs. The navigating properties of radial acquisitions – corroborated by multiple receiver coils – are exploited to detect actual instances of motion. Pseudo-random projection ordering provides flexibility of reconstructing navigator images from the obtained motion-free variable-width subsets for subsequent estimation of rigid-body motion parameters by co-registration. The proposed approach does not require any additional navigators or external motion estimation schemes. The capabilities and limitations of the method are described and demonstrated through simulations and representative volunteer cranial acquisitions.

INTRODUCTION

Magnetic resonance imaging (MRI) is highly sensitive to patient motion. Depending on the k-space acquisition trajectory, motion can cause blurring, ghosting, or other artifacts that negatively affect image quality (1), reduce diagnostic information or require repeated scans. Especially challenging groups include pediatric, uncooperative, and impaired patients. In Cartesian k-space sampling, the approach widely adopted on clinical MRI scanners, patient motion causes significant ghosting artifacts. As prior problems such as gradient and timing instability continue to diminish on new scanners, non-Cartesian trajectories are becoming a more attractive option for providing imaging solutions to these challenging groups. Non-Cartesian trajectories allow for longer data acquisition intervals per TR that allow shorter scans. The variable sampling density of many non-Cartesian scans often allow accelerated imaging through undersampling, especially with time-resolved angiography and DCE-MRI (2). Non-Cartesian sampling started playing an important role in many emerging applications including sodium imaging (3) and ultra-short echo time imaging (4). Furthermore, non-Cartesian sampling provides a practical platform for acceleration with advanced image reconstruction techniques such as constrained reconstruction and compressed sensing (5-6). For non-Cartesian k-space trajectories such as radials and spirals (1,7-9), image artifacts caused by physiological motion (i.e., respiration, cardiac pulsatility, and flow) are more tolerable since they manifest themselves as local blurring (1). The ability to design a radial projection ordering scheme that provides more uniform k-space coverage further diminishes the effect of data inconsistencies due to motion, producing dispersed streaking artifacts, which are much less detrimental for radiological examination than ghosting in Cartesian imaging. These benefits become even more pronounced in 3D radial imaging where the point spread function is less coherent than for 2D radial acquisitions. A distinct advantage of radial view ordering is that it samples the center of k-space every repetition time (TR), thereby obtaining partial or full navigation information, which may be useful for motion correction in some applications (7,10-11).

While radial sampling provides some tolerance against physiological motion, bulk motion remains a significant problem, particularly in 3D imaging where prolonged acquisition times increase the likelihood of the occurrence of motion artifacts. Analysis of projection moments in a radial acquisition may provide a way to characterize object motion continuously based solely on the acquired data. Previous work successfully estimated and corrected rigid body translation and rotation using analysis of center of mass (COM) and higher order projection moments (10), respectively. In theory, these methods apply to both 2D and 3D radial acquisitions; however, 3D implementation is non-trivial due to a large complex search space to correct for rotational motion. Furthermore, the method of translational and rotational motion estimation from projection moments is not robust in the presence of noise, susceptibility artifacts, and trajectory deviations. Finally, as we will demonstrate, analysis of projection moments fails to describe object displacement accurately when imaging with stationary multi-channel coils with non-uniform sensitivity profiles, such as those used in parallel MRI.

Alternatively, motion can be tracked with the use of periodically acquired low-resolution navigator images. Many retrospective motion correction techniques (12-13) rely on assumptions that the object is rigid, and its position and orientation do not change significantly during acquisition of the navigator images. These methods sample central k-space periodically during short segments. Low-resolution images reconstructed from these segments act as navigators for consequent motion correction. One such approach, PROPELLER (12), has achieved widespread use in clinical applications, particularly in cranial imaging where motion conforms well to a rigid-body model. PROPELLER acquires Cartesian k-space data in successively rotated strips of parallel lines (“blades”). The original 2D PROPELLER approach relies on the assumptions that no motion occurs during the acquisition of each blade and that any occurring rigid body motion happens mostly in-plane. The first assumption is valid for typical implementations, which acquire individual 2D blades in approximately 100 ms. The second assumption may be more prone to violation, depending on the anatomy of interest, but is common to many 2D motion correction schemes. Parameters for translational and rotational in-plane motion can then be accurately determined by pre-processing and co-registering low-resolution data from fully sampled k-space centers of individual blades. While the original 2D PROPELLER algorithm may in principle be modified to suit different pulse sequences (14) and acquisition trajectories including 2D radials (15), it has notable challenges. In particular, to allow for sub-voxel motion estimation, wider blades are desired (16). In multi-echo sequences, it is often problematic to satisfy this design criterion due to the finite number of available echoes in the echo-train and requires exploring available tradeoffs between long readouts and related image artifacts (17). At the same time, increasing the number of readouts per blade also increases the probability of intra-blade motion, potentially violating the method's assumptions and compromising its accuracy. These problems may be partially alleviated for 2D imaging through parallel MRI with multiple coil receivers (18). However, a straightforward extension of PROPELLER to 3D for full rigid body motion correction is significantly complicated by a large increase in data sampling requirements.

In this work, we propose a novel adaptive fully 3D motion correction technique based on the use of a 3D radial sampling scheme and multi-coil arrays. This method is designed to overcome challenges of the aforementioned motion correction techniques. We assume that patient motion, such as muscle twitching or adjusting for comfort, occurs in a discontinuous manner alternating with relatively motionless periods. This assumption is consistent with related methods (12-13), which assume that motion is negligible within the acquisition of a navigator image. We demonstrate that although regular COM analysis does not provide accurate estimates of motion parameters in the presence of non-homogeneous coil sensitivity profiles of stationary phased arrays, it can be a powerful tool for retrospective detection of not only translational but also rotational motion. Thus, we avoid making a priori assumptions about when motion occurs during a scan. Instead our method identifies consistent variable-width data subsets based on multi-coil COM analysis, that are used as navigators for estimation of rigid body motion parameters through co-registration. The obtained motion parameters are used to correct the data from the various motionless positions before final reconstruction.

THEORY

COM Analysis for Translational Motion Correction in Radial Acquisitions

If an object is a rigid body, its position – though not its orientation – can be completely characterized by its center of mass (COM). By definition, the COM of an object described by a function f is calculated as the ratio of its 1^st and 0^th moments:

$${\mathbf{x}}_{COM}=\frac{\int \mathbf{x}f\left(\mathbf{x}\right)d\mathbf{x}}{\int f\chi \left(\mathbf{x}\right)d\mathbf{x}}$$ [1]

There is a rather straightforward relationship between COM of an object and its sinogram (11), namely, a projection of the object COM onto a radial line is equivalent to the ratio of 1^st and 0^th moments of the object's sinogram along this line, or:

$${\mathbf{x}}_{COM}\cdot \gamma \left(\theta \right)\frac{\int rR(r,\theta )dr}{\int R(r,\theta )dr}=\frac{\int r{F}_r^{-1}\left[S\right](r,\theta )dr}{\int F_r^{-1}\left[S\right](r,\theta )dr}$$ [2]

where g (q) is the unit vector defining the radial line, R and is the Radon transform (sinogram) of the object, S(r, q) denotes the k-space values along the radial line and $F_r^{-1}$ stands for one-dimensional inverse Fourier transform along the projection axis. This relationship provides a theoretical foundation for self-navigating properties of radial trajectories. Previously proposed algorithms for translational motion correction used calculated COM coordinates to shift projections to align their COMs (10-11,19) before final image reconstruction, successfully correcting bulk object translation. Theoretically, only three projections are required to estimate the object COM coordinates from the above relationships (in 3D). In practice, more projections are desirable to obtain a robust least squares solution, since k-space measurements can be corrupted by noise and trajectory deviations. In our approach, the number of projections used to calculate the COM determines the timescale for motion correction.

COM for Motion Detection with Multiple Coil Receivers

MRI signal is measured by one or more coil receivers with spatially varying sensitivity profiles. The coil sensitivity modulates the imaged object in multiplicative fashion. It is generally assumed that effect of coil sensitivities on the analysis of the projection moments is negligible (10,19), which may be the case for a relatively uniform coil sensitivity profile (e.g., when imaging with transmit/receive birdcage coils, such as a body coil). In the typical multi-coil case, however, coil sensitivity variations are significant and each coil signal in effect corresponds to a different object. Hence, the full analysis of the projection moments (Eq. [2]) should additionally include the description of object motion with respect to the coil system. When the object moves within the stationary coil receiver system (such as a head array), the actual image content of each effective coil object changes. While these changes are correlated, they nonetheless disrupt the linear relationship between the translational motion vector and measured COM values. As we will demonstrate, this diminishes the ability to accurately estimate object COM coordinates and translational motion from projection COM data. At the same time, as demonstrated in the results section, varying modulation of the object by multiple coil sensitivities makes COM analysis an even more robust method of motion detection, sensitive to not only translation but also rotation. We should note that this property does not hold in traditional COM analysis with uniform coil sensitivities (for example, consider a case when center of a rotation coincides with the object COM), although analysis of higher order projection moments has been used in 2D imaging to reject inconsistent projections (7). In the multi-coil case, however, COM coordinates of the object estimated from individual coil data would generally have different values. Therefore, no matter where a center of rotation is located, we expect to see a change in the COM for at least one coil in response to any rotation. We explored the effects of coil sensitivity modulations on estimated COM through two simulations, presented in the results section.

Pseudorandom Radial Acquisition

In addition to their self-navigating properties, a notable advantage of radial acquisitions is the ability to implement pseudo-random projection ordering, which allows for relatively even filling of k-space from the center out (Fig. 1). This enables reconstruction and registration of angularly undersampled images from subsets of data that are defined retrospectively, instead of being inherently constrained by the acquisition trajectory. Angular undersampling of 3D radial data results in a reduced artifact-free FOV (radius r) relative to the full FOV (radius R) Cartesian scans for a given matrix size across the FOV (N_R). This relationship is defined (20) in terms of the number of acquired projections (N_P) by:

$$\frac{r}{R}=\frac{2}{N_R}\sqrt{\frac{N_p}{2p}}$$ [3]

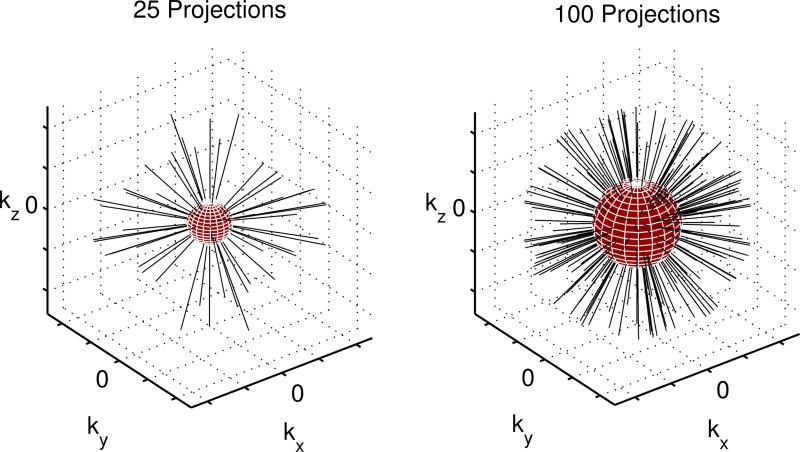
Thus, the Nyquist radius (extent of fully sampled central k-space) of pseudo-random projection ordering grows approximately with the square root of the number of projections as data acquisition proceeds in time. If the scan consists of several sufficiently long motion-free periods, a more efficient utilization of data may be possible. Longer motion-free periods as detected in the method introduced below would result in higher resolution navigator images, which in turn would result in higher accuracy of registration and the ability to correct motion on a smaller scale.

Figure 1.

Pseudorandom 3D radial trajectory. The region where average sampling density satisfies Nyquist limit (navigator data) is within the red sphere. The resolution of navigator data increases in time as the number of acquired projections grows.

METHODS

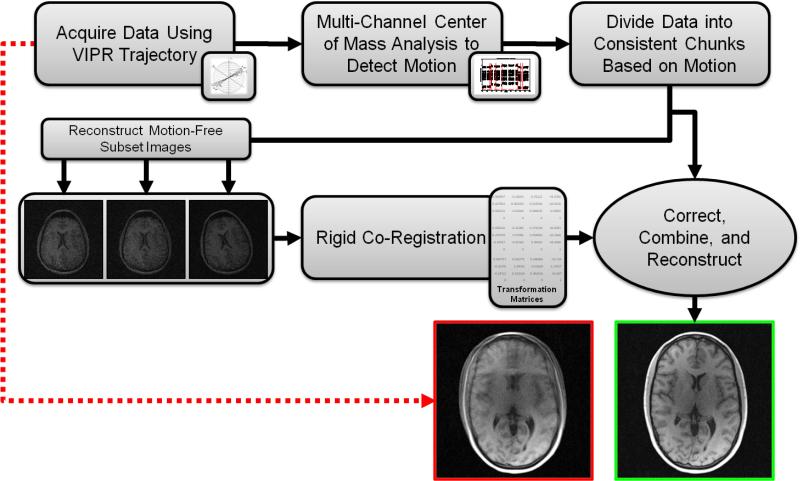
The proposed motion correction method is depicted in Figure 2. First, the acquired radial data are analyzed to identify consistent motion-free subsets of individual interleaves based on motion detection algorithms that analyze multi-channel projection data. In the second step, undersampled images are reconstructed for each such subset (frame) and inter frame motion parameters are estimated via co-registration analysis. Finally, the k-space data from the subsets are corrected using the determined motion parameters and combined to produce a single high quality image volume. The following subsections describe details of the implementation.

Figure 2.

The proposed motion correction method.

Trajectory Design

Our method uses a combination of coherent and randomized sampling. The elementary building block of our k-space acquisition is an interleaf containing relatively few projections with isotropic spacing in 3D. These interleaves are distributed in time in a bit-reversed order (21-22) based on the index of the initial projection, though other schemes are possible (23). The purpose of acquiring projections sequentially within each interleaf is to minimize differences in gradient amplitude for successive TRs, and to ensure consistent COM calculation. As explained in the previous section, the purpose of randomization through bit-reverse acquisition is to use the benefit of relatively isotropic k-space filling with uniformly growing Nyquist radius for reconstruction of arbitrary subsets of data, and to enable more accurate motion correction. Moreover, such randomization minimizes artifacts from discarding or down-weighting uncorrectable data, as residual gaps in k-space become less structured.

Motion Detection

After acquisition, the radial data are first transformed into sinogram space by inverse Fourier transform (see comments to Eq. [2]) where projection COM values are calculated. To subdivide the data into consistent subsets, N_d-dimensional COM vectors (N_d = 2 or 3 spatial dimensions) are estimated using data from each successive interleaf (total N_i interleaves) on a per coil basis (total N_c coil channels). This creates N_cN_d independent detection channels with N_i samples in the temporal dimension, each affected by motion to a different degree depending on the spatial dimension and coil channel. In the absence of motion and noise, each detection channel plot is represented by a constant function, while rigid motion of the object makes these plots piecewise constant, and noise in the measurements induces noise in the detection channels. Therefore, incidents of motion correspond to jump discontinuities or edges in the detection channel plots. We process the channels individually using a multi-level Gaussian 1D edge-detection technique (24) (http://www.cs.unc.edu/~nanowork/cismm/download/edgedetector/index.html), although other edge-detection techniques can be used instead. Our current implementation uses four scales (1, 2, 4, and 8) with local extrema detection thresholds of .1, .2, .3, and .4 respectively. For robustness, a detected edge location is classified as motion only if it is corroborated by a predetermined number of detection channels. We set this threshold empirically to three for a 3D acquisition with an 8-channel coil array.

Motion Estimation and Correction

The above procedure identifies consistent (motion-free), variable-size subsets of interleaves, which are reconstructed individually to create undersampled navigator images. These navigators are co-registered (using the largest motion-free subset as a reference) to estimate rigid object motion parameters. Affine registration of navigator images was performed with FLIRT, a registration tool provided in the FMRIB Software Library (FSL) (25), using the correlation ratio cost function. Translational motion is corrected by applying corresponding linear phase to the k-space data on per subset basis, and rotational motion is corrected by applying corresponding rotational transformation to the affected k-space coordinates. The corrected subsets are then concatenated and reconstructed using standard non-Cartesian methods. Subsets deemed too small for reasonably accurate registration (less than 5% of the total number of projections necessary for full sampling) and interleaves acquired during motion are discarded in the current implementation, although methods of incorporating these data into reconstruction in a meaningful way are the subject of future investigation.

Simulations

To evaluate the effects of non-uniform coil sensitivities on estimated COM values, we performed three simulations using 2D digital phantoms. In the first simulation, a realistic slice of a 3D cranial image from the BrainWeb database (26) was shifted (0 to 15 pixels) relative to: i) a uniform coil, and ii) an array of four surface coils with realistic sensitivity profiles. Translation parameters were estimated by COM analysis using the uniform coil and each individual surface coil and the estimation errors recorded for each case.

In the second simulation, COM coordinates were calculated for: i) the Shepp-Logan phantom modulated by each of two individual coils with realistic sensitivity profiles, ii) the coil-combined (sum of squares) object, and iii) the actual object (i.e. the Shepp-Logan phantom modulated by a uniform coil). Each of the calculated coordinates then served as a center of rotation of the object by 15°. In each rotation instance, the COM coordinates of the rotated object were calculated again as described above. Total displacements of COMs were calculated to estimate how detectible each rotation was for the various coil set-ups.

The third simulation implemented a Monte-Carlo approach to determine detectability of motion in the presence of trajectory deviations and noise. This experiment used the same 2D brain phantom as described in the first simulation with eight complex spatially-varying coil sensitivity maps. Radial k-space data were synthesized based on a measured 2D radial trajectory consisting of 332 projections. The measured trajectory provided realistic trajectory deviations due to gradient delays. Various levels of Gaussian noise were added to the k-space data resulting in image SNR values of 25, 50, 75, 100, and infinity. Simulated translations (0.25, 0.5, 0.75, and 1 pixel) and rotations (0.25°, 0.5°, 0.75°, and 1°) were applied for 1000 noise realizations for each case. Translation direction was randomized for each noise realization; rotations were all counter-clockwise about the COM of the actual image object. COM values were calculated for each successive set of 8 projections for each coil, and motion detection was performed to assess sensitivity and specificity of the procedure.

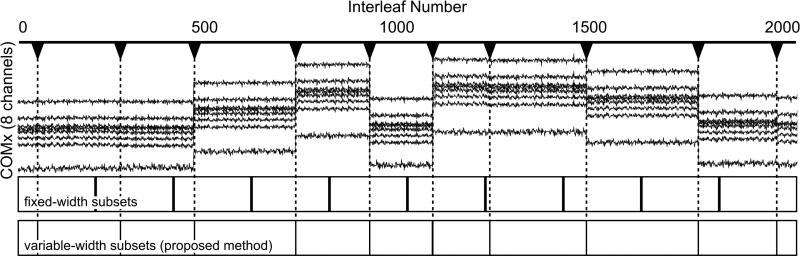
As discussed in the introduction, a straightforward approach to motion correction with 3D radials is to use radial interleaves with predefined width. To compare the performance of our proposed variable-width subset technique with such fixed-subset-width method, a 3D simulation was performed. A corrupted dataset was generated from a motion free cranial VIPR (Vastly undersampled Isotropic PRojection, a fully radial 3D trajectory (27)) scan (100,000 total projections) by simulating 10 instances of translation and rotation. Each instance of motion consisted of random translation (-10 to 10 pixels) and rotation (-2.5° to 2.5°) along or about each primary axis. To avoid the worst-case performance (motion occurs in the middle of the interleaf), we simulated these instances of motion at semi-random intervals such that every subset of 10,000 projections contained one instance of motion (Fig. 3). Motion compensated images were reconstructed for comparison using co-registration with a priori fixed width sequential subsets and using the proposed variable width subset method with COM-based motion detection.

Figure 3.

Setup of the 3D motion simulation. The top plot depicts the x coordinates of the COM for eight channels vs. interleaf number. Steps in the plot correspond to simulated translations and rotations. The boxes below represent subsets used for co-registration and motion estimation defined a priori (fixed-width) and adaptively as proposed. Note the actual incidents of motion corrupt the fixed-width subsets.

Volunteer Experiments

After obtaining informed consent in accordance with IRB protocol, four human volunteers were imaged to assess the overall performance of the technique on realistic data. Data were acquired using an undersampled 3D radial spoiled gradient echo sequence (VIPR) (27). A preliminary scan was used to determine gradient delays, which were compensated using modified prewinder gradients in the subsequent scans to reduce trajectory errors (28). This sequence was implemented on a clinical 3.0 T scanner (Discovery™ MR750, GE Healthcare, Waukesha, WI) using an 8-channel brain imaging array. Typical scan parameters included: TE/TR = 2.9/7.0 ms, BW = 62.50 kHz, flip angle = 17°, voxel size = 0.94 mm isotropic, FOV = 240 mm isotropic, with 100,000 projections for a total scan time of 11 minutes 40 seconds. Acquisitions were performed in an interleaved fashion with 50 sequential projections per interleaf, with 2000 interleaves acquired in bit-reverse order based on the index of the first projection. This set the timescale for motion detection to 350 ms (50 projections times 7 ms TR). Singular value decomposition (SVD) was used to find the least squares solution to an over-determined system in Eq. [2] for each interleaf to yield (in total) 24 motion detection channel plots (each of length 2000 time points). Volunteers were instructed to adjust their head position arbitrarily several times throughout the scan to provide motion corrupted data, and asked to remain still during a subsequent scan to provide motion-free comparisons.

RESULTS

Simulations

Table 1 shows the errors of motion parameter estimates obtained in both multi-coil and single coil setups using COM values. Note that while in the single uniform coil case estimated parameters provide good approximations to the true shift values, the situation changes drastically in the multi-coil case, which limits applicability of traditional COM analysis for motion correction with phased arrays.

Table 1.

Translational motion parameter estimation error obtained in both single- (uniform) and multi-coil setups using COM values in 2D simulations. Surface coil results correspond to the minimum error among all four used coils.

Shift (pixels)	Uniform coil error	Best surface coil error
0.25	7.26%	14.46%
0.50	3.02%	14.13%
0.75	2.07%	14.84%
1	0.00%	11.94%
2	0.00%	11.95%
5	0.00%	11.93%
10	0.00%	11.83%

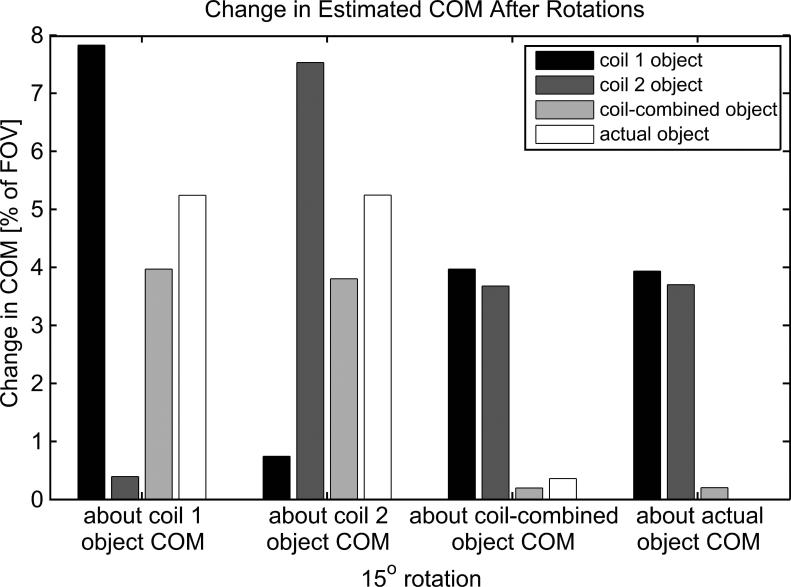
Figure 4 shows the change in COM values for various coil setups after a 15° rotation about various points. As expected, for the cases when the center of rotation and COM analysis are done based on uniform or relatively uniform effectual coil sensitivity (when images were formed by coil combination), the change in the obtained COM values was either zero (actual object case) or noticeably smaller than 1% of the FOV. As a result, COM analysis cannot be a reliable way to detect rotational motion in these cases, especially in the presence of noise. At the same time, COM analysis for individual coils was able to detect rotational motion in all instances, regardless of the location of the center of rotation. Detection sensitivity varied among different coil channels depending on the center of rotation, but the change in COM values was always significant in at least one coil channel. Note that in all instances of COM analysis there was no apparent relationship between the calculated COM displacements and the actual object COM displacement (except for the trivial case of rotation of actual object around its COM).

Figure 4.

Variations in COM values due to rotational motion about four different rotation points in case of uniform (actual object) and phased array coils.

Table 2 shows sensitivity and specificity of the proposed motion detection scheme for various amount and types of motion at several noise levels, as determined by Monte-Carlo simulations. The technique reliably (sensitivity and specificity greater than 90%) detected one pixel shifts and .75° rotations for SNR values of 50 and higher, with performance rapidly growing with SNR.

Table 2.

Sensitivity and specificity of the motion detection scheme (2D Monte-Carlo simulations). Specificity is given by values in parenthesis for each SNR level.

		Image SNR
		25 (92%)	50 (94%)	75 (96%)	100 (96%)	∞ (100%)
Shifts	.50px	35%	70%	84%	91%	99%
	.75px	54%	88%	94%	98%	100%
	1px	75%	96%	99%	100%	100%
Rotations	.50°	23%	66%	89%	96%	100%
	.75°	47%	94%	99%	100%	100%
	1°	75%	99%	100%	100%	100%

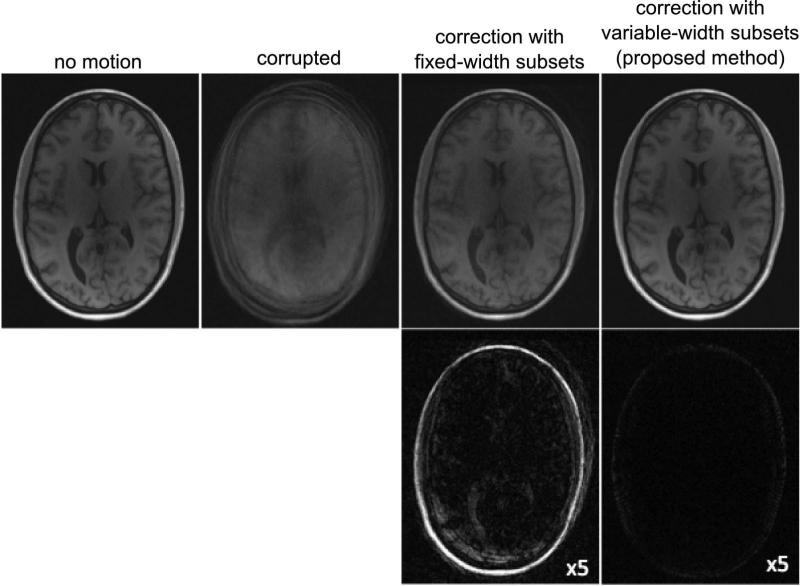
Figure 5 compares results of motion correction using the proposed variable subset width method with a fixed subset approach. Image quality is improved with both methods compared to the corrupted dataset. However, the adaptive selection of subsets led to a more consistent corrected k-space dataset, while using the a priori subset determination approach left large data inconsistencies even after correction. As a result, the adaptive subset selection algorithm produces noticeably smaller reconstruction errors than the fixed-width one.

Figure 5.

Comparison of motion correction using fixed-width subsets and variable-width subsets (proposed method) for a dataset with simulated motion. Top: Reference, corrupted, and corrected images. Bottom: Corresponding error images (scaled by factor of 5.

Volunteer Experiments

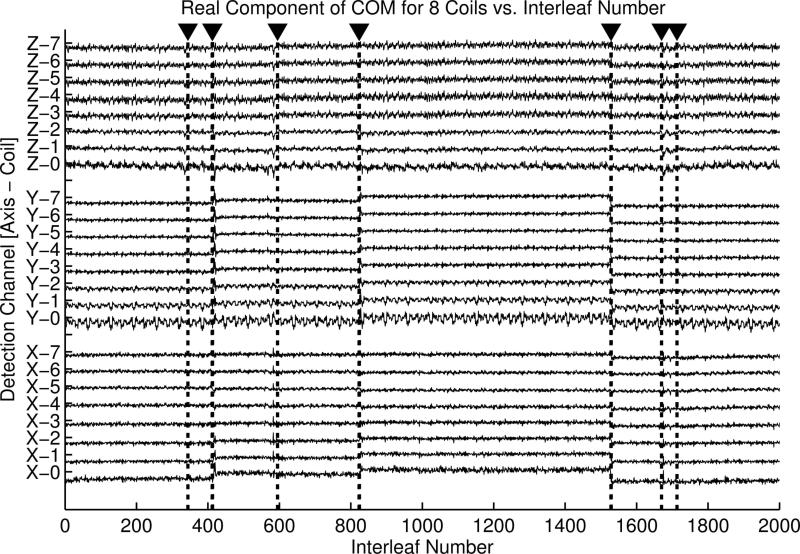
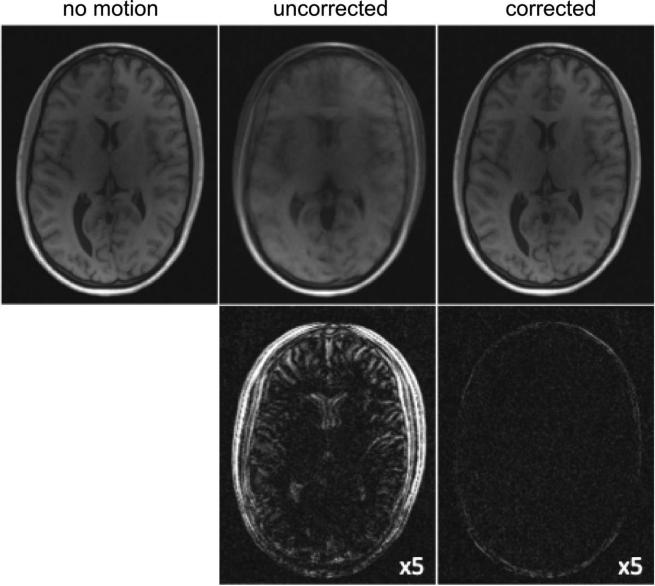
Figure 6 provides an illustration of the typical detection channels. The plots represent the real components of the x-coordinates of the estimated COM for all eight coil channels from a volunteer in vivo cranial exam. Detected instances of motion are identified by dotted vertical lines and arrows (y- and z-coordinates were also used in detection, but are not shown). Seven instances of motion – and thus eight consistent subsets – were detected in this case, with 6% of the total projections rejected as unrecoverable. Figure 7 shows the results of the proposed motion correction process for the same volunteer. Representative slices from the original corrupted image and a subsequent motion-free scan are provided for comparison with the corrected image. Corresponding difference images in the bottom row depict residual error in the reconstructions.

Figure 6.

Example motion detection plots from a volunteer scan (see Fig. 7 for corresponding images). Note that COM detection channels corresponding to individual coils and coordinates have different sensitivity to the motion instances, which necessitates combined detection for improved robustness.

Figure 7.

Top: Representative volunteer scans: motion-free, motion corrupted, and motion corrected by the proposed technique. Bottom: Corresponding difference images (scaled by factor of 5) illustrate motion artifacts are drastically minimized by the proposed correction scheme.

DISCUSSION

We proposed a novel adaptive technique for retrospective 3D motion correction in multi-coil 3D projection imaging. The method derives from two existing motion correction approaches, namely projection moments analysis (7,10-11) and correction by means of co-registration of low-resolution image navigators calculated from time-localized subsets of radial data (12-13,15,29-30). As we demonstrated (Table 1, Fig. 4), existing techniques may become suboptimal for radial imaging with multi-coil receivers with highly varying coil sensitivity profiles. In particular, the accuracy of motion parameter estimation using COM analysis drops significantly for stationary multi-coil receiver systems (Table. 1). At the same time, the non-trivial propagation of coil sensitivity information during motion enhances the ability of COM analysis to detect the motion instances including rotational motion (Fig. 4). In radial acquisitions, each readout samples the central part of k-space, which contains a major portion of the image information content. Hence, data inconsistencies due to motion within datasets used to obtain low-resolution navigators may significantly affect the quality of such navigators and subsequently derived motion parameters. While the use of predefined fixed-subset navigators still results in noticeable improvement of image quality (Fig. 5), its performance is hard to predict and will vary depending on when motion occurs within any given subset.

These shortcomings are eliminated with the proposed technique, which makes no a priori assumptions about when motion will occur. Instead, our method takes advantage of self-navigating properties of radial trajectories to determine consistent subsets of readouts based on actual occurrences of motion as detected by COM analysis. This decouples the process of motion detection from the process of motion estimation, leading to significant improvements in image quality (Figs. 6 and 7). An additional advantage of this adaptive approach stems from the fact that the width of motion-free data subsets is critical for success of co-registration based motion correction (29). Our assessment of registration accuracy (results not shown) indicates that motion free subsets should consist of at least 10% of the total number of projections for accurate subvoxel motion estimation in a 3D acquisition, which is consistent with previously published results for 2D motion correction (29). As our method relies on learning consistent subsets in an adaptive fashion, it allows for better utilization of motion-corrupted data in cases where motion-free periods exceed the duration of an a priori fixed-width navigator images (Figs. 3 and 5). This is particularly important for 3D imaging where the need for encoding in an additional spatial dimension skews the tradeoff between spatial and temporal resolution of navigator images, which in turn determine the time scale and sensitivity of the motion correction scheme.

Although resolution appeared to be entirely recovered in our studies, there is a small loss of apparent SNR in the restored images (Fig. 7). This effect is likely due to residual gaps in k-space resulting from rotation corrections and rejected interleaves. Missing data manifests itself in the resulting images in the form of streaking artifacts, thereby increasing the signal in the background. This issue is common to many retrospective motion compensation schemes, but in our method, the impact of gaps is minimized by the use of properly distributed radial interleaves. For example, in an extreme case of rotation, a PROPELLER scan may effectively acquire the same blade twice, leaving a full blade width gap in the k-space data. In a similar case using radial interleaves, narrower gaps (wedges with an arc-angle equal to the angular difference between adjacent interleaves) would be introduced in an isotropic pattern. The smaller gaps in the interleaved case should correspond to less intrusive artifacts, similar to the effects of radial undersampling. An optimized reconstruction incorporating iterative density compensation (31) or parallel imaging such as that proposed by Bammer et al (32) may reduce streaks caused by the residual gaps in k-space, and be more apt for interpolating narrow gaps in k-space. Additionally, the iterative estimation may provide an efficient way to incorporate now-rejected small subsets of data for improved SNR by applying data weighting schemes (33) to reduce their relative contribution to the reconstructed image.

The efficiency of the proposed method depends on the accuracy of COM calculations, which may be affected by systematic errors caused by trajectory deviations due to gradient delays and eddy currents (34). In addition to the acquisition-time gradient corrections used here, in vivo trajectory calibration may further improve COM estimates calculated from k-space data. Additionally, the temporal fidelity of our method depends on the repetition time of the pulse sequence, number of projections in each interleaf, and noise level (Table 2). Although the time scale for motion correction in our current implementation is higher than that of 2D PROPELLER (300 ms vs. 100 ms), it provides a fully 3D motion correction. The time scale may be reduced by using parallel MRI reconstruction to decrease the number of projections in each interleaf (35). Improvements in COM estimation may also allow reducing the number of projections used to calculate the COM, thus further refining the time-resolution for motion detection and in turn providing more accurate subset delineations.

The proposed method is especially well suited to cranial imaging since typical motion during these exams conforms to our assumptions of rigid-body and intermittent motion. As with any global registration-based motion correction technique, rapid continuous and non-rigid motions remain problematic for the proposed method (36). This is a limitation of the proposed technique, which relies on the assumption that there exist time periods sufficient for acquisition of the navigator images, during which position and orientation of the object do not change. One potential way to overcome this limitation is by employing temporal interpolation to approximate object positions to correct all data points corrupted by continuous motion. To this end, alternative motion detection schemes based on other types of data consistency checks (37-39), correlation-based techniques (40-42) or external motion detection (43-44) are the subject of future research.

CONCLUSIONS

While radial imaging is inherently less sensitive to bulk motion than Cartesian imaging, motion detection and correction can be an important step to increase clinical usefulness of radial acquisitions. We proposed a technique that enables robust 3D rigid body motion correction in 3D radial acquisitions, without the need for additional scan time or external motion estimation. Instead, the proposed method uses inherent self-navigation properties of radial trajectories – with redundancy provided by multiple receiver coils – to detect actual instances of motion. The proposed method is well suited for intracranial imaging. Our approach does not require substantial acquisition modifications, and can thus be used with a wide variety of existing pulse sequences, including steady-state acquisitions, on currently deployed hardware.