Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2014 Nov 11;4:7001. doi: 10.1038/srep07001

Magnetically tunable Mie resonance-based dielectric metamaterials

Ke Bi 1, Yunsheng Guo 2, Xiaoming Liu 2, Qian Zhao 2, Jinghua Xiao 1,a, Ming Lei 1,b, Ji Zhou 2,c
PMCID: PMC4227011  PMID: 25384397

Abstract

Electromagnetic materials with tunable permeability and permittivity are highly desirable for wireless communication and radar technology. However, the tunability of electromagnetic parameters is an immense challenge for conventional materials and metamaterials. Here, we demonstrate a magnetically tunable Mie resonance-based dielectric metamaterials. The magnetically tunable property is derived from the coupling of the Mie resonance of dielectric cube and ferromagnetic precession of ferrite cuboid. Both the simulated and experimental results indicate that the effective permeability and permittivity of the metamaterial can be tuned by modifying the applied magnetic field. This mechanism offers a promising means of constructing microwave devices with large tunable ranges and considerable potential for tailoring via a metamaterial route.

Electromagnetic metamaterials with exotic physic properties have stimulated tremendous fundamental and practical interests during past decade1,2,3,4,5. Metamaterials are a class of materials in which subwavelength features, rather than the constituent materials, control the macroscopic electromagnetic properties6. Up to now, most of present metamaterials are constructed by using artificial metallic microstructures such as split ring resonator (SRR) or wire, whose size and periodicity are far smaller than the operating wavelengths so that the response of metamaterial to electromagnetic wave can be interpreted by using effective parameters7,8,9,10. The unusual electromagnetic properties of metamaterials originate from artificial structure rather than being inherited directly from the materials, which opens a way to design material with more freedom11,12,13.

Recently, Mie resonance-based metamaterials have been theoretical and experimentally studied14,15,16,17,18. The electromagnetic wave interaction of dielectric particles with relative high permittivity can exhibit a strong magnetic or electric resonance. From the oscillation of resulting magnetic or electric dipole, negative permeability or permittivity can be produced19. Compared to SRR and related structures, Mie resonance-based metamaterial can be expected to realize low loss and isotropic properties because it does not suffer from conductive currents and capacitance gap20. It is well known that the permeability and permittivity of the materials are key factors for the propagation of the electromagnetic wave. In order to decrease the number of parts, materials for microwave devices are required to have field dependence properties and one of the easiest ways to satisfy this need is to find materials where the parameters show magnetic DC bias dependence. However, the effective parameters cannot be tuned as a result of the settled characteristic frequency band in artificial metallic structure or Mie resonance-based metamaterials, since the size and structure of those metamaterials are confirmed.

Here, we report a magnetically tunable metamaterials based on the coupling of the Mie resonance of dielectric cube and ferromagnetic precession of ferrite cuboid. The electromagnetic properties of the metamaterials were investigated by simulations and experiments. Our results demonstrate the effective permittivity and permeability of the metamaterial can be tuned by applied magnetic field.

Results

Design and characterization of the magnetically tunable Mie resonance-based dielectric metamaterial

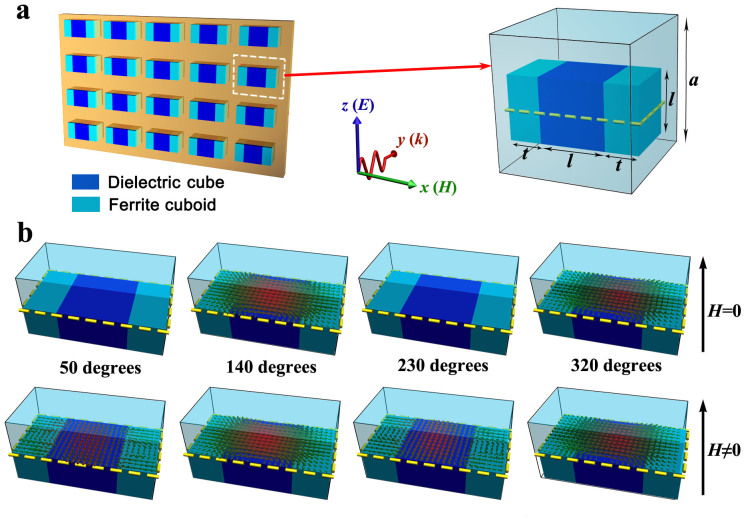
Figure 1a shows the schematic diagram of the magnetically tunable Mie resonance-based dielectric metamaterial. The unit cell of the metamaterial is composed of one dielectric cube and two ferrite cuboids surrounded by air. Dielectric particles support an electric and magnetic dipole response attributable to Mie resonances. The effective permittivity and permeability of an array of dielectric spherical particles embedded in a matrix can be expressed as follows21:

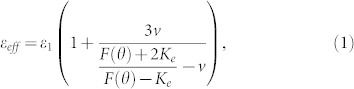graphic file with name srep07001-m1.jpg
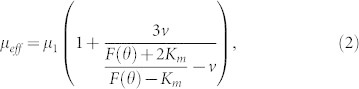graphic file with name srep07001-m2.jpg

where

Figure 1. Schematic diagram of the magnetically tunable Mie resonance-based dielectric metamaterial.

Figure 1

Open in a new tab

(a) The metamaterial and the unit cell consisting of one dielectric cube and two ferrite cuboids. The propagation of the incident electromagnetic wave is along the y axis, and the electric field and magnetic field are along the z and x axes, respectively. The bias magnetic field is applied in the z direction. (b) Magnetic field distributions at Mie resonance frequency illustrating the effect of applied magnetic field on Mie resonance. Four maps with different phase (50, 140, 230 and 320 degrees) are chosen to indicate the dynamic changes of magnetic field distributions in the unit cell. The upper and lower maps show the magnetic field distributions for the unit cell without and with applied magnetic field, respectively.

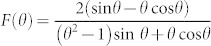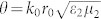Inline graphic, Inline graphic, k0 = 2π/λ, Ke = ε1/ε2, Km = μ1/μ2, 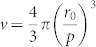Inline graphic is the volume fraction of dielectric particles, r0 and p are the particle radius and the lattice constant, respectively; ε1 and μ1 are the permittivity and permeability of the background matrix, respectively; ε2 and μ2 are the permittivity and permeability of the dielectric particles, respectively. From Eqs. (1) and (2), we observe that the effective permittivity εeff and permeability μeff can be not only influenced by the permittivity ε2 and the permeability μ2 of the dielectric particles, but also affected by the permittivity ε1 and the permeability μ1 of the background matrix. Meanwhile, by interacting with the magnetic field of an electromagnetic wave, ferromagnetic precession can arise in ferrite under an applied magnetic field. The effective permeability of the ferrite around the frequency area of ferromagnetic resonance can be expressed as follows22:

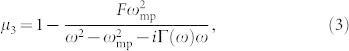graphic file with name srep07001-m3.jpg

where Γ(ω) = [ω2/(ωr + ωm) + ωr + ωm]α; 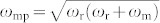Inline graphic; ωm = 4πMsγ; ωr = γH; α is the damping coefficient of ferromagnetic precession; γ is the gyromagnetic ratio; F = ωm/ωr; ωm and ωr are the characteristic frequency and ferromagnetic resonance frequency of the ferrite, respectively; Ms is the saturation magnetization caused by the applied magnetic field; and H is the applied magnetic field. According to Eq. (3), the permeability of the ferrite can be tuned by adjusting the applied magnetic field. Because ferrite is one of the two important parts in this metamaterial, the effective permeability of the metamaterial can be influenced by the permeability of the ferrite cuboids, which means that the effective permeability of the metamaterial can be tuned by adjusting the applied magnetic field. To simplify fabrication, cubes rather than spheres were used as the dielectric particles to prepare the metamaterial.

In order to understand the influence of applied magnetic field on the electromagnetic properties of the metamaterial, the dynamic magnetic field distributions of the unit cell were simulated. Figure 1b shows the magnetic field distributions for the unit cell with or without applied magnetic filed. Four maps with different phase (50, 140, 230 and 320 degrees) are chosen to indicate the dynamic changes of magnetic field distributions in the unit cell. For the unit cell without applied magnetic field, the dielectric cube plays a key role in interacting with electromagnetic wave, and the ferrite cuboids do not interacts with electromagnetic wave due to they have not been magnetized. At a certain frequency (Mie resonance frequency, 11.37 GHz), the magnetic field distributions in the xy-plane (the upper four maps in Fig. 1b) show a typical magnetic Mie-resonance mode. First, the magnetic fields are mainly localized in the cubes at the Mie-resonance frequency16. Second, it can be seen that the displacement currents at 50 and 230 degrees are nearly disappeared and that at 140 and 320 degrees localize in the center of the unit cell. The direction of the linearly polarized displacement currents at 140 degrees is opposite to that at 320 degrees along the x axis, which exhibits a magnetic dipole characteristic. Ferrite can be magnetized in presence of a certain external magnetic field. When a bias magnetic field (1500 Oe) is applied along z direction, the ferromagnetic precession takes place in the ferrite cuboids by interacting with the electromagnetic wave, which could influence the Mie resonance of the dielectric cube. The magnetic field distributions at 11.60 GHz for the unit cell with applied magnetic filed are shown in the lower four maps of Fig. 1b. The magnetic field distributions at 140 and 320 degrees for the unit cell with applied magnetic filed are the same as that for the unit cell without applied magnetic filed. However, at 50 and 230 degrees, the magnetic field distributions for the unit cell with and without applied magnetic filed are much different. According to the dynamic simulation, when a bias magnetic field is applied along z direction, the linearly polarized displacement currents in dielectric cube rotate clockwise and that in ferrite cuboids rotate anticlockwise. At 140 and 320 degrees, the behavior of the displacement currents exhibits a magnetic dipole characteristic. At 50 and 230 degrees, the magnetic field distributions in ferrite cuboids show a vortical pattern, which exhibits an electric dipole characteristic. On the basis of the analysis of the magnetic field distributions for the unit cell with or without applied magnetic filed, one can predict that the applied magnetic filed not only influences the permeability of the metamaterial, but also affects the permittivity of the metamaterial.

Numerical simulations

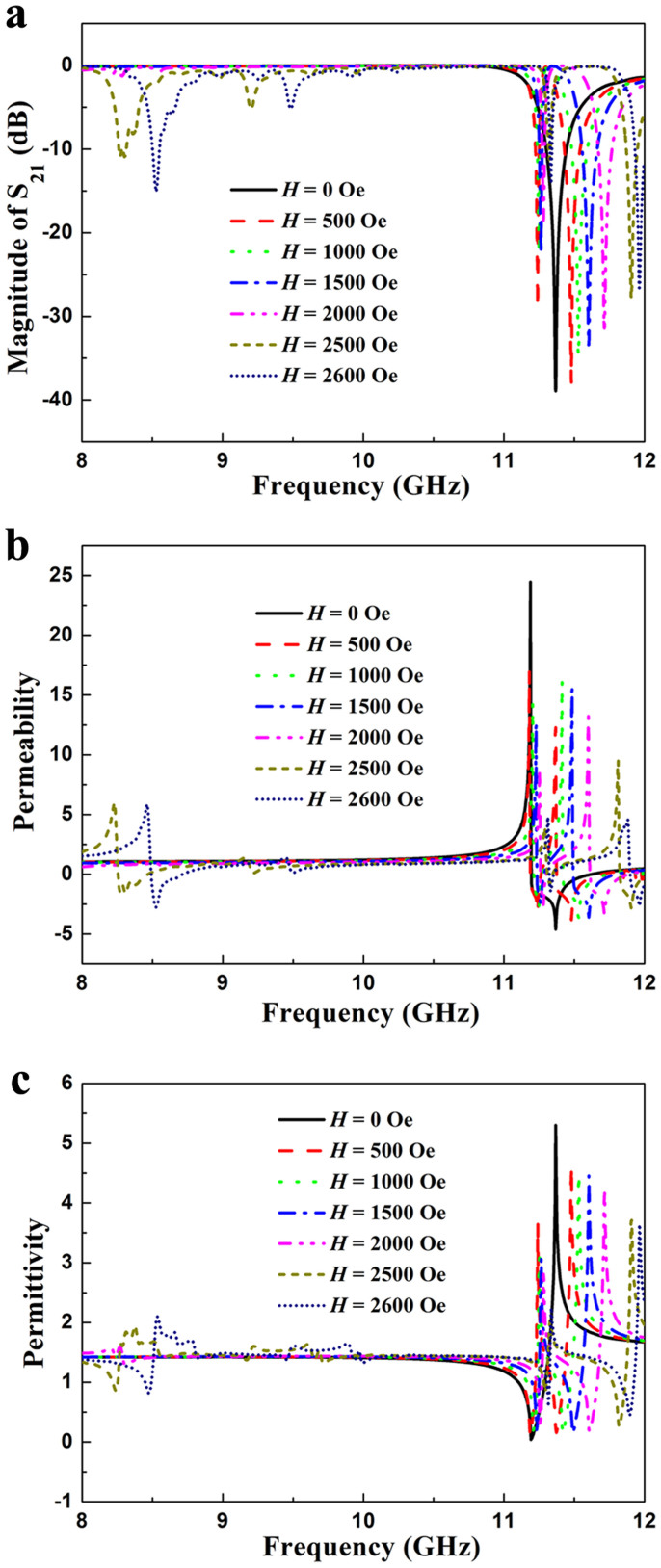
Figure 2a shows the simulated transmission spectra for the unit cell of the metamaterial under a series of applied magnetic fields H. A transmission dip appears at 11.37 GHz in the absence of an applied magnetic field, which corresponds to the magnetic Mie-resonance20. When a magnetic field of H = 500 Oe is applied, one can see that two transmission dips appear at 11.24 GHz and 11.48 GHz, respectively. This indicates that the electromagnetic properties of the metamaterial can be affected by the applied magnetic field. When H is increased from 500 Oe to 2000 Oe, two transmission dips move to higher frequency region, which exhibits a magnetically tunable behavior. When H is increased to 2500 Oe, the third transmission dip appears at 8.29 GHz, corresponding to the ferromagnetic resonance of the ferrite cuboids23. The effective permittivity and permeability of the unit cell of the metamaterial under the same series of applied magnetic fields H was extracted from the simulated scattering parameters using a well-developed retrieval algorithm24,25,26. Figure 2b shows the dependence of the calculated effective permeability on frequency. For the unit cell without applied magnetic field, one remarkable Lorentz-type dispersion occurs in the range of 11–12 GHz. When a certain magnetic field is applied, instead of one dispersion, two or three frequency dispersions appear in the range of 11–12 GHz, which also exhibit magnetic resonance characteristic. The resonance frequency increases as H increases, consistent with the behavior observed in Fig. 2a. In addition, between the magnetic resonance frequency and the magnetic plasma frequency, the value of the effective permittivity is negative. This characteristic makes this metamaterial suitable for applications in negative refractive index materials. Figure 2c shows the dependence of the calculated effective permittivity on frequency. Corresponding to each Lorentz-type dispersion for the effective permeability shown in Fig. 2b, a concurrent anti-resonance state of the effective permittivity appears due to the periodicity effect27. Besides that, the electric resonance frequency increases as H increases. From the above analysis, both the effective permittivity and permeability of the metamaterial can be tuned by applied magnetic field.

Figure 2. Simulation demonstrating the magneto-tunable behavior.

Figure 2

Open in a new tab

(a) Simulated transmission spectra for the unit cell of the metamaterial under a series of applied magnetic fields H. Real parts of the effective (b) permeabilities and (c) permittivities retrieved from the simulated scattering parameters under a series of applied magnetic fields H.

Microwave measurement system

To confirm the results of the above simulations, experimental investigations of the electromagnetic properties of this metamaterial were conducted. The photograph of the microwave measurement system and the metamaterial are shown in Fig. 3. The upper and lower metal plates form the planar waveguide, which restrict the polarization of the electric field to lie uniformly along the z direction and further restrict propagation to the x-y plane. Two horn antennas connected to the output and input ports of the vector network analyzer (Agilent ENA5071C) are installed at both ends of planar waveguide (between the upper and lower metallic plates) as the waveguide adapter to excite and receive a plane wave (8–12 GHz). The sample is placed between two horn antennas. The propagation of the incident electromagnetic wave is along the y axis, and the electric field and magnetic field are along the z and x axes, respectively. The bias magnetic field is generated by an electromagnet in the z direction and can be tuned by adjusting the input current. A teslameter is used to detect the magnetic field. The inset shows a photograph of the metamaterial and the horn antenna.

Figure 3. Experimental microwave setup.

Figure 3

Open in a new tab

The sample is placed between two horn antennas. The propagation of the incident electromagnetic wave is along the y axis, and the electric field and magnetic field are along the z and x axes, respectively. The bias magnetic field is generated by an electromagnet in the z direction. The inset shows a photograph of the metamaterial.

Experimental results

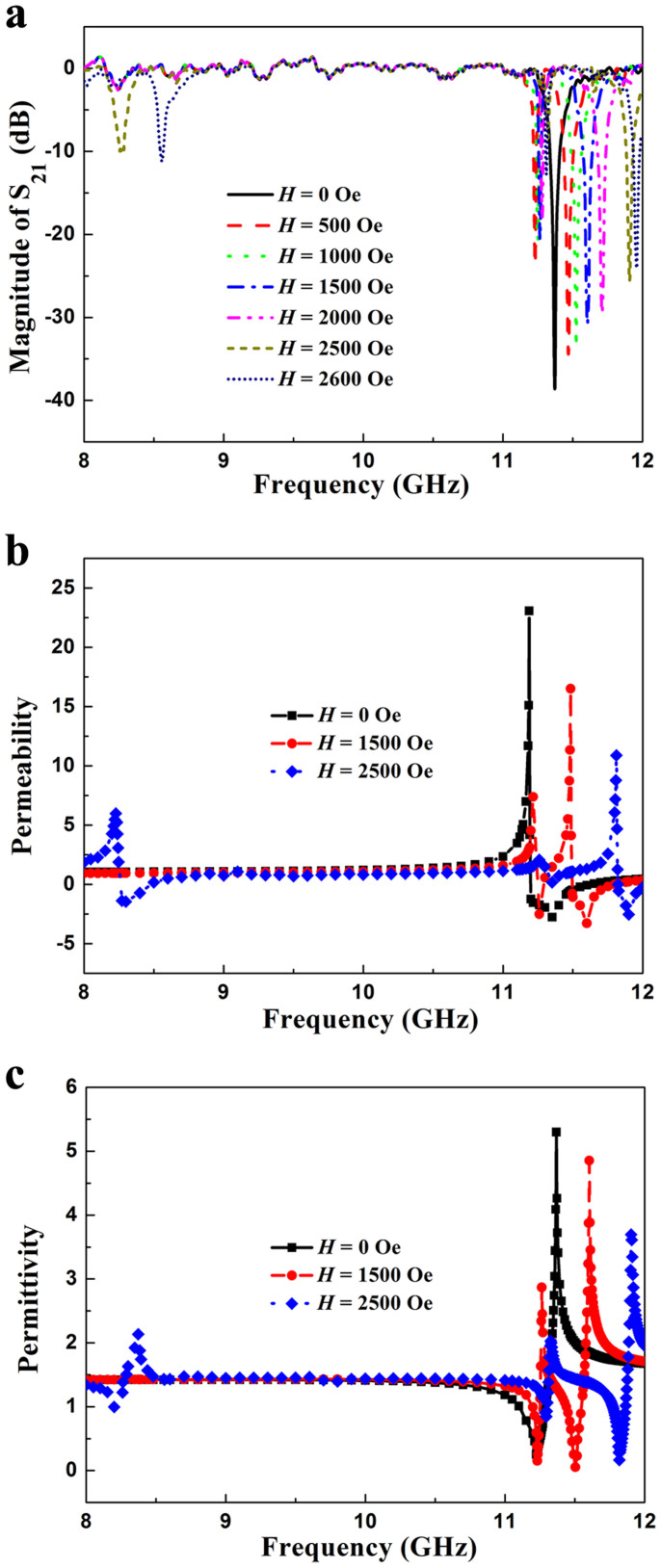
Figure 4a presents the experimental transmission spectra for the metamaterial under a series of applied magnetic fields H. First, a transmission dip induced by magnetic Mie-resonance of dielectric cube occurs in the transmission spectrum for the metamaterial without applied magnetic field. Second, when a certain magnetic field is applied in the z direction, two transmission dips appear in the range of 11–12 GHz. The resonance frequency of the transmission dip increases as H increases, which exhibits a magnetically tunable behavior. Third, when H is increased from 2500 Oe to 2600 Oe, the third transmission dip induced by ferromagnetic resonance of the ferrite cuboids appear in the range of 11–12 GHz. When H = 0, the ferrite cuboids are not magnetized and almost have no effect on the magnetic field distributions of the unit cells, as shown in the upper four maps in Fig. 1b. The typical magnetic Mie-resonance is induced by the dielectric cube, which results in one transmission dip appeared in the spectra. The ferrite cuboids will be magnetized when H > 0. By interacting with the electromagnetic wave, the ferromagnetic precession takes place in the ferrite cuboids. As shown in the lower four maps in Fig. 1b, the magnetic Mie-resonance in the dielectric cube is influenced by the ferromagnetic precession. Hence, two transmission dips appear in the transmission spectra. The ferromagnetic precession in the ferrite cuboids will enhance as H increases. As a result, the resonance frequency of the transmission dip increases as H increases.

Figure 4. Experimental results of the magnetically tunable Mie resonance-based dielectric metamaterial.

Figure 4

Open in a new tab

(a) Experimental transmission spectra for the metamaterial under a series of applied magnetic fields H. Real parts of the effective (b) permeabilities and (c) permittivities retrieved from the experimental scattering parameters under a series of applied magnetic fields H.

The real parts of the effective permeabilities retrieved from the experimental scattering parameters under the same series of applied magnetic fields H are depicted in Fig. 4b. The results reveal remarkable frequency dispersion in the range of 11–12 GHz in all cases. The number of the Lorentz-type dispersion in the range of 11–12 GHz is one, two and three when H = 0 Oe, 1500 Oe and 2500 Oe, respectively. The value of the effective permittivity is negative between the magnetic resonance frequency and the magnetic plasma frequency. Figure 4c shows the real parts of the effective permittivities retrieved from the experimental scattering parameters under the same series of applied magnetic fields H. The effective permittivity shows the anti-resonance state. The electric resonance frequency increases as H increases, thus, magnetically tunable behavior is demonstrated. From the analysis presented above, it is evident that the behavior of the experimental data is in good agreement with that of the simulated data.

Discussion

We experimentally and numerically demonstrated a magnetically tunable Mie resonance-based dielectric metamaterials. The tunable property is attributable to the coupling of the Mie resonance of dielectric cube and ferromagnetic precession of ferrite cuboid. When a certain magnetic field is applied, two or three resonance frequency dispersions appear in the range of 8–12 GHz, which indicates two or three peak values can be obtained. In particular, both the effective permittivity and permeability of the metamaterial can be tuned by adjusting the applied magnetic field. This work provides a new way to fabricate the tunable metamaterials, which has greater potential for wireless communication and radar technology.

Methods

Sample fabrication

The dielectric material chosen for this work was Barium Strontium Titanate (BST) ceramic. BST cubes were cut to dimensions of 2 × 2 × 2 mm3. The relative permittivity and dielectric loss are 120 and 0.015, respectively. The ferrite material chosen for this work was yttrium iron garnet (YIG) ferrite. YIG cuboids were cut to dimensions of 2 × 2 × 1 mm3. The saturation magnetization 4πMs, linewidth ΔH, and relative permittivity εr of the YIG rods were 1950 Gs, 10 Oe, and 14.5, respectively, and the same values were used in the simulations. The unit cell of the metamaterial is composed of one dielectric cube and two ferrite cuboids. Two ferrite cuboids were bonded with both ends of the dielectric cube. The sample was fabricated by inserting the dielectric cubes and ferrite cuboids into a Teflon substrate, as shown as an inset in Fig. 3. The distance between the dielectric cubes in the x direction is the same as that in the z direction (5 mm).

Simulations

The dimensions of the unit cell were 5 × 5 × 5 mm3. All the parameters of the dielectric cube and ferrite cuboid were the same as those in the experiments. A plane wave was assumed for the incident electromagnetic field, with polarization conditions corresponding to an electric field along the x axis and a magnetic field along the y axis. The bias magnetic field was applied in the z direction. Numerical predictions of the transmission spectra were calculated using the commercial time-domain package CST Microwave Studio TM.

Microwave measurements

The sample was placed between two horn waveguides connected to an HP 8720ES network analyzer, as shown in Fig. 3. The propagation of the incident electromagnetic wave was along the y axis, and the electric field and magnetic field were along the z and x axes, respectively. The bias magnetic field provided by the electromagnets was applied in the z direction.

Author Contributions

K.B. conceived the idea and designed experiments. K.B., Y.S.G. and X.M.L. performed the experiments. K.B., Q.Z., M.L. and J.H.X. developed the post-processing treatments of the experimental data. K.B. and Y.S.G. carried out numerical calculations and figures. K.B. and J.Z. wrote the paper. All authors contributed to scientific discussion and critical revision of the article.

Acknowledgments

This work was supported by the National High Technology Research and Development Program of China under Grant No. 2012AA030403; the National Natural Science Foundation of China under Grant Nos. 51402163, 61376018, 61377067, 51032003, 11274198, 51102148 and 51221291; and the China Postdoctoral Research Foundation under Grant Nos. 2013M530042 and 2014T70075.

References

  1. Veselago V. G. The electrodynamics of substance simultaneously negative values of ε and μ. Sov. Phys. Usp. 10, 509–514 (1968). [Google Scholar]
  2. Pendry J. B. Negative Refraction Makes a Perfect Lens. Phys. Rev. Lett. 85, 3966–3969 (2000). [DOI] [PubMed] [Google Scholar]
  3. Schurig D. et al. Metamaterial Electromagnetic Cloak at Microwave Frequencies. Science 314, 977–980, 1133628 (2006). [DOI] [PubMed] [Google Scholar]
  4. Yuan G. et al. A broadband slab lens antenna formed from gradient refractive index metamaterials composed of cross-shaped cells. Microwave Opt. Technol. Lett. 56, 1124–1129 (2014). [Google Scholar]
  5. Hoffman A. J. et al. Negative refraction in semiconductor metamaterials. Nat. Mater. 6, 946–950 (2007). [DOI] [PubMed] [Google Scholar]
  6. Smith D. R., Pendry J. B. & Wiltshire M. C. K. Metamaterials and Negative Refractive Index. Science 305, 788–792 (2004). [DOI] [PubMed] [Google Scholar]
  7. Liu M. et al. Terahertz-field-induced insulator-to-metal transition in vanadium dioxide metamaterial. Nature 487, 345–348 (2012). [DOI] [PubMed] [Google Scholar]
  8. Paul T., Menzel C., Rockstuhl C. & Lederer F. Advanced Optical Metamaterials. Adv. Mater. 22, 2354–2357 (2010). [DOI] [PubMed] [Google Scholar]
  9. Gu J. et al. Active control of electromagnetically induced transparency analogue in terahertz metamaterials. Nat. Commun. 3, 1151 (2012). [DOI] [PubMed] [Google Scholar]
  10. Ren M. et al. Nanostructured Plasmonic Medium for Terahertz Bandwidth All-Optical Switching. Adv. Mater. 23, 5540–5544 (2011). [DOI] [PubMed] [Google Scholar]
  11. Chen P.-Y., Farhat M. & Alù A. Bistable and Self-Tunable Negative-Index Metamaterial at Optical Frequencies. Phys. Rev. Lett. 106, 105503 (2011). [DOI] [PubMed] [Google Scholar]
  12. Wu Y., Lai Y. & Zhang Z.-Q. Elastic Metamaterials with Simultaneously Negative Effective Shear Modulus and Mass Density. Phys. Rev. Lett. 107, 105506 (2011). [DOI] [PubMed] [Google Scholar]
  13. Liu H., Zhao X., Yang Y., Li Q. & Lv J. Fabrication of Infrared Left-Handed Metamaterials via Double Template-Assisted Electrochemical Deposition. Adv. Mater. 20, 2050–2054 (2008). [Google Scholar]
  14. Kang L. & Lippens D. Mie resonance based left-handed metamaterial in the visible frequency range. Phys. Rev. B 83, 195125 (2011). [Google Scholar]
  15. Kuznetsov A. I., Miroshnichenko A. E., Fu Y. H., Zhang J. & Luk'yanchuk B. Magnetic light. Sci. Rep. 2, 492 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Zhao Q. et al. Experimental Demonstration of Isotropic Negative Permeability in a Three-Dimensional Dielectric Composite. Phys. Rev. Lett. 101, 027402 (2008). [DOI] [PubMed] [Google Scholar]
  17. Vynck K. et al. All-Dielectric Rod-Type Metamaterials at Optical Frequencies. Phys. Rev. Lett. 102, 133901 (2009). [DOI] [PubMed] [Google Scholar]
  18. Kim J. & Gopinath A. Simulation of a metamaterial containing cubic high dielectric resonators. Phys. Rev. B 76, 115126 (2007). [Google Scholar]
  19. Zhang F., Kang L., Zhao Q., Zhou J. & Lippens D. Magnetic and electric coupling effects of dielectric metamaterial. New J. Phys. 14, 033031 (2012). [Google Scholar]
  20. Zhao Q., Zhou J., Zhang F. L. & Lippens D. Mie resonance-based dielectric metamaterials. Mater. Today 12, 60–69 (2009). [Google Scholar]
  21. Lewin L. The electrical constants of a material loaded with spherical particles. Proc. Inst. Elec. Eng. 94, 65–68 (1947). [Google Scholar]
  22. Zhao H., Zhou J., Kang L. & Zhao Q. Tunable two-dimensional left-handed material consisting of ferrite rods and metallic wires. Opt. Express 17, 13373–13380 (2009). [DOI] [PubMed] [Google Scholar]
  23. Bi K., Zhou J., Zhao H., Liu X. & Lan C. Tunable dual-band negative refractive index in ferrite-based metamaterials. Opt. Express 21, 10746 (2013). [DOI] [PubMed] [Google Scholar]
  24. Smith D. R., Schultz S., Markoš P. & Soukoulis C. M. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B 65, 195104 (2002). [Google Scholar]
  25. Croënne C., Fabre B., Gaillot D., Vanbésien O. & Lippens D. Bloch impedance in negative index photonic crystals. Phys. Rev. B 77, 125333 (2008). [Google Scholar]
  26. Chen X., Grzegorczyk T. M., Wu B., Pacheco J. & Kong J. A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E 70, 016608 (2004). [DOI] [PubMed] [Google Scholar]
  27. Koschny T. et al. Impact of inherent periodic structure on effective medium description of left-handed and related metamaterials. Phys Rev B 71, 245105 (2005). [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES