Long-Range Distance Measurements in Proteins at Physiological Temperatures Using Saturation Recovery EPR Spectroscopy

Abstract

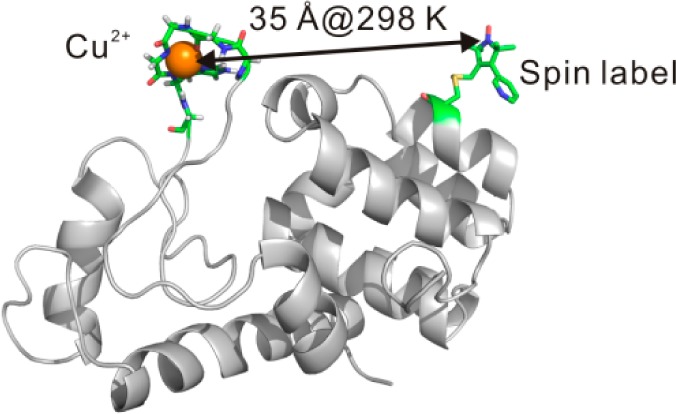
Site-directed spin labeling in combination with EPR is a powerful method for providing distances on the nm scale in biological systems. The most popular strategy, double electron–electron resonance (DEER), is carried out at cryogenic temperatures (50–80 K) to increase the short spin–spin relaxation time (T₂) upon which the technique relies. A challenge is to measure long-range distances (20–60 Å) in proteins near physiological temperatures. Toward this goal we are investigating an alternative approach based on the distance-dependent enhancement of spin–lattice relaxation rate (T₁^–1) of a nitroxide spin label by a paramagnetic metal. With a commonly used nitroxide side chain (R1) and Cu²⁺, it has been found that interspin distances ≤25 Å can be determined in this way (Jun et al. Biochemistry2006, 45, 11666). Here, the upper limit of the accessible distance is extended to ≈40 Å using spin labels with long T₁, a high-affinity 5-residue Cu²⁺ binding loop inserted into the protein sequence, and pulsed saturation recovery to measure relaxation enhancement. Time-domain Cu²⁺ electron paramagnetic resonance, quantum mechanical calculations, and molecular dynamics simulations provide information on the structure and geometry of the Cu²⁺ loop and indicate that the metal ion is well-localized in the protein. An important aspect of these studies is that both Cu²⁺/nitroxide DEER at cryogenic temperatures and T₁ relaxation measurements at room temperature can be carried out on the same sample, allowing both validation of the relaxation method and assessment of the effect of freezing on protein structure.

Introduction

Development of techniques to determine protein structure and dynamics in solution is attracting attention because such information is essential to elucidate mechanisms of function. Among the existing experimental approaches, site-directed spin labeling in combination with electron paramagnetic resonance (SDSL-EPR) is uniquely powerful due to advantages of high sensitivity (μg of protein), wide dynamic range (ps–ms), and the ability to study large proteins, including membrane proteins and complexes thereof with minimal structural perturbation.¹⁻⁵ For a doubly labeled protein, SDSL-EPR also allows determination of distances between spin labels, providing information on structure and function-associated structural changes of the protein. Measurement of internitroxide distances can be carried out at physiological temperatures using magnetic dipolar broadening of Continuous Wave (CW) EPR spectra, but the maximum distance determined is limited to ∼20 Å.^6,7 Distances to ∼80 Å together with a distance probability distribution can be measured with pulsed dipolar spectroscopy (PDS), which includes double electron–electron resonance (DEER) and double quantum coherence (DQC).^8,9 However, PDS for proteins is generally carried out at cryogenic temperatures to prevent protein rotational diffusion which averages the dipolar interaction and to maintain a sufficiently long spin–spin relaxation time (T₂) of the electron spin on which the spin–echo based method depends.

While current evidence shows that the distance distributions obtained from cryogenic PDS are in reasonable agreement with expectation, there remains uncertainty as to possible freezing effects on protein conformational equilibria. Moreover, in membrane proteins, the cooling process could also cause phase changes of the membrane lipids, potentially affecting the conformation of the protein. Such considerations apply equally to any method conducted at low temperature. Consequently, an important improvement to the EPR distance measurement methodology would be to remove the requirement of cryogenic temperature for medium- to long-range distance measurement, beyond 20 Å.

Advances have been made in this direction. For example, PDS was recently shown to measure distances to ≈25 Å in liquid solution using novel triarylmethyl (TAM) spin labels in a protein immobilized on a solid support, and modifications to the TAM labels could increase the measurable distance range.¹⁰ Non-adiabatic rapid scanning (NARS) EPR, also based on magnetic dipolar interactions, was demonstrated to increase the maximum distance range to ≈30 Å for proteins with slow rotational diffusion.¹¹ More recently, distances up to 46 Å were measured at 37 °C on an immobilized DNA containing a TAM pair, but the method was not generalized to proteins.¹²

Relaxation enhancement (RE) methods offer an alternative to those that depend on static dipolar interactions for determination of interspin distances. In principle, distances up to 150 Å can be obtained at low temperatures using the distance-dependent enhancement of nitroxide or natural radical spin–lattice relaxation rate (T₁^–1) by fast-relaxing metal ions,¹³ provided that the protein has an endogenous metal center^14,15 or that one can be introduced at the desired sites.¹⁶⁻²⁰ Recent progress in RE technological development and its application to obtain structural information in biological systems at low temperatures have been reported.²¹⁻²⁹ It is challenging to generalize the RE method to near-room temperature because the relaxation rates of most metal ions at room temperature are usually <ps, generating marginal or zero effects on the relaxation rates of the spin label. An exception is Cu²⁺, which has ns relaxation time at room temperature.³⁰

In the present study, we revisit the Cu²⁺-enhanced T₁ relaxation of nitroxides that was introduced by Jun et al.²⁰ In that work, inversion recovery methods were used to measure relaxation enhancement for mapping distances to 25 Å at room temperature in synthetic peptides that contained an endogenous Cu²⁺ binding site. To generalize the method for application to larger proteins, a Cu²⁺ binding site must be introduced into the protein, and saturation recovery (SR) rather than inversion recovery must be used to measure T₁ due to the short nitroxide T₂ in the intermediate correlation time range typically found for nitroxides in proteins with MW > 10 kDa. Introduction of a Cu²⁺ binding site can be achieved using histidine pairs^16,18 or unnatural amino acids,³¹ but the affinity of these ligands is relatively low (K_d ≈ μM), and as shown below, nonspecific binding of Cu²⁺ can compete with such sites. In this study a five-amino acid peptide with a high-affinity for Cu²⁺ is genetically engineered in the protein of interest and the distance-dependent enhancement in T₁ relaxation is measured with pulsed SR EPR at room temperature. In order to extend the distance range beyond 25 Å, nitroxide spin labels with long T₁s are employed. An appealing feature of this method is that interspin distance can be measured at both low and high temperature to evaluate the effect of freezing and compared with Cu²⁺-nitroxide distance distributions determined from DEER on the same sample to provide information on the location and inherent flexibility of the engineered Cu²⁺ binding site.

Results

General Strategy

The theoretical framework of EPR relaxation-based distance measurements has been developed for the case where the interspin vector reorients on a time scale fast compared to that for the dipolar interaction (the fast motional limit) and in the absence of motion (the rigid limit).^{13,20,32−34} Figure 1A shows the estimated maximum measurable distance for a Cu²⁺/nitroxide pair as a function of the intrinsic T₁ of the nitroxide based on the fast motional limit (see below).²⁰ As is evident, the maximum distance measurable increases with increasing nitroxide T₁. The T₁ of a nitroxide increases with decreasing correlation time in the ns range,^35,36 so nitroxide side chains with constrained internal motion are expected to have long T₁s. At solvent exposed sites in a protein, where the spin label has minimal perturbation, the most commonly used nitroxide side chain R1 (Figure 1B) typically has T₁ ≈ 2 μs, corresponding to a maximum measurable distance ≈25 Å. On the other hand, the nitroxide side chains designated R1p and RX (Figure 1B) are immobilized relative to the protein^37,38 at such sites and have T₁s of 3.6–5 μs and 6–10 μs, respectively. According to Figure 1A, R1p and the RX can theoretically extend the maximal measurable distances up to 35 and 40 Å, respectively.

Figure 1.

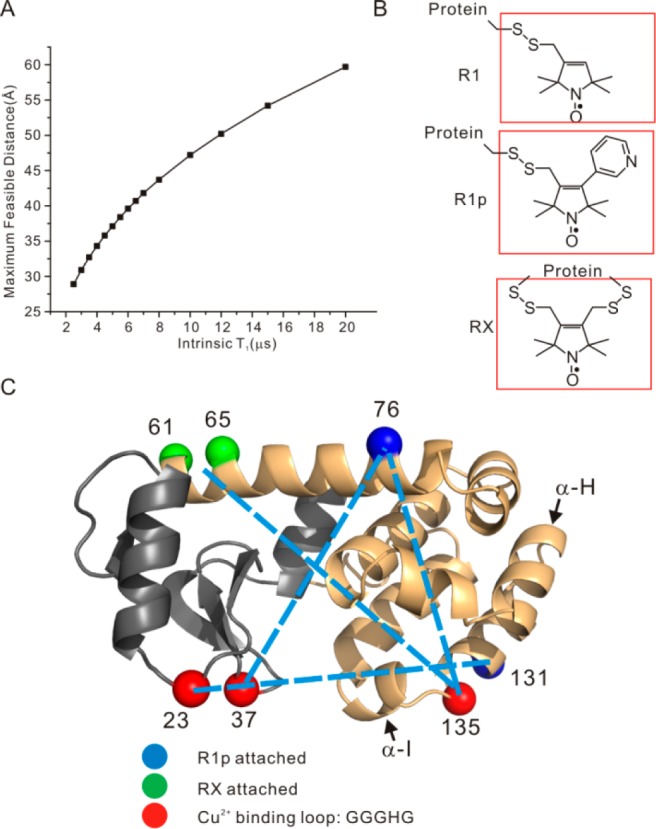
(A) A plot of the maximum measurable distances as a function of nitroxide intrinsic T₁ using the fast motional approximation (eq 1). The maximum measurable distances were estimated by taking the minimum measurable drop in T₁ due to the presence of a fast-relaxing spin to be 0.5 μs (the uncertainty in T₁ for SR measurement is typically ±0.1 μs, see SI), using 3 ns as the Cu²⁺ electron spin relaxation times (eq 1). (B) The schematic structures of R1 and the two restrained spin labels employed in this study (cf. refs (37 and 38)). (C) A ribbon model of T4 lysozyme. The two subdomains of the protein, the N- and the C-domain, are color coded with gray and orange, respectively. The cyan and green spheres represent the locations of the Cα atoms of the residues where the R1p and the RX spin label were attached, respectively. The red spheres identify the positions where the GGGHG loop was inserted. Dotted bars indicate spin pairs used in distance measurement in this work. The α-helices of H and I are indicated by arrows.

To reliably employ Cu²⁺ -induced RE in proteins, the Cu²⁺ binding site must be of extremely high affinity in order to avoid complication of data analysis caused by the presence of low affinity, nonspecific Cu²⁺ binding site(s). The Cu²⁺ complex of the methyl amide of glycylglycyl-l-histidine (GGH) was reported to have a K_d of 10^–21 M, the smallest for any Cu²⁺ complex reported in the literature.³⁹ Based on this result, the five amino acid sequence GGGHG was selected for introduction into proteins as a high affinity Cu²⁺ binding site. The additional glycine residues at both ends were incorporated to minimize strain at the site of introduction.

T4 lysozyme (T4L) was selected as a well-studied model protein to evaluate the overall strategy. The GGGHG sequence was inserted, one at a time, between residues 23 and 24, 37 and 38, and 135 and 136 in T4L as shown in Figure 1C (red spheres); in each case, the site of introduction is in a loop spanning helical segments. In addition, cysteine was substituted for a native residue at a selected site to introduce the R1p side chain; introduction of RX requires two cysteine residues (Figure 1C). Details of mutagenesis, protein expression/purification, and spin labeling are provided in the Supporting Information (SI). The resulting proteins containing R1p are designated as iL/j, where iL indicates that the GGGHG loop was inserted in between residues i and i + 1 and R1p is at residue j. The single RX labeled mutant is designated as 135L/61RX65, meaning RX was attached to residues 61 and 65, and the GGGHG loop was inserted between residues 135 and 136.

Far UV CD Studies on Protein Secondary Structure upon Insertion of Cu²⁺ Binding Loop

To determine the structural integrity of the loop-inserted T4L mutants, far UV CD measurements were carried out for each of the copper loop mutants containing a spin label. For comparison, the far UV CD spectrum of the pseudo-wild-type (WT*) T4L protein (wild-type T4L containing the substitutions C54T and C97A)⁴⁰ was recorded under the same experimental conditions (see Methods section) (Figure 2). For the mutants 23L/131R1p and 37L/76R1p, the far UV spectra are the same as the WT* protein within experimental error, suggesting that the mutants retain WT*-like secondary structure. Interestingly, for the 135L/61RX65 mutant, there is a statistically significant decrease in the mean residue ellipticity suggesting a small change in the secondary structure. Estimation of the difference in helical content between 135L and the WT* based on the mean residue ellipticity at 208 and 222 nm^41,42 indicates a reduction of ≈6% (≈1–2 turns), likely due to localized distortions in flanking helices H and/or I (Figure 1C). In the WT* protein, the loop connecting H and I is short and structured (residues 135–136).

Figure 2.

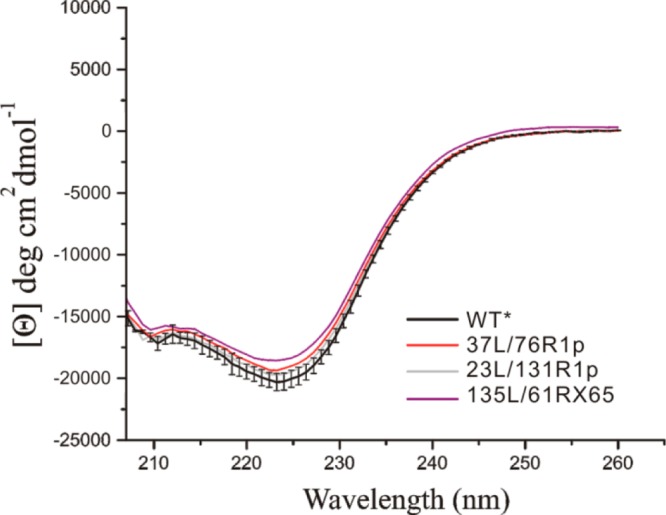
Far UV CD spectra of the indicated mutants of T4L. The black vertical bars represent the standard deviation of the mean residue ellipticity for the WT* protein based on triplicate measurements.

Cu²⁺ Binding Affinity of Loop-Inserted Mutants

The Cu²⁺ binding affinity of loop-inserted T4L mutants was determined by titration with CuCl₂ using a Cu²⁺ selective electrode.⁴³ The results, including a control experiment with 131R1 without the GGGHG loop, are shown in Figure 3. The titration data are compared with theoretical curves simulated for 1:1 stoichiometry with K_d from 50 μM to 1 nM (solid traces) in order to estimate the K_d of each mutant. The data on 131R1 indicate that nonspecific Cu²⁺ binding site(s) are present in T4L with an affinity of tens of μM in K_d. The titration results of three loop-containing samples, 23L/131R1p, 37L/76R1p, and 135L/76R1p indicate K_ds of <50 nM, consistent with a value of ≈5 nM estimated through quantum mechanical (QM) calculations (Figure S1). Note that above the saturating Cu²⁺ concentration (when 50 μM or more Cu²⁺ was added), nonspecific binding is evident. Collectively, the data show that addition of stoichiometric amounts of Cu²⁺ and protein saturates the specific binding with little contribution from nonspecific sites.

Figure 3.

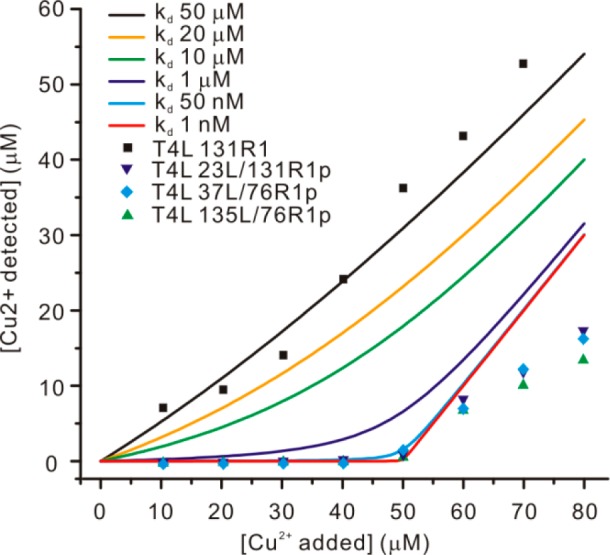
Summary of the Cu²⁺ titration study. The equilibrium free Cu²⁺ concentration is plotted as a function of total added Cu²⁺. Theoretical titration curves using different K_d values are color-coded as listed in the inset. Experimental titration data from four samples, including a control sample, are also listed in the inset. In all titration studies, the concentration of protein was maintained at 50 μM.

Geometry of the Cu²⁺ Binding Sites in the Loop-Containing Mutants

After confirming the existence of high affinity Cu²⁺ binding sites in the loop-containing mutants, the geometry of the Cu²⁺ coordination was investigated using a combination of EPR and computational techniques. The field-swept electron spin echo (FS-ESE) detected absorption spectra of Cu²⁺ on each loop-containing protein are consistent with a square-planar geometry of 3 nitrogen and 1 oxygen atoms around the metal (3N1O) based on an A_|| of ∼165 G⁴⁴ and electron spin echo envelope modulation (ESEEM) data that indicate the presence of a histidine ligand on Cu²⁺ (cf. Figure S2).⁴⁵ These results are in agreement with those from computational modeling, where QM optimization algorithms were used to determine the structure of the Cu²⁺ binding center in a GGH tripeptide model capped with terminal amide groups (see Methods and SI). The results show that the 3N1O square-planar geometry in which two deprotonated Gly backbone amides, a His side chain and a Gly backbone carbonyl are coordinated, is the optimal geometry for the Cu²⁺ binding motif (Figure 4A). This arrangement is similar to that found in α-synuclein during the Cu²⁺-induced misfolding of Parkinson’s disease protein.⁴⁶ It is noted that in the Cu²⁺-coordinated GGH tripeptide crystal structure, the Cu²⁺ binding geometry involves four nitrogen atoms around copper (4N), one from the free amino group of the terminal glycine (Figure 4B). This geometry is unlikely for the loop in proteins since three amides would be deprotonated yielding a unstable anionic motif (calculated to be 56 kcal mol^–1 less stable than the 3N1O motif) and the backbone will have considerable steric stress (Figure 4C). The absence of the fourth amino ligand may be the reason for the lower (nM) affinity observed for the GGGHG in proteins compared to the 10^–21 M K_d reported for the isolated GGH tripeptide.

Figure 4.

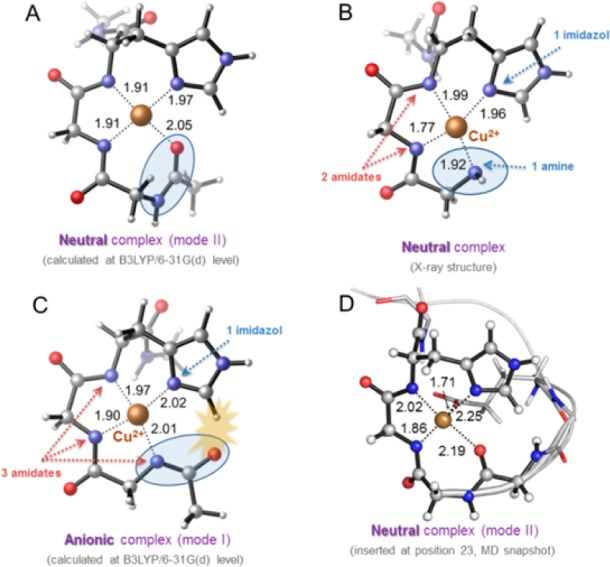
(A) Square-planar coordination mode of Cu²⁺ to NHCOMe-Gly-Gly-His-CONHMeCu optimized through DFT calculations. (B) Crystallographic structure of copper(II)-glycylglycyl-l-histidine-N-methyl amide complex (ref (39)). (C) A different square-planar coordination mode of Cu²⁺ to NHCOMe-Gly-Gly-His-CONHMeCu optimized through DFT calculations. Steric clash between the imidazole ring and an amide carbonyl group is represented with a yellow star. (D) Cu²⁺-binding loop (coordination mode II) inserted in position 23 of T4 lysozyme, after 2 ns of MD simulation.

Molecular dynamics (MD) simulations in explicit solvent (see Methods and SI) for the GGGHG loop in T4L revealed that often after a short equilibration other carbonyl groups from adjacent Asp and backbone residues, together with solvent molecules, participate in additional coordination to the metal center, providing an octahedral environment (Figure 4D). Nevertheless, the coordination of Cu²⁺ to the different loops was maintained along the whole simulation time (100 ns).

Effects of Molecular Rotational Motion on Distance Measurements

Figure 5 shows example SR data for the RE due to Cu²⁺ binding for 23L/131R1 and 23L/131R1p. The data illustrate the greater enhancement for R1p relative to R1 at the same distance (∼32 Å) from the Cu²⁺ site, reflecting the longer maximum measurable distance for R1p predicted in Figure 1A.

Figure 5.

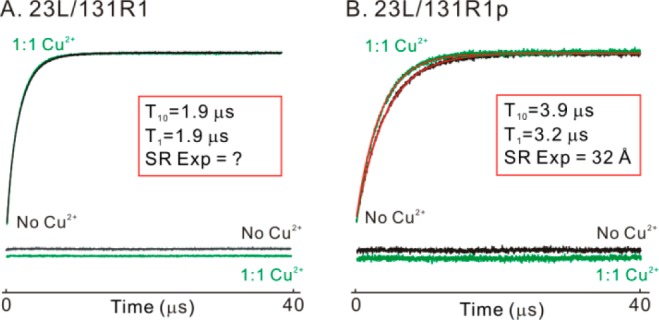
SR data for the relaxation enhancement due to Cu²⁺ binding for 23L/131R1 (A) and 23L/131R1p (B), in the absence (black) and presence (green) of saturated Cu²⁺. Fits to each trace using a single exponential function are shown in red, with corresponding residual signal provided below the SR data. The time constants from each fit and the Cu²⁺-nitroxide distance calculated based on the fast motional limit are reported in the inset. For 23L/131R1, no enhancement was observed.

To compute interspin distances from RE data like those in Figure 5, the rotational motion of the interspin vector must be considered; for the immobilized residues R1p and RX, this is the same as the rotational diffusion of the entire protein with correlation time τ_C. There are two limiting cases: the fast motional and the rigid limits. For peptides and small globular proteins the fast motional limit model is likely to be appropriate for calculating the interspin distance. For the fast motional limit to apply, τ_C must be such that⁴⁷

where r is the interspin distance, μ₀ is the vacuum permeability, ℏ, g_f, g_s, and β_e are the reduced Plank constant, g values of the fast (Cu²⁺) and slowly (nitroxide) relaxing electron spins, and the Bohr magneton, respectively. In the fast motional limit, the RE of a nitroxide upon Cu²⁺ binding is related to the average Cu²⁺-nitroxide distance according to,²⁰

1

where T_1s and T_1s^o are the T₁ values of the nitroxide in the presence and absence of Cu²⁺, respectively, ω_s and ω_f are the resonant frequencies of the nitroxide and the Cu²⁺, and T_1f and T_2f are the spin–lattice and spin–spin relaxation time of the Cu²⁺.

In the rigid motional regime, the corresponding expression is¹⁴

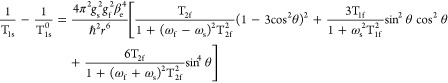2

In this limit, calculation of the RE requires integration over the angle θ, which describes the relative orientation between the spin–spin vector and the external magnetic field.

For distances in the desired target range of 25–40 Å, the correlation time for T4L in water lies at the upper edge of the fast motional limit (τ_C ≈ 6 ns).⁴⁷ The correlation time for the protein can be “tuned” by changing the solution viscosity or by immobilizing the protein on a solid support, thus in principle moving from the fast motional limit to the rigid limit and hence from eqs 1 to 2 as the appropriate method for determining r. To test these ideas and to provide a validation for the RE method, a value for the “true” r is required. Two approaches are possible, namely modeling of the Cu²⁺ site and nitroxide spin label in the crystal structure of T4L or a direct experimental measurement of the interspin distance using DEER spectroscopy.^8,48−51 The latter approach is preferred and presented first.

The RE provides a distance-weighted average value for r in the general case where a distribution of interspin distances exists. On the other hand, DEER directly provides the distance distribution. Thus, the opportunity exists to determine the Cu²⁺-nitroxide distance distribution from DEER at cryogenic temperatures.⁵¹ From this distance distribution, one can compute the distance-weighted average r value that should correspond to that measured by RE.⁵² The distance-weighted average r value computed from this distribution is referred to as a “DEER-averaged” distance and can be directly compared to the average r found from RE measured at any temperature according to eq 1 or 2.^20,52

To calculate the “DEER-averaged” Cu²⁺-nitroxide distance, a relaxation curve corresponding to each distance of the distribution is constructed by calculating the corresponding T_1s using eq 1 or 2, and all relaxation curves are summed with weighting according to the experimental distance distribution function. A fit to the summed relaxation curve will yield the “averaged” T_1s, which can be used in either eq 1 or 2 to calculate the “DEER-averaged” Cu²⁺-nitroxide distance. This procedure was carried out for the 23L/131R1p mutant in buffer, 30% (w/v) sucrose with a relative viscosity of 3 cP and covalently attached via native lysine residues to CNBr-activated sepharose 4B to modulate τ_C.⁵³

Figure 6 shows a summary of the results; for each case, the DEER distributions are taken to be the same due to the absence of motion at cryogenic temperatures. At 298 K in buffer, analysis of RE data yields 32.0 and 30.9 Å average Cu²⁺-R1p distances using the fast motional and the rigid approximation, respectively. The “DEER-averaged” distances of 32.0 and 31.9 Å are obtained using the fast motional and the rigid approximation, respectively. An excellent agreement between the “DEER-averaged” and RE values for r is achieved when the fast motional approximation was assumed; the “DEER-averaged” distance overestimates the distance using the rigid limit approximation. Thus, for distances ≥30 Å and protein molecules tumbling at ∼6 ns, the fast motional limit is apparently valid within experimental error (see SI). On the other hand, when the mutant was attached to the CNBr-activated solid support, where the protein is known to be essentially immobilized,⁵³ the “DEER-averaged” distances calculated using the rigid limit match well with r from RE (Figure 6 bottom level). Lastly, when T4L is in solution but in the presence of 30% (w/v) sucrose, which results in a correlation time of ∼18 ns, the “DEER-averaged” distance calculated using the rigid approximation again matches well with r from RE. In each case, an average Cu²⁺-R1p distance of 32.0 Å was determined.

Figure 6.

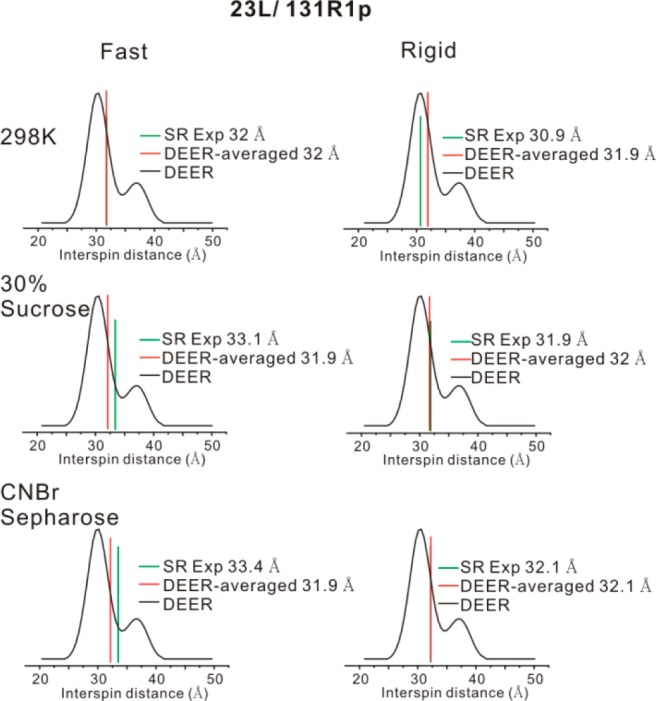
Effects of molecular rotational motion on distance measurements on the 23L/131R1p mutant. Three different conditions were investigated, namely protein in buffer at 298 K, protein in buffer with 30% (w/v) sucrose (298 K), and protein immobilized on the CNBr-sepharose (298 K, see row labels). For each row, two theories, the fast motional approximation (the “Fast” column) and the rigid motional approximation (the “Rigid” column), were used to calculate the average Cu²⁺-R1p distances based on SR data (green bars) and the “DEER-averaged” distance (red bars). Black curves are the Cu²⁺-nitroxide distance distribution measured from DEER on 23L/131R1p with 25% (v/v) glycerol as a cryoprotectant.

Very similar results were obtained for another pair, 37L/76R1p (Figure S3). Collectively, the results suggest that for a protein of smaller size (ca. 18.7 kDa), the fast motional approximation can be used to estimate the average Cu²⁺-R1p distance at ambient temperatures using RE. For larger globular proteins and membrane bound proteins, the rigid motional approximation is appropriate, although it is clear that the differences are relatively small.

To test the generality of the method Cu²⁺-nitroxide distance measurements at 298 K were made on the other Cu²⁺ binding loop inserted mutants, 37L/76R1p and 135L/76R1p. For 37L/76R1p, using the fast motional approximation, RE yields a 28.8 Å distance, close to the 29.2 Å “DEER-averaged” distance (Figure 7A). Similarly, for 135L/76R1p, RE yields a 30.0 Å distance, close to the 29.5 Å “DEER-averaged” distance (Figure 7B). Using R1p as the slowly relaxing spin label and the fast motional approximation, we foresee that distances up to 35 Å can be measured in proteins in liquid solution (Figure 1A).

Figure 7.

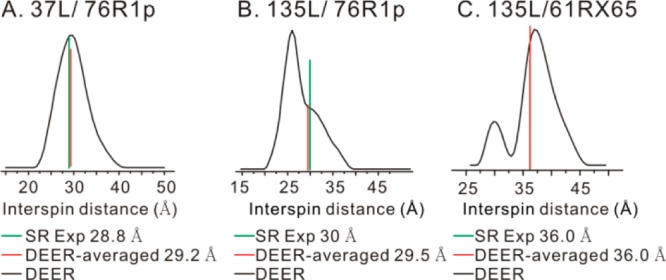
SR-based distance measurements on 37L/76R1p (A), 135L/76R1p (B), and 135L/61RX65 (C) in liquid solution at 298 K. For each sample, the fast motional approximation was used for distance calculations based on SR data (green bars). The “DEER-averaged” distances are indicated by the red bars.

The RX Spin Label Increases the Upper Limit of RE Distance Measurement

The T₁ of the RX spin label in T4L is in the range of 6–10 μs and is predicted to extend the upper limit of distance measurement to ∼40 Å according to Figure 1A. In order to examine this, the mutant 135L/61RX65 was prepared. At 298 K, using the fast motional approximation, an average distance of 36.0 Å was obtained using RE, the same as the “DEER-averaged” distance (Figure 7C).

Freezing Effects on RE Distance Measurement

Potential freezing effects on the protein conformation can be directly evaluated using RE measurements because it can be made at any temperature. To address this issue, low-temperature (LT) SR and room-temperature (RT) SR results were compared for four mutants involving each of the three Cu²⁺ binding loops. LT SR was carried out at 110 K in order to maintain a relatively fast Cu²⁺ relaxation rate⁵² so that the Redfield’s limit, T_2f ≪ T_2s, is applicable and eq 2 can be employed to compute r from RE data.¹⁴ In our case, T_2f and T_2s are ∼250 ns and ∼2 μs, respectively, at 110 K satisfying the condition.⁵² For the 23L/131R1p and the 37L/76R1p variants the average Cu²⁺-R1p distances differed by only 0.7 Å, at the two temperatures, indicating that the freezing effects were minimal. On the other hand, small differences (≈ 2 Å) were seen for the 135L/76R1p and the 135L/61RX65 mutants. Such small difference can be attributed to local structural changes in regions close to the Cu²⁺ binding loop upon freezing the sample, possibly due to the conformational flexibility resulting from perturbation of the structure by the strained loop region (Figure 2). This issue is further discussed below.

Flexibility of the GGGHG Loop

To use the Cu²⁺ binding loop in distance measurements the flexibility (localization) of the Cu²⁺ binding motif requires consideration. This information is directly available in the DEER distance distribution between the Cu²⁺ and the nitroxide. The measured distributions are a convolution of those for the individual spins, but the nitroxides of the R1p³⁷ and RX side chains³⁸ are spatially localized and the overall distributions are expected to reflect to a large extent structural heterogeneity in the engineered loop and/or the protein.

The distributions measured are generally multimodal with a dominant population whose width is in the range of 5–10 Å (Figures 6 and 7), not substantially different than that for internitroxide distances in R1 labeled proteins,^5,54 suggesting a similar degree of localization for the Cu²⁺ loop and making it an equally useful spin label for distance mapping. The origin of the secondary peaks in the distributions is uncertain, but for the interdomain distances measured by 23L/131R1p and 37L/76R1p it may be attributed to the hinge-bending mode in T4L that moves one domain relative to the other.^47,55 Indeed, modeling of R1p and the Cu²⁺ loop in the structure indicates that the two populations resolved in the 23L/131R1p distance distribution (separated by about 7 Å) can be accounted for by the “open” and “closed” forms observed in crystal structures (see Figure S4).⁵⁶ For 37L/76R1p, the interspin distance would only differ by ≈2 Å; the experimental distance distribution is monomodal but relatively broad.

The two intradomain distances in 135L/76R1p and 135L/61RX65 might be expected to be monomodal and relatively narrow because they are within a single domain and not influenced by hinge bending and because the RX side chain is completely rigid. The fact that this is not the case and both pairs involving the 135L are bimodal suggests some disorder in the 135 loop structure due to perturbations incurred by introduction of the GGGHG sequence into a very tight and structured loop; again, this is supported by the helical loss of ≈6% which could be unfolding of proximal segments of helices H and I to accommodate the loop. Thus, it is possible that the two modes in the distributions involving 135L originate in loop flexibility. One of the attractive features of the overall experimental method is that such issues can be directly evaluated in each case by determining the DEER distribution between Cu²⁺ in the loop and a reference nitroxide.

As another approach to evaluating loop flexibility, 100 ns MD simulations in explicit water were carried out for the three loops in T4L. The distance distributions of the Cu²⁺ atoms were determined relative to reference Cα atoms located in the same domain of the protein so as to reflect only motion of the loop; two different references were selected for each loop to examine the anisotropy of the motion in approximately orthogonal directions. The results are shown in Figure 8. The overall widths of the distributions for the apparently isotropic motion of 37L are similar to those observed in DEER distributions for 37L/76R1p; for 23L the motion is anisotropic; and for one direction the width is again on the order of that observed in DEER for 23L/131R1p. Interestingly, the distribution for 135L was mainly monomodal and narrower than that seen in DEER for 135L/76R1p. This is rationalized that in the MD simulations, the helical content of the flanking H and I helices is retained in the 100 ns trajectories.

Figure 8.

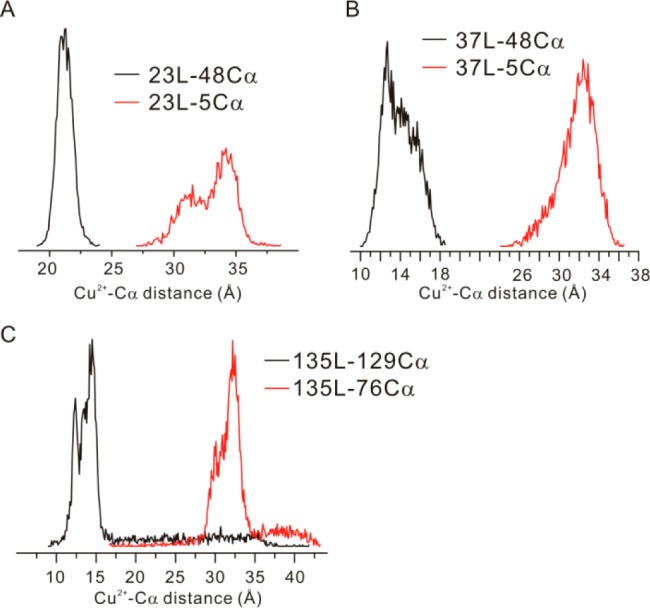
Intrinsic flexibility shown from MD simulations for the three Cu²⁺ binding loops studied in this work. The reference sites (Cα atoms) were selected to be located in the same terminus of T4L on the backbone of the protein.

Discussion

PDS methods are clearly the current “gold standard” for distance mapping on the nm scale, but the requirement for cryogenic temperatures may be problematic in particular cases. The purpose of the present study was to generalize and extend the range of applicability of the RE methods for distance measurement beyond 20 Å in proteins at physiological temperatures. To this end, the enhancement of T₁ relaxation of nitroxides by Cu²⁺ is explored. The key innovations of this paper are the characterization of a high affinity Cu²⁺ binding site for facile introduction into proteins, the use of nitroxide side chains with long T₁ relaxation times to extend the range of distance measurement and the validation of the method using a combination of time-domain EPR, QM calculations, and MD simulations.

For practical application, a general method for introduction of a high affinity and well-localized Cu²⁺ binding site in the protein is required. The use of unnatural amino acids (ie, a bipyridyl derivative)³¹ and histidine pairs¹⁸ as Cu²⁺ ligands has been explored, but the affinities, which lie in the μM range, are too low to effectively compete with nonspecific Cu²⁺ binding as shown here for T4L. On the other hand, the extremely high affinity (K_d < 50 nM) of the GGGHG loop is ideally suited to form stoichiometric complexes without involvement of nonspecific sites (Figure 3). The high Cu²⁺ binding affinity is also confirmed by the fact that only a single exponential function is required to fit SR data for samples in the presence of a 1:1 Cu²⁺-to-protein stoichiometry (Figure S5); unbound protein would have a different T₁₀, and a biexponential function would be required to best describe the data. The peptide can in principle be introduced into any loop connecting regular secondary structural elements, and this was illustrated here by introduction at three different sites in T4L. However, introduction of the peptide into very short and structured loops can result in some degree of destabilization, as found here for the 135L in T4L, and such sites should in general be avoided. On the other hand, a loop with high flexibility should be avoided as the insertion point, since structural information obtained from distance measurements could be obscured by disorder in the Cu²⁺ center.

With a tightly bound Cu²⁺, distance-dependent RE of a nitroxide in the same protein is observed. The calculation of interspin distance from the experimentally measured RE using eq 1 or 2 assumes that the enhancement is due only to fast spin relaxation of the Cu²⁺. However, other mechanisms exist. At room temperature, modulation of the magnetic dipolar interaction by rotational motion of the protein, and hence the interspin vector, can in principle contribute to RE of the nitroxide, i.e.

3

where Δ(1/T_1,rot) is the RE contribution from rotational diffusion and Δ(1/T_1,realx) is that from Cu²⁺ relaxation and given by eq 1 or 2. The RE from protein rotational motion can be described by^20,57

4

where τ_C is the rotational correlation time of the protein molecule, S is the spin quantum number of the slowly relaxing electron spin, and ω is the resonance frequency of the slowly relaxing electron spin. For T4L in water, τ_C ≈ 6 ns⁴⁷ and for interspin distances in the range of 25–40 Å, the RE from rotational motion (eq 4) is more than 2 orders of magnitude smaller than that from Cu²⁺ relaxation. In cases where a slower τ_C is encountered, such as for T4L in 30% sucrose or attached to a solid support (Figure 6), the contribution from rotational motion is even less. Therefore, only the modulation of dipolar interaction due to Cu²⁺ relaxation contributes significantly to the nitroxide RE for the cases considered here; a similar conclusion was reached earlier for Cu²⁺ RE of nitroxides in peptides.²⁰ An additional mechanism for RE exists in liquid solution if the nitroxide and Cu²⁺ sites fluctuate in relative position on the ns time scale, thus modulating the dipolar interaction. However, for motions on this time scale, the R1p and RX nitroxides are well-localized,^37,38 and both DEER data (Figures 6 and 7) and MD simulations (Figure 8) indicated that the Cu²⁺ site is also relatively constrained. Thus, strong modulation of the dipolar interaction on the ns time scale is not expected. If this mechanism were important, the interspin distance calculated from eq 1 or 2 would underestimate the true distance, but the good agreement between interspin distances from RE, modeling, and DEER measurements suggests that contributions from this mechanism are not significant.

The SR data of Figure 5 provide experimental verification that nitroxides of longer T₁₀ can extend the upper limit of distances that can be measured (Figure 3) by RE methods. The results of the present study show that distances of ≈36 Å can be measured with Cu²⁺ enhanced T₁ relaxation of the RX side chain, thus extending the range for measurement by at least 10 Å. Recently, a novel triarylmethyl radical with very long T₁ (≈ 12 μs) was introduced as a spin label for proteins.⁵⁸ With this label, distances up to ≈50 Å can in principle be measured with RE using Cu²⁺ in proteins.

T4L was selected as a model system in part because previous studies have shown the absence of freezing artifacts on the protein conformation.⁵⁹ This being the case, DEER spectroscopy can be used to predict the expected outcome of RE measurements for validation of the method. Distance-weighted averages determined from the DEER distributions are in excellent agreement with the corresponding RE measured values when computed according to the theoretical framework applicable to the rotational correlation time of the protein, thus validating the general RE methodology. A potentially useful aspect of the RE method using Cu²⁺/nitroxide pairs is that average distances can be determined at both physiological temperatures and in frozen solution, thus providing a means of evaluating the effect of freezing on conformation. This is demonstrated for T4L, where no effect of freezing was found, as expected. In other situations, RE can be used to evaluate the effect of freezing on a system prior to determination of distance distributions by DEER analysis.

Despite the advantage of RE for use at physiological temperature, the method has a disadvantage relative to PDS in that only a distance-weighted average is found rather than a full distance distribution. If the distribution is narrow and relatively symmetric, the RE distance is close to the mode of the true distribution. On the other hand, highly asymmetric distributions will give RE distances biased to short distances, but this situation can be readily identified by DEER on the same sample. These effects have been discussed in detail by Sarver et al.⁵²

The uncertainty in SR distance measurements has contributions from random instrumental error, the signal-to-noise ratio (SNR) of the data that determines statistical errors in fitting, and a possible systematic error from the estimated value of the Cu²⁺ relaxation times. To estimate the random instrumental error, each SR experiment was repeated three times. For RT SR, the uncertainty in each T₁ reported is in the range of 50–100 ns, leading to uncertainty in distance of 0.5–1 Å. Because the SR distances calculated using the fast motional limit and the rigid limit differ by over 1 Å (Figures 6 and S3), we attribute these differences to different motional limits, rather than random errors. For LT SR, the uncertainty in each T₁ reported is in the range of 5–10 μs, resulting in uncertainties in distance of 1–2 Å. As shown in Table S2, the difference between RT SR and LT SR is within the uncertainty caused by instrumental error, indicating that consistent results were obtained from RT and LT measurements. SNR is not a significant source of uncertainly in the present experiments, where high concentrations of protein (500 μM) were employed to maximize SNR for the purpose of validating the methodology. For example, fitting error for a typical data set is on the order of 5–15 ns. For general use, such a high protein concentration is not necessary. For example, at 200 μM the increased noise level in SR data yields <50 ns uncertainty in fitting, less than the instrumental error. In addition, time constants from single exponential fitting are not strongly dependent on noise level. Lastly, use of improper Cu²⁺ relaxation times T_1f and T_2f in eqs 1 and 2 will contribute a systematic error to the distance determination. Experimental determination puts these values in the range of 1–5 ns.⁶⁰ The selection of 3 ns for T_1f and T_2f in the present work was based on the room temperature RE study of Jun et al.²⁰ where this value gave good agreement between experimental and modeled distances in two polypeptides.²⁰ Distances calculated between four different pairs using 3 ns in the present experiments are consistent with SR, DEER, and MD results. Collectively, the above results suggest that, at near room temperature, the Cu²⁺ electron spin relaxation time must be fairly close to 3 ns. Variation by ±1 ns yields ∼5% error in distance calculation (∼1–2 Å). Since both eqs 1 and 2 contain T_1f and T_2f, this error does not affect the comparison between different motional conditions (Figures 6 and S3).

The Cu²⁺-nitroxide dipolar interaction provides an opportunity to monitor time-dependent distance changes. The principle is that interspin distance changes modulate the nitroxide T₁ and changes in T₁ can be followed by intensity of the central nitroxide resonance line under saturating microwave power.⁶¹ Alternatively, the intensity of the three quantum multiquantum EPR absorption spectra, which is proportional to T₁,⁶² can be followed in time. Although the time resolution is in principle determined by either the modulation frequency or T₁ itself, signal-to-noise considerations probably limit the time resolution to the ms range. For changes that occur on the second time scale, direct SR detection is possible.

Methods

A summary of methods is given below; additional details are provided in the SI.

T4L Sample Preparation

Protein expression, purification, and spin labeling with R1, R1p, and RX spin probes were performed following reported methodologies.^37,38 The typical sample concentration was 500 μM for RT SR experiments and 200 μM for LT SR and DEER experiments.

Far UV CD Spectroscopy

The CD spectra were recorded at room temperature on a Jasco J-810 spectropolarimeter using a 1 mm quartz cell. Details of sample preparation and data analysis are provided in SI.

Cu²⁺ Titration

The concentration of free Cu²⁺ in solution was determined by titration using Cole-Parmer combination ion-selective electrodes (product no. YO-27504-10). To avoid contamination of the electrode membrane caused by protein, the protein samples (50 μM, 2 mL volume) were maintained in a Millipore centrifugal concentrator. After addition of an aliquot of Cu²⁺ (CuCl₂, Sigma), the protein-Cu²⁺ mixture was incubated at room temperature for at least 10 min, followed by centrifugation for ∼12 min. The concentration of unbound Cu²⁺ was measured in the filtrate solution using the cupric ion electrode. Control experiments showed no Cu²⁺ absorbance by the filter membrane of the Millipore concentrator.

SR EPR Spectroscopy

All SR measurements were performed at X-band. The RT SR experiments were carried out using experimental procedures as described earlier.³⁶ The only exception was the use of a longer saturating pulse (1 μs) in order to increase the sensitivity. The LT SR experiments were carried out using a Bruker MS2 split-ring resonator and a traveling-wave tube signal amplifier.⁶³ The experimental temperature (110 K) was controlled using an Oxford temperature controller and liquid nitrogen or liquid helium. Pulse sequences and all SR data are presented in the SI (Figures S5 and S6). Each SR curve was fitted with a single exponential function; the resultant time constants are provided in Table S3. Details of distance computation are provided in the SI.

DEER EPR Spectroscopy

All DEER experiments were performed using the same instruments as in the LT SR experiments, except the temperature was adjusted to be 20 K. The standard DEER pulse sequence was used, where the π/2 pulse length was adjusted to be 6–8 ns in order to remove the effects of orientational selectivity due to Cu²⁺.^52,64 The stepsize was 16 ns in all DEER measurements with a total of 110 to 150 points. The pump and the observe pulses were applied to the maximum absorbance of the nitroxide and the Cu²⁺ absorbance spectrum, respectively. For some samples, the observe pulses were applied to different positions of the Cu²⁺ absorption spectrum in order to confirm that the orientational effect was removed. The typical signal averaging time was 4–12 h. DEER data were analyzed using LongDistances.⁶⁵

FS-ESE and ESEEM Spectroscopy

The instrument used was the same as in the LT SR experiments. Pulse sequence and data analysis are provided in the SI.

QM Calculations

Full geometry optimizations were carried out with the B3LYP hybrid functional^66,67 and 6-31G(d) basis set using the Gaussian 09 package.⁶⁸ The possibility of different conformations and coordination modes was taken into account for all structures. Frequency analyses were carried out at the same level used in the geometry optimizations, and the nature of the stationary points was determined in each case according to the appropriate number of negative eigenvalues of the Hessian matrix. Scaled frequencies were not considered since significant errors in the calculated thermodynamic properties are not found at this theoretical level.⁶⁹⁻⁷¹ The quasiharmonic approximation reported by Truhlar et al.⁷² was used to replace the harmonic oscillator approximation for the calculation of the vibrational contribution to enthalpy and entropy. Bulk solvent effects were considered implicitly by performing single-point energy calculations at the B3LYP/6-311+G(d,p) level on the gas-phase optimized geometries, through the SMD polarizable continuum model of Cramer and Thruhlar⁷³ as implemented in Gaussian 09. The internally stored parameters for water were used to calculate solvation free energies (ΔG_solv). Free Gibbs energies (ΔG) in solution were used for the discussion on the relative stabilities of the considered structures. Cartesian coordinates, electronic energies, entropies, enthalpies, Gibbs free energies, lowest frequencies of the different conformations of all structures considered are available in the SI.

MD Simulations

Parameters for the Cys-ligated R1p spin label and the unnatural GGH-Cu²⁺ motif in which the two Gly backbone amides are deprotonated were generated with the antechamber module of Amber12⁷⁴ using the general Amber force field, with partial charges set to fit the electrostatic potential generated at HF/6-31G* by restrained electrostatic potential.⁷⁵ The charges are calculated according to the Merz–Singh–Kollman scheme using Gaussian 09.⁶⁸ The G(GGH-Cu²⁺)G loop was inserted one at a time at the desired positions of a mutated bacteriophage T4 lysozyme, together with the spin labels, by homology modeling using a crystallographic structure as the template (PDB code 3LZM).⁴⁰ Each modified protein was immersed in a truncated octahedral box with a 10 Å buffer of TIP3P⁷⁶ water molecules. The systems were neutralized by adding explicit counterions (Na⁺Cl^–). All subsequent simulations were performed using the Stony Brook modification of the Amber 99 force field.⁷⁷ As is well-known, copper and other transition metals are difficult to describe with force fields, due to the importance of quantum effects, particularly charge–dipole interaction.⁷⁸ In our study, the copper cation was modeled by using the parameters recently developed by Merz et al.⁷⁹ and represented by a set of springs which kept the copper geometry close to that optimized by QM calculations. Four springs with constants of 500 kcal/(mol A²) were used to represent copper-ligand bonds. This value reproduced the vibrational amplitudes of the quantum calculations. A two-stage geometry optimization approach was performed. The first stage minimizes only the positions of solvent molecules and ions, and the second stage is an unrestrained minimization of all the atoms in the simulation cell. The systems were then gently heated incrementing the temperature from 0 to 300 K under a constant pressure of 1 atm and periodic-boundary conditions. Harmonic restraints of 30 kcal/mol are applied to the solute, and the Andersen equilibration scheme is used to control and equalize the temperature. The time step was kept at 2 fs during the heating stages, allowing potential inhomogeneities to self-adjust. Each system was then equilibrated for 4 ns with a 2 fs time step at a constant volume. Water molecules are treated with the SHAKE algorithm such that the angle between the hydrogen atoms is kept fixed. Long-range electrostatic effects are modeled using the particle mesh Ewald method.⁸⁰ Production trajectories were then run for additional 100 ns under the same simulation conditions.

Conclusions

In conclusion, we present an experimental approach to measure interspin distances up to 40 Å in proteins at physiological temperatures based on the relaxation enhancement (RE) of spin labels due to a bound paramagnetic metal, Cu²⁺. While the general idea has been employed earlier, two points distinguish this study. First, a short pentapeptide with an extremely high affinity for Cu²⁺ has been found that can be inserted in unstrained loops between secondary structural elements, and the method should be general for introducing a tightly bound Cu²⁺ into a protein. Using EPR and computational methods the introduced Cu²⁺ center was found to be well-localized and suitable as a spin probe for interspin distance measurements using either RE or Cu²⁺-nitroxide DEER. The second distinguishing feature of the work is the use of spin labels with restricted motion and hence long T₁s that extend the range of distance measurement. A combination of time-domain EPR, QM calculations, and MD simulations validates the overall method, which can be applied at both physiological and low temperatures to identify freezing artifacts which could be of concern in DEER measurements done exclusively at cryogenic temperatures. The use of TAM spin labels that have T₁s much longer than nitroxides should greatly extend the distance range measured; this possibility is currently under investigation.

Supporting Information Available

Experimental procedures of EPR experiments, details of QM calculations and MD simulations, all EPR data, additional supporting materials, and complete refs (68 and 74). This material is available free of charge via the Internet at http://pubs.acs.org.

Author Present Address

^§ Department of Chemistry and Biochemistry, California State University, Fullerton, CA 92831.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States