Uncovering pH-Dependent Transient States of Proteins with Buried Ionizable Residues

Abstract

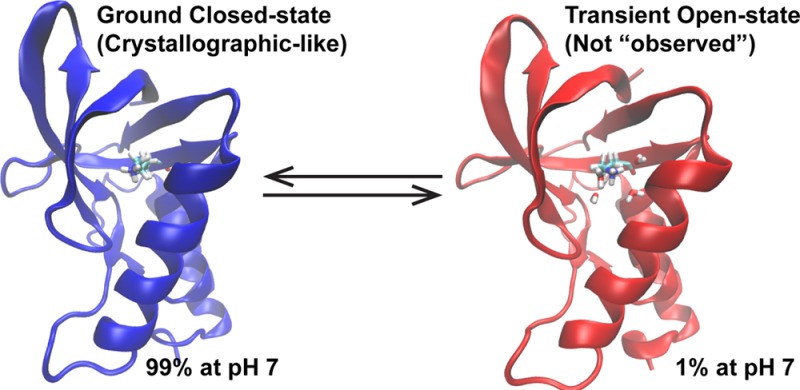
The role of pH in regulating biological activity is ubiquitous, and understanding pH-mediated activity has traditionally relied on analyzing static biomolecular structures of highly populated ground states solved near physiological pH. However, recent advances have shown the increasing importance of transiently populated states, the characterization of which is extremely challenging but made plausible with the development of techniques such as relaxation dispersion NMR spectroscopy. To unlock the pH dependence of these transient states with atomistic-level details, we applied the recently developed explicit solvent constant pH molecular dynamics (CPHMD^MSλD) framework to a series of staphylococcal nuclease (SNase) mutants with buried ionizable residues and probed their dynamics in different pH environments. Among our key findings is the existence of open states in all SNase mutants containing “buried” residues with highly shifted pK_a’s, where local solvation around the protonation site was observed. The calculated pK_a demonstrated good agreement with experimental pK_a’s, with a low average unsigned error of 1.3 pK_a units and correlation coefficient R² = 0.78. Sampling both open and closed states in their respective pH range, where they are expected to be dominant, was necessary to reproduce experimental pK_a’s, and in the most extreme examples of pK_a shifts measured, it can be interpreted that the open-state structures are transient at physiological pH, contributing a small population of 1–2%. This suggests that buried ionizable residues can trigger conformational fluctuations that may be observed as transient-state structures at physiological pH. Furthermore, the coupled relationship of both open and closed states and their role in recapitulating macroscopic experimental observables suggest that structural analysis of buried residues may benefit from looking at structural pairs, as opposed to the conventional approach of looking at a single static ground-state conformation.

One of the critical regulators of biological activity is pH, and misregulated pH is a hallmark of cancer-related physiology.⁵ Ionizable groups that change their protonation states as a function of pH and their local electrostatic environment are often the key residues that govern pH-dependent activity. Due to their charged nature, the majority of them are expressed near the protein surface; however, in some systems, such as membrane proteins, they can be found in more hydrophobic environments. Until recently, the dominant approach to probe the mechanism of such pH-dependent activity has been focused on the analysis of static structures typically solved at physiological pH. However, recent studies have demonstrated the increasingly important role of biomolecular excited-state structures, typically referring to populations that are 0.1% to a few percent of the total population under physiological conditions⁶ (hereon referred to as “transient states” to avoid confusion with electronically excited states), in protein folding⁷ and ligand binding.⁸ While the list of examples of pH-dependent transient states is not that long, there is precedence for their importance, such as in membrane fusion involving the influenza hemagglutinin HA2 subunit.¹⁰

The characterization of transient states is beyond the detection limits of conventional experimental techniques, but recent developments in relaxation dispersion NMR spectroscopy¹¹ and room-temperature X-ray crystallography¹² have made this endeavor feasible. Probing pH-dependent transient states will undoubtedly be similarly challenging. In this context, we report on the application of novel computational techniques to model pH-dependent dynamics of proteins and to probe their transiently populated minor states, which can serve as complementary tools in the field since simulations are not subject to the same detection limits as experiments. One major approach to model accurate pH-dependent dynamics is the constant-pH molecular dynamics (CPHMD) framework, where MD simulation is coupled to the protonation state of the titrating residue.¹³ In the continuous variant of CPHMD used in this study, the titration coordinate represents an instantaneous microstate, and it is propagated continuously between the protonated and unprotonated states using the λ dynamics approach.¹⁶ We focus our investigation on modeling the pH-dependent dynamics of a series of engineered mutants of staphylococcal nuclease (SNase) with Lys residues buried in the hydrophobic core¹⁸ using the recently developed explicit solvent CPHMD^MSλD framework for proteins.¹⁷ While the effectiveness of CPHMD has been demonstrated on numerous systems,¹⁹ almost all work reported to date was based on an implicit solvent model.¹³ Applications of explicit solvent CPHMD on biomolecules thus far have only a few reported successes.^17,24 More importantly, none of the existing works have attempted a comprehensive investigation of buried ionizable residues, where, we hypothesize, the contrast in electrostatic environment between a hydrophobic pocket and a solvent-exposed environment will provide a key driving force for pH-mediated conformational fluctuations and, possibly, transient states formation.

As shown in Figure 1a, the mutants for this study comprise a set of diverse mutation sites, with residues varying in the magnitudes of pK_a shifts. In addition, experiments have demonstrated that, for the mutants that we selected, the titration of the internal Lys is decoupled from the ionization of Asp and Glu residues.¹⁸ Thus, to facilitate convergence within a reasonable time, we titrated only the buried Lys and performed an initial check of the accuracy of our simulations by calculating its pK_a value, using the crystallographic structures as the starting models (see Supporting Information (SI) for details). As summarized in Figure 1b and Table S1, most of the buried residues have a predicted pK_a < 1, which is shifted by nearly 10 pK_a units from the reference value of 10.4. pK_a calculations on the V66D and V66E mutants produced a predicted pK_a > 14, which is dramatically shifted from their reference values of 4.0 and 4.4, respectively. In both cases, the pK_a shifted toward the direction stabilizing the neutral state of each titrating species (upward for Asp/Glu; downward for Lys). The dramatic pK_a shifts observed in our simulations mirror the experimental spectrophotometric measurements of Brønsted acids and bases, where a similar pK_a shift of 10–20 units was recorded when moving from an aqueous to an organic environment.²⁸ For example, acetic acid, which has the same functional group as Asp and Glu, has its pK_a value shifted from 4.8 to ∼23 in water (ε = 80) vs acetonitrile (ε = 37).²⁹ Even though the dielectric constant of a typical hydrophobic pocket in SNase, which ranges from 4 to 20,³⁰ is lower than that of acetonitrile, such dramatic pK_a shifts of more than 10 units have never been observed in the protein. In fact, some of the largest pK_a shifts for Asp, Glu, and Lys reported in the literature are perturbed by a mere 5 units from their reference values.^18,33 Thus, there is an inconsistency in the magnitude of experimental pK_a shifts observed in SNase compared to historical experimental pK_a shifts observed in organic solvents, even though both environments have similarly low dielectric values, which indicates that additional factors have to account for the apparent inconsistency.

Figure 1.

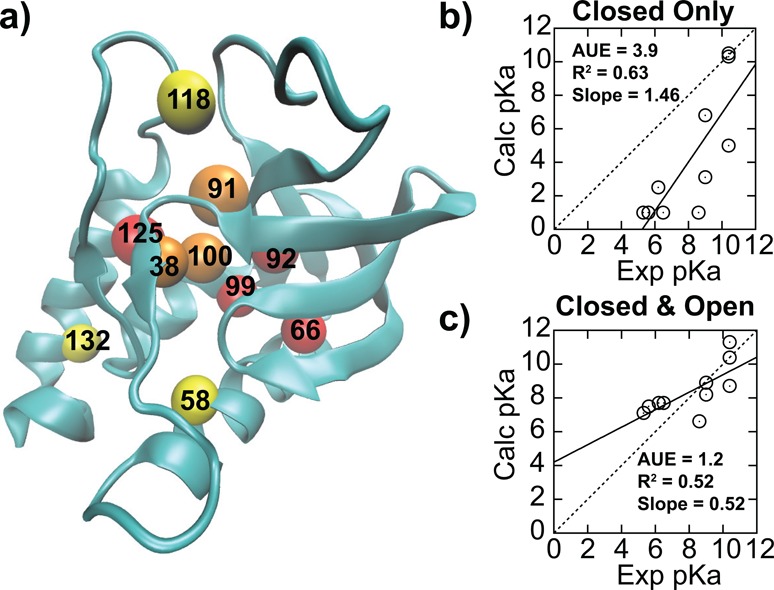
(a) Distribution of internal Lys residues of SNase mutants, color-coded depending on the pK_a shift: yellow, not shifted; orange, shifted by 1–2 units; red, shifted by >2 units. Comparison between experimental and calculated pK_a’s from explicit solvent pH-REX CPHMD^MSλD simulations using (b) only closed crystallographic like structures and (c) both open and closed states.

Strong coupling between pK_a and conformational sampling has been previously reported,³⁴ and, while the importance of conformational sampling has been observed in some SNase mutants, no connection to experimental pK_a values has been reported.³⁸ Based on these observations, we performed an additional series of extended-run explicit solvent pH-REX CPHMD^MSλD simulations on the structures that were pre-equilibrated for 50 ns at high and low pH (see SI for details). The findings, summarized in Figure 1c and Table S1, demonstrate significantly improved results, with the averaged unsigned error (AUE) reduced from 3.9 to 1.2 pK_a units. We observed that the longer equilibration allowed the sampling of “open” solvated structures that were critical for reproducing the experimental pK_a values reported for all Lys mutants with highly shifted pK_a values. This is in contrast to the “closed” crystallographic-like structure where there is little to no water present within 3 Å of the protonation site (Figure 2a). Using the V66K mutant as an example, we demonstrate that SNase conformations sampled in our simulations interconvert between closed and open states (Figure 2b,c) when the external pH is close to the calculated pK_a value. While the coupling between pK_a and conformational sampling has been reported for a few isolated examples,^36,37 and the importance of sampling such alternative conformational states has been previously postulated by experiments,³⁹ there has been no comprehensive proof for their role. Our work presents the first interpretation that pH-dependent transient states exist and may be of general importance for proteins with buried ionizable groups. For all mutants with highly shifted pK_a values, we observed that protonation of the internal Lys was concomitant with an increase in local solvation around the protonation site, as illustrated in Figure 2a. The backbone RMSD of the entire structure between both closed and open states in these mutants is small, ranging from 1.2 to 1.9 Å (also see Figure S1), which suggests that the conformational relaxation to accommodate a buried charged residue does not require significant structural rearrangement. Our observations are consistent with experimental measurements indicating that buried ionizable residues in SNase are readily accommodated without any special structural adaptation or distortion to the overall protein conformation.^18,33

Figure 2.

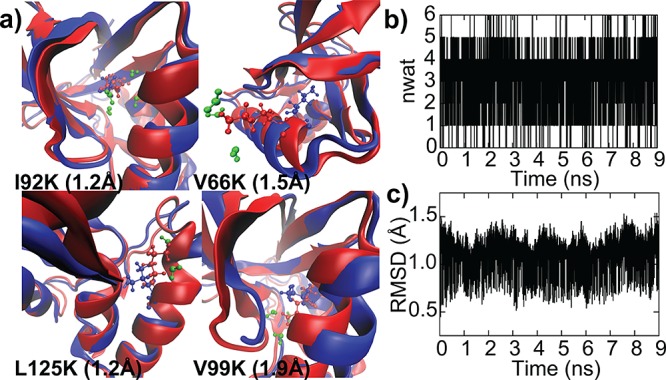
(a) Structures of the four most highly shifted Lys mutants at high-pH “closed” conformation (blue) and low-pH “open” conformation (red), with the backbone RMSD between the two structures in parentheses. Water molecules within 3 Å of the protonation site at low pH (green) are included; no water molecules were observed at high pH. Using V66K, we show the conversion between the two states at external pH close to the calculated pK_a in the time evolution of (b) number of waters within 3 Å of the protonating site and (c) backbone RSMD relative to the crystallographic structure.

Having established that buried ionizable residues can trigger pH-dependent structural fluctuations, we extend our analysis to determine the relevance of these alternative states at pH 7. Using a two-state model that assumes a conversion between one dominant open state and one dominant closed state, we derive an equation (see SI for derivation) describing the ratio of open to closed states, R_OC:

This function can be decomposed into pH-dependent (K_pH) and pH-independent (K⁰) terms. The K_pH term depends on the microscopic pK_a of each state (pK_closed, pK_open) and external pH. The K⁰ term can be physically related to the free energy difference of the open and closed states in their protonated form (SI). However, as each form favors opposing protonation states, this free energy is usually not measured by experiments. Thus, it may be advantageous to express K⁰ as a function of the system’s readily measured macroscopic or apparent pK_a (pK_app) and the microscopic pK_a of each state (pK_closed, pK_open). Based on the R_OC equation, one may also derive the fraction of the open state (F_open), a more intuitive metric for open states at a specific pH:

Due to the rapid dynamics and/or low population of the minor state, it is often beyond the detection limits of experiments to establish the pK_a values of each microscopic state.³⁹ However, because the open state is solvent-exposed, pK_open may be approximated as the reference pK_a of the free amino acid. Using the range of pK_a shifts of 10–20 units recorded from spectrophotometric measurements of organic acids and bases in a low dielectric solvent,²⁸ we have conservatively assigned pK_closed to be shifted by 10. As shown in Figure 3, one can use the R_OC equation to derive the pH-dependent fraction of the open state for a series of hypothetical pK_app for buried Lys or Glu.

Figure 3.

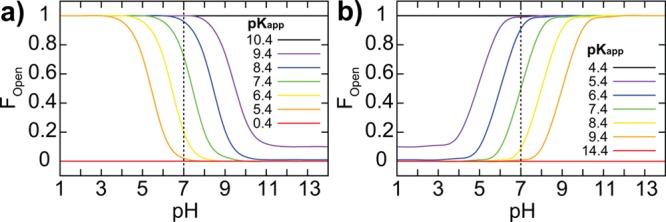
pH-dependent distribution of the fraction of open states (F_open) for buried (a) Lys and (b) Glu residues. Several color-coded hypothetical apparent pK_a (pK_app) values are illustrated, shifted by 1−5 pK_a units. In the limits of extreme (i.e., 10) or null pK_a shift, the expected population of 100% closed or open states is recovered. For this plot, pK_open = 10.4 and 4.4, and pK_closed = 0.4 and 14.4, for Lys and Glu, respectively.

Our analysis indicates that pH-dependent transient open states may contribute as much as 2% of the total population at pH 7 when the apparent pK_a of Lys is shifted by as much as 5 units, which appears to be the upper limit of pK_a shift as recorded in current literature.^18,33 For Asp and Glu, a pK_app shifted by 5 pK_a units represents a 1% contribution of the transient state at pH 7. Thus, for the residues with highly shifted pK_a values, the low-population transient states are likely to contribute significantly to the apparent pK_a and, thus, need to be elucidated to correctly compute the apparent pK_a. Although the existence of transient states involving buried ionizable groups does not necessarily imply a functional relevance, there is increasing precedence that the inclusion of transient states is needed to fully account for biological properties.⁶⁻⁸ In the context of our work, we suggest that the effect of such pH-dependent transient states will be pronounced when an ionizable group transitions between hydrophilic and hydrophobic environments, such as in membrane fusion processes, where activated/transient states have been postulated to play a crucial role.¹⁰ In addition, traditional studies of catalytic mechanisms have always assumed that crystallographic structures correlate to measured pK_a, but, as we have shown, that may not be true for buried residues with highly shifted pK_a values. Moreover, the coupled relationship between open and closed states and their role in recapitulating macroscopic experimental observables suggests that structural analysis of buried residues should be performed from the perspective of looking at structural pairs, as opposed to the conventional approach of looking at a single static ground-state conformation. For such analyses, the equations we have provided will prove useful for a quick, “back of the envelope” estimation of the population of proposed transient states. For example, one could use the experimentally measured pK_app to select the appropriate curve in Figure 3, and use it to estimate the fraction of the open state at a given pH, as a means to evaluate the plausibility of experimental characterization within the detection limits of the methods employed. Alternatively, it could also be used to estimate the pH range where the population of proposed transient states will enter the detection range of experiments.

Lastly, we investigate the various computational models, specifically previous CPHMD implementations, to ascertain the robustness of predictions obtained from simulations. One insightful observation is that our calculated pK_a for the N100K mutant of SNase is 6.6, which is close to the calculated pK_a of 7.0 reported by Shen and co-workers,³⁷ despite the differences in the solvation model and cutoff schemes utilized. This suggests that the CPHMD framework is not overly sensitive to specifics of the simulation setup. This is because CPHMD calculates the free energy of protonation relative to a reference compound, and, as long as the simulations of the protein and the reference are performed under identical conditions, the differences originating from the simulation setup approximately cancel out. To test this hypothesis, we compare our pK_a predictions from explicit solvent pH-REX CPHMD^MSλD simulations with those obtained from the GBSW¹⁴ implicit solvent pH-REX CPHMD framework, using the refined protocol presented in this paper. Our results (Figure 4a,b and Table S2) show excellent correlation of R² = 0.89 between the pK_a’s predicted from both explicit and implicit models. However, unlike the explicit solvent CPHMD^MSλD simulations, which resulted in a pK_a shift of more than 10 units when only the closed state was used, the implicit solvent CPHMD simulations produced pK_a shifts that were smaller in magnitude. The van der Waals surface representation used to define the solute–solvent dielectric boundary in GBSW is known to form small crevices of high dielectric region between atoms, which results in the underestimation of the Born radii and overestimation of the solvation free energy.⁴⁰ Therefore, despite the actual hydrophobicity of the environment near the protonating site, the GBSW model may be too “wet”, causing a smaller pK_a shift. Alternatively, the same effect can be achieved as a result of the faster conformational dynamics in the GBSW model, which may sample both open and closed states more frequently.

Figure 4.

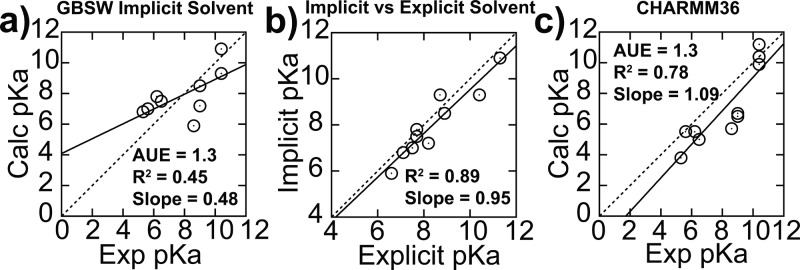
(a) Accuracy of calculated pK_a from implicit solvent pH-REX CPHMD simulations is similar to that of explicit solvent results, and (b) both sets of calculated pK_a values are highly correlated with each other. (c) Calculated pK_a values from explicit solvent pH-REX CPHMD^MSλD simulations using the CHARMM36 force field result in improved correlation with experimental pK_a values. All simulations were initiated using both closed and open structures.

To distinguish between these two possibilities, additional simulations, with the structures of the V66K, V99K, L125K, and I92K mutants rigidified by applying harmonic restraints to all heavy atoms, were performed, and the resulting pK_a values were similar to those calculated without restraints (Table S2). These results suggest that smaller pK_a shift in the implicit solvent primarily stems from the “wetness” of the GBSW model, rather than its faster conformational dynamics. Finally, we investigated the effect of using the recently released CHARMM36 all-atom force field for proteins on our predictions, as it has been previously shown to yield superior reproduction of experimental dynamic data.⁴¹ We recalculated the biasing potentials for the common titrating residues of proteins using the CHARMM36 force field (Table S4), and revised pK_a values, as shown Figure 4c, indicate an improvement in the predictive performance over the older CHARMM22/CMAP force field, with R² increasing from 0.52 to 0.78, and the slope of the regression moving from 0.52 to 1.09, while maintaining the same level of accuracy with an average unsigned error of 1.3 pK_a units.

In conclusion, we have applied the recently developed explicit solvent constant pH molecular dynamics framework to simulate the pH-dependent dynamics of a comprehensive set of SNase mutants with buried ionizable residues that have varying degrees of pK_a shifts. Among our key findings are that a buried charged residue cannot be accommodated inside a purely hydrophobic pocket, and that an open-state structure for these “buried” residues, characterized by local solvation around the protonating site, was observed in all SNase mutants with highly shifted pK_a’s. At physiological pH, buried ionizable groups with large pK_a shifts have transiently populated open states, where they contribute a small but non-zero population of 1–2%. Nevertheless, sampling these open states is a necessary condition for accurately reproducing experimental pK_a measurements, with which calculated pK_a from our explicit solvent CPHMD^MSλD simulations demonstrated good agreement, with a low average unsigned error of 1.3 pK_a units and correlation coefficient R² = 0.78. This work provides the first validation that buried ionizable residues can readily trigger pH-mediated conformational fluctuations that may be observed as transient-state structures at physiological pH. Lastly, the discovery of a coupled relationship of both open and closed states and their role in recapitulating macroscopic experimental observables suggests that structural analysis of buried residues may benefit from looking at structural pairs, as opposed to the conventional approach of looking at a single static ground-state conformation.

Supporting Information Available

Details of computational protocol, derivation of R_OC equation, and additional pK_a calculations. This material is available free of charge via the Internet at http://pubs.acs.org.

The authors declare no competing financial interest.

Funding Statement

National Institutes of Health, United States